RAP: Accurate and Fast Motif Finding Based on Protein-Binding Microarray Data

Abstract

The novel high-throughput technology of protein-binding microarrays (PBMs) measures binding intensity of a transcription factor to thousands of DNA probe sequences. Several algorithms have been developed to extract binding-site motifs from these data. Such motifs are commonly represented by positional weight matrices. Previous studies have shown that the motifs produced by these algorithms are either accurate in predicting in vitro binding or similar to previously published motifs, but not both. In this work, we present a new simple algorithm to infer binding-site motifs from PBM data. It outperforms prior art both in predicting in vitro binding and in producing motifs similar to literature motifs. Our results challenge previous claims that motifs with lower information content are better models for transcription-factor binding specificity. Moreover, we tested the effect of motif length and side positions flanking the “core” motif in the binding site. We show that side positions have a significant effect and should not be removed, as commonly done. A large drop in the results quality of all methods is observed between in vitro and in vivo binding prediction. The software is available on acgt.cs.tau.ac.il/rap.

1. Introduction

Gene expression is regulated mainly by proteins that bind to short DNA segments. These proteins, termed transcription factors (TFs), bind to short DNA sequences with variable affinity. These sequences, called binding sites (BSs), are usually found upstream to the gene transcription start site. This TF-BS binding regulates gene expression, either by encouraging or impeding gene transcription.

Many technologies have been developed to measure the binding of TFs to DNA sequences. Chromatin immunoprecipitation (ChIP) extracts bound DNA segments, which are then either hybridized to a predesigned DNA microarray (Aparicio et al., 2004) or directly sequenced (Johnson et al., 2007; Rhee and Pugh, 2011). These technologies can produce reasonably accurate in vivo binding profiles. However, they present some difficulties. The binding is tested against genomic sequences only, which have sequence biases (e.g., they do not cover all k-mers uniformly and thus can affect constructed models). In addition, many binding events are due to cooperative binding by more than one TF. Moreover, accurate modeling of these binding events must account for other significant factors that affect binding, such as nucleosome occupancy and chromatin state.

In vitro technologies, such as protein-binding microarray (PBM) (Berger et al., 2006) and MITOMI (Fordyce et al., 2010), measure binding of a TF to thousands of synthesized probe sequences. The sequences are designed to cover all DNA k-mers and so give an unbiased measurement of TF binding to a wide spectrum of sequences. The binding is due to TF affinity without additional binding effects found in vivo (albeit, with some technological biases). Current implementations of PBMs cover all DNA 10-mers and are available in two different array designs. Another technology, based on high-throughput sequencing, measures binding to random k-mers, with complete coverage of all 12-mers (Nutiu et al., 2011). The latter study showed that some TFs bind to motifs of length greater than 10 and emphasized the importance of greater k-mer coverage.

Several algorithms were developed for the specific task of learning binding-site motifs from protein-binding microarray data. These include Seed-and-Wobble (SW) (Berger et al., 2006), RankMotif++ (RM) (Chen et al., 2007), and BEEML-PBM (BE) (Zhao and Stormo, 2011). All produce the binding-site motif as a position weight matrix (PWM). For each position, the binding preference is given by a probability distribution over four nucleotides. Agius et al. (2010) developed a much more complex model based on a collection of 13-mers, but we will focus here on the PWM model, which is far more common and transparent. A previous study by our group compared these different methods using several evaluation criteria (Orenstein et al., 2012). Weirauch et al. (2012) compared methods for TF-binding prediction using PBMs. A key observation that emerged from both studies is a dichotomy of current motif construction methods: Some produce motifs that accurately predict in vitro binding; other methods produce motifs with higher information content that are more similar to literature motifs. No method performed well in both tasks.

The current state of affairs of PBM-based motif prediction raises several questions: Can one develop a method that produces motifs that are both similar to literature motifs and accurately predict in vitro binding? What is the best model for TF-binding preference? Is it a PWM with low or high information content motifs? What is the best length of the binding site that can be learned from PBM data?

In this study, we address all these questions. We developed a new simple method to extract binding-site motifs, represented in PWM format, from PBM data. In spite of its simplicity, the method produces motifs that achieve top performance both in predicting in vitro binding and in similarity to known motifs. By comparing the performance of motifs of different lengths we conclude that longer motifs are better and that inclusion of flanking positions—even with relatively low information—has a positive effect on predicting binding affinity. We also give evidence to a large gap between the quality of in vitro and in vivo binding prediction.

2. Results

2.1. The RAP algorithm

We developed a new method for finding binding-site motifs using PBM data. The method works in four phases. (1) Ranking phase: rank all 8-mers by the average binding intensity of the probes in which they appear. (2) Alignment phase: align the top 500 8-mers to the top-scoring 8-mer using star alignment (Altschul and Lipman, 1989). 8-mers must align with an overlap of at least five positions, at least four matches, and at least three consecutive matches, otherwise, they are discarded. (3) PWM phase: use the aligned 8-mers to build a PWM. The core matrix is of length 8. In each column of the PWM, the nucleotide probabilities are calculated according to a weighted count in the corresponding column of the alignment. (4) Extension phase: the matrix is extended to both sides according to the original probes that contain each of the aligned 8-mers. In each peripheral position, the probe sequences and their scores are used to calculate nucleotide probabilities in a similar fashion as for the core positions. The method is called RAP (for rank, align, PWM). Its running time is less than 2 seconds for one PBM data file, where most of the time is needed to read the file.

2.2. Performance comparison: predicting in vitro binding

We tested RAP, SW (Berger et al., 2006), RM (Chen et al., 2007), and BE (Zhao and Stormo, 2011) in predicting high-affinity binding. Most TFs studied by PBMs to date were measured in a pair of experiments using two different array designs. This allows an elegant way to test performance, as suggested in Chen et al. (2007): The binding site is learned according to one array and tested on the other. For this test, we used all TFs in the UniPROBE database that had such paired experiments. PBM experiments that had a positive set of less than 20 probes (see Methods) were excluded from the testing results. In total, the results reported below cover 316 PBM experiments.

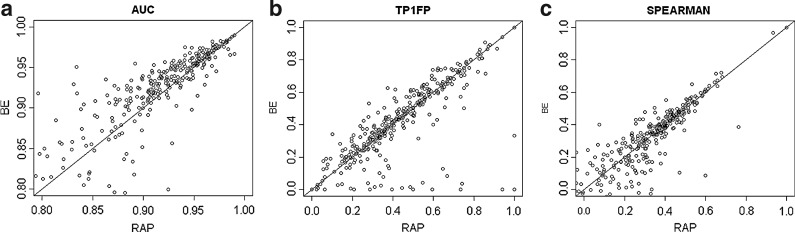
A PWM learned using one array was used to rank the probes of its paired array. This ranking was compared to the ranking according to true binding intensity using three criteria: area under the ROC curve (AUC), sensitivity at 1% false positive (TP1FP), and Spearman rank coefficient (see Methods). RAP achieves best average performance in all criteria, followed by BE, RM, and SW in this order (Table 1). The advantage of RAP over BE is not significant in all criteria, while the advantage of both RAP and BE over RM and SW is significant (p < 0.05, Wilcoxon rank-sum test). In terms of median performance, BE is slightly better than RAP. Figure 1 shows a dot plot comparison of RAP and BE.

Table 1.

Predicting In Vitro Binding

Method/criterion	AUC	TP1FP	Spearman
RAP	0.880	0.435	0.293
BEEML-PBM	0.873	0.418	0.283
Seed-and-Wobble	0.858	0.332	0.239
RankMotif++	0.869	0.292	0.245

The table shows average results in three different criteria for each method over 316 PBM pairs. In each experiment, a PWM was learned using one array and then used to rank probes of its paired array. This ranking was compared to the original probe ranking using AUC, sensitivity at 1% false positive (TP1FP), and Spearman rank coefficient. AUC, area under the curve; PWM, position weight matrix; RAP, rank, align, PWM; PBM, protein-binding microarray.

FIG. 1.

Comparison of RAP and BEEML-PBM (BE) in predicting in vitro binding. Data and performance criteria are as in Table 1. Each dot corresponds to a PBM experiment, and the x- and y-axis are RAP and BE performance results for that experiment, respectively. Note that in the AUC plot experiments with low score are not shown. RAP, rank, align, PWM; PBM, protein-binding microarrays.

2.3. Performance comparison: similarity to literature motifs

We compared motifs learned by the different methods to motifs learned from non-PBM technologies. We used 58 mouse and 51 yeast PWMs taken from the JASPAR (Bryne et al., 2008) and ScerTF (Spivak and Stormo, 2012) databases, respectively, and calculated the similarity to PWMs learned by the different methods (on two paired PBM profiles together, when available). We measured dissimilarity using Euclidean distance. In addition, we calculated the average information content (IC) of the PWMs of each method (see Methods). The results are summarized in Table 2.

Table 2.

Dissimilarity to Literature Motifs and Information Content

Method/criterion	Dissimilarity	Information content
RAP	0.197	0.992
Seed-and-Wobble	0.201	1.330
RankMotif++	0.222	0.884
BEEML-PBM	0.232	0.689

We calculated Euclidean distances between PWMs learned by each method and the corresponding matrices in JASPAR and ScerTF (51 mouse and 58 yeast PWMs, respectively). The table shows average distance for each method. Information content averages are calculated for the PWMs learned by each method.

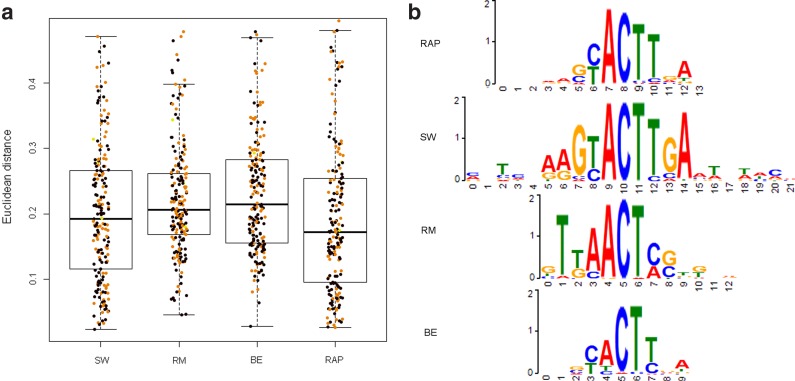
RAP achieves best similarity, followed closely by SW (p-value = 0.14, Wilcoxon rank-sum test), while RM and BE are far less similar to literature motifs (p-value < 0.0003). SW had the highest average IC (1.33), significantly higher than RAP, RM, and BE in that order. Figure 2a shows a boxplot of similarity to known motifs, with colors depicting the IC of each PWM. On average higher IC correlates with lower Euclidean distance, e.g., about −0.4 correlation for BE and RM. Figure 2b shows examples of PWMs in logo format.

FIG. 2.

Dissimilarity to literature motifs and logo comparison. (a) Dissimilarity values boxplots. Binding sites were learned by each method, and the Euclidean distance was measured against 109 PWMs from JASPAR and ScerTF. Dots correspond to transcription factors (TFs) where height is the distance and color reflects the information content (IC) of the PWM. Black: IC > 1.3; orange: 1.3 ≥ IC > 0.9; yellow: IC ≤ 0.9. (b) PWM logos for Ceh-22 protein.

2.4. The effect of motif length and flanking sequences

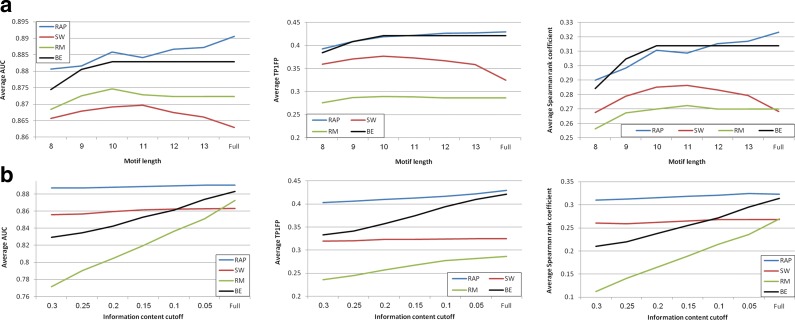
We tested the effect of motif length and flanking sequences on the ability to predict in vitro binding. We took the PWMs produced by the different methods, and for different values of k, we kept the k contiguous positions with the highest IC. In another test, since different TFs may have different lengths, we also trimmed side positions by using an IC threshold. Figure 3 summarizes the results of both tests.

FIG. 3.

Effect of motif length and information content on predicting in vitro binding. (a) Performance as a function of motif length. For each PWM, we kept the k most informative contiguous positions and tested the ability of the resulting motif to predict in vitro binding. When the motif length was smaller than k, we used all positions. Average results of three criteria are shown in the graphs. (b) Performance as a function of IC cutoff. For each PWM, we removed all contiguous side positions with IC below the cutoff until reaching the first position with higher IC. The graphs show average results using the same three criteria.

For most methods, longer motifs are better. The performance of RAP, BE, and RM declined as motif length decreased. On the other hand, SW's performance peaked at length 11 and decreased for longer motifs (Fig. 3a). All four methods did not benefit from trimming flanking positions with low IC (Fig. 3b). Both BE and RM deteriorated sharply as the cutoff increased, since they produce PWMs with low IC (compare Table 2). RAP and SW were barely affected.

2.5. Predicting in vivo binding

We also tested the performance of the methods in predicting in vivo binding. We used the Harbison et al. (2004) data set and its definition of a positive promoter set, focusing on 69 yeast ChIP-chip experiments with corresponding TFs in the UniPROBE database. We used the PWM learned using PBM data to predict ranking of yeast promoter sequences and compared it to the true ranking reported by Harbison et al., using the same three criteria. The results are summarized in Table 3.

Table 3.

Predicting In vivo Binding

Method/criterion	AUC	TP1FP	Spearman
RAP	0.662	0.108	0.149
Seed-and-Wobble	0.659	0.118	0.145
RankMotif++	0.655	0.092	0.158
BEEML-PBM	0.665	0.084	0.146

The table shows average results for each method over 69 ChIP-chip experiments. In each experiment, a PWM learned using PBM data was used to rank yeast promoter sequences. This ranking was compared to the original promoter ranking using AUC, sensitivity at 1% false positive (TP1FP), and Spearman rank coefficient.

In terms of AUC and Spearman score, all methods performed roughly equally. SW and RM performed slightly (but not significantly) better in the sensitivity and Spearman criterion, respectively. Notably, all methods performed much worse in predicting in vivo binding than in predicting in vitro binding (compare Table 1).

3. Discussion

We have developed RAP, a new algorithm to extract binding-site motifs in PWM format from protein-binding microarray data. Previous studies observed that algorithms for this task fall into two categories (Orenstein et al., 2012; Weirauch et al., 2012). Some algorithms predict in vitro binding well but produce motifs that show low resemblance to motifs reported in the literature. Others match literature motifs (extracted using other technologies) well, but are less successful in in vitro binding prediction. This raised the question whether the dichotomy is inevitable. Here we show this is not the case. The RAP algorithm achieved top performance in both criteria. In terms of in vitro binding, it is on a par with BE; its motifs are as similar to literature motifs as those of SW. Notably, its running time is a couple of seconds, 2–3 orders of magnitude faster than the other algorithms.

We note that while RAP is slightly better on average than BE, the latter was slightly better in median. For more TFs, BE results are better than RAP's (Fig. 1). But for some, it fails to capture the binding preference correctly. For example, BE achieves AUC < 0.5 for 10 TFs, while only one such case exists for RAP. Hence, BE performs slightly better in more samples, but has a few failures, whereas RAP is robust and produces accurate motifs in almost all cases.

In spite of its very simple algorithm, RAP was shown to be powerful and quite accurate. What explains RAP's performance? Like other methods, it combines information about binding intensities of 8-mers using their occurrences in multiple probes in order to evaluate robustly the 8-mers binding intensity. Unlike other methods, it then focuses solely on the top-binding 8-mers. Star alignment of the top 500 8-mers to the top-ranked one is a simple yet effective way to extract an initial core motif, which is then extended using the original probes. Our tests showed that the use of 500 top 8-mers is optimal, with performance dropping when more k-mers are used. It is possible that a part of the advantage of RAP is gained by focusing on the top 8-mers: They are informative enough to reveal a PWM with good binding-prediction quality, and this approach avoids noise and reduced IC that would be caused by incorporating information from lower intensity probes.

Previous studies suggested that TF-binding preference is best modeled by low IC motifs (cf. Weirauch et al., 2012). This is a natural conjecture derived from the dichotomy of previous methods, since literature motifs tend to have high IC. The RAP algorithm goes against this suggestion: It produces motifs with relatively high IC, which are on par with the best in predicting in vitro binding. (SW motifs have substantially higher IC, but they do not perform highly in both criteria).

Our tests of the effect of motif length on performance showed that peripheral positions do affect TF binding. For RM, BE, and RAP, the performance deteriorated as the motif was shortened. Only SW (whose performance was generally lower) did worse for motifs of length ≥11. Hence, while the core motifs are easier to comprehend, keeping flanking positions in the model is beneficial. As current PBM techniques are limited to covering all 10-mers (or 12-mers) (Nutiu et al., 2011), producing larger arrays would allow more accurate inference of longer motifs. Our analysis also shows that using IC cutoffs to remove flanking positions is too crude and is particularly damaging to low IC motifs. Hence, both tests suggest that side positions should be kept in the model, in agreement with conclusions reported in Nutiu et al. (2011). To our knowledge, this is the largest-scale rigorous test of the effect of motif length.

Our results show that all algorithms give much poorer prediction on in vivo compared to in vitro data (Table 3): AUC drops from 0.88 to 0.665, and sensitivity deteriorates from 0.435 to 0.118. While the complexity of the in vivo environment may explain this in part, the severity of the gap in the quality of the results questions our ability to carry over the powerful results achievable using PBMs to the natural environment. More complex in vivo models that could combine “naked” in vitro motifs with epigenetic marks and other parameters may help to narrow this gap.

In summary, we developed a new algorithm and showed that it is highly accurate in both predicting in vitro binding and producing interpretable motifs. Our results question the claim that TF binding preference is best modeled with low IC motifs and highlight the importance of using long motif models and of learning peripheral positions correctly. Carrying these results over to in vivo predictions remains an important challenge.

4. Methods

4.1. Data

We downloaded all paired PBM profiles from the UniPROBE database (Robasky and Bulyk, 2011), obtaining 364 PBM profiles (182 pairs). From these we removed all PBM profiles, where the size of the positive set (see definition below) on the test array was smaller than 20. This resulted in 316 PBM profiles to test the methods performance.

We compared similarity between motifs learned from PBM data and motifs learned by independent technologies. For this aim, we used 58 mouse TFs that had a PBM profile in the SCI09 study (Badis et al., 2009) and had a model not based on PBM in the JASPAR database (Bryne et al., 2008). Similarly, we collected 51 yeast TFs that had a PBM profile in the GR09 study (Zhu et al., 2009) and were present in ScerTF database (Spivak and Stormo, 2012). The motif was learned using the PBM profile or two paired profiles, when available, and compared against the PWM from the database.

For the in vivo binding prediction we used Harbison et al. ChIP-chip dataset (Harbison et al., 2004). The positive promoter set included all promoters with p-value < 0.001 according to Harbison et al. (2004). We used all experiments with a TF in the GR09 dataset (Zhu et al., 2009). This resulted in 69 different experiments.

4.2. Comparison criteria

We tested the ability of each method to predict in vitro binding of another PBM array. A binding site in PWM format was learned using one PBM profile. The PWM was used to rank all probe sequences of the paired array. For each probe an occupancy score was calculated, which is the sum of the probability of the TF to bind over all positions (Tanay, 2006). This score is used to rank all probes. For probe sequence s and PWM Θ of length k, the sum occupancy score is

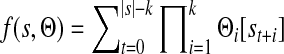where Θ_i(x) is the probability of base x in position i of the PWM. The ranking due to the occupancy score is compared to the original probe ranking according to the binding intensity. A positive set of probes is defined as the probes with binding intensity greater than the median by at least 4 * (MAD/0.6745), where MAD is the median absolute deviation (MAD = 0.6745 for the normal distribution N(0,1)) (Chen et al., 2007). Three criteria are used to gauge the ranking: AUC of ROC curve, sensitivity (true positive rate) at 1% false positive (TP1FP), and Spearman rank coefficient among the positive set (Orenstein et al., 2012).

For interpretability and motif similarity we used average IC and average Euclidean distance. The IC for vector (v₁, v₂, v₃, v₄) (where ∑_i v_i = 1) is defined as 2+∑_i v_i log(v_i) (Schneider et al., 1986). The IC for a PWM is the average IC of the most informative eight contiguous positions, since peripheral positions tend to be of low IC and bias the results. To measure the similarity between two motifs we used Euclidean distance (Harbison et al., 2004). For two PWMs, we tried all possible offsets, with an overlap of at least five positions, and chose the one with minimal average Euclidean distance between columns. Motif logos were plotted using http://demo.tinyray.com/weblogo

In vivo binding prediction is tested in the same fashion as for probe ranking. Yeast promoters are ranked according to occupancy score using a PWM learned by one of the methods. The ranking is compared to the original ranking by p-value. AUC, TP1FP, and Spearman rank coefficient are used to gauge the ranking (Orenstein et al., 2012).

4.3. Implementation details

The method is implemented efficiently in Java. Each nucleotide is coded by 2 bits. The 8-mers are kept in a hash table, together with pointers to the original probes in which they appear. The software is available on acgt.cs.tau.ac.il/rap.

Acknowledgments

This study was supported in part by the European Community's Seventh Framework grant [HEALTH-F4-2009-223575] for the TRIREME project, and by the Israel Science Foundation (grant no. 802/08). Y.O. was supported in part by a fellowship from the Edmond J. Safra Center for Bioinformatics at Tel-Aviv University and by a Dan David PhD Fellowship. We thank David Glauber for his help during the early phase of this study.

Disclosure Statement

All authors state that no competing financial interests exist.