Abstract
Inborn errors of metabolism (IEM) are genetic diseases caused by mutations in enzymes or transporters affecting specific metabolic reactions that cause a block in the physiological metabolic fluxes. Therapeutic treatment can be achieved either by decreasing the metabolic flux upstream of the block or by increasing the flux downstream of the block. The identification of upstream and downstream fluxes however is not trivial, since metabolic reactions are intertwined in a complex network. To overcome this problem, we propose an innovative computational workflow to model the alteration of metabolism caused by IEM and predict the metabolites and reactions that are affected by the mutation. Our workflow exploits a recent genome-scale metabolic network model of hepatocyte metabolism to identify metabolites accumulating in hepatocytes due to single gene mutations in IEM via an innovative “differential flux analysis.” We simulated 38 IEMs in the liver, and in about half of the cases, our workflow correctly identified the metabolites known to accumulate in the blood and urine of IEM patients.
Key words: differential flux analysis, flux balance analysis, hepatocyte metabolism, inborn errors of metabolism, mathematical modeling
1. Introduction
Inborn errors of metabolism (IEM) are genetic diseases caused by alterations of specific metabolic reactions, which in turn affect one or more metabolic fluxes. A metabolic flux can be defined as “the production or elimination of a quantity of metabolite per mass of organ over a specific time” (Lanpher et al., 2006). IEMs are individually rare but collectively common in the population.
These disorders are generally caused by single-gene mutations (monogenic) causing a loss- or gain-of-function1 in the encoded protein (usually an enzyme or a transporter). The accepted explanation for the pathogenesis of IEM diseases is that a mutated enzyme will cause an altered metabolic flux in the same pathway of which it is a part. Therapeutic avenues include dietary restrictions or supplements, enzyme replacement therapy where possible, or substrate reduction therapy (Lanpher et al., 2006). The hypothesis underlying such therapeutic strategies is that treatment can be achieved if the block in the physiological metabolic fluxes caused by an IEM can be restored. This can be achieved either by decreasing the metabolic flux upstream of the block or by increasing the flux downstream of the block. The identification of upstream and downstream fluxes, however, is not as trivial as it may seem since metabolic reactions are intertwined in a complex network, which may give rise to unpredictable behaviors if perturbed even by a single gene mutation.1
Our work builds on the hypothesis that a genome-scale metabolic network model of hepatocyte metabolism (Gille et al., 2010) may be used to identify novel therapeutic targets whose modulation can restore the physiological metabolic fluxes in inborn errors of liver metabolism. Moreover, it may also explain the pathomechanism of IEM, which may have been missed by currently biased approaches and may allow the identification of novel disease biomarkers.
Toward this goal, we first extended the HepatoNet1 model (Gille et al., 2010), which comprises 2539 reactions for 777 metabolites to include enzymes whose function is specifically altered in liver IEM disorders such as Primary HyperOxaluria Type I and II (PH1 and PH2). We then developed an innovative computational workflow to predict the metabolites and reactions that are the most affected by a single gene gain- or loss-of-function mutation typical of inborn errors of liver metabolism (Lanpher et al., 2006).
The proposed workflow, in Figure 1, consists of four steps comprising the entire process of modeling, simulating, and in silico phenotyping of liver IEM, starting from the first genome-scale model of a comprehensive metabolic network of human hepatocytes (Gille et al., 2010). The first step concerns the genome-scale metabolic network reconstruction of liver metabolism. In the second one, flux balance analysis (Orth et al., 2010) is applied to the metabolic network to simulate physiological and pathological metabolic flux distributions. The third step involves a “differential flux analysis” (DFA), which we developed, to identify those metabolites and reactions predicted to be most affected by a gene loss- or gain-of-function. Finally, in order to evaluate the predicted in silico phenotypes, we simulated 38 IEMs affecting hepatocytes resulting from single mutation, and assessed if the metabolites identified by the DFA as the most affected include those metabolites known to be altered in the disease.
FIG. 1.
Steps of the workflow for studying the effect of gene perturbation on liver metabolism.
We achieved very promising results from the application of our workflow, thus demonstrating for the first time that these genetic disorders can be modeled computationally and that the model can be used to identify new therapeutic targets in an unbiased and inexpensive way.
2. Material and Methods
2.1. Extension of a hepatocyte-specific genome-scale metabolic network model
Current genome-scale metabolic models provide a computational platform to study in silico the metabolic fluxes in a given condition and cell type. Recently, a genome-scale reconstruction of the metabolic network of the human hepatocyte HepatoNet1 (Gille et al., 2010) has been generated. In this network, 777 metabolites and 2539 reactions are arranged in six intracellular and two extracellular compartments, thus providing a model able to simulate a large set of known metabolic liver functions.
We extended HepatoNet1 to include: i) all the reactions and metabolites known to be involved in glyoxylate metabolism, causative of two IEM disorders (Primary Hyperoxaluria Type I and II), starting from published models (Duarte et al., 2007; Ma et al., 2007), public databases (Cerami et al., 2011; Kanehisa and Goto, 2000; Matthews et al., 2009), and literature analysis (Danpure, 2006; Danpure and Jennings, 1986); and ii) transport reactions useful to balance the fluxes in the different compartments. At the end of this step, we obtained a single tissue-specific metabolic model of human hepatocytes, which can be used to study hepatocyte functions. (A list of the new reactions and metabolites added can be found in Table 1).
Table 1.
The Set of Reactions that Extends the Genome-Scale Model Developed in Gille et al, (2010)
| Peroxisomal enzymatic reactions |
| Alanine(p) + Glyoxylate(p) → Glycine(p) + Pyruvate(p) |
| Serine(p) + Pyruvate(p) → Hydroxypyruvate(p) + Alanine(p) |
| Glyoxylate(p) + O2(p) → H2O2(p) + Oxalate(p) |
| Glycolate(p) + O2(p) → Glyoxylate(p) + H2O2(p) |
| Glycine(p) + H2O(p) + O2(p) → Glyoxylate(p) + H2O2(p) + NH3(p) |
| Chenodeoxycholoyl-CoA(p) + Glycine(p) → CoA(p) + Glycochenodeoxycholate(p) |
| Choloyl-CoA(p) + Glycine(p) → CoA(p) + Glycocholate(p) |
| H2O(p) + O2(p) + Sarcosine(p) → Formaldehyde(p) + Glycine(p) + H2O2(p) |
| H2O2(p) ⇌O2(p) + H2O(p) |
| Cytoplasmic enzymatic reactions |
| Glyoxylate(c) + NAD + (c) → NADH(c) + Oxalate(c) |
| Glyoxylate(c) + NADPH(c) → Glycolate(c) + NADP+(c) |
| Glyoxylate(c) + NADH(c) → Glycolate(c) + NAD+(c) |
| 3htmelys(c) + H+(PG)(c) → 4tmeabut(c) + Glycine(c) |
| Gcald(c) + H2O(c) + NAD+(c) → Glycolate(c)+ 2 H+(PG)(c) + NADH(c) |
| Glyoxylate(c) + Alanine(c) → Glycine(c) + Pyruvate(c) |
| Glycine(c) → Glyoxylate(c) |
| Glycolate(c) → Oxalate(c) |
| Serine(c) ⇌ Glycine(c) + H2O(c) |
| Glycolaldehyde(c) + NAD+(c) → Glycolate(c) + NADH(c) |
| Hydroxypyruvate(c) → Glycolaldehyde(c) + CO2(c) |
| Hydroxypyruvate(c) + NADH(c) → Glycerate(c) + NAD+(c) |
| Tryptophan(c) → Oxalate(c) |
| Mitochondrial enzymatic reactions |
| Alanine(m) + Glyoxylate(m) → Glycine(m) + Pyruvate(m) |
| Glyoxylate(m) + H+(PG)(m) + NADPH(m) → Glycolate(m) + NADP + (m) |
| Glycine(m) + H+(PG)(m) + Lipoamide(m) ⇌ Alpam(m) + CO2(m) |
| Glycine(m) + H+(PG)(m) + Lpro(m) ⇌Alpro(m) + CO2(m) |
| FAD(m) + Sarcosine(m) + THF(m) → FADH2(m) + Glycine(m) + 5,10-Methylene-THF(m) |
| Transport reactions |
| H2O2(c) ⇌ H2O2(p) |
| H2O2(c) ⇌ O2(c) + H2O(c) |
| NH3(p) ⇌ NH3(c) |
| H+(PG)(p) ⇌ H+(PG)(c) |
| Alanine(c) ⇌ Alanine(p) |
| Pyruvate(p) ⇌ Pyruvate(c) |
| Serine(p) ⇌ Serine(c) |
| Glycochenodeoxycholate(p) ⇌ Glycochenodeoxycholate(c) |
| Glycocholate(p) ⇌ Glycocholate(c) |
| Sarcosine(p) ⇌ Sarcosine(c) |
| Formaldehyde(p) ⇌ Formaldehyde(c) |
| NH4 + (p) ⇌ NH4 + (c) |
| Glycine(c) ⇌ Glycine(p) |
| Glycolate(c) ⇌ Glycolate(p) |
| Glyoxylate(c) ⇌ Glyoxylate(m) |
| Oxalate(p) ⇌ Oxalate(c) |
| Hydroxypyruvate(p) ⇌ Hydroxypyruvate(c) |
| Consuming reactions |
| Glycerate(c) → |
| Oxalate(c) → |
| Glycolate(c) → |
| Glycolaldehyde(c) → |
(c), cytosol; (m), mitochondrial matrix; (p), peroxisome.
In order to validate this extended model, we performed producibility analysis to test that the model is able to produce all the compounds in the glyoxylate metabolism, as well as flux-balance analyses to establish a flux distribution for each of the different metabolic objectives listed in Gille et al (2010).
A metabolite xi is producible by a metabolic network if the network can sustain its synthesis under the steady state and thermodynamic constraints. To test the producibility of xi, we added a reaction rj in the cytoplasmic compartment that consumes xi, and then a flux-balance problem is solved to check if the network can produce strictly positive flux through rj.
2.2. Flux balance analysis and thermodynamic constraint-base modeling
The extended Hepatonet1 network topology can be mathematically described by a stoichiometric matrix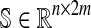 
, where n is the number of metabolites and m of reactions,2 which indicates how metabolic fluxes affect the concentrations of metabolites. More in detail, this matrix is formed from the stoichiometric coefficients of the reactions, which are integers that comprise the network. This matrix is organized such that each column corresponds to a reaction and each row to a metabolite.
Considering the stoichiometric matrix, the flux balance statement is given by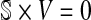 
where 
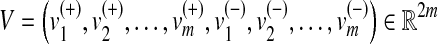is the vector of fluxes associated with the forward and reverse reactions of the network. Moreover, additional constraints, including those that relate to the maximal fluxes that can be supported by each reaction, can be introduced as inequalities. Furthermore, we need to specify the metabolic input(s) and output(s) of the network—the boundary reactions—which define the set 
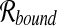. If we consider k boundary reactions, we then obtain an extended stoichiometric matrix 
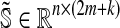and an extended vector of fluxes 
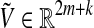. Moreover, to accomplish a particular functional state, the fluxes through a certain number of essential reactions, also called target reactions (
), have to be maintained at nonzero values. This is obtained by equality constraints of the form vj = κj > 0.
In the constraint-base modeling, a metabolic network is assumed to optimize a biological objective function. We consider the principle of flux-minimization (Holzhütter, 2004), which states that given the value of relevant target fluxes, the most likely distribution of stationary fluxes within the metabolic network is such that the weighted sum of all fluxes is a minimum. Employing the principle of flux minimization results in the solution of the following constrained linear optimization problem for the calculation of stationary metabolic fluxes:
 |
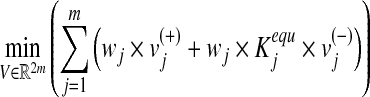(1) |
where wj is the weight associated with vj (in our simulations, fluxes in the objective function are weighted equally by default unless modified in selected cases to reflect differential activity of enzymes with alternative substrates or cofactors), while the equilibrium constants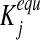 
are introduced to constraint fluxes according to Gibbs free energy calculations. Weighting the backward flux with the thermodynamic equilibrium constants takes into account the thermodynamic effort connected with reversing the natural direction of the reaction (Holzhütter, 2004). The minimization problem Equation (1) is subject to the following constraints:
 |
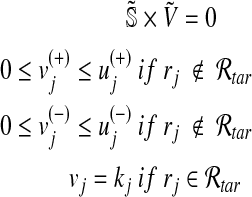(2) |
where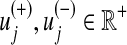 
represents the upper bounds of 
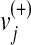and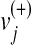 
, respectively, while wj is the weight associated with the flux vj.
2.3. Simulating wild-type and loss- or gain-of-function metabolic flux distributions
The consequence of an enzyme mutation on the metabolic network can be simulated by solving a flux minimization problem (Subsection 2.2) where the flux through the affected reaction is constrained to zero (in case of a loss-of-function) or to a value greater than zero (in case of a gain-of-function).
Let rj be the reaction catalyzed by an enzyme. In order to simulate the effect of a loss-of-function mutation of this enzyme in l different metabolic conditions, we first need to solve l optimization problems of type (1) to compute the wild-type flux distributions for the l different functions. Secondly, the same flux-balance problems must be solved by constraining the fluxes through vj to zero (loss-of-function mutation), that is, 
. The results of the simulations are stored in two matrices: i)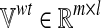 
, which contains the fluxes of the m internal reactions computed in the wild-type simulations, and ii) 
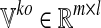storing the fluxes obtained by the loss of function simulations. Namely, 
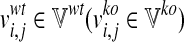represents the flux of reaction ri in the j-th metabolic functions, with 
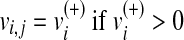and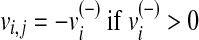 
. We follow this rule to store the value of a metabolic flux vi and to take the direction of ri into account.
2.4. Differential flux analysis
We would like to identify those metabolites and reactions that are likely to be most affected by the loss-of-function of an enzyme or transporter. To perform “differential flux analysis,” (DFA) we first apply flux balance analysis in both wild-type and loss-of-function conditions for each of the l different metabolic functions to obtain the matrix of fluxes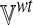 
and 
as defined previously. We then compute the difference Δ of each of the m fluxes between the two conditions (wt and ko) for the l different metabolic functions:
 |
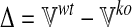(3) |
with 
. Next, we compute for each of the m reactions the mean of flux differences across the l different metabolic functions:
 |
(4) |
where δi,j is the element of Δ having indexes i and j. We indicate with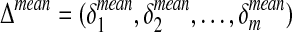 
the vector containing the average of flux differences.
Δmean is then directly used to obtain a ranked list of fluxes (and hence reactions) arranged in ascending order. In this way, at the top and at the bottom of the list, we will find the reactions having the metabolic flux most affected by the loss-of-function (or gain-of-function) mutation. More in details, the top of the list contains the reactions for which the flux is decreased in the simulated disorder, while in the bottom of the list we find the reactions having an increased flux.
Metabolites are instead ranked by taking into account also the stoichiometry of the network. We thus estimate the impact of an enzymatic defect on a metabolite concentration xi by means of the following index:
 |
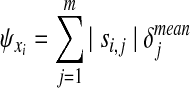(5) |
where si,j is the element of matrix 
of index (i, j).
The vector 
is then used to obtain a ranked list of metabolites, named Xord, arranged in ascending order. Also in this case, at the top and at the bottom of the list, we will find metabolites whose concentration changes the most.
The resulting ranked list Xord may contain the same metabolite associated with different compartments in different positions. In order to study the in silico phenotype, we would like to have only one instance for each metabolite. To this aim, we decided to keep, for each compound, the one having the maximal absolute value of ψxi across all the different compartments.
2.5. Metabolite enrichment analysis
The ranked lists resulting from the previous step allow us to analyze how a loss-of-function changes the metabolic flux distribution. In order to validate whether the in silico results for a given loss-of-function mutation resemble clinically observed phenotypes of the IEM, we applied a variant of the gene set enrichment analysis (GSEA) (Subramanian et al., 2005) to test if metabolites that are clinically known to accumulate due to a loss-of-function mutation occur toward the bottom of the list Xord and vice versa. In order to avoid confusion, we named this statistical analysis “metabolic enrichment analysis” (MEA).
We considered 760 disease-associated metabolite sets comprising 500 different diseases, from a public repository (Xia and Wishart, 2010). These sets are divided into two subcategories based on the biofluids in which they have been measured: i) 414 sets in blood and ii) 346 in urine. Let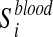 
, 
, be the i-th disease-associated metabolite set in blood, and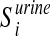 
, 
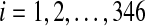, be the i-th disease-associated metabolite set in urine. We then consider their union, namely, 
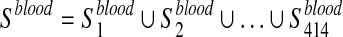and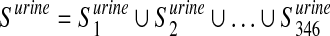 
.
After that, we start from the list Xord to obtain two new lists, namely, Xblood and Xurine. The first one is obtained by removing from Xord the metabolites that are not elements of the set Sord ∩ Sblood, while the second one by removing the ones that are not in the set Sord ∩ Surine, where Sord is a set containing all the metabolites in Xord.
Metabolite enrichment analysis is performed by checking whether the disease-associated metabolites for a given IEM tend to be ranked at top (or bottom) of the ranked list Xblood and Xurine obtained by simulating the IEM under investigation. More in details, let us consider the disease-associated metabolite sets in blood (the same approach is applied to disease-associated metabolite sets in urine). For each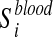 
, enrichment analysis is performed to compute an enrichment score 
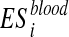, which reflects the degree to which 
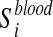is overrepresented at the top or bottom of Xblood. This score, which corresponds to a Kolmogorov-Smirnov test, evaluates if the metabolites of 
tend to be found at top or bottom of Xblood or if they are randomly distributed (Subramanian et al., 2005).
We applied a permutation test to asses the statistical significance of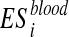 
(Edgington, 1986). The significance of a permutation test is represented by its p-value. It is the probability of obtaining a result at least as extreme as the test statistic given that the null hypothesis is true. In permutation tests, the null hypothesis is defined as: “the elements of a list are interchangeable.” Significantly low p-values indicate that the elements are not interchangeable and that the original list is relevant with respect to the data.
The p-value is assessed by performing a set of permutations and computing the fraction of permutation values that are at least as extreme as the test statistic from the unpermuted data. Then, the enrichment score is computed after a random shuffling of Xblood. Let I(·) be the indicator function. The permutation procedure is repeated t times and 
, are computed. The p-value associated to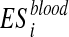 
is calculated as:
 |
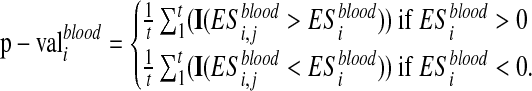(6) |
The disease sets are ranked in ascending order according to absolute values of the enrichment scores, and then the rank is pruned by removing the sets for which the p-value is above a fixed threshold, usually set as 0.05 or 0.01.
3. Results
3.1. In silico simulation of inborn errors of liver metabolism
We applied our computational workflow to simulate the metabolic phenotypes of 38 IEMs reported in Table 2. For each of the 38 IEMs, flux-balance analysis, as outlined in Subsections 2.2 and 2.3, was applied to the extended HepatoNet1 metabolic network model to compute both wild-type and loss-of-function metabolic flux distributions across 8843 different metabolic objectives, simulating different physiological functions of the hepatocyte.
Table 2.
The Simulated Inborn Errors of Metabolism
| Disease | Enzyme | OMIM | Pathways |
|---|---|---|---|
| Argininemia | EC 3.5.3.1 | 207800 | Arginine and proline metabolism |
| Argininosuccinic aciduria | EC 4.3.2.1 | 207900 | Alanine, aspartate, and glutamate metabolism Arginine and proline metabolism |
| Gaucher disease | EC 3.2.1.45 | 230800 | Sphingolipid metabolism Lysosome |
| Von Gierke disease | EC 3.1.7.9 | 232200 | Starch and sucrose metabolism Insulin signaling pathway Lysosome |
| Phenylketonuria | EC 1.14.16.1 | 261600 | Phenylalanine metabolism Phenylalanine, tyrosine, and tryptophan biosynthesis Folate biosynthesis |
| Ornithine transcarbamylase deficiency | EC 2.1.3.3 | 311250 | Arginine and proline metabolism |
| Methylmalonic acidemia | EC 5.4.99.2 | 251000 | Valine, leucine, and isoleucine degradation Glyoxylate and dicarboxylate metabolism Propanoate metabolism |
| Galactosemia type I | EC 2.7.7.12 | 230400 | Galactose metabolism Amino sugar and nucleotide sugar metabolism |
| Galactosemia type II | EC 2.7.1.6 | Galactose metabolism Amino sugar and nucleotide sugar metabolism |
|
| Galactosemia type III | EC 5.1.3.2 | Galactose metabolism Amino sugar and nucleotide sugar metabolism |
|
| Pyruvate carboxylase deficiency | EC 6.4.1.1 | 266150 | Citrate cycle (TCA cycle) Pyruvate metabolism |
| Medium-chain acyl-CoA | EC 1.3.99.3 | 201450 | Fatty acid metabolism Valine, leucine and isoleucine degradation beta-Alanine metabolism Propanoate metabolism |
| Fructose intollerance | EC 4.1.2.13 | 229600 | Glycolysis / Gluconeogenesis Pentose phosphate pathway Fructose and mannose metabolism |
| Maple Syrup Type II | EC 1.2.4.4 | 248600 | Valine, leucine, and isoleucine degradation |
| Maple Syrup Type III | EC 1.8.1.4 | 248600 | Glycolysis / Gluconeogenesis Citrate cycle (TCA cycle) Glycine, serine, and threonine metabolism Valine, leucine, and isoleucine degradation Pyruvate metabolism |
| Tyrosinemia type I | EC 3.7.1.2 | 276700 | Tyrosine metabolism Phenylalanine metabolism |
| Homocystinuria | EC 4.2.1.22 | 236200 | Glycine, serine, and threonine metabolism Cysteine and methionine metabolism |
| Tay-Sachs | EC 3.2.1.52 | 272800 | Other glycan degradation Various types of N-glycan biosynthesis Amino sugar and nucleotide sugar metabolism Glycosaminoglycan degradation Glycosphingolipid biosynthesis - globo series Glycosphingolipid biosynthesis - ganglio series Lysosome |
| Adenosine deaminase deficiency | EC 3.5.4.4 | 102700 | Purine metabolism |
| Smith-Lemli-Opitz Syndrome | EC 1.3.1.21 | 270400 | Steroid biosynthesis |
| Niemann-Pick Type A | EC 3.1.4.12 | 257200 | Sphingolipid metabolism Lysosome |
| Lesch-Nyhan-Syndrome | EC 2.4.2.8 | 300322 | Purine metabolism Drug metabolism - other enzymes |
| Carbamyl phosphate synthetase | EC 6.3.4.16 | 237300 | Arginine and proline metabolism |
| Carbamyl phosphate synthetase B | EC 6.3.5.5 | 237300 | Arginine and proline metabolism |
| Glycogen storage disease 0 | EC 2.4.1.11 | 611556 | Starch and sucrose metabolism Insulin signaling pathway Lysosome |
| Glycogen storage disease II | EC 3.1.3.9 | 232200 | Starch and sucrose metabolism Insulin signaling pathway Lysosome |
| Hers disease | EC 2.4.1.1 | 232700 | Starch and sucrose metabolism Insulin signaling pathway Lysosome |
| Andersen disease | EC 2.4.1.18 | 232500 | Starch and sucrose metabolism Insulin signaling pathway Lysosome |
| Tarui disease | EC 2.7.1.11 | 610681 | Starch and sucrose metabolism Insulin signaling pathway Lysosome |
| Cori disease (GSD III) | EC 3.2.1.33/2.4.1.25 | 232400 | Starch and sucrose metabolism Insulin signaling pathway Lysosome |
| ACYL-CoA dehydrogenase, medium chain | EC 1.3.99.3 | 607008 | Fatty acid metabolism Valine, leucine, and isoleucine degradation |
| ACYL-CoA dehydrogenase, short chain | EC 1.3.99.2 | 606885 | Fatty acid metabolism Valine, leucine, and isoleucine, degradation |
| Glutaric acidemia | EC 1.3.99.7 | 231670 | Fatty acid metabolism Fatty acid metabolism Lysine degradation |
| Isovaleric acidemia | EC 1.3.99.10 | 231670 | Valine, leucine, and isoleucine degradation |
| Propionic acidemia | EC 6.4.1.3 | 606054 | Valine, leucine, and isoleucine degradation Propanoate metabolism |
| Alkaptonuria | EC 1.13.11.5 | 203500 | Tyrosine metabolism |
| Carnitine palmitoyltransferase deficiency I | EC 2.3.1.21 | 600528 | Fatty acid metabolism Valine, leucine, and isoleucine degradation |
| Primary hyperoxaluria type I | EC 2.6.1.44 | 259900 | Glycine, serine, and threonine metabolism Glyoxylate and dicarboxylate metabolism |
The KEGG database has been used as reference for the patnwas associated with each disease.
Following FBA, we then applied differential flux analysis (Sec. 2.4 and 2.5) to identify the metabolites predicted to change the most in each of the 38 IEMs due the loss-of-function mutation.
Next, we applied Metabolite Enrichment Analysis (MEA) (Sec. 2.5) to check whether metabolites whose levels are known to be altered in blood or urine of patients are correctly identified as the most changed by the in silico simulations. MEA assigns an enrichment score and a p-value to each one of 500 distinct metabolic sets known to be altered in 500 distinct metabolic disorders (including the 38 IEMs). We deemed a simulated metobolic phenotype correct (true positive), if the p-value of the metabolic set associated with the simulated IEM was significant (i.e., below 0.01 or 0.05).
To assess the performance of our in silico workflow, we used the positive predictive value (PPV): for each of the 38 simulated disorders, we counted the number of true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN), and computed the PPV as TP/(TP + FP) and sensitivity as TP/(TP + FP).
Figures 2 and 3 plot the PPV versus rank and PPV versus sensitivity for the ranked list obtained by using, respectively, p–value ≤ 0.05 and p–value ≤ 0.01 to select TPs. As shown in Figure 2, the PPV reaches a maximum of approximately 15% for disease-associated metabolite sets in blood, and of approximately 23% for disease-associated metabolite sets in urine. Moreover, the sensitivities are approximately 47% and 34%, respectively.
FIG. 2.
Workflow performances on 38 IEMs, considering p-value = 0.05 as threshold to select true positives. (a) PPV vs. rank, and (b) PPV vs. sensitivity for disease-associated metabolite sets in blood. On the bottom part, the plots show the results for disease-associated metabolite sets in urine. (c) PPV vs. rank, and (d) PPV vs. sensitivity for disease-associated metabolite sets in urine. The peaks of the curve are at 15% and 23% for blood and urine, respectively. The workflow performance (blue line) outperforms the random performance (red line). IEM, inborn errors of metabolism; PPV, positive predictive value.
FIG. 3.
Workflow performances on 38 IEMs, considering p–val = 0.01 as threshold to select true positives. (a) PPV vs. rank, and (b) PPV vs. sensitivity for disease-associated metabolite sets in blood. On the bottom part, the plots show the results for disease-associated metabolite sets in urine. (c) PPV vs. rank, and (d) PPV vs. sensitivity for disease-associated metabolite sets in urine. The peaks of the curve are at 15% and 23% for blood and urine, respectively. The workflow performance (blue line) outperforms the random performance (red line).
On the other hand, when the lists are filtered by using 0.01 as thresholds for the p-values, then the PPV significantly increases. In fact, we obtained a maximum of 31% for disease-associated metabolite set in blood and of approximately 38% for disease-associated metabolite sets in urine.
In Tables 3 and 4, we report the ranks of the simulated diseases that are present in the final ranked lists, considering the two p-value thresholds. Due to the fact that some disorders can have different clinical manifestations, we associated more than one rank to some of them.
Table 3.
Ranks of the Simulated Diseases in the Final Ranked Lists of Disease-Associated Metabolite Sets in Blood After the Pruning
| Disease | Rank p-val = 0.05 | Rank p-val = 0.01 |
|---|---|---|
| Argininemia | 2 | |
| Argininosuccinic aciduria | 29 | 15 |
| Gaucher disease | 1 | 1 |
| Von Gierke disease | 1 | 1 |
| Ornithine transcarbamylase dificiency | 30 | 13 |
| Methylmalonic aciduria | 9, 12, 19, 20 | 4 |
| Galactosemia type I | 1 | 1 |
| Galactosemia type II | 2 | 2 |
| Galactosemia type III | 7 | |
| Fructose intollerance | 19 | |
| Maple syrup type II | 32 | |
| Tyrosinemia type I | 6, 18 | 7 |
| Homocystinuria | 7 | |
| Glycogen storage disease | 2 | 2 |
| Acyl-CoA dehydrogenase medium chain | 8, 16 | 6 |
| Acyl-CoA dehydrogenase short chain | 10, 21 | |
| Glutaric aciduria | 2 | |
| Carnitine palmitoyltransferase deficiency I | 10, 12 | 6 |
Table 4.
Ranks of the Simulated Diseases in the Final Ranked Lists of Disease-Associated Metabolite Sets in Urine, After the Pruning
| Disease | Rank p-val = 0.05 | Rank p-val = 0.01 |
|---|---|---|
| Methylmalonic aciduria | 2, 3 | 2, 3 |
| Argininosuccinic aciduria | 29 | 15 |
| Gaucher disease | 1 | 1 |
| Von Gierke disease | 1 | 1 |
| Ornithine transcarbamylase deficiency | 30 | 13 |
| Methylmalonic aciduria | 9, 12, 19, 20 | 4 |
| Galactosemia type I | 1 | 1 |
| Galactosemia type II | 2 | 2 |
| Galactosemia type III | 6 | |
| Tyrosinemia type I | 7 | |
| Homocystinuria | 4,8 | 5 |
| Adenosine deaminase deficiency | 9 | |
| Lesch-Nyhan sindrome | 2 | |
| Glutaric aciduria | 2 | |
| Primary hyperoxaluria type I | 1 | 1 |
4. Conclusions and Ongoing Work
In this article, we proposed a computational workflow, based on a genome-scale metabolic model of hepatocytes, to simulate in silico the changes in metabolites observed in patients affected by IEM. In this work, we considered Mendelian disorders, but we would like to point out that our method might have broader applications for the study of other aspects of the metabolism and common human diseases, such as obesity, diabetes, and cancer.
To validate our computational approach, we simulated the in silico phenotype of a representative set of inborn errors of metabolism capturing the wide spectrum of pathophysiology, clinical presentation, and clinical management of these Mendelian disorders. The results here presented prove that our workflow can be a valuable tool to simulate IEM in liver and to identify new therapeutic targets in an unbiased and inexpensive way.
As an ongoing work, we are testing the usefulness of such a system-level approach in automatically identifying the most promising therapeutic targets by focusing on Primary Hyperoxaluria Type I, which is caused by a loss-of-function mutation of the liver-specific AGT enzyme. In the peroxisomes of normal human hepatocytes, this enzyme catalyzes the transamination of the intermediary metabolite glyoxylate to glycine. This is a detoxification reaction because its dysfunction in an IEM known as Primary Hyperoxaluria Type 1 (PH1) allows glyoxylate to escape from the peroxisomes into the cytosol where it is oxidized to oxalate, catalyzed by lactate dehydrogenase, and reduced to glycolate, catalyzed by glyoxylate/hydroxypyruvate reductase (Danpure, 2006). In humans, at least, oxalate cannot be further metabolized, and its increased synthesis and urinary excretion leads to the progressive deposition of insoluble calcium oxalate (CaOx) in the kidney and urinary tract, resulting in various combinations of nephrocalcinosis (diffuse deposition throughout the renal parenchyma) and/or urolithiasis (calculi). This eventually leads to renal failure and a multi systemic disorder due to widespread tissue CaOx accumulation, following which the combined effects of increased oxalate synthesis and failure to remove it from the body results in the deposition of CaOx almost anywhere.
As shown in Table 4, the metabolites known to accumulate in the urine of PH1 patients match very well with the list of metabolites predicted to change the most by a loss-of-function mutation of AGT by our computational method (first rank in the disease sets associated to urine). To analyze in more details the simulated PH1 phenotype, we observed that in the associated ranked lists of metabolites, namely Xurine and Xord, the top two metabolites predicted to increase the most are glycolate and oxalate in the cytosolic compartment; this prediction is in agreement with the known increased conversion rate of glyoxylate to oxalate and glycolate in PH1 patients (Beck and Hoppe, 2006).
Moreover, we observed that metabolites and fluxes involded in the pathways that convert hydroxypyruvate and tryptophan to oxalate are predicted to significantly change. It is known that hydroxypyruvate is a precursor of oxalate (Gambardella and Richardson, 1978; Raghavan and Richardson, 1983), that is, it increases endogenus oxalate via glycolaldehyde → glycolate → glyoxylate → oxalate. Moreover, tryptophan has been shown to be converted to oxalate (Gambardella and Richardson, 1977).
These results show that our proposed methodology is able to perform nontrivial predictions and that it can be ultimately used to identify alternative therapeutic strategies proposing nontrivial substrate reduction therapies or enzymes whose modulation could restore physiological metabolic fluxes in IEM.
Footnotes
Gain-of-functions are extremely rare among IEMs.
In our model, we consider 2m reactions because a metabolic flux can be positive or negative. Therefore, to deal with non-negative variables, each reaction is decomposed into an irreversible forward one and an irreversible backward one.
We simulated the 442 physiological funtions of the hepatocyte (Gille et al., 2010) by considering two different sets of flux constraints for the reaction exchanging glycine between cytosol and peroxisome.
Acknowledgments
This work was funded by the European Community's Seventh Framework Programme [FP7/2007-2013] under grant agreement n 259743 (MODHEP) and by the Telethon Foundation Grant TGM11SB1 to DdB.
Author Disclosure Statement
The authors declare that no competing financial interests exist.
References
- Beck B.B. Hoppe B. Is there a genotype-phenotype correlation in primary hyperoxaluria type 1? Kidney Int. 2006;70:984–6. doi: 10.1038/sj.ki.5001797. [DOI] [PubMed] [Google Scholar]
- Cerami E.G. Gross B.E. Demir E. Rodchenkov I, et al. Pathway Commons, a web resource for biological pathway data. Nucleic Acids Res. 2011;39:D685–D690. doi: 10.1093/nar/gkq1039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danpure C. Jennings P. Peroxisomal alanine:glyoxylate aminotransferase deficiency in primary hyperoxaluria type I. FEBS Lett. 1986;201:20–34. doi: 10.1016/0014-5793(86)80563-4. [DOI] [PubMed] [Google Scholar]
- Danpure C.J. Primary hyperoxaluria type 1: AGT mistargeting highlights the fundamental differences between the peroxisomal and mitochondrial protein import pathways. Biochimica et Biophysica Acta BBA Molecular Cell Research. 2006;1763:1776–1784. doi: 10.1016/j.bbamcr.2006.08.021. [DOI] [PubMed] [Google Scholar]
- Duarte N.C. Becker S.A. Jamshidi N., et al. Global reconstruction of the human metabolic network based on genomic and bibliomic data. Proc. Natl. Acad. Sci. U S A. 2007;104:1777–1782. doi: 10.1073/pnas.0610772104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgington E.S. Randomization tests. Marcel Dekker, Inc.; New York, NY: 1986. [Google Scholar]
- Gambardella R.L. Richardson K. The formation of oxalate from hydroxypyruvate, serine, glycolate and glyoxylate in the rat. Biochimica et Biophysica Acta BBA General Subjects. 1978;544:315–328. doi: 10.1016/0304-4165(78)90100-9. [DOI] [PubMed] [Google Scholar]
- Gambardella R.L. Richardson K.E. The pathways of oxalate formation from phenylalanine, tyrosine, tryptophan and ascorbic acid in the rat. Biochimica et Biophysica Acta BBA General Subjects. 1977;499:156–168. doi: 10.1016/0304-4165(77)90238-0. [DOI] [PubMed] [Google Scholar]
- Gille C. Bolling C. Hoppe A., et al. HepatoNet1: a comprehensive metabolic reconstruction of the human hepatocyte for the analysis of liver physiology. Mol. Syst. Biol. 2010;6 doi: 10.1038/msb.2010.62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzhütter H.G. The principle of flux minimization and its application to estimate stationary fluxes in metabolic networks. European Journal of Biochemistry. 2004;271:2905–2922. doi: 10.1111/j.1432-1033.2004.04213.x. [DOI] [PubMed] [Google Scholar]
- Kanehisa M. Goto S. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 2000;28:27–30. doi: 10.1093/nar/28.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanpher B. Brunetti-Pierri N. Lee B. Inborn errors of metabolism: the flux from Mendelian to complex diseases. Nat. Rev. Genet. 2006;7:449–459. doi: 10.1038/nrg1880. [DOI] [PubMed] [Google Scholar]
- Ma H. Sorokin A. Mazein A., et al. The Edinburgh human metabolic network reconstruction and its functional analysis. Mol. Syst. Biol. 2007;3 [Google Scholar]
- Matthews L. Gopinath G. Gillespie M., et al. Reactome knowledgebase of human biological pathways and processes. Nucleic Acids Res. 2009;37:D619–D622. doi: 10.1093/nar/gkn863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orth J.D. Thiele I. Palsson B.O. What is flux balance analysis? Nat. Biotechnol. 2010;28:245–248. doi: 10.1038/nbt.1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raghavan K.G. Richardson K. Hydroxypyruvate-mediated regulation of oxalate synthesis by lactate dehydrogenase and its relevance to primary hyperoxaluria type II. Biochemical Medicine. 1983;29:101–113. doi: 10.1016/0006-2944(83)90059-5. [DOI] [PubMed] [Google Scholar]
- Subramanian A. Tamayo P. Mootha V.K., et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. U S A. 2005;102:15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia J. Wishart D.S. MSEA: a web-based tool to identify biologically meaningful patterns in quantitative metabolomic data. Nucleic Acids Res. 2010;38:W71–77. doi: 10.1093/nar/gkq329. [DOI] [PMC free article] [PubMed] [Google Scholar]