Locally-Constrained Region-Based Methods for DW-MRI Segmentation

Abstract

In this paper, we describe a method for segmenting fiber bundles from diffusion-weighted magnetic resonance images using a locally-constrained region based approach. From a pre-computed optimal path, the algorithm propagates outward capturing only those voxels which are locally connected to the fiber bundle. Rather than attempting to find large numbers of open curves or single fibers, which individually have questionable meaning, this method segments the full fiber bundle region. The strengths of this approach include its ease-of-use, computational speed, and applicability to a wide range of fiber bundles. In this work, we show results for segmenting the cingulum bundle. Finally, we explain how this approach and extensions thereto overcome a major problem that typical region-based flows experience when attempting to segment neural fiber bundles.

1. Introduction

Region-based approaches to image segmentation constitute a key methodology for numerous applications. In these approaches, the objective is to find the segmentation which optimally separates features exterior to a closed curve or surface from features contained in the interior. These approaches have been shown to accurately segment datasets with low signal to noise ratio, frequently outperforming edge-based techniques.

For example, in the work by Chan and Vese, a flow is proposed which optimally separates the first moments of the intensity distributions [4]. In more recent work, Rathi et al. demonstrate a method based on the Bhattacharyya distance for separating entire distributions [30]. In both of these cases, features from the entire interior of the curve are compared against features from the entire exterior.

In this present work, we propose a region-based algorithm for the segmentation of neural fiber bundles from diffusion weighted magnetic resonance imagery (DW-MRI). Specifically, we describe why classical approaches (i.e. those which compare features across the full interior with features from the full exterior) may not be well-suited for DW-MRI fiber bundle segmentation. Then, we explain how one can leverage the results of optimal or geodesic path algorithms to locally constrain region-based approaches in such a manner which will both retain the beneficial attributes of region-based methods while also handling the challenges posed by DW-MRI data. Starting from an optimal path (or anchor tract), a fiber bundle is segmented using a Bayesian framework. The priors are based on anatomical knowledge of the bundle being segmented, for instance, a simple nonlinear anatomically derived function of the distance to the anchor tract works well for the cingulum bundle. The likelhoods are based on local measures of tensor compatibility (local uniformity), adapting a Chan and Vese approach to active contours without edges. The Bayesian formulation is cast as an energy minimization problem which is solved using a greedy flood fill motivated algorithm.

We now briefly describe the remainder of this paper. First, in Section 2, we provide a literature review and background of tractography and fiber bundle segmentation algorithms. Second, in Section 3, we motivate our interest in applying this algorithm to the segmentation of the cingulum bundle. Third, in Section 4, we describe the algorithm for locally constraining the region-based method. Fourth, in Section 5, we provide initial results on the segmentation of the cingulum bundle using a simplistic implementation. Finally, in Section 6, we provide an extensive explanation of how these ideas and results may be adapted for use in a variety of implementations and algorithms.

2. Background

Since the advent of diffusion weighted magnetic resonance imaging, a great deal of research has been devoted to finding and characterizing neural connections between brain structures. Image resolution is typically high enough so that major white matter tracts, or bundles of densely packed axons, are several voxels in cross-sectional diameter [20]. The goal of tractography algorithms is to segment these fiber bundles from the DW-MRI datasets.

Early tractography methods were based on streamlines which employed local decision-making based on the principal eigenvector of diffusion tensors [19, 33, 2, 5]¹.

In these techniques, tracts are propagated from a starting point until the tracts reach some termination criterion. Due to the local decision-making process, these methods have been shown to perform poorly in noise and often stop prematurely. These techniques do not provide a measure of connectivity for the resulting tracts. Furthermore, several of these methods do not use the full tensor, reducing the data to the principal eigenvectors, and subsequently are unable to handle fiber crossings, branchings, “kissings,” etc.

Despite the shortcomings of this approach, due to its ease-of-use, streamlining has quickly become the most popular method for fiber segmentation. To infer fiber bundles from streamline tractography results, several groups have successfully worked on methods for fiber clustering. The goal of clustering is to capture group behavior of a population of streamlines and to use this group behavior to drive fiber bundle segmentation. The end result of clustering algorithms has been shown to accurately capture many neural fiber bundles, see for example [22, 18].

Recently, another line of work has emerged which seeks to avoid the use of the problematic streamlines. Tractography advances have been made which provide full brain optimal connectivity maps from predefined seed regions. These methods are more robust to noise and depending upon the underlying metric, may be able to more fully use the complete DW-MRI data. These approaches can be subdivided into stochastic and energy-minimization approaches.

Stochastic approaches produce probability maps of connectivity between a seed region and the rest of the brain. Parker et al. developed PICo, a probabilistic index for standard streamline techniques [24]. Perrin et al. presented probabilistic techniques for untangling fiber crossings using q-ball fields [26]. In other work, Friman et al. proposed a method for probabilistically growing fibers in a large number of random directions and inferring connectivity from the resulting percentages of connections between seed and target regions [7]. While providing a measure of connectivity between brain regions, these stochastic approaches do not provide an explicit segmentation of the fiber bundle itself and often do not explicitly provide the optimal connection between regions of the brain.

Energy-minimization techniques have also been developed. Parker et al. proposed fast marching tractography which minimizes an energy based on both the position and direction of the normal to a propagating front [25]. O’Donnell et al. cast the tractography problem in a geometric framework finding geodesics on a Riemannian manifold based on diffusion tensors [23]. Similarly, Prados et al. and Lenglet et al. demonstrated a Riemannian based technique, GCM (Geodesic Connectivity Mapping), for computing geodesics using a variant of fast marching methods adapted for directional flows [29, 15]. Jackowski et al. find Riemannian geodesics using Fast Sweeping methods as given by Kao et al. [8, 11, 12]. Pichon et al. and Melonakos et al. use the more general Finsler metric to find optimal connections [27, 28, 17, 16]. Finally, Fletcher et al. propose a new Hamilton-Jacobi-Bellman numeric solver on the graphics processing unit to find Riemannian geodesics in near real-time speeds [6]. In each of these cases, an optimal path is found which represents the best connection between the two regions under the given metric.

3. The Cingulum Bundle

In this section, we motivate the problem of segmenting the cingulum bundle. The cingulum bundle is a 5–7 mm in diameter fiber bundle that interconnects all parts of the limbic system. It originates within the white matter of the temporal pole, and runs posterior and superior into the parietal lobe, then turns, forming a ”ring-like belt” around the corpus callosum, into the frontal lobe, terminating anterior and inferior to the genu of the corpus callosum in the orbital-frontal cortex [32]. Moreover, the cingulum bundle consists of long, association fibers that directly connect temporal and frontal lobes, as well as shorter fibers radiating into their own gyri. The cingulum bundle also includes most afferent and efferent cortical connections of cingulate cortex, including those of prefrontal, parietal and temporal areas, and the thalamostriatae bundle. In addition, lesion studies document a variety of neurobehavioral deficits resulting from a lesion located in this area, including akinetic mutism, apathy, transient motor aphasia, emotional disturbances, attentional deficits, motor activation, and memory deficits. Because of its involvement in executive control and emotional processing, the cingulum bundle has been investigated in several clinical populations, including depression and schizophrenia. Previous studies, using diffusion tensor imagery, in schizophrenia, demonstrated decrease of fractional anisotropy in the anterior part of the cingulum bundle [13, 34], at the same time pointing to the technical limitations restricting these investigations from following the entire fiber tract.

4. The Algorithm

In this section, we present our method for applying local constraints to region-based flows.

4.1. Motivation for Local Constraints

An implicit assumption of classical (i.e., those which compare features across the full interior with features from the full exterior) region-based approaches is that the entire interior of the contour contains fairly homogeneous features, such as mean intensity. Under this assumption, these algorithms proceed by evolving the closed curve or surface to minimize an energy defined over these features.

However, if there are no homogeneous features across the entire interior or exterior of the object of interest, it becomes difficult to define a region-based approach which will accurately segment the image. For instance, in the case of the cingulum bundle which curves around the ventricles, the tensors across the fiber bundle vary in both anisotropy and orientation across the length of the bundle, as shown in Figure 1. In this sagittal view, we see that it is difficult to define a feature on the space of tensors which uniquely separates the entire interior of the cingulum bundle from the exterior. However, we also notice that the tensor shape and anisotropy vary smoothly across the bundle. Hence, locally across the fiber one can define tensor features which are distinguishable from the exterior.

Figure 1.

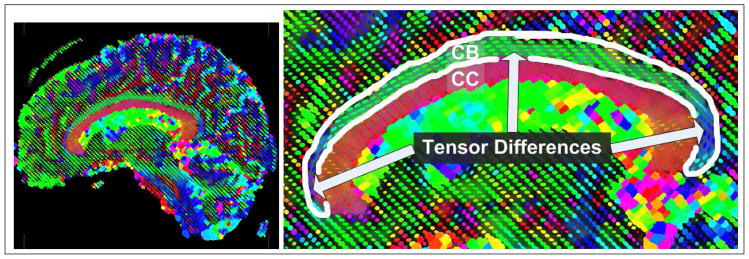
Example of the need for local constraints on region-based segmentation algorithms which attempt to segment the cingulum bundle. Notice that tensor anisotropy and orientation vary across the length of the cingulum bundle.

4.2. Prior Work

Surface evolution approaches have been described for fiber bundle segmentation. Rousson et al. [31] use a multivariate Gaussian distribution of the tensor components in a geodesic active region model to drive a surface evolution towards the segmentation of fiber bundles. The method is applied to the segmentation of the corpus callosum, but is unable to fully capture its curved character as discussed by the authors. In a follow-up paper [14] a similar segmentation framework in combination with a geodesic distance between tensors is shown to yield superior segmentation results, in particular, when segmenting curved fiber bundles. Jonasson et al. propose two different ways to address the segmentation of curved fiber bundles in a surface evolution setting: (i) a local approach [9], where the surface evolution speed is influenced by the similarity of a tensor in comparison to its interior neighbors, and (ii) a region-based approach, where the similarity measure is based on the notion of a most representative tensor within the segmented region [10]. In the latter case, capturing highly curved fiber bundles will be problematic. In both cases the segmentation algorithm is combined with a surface regularization to prevent leaking. The approach proposed in this paper is related to Jonasson’s work [9] in as much as it uses local tensor similarities to drive the segmentation, however, no surface evolution is used and a tensor similarity measure is combined with prior information as given by an initially computed anchor tract (also preventing large-scale leaking). The extension of the approach proposed in this paper (see Section 6) can be seen as complementary to the method by Lenglet et al. [14]. Instead of disentangling tensor shape and orientation through an appropriate tensor distance (and statistic) the anchor tract may be used to warp the space initially, thus effectively removing large orientation differences². Further, due to the absence of a surface evolution, our approach is computationally very efficient.

4.3. Bayesian Framework

In this section, we describe how the algorithm can be formulated in a Bayesian framework. We follow the approach by Mumford [21] and cast the Bayesian estimation problem into an energy minimization. The probability of observing the classification C, consisting of points belonging to the fiber and points belonging to the background given the tensor information T is (using Bayes’ formula):

$$p(C\mid T)=\frac{p(T\mid C)p(C)}{p(T)}~p(T\mid C)p(C),$$ (1)

where C is an element of the set of all possible assignments of voxels to the fiber and the background respectively, p(T|C) is the likelihood of observing T given the classification C and p(C) is the prior. By taking the logarithm on both sides and noting that p(T) is independent of the classification C, Equation (1) can be written as an energy minimization problem [21]

$$\begin{array}{l}E(C)=-log(p(C,T))\\ =-log(p(T\mid C))-log(P(C))\\ =E_d(T,C)+E_p(C),\end{array}$$ (2)

where E_d(T, C) denotes the data energy and E_p(C) the prior (or regularization) energy. Instead of solving the Bayesian estimation problem (1) directly we may thus instead minimize the energy (2). Which leaves us with defining these energies. We use a flood-fill algorithm approach that solves the energy minimization problem (2) for an individual point only considering its local neighborhood N. In what follows we first describe the continuous setting, to make connections with existing approaches, and then describe the discrete implementation in the context of the proposed Bayesian flood-fill algorithm. Given the local neighborhood N of a point x we want to decompose it into a subregion belonging to the fiber and a subregion belonging to the background. The goal of our algorithm is to make each of these two subregions individually as uniform as possible, while at the same time using anatomically meaningful prior information. The prior information is encoded based on the distance of the pre-computed anchor tract, which is the lowest cost path connecting two maximally spaced-out, pre-defined regions of interest of the fiber bundle of interest (in our case the cingulum bundle). Specifically, we choose p(C) as

$$p(\mathbf{x})=s_G(d(\mathbf{x})),$$ (3)

where d(x) is the distance of point x from the anchor tract and

$$s_G(r)=G_{\sigma }\ast \{\begin{array}{ll}\hfill 1\hfill & \text{for}\mid r\mid >{\mu }_{\mathit{min}}\hfill \\ \hfill \frac{1}{2}\hfill & \text{for}{\mu }_{\mathit{min}}\le \mid r\mid \le {\mu }_{\mathit{max}}\hfill \\ \hfill 0\hfill & \text{otherwise},\hfill \end{array}$$

where G_σ is a Gaussian with standard deviation σ and * is the convolution operator; μ_min and μ_max are set to the range of expected radius values. Note, that the prior could also be replaced by a probabilistic atlas. Equation (3) describes an initial zone of high fiber confidence close to the anchor tract, a transitioning region (where p(C) = 1/2) where the prior information will not be used³, and an anatomically implausible region, where the prior probability decreases to zero. The prior energy is then defined as

$$E_p(C)=\frac{1}{\mid N\mid }\left({\int }_{N_f}1-p(\mathbf{x})d\mathrm{\Omega }+{\int }_{N_b}p(\mathbf{x})d\mathrm{\Omega }\right),$$ (4)

where N_f is the region belonging to the fiber N_b is the region belonging to the background and |·| denotes cardinality, i.e., |N| is the volume of the neighborhood. Given a measure of uniformity $D:\mathcal{T}\times {\mathcal{S}}_N\mapsto {\mathbb{R}}_0^{+}$ mapping from the space of tensors and the space of neighborhood sets of tensors 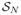∋ T(N) := {T(x) ∈ |x ∈ N} to a nonnegative real value, we write the data energy as

$$E_d(T,C)=\frac{1}{\mid N\mid }\left({\int }_{N_f}D(T(\mathbf{x}),T(N_f))d\mathrm{\Omega }+{\int }_{N_b}D(T(\mathbf{x}),T(N_b))d\mathrm{\Omega }\right),$$ (5)

where T(x) denotes a tensor at position x and T(N) denotes the set of tensors in the region N. This is an energy similar to the one proposed by Chan and Vese [4] for the segmentation of intensity images⁴. Note, however, that instead of using this energy globally to perform tensor segmentation, we are proposing to use this energy in a local neighborhood to make a local decision for a flood-fill algorithm, thus avoiding global tensor orientation issues for strongly curving fiber bundles. To minimize this energy in the discrete flood-fill setting, we simply compute the difference of the energies when adding the voxel in question to either the fiber (resulting in energy E^f) or to the background (resulting in energy E^b). The difference of these energies ΔE = E^b − E^f corresponds to a discretized gradient. Since our goal is to minimize the overall energy, a voxel x will be added to the set of fiber voxels if ΔE > 0. All integrals in Equations (4) and (5) become sums in the discretization. Many uniformity measures are possible (see for example [10, 9, 1] for some ideas on how-to compare tensors), we constructed a simple one based on fractional anisotropy and the major diffusion direction:

$$D(T(\mathbf{x}),T(N))=\frac{1}{2}\left(D_{FA}(T(\mathbf{x}),T(N))+D_{e_1}(T(\mathbf{x}),T(N))\right),$$

where

$$D_{FA}(T(\mathbf{x}),T(N))=\mid FA(T(\mathbf{x}))-\overline{FA(T(N))}\mid$$

measures the uniformity in fractional anisotropy and

$$D_{e_1}(T(\mathbf{x}),T(N))=1-\sqrt{FA(T(\mathbf{x}))\overline{FA(T(N))}}\times e_1{(T(\mathbf{x}))}^T\frac{\overline{{\lambda }_1(T(N))e_1(T(N))}}{\left|\right|{\lambda }_1(T(N))e_1(T(N))\left|\right|}$$

measures the uniformity in direction. Fractional anisotropy (FA) is defined as [3]

$$FA=\sqrt{\frac{3}{2}}\frac{\sqrt{{({\lambda }_1-{\lambda }_2)}^2+{({\lambda }_1-{\lambda }_3)}^2+{({\lambda }_2-{\lambda }_3)}^2}}{\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}$$

where e₁(T) denotes the major unit eigenvector of the tensor T, λ_i(T) its eigenvalues (with λ₁ ≥ λ₂ ≥ λ₃ ≥ 0), and the overhead bar signifies the mean⁵. D_e1 is scaled by fractional anisotropy to discard tensors that are close to being isotropic, since in these cases eigenvector computations become numerically problematic. The continuous approach could alternatively be implemented using fast marching or level sets. In this work, we use a very simple flood-fill approach which propagates away from the anchor tract. Certainly other methods would offer a more continuous and numerically accurate approach. However, our simple flood-fill implementation is sufficient as a proof-of-concept.

The algorithm proceeds in the following steps:

1. Declare all voxels on the anchor tract as fiber voxels.

2. Consider all 6-connected neighbors to the fiber voxels that are not fiber voxels themselves as candidate voxels.

3. Decide whether a candidate voxel should belong to the fiber based on the simple local energy minimization described above (where the neighborhoods N_f and N_b are given by the voxels in the current neighborhood N that already belong to the fiber or are so far classified as background respectively). If a candidate voxel should be part of the fiber according to the local energy minimization, add it as a fiber voxel.

4. Repeat from step (ii) until no more new fiber voxels are found.

Using the Bayesian framework, the outward propagating front stops once the Bayesian detection threshold is reached, i.e., once all boundary voxels are in locally minimal energy configurations.

5. Experiments

In this section, we show results of the algorithm applied to DW-MRI datasets of 51 sampling directions. We used the Finsler tractography method proposed by Melonakos et al. to compute the anchor tracts or optimal paths between two input seed regions [16]. The seed regions were manually segmented, one under the anterior tip of the ventricles and the other under the posterior tip of the ventricles.

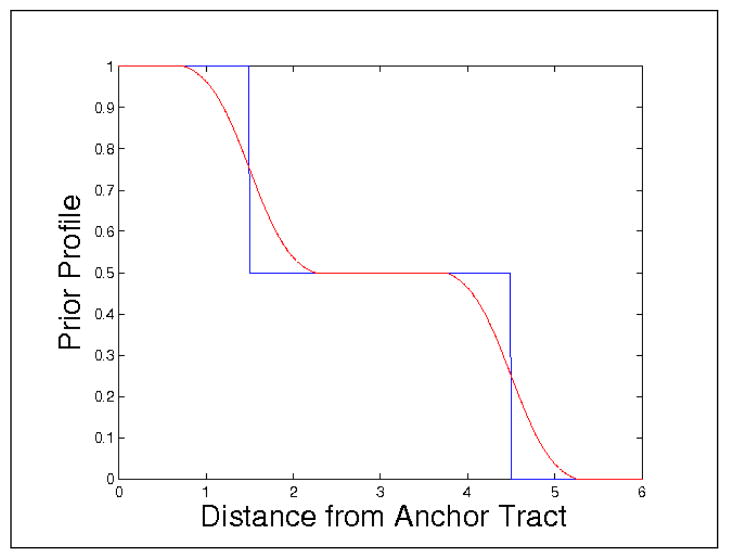
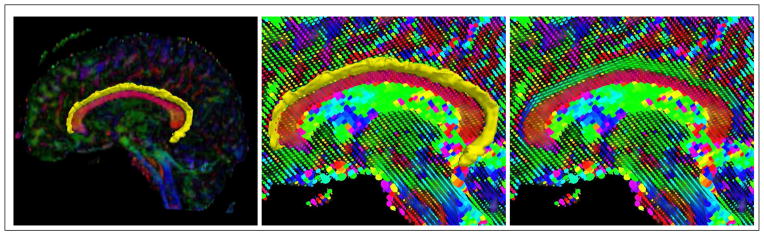
Using precomputed anchor tracts, we were able to construct our priors using the function shown in Figure 2, as previously described (mean radius r̄ = 3 mm, ${\mu }_{\mathit{min}}=\frac{1}{2}\overline{r}=1.5\text{mm},{\mu }_{\mathit{max}}=\frac{3}{2}\overline{r}=4.5\text{mm},\sigma =\frac{1}{8}\overline{r}=\frac{3}{8}$). Applying this function to a distance map from the anchor tract, the prior image is as shown on the left side of Figure 3. The white colored area is where the uniform priors are centered on the mean value of the cingulum bundle radius, which we take to be 3 mm as described in Section 3. In the middle of Figure 3, we show the likelihood energy gradient computed from the evolution (where positive values are likely to belong to the bundle and negative values are not likely to belong to the bundle). Notice how the likelihood energy function captures an appropriate boundary across a majority of the cingulum fiber bundle. The orientation dependent terms had the strongest influence on the inferior edge against the corpus callosum. The anisotropy dependent terms had the strongest influence on the superior edge. On the right side of Figure 3, we show the posterior energy gradient, which results from the combination of likelihood energy and prior energy terms.

Figure 2.

The prior profile: Blue is the initial step function, Red is the actual profile after smoothing. Note the region of uniform priors (0.5), centered around the clinically defined mean fiber radius.

Figure 3.

The prior energy (left), likelihood energy (middle), and posterior energy (right).

In Figure 4, we show a 3D model view of the resulting segmentation. Then, in Figure 5, we show three separate time steps in the flood-fill evolution. The first column is at 1 iteration, the second column is at 3 iterations, and the final column is at 18 iterations-where all three methods had converged. The top row shows the evolution using only the priors. Notice how the result is a smooth tube exactly matching the prior that is too wide for this individual and ends up overlapping proximal anatomy, such as the corpus callosum. The middle row shows the evolution using only the likelihoods. While this result appropriately captures the majority of the bundle, it is subject to a few leaks as shown. The bottom shows the evolution using the Bayesian combination of the likelihoods and priors. This result shows an appropriate combination of the likelihood boundary stopping and the prior leakage constraints.

Figure 4.

A 3D view of the result.

Figure 5.

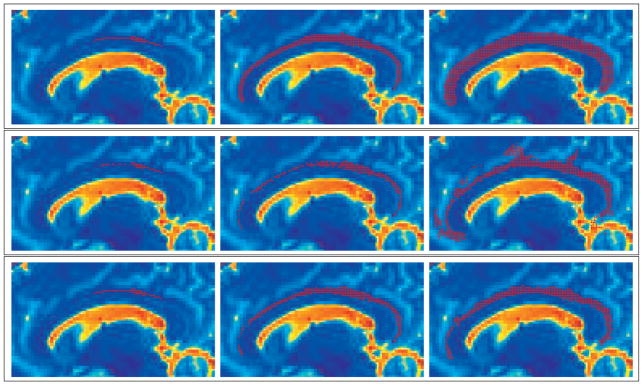
Front evolution time steps: Top Row is the evolution with only the priors. Middle Row is the evolution with only the likelihoods. Bottom Row is the evolution from the Bayesian inclusion of both the likelihoods and priors.

We also note that the few parameters used in this method can be chosen given anatomical information about the mean radius of the fiber bundle. The prior energy function is only dependent upon this parameter, as mentioned previously. Also, the neighborhood size is chosen to be large enough so that at least 20% of the neighborhoods on the first iteration include voxels exterior to the fiber bundle. In this case, we chose a neighborhood radius of 7 mm. No other parameters were needed in this computation.

6. Future Work and Conclusions

This paper proposed a novel segmentation method for diffusion tensor images. The approach is based on a Bayesian region growing, where the prior depends on the distance to a pre-computed anchor tract. The anchor tract is given by the optimal path in a Finsler metric (though any other robust method giving a representative fiber path could be used), utilizing the full diffusion profile. The likelihood is determined based on the consistency of a candidate voxel with its neighbors that are already part of the segmentation. (i.e. the likelihood is dynamically updated as the region is growing.) The Bayesian combination of likelihood and prior allows for a balanced combination of local consistency and distance from the optimal path, which also inhibits segmentation leakage. The approach is computationally efficient.

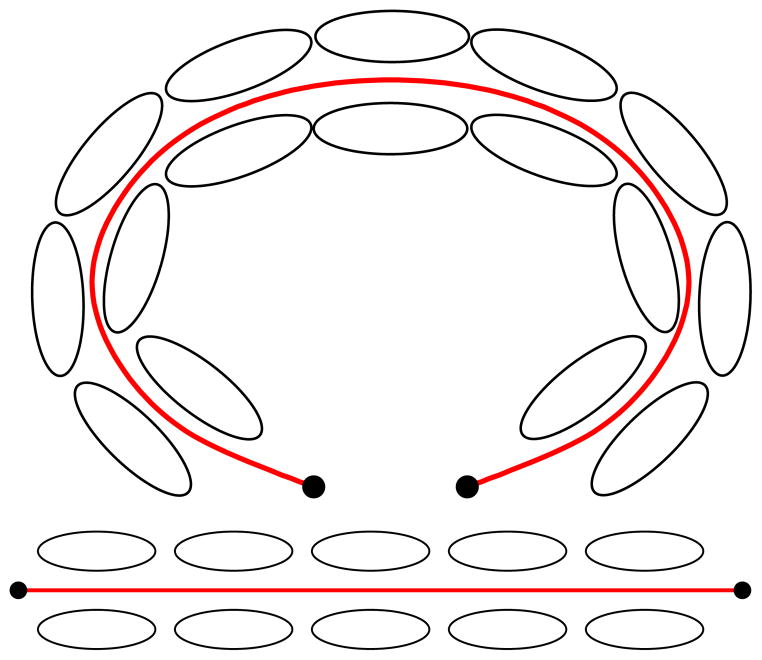
Region-based segmentation algorithms have been highly successful in segmenting uniform (in a given measure) regions. Translating this global region-based approach to diffusion weighted imaging for the segmentation of fiber bundles is challenging, since it is not obvious how to define a criterion to incorporate shape and directional information over an entire region. In particular, many fiber bundles in the brain curve strongly (e.g. the cingulum bundle, the arcuate fasciculus, the corpus callosum). Figure 6 shows some exemplary tensors aligned along an anchor tract. Warping the anchor tract to a straight line may greatly simplify the design of region-based statistics, by “flattening” the geometry to remove large-scale deformation. Further, by establishing correspondences between the anchor tract and the rest of the domain, other interesting neighborhoods may be defined. This will be the topic of future research.

Figure 6.

Tensors aligned along the anchor tract (top) and tensors aligned along the anchor tract warped to a straight line (bottom). Warping the tensors based on the geometry of the anchor tract greatly simplifies the tensor segmentation problem.

Many more extensions are conceivable, such as the use of more sophisticated distance and similarity measures. The locally-constrained method proposed as well as global region-based segmentation methods will benefit from similarity metrics using the complete tensor information. In particular, more suitable tensor-based statistics may be explored in this framework, such as those shown by Lenglet et al. [14]. Further, a continuous formulation, based on a variant of the Eikonal equation or as a complete surface evolution (with the easy possibility of directly integrating smoothing terms) will be desirable, and validations with respect to manual segmentations should be performed.