Chromatic confocal microscopy for multi-depth imaging of epithelial tissue

Abstract

We present a novel chromatic confocal microscope capable of volumetric reflectance imaging of microstructure in non-transparent tissue. Our design takes advantage of the chromatic aberration of aspheric lenses that are otherwise well corrected. Strong chromatic aberration, generated by multiple aspheres, longitudinally disperses supercontinuum light onto the sample. The backscattered light detected with a spectrometer is therefore wavelength encoded and each spectrum corresponds to a line image. This approach obviates the need for traditional axial mechanical scanning techniques that are difficult to implement for endoscopy and susceptible to motion artifact. A wavelength range of 590-775 nm yielded a >150 µm imaging depth with ~3 µm axial resolution. The system was further demonstrated by capturing volumetric images of buccal mucosa. We believe these represent the first microstructural images in non-transparent biological tissue using chromatic confocal microscopy that exhibit long imaging depth while maintaining acceptable resolution for resolving cell morphology. Miniaturization of this optical system could bring enhanced speed and accuracy to endomicroscopic in vivo volumetric imaging of epithelial tissue.

1. Introduction

Reflectance confocal microscopy (RCM) and optical coherence tomography (OCT) techniques, and combinations thereof, are the primary high resolution volumetric reflectance-based optical imaging modalities being explored for early cancer detection in epithelial tissues. These techniques can provide morphological and architectural information on the tissue, cellular, and sub-cellular scale based on elastic light scattering properties and differences in refractive index [1]. Low-coherence interferometric detection in OCT enables high axial resolution and relatively deep imaging in tissue. However, low numerical aperture (NA) lenses are typically employed, resulting in a lateral resolution insufficient for sub-cellular imaging. In contrast, the high NA objective lenses typically used in RCM enable high lateral and axial resolution for sub-cellular imaging in three dimensions. In comparison to OCT, confocal imaging has shallower penetration in tissue; however, RCM with near infrared (NIR) illumination has sufficient penetration depth for epithelial imaging [2].

RCM frame rates have approached video-rate as a result of methods to increase lateral scanning speed, including fast scanning mirrors, slit-scanning, and spectral encoding of spatial position in the lateral direction [3–5]. Volumetric imaging is typically accomplished by mechanical axial scanning of the imaging optics relative to the sample or the sample relative to the optical system. Mechanical scanning is 1) cumbersome in endoscopic systems, which generally results in larger diameter probes, and 2) time-consuming, which can lead to severe motion artifacts in reconstruction of volumetric images in living subjects. Hence, a technique to accomplish rapid nonmechanical axial scanning can potentially mitigate image degradation by motion artifact and foster more compact endoscope designs.

A promising approach is to take advantage of traditionally undesirable chromatic aberrations to generate a longitudinal line focus in the sample that is spectrally encoded in depth [6–8]. Spectrally encoding depth enables simultaneous detection of reflectance signal from all points along the line focus, thus enabling significant increases in volumetric image acquisition speed while obviating the need for mechanical axial scanning. This technique, called chromatic confocal microscopy (CCM), has been used primarily for measurement of optical thickness, topography, and stereoscopy of semiconductor and biological samples [7–10]. Lane et al. [8], presented a promising CCM microendoscope using a GRIN lens; however, images were limited to a resolution target and a microprocessor chip to demonstrate lateral resolution and optical sectioning capability. Shi et al. [11], employed a supercontinuum laser for improved illumination efficiency, but only achieved 7 µm of focal shift and only images of a transistor were presented.

Here we present our effort to design and develop a bulk optic chromatic confocal microscope. Previous CCM systems have exploited the chromatic aberrations in GRIN [8] and Fresnel [7] lenses, both of which suffer from nontrivial spherical aberrations, which limit image quality and resolution in a high-resolution imaging system. In our system, a series of plastic aspherical lenses provide sufficient chromatic shift. With this system, we have obtained the first microstructural images in non-transparent biological tissue using the prototype CCM system, successfully imaging over larger depths than some previous systems while maintaining acceptable resolution for resolving cell morphology.

2. Materials and methods

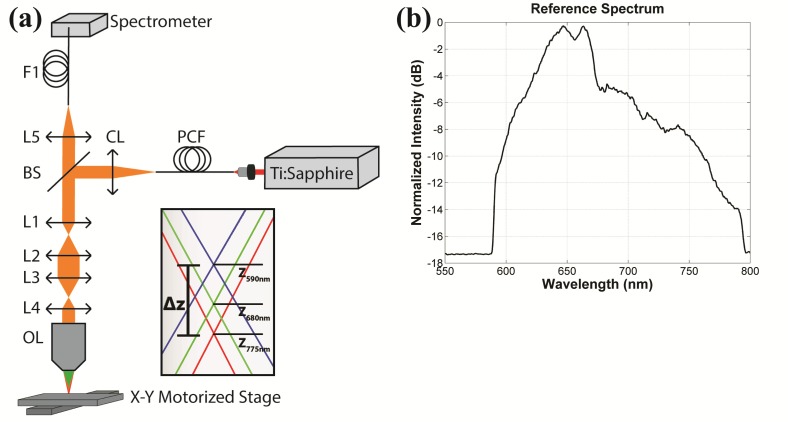
The prototype CCM system schematic is shown in Fig. 1(a). A broad spectral bandwidth source [Fig. 1(b)] is created by supercontinuum generation in a photonic crystal fiber, PCF (NL-1.8-845, Crystal Fibre), illuminated with a 140 fs Ti:Sapphire laser (Chameleon, Coherent Inc.) tuned to 800 nm. The maximum pulse energy into the PCF is 50 nJ which provides sufficient power continuously over a broad range of 590-775 nm. After the collimating lens, a 45:55 pellicle beamsplitter (CM1-BP145B2, Thorlabs) reflects the broad bandwidth light into the optical imaging path.

Fig. 1.

(a) Schematic of the chromatic confocal microscope. PCF: photonic crystal fiber supercontinuum source; CL: collimating lens; BS: beam splitter; L1, L2, L3, and L4: aspheric lenses; OL: objective lens; L5: detection lens; F1: detection fiber. Inset shows a generic chromatic focal shift for any beam focus within the lens system. (b) Reference spectrum of the supercontinuum source measured by the spectrometer through the optical system.

Using ZEMAX software to model the chromatic dispersion, the optical design was optimized for maximum chromatic shift using commercially available lenses. Two sets of relay lenses expand the beam to fill the back aperture of the objective lens and contribute to the chromatic aberration. The two relays consist of four aspheric lenses, L1 (f = 8 mm; A240TM-B, Thorlabs), L2 (f = 17.5 mm; NT66-020, Edmund Optics), L3 (f = 40 mm; NT66-024, Edmund Optics), and L4 (f = 20 mm; NT66-021, Edmund Optics). Aspheres are well corrected for spherical aberration, but exhibit strong longitudinal chromatic aberration. The dispersion of the lenses is characterized by the Abbe number of the lens material, where lower Abbe numbers translate to stronger dispersion. L1 is made from S-LAL13 glass, Abbe number 53.2, and L2-L4 are made from Zeonex E48R plastic, Abbe number 51.66. A well-corrected, water immersion 40 × 0.8 NA lens (CFI Apo 40XW NIR, Nikon) is used as the objective. This lens should not add significant aberrations (desired or otherwise) to the system. Each wavelength is focused to a different relative position in the object determined by the dispersion and magnification of the preceding lenses, illustrated in Fig. 1(a). Based on the ZEMAX model, the chromatic focal shift, Δz in Fig. 1(a), for the 590-775 nm wavelength range, at the beam focus between L1 and L2 is 98 µm. After passing through L2 and L3, Δz at the beam focus between L3 and L4 is 1.939 mm. Although the ZEMAX lens data is not available for the Nikon objective lens, we model the longitudinal magnification of the objective using a simple lens with the same focal length, 5 mm, and then, assuming no chromatic aberration in the objective, remove the chromatic shift associated with that simple lens to estimate the chromatic focal shift of the total lens system. We estimate approximately 159 µm chromatic focal shift in the object for the 590-775 nm wavelength range.

Since the lens system obeys the principle of reversibility, the reflectance signal from each focal point in the object is recombined into a single collimated beam before the beam splitter. The detection lens, L5 (f = 100 mm; AC254-100-A-ML, Thorlabs), couples the light into the detection fiber F1 (P2-2000-PCSMA-1, Thorlabs), with a core diameter of 11 ± 1 µm. The detection lens and fiber are designed to be a fairly typical confocal spatial filter by making the spot size and fiber core diameter approximately equal. A commercial spectrometer (USB4000, Ocean Optics) captures the spectrum of the reflectance signal directly from the detection fiber, which corresponds to an A-scan, or axial depth scan. Three dimensional volumetric images are acquired by two dimensional raster scanning of the sample using a pair of X-Y mounted motorized stages (T-LSM, Zaber, Inc). The collected volume was normalized to the reference spectrum. To reduce the file size, the spectral data was resampled from 0.19 nm/pixel to 0.95 nm/pixel by window averaging every 5 samples in wavelength; this results in an average pixel size of 1 µm in the axial direction. The resolution is not affected by the reduction of the sample size since the optical resolution is oversampled in the spectrometer.

In CCM, the range of wavelengths results in a number of factors affecting the wavelength-dependent resolution, including objective lens NA, focused spot size on the fiber core, fiber V parameter, and spectral resolution of the spectrometer. Additionally, changes in the fiber V parameter affect mode excitation and fiber coupling. The axial optical point spread function in the sample space [oPSF(λ)] of CCMs has been modeled for finite pinhole sizes and for single-mode fibers as detection apertures [12,13]. Based on the range of fiber V parameter over the bandwidth, we estimate between 14 and 26 modes are excited in the fiber; therefore, we use the finite pinhole model.

The theoretical axial point spread function of a CCM is calculated by modeling the detected intensity [14],

$$I(u)={\displaystyle {\int }_0^{v_p}{\left|{\displaystyle {\int }_0^{1}P(\rho )\exp (ju{\rho }^2)J_0(v\rho )\rho \text{d}\rho }\right|}^2}v\text{d}v$$ (1)

as a function of the normalized optical units,

$$u=\frac{2\pi }{\lambda }\frac{N{A}^2}{n}z$$ (2)

$$v=\frac{2\pi }{\lambda }NAr$$ (3)

where P(ρ) is the pupil function of the objective, v_p is the pinhole radius in normalized units, λ is wavelength, NA is the objective numerical aperture, n is the refractive index of the immersion medium, and z and r are the real axial and radial optical coordinates, respectively. The CCM detector is a spectrometer which has a resolution in part defined by the optical point spread function on the line detector, sPSF(λ). Since the axial space is encoded in the spectral domain, the sPSF of the spectrometer contributes to the width of the measured axial point spread function PSF(λ). Assuming a perfect detector, the PSF(λ) measured at the spectrometer is therefore the convolution of the oPSF(λ) and the sPSF(λ) determined by the spectrometer’s optics, i.e.

$$PSF(\lambda )=oPSF(\lambda )\otimes sPSF(\lambda )$$ (4)

As wavelength increases, the normalized pinhole, v_p, decreases and optical sectioning is enhanced (i.e. smaller oPSF), since the spot in the detector plane grows larger compared to the fiber core. In opposition, longer wavelengths yield a larger oPSF in the object (sample) space. In the wavelength range where the spot size is smaller than the pinhole, the FWHM plot as a function of wavelength exhibits a low amplitude oscillating pattern [12]. The slight decrease in NA increases the oPSF for longer wavelengths; however, the effect is negligible for small focal shifts.

Using the design NA of the objective (0.8 in water) to estimate the axial resolution of the CCM, the resulting theoretical axial full-width half-maximum (FWHM) of the oPSF varies from 1.13 to 1.43 µm over the 590-775 nm wavelength range, respectively. The sPSF is approximated by a Gaussian function with a FWHM (given from specifications) of 1.5 nm. The oPSF is converted to wavelength using the measured dispersion curve (Eq. (5)), convoluted with the sPSF, and the resulting PSF is converted back to axial coordinates using Eq. (5). The convolution of the oPSF with the sPSF yields a theoretical FWHM of the total PSF ranging from 2.17 to 1.57 µm over the 590-775 nm range, respectively. The spreading effect from the sPSF affects the shorter wavelengths more strongly since the dispersion is much stronger in this range.

The axial resolution as a function of wavelength was experimentally measured by translating a mirror through the foci of the CCM system and recording spectra as a function of axial position of the mirror. This data also served to measure chromatic shift over the full spectrum of the system and was used to normalize subsequent spectra.

To evaluate imaging of non-transparent tissue, a thick tissue sample of porcine buccal mucosa was imaged ex vivo. The tissue was immersed in acetic acid for 30 seconds to enhance backscattering from cell nuclei [15]. 500x500x157 µm³ volumes were captured using a 1 µm lateral sampling interval and 7 ms integration time. The lateral direction is intentionally undersampled to improve speed and reduce memory requirements. Images were compared to traditional reflectance confocal images acquired with a Lucid Vivascope 2500 confocal microscope with 830 nm illumination wavelength, 0.9 NA, and <2.0 µm lateral and <5.0 µm axial resolution.

3. Results

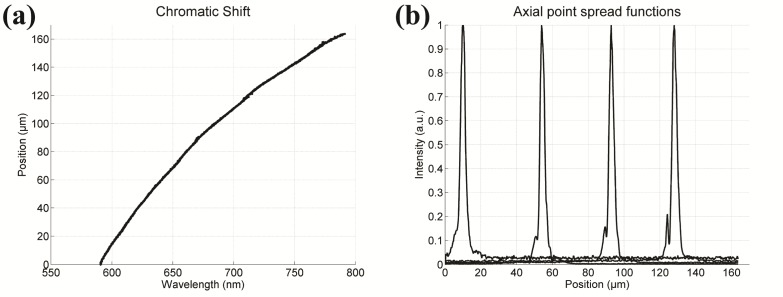
In order to evaluate the performance of the imaging system, we translated a mirror through the foci and recorded the spectra as a function of axial position of the mirror. The chromatic focal shift [Fig. 2(a)] is plotted by finding the peak intensity wavelength for each axial position. Over the 590-775 nm wavelength range, the foci span a depth range of 157 µm, which corresponds well with our optical model. A quadratic fit (R² = 0.999) to the experimental measurements yielded a calibration curve to convert wavelength in µm to relative axial position in µm,

$$z(\lambda )=-2213{\lambda }^2+3850\lambda -1498.045$$ (5)

where z = 0 µm represents the shortest focal position, at λ ≈590 nm. The signal versus mirror position can be plotted to show the axial PSF for each wavelength. Figure 2(b) shows the axial PSF for four wavelengths. Over the entire wavelength range of 590-775 nm, the average measured FWHM axial resolution was 3.1 µm; however, the value varies irregularly between 2.0 to 4.4 µm due to the multifarious wavelength dependence of axial resolution discussed in the Methods. The lateral resolution was obtained by imaging a Ronchi grating with the center wavelength and measuring the edge resolution (10%-90%). The pixel size of the grating image was set to oversample a Ronchi edge at 0.17 µm/pixel. The measured lateral resolution is 0.7 µm, whereas the theoretical lateral resolution, based on the Rayleigh criterion, is 0.5 µm.

Fig. 2.

(a) The chromatic shift shows the relative focus for each wavelength. The total shift is 157 µm over a 185 nm range. (b) Four axial PSFs are shown at 10, 50, 90, and 130 µm depth at wavelengths of 595, 635, 675, and 725 nm, respectively. The peak of each PSF corresponds to a single wavelength which is converted to relative depth using a calibration curve. The FWHM from left to right is 3.2, 2.9, 3.1, and 3.1 µm.

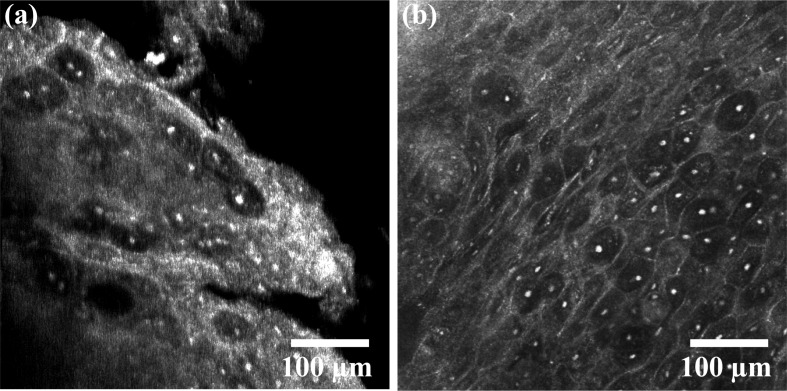
The porcine buccal mucosa volumes demonstrate the ability to resolve cellular features. A video from a shallow depth in the tissue (~0-150 µm) is shown from the CCM volume [Fig. 3(a), Media 1 ^{(6.3MB, AVI)} ] with an image captured with the commercial confocal microscope of a similar region [Fig. 3(b)]. Figure 4(a) (Media 2 ^{(8.8MB, AVI)} ) is a video captured from a CCM volume deeper in the tissue (~100-250 µm). Basal cell nuclei, which are more crowded than superficial cell nuclei, can be seen in the video. Figure 4(b) shows an image of a similar region in depth taken with the commercial confocal microscope. To find the absolute depth in tissue with the Vivascope, a slide is used as an axial reference point in the inverted microscope. In the CCM system, the tissue surface is the only reference point. Since imaging speed is slow in this CCM system, finding the absolute depth in tissue at which to begin imaging was done by acquiring A-scans in time (M-scans) then adjusting the stage so that signal begins at the shallowest point in the depth scan. This method was unreliable and, as a consequence, imaging required multiple trials. For imaging where the shallowest depth was within the tissue, the z-stage was adjusted such that the absolute depth was known with an accuracy of ~10 μm. In this case, the absolute depth is only known at the starting point since the tissue surface topology is not known. The depths of the images in Figs. 3(a) and 4(a) were therefore estimated based on apparent morphology compared with images at known depths from the Vivascope microscope. The contrast of Figs. 4(a) and 4(b) was enhanced for viewing on print.

Fig. 3.

(a) CCM video (Media 1 ^{(6.3MB, AVI)} ) of porcine buccal mucosa compared with (b) an image of the same tissue from the Lucid Vivascope confocal microscope.

Fig. 4.

(a) CCM video (Media 2 ^{(8.8MB, AVI)} ) of the basal layer of porcine buccal mucosa. (b) The same cell morphology can be seen in an image taken with the Lucid Vivascope confocal microscope.

4. Discussion

As noted above [see Fig. 2(b)] the measured PSF has a FWHM of 3.1 μm at 650 nm. Without considering the spectrometer optics the axial FWHM at 650 nm is 1.21 µm; however, the limited spectral resolution of our spectrometer yields a 1.90 µm theoretical axial FWHM. This result is in better agreement with our measurement and demonstrates the influence of spectral resolution on the axial resolution in our system. From an inspection of the PSFs in Fig. 2(b) it is clear from the asymmetry that there is uncorrected aberration in the microscope and/or spectrometer optics which is the likely source of most of the residual difference between measured and calculated resolution. The shoulders on the PSFs can also contribute to reduced contrast in the image.

The porcine buccal mucosa volumes presented here demonstrate the capability of the described chromatic confocal microscope to image epithelial tissue with sufficient spatial resolution and chromatic shift to resolve cell nuclei over multiple cell layers. The cellular features resolvable in single-depth CCM images in Figs. 3(a) and 4(a) obtained from three dimensional data sets are comparable to those obtained by a commercial reflectance confocal microscope that uses traditional single-depth imaging without chromatic aberration [Figs. 3(b) and 4(b)]. While traditional confocal microscopes require physical translation of the sample or objective lens to acquire data in depth, the CCM captures confocal reflectance data over the 157 µm depth range of the chromatic shift in a single shot. The spectral encoding of depth is decoded using a spectrometer. Although relatively simple changes are made to a reflectance confocal microscope to achieve depth encoding, the same changes cannot be applied to one-photon fluorescence confocal microscopes due to the Stokes shift of the fluorescence emission. The emission spectra of fluorophores are independent of excitation wavelength; therefore, all depth-to-wavelength codification is lost and emission light would be spatially filtered out by the confocal pinhole. In contrast, chromatic axial scanning has been applied to transmission second harmonic imaging and demonstrated over an 8 µm axial scan range using ~8 nm second harmonic wavelength range [16]. Additionally, one-photon fluorescence imaging has been achieved using spectral encoded imaging by correlating temporal signal with a wavelength-swept source [17]; however, this system is not confocal and therefore not optimized for thick turbid samples.

Ideally, the chromatic focal shift at the sample would span up to 300 µm, which would cover the full epithelium and the full range of imaging depth with NIR RCM in most epithelial tissues. For shorter wavelengths, penetration depth is limited; however, dispersion from refracting optics focuses shorter wavelengths to shallower depths. Extending the spectral range of our source further into the NIR wavelengths will reduce scattering and improve penetration depth but will not yield significant chromatic focal shift due to flattening of the dispersion curve. The effect can be seen at longer wavelengths in the chromatic shift curve in Fig. 2(a). If a custom lens is designed for this application, lens material with stronger dispersion in the NIR range could provide the necessary chromatic shift. Using hyperchromat theory in the lens design [18] could also increase chromatic dispersion as well as linearize the focal shift. Hyperchromats are not currently used due to limited selection of commercially available sizes and focal lengths. Magnification is an important factor when optimizing chromatic shift. Typically the objective demagnifies a chromatic shift from back aperture to the focal plane. If the magnification from source to sample is increased (less demagnification), the chromatic shift will be greater. However, the beam size in the Fourier plane of the objective is reduced, decreasing numerical aperture and therefore diminishing resolution. Designing a custom objective would allow better control over optimization of numerical aperture and magnification.

Increasing dispersion to gain chromatic shift also places more demands on the detection spectrometer. The axial point spread function (PSF) remains constant in space; hence an increase in dispersion results in a decrease in the spectral width of the PSF and a concomitant increase in the required spectral resolution. This is evident in the performance of our current system and is considered in our theoretical axial FWHM calculations above. Going forward, the development of a custom spectrometer with optimized resolution for the designed chromatic dispersion with well corrected optics will be key to realizing the full potential of the CCM system.

In principle, the CCM technique can enable high speed volumetric imaging; however, the current prototype is limited by the translation stages used for x,y scanning and the slow read-out time (7.5 ms) and optical inefficiency of the commercial spectrometer detector. Currently, a 500x500 µm² x,y scan at 1 µm sampling interval can take up to 30 minutes. Slow scanning speed can readily be addressed by incorporating more traditional galvo mirror based x,y scanning. Likewise, a custom built efficient spectrometer incorporating a high-speed line scan camera with the appropriate spectral resolution would address the limitations of our current spectrometer.

We can estimate the ultimate imaging speed of our CCM system by making a few reasonable assumptions about our system and sample. We will define the limit of detection as the power at which the signal to noise ratio (SNR) is equal to one. The power that reaches the detector is determined by the losses in the system, the power incident on the sample, and the reflectivity of the sample. The losses in the system can be estimated based on our current CCM system and replacing the spectrometer with a high efficiency design; the loss from the optics and pinhole results in approximately 4.5% transmission, so a spectrometer with a grating efficiency of 80% would bring the total efficiency to 3.5%. The maximum power incident on the sample is determined by the ANSI maximum permissible exposure (MPE) [19]. The MPE is a function of the dwell time on the sample or the number of pixels times the sum of the integration and read-out times. The maximum SNR can then be defined as (modified from [20]),

$$SNR=\frac{\frac{\text{MPE}}{p_{x}E}QFR}{{\left(\frac{\text{MPE}}{p_{x}E}QFR+n_d^2+n_r^2\right)}^{1/2}}$$ (6)

where Q is quantum efficiency, F is the efficiency of the system, R is the reflectivity of the sample, p_x is the number of pixels in an image, E is the energy of a photon, n_d is the dark noise, n_r is the readout noise, and

$$\text{MPE}=1.1A{(p_x{t}_p)}^{0.25}\left[J\right]$$ (7)

where A is the area of the limiting aperture (3.5mm diameter for skin), and t_p is integration time. Equation (7) assumes we will not image an area larger than the limiting aperture and that there is only one exposure, repeated exposures would have a lower MPE. At low light levels and low integration times, readout noise is the main source of noise; therefore, the SNR can be simplified to

$$SNR=\text{MPE}\frac{QFR}{p_{x}E{n}_r}$$ (8)

We can then solve for R assuming a limit of detection of SNR = 1 and define this quantity as the noise equivalent reflectivity (NER). If we assume a commercial linear CCD array (E2V, AVIIVA EM4) with 210 kHz line rate, a quantum efficiency of 0.8, and a readout noise of ~50 e^- RMS, we can calculate the NER. Given an image size of 500x500 px² and 600 nm wavelength light, the NER would be ~5x10⁻⁷. Cell nuclei have a reflectivity between 10⁻⁴-10⁻⁶ [20], well above the NER. When the reflectivity is much higher than the NER, shot noise becomes important and Eq. (6) is more appropriate. Under these conditions we could collect a 500x500 px² volume in 1.2s.

5. Conclusion

In summary, we have developed a CCM that utilizes a supercontinuum source, incorporates aspheric lenses for chromatic dispersion, and utilizes spectroscopic detection to simultaneously capture reflectance confocal signal over a 157 μm axial range in tissue. Volumetric images of cells in pig oral epithelium are presented. Although the current imaging speed is slow, straightforward improvements in the experimental design can decrease imaging time to less than 2 seconds per volume. The ability to capture volumetric reflectance confocal imaging data without mechanical axial scanning is attractive for clinical endoscopy applications due to the reduced complexity in the endoscope and a reduced susceptibility to motion artifact. Most current confocal endoscope designs either only collect 2-D images or utilize relatively slow axial scanning mechanisms.