Evidence for trapped surface bubbles as the cause for the twinkling artifact in ultrasound imaging

Abstract

The mechanism of the twinkling artifact (TA) that occurs during Doppler ultrasound imaging of kidney stones was investigated. The TA expresses itself in Doppler images as time-varying color. To quantitatively define the TA, beamforming and Doppler processing were performed on raw per-channel radio-frequency (RF) data collected when imaging human kidney stones in vitro. Suppression of twinkling by an ensemble of computer generated replicas of a single RF received signal demonstrated that the TA arises from variability among the acoustic signals and not from electronic signal capture or processing. This variability was found to be random. Its suppression by elevated static pressure and return when the pressure was released suggest the presence of bubbles on the stone surface is the mechanism that gives rise to the TA.

Introduction

The twinkling artifact (TA) (Rahmouni et al. 1996) appears as a dynamic color mosaic on the image of hard objects in a color-Doppler ultrasound display. Recent studies (Vasiliev and Gromov 1997; Aytac and Ozcan 1999; Lee et al. 2001; Trillaud et al. 2001; Gromov and Zykin 2002; Turrin et al. 2007; Mitterberger et al. 2009; Shabana et al. 2009; Kim et al. 2010; Winkel et al. 2012) have reported that the TA, as a Doppler ultrasound artifact has a great potential to improve kidney stone detection. However, this artifact is inconsistent precisely because its origins are unknown: Its manifestation depends on the specific ultrasound imager, the sonographer skills, the machine parameter settings, and the type of stone. Our goal is to improve the understanding of the mechanism(s) that give rise to the TA as a step toward making the TA a reliable clinical tool.

Several studies have investigated the mechanism of the TA displayed by kidney stones. The sources of the artifact were attributed either “to the acoustics” or “to the machine”, i.e., to peculiarities either of ultrasound scattering from the stone or in the system processing of the unique scattered signal. In one study of the acoustics, the TA was explained as a result of the random scattering of the ultrasound beam at multiple reflectors associated with the rough interface typical for the stones (Rahmouni et al. 1996). A study of the TA from different types of stones showed that the intensity/character of the TA might depend on the morphology and biochemical content of stones (Chelfouh et al. 1998). A more recent study showed that the strength of the twinkling is color-Doppler carrier frequency dependent (Gao et al. 2012). Other investigators believe that the appearance of the TA is determined by the ultrasound machine or machine settings, such as the scan type, technical parameters, gain, and scan settings (Aytac and Ozcan 1999; Lelyuk et al. 2003; Rubaltelli et al. 2000). One of the more recent mechanism studies has suggested that the cause for the artifact is narrow-band internal noise due to “phase jitter”, and the irregular stone surface is only secondary and only serves for broadening the spectrum (Kamaya et al. 2003). However, they also concluded that “experiments were limited by the inability to control all machine settings separately”, which leaves many steps in their outline unexplained.

For most of the studies listed above, the conclusions were drawn based on analyzing the Doppler images and Doppler spectrum that were generated by commercial ultrasound machines. Those images may vary between machines, depending on the imaging processing methods employed and different machine settings. The commercial ultrasound machines are “black boxes” in that it is very difficult to separate the acoustical effects (i.e., scattering from a rough surface, stone reverberation, etc.) from the effects of the machine (i.e., phase jitter, machine settings and signal processing, etc.). In addition, clinical ultrasound machines rarely provide users access to the raw radio-frequency (RF) data that are more fundamental than the images, since the raw per-channel RF signals originate directly from the ultrasound array elements, i.e., are not distorted by any post-processing from the machine.

In this study, the raw per-channel RF data immediately following the analog-to-digital converter (ADC) were used. According to the conventional color Doppler imaging algorithm (Evans and McDicken 2000), the color pixels shown on the image are always encoded based on the variability within the Doppler ensemble that corresponds to strong Doppler power. Bearing that in mind, the Doppler power was used as the criterion of the TA. Based on the RF data analysis, the dominant reason for the occurrence of the TA was investigated by estimating whether the variability within the Doppler ensemble is introduced from the acoustic field or from the machine; in addition, a high static pressure study and other studies were performed to further investigate the mechanism(s) for the generation of the TA.

Materials and Methods

Rationale for the chosen materials and methods

The experiments were preceded by many observations not reported here of the distinct features of the twinkling artifact in vivo and in vitro. Although the TA is frequently seen when imaging stones in patients, it was important for the mechanistic study to mimic the clinical situation in vitro, for which the stone position and medium around it could be controlled. In order that the in vitro conditions would be close to the in vivo ones and no patterns of difference between the raw signals from both were detected, real human kidney stones were used as imaged objects. The stones were either embedded in a degassed gel block, or were held fixed in degassed water. Several stones under study that showed twinkling with the Verasonics Ultrasound Engine (VUE) used in the studies reported here were additionally imaged by other ultrasound machines, namely ATL-Philips HDI 5000 and Ultrasonix RP, which also showed the TA. Although the details of the stone images were not identical, there are also undefined differences in signal processing and image formation in different ultrasound machines. The fact that the VUE showed the TA to be similar to that produced in other machines supported the choice of the VUE as the main experimental tool (an open architecture ultrasound imager). To make clearer the rationale for the performed experiments, we mention in this section, in advance, some results. The first fundamental question to answer was as follows: What is the primary cause of the TA; namely, is it the acoustics (i.e., the ultrasound propagation and scattering) or the machine (i.e., the electronics of the transmitter/receiver and the Doppler signal processing)? The answer (it is the acoustics) was obtained by examining the machine aspect with a stable signal from a function generator that mimicked the signals originated from ultrasound scattering; thus, we removed the potential pulse-to-pulse variability. The next logical step was to investigate the acoustic origin of the TA: It was determined that the signal variability was uniformly distributed within the Doppler pulse ensemble. Since the origin of the TA was thus in the acoustics, bubbles, as random scatterers, were a reasonable mechanism to investigate. Of course, other causes, e.g., speckle noise due to the rough surface of a stone, could also play a role. To test the bubble hypothesis, a special chamber was built that allowed imaging of the stones under elevated static pressure. The application of sufficient overpressure should collapse any bubbles present on the stone surface, and thus suppress the twinkling artifact — which it did. To further confirm this rather surprising observation, scratches, which would harbor bubbles, were created in smooth plastic stone models. These scratched models displayed the TA, while their smooth predecessors did not. It was also discovered that immersing the stones in ethanol, which would modify the bubble-stabilization mechanism, and thus reduce the size and number of surface bubbles (Crum 1979, 1982), also suppressed the TA. Therefore, the experiments of the current study consisted of multiple steps, and different physical and signal processing tools were used. These are described in more detail below.

Platform

A Verasonics Ultrasound Engine (VUE, Verasonics, Redmond, WA) and a 128-element linear ultrasound array with 5 MHz central frequency (a clinical probe ATL/Philips HDI L7-4, Bothell, WA, US) were used for all experiments. The pressure waveform radiated from the transducer was measured by a broadband calibrated hydrophone (HGL0085, ONDA, US) having sensitivity 48 nV/Pa at 5 MHz. The acoustic pulse was similar to the transducer voltage, i.e., it had the form of a 3-cycle tone burst with the central frequency 5 MHz. At the location 4 cm away from the transducer in water the measured peak positive and negative pressures were, correspondingly, P₊ ≈2 MPa and P₋≈ −1 MPa; knowing these values was important in choosing a sufficiently high level of the static pressure in the overpressure test (see below). The imaging was performed in “flash” transmitting mode when all the array elements were excited simultaneously to emit a quasi-plane wave in the direction orthogonal to the radiating surface (zero degrees incident angle); such a mode simplified the analysis of the received signals without limiting the possibility of stone imaging. Both B mode and Doppler mode were employed. In the Doppler mode (that showed the TA) the array elements were excited by a series of 14 identical pulses emitted one-after-another with 3 kHz pulse-repetition frequency (PRF), which is typical to Doppler regimes of conventional ultrasound machines. The PRF could be changed; the value of 3 kHz was used because it was a default setting for the machine. Each pulse in the aforementioned 14-pulse Doppler ensemble was a tone burst consisting of 3 cycles at the central frequency 5 MHz. As in conventional ultrasound imagers, the scattered acoustic signals were received by the same array. The corresponding electrical signals of the array elements went through an anti-aliasing band-pass filter of 0.7–17 MHz bandwidth, an amplifier with the time-gain compensating feature (TGC), clipping diode (to limit excessive signals), and finally were sampled at 20 MHz frequency by a 12-bit analog-to-digital convertor (ADC). The digitized signals were then processed in MatLab either by the VUE software or by a separate in-house code written in MatLab. The signals could be processed either in real time or be stored in a buffer and post-processed later. The saved signals were radio-frequency (RF) data from the output of ADCs of each channel. Access to these RF data provides a possibility to study the “raw” ultrasound signals associated with the TA.

To test the response of the receiving electronic tract and signal processing of typical Doppler signals without using the ultrasound probe, a special break-out board was connected to the entrance of the electronic tract, which enabled sending, to any selected receiving channel, an electric signal from an external source. In particular, such a source could provide an electric signal similar to that appearing at the array element when receiving an ultrasound pulse scattered from a stone. Such a replacement of acoustically-originated signal by a controlled-source signal allowed us to determine if the TA originated in the machine (i.e., in the electronic tract and signal-processing box) independently from whether the TA originated in the acoustics (i.e., from fluctuations during acoustic scattering and propagation). As an external voltage source, a function generator (AFG 3022B, Tektronix, OR) was used. The generator signal was programmed to be identical to the acoustically originated signal as detailed below.

Signal processing

B-mode images combined with Doppler-mode images were prepared by employing the signal processing internal algorithms provided by the Verasonics (Daigle 2011). In doing so, the Doppler threshold, which accepts the color information for a certain sample volume based on the comparison of the corresponding Doppler power of the sample volume to a certain percentage of the maximum Doppler power was decreased to the minimum possible level, i.e., it was set just above the level of the appearance of the background noise. The color-write priority was set to the highest level that the color information rather than the B-mode information was always plotted on the screen. In the experiments where the raw signals were analyzed to reveal the origin of the TA, the signal processing was performed using in-house MatLab codes. In particular, such characteristics as the Doppler residual and Doppler power were calculated to correlate them with the TA. Because those parameters will be used in the consequent sections, they are described below in some detail.

Consider N pulses U_n (t), n = 1, 2, …, N, which represent an ensemble of signals received from one of the elements of the ultrasound probe in the course of Doppler imaging. The pulses follow each other with the PRF. In the VUE, the default Doppler ensemble consists of 14 pulses. However, the first two pulses are omitted to avoid possible unrepeatable tissue reverberation; therefore, N =12 is used. The Doppler shift can be measured by comparing signals U_n (t − nT) for different n, where T =1/PRF is the ensemble period. When those signals are identical, no Doppler shift appears. Any differences between the signals would signify that the scatterer is changing from pulse to pulse. For example, the signals U_n (t − nT) for different n would arrive at different times if such a scatterer moved with a certain velocity. The velocity can be calculated from the time shift, which is one of the methods for the velocity estimation in the Doppler mode. If the signals U_n (t) are not only delayed/advanced but fluctuate in a more general manner, then the Doppler processing would also provide some velocity, but it will not necessarily be related to true scatterer movement, i.e., the corresponding Doppler signal would be an artifact. The twinkling artifact is one of such signals.

Although Doppler processing is a well-known procedure, it can be realized in several alternative ways. To clarify the TA analysis of the current study, below the Doppler processing is described as it was implemented in the in-house algorithm. After ADC, the signals U_n (t) are transformed to a digital form

$$U_{nm}=U_n(t_m=m\mathrm{\Delta }t),$$ (Eq #1)

where Δt is the signal sampling step (50 ns for our 20 MHz sampling frequency), m = 1, 2, … M, M is the total number of samples recorded in one period of the Doppler ensemble. In the reported experiment, M =1024. In addition to analysis of received signals from the individual elements of the array, beamformed signals were calculated and processed for each channel. Such signals were formed by the conventional “delay-and-sum” beamforming method. Let U_nm be the digitized signal for either non-beamformed or beamformed single channel data. The first step in the signal processing of the channel data was the calculation of the quadrature components of the signals U_nm using the Hilbert transform. The transform was made in MatLab by the corresponding tool V = hilbert (U). As a result, for each n, a complex (“analytic”) signal

$$V_{nm}=U_{nm}+{iQ}_{nm}$$ (Eq #2)

was calculated, where the quadrature signal Q_nm is the Hilbert transform of U_nm, and i is the imaginary unit. The next step was “wall-filtering” that reduced the signal fluctuations due to possible slow-moving scatterers. For that, the 1^st order regression filter was applied to the analytic signal V_nm. Specifically, for each fast time-moment m, the corresponding signals from different pulses within the Doppler ensemble were considered as a function of the pulse number n, and a linear fit

$${\overline{V}}_{nm}=a_m+n{b}_m$$ (Eq #3)

was found for V_nm using the least squares estimation (here a_m and b_m are some coefficients that do not depend on the pulse number n ). Then the residual signal

$${\stackrel{\sim }{V}}_{nm}=V_{nm}-{\overline{V}}_{nm}$$ (Eq #4)

is wall-filtered signal. The absolute value of that signal, the residual amplitude

$$A_{nm}=\left|{\stackrel{\sim }{V}}_{nm}\right|,$$ (Eq #5)

can be used to represent the signal fluctuations within the Doppler ensemble. The average power

$$W_m=\frac{1}{N}\sum _{n=1}^N{\left|{\stackrel{\sim }{V}}_{nm}\right|}^2$$ (Eq #6)

provides the strength of the fluctuations at the moment of time t_m = mΔt and is usually called the Doppler power.

As the TA is a fluctuating (i.e., random) phenomenon, additional averaging both in time and space would give a more representative description for the effect. This averaging can be done in a way mimicking what the sonographer does when observing the twinkling color around the stone image. The following procedure was developed for such a characterization. (1) The RF data was used to calculate the beamformed channel data using a conventional sum-and-delay algorithm. (2) One pulse of the Doppler ensemble of each channel was used to build the B-mode image of the stone. The stone contour was defined based on the brightness of the image, and the total number of pixels, N_total, within this contour was counted. (3) The Doppler power traces W_m were calculated for all the beamformed channels, so that the Doppler power was found for each pixel of the B-mode image. (4) The background noise level was defined as the average of the Doppler powers over all pixels in the entire image. (5) If the Doppler power exceeded the background noise level by more than 6 dB, the corresponding pixel was counted as a “color pixel”. (6) The number of color pixels, N_color, was counted within the stone contour, and the color percentage was calculated for the twinkling image of the stone under study:

$$C=\frac{N_{\mathit{color}}}{N_{\mathit{total}}}\times 100\%$$ (Eq #7)

The value of N_total for each imaged stone was a constant number, but the N_color varied from frame to frame, so the color percentage C was also fluctuating from frame to frame. To analyze the difference of some two cases (e.g., images of the same stone under different static pressures) the mean value of C was calculated in those cases by averaging over 100 frames, and the comparison was made using Student’s t-test with the p<0.05 criterion for the decision whether the two mean values were statistically different.

Experimental Targets

Human kidney stones from a stone laboratory (Beck labs, Indianapolis, IN) that consisted of more than 90% calcium oxalate monohydrate (COM) were used for the majority of the experiments. The stones were 5-12 mm in diameter. In total, 18 of such stones were used. Half of them (9) were imaged while embedded in a tissue-mimicking gel; the other 9 stones were held on a metal needle and imaged directly in degassed water. Gel was used in order to better mimic the stone surroundings in vivo. The ultrasound absorption coefficient of gel was similar to tissue (see below). However, no obvious differences were observed in the TA manifestation between the stones in gel and in water, so several experiments (in particular, the overpressure tests) were made directly in water. In those cases the stones were immersed in the degassed water for over 48 hours prior to imaging.

The tissue-mimicking gel used in a part of the experiments was a polyacrylamide hydrogel (Sigma-Aldrich, US). The liquid mixture was first degassed for at least one hour in a desiccant chamber. Then it was poured into a plastic container of W×L×H=10×10×13 cm dimensions to 6 cm height, and a polymerization agent was added. When it was set, the studied kidney stones, which were previously immersed in degassed water for 48 hours, were placed on the concretionary gel surface, and another portion of degassed liquid mixture was poured in the container with polymerization agent to 10 cm height. The end result was gel with stones suspended in the middle of the container at the depth of 4 cm. The empty top part of the container was later filled with degassed water, and the imaging probe was immersed in that water layer facing the stone. The attenuation coefficient, sound speed and impedance of the gel are 0.08 dB/cm/MHz, 1546 m/s and 1.58 MRayl, respectively (Prokop et al. 2003).

In addition to the stones from the stone laboratory, kidney stones recently removed from patients by performing percutaneous nephrostomy were used. Since there is some possibility of bubbles being created on stones that have been exposed to air, it was desirable to test stones that were freshly removed from the in vivo environment. Those stones were placed in degassed saline immediately after removal and tested within 12 hours. Only 2 stones were tested since the possibility of getting such stones was limited. The two stones were 6 and 7 mm in diameter.

Besides natural kidney stones, stone-mimicking plastic spheres were also examined. Acrylic spheres (Small Parts, Inc. Logansport, IN, USA) with two different diameters (9.5 mm and 6.4 mm) were used in the tests. Those spheres originally had a smooth surface and did not show any twinkling artifact. The TA appeared after their surface was scratched. The corresponding rough spots were created by making multiple cuts by a knife with a 0.3 mm thick blade. The acoustic parameters of acrylic are as follows: longitudinal sound speed 2750 m/s and density 1200 kg/m³ (Selfridge 1985). An acrylic scatterer is easy to image by ultrasound, although it has lower acoustical contrast to water in comparison with a natural kidney stone: e.g., COM stones have longitudinal sound speed 4530 m/s and density 2040 kg/m³ (Heimbach et al. 2000).

Experimental design and methods

Test #1. Simulated acoustic source experiment

The experimental arrangement and procedure are shown in Fig. 1. The kidney stones within the tissue-mimicking gel phantoms were placed in front of the center of the ultrasound probe at a 4 cm distance and imaged in Color Doppler mode. During the experiment, the time-gain-compensation (TGC) was set to the minimum level for RF data acquisition to avoid signal saturation. The cases that showed the TA were chosen. For those cases, the RF data were acquired at the output of the ADC of the VUE. The Doppler power was calculated for all the channels, and the channel with the highest level of the Doppler power was selected; typically, it corresponded to one of the elements close to the center of the probe, e.g., #64. To prepare an artificial signal that mimicked the scattered signal for that channel, one of the pulses of the Doppler ensemble was picked (because all the pulses were almost identical; this could be any pulse of the 14-pulse sequence). The chosen pulse (e.g., #7) was interpolated using MatLab function “interpft” to resample with the higher sampling frequency of 200 MHz and thus smooth the waveform. Then this waveform was repeated 14 times to build a periodic sequence mimicking the Doppler ensemble, which was programmed into the function generator. Next, the ultrasound probe was disconnected from the VUE and the function generator was connected to the chosen channel in place of the probe. The generator was triggered directly from the VUE, so that the machine received the generator signal in the same way as it would in real imaging. The function generator amplitude level was adjusted so that the RF signal measured at the output of the ADC was of the same level as that measured in the original imaging experiment. After that, the Doppler power of the generator-born ensemble was calculated by employing the same algorithms as in the actual ultrasound imaging.

Figure 1.

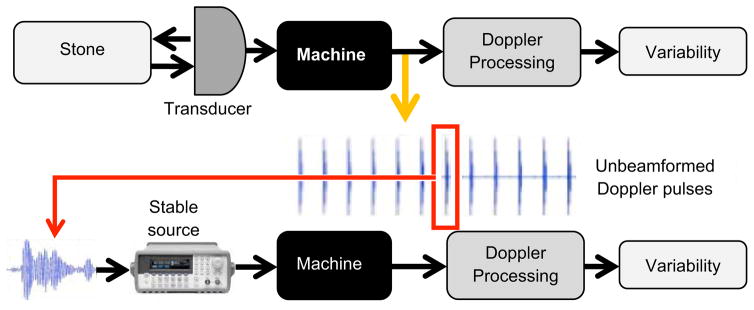
Diagram of the experimental setup and procedure. The upper part shows the flow chart of RF data acquisition. The RF data for unbeamformed Doppler ensemble that corresponds to the TA was recorded. The variability was examined based on the Doppler power estimation by using self-developed signals and Doppler processing algorithms. One pulse within multiple pulses was picked randomly and interpolated in the frequency domain. The function generator (lower part) was connected to the machine directly and triggered by the same trigger signal used in the VUE. The interpolated chosen Doppler pulse was programmed into the function generator. Simulated stable Doppler signals were sent back to the machine and then the same signal and Doppler processing algorithms were employed. Doppler power was calculated for identifying whether there is variability within the Doppler ensemble.

Test #2. Overpressure experiment

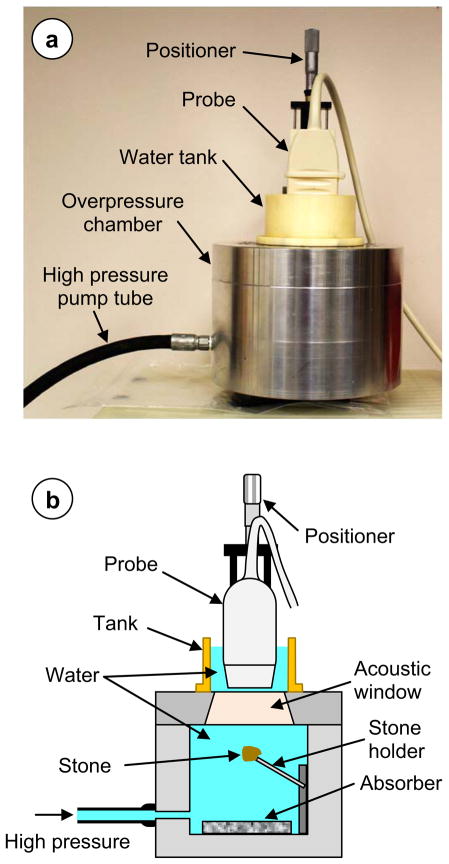
A well-known technique – an overpressure test (Bailey et al. 2000; Sapozhnikov et al. 2002) was used to test for the possible role of bubbles. The overpressure system and experimental design are shown in Fig. 2. The chamber was of cylindrical shape with the inner diameter 11.2 cm and height 7 cm. Its walls, bottom, and upper lid were made of aluminum. The walls were 4.5 cm thick, and the bottom and the lid were 3.6 cm thick, to sustain high pressures. A rubber acoustic absorber (1 cm thick) was placed on the bottom of the chamber to dampen the possible reverberations during the stone imaging. The stone under study was fixed on the tip of a brass needle of 1.6 mm in diameter that was rigidly attached to the chamber wall. A polystyrene puck was fixed in the middle of the lid to serve as an acoustic window for better ultrasound transmission. It had 5.3 cm diameter and 2.16 cm thickness. The window material parameters were the following: Longitudinal sound speed 2400 m/s; shear wave speed 1150 m/s; density 1050 kg/m³; acoustical impedance 2.52 MRayls; absorption coefficient 1.8 dB/cm at 5 MHz (Selfridge 1985). The ultrasound refraction in the acoustic window due to different sound speed from that of water was later taken into account in the beamforming in-house algorithm. On the top of the lid, a plastic cylinder of 8.8 cm diameter and 5.1 cm height was attached to form an external water tank, where the imaging transducer was immersed. The transducer was fixed on the positioning system with its axis oriented perpendicularly to the chamber lid. The surface of the transducer was close (less than 1 mm) but did not touch the acoustic window during the experiment; this was done so in order to avoid transducer displacement that could be caused by the acoustic window bending under high-pressure. The transverse position of the transducer was adjusted by the positioning system to find the best twinkling location on the stone. High static pressure was generated inside the chamber by a piston screw pump (model 37-6-30, High Pressure Equipment Company, Erie, PA). This pump was capable of producing pressure up to 200 MPa, although lower pressures (less than 9 MPa) were used in the experiment, because it was high enough to exceed several times the peak negative pressure of the ultrasound pulses (P₋≈−1 MPa) A gauge of maximum scale 13.8 MPa was used for determining pressure in the chamber (Ashcroft 1008, Huntington Beach, CA).

Figure 2.

a) The picture of the high-pressure chamber with the probe. b) The sketch of the internal structure of the high-pressure chamber with the probe.

The experimental procedure was as follows. The stone under study was glued to a brass needle using 5-minute epoxy (McMaster, CA) and fixed in the chamber. The open chamber was completely immersed in degassed water in an auxiliary plastic tank. Then the lid was closed and screwed to the chamber. After that the chamber was removed from the water tank and placed on a bench for the consequent experiment. The pressure was changed by winding the wheel of the pump. Three different pressure conditions were used: (a) Before applying excess pressure, (b) under high-pressure, and (c) after pressure was released back to the normal value. For the high-pressure condition, the stone was left under 8.5 MPa pressure for at least 4 hours. This pressure level was chosen because it exceeded several times the absolute value of the peak negative pressure of the original ultrasound pulse (P₋≈−1 MPa), i.e., a negative pressure (tension) could not appear during the stone imaging, and thus the possible ultrasound-induced bubble growth was suppressed. For each pressure condition, the image on the ultrasound machine display was filmed by a camcorder for 1 hour to obtain the whole twinkling pattern. The corresponding RF data were collected periodically. All videos were compared for different pressure conditions and the corresponding RF data were analyzed for the quantitative description of the TA. The overpressure tests were applied to laboratory stones, fresh stones and acrylic spheres with rough surfaces. For the overpressure test with fresh (recently removed from patients) stones, in order to keep the stone contact with air minimal, the preparation of the experiment was performed in degassed water, including the stone gluing to the holder.

Test #3. Imaging of acrylic spheres in liquids with different surface tension

In addition to water, ethanol was used to improve wetting of the acrylic spheres, reducing or eliminating bubbles stabilized on the stone surface, and thus suppressing bubble effects. The surface tension of ethanol (25 mN/m) (Vazquez et al. 1995) is several times lower than that of water (72 mN/m) (Vargaftik et al. 1983). Five acrylic spheres were used in this study. The transducer was fixed in the positioning system, and the sphere was placed 4 cm away from the transducer in front of its center, as in the experiments with natural kidney stones. The rough side of the sphere faced the transducer. Both the transducer and sphere were placed in a tank filled with liquid. The TA was filmed, and RF data were collected first in degassed water, then water was replaced with ethanol of 70% volume concentration, and afterwards ethanol was again replaced with degassed water. Every time a new liquid was filled, a plastic pipette was used to create agitation around the sphere to remove possible bubbles and clean the surface from the remnants of the previous liquid.

Results

Figure 3 shows typical signals that were analyzed to reveal the TA features. The left-hand side plots (A – C) describe data for imaging of a natural kidney stone from the stone laboratory, which was placed in gel. The plots A and B overlays 12 successive waveforms of the Doppler ensemble ultrasound pulses scattered from the stone recorded at the central element of the array. Here the imaging depth d corresponds to the time delay of the scattered signal t in accordance with the formula

Figure 3.

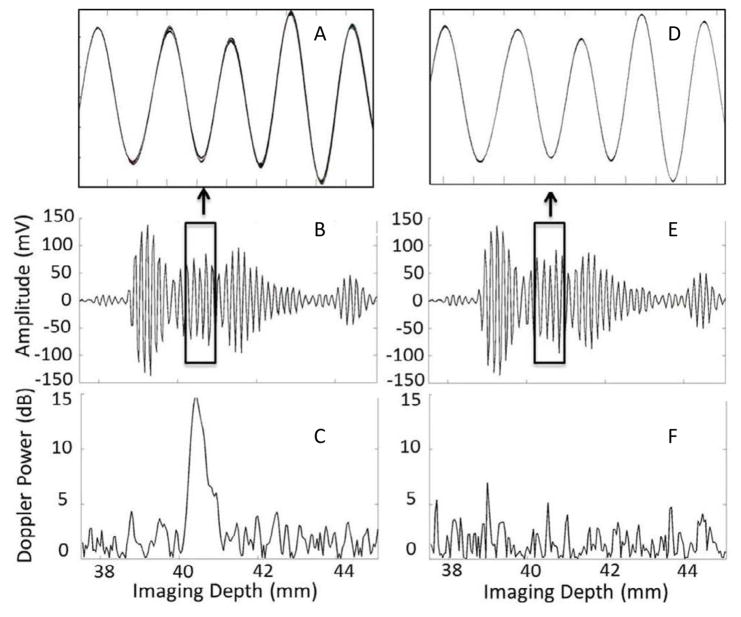
Results of natural kidney stone imaging and simulated acoustic source experiments. On the left column, figures A and B show the unbeamformed Doppler pulses (12 pulses on top of each other) recorded from natural kidney stone imaging and figure C shows the corresponding Doppler power of the Doppler ensemble. On the right column, figures D and E show the unbeamformed Doppler pulses (12 pulses on top of each other) acquired from simulated acoustic source experiment and F shows the corresponding Doppler power of the Doppler ensemble shown in figure E. The y-axis of figure B and E is the amplitude of the Doppler pulses in mV and the y-axis of figure C and F are the relative strength of the Doppler power to the background noise level in dB. The x-axis of all figures represents the imaging depth in units of mms.

$$d=ct/2,$$ (Eq #8)

where c=1540 m/s. The waveforms that are plotted on top of each other are barely distinguishable, because the corresponding changes are small. To reveal the difference between them in more detail, the Doppler power calculated from those waveforms is shown on the plot C. The Doppler power is shown in dB scale, relative to the background noise level. An obvious spike occurs about 2 – 3 μs after the arrival of the front of the stone-scattered pulse, which indicates that the corresponding part of the signal within the Doppler ensemble is fluctuating from pulse to pulse. Such a spike was observed for all studied stones and corresponded to the twinkling part of the color Doppler image. On the right-hand-side of Fig. 3(D – F), results obtained for the simulated acoustic source experiment test are shown (Test #1, described earlier). The waveforms of the simulated Doppler ensemble pulses are shown in Figs. 3D and 3E, also 12 waveforms on top of each other. The waveforms of Figs. 3B and 3E are visually identical, which indicates the high quality of the mimicking procedure. As was described, the artificial Doppler ensemble was sent through the same signal path inside the machine as the original Doppler sequence. Figure 3F represents the result for the Doppler power calculated from the waveforms shown above. No obvious spike is seen in Fig. 3F. Again, this test was made for 6 stones, and the result was repeatable. This repeatability is an important observation, because it strongly suggests that the origin of the twinkling artifact is not related to the machine. Therefore, the TA appearance must result from some effect, which we assume is acoustics.

In order to understand the properties of the scattered signals during the TA manifestation, the residual amplitude A_nm was calculated for each Doppler pulse within the ensemble. To make the data processing closer to that used in the Color Doppler imaging, beamformed channel data were analyzed. A typical result is shown in Fig. 4a. It is seen that the residual amplitudes vary from pulse to pulse, which indicates that the scattered pulses have different waveforms. Some of the pulses show spikes in the residual amplitude, which occur at the same depth as the spike of the corresponding Doppler power W_m, in accordance with the definition of the Doppler power (see Eq #6). It is useful to determine if these spikes in the residual amplitude occur only at specific pulses within the Doppler ensemble, or if they are randomly distributed within the ensemble. To perform such a test, we considered the appearance of a spike of the Doppler residual amplitude as “an abnormal event” in the given pulse of the ensemble when the waveform is noticeably distorted. For that, the following criterion was used: For the abnormal event to occur, the maximum residual amplitude for the given pulse should exceed more than 3 dB the averaged maximum residual amplitude for that ensemble. The distribution of the abnormal events within the 12 pulses of the Doppler ensemble is shown on Fig. 4b. The data were collected for 3 stones by repeatedly detecting the appearance of abnormal events during 800 imaging frames for each stone. The diagram shows the net result. The probability for the event to happen appeared to be fairly uniform within the ensemble. This result suggests that the origins of the TA are random scatterers.

Figure 4.

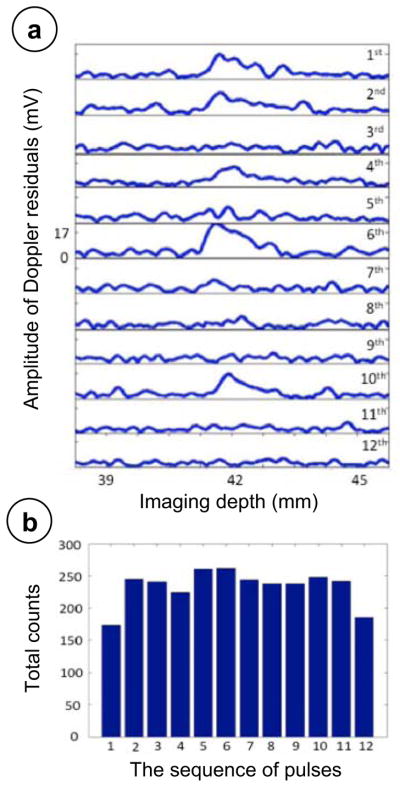
a) The amplitude varies among 12 Doppler wall-filter filtered pulses (from top to the bottom, 1st pulse to 12th pulse). The 1st, 2nd, 6th, and 10th pulse showed larger amplitude than any other pulses within the Doppler residuals. The x-axis is the imaging depth in mm; the y-axis is the amplitude of the Doppler residuals in millivolts. b) The total counts of abnormal events happened among 12 Doppler wall-filtered pulses in stone phantom imaging cases that showed the twinkling artifact. The x-axis is the sequence of the pulses within the Doppler ensemble. The y-axis is the count of the abnormal events happened.

Common candidates for random ultrasound scatterers are bubbles. Indeed, the gas bubbles may interact stochastically with ultrasound (Leighton 1994). The bubbles may be present in the bulk of propagation medium, or they may also rest on the stone surface, especially if there are microscopic cracks and crevices. The possible presence of bubbles was studied using Test #2 described in the Materials and Methods section. Figure 5 shows Color Doppler image of a stone positioned in the overpressure chamber under varied static pressure. The images were recorded by a camcorder directly from the VUE display. There is an obvious TA in the images a and c that correspond to ambient pressure conditions. The image b shows the stone image when high-pressure was applied. The TA has completely disappeared. After the pressure was released, the twinkling reappeared almost immediately. Nine stones were tested, and the results similar to those shown in Fig. 5 were observed, i.e., the TA suppression by high static pressure was repeatable. In addition to the measurements at 8.5 MPa static pressure, the TA behavior was monitored during varying static pressure to find the TA disappearance threshold. This threshold varied from stone to stone and lay within the range 0.34 MPa to 1.38 MPa. Interestingly, this pressure level is of the same order as the peak negative pressure of the imaging pulse measured at the stone location (P₋ = −1 MPa).

Figure 5.

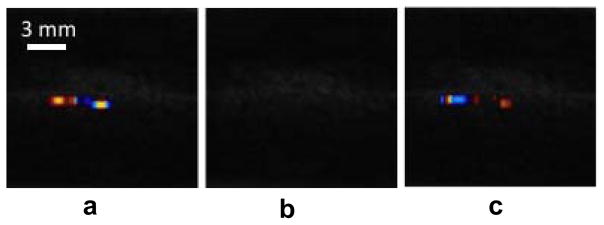
Results of the overpressure experiment on natural kidney stones. From the left to the right, there was twinkling shown before increasing pressure (a), no twinkling during the high-pressure of 8.5 MPa (b) and twinkling returned after the pressure was released (c).

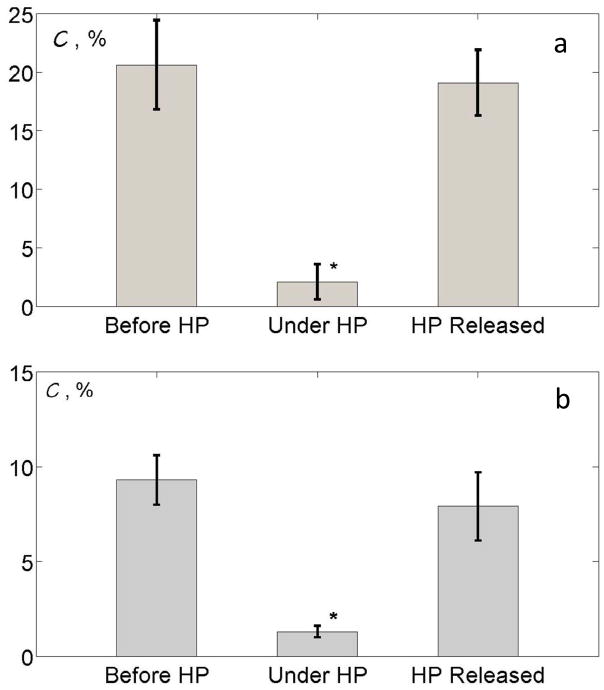
Figure 6a shows the color percentage C (see Eq #7) calculated for the three pressure conditions (1, 8.5, and 1 MPa) for one of the nine tested stones. The parameter C was 20.6%, 2.1% and 19.1% for the cases before increasing pressure, under high pressure, and after pressure was released, respectively. The statistical analysis showed that the color percentage C in the first and last cases within the criterion p>0.05 were statistically identical (p =0.3), but the high-pressure case showed a significant drop in the value of C (p=5.8×10⁻¹² and 1.6×10⁻¹⁵, when compared to C for before increasing pressure and after pressure was released, respectively). These results confirmed more quantitatively the observations shown in Fig. 5. A comparison was made for other stones (9 in total), and the results were similar.

Figure 6.

a) The color percentage C of three different pressure conditions. The human kidney stones are from a stone laboratory. From left to right, the parameter C of before increasing high pressure (HP), under HP and after HP was released was 20.6%, 2.1% and 19.1%, respectively. The Student’s t-tests were applied between cases. The p-value of the parameter C before HP and HP released was >0.05 (p = 0.3) and the p-value of the parameter C for before HP and under HP or HP released and under HP was ≪ 0.05. The results showed that the TA recovered close to the initial status after the HP was released. b) Same measurements for a fresh human kidney stone. From left to right, the parameter C before increasing HP, under HP and after HP was released was 9.3%, 1.3% and 7.9%, respectively.

The overpressure test was performed for the two stones recently removed from patients; again, similar results were obtained. The pressure threshold of the TA disappearance was found to be 0.34 MPa and 1.72 MPa for those stones. Figure 6b shows the color percentage C change following the change in pressure from 1 to 8.5 and back to 1 MPa for the first stone. Similar to the laboratory stone test, the TA was statistically identical at normal pressure before and after the overpressure test, and statistically different as compared to the high-pressure case.

The aforementioned results show that the random scatterers that cause the TA are suppressed by overpressure, which is a strong indication that those scatterers are gas bubbles. The application of external pressure shrinks the bubbles that are presumably stabilized in cracks and crevices on the stone surface; and they then return with the release of pressure. However, the natural kidney stones may contain internal cracks that could also behave similarly to bubbles; namely, they could scatter the sound randomly and be sensitive to static pressure (Solodov and Korshak 2001; Klepka et al. 2012). To exclude such a possible role, the overpressure test was also performed for acrylic spheres that had a uniform internal structure, but roughened surfaces that would presumably contained stabilized bubbles. Figure 7 shows the color Doppler images of a 9.5 mm diameter sphere under different pressure levels, similar to Fig. 5. The results of this observation, as well as the results of the color percentage C analysis, demonstrated that overpressure suppressed the TA, as in case of natural kidney stones.

Figure 7.

Overpressure experimental results of acrylic spheres with rough surfaces: before increasing pressure (a), under high-pressure (b), and after high-pressure was released (c). The results are similar to that of natural kidney stone overpressure experiments. The TA was suppressed under high-pressure. This figure is available in movie form in supplement 1.

To provide additional evidence for the vital role of crevice bubbles in the TA appearance, an alternative bubble-influencing factor was used, namely that of surface tension. The corresponding Test #3 was performed (see Materials and Methods). The TA for the acrylic spheres was compared in water and ethanol – which wet the surface differently, and presumably affect the bubble stabilization mechanisms. The results are shown in Fig. 8. There was obvious twinkling when the sphere was immersed in water, while the TA almost disappeared when water was replaced by ethanol. When the ethanol was replaced back with degassed water, the twinkling returned to its original level. Note that Fig. 8 is similar in appearance to Fig. 7, which suggests that static pressure and a low surface tension fluid have similar effects, namely, that they reduce the effect of surface bubbles.

Figure 8.

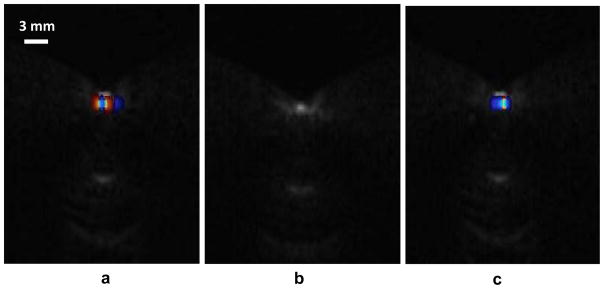
Results of the TA on acrylic spheres with rough surfaces immerged in different liquids. The TA on the sphere immerged in water (a), ethanol (b), and water again (c). The results are similar to results shown in Fig. 7. The TA was suppressed under ethanol. This figure is available in movie form in supplement 2.

Discussion

Interaction of gas bubbles with a pressure field is an important subject in acoustics of liquids. The corresponding phenomenon (acoustic cavitation) is especially initiated when the ultrasound intensity is high and the frequency is low (Leighton 1994). Bubbles are activated by the tension created during the negative pressure phase of the acoustic wave. The onset of cavitation depends not only on the acoustic pressure but also on whether there are impurities in the liquid (“cavitation nuclei”), where the bubbles appear and grow. Cavitation can happen in biological tissue as well. This is an important subject in medical ultrasound, especially in relation to ultrasound therapy and safety of ultrasound imaging (Bailey et al. 2003). To characterize a possible appearance of cavitation in tissue during ultrasound imaging, the original Mechanical Index was introduced by Apfel and Holland (1991):

$$MI=\left|P_{-}\right|/\sqrt{f},$$ (Eq #9)

where P₋ is negative pressure in MPa, and f is ultrasound frequency in MHz. The condition MI >1 is usually considered to be an indication of a possibility of cavitation damage. In the experiments of the current study |P₋| =1 MPa and f =5 MHz, which gives MI ≈ 0.45, i.e., the pressure is below the critical level, although close to it. However, the concept of Mechanical Index was proposed in relation with cavitation in soft tissue, not kidney stones or other concretions that are exposed to ultrasound. In the presence of such inclusions, the cavitation threshold may be significantly reduced and pressures might increase by superposition with reflections. The reason is that the surface of the solid objects may be weaker to tension, e.g., when the liquid does not fully wet the surface. The bubbles can be activated even easier if there are pre-existing gas pockets on the surface. Those pockets are associated with microscopic cracks and crevices or other irregularities of the surface. The role of crevices in the strength of liquids against tension has been studied for many years (Strasberg 1959), and specifically in relation to acoustic cavitation (Apfel 1970; Crum 1979, 1982). Note that the crevices and the corresponding bubbles are frequently of micron or submicron size, so they are invisible to the naked eye, and even to many microscopy techniques; thus, they are usually detected only indirectly from the effects they produce. It is likely that any bubbles that have been stabilized on a stone will be very small and since the acoustic pulse length is not that long, will not grow to visible sizes. It is also likely that there will be some rectified diffusion (Crum 1980), but perhaps just enough to change the scattering coefficient, and possibly the phase of the reflected signal.

Although the overpressure experiments provide strong evidence for the important role of bubbles, we have also considered other factors that might influence the scattering and thus modify the TA. One of them is change of speed of sound in the liquid under overpressure. Increase in speed of sound Δc due to excess pressure Δp can be calculated as

$$\mathrm{\Delta }c=\frac{\beta -1}{{\rho }_0{c}_0}\mathrm{\Delta }p,$$ (Eq #10)

where c₀ and ρ₀ are the ambient speed of sound and density, β is parameter of acoustic nonlinearity (Hamilton and Blackstock 1997). For water c₀ =1500 m/s, ρ₀ =1000 kg/m3, β = 3.52, which gives Δc =12.6 m/s for the excess pressure Δp =7.5 MPa used in the reported experiments. It is noted that this sound speed change is quite small; such an increase is even smaller than the difference between speed of sound in water and in soft tissue (1540 m/s). In the Verasonics imager, the speed of sound can be set manually; no difference in the TA appearance was seen between the cases of c = 1500 m/s and c = 1512.6 m/s.

Another potential effect is the shift of the plastic acoustic window of the chamber (see Fig. 2) when the water is pressurized. The corresponding displacement was measured based on the delay in the RF signal, and appeared to be less than 0.2 mm. This shift was not significant as well, which was determined by displacing the ultrasound probe within several millimeters; the TA was not sensitive to such a change. Note that the transducer was always distant from the acoustic window (more than 0.2 mm but less than 1 mm), i.e., it never was touched the acoustic window.

Analysis of the RF signals has shown that the spike in the Doppler power occurred not at the front of the imaging pulses but a little later, around 2—3 μs (Fig. 3). This delay was consistent for different stones. A possible explanation for the delay could be time needed for a bubble to grow or to leave the crevice in order to become an efficient scatterer. The delay could be also caused by bulk and surface waves in the stone and how they are affected by the variable loading of changing surface bubbles. More studies are needed to clarify this peculiarity. An important feature shown in Figs. 5–7 is the almost complete recovery of the TA to its initial status after the high pressure was released. That was an indication that the bubbles were compressed but not dissolved during the overpressure stage, which is a typical behavior of bubbles in the crevice (Apfel 1970). Some visible reduction in the color percentage C after the pressure was released as compared to its initial value (Fig. 6) could be explained that part of the bubbles were not associated with the crevices and thus were completely dissolved by overpressure. Note, however, that this change was not statistically significant. Also the TA is weaker in the fresh stones, which suggests that fresh stones have less contact with air and therefore have fewer bubbles.

Our hypothesis that stabilized surface bubbles is the mechanism for the appearance of the TA, as proposed in this paper, does not contradict many of the existing observations reported in previous publications on this subject. For example, the evidence that roughness of the stone surface enhanced the TA agrees well with the fact that a rough surface could harbor more bubbles (Rahmouni et al. 1996; Kamaya et al. 2003; Louvet 2006). Observations that the biochemical content of the stones correlates with the TA efficiency also can be explained by the bubble hypothesis, because surface wetting is sensitive to the composition of the stone (Chelfouh et al. 1998). A recent study on the effect of ultrasound frequency on the TA indicating that the artifact is pronounced at low frequencies (Gao et al. 2012), is a typical feature of acoustic cavitation, and thus also supports the bubble hypothesis.

An adequate depiction of how the bubbles are formed on the stone surface is not a simple task, and beyond the scope of this paper. See (Crum 1982) for more details on this phenomenon. What is lacking for this specific case is a fuller understanding of kidney stone biochemistry and surface microstructure. A typical stone consists of proteins and crystals. Some hydrophobic regions on the stone surface (e.g., proteins) may trap gas and form crevice bubbles. The crevice bubbles are probably extremely small (submicron or even nanometer size) and thus may not be seen even with μCT and other imaging technologies; e.g., we have been unsuccessful in detecting these bubbles via diagnostic ultrasound. Nevertheless, considerable evidence has been presented here that the twinkling artifact is caused by bubbles on the surface of stones, even those taken freshly from the body of patients. This observation raises the question that if in vivo stones, or other calcifications in the body twinkle, then does this mean that any object that twinkles has bubbles on (or in) it? And if so, where do these bubbles come from and what role do they play in body chemistry?

Conclusions

The current study provides several important experimental facts concerning the twinkling artifact: 1) The TA is caused by acoustic effects, not by an abnormal response of the machine electronic circuits or improper signal processing; 2) The acoustic scatterers that cause the artifact respond to the imaging Doppler pulses randomly; 3) The TA is suppressed by overpressure and by more efficient wetting of the stone surface. Those results provide strong evidence that the twinkling artifact is caused by small bubbles that are trapped and stabilized in cracks and crevices on the stone surface. Such bubble stabilization mechanisms have long been known as the principal nucleation sites for cavitation (Apfel 1970; Crum 1979, 1982). Indeed, other possible sources of the TA (e.g., radiation force, phase jitter of the machine, scattering from the rough surface) would not be sensitive to overpressure or the type of liquid in which the stone is immersed.