Structural Ensemble and Dynamics of Toroidal-like DNA Shapes in Bacteriophage ϕ29 Exit Cavity

Abstract

In the bacteriophage ϕ29, DNA is packed into a preassembled capsid from which it ejects under high pressure. A recent cryo-EM reconstruction of ϕ29 revealed a compact toroidal DNA structure (30–40 basepairs) lodged within the exit cavity formed by the connector-lower collar protein complex. Using multiscale models, we compute a detailed structural ensemble of intriguing DNA toroids of various lengths, all highly compatible with experimental observations. In particular, coarse-grained (elastic rod) and atomistic (molecular dynamics) models predict the formation of DNA toroids under significant compression, a largely unexplored state of DNA. Model predictions confirm that a biologically attainable compressive force of 25 pN sustains the toroid and yields DNA electron density maps highly consistent with the experimental reconstruction. The subsequent simulation of dynamic toroid ejection reveals large reactions on the connector that may signal genome release.

Introduction

Double-stranded DNA (dsDNA) bacteriophages are sophisticated biological machines that pack their micron-length genome into a preassembled capsid only tens of nanometers wide (1). The well-studied bacteriophage ϕ29 is one of the smallest dsDNA bacteriophages and it has long served as a model system to study virus structure, assembly, and ejection. Its relatively small genome consists of ∼19.3 kilo-basepairs (kbp), which encode for only ∼20 genes. Despite this small genome, the DNA is packed to near-crystalline density within the confines of the capsid by one of the most powerful ATP-driven molecular motors (2). These remarkable viral DNA packing motors overcome considerable energetic barriers (due to DNA bending/twisting, electrostatic self-repulsion, and entropy) by generating forces at ∼100 pN (2–5).

At the heart of the packing motor is the ϕ29 connector, a 12-mer ring of gene product 10 (gp10) proteins, which acts as a portal through which DNA is threaded. The connector actively participates in almost every stage of the phage lifecycle. Bacteriophage ϕ29, unlike many other tailed DNA bacteriophages, packages a unit-length genome with a terminal protein (gp3) covalently linked to the 5′ ends of the genome. After packing the DNA-gp3 complex, the motor assembly is broken down by dissociation of the ATPase (gp16) and pRNA. The connector is then left available as the binding site for the tail assembly including the lower collar/tail tube (gp11), tail knob (gp9), and appendages (gp12) (6). This process may be initiated through interactions between the motor and gp3 on the terminal end of the genome (7). However, the connector must somehow prevent the highly pressurized DNA from leaking from the prohead after motor disassembly but before tail assembly. Recently, Grimes et al. (7) implicated the connector channel loops, structures that protrude into the center of the connector and contact DNA, as the mechanism responsible for genome retention. In these experiments, mutated connectors with altered channel loops did not significantly affect DNA translocation but significantly hindered phage maturation. Additionally, Geng et al. (8), Jing et al. (9), and Fang et al. (10) revealed that the connector exhibits genome gating behavior and undergoes a conformational change through a sequence of steps, possibly triggered by interactions between DNA and the C-terminal flexible domain.

Whereas monumental efforts have been made to provide us with a complete picture of the ϕ29 lifecycle, many of the mechanistic details underlying a number of phage functions are only now emerging. For instance, a recent high-resolution (7.8 Å) cryo-electron microscopy (cryo-EM) reconstruction of ϕ29 has uncovered a previously undetected feature: an intriguing toroidal structure lodged in the cavity formed between the connector (gp10) and lower collar (gp11) (11) (see Fig. 1). Whereas a previous study (6) reports that the terminal protein gp3 occupies the cavity, Tang et al. (11) report densities consistent with DNA inside the connector-lower collar cavity and gp3 instead resides in the center of the tail channel below the cavity. The DNA density reveals a toroid believed to consist of 30–40 bp of highly bent dsDNA surrounding a central void (11). Although the mechanism needed to form such a highly bent DNA toroid remains unclear, we hypothesize that after DNA packing is completed and the tail is assembled, the connector undergoes a conformational change that opens the channel and allows the capsid pressure to drive DNA out of the capsid. The capsid pressure, in turn, fills the tail with DNA and forms the toroid. Before the connector opening, the terminal protein gp3 may likely be constrained inside the cavity/tail. Our hypothesis may explain how gp3, with its smallest dimension larger than the diameter of the tail channel (6,12), is compressed and driven to the distal end of the tail. Indeed, the connector has been observed to undergo conformational changes between prohead and maturity stages (6,11). Thus, the ϕ29 cavity not only permits dsDNA to pass through but is also large enough to allow DNA to bulge outward in forming the observed toroidal supercoil.

Figure 1.

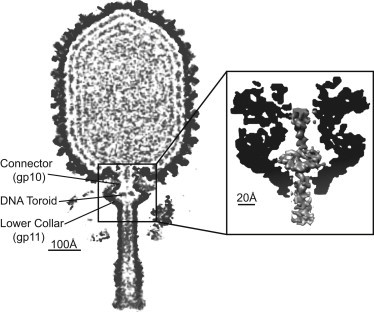
Cross section of the three-dimensional cryo-EM ϕ29 reconstruction (11). The virion map (purple, color online) is overlaid with the emptied map to highlight the genome. (Inset) Region to be simulated; the toroid constrained in the connector/lower collar cavity. Density maps generated with UCSF CHIMERA (36).

Should ϕ29 compress DNA so tightly that it forms a 30–40-bp toroid of DNA, it would present one of the most extreme cases of DNA bending known to occur in nature. It would also present a unique model system for understanding DNA under extreme compression/bending, a stress state of DNA that has yet to be examined. Close examination of the experimental density map of Tang et al. (11) reveals a 20 Å-thick toroid with outer and inner radii of 29 Å and 9 Å, respectively. This sub-persistence-length toroid shares the same extreme curvature as a 30–40-bp minicircle. By contrast, experiments (13) and atomistic simulations (14) of larger unconstrained 65-bp minicircles reveal a host of noncanonical DNA structures including bubbles, kinks, and wrinkles that form under high bending and torsional stress. Integration host factor has proven capable of wrapping 35 bp of DNA around itself to form a U-turn bend-angle >160° enabled by two kinked regions (15). Thus, the ϕ29 protein cavity may similarly preserve dsDNA despite the sharp bending.

Although the biological function of this sub-persistence-length toroidal DNA supercoil remains unknown (16), the mechanical energy stored within such a distinctive structure has led us to question the possible biological function(s) it may serve. In this study, we use computational models to address two major issues.

The first issue is whether dsDNA within the ϕ29 cavity can form a 30–40-bp toroid under mechanical compression alone. That is, can the virus provide adequate forces to compress DNA into the toroid proposed by Tang et al. (11)? If such a toroid forms, does the DNA remain intact?

The second issue addresses the possible biological functions of this highly energetic DNA structure. Hypotheses we explore include the possible role of the toroid in signaling genome release, stabilizing the pressurized virion, and initiating host infection. Our analysis exploits a multiscale model for DNA involving a coarse-grain elastic rod model and an all-atom molecular dynamics (MD) model. Our models not only reveal that a DNA toroid can be maintained at force levels below those predicted by experiments, but that the atomic toroidal DNA structure is largely preserved. The predicted density maps compare favorably with that of Tang et al. (11) and suggest an ensemble of different-sized toroids. We also demonstrate that a toroid can fulfill all three proposed hypotheses.

Methods

We open with a description of our multiscale modeling approach. Simulating DNA buckling under biologically relevant forces in all-atom MD requires prohibitively large computational resources. One strategy to shorten computation time is to apply significantly higher forces on DNA than exists in the biological system. However, this approach greatly increases the likelihood of forcing the system away from the physical pathway and thereby introducing artifacts into the computed DNA structure. Alternatively, a coarse-grained rod model can efficiently simulate buckling but faces the challenge of representing the true atomistic structure on length scales approaching a helical turn. Therefore, we exploit equilibrium conformations predicted by the rod model as initial conditions for refinement in MD, which significantly reduces computation time yet preserves biologically relevant force levels.

Modeling cavity contact with the elastic rod

We build upon the computational rod model of Goyal et al. (17,18) and Lillian et al. (19), which describes the dynamic, three-dimensional bending and twisting of the DNA helical axis in response to DNA elasticity, dissipation, and prescribed body forces/torques. The rod stiffness is determined by the bending and torsional persistence length of DNA. The feature that distinguishes this study from related formulations (20–26) is the inclusion of body forces representing the interaction of DNA with the protein cavity formed by the connector and lower collar (refer to Fig. 2 C). We summarize the salient features of this DNA-cavity interaction model by also drawing upon results from Hirsh et al. (27). In addition, an overview of the computational rod model is provided in the Supporting Material.

Figure 2.

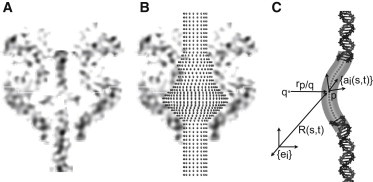
(A) Cross section of the connector/lower-collar cavity with toroidal DNA from Tang et al. (11). (B) Point-wise discretized constraint surface, derived from the protein cavity walls, specifies the location of computational grid points in the rod model or inert atoms in MD rigidly positioned on the cavity surface. (C) The atomic structure of DNA superimposed with an elastic rod with equivalent elastic properties. $\overrightarrow{R}\left(s,t\right)$ defines the position of the helical axis as a function of contour length s and time t with respect to the inertial frame e. We also define a body-fixed reference frame a(s,t), which is also a function of s and t. The interaction forces are dependent on all pairwise vectors between rod grid points p and points q representing the cavity surface.

The ϕ29 connector/lower collar cavity dictates the constraints for DNA buckling and eventual toroid formation. Although a crystal structure of the monomer of the ϕ29 connector exists (28), the atomic resolution structure of the lower collar/tail tube is unfortunately unknown. Thus, we must necessarily make simplifying assumptions to approximate the cavity geometry. We assume, that the cavity is axisymmetric about the viral tail axis. To obtain a smooth cavity, we analyze the cryo-EM density map (see cross section in Fig. 2 A) and employ averaging. Specifically, the density map is sampled at 12 azimuthal angles (each hour on a clock face). For example, the right and left side of the cavity in Fig. 2 A are at 3 and 9 o’clock, respectively. At each azimuthal cross section, we identify the innermost points with nonzero density value. Each of these points is a known distance from the central axis and, upon collecting all points, we construct a best-fit line through the collocation of points that extends from top to bottom on the density map. The best-fit line is used to define the constraint surface, which is then point-wise discretized (see Fig. 2 B).

Although it has been proposed that the negatively charged connector channel interior is responsible for centering DNA in the portal during packaging (28), the charge on the lower collar/tail remains unknown. Therefore, we approximate repulsion by modeling (hard) mechanical contact between DNA and the cavity with an inverse power law given by

$${\overrightarrow{F}}_{p,q}=\frac{{\rho }_{\text{DNA}}{l}_o{\rho }_{\text{cavity}}AC}{{\left(r_{p,q}-r_o\right)}^{\beta }}\frac{{\overrightarrow{r}}_{p,q}}{r_{p,q}}.$$ (1)

In the equation, r_p,q is the distance between a pair of rod (p) and cavity (q) grid points; r_O = 10 Å is the assumed physical radius of dsDNA; β = 6 is the degree of the power law; l_o = 1.7 Å is the discretization length of the rod; A = 16 Å² is the approximate surface area surrounding each cavity point (cavity grid points are spaced ∼4 Å apart); ρ_DNA = ρ_cavity = 1 is the local charge density of each DNA and cavity grid point, respectively; and C = 0.1 pN · Å⁶ is a tunable constant. In Hirsh et al. (27), we examined the sensitivity to the above computational parameters, including setting β to 4 and 8 and order-of-magnitude changes to C, and observed only minuscule differences in computed solutions. To determine if solutions remain invariant to finer cavity point spacing, we used values of 2 Å and 1 Å, and observed insignificant changes that assure convergence for 4 Å. The net cavity contact force acting on rod grid point p is the sum over all pairwise interactions with M cavity grid points, per

$${\overrightarrow{F}}_{p,\text{cavity}}=\sum _{q=1}^M\frac{{\rho }_{\text{DNA}}{l}_o{\rho }_{\text{cavity}}AC}{{\left(r_{p,q}-r_o\right)}^{\beta }}\frac{{\overrightarrow{r}}_{p,q}}{r_{p,q}}.$$ (2)

This contact force is inserted into the discretized equations of motion for the rod as an additional contribution to the body force ${\overrightarrow{F}}_{\text{body}}$ appearing in the Supporting Material.

Constructing the two-dimensional energy landscape

Each equilibrium conformation of DNA inside the cavity predicted by the rod model was energy-minimized in an all-atom force field. To overcome the absent atomic structures required for simulating the atomistic cavity constraints, we make the following simplifying approximations. We represent the cavity points as Lennard-Jones atoms (with mass and van der Waals radius of a helium atom equal to 1.48 Å and fixed in Cartesian space at points shown in Fig. 2 B) to enforce hard contact between DNA and the cavity wall. This approach permits simulation of DNA within the constraints of the cavity, and it can be refined to capture atomic details when additional crystal structure data is available.

A free parameter in the interaction potential with the cavity boundaries is the depth of the L-J potential well, ε, and we conduct identical MD simulations varying ε over various orders of magnitude (ε = 0.02, 0.2, 2.0, and 20 kcal/mol). The most stable DNA structures are observed for ε = 0.2 kcal/mol and this value is adopted in all energy minimization runs (see Fig. S1 and text in the Supporting Material for additional results and a discussion of sensitivity to ε).

The minimization procedure was performed with CHARMM package (29) using the generalized Born molecular volume (GBMV II) implicit solvation model (30–32). The minimization protocol consisted of 1000 steps of steepest decent minimization followed by 1000 steps of minimization using the Adopted Basis Newton-Raphson algorithm. The total energy of the system for each of the DNA conformations was calculated as an average over the last 100 steps from the minimization run.

Minimization, equilibration, and production runs were performed using the CHARMM27 force field (33). During all MD simulations, the nonbonded list was generated with a cutoff of 21 Å; the cutoff for nonbonded interactions and the onset of switching for nonbonded interactions were set to 18 Å and 16 Å, respectively.

MD simulation details

The equilibrium conformation of DNA with a toroid size of 33 bp and DNA registry value of 280° predicted by the elastic rod model was used as the initial structure for all-atom MD simulation. All MD trajectories were obtained with the NAMD package (34). The solvation effects during the simulation were described by the generalized Born implicit solvent model of Onufriev et al. (35) with a cutoff of 16 Å for calculating the Born radius. The salt concentration was set to the default value of 0.2 M.

Initially, the system was energy-minimized for 5000 integration steps. Next, the system was slowly heated to 300 K in 50 K increments for each 200 ps. To prevent translation of the DNA ends along the tail tube, the motion of the terminal DNA basepairs along the tail tube direction was harmonically restrained by a force constant of 50 kcal/mol/Ų. To preserve the duplex DNA structure during heating, two types of harmonic restraints, each with force constant of 100 kcal/mol/Ų, were applied on the DNA atoms:

• 1.Root-mean-square displacements of heavy atoms were restrained to an initial structure; and
• 2.Donor-acceptor distances between complementary DNA bases were restrained to 3 Å.

This heating stage was followed by constant temperature equilibration with 8 ns of slow release of the harmonic restraints (further details are given in Table S1 in the Supporting Material). The average temperature of the system was maintained at 300 K via Langevin thermostat with a coupling coefficient of 5 ps⁻¹. The vibrations of covalent bonds to hydrogen atoms were harmonically restrained, which allowed 2-fs integration time steps during the MD runs. After equilibration, the simulation proceeded for 2 ns with the only restraints applied on the terminal DNA basepair. The final 2 ns of simulation time were used for the collection and analysis of equilibrium data.

Constructing predicted density maps

UCSF CHIMERA (36) was used to generate the predicted density maps from rod-model computed toroids using the built-in function MOLMAP. Grid spacing is set to 1 Å and the width of the Gaussian distribution used to describe each atom, σ-factor, is set to 0.425. Rotational averaging is performed using cyclic symmetry by placing 100 equivalent copies around the vertical tail axis. A cross section is taken and 20 color bins are scaled between the highest volume data value (yellow) relative to the lowest (dark blue). The density maps remain unchanged upon adding more copies so long as the number of copies is sufficient. Thus, the maps are well converged using 100 copies. To smooth the color gradients, per-pixel coloring is selected. All other settings are default.

Results

Toroid conformations predicted by rod model

After the tail machinery (including the lower collar, tail tube, and tail knob) is installed, the connector presumably allows an amount of DNA to escape, which, driven by high capsid pressure, descends to fill the tail and cavity. The resulting equilibrium conformations of a short (75-bp) segment of DNA are computed from the rod model including DNA within the cavity and short sections in the tube above and below the cavity. In the simulations, DNA is compressed from a nearly straight conformation to a highly buckled toroidal conformation. The buckling is simulated by allowing 1 bp at a time to descend from the top portion of the connector tube into the cavity until an excess of 33 bp fills the cavity, forming a buckled toroid. During this simulation, the lower boundary is held fixed against translation while the upper boundary undergoes a quasi-static prescribed translation. The excess DNA fills the cavity and increases the toroid size.

In addition, the only rotation permitted at the lower boundary is rotation about the helical axis, which relieves any additional DNA twist during buckling. No rotations are permitted at the upper boundary. Images of selected equilibrium conformations during buckling are shown in Fig. 3 and the associated terminal compressive force and elastic strain energy of the DNA are reported in Fig. 4. Although all equilibrium conformations remain twist-free, the initial condition is a nearly straight right-handed supercoil that biases the formation of a right-handed toroid thereafter. Although it is unknown whether the actual toroid is right- or left-handed, Yu et al. (37) determined that the packing motor twists DNA in a left-handed sense during packaging. As DNA exits the capsid, we hypothesize that DNA will relax by twisting in the opposite direction, thereby biasing the formation of a right-handed toroid.

Figure 3.

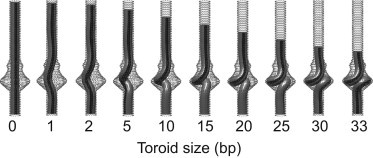
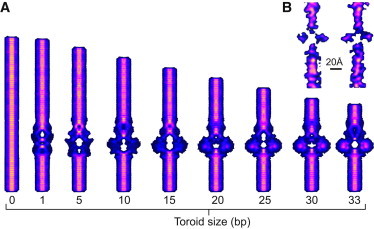
Rod model predicts toroid formation in the ϕ29 cavity. Snapshots of twist-free equilibrium conformations as a function of toroid size (basepairs). (Black stripe) Aid in visualizing the twist state of DNA. During supercoil formation, twist is relieved through the lower boundary.

Figure 4.

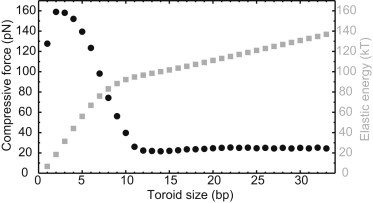
Compressive force required to form a toroid is well within packing motor capabilities (25 pN for toroids >10 bp). Plotted are DNA internal (elastic strain) energy (gray squares) and compressive force (black circles) as a function of toroid size. DNA is initially nearly straight while the top boundary descends in the tube one basepair (3.4 Å) at a time.

Structural equilibration of toroids using MD simulations

The initial condition for atomistic simulation is obtained by fitting an all-atom representation of B-form DNA around the DNA helical axis predicted by the rod model (using the Model.it toolset (38)). Because fitting involves placing preoptimized basepair geometries perpendicular to the helical axis, we are left with a free parameter, referred to as the registry parameter. Specifically, the DNA atoms can be barrel-rolled about the helical axis without changing the linking number. This registry parameter may play an important energetic role because it dictates how the negatively charged sugar-phosphate backbones align at the entry and exit of the toroidal DNA, an effect not included in the rod model. We next perform all-atom energy minimizations of the DNA structures over a two-parameter space defined by toroid size and registry. The result for right-handed toroids, Fig. 5, illustrates the total potential energy landscape and its constituent parts. The limiting 33-bp case represents the largest toroid contained in the cavity without nonphysical overlap of the sugar-phosphate backbone. For completeness, the energy landscape for left-handed toroids is shown in Fig. S2 in the Supporting Material.

Figure 5.

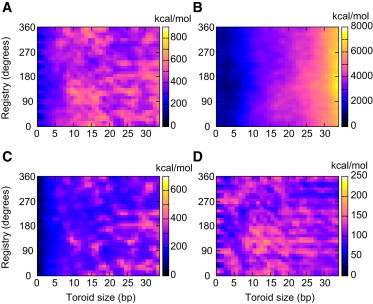
Energy landscape of all possible DNA conformations over the two-parameter space of toroid size and registry. (A) Potential energy landscape and its (B) electrostatic, (C) bonded, and (D) van der Waals components for right-handed toroids. To highlight energetic differences between conformations, energy values are scaled relative to the minimum value in the corresponding landscape.

The absolute energies of the all-atom force field are associated with a rapid increase in the repulsive electrostatic energy of the system as the highly charged DNA is being compressed within a confined volume. The hard (Lennard-Jones) interaction potential between DNA and the cavity wall, whose rigidity is enforced in our model, confines this highly energetic DNA state and mimics the way the protein environment would confine it. Although the absolute energy values are high, they are not, in relative considerations, higher than those expected in the real biological case of a protein viral capsid where DNA is highly pressurized to ∼40 atm (39). Additionally, measurements of Young’s modulus using scanning force microscopy show that the protein shells of bacteriophages are extremely resilient and can withstand nanoNewton forces (40). Moreover, the forces derived in our models are of the same order of magnitude as those reported in Smith et al. (2) and we therefore expect that the cavity can accommodate these force levels without significant deformation. Although the formal possibility exists that the energy values associated with DNA compression inside the protein cavity can be smaller than those predicted with our simplified approach (because of the simplifications in the potential), the model gives important insights into the energetic dependence of various DNA toroidal shapes inside the confined volume of the exit cavity of ϕ29.

To determine the atomic equilibrium structure of the toroid, we choose a representative toroid from the described landscape (33 bp, registry 280°) (Fig. 6, A and B) and perform an equilibration in MD. Equilibration proceeds for 8 ns, followed by 2 ns of production run (see Methods for simulation protocol). To enforce identical boundary conditions in MD, the terminal basepairs are harmonically restrained against translation along the tail tube but permitted to rotate about the tail axis. Fig. 6, C and D, shows front and top views of the equilibrated structure, respectively.

Figure 6.

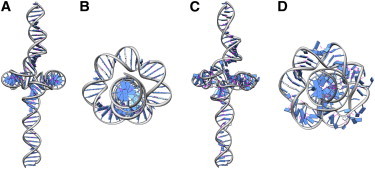
Molecular dynamics model of atomic DNA structure highly bent and under extreme compression. (A and B) Front and top views of all-atom initial condition of a 33-bp toroid with helical axis predicted by rod model inside the constraints of the cavity. The DNA sequence is the first 75 bps from the ϕ29 genome. (C and D) Same views of final conformations after MD equilibration within the constraints of the cavity show that basepairing is preserved. (Magenta) Hydrogen bonds. All atomistic DNA graphics generated with UCSF CHIMERA (36).

Comparison with experimental cryo-EM density map

The all-atom energy-minimized conformations are used to generate predicted density maps for direct comparison with the experimental cryo-EM density map (two orthogonal cross sections are shown in Fig. 7 B) (11). In the experimental reconstruction, density attributed to DNA is obtained through subtraction of two maps: the virion reconstruction (EMD-1420) minus the post-ejection emptied reconstruction (EMD-1419) found in the EBI-MSD EMD database. Recall that the capsid exhibits fivefold symmetry whereas the connector/tail exhibits 12-fold symmetry. Although these components aid in aligning the exterior of the two-dimensional particle images, the interior toroid may not possess the same azimuthal orientation from particle to particle. That is, if the buckled DNA is randomly oriented within the interior cavity, then the resulting EM map will appear smeared-out upon rotational averaging of images about the tail axis. To mimic this process, we rotationally average conformations of increasing toroid size (while maintaining, e.g., 280° registry) with the resulting cross sections of predicted density maps shown in Fig. 7 A (see Fig. S3 and text in the Supporting Material for additional maps with varying toroid registry and handedness).

Figure 7.

Predicted density maps compared side by side with experimental data. (A) Predicted maps for different-sized toroids. (B) Two orthogonal cross sections of the experimental cryo-EM density map (11). (Yellow and dark blue) Regions of highest and lowest intensity, respectively. Rotational averaging of the conformation was performed using UCSF CHIMERA (36). Consistent with the experimental results, the color scale is determined by scaling the highest intensity bin relative to the lowest intensity bin (see Methods).

Simulating ejection dynamics

During infection, the distal end of the tail knob opens to allow the genome to exit the virus (6). Once opened, the highly energetic toroid will undergo dynamic collapse and ejection from the cavity. We hypothesize that toroid collapse/ejection could play an important role in initiating infection, for example, by acting as a signaling mechanism. To address this hypothesis, we return to the rod model to simulate the ejection dynamics induced by toroid collapse and over long timescales that are practically inaccessible to MD.

The initial condition to the ejection simulation is adapted from the rod-model-predicted equilibrium conformation (the 33-bp toroid in Fig. 3). To account for viscous drag effects, an additional 80 bp of DNA is added beneath the toroid to the opening of the tail tube. The viscous drag model for DNA (41) follows the numerical implementation of Lillian et al. (19) and Hirsh et al. (27) (see the Supporting Material). At the opening of the tail tube (bottom), the rod remains restrained against rotation about the two transverse axes, but is now free to translate along and rotate about the tail (vertical) axis after the (assumed instantaneous) opening of the tail knob. The upper boundary remains clamped and fixed by the possible pinching of the connector and reacts to highly dynamic forces and torques induced during toroid collapse. The predicted axial reaction force and torque during this collapse are reported in Fig. 8 as functions of reduced time.

Figure 8.

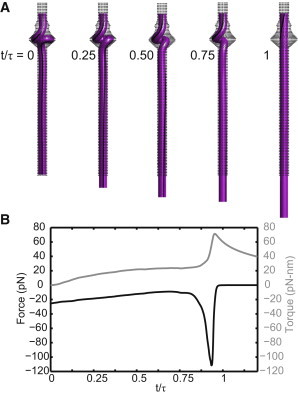
Rod model of toroid collapse predicts large reaction force/torque at the connector. (A) Snapshots show instantaneous conformations during ejection. (B) Axial reaction force and torque at the upper boundary as a function of reduced time t/τ, where τ is the time required for the toroid to fully straighten and can range from ∼τ = 6.8–68 μm (see text for discussion).

The reduced timescale in Fig. 8 B is obtained by dividing simulation time (t) by the time required for the toroid to completely straighten and eject (τ). Thus Fig. 8 A illustrates the conformation of the DNA toroid at times corresponding to 0, 25, 50, 75, and 100% of full ejection. Whereas τ obviously depends on the selected friction model, the important findings illustrated in Fig. 8 do not. In particular, note the large reaction force and torque developed at the upper boundary right as the toroid straightens. These large reactions arise regardless of the assumed friction model which, for computational expediency, presently underestimates the total friction; it accounts for hydrodynamic drag and not the (unknown) friction of DNA within the tail tube of ϕ29. If one were to adopt the much larger (by 2–3 orders of magnitude) friction coefficients estimated from experiments on bacteriophage-λ ejection (42) (0.17–2.4 N·s/m²), then the predicted ejection times would range from 6.8 $<\tau <$ 68 μm.

Discussion

The existence and geometry of the toroid

Both the rod and MD models corroborate the existence of a highly strained toroid within the small connector-lower collar cavity. Results from the rod model confirm that the capsid pressure is sufficient to mechanically compress and maintain DNA in a toroidal shape within the cavity. Inspection of Fig. 4 reveals that as the bucking process begins, the DNA deflects outward into a slender but stiff helical buckle that requires high compressive force (refer to Fig. 3). After 2 bp are inserted, DNA contacts the cavity wall, which further constrains the structure and results in maximum compression (∼160 pN). As the upper boundary descends further, the DNA buckles dramatically to fill the cavity interior. This large-scale buckling creates a substantially more compliant structure, and significantly smaller compressive forces are therefore required for DNA equilibrium (refer to Fig. 4 for bp > 10 where compressive forces is reduced to a modest ∼25 pN). Therefore as the toroid evolves, the compressive forces remain nearly constant at ∼25 pN which, by comparison, is ∼25% of the maximum force achievable by the packing motor.

During the initial buckling of DNA (Fig. 4), the rod model also predicts forces that exceed those achievable by the packing motor. However, these high initial forces result from the particular pathway to toroid formation chosen for this computation. The results illustrated in Fig. 4 follow from a near perfectly straight DNA segment that also remains torque-free—both limiting conditions that require the greatest compressive force to initiate buckling. The addition of any intrinsic DNA curvature, torque, or localized defects would significantly reduce the compressive force required to initiate buckling. For instance, the supercoiled capsid DNA would likely impart torque to the DNA as it descends through the tail tube, which in turn will reduce the compressive force required to initiate buckling (43). Therefore, our results demonstrate that the capsid pressure provides sufficient driving force to buckle DNA into a toroid in this confined volume.

Upon refining the rod-predicted initial condition, the computed energy landscape in Fig. 5 illustrates energetic dependence on both toroid size and registry. The potential energy (Fig. 5 A) and the elastic strain energy estimated with the rod model (Fig. 4) both increase with toroid size as expected. Furthermore, both models predict a rapid energy increase at the initial stage of compression (for toroids up to ∼10 bp). Inspection of Fig. 5 B reveals that the electrostatic energy component monotonically increases as more DNA enters the cavity, an effect independent of registry as expected. By contrast, DNA-bonded energy and the van der Waals energy of the system exhibit dependence on size and registry. The variations in the potential energy (Fig. 5 A), which largely follow that of the bonded and van der Waals components, do not suggest a single favorable toroid size or registry. Instead, these results suggest that an ensemble of toroids may exist. Additionally, the energy landscape for left-handed toroids (see Fig. S2) remains energetically equivalent to the right-handed landscape, suggesting no energetic preference exists regarding toroid handedness.

The predicted maps in Fig. 7 A share many qualitative characteristics with the experimental map (11) and further argue for an ensemble of toroids. Note the appearance of a central void as soon as DNA buckles and the toroid intensity increases with toroid size as more DNA fills the cavity. In the straight tube sections above and below the toroid, observe extensive low (dark blue) and intermediate (light blue) intensity regions with patches of high intensity (magenta and yellow) near the center of the tail axis consistent with the experimental map. Also observe the low-intensity region joining the toroid to the high-intensity straight segments above and below it, as noted in Tang et al. (11). All predicted maps for toroids larger than ∼20 bp similarly exhibit sharp (nearly 90°) density transitions between straight and toroidal sections. For these larger toroids, note the dominant regions of intermediate (light blue) and high (magenta) intensities in the toroid that are consistent with the intensities reported in the experiments. Smaller toroids, by contrast, do not possess the high-intensity regions observed in the experiments. Although difficult to discern exact toroid size and registry, we observe matching high (magenta) intensity in the toroid for sizes of ∼20 bp and larger. Thus, the experimental density map may reflect an averaged ensemble of toroids weighted toward larger ones (consistent with results in Fig. 5). Additionally, the shape of the void at the center of the toroid (as well as the existence and shape of the smaller voids above and below the toroid) changes with toroid size, registry, and handedness, but an ensemble average would also mask these dependencies (see Fig. S3 for predicted density maps for varying handedness and registry).

Beyond the qualitative similarities noted above, the predicted density maps (Fig. 7 A) also share remarkable quantitative similarities to the experimental map. Tang et al. (11) report a 20 Å-thick toroid possessing an outer and inner diameter of 58 Å and 18 Å, respectively. Despite the small differences in the central void, the dimensions of the larger toroids remain remarkably consistent with these experimental measurements. In particular, the predicted toroid thickness and the inner diameter (distance between the high intensity regions) are ∼20 Å, whereas the outer diameter is ∼60 Å (dictated of course by the diameter of the cavity).

Equilibration in all-atom MD simulations reveal that the initial toroid predicted by the rod model is largely preserved despite sharp bending and compression. Observe in Fig. 6 that the initial condition matches reasonably well with the MD-equilibrated structure and both confirm the existence of a central void. Aside from a few regions where we observe basepair flipping, the DNA remains double-stranded. The small denatured regions may also be an artifact arising from the assumed interaction potential with helium atoms, which likely do not fully represent the biological system. To explore the implications of our assumptions, we have applied the model using several interaction potentials, characterized the sensitivity to this parameter, and speculate on the biological implications (see Supporting Material text and Fig. S1). From our systematic analysis emerges a model whereby dsDNA denaturation is limited in large part by the nonspecific interaction with the cavity.

The objective of this article is to explore the hypothesis put forth by Tang et al. (11) that DNA forms a toroidal structure. A coarse-grain model, an MD model, and predicted cryo-EM density maps all provide consistent evidence for a toroid. However, for completeness we must also recognize that there are other structures that could yield the split density in the entry/exit cavity including DNA strand separation, as observed in Podovirus P-SSP7 (44), flipped bases, a cruciform, etc.

Possible functions of the toroid

Recent experiments conducted after the reconstruction of Tang et al. (11) have increased our understanding of the sequence of conformational changes in the ϕ29 connector. In light of these discoveries, we explore several possible biological functions of the toroid, including its ability to not only stabilize the mature virion but possibly trigger a conformational change.

• 1.Toroid collapse triggers genome release: The dynamic collapse of the toroid could function as a signalizing mechanism to initiate the release of the capsid DNA. Our simulations predict a rapid dynamic collapse of the toroid, which would occur well before the remainder of the genome would be ejected from the capsid. During collapse, the compressive force on the connector increases fourfold from its value at equilibrium (see Fig. 8). In fact, this reaction force as well as the reaction torque achieve maxima right as the toroidal DNA straightens. It is impressive that rapid toroid collapse generates forces (∼110 pN) on par with the strongest known molecular motors and without the need for additional ATP. This tandem reaction force/torque shock might disturb the highly organized genome. Additionally, a recent study by Geng et al. (8) on the gating mechanism in the ϕ29 connector concluded that it could undergo stages of conformational change mediated by contact between DNA and the C-terminal flexible domain. If the C-terminal domain acts as the trigger to induce conformational changes, then it is possible that the large reaction forces/torques could cause DNA/trigger contact, initiating yet another conformational change. While the connector undergoes a conformational change upon DNA packing (7) to hold the pressurized genome inside the capsid, we hypothesized that it must also undergo a second conformational change to open the connector and allow DNA leakage back through the tail. Toroid collapse may further dilate the connector to allow unhindered genome escape. Additionally, it has been proposed that a triggered conformational change in bacteriophage SPP1 (45) and P22 (46) opens the connector and enables genome ejection. Finally, the large force/torque occurs right as DNA straightens and their magnitude is independent of toroid size. This size independence renders toroid collapse a robust signaling mechanism.
• 2.Toroid stabilizes pressurized virion: At first glance, the toroid resembles a single turn of a helical spring that may help stabilize the densely packed genome. Changes in environmental conditions (e.g., temperature or ionic conditions) over the life of ϕ29 cause fluctuations in the highly pressurized capsid DNA. In fact, the dynamics of bacteriophage genome ejection have been probed by perturbing ionic conditions, which in turn affect capsid pressure (47). The flexible toroid could serve as an essential source of mechanical compliance, allowing the tightly packed capsid to remain stable despite environmentally induced pressure fluctuations. This possibility follows from the force-deflection curve of Fig. 4, which confirms that a large change in toroid size produces little-to-no change in DNA compression (remains at ∼25 pN for toroids larger than 10 bp). By contrast, a straight column of DNA provides little compliance and potentially induces much larger stresses in the capsid protein shell in response to environmental disturbances.
• 3.Toroid initiates host infection: Upon opening the tail knob during infection, toroid collapse may rapidly push the terminal protein gp3 ∼30–40 bp into the host cell, a process requiring no aid from the capsid pressure or additional ATP. Hydrolytic enzymes decorating the tail knob (gp13) help degrade the ∼250 Å host cell wall (48–50). Thus, as the tail knob bores into the host, the toroid could push gp3 significantly into the cell wall/membrane to help degrade/puncture it.

Conclusions

In summary, we employ a continuum-elastic rod and an all-atom MD model to simulate DNA buckling into a toroid and its subsequent ejection from the connector-lower collar cavity. The rod model predicts that an ensemble of toroids can mechanically form under biologically relevant force levels. Equilibration in MD reveals that the dsDNA structure is largely preserved under sharp bending through nonspecific interactions with the cavity. Both the energy landscape and the predicted density maps support the likelihood of an ensemble of different-sized toroids that combine to form the averaged experimental density map. Upon simulating the dynamic ejection of the toroid, we compute large reaction forces/torques at the connector, which may signal an additional conformational change to allow the capsid DNA’s unhindered escape into the host cell. We hypothesize that the mechanics of DNA may not only help stabilize the phage, but also play an active role in governing genome release. Higher-resolution reconstructions of other bacteriophages may reveal similar DNA structures in the phage portal/tail.