Abstract
Fluorescence recovery after photobleaching (FRAP) is a widespread technique used to determine intracellular reaction and diffusion parameters. In recent years, due to technical advances and an increasing number of mathematical models for analysis, there was a resurging interest in FRAP applications. However, care has to be taken when inverting parameters from such data. We study potential influences on FRAP acquisition and analysis like initial fluorescence distribution, membrane passage, and geometrical aspects. Monte Carlo simulations are employed for the investigation of reaction-diffusion processes to additionally include cases in which no analytical description is available. To assess the importance of influencing factors we apply a sensitivity method based on elementary effects providing an estimate for the global parameter space. The combination of simulations and sensitivity measure helps us to predict ranges of parameters used in acquisition and analysis for which a reliably inversion of reaction-diffusion parameters is possible. Using this approach, we show that FRAP data are highly susceptible to misinterpretation. However, by identifying the parameters of susceptibility, our analysis provides the means for taking measures to significantly improve FRAP data interpretation and analysis.
Introduction
The interest in molecular interaction and dynamics in living cells is steadily increasing. Several experimental approaches based on fluorescent microscopy have been developed over the years. One of the most widespread techniques to investigate molecular mobility in living cells is fluorescence recovery after photobleaching (FRAP) (1–9).
The underlying strategy of a FRAP experiment is quite simple. A region of interest (ROI) is chosen and the fluorescence in this area is irreversibly bleached by a laser beam. Subsequently, the reoccurrence of the fluorescence in the ROI is monitored over time, giving rise to a so-called recovery curve. The shape of this curve is determined by the characteristics of mobility, e.g., molecular interaction, diffusion, or directed movement. Therefore, FRAP experiments can be used to deduce parameters characterizing processes such as diffusion coefficients or reaction rates (10–15).
Due to the implementation of FRAP acquisition tools on commercially available microscopes, and the introduction of fluorescent proteins like GFP, the interest in FRAP applications experienced a resurge in recent years. Despite these technical advances and an increasing number of mathematical models for analysis (16–18), some considerations are still warranted when inverting parameters from such experiments. Not only the experimental setup, but also the subsequent mathematical analysis of the generated FRAP data, can have a marked effect on the parameter outcome. In this respect, we evaluated the importance of FRAP acquisition and analysis parameters, employing Monte Carlo simulations coupled with a sensitivity measure.
Simulations (i.e., numerical models) can facilitate the understanding of cellular systems in particular if spatio-temporal parameters take on importance. Evaluating which model parameters are most influential and which are negligible can provide further insight into the system investigated. However, for a comprehensive model assessment, the overall impact of all parameters on the model output should be determined by using as small a number of model evaluations as possible. Several methods are available for such a sensitivity analysis to provide a quantitative measure of the parameter importance. These methods differ in complexity and in the parameter information generated (19). Methods used to determine the influence of a single parameter on the model response while neglecting interaction between parameters are known as screening methods. These are based on sampling. Parameter sets are sampled from a distribution and used subsequently to drive the model.
One particularly useful screening method for computationally expensive models is based on elementary effects, because this approach only needs a small number of model evaluations to determine a sensitivity measure for each parameter. The concept of the elementary effects method was introduced by Morris (16). A derivative choosing the parameter sets such that the complete feasible domain of parameter values is covered was introduced by Saltelli et al. (17). We used this approach to determine the importance of parameters used in acquisition and analysis of FRAP.
Numerical models are computationally very expansive, therefore the reaction-diffusion parameter inversion from FRAP data commonly relies on simplified analytical models. These simplifications are based on assumptions that usually do not hold in the environment of a living cell. It is easy to imagine that, by these model assumptions, only approximate model functions describing the time course of the fluorescence recovery within the ROI can be deduced, which will lead to inaccurate parameter values (i.e., diffusion coefficients and reactions rates).
In this article, the influence of these model assumptions as well as the influence of the experimental setup (e.g., the position of the bleaching spot, and the geometry of the bleached compartment) will be studied.
We will show that FRAP experiments are highly susceptible to misinterpretation. A prerequisite for the successful combination of biological observations with mathematical models is an accurate data acquisition as well as an appropriate model assumption set. Therefore, it seems evident to use simulations of FRAP measurements in combination with a sensitivity measure to determine the main influencing factors on FRAP recovery curves to significantly improve their interpretation and analysis.
Simulations and Sensitivity Analysis
To determine possible influencing factors of FRAP experiments, we use a simulation framework of such experiments as well as a strategy to quantitatively determine the impact of each of these factors.
We start out by describing our general setup of FRAP simulations. Subsequent to the verification of the simulator, we investigate the impact of different experimental and analytical aspects of a FRAP experiment. To gain a quantitative measure, we apply a sensitivity method allowing a direct comparison of various influencing factors on the output of a FRAP experiment.
Simulations
FRAP data reflect intracellular spatio-temporal processes. The mathematical description of these processes necessitates partial differential equations (PDEs). Such PDEs consist of four different components:
-
1.
Spatio-temporal processes.
-
2.
Initial conditions.
-
3.
Boundary conditions.
-
4.
The feasible domain.
Therefore, our FRAP simulator integrates:
Processes
The most important intracellular molecular processes that have to be addressed are movement and interaction. Our simulator considers reaction and diffusion. Although advection would be a special case covered by our simulation framework, it was not further investigated.
Initial conditions
In general, the initial condition describes the characteristics of the modeled system at time step t = 0. Specifically, for FRAP simulations, the experimentally observed fluorescence distribution immediately after bleaching has to be approximated. Different types of such approximations are considered.
Boundary conditions
The boundary condition specifies the behavior of the modeled system at the boundaries of the geometries. Regarding fluorescent particles, the boundary condition specifies, e.g., a possible passage over a membrane.
Geometry of the feasible domain
The cellular space in which the experiment is performed has to be taken into account. Corresponding geometries can be simplified, or real cell geometries can be used.
The explicit system of PDEs for (S + 1) diffusing and reactively coupled compounds Bi is given in Eq. 1, where , , and are the diffusion coefficients and the association and dissociation rate of the compound Bi, respectively. The initial as well as the boundary conditions have to be chosen corresponding to the application examples given in Mai et al. (18):
| (1a) |
| (1b) |
| (1c) |
The detailed specifications of the implementation of the above-mentioned processes and methods can be found in the Supporting Material, including excerpts of the source code.
Numerical implementation
We employed Monte Carlo simulations to solve our numerical models and define their realizations as particles, although they do not have a spatial dimension. The advantage of these Monte Carlo simulations is that only the boundaries of the simulation domain (in our case plasma or nuclear membrane) have to be discretized, and no mesh of the whole domain has to be generated.
Discretization
To assure comparability of the simulation results we chose a standardized simulations setup.
Simulations were performed using 1000 time steps, 10,000 particles, and a time discretization of Δt = 0.005. To achieve a smooth recovery curve, 10 simulations per model and parameter set were averaged. These averaged curves were then compared with either the analytical solutions or, where applicable, the simulation results.
Simulations of two reactively coupled, diffusing particle types were performed. Parameter ranges for reaction and diffusion were chosen corresponding to the literature (18–20) and can be found in Table 1.
Table 1.
Reaction-diffusion parameter values and ranges
| D1 | D2 | kon | koff | |
|---|---|---|---|---|
| IA | 10 | 1 | 0.5 | 0.5 |
| IB | [5, 10] | [0, 5] | [0.001, 1] | [0.001, 1] |
| IIA1 | 10 | 1 | 0.5 | 0.5 |
| IIA2 | 10 | 1 | 0.5 | 0.5 |
| IIB1 | [5, 10] | [0, 5] | [0.001, 1] | [0.001, 1] |
| IIB2 | [5, 10] | [0, 5] | [0.001, 1] | [0.001, 1] |
| IIIA1 | 10 | 1 | 0.3 | 0.05 |
| IIIA2 | 10 | 1 | 0.3 | 0.05 |
| IIIA3 | 10 | 1 | 0.3 | 0.05 |
| IIIA4 | 10 | 1 | 0.3 | 0.05 |
| IIIB | [5, 10] | [0, 5] | [0.001, 1] | [0.001, 1] |
Reaction-diffusion parameter values and ranges used for Monte Carlo simulations. Two reactively coupled, diffusing particle types are simulated. The diffusion coefficients are D1 and D2 whereas the reaction is determined by the association and dissociation rates kon and koff, respectively.
The overall number of simulations depended on the amount of parameters studied and was set according to the Morris method (see Section S2.3 in the Supporting Material).
Code verification
The performance of all algorithms implemented for the particle-based simulations had to be confirmed. Therefore, we employed analytical solutions of reaction-diffusion problems as described in Mai et al. (18) and compared them with simulations of such experiments under the same conditions used for calculating the analytical solutions. The models used include multiple diffusion and reaction schemes (see Section S3 in the Supporting Material).
We demonstrate exemplarily the results for two different model types:
-
1.
Diffusion of only one fraction of reactively coupled particles while the other fraction is immobile; and
-
2.
Diffusion of both particle fractions (Fig. 1).
The initial bleaching profile applied corresponds to the adapted constant initial condition (see Section S3.1 in the Supporting Material). For both models an analytical solution has been described previously (18).
Figure 1.
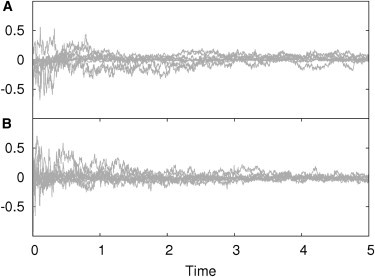
Analysis of simulation accuracy. Relative error between FRAP simulations and analytical solutions. Each subplot shows the error at each simulated time step using 10 different parameter sets. (A) Simulation of two reactively coupled particle fractions, one diffusing and the other one immobile. (B) Both reactively coupled particle fractions are diffusing.
Sensitivity analysis
The results of simulations using the previously described implementations, are strongly dependent on the parameterization of the processes, i.e., the result will change by variation of diffusion coefficients or the simulation domain. The following section will describe the elementary effects-based method we used to quantify these changes allowing for a comparability of parameter impacts.
In general, an elementary effect is the change of the model output given by adjusting one parameter whereas all others kept constant. It is defined as
| (2) |
where EEi is the elementary effect of the ith parameter, M is the model dependent on the N parameters p1,…,pN, and Δ is the change of the ith parameter. The parameters have to be scaled to the unit interval [0,1], because the scaling of the parameter to true values is already a part of the model. Therefore, Δ will also range between 0 and 1.
To obtain the elementary effect of a certain parameter i, the EEi has to be calculated for K different parameter constellations to assure a mean effect of this parameter i. An overall number of 2NK parameter sets would be necessary to estimate the elementary effect of the N parameters based on K single samples (NK reference sets and NK sets with adjusted parameter values). In turn, 2NK model runs are needed to calculate the elementary effects. To reduce the number of parameter sets and therefore the number of model runs, an efficient way to sample is the use of K parameter trajectories.
A parameter trajectory is generated as follows:
-
(A)
A permutation of the vector m = (1,2,…,N) is calculated;
-
(B)
A random, initial parameter set p(0) is generated;
-
(C1)
The second parameter set p(1) is determined by p(0), with the parameter corresponding to the first entry of m adjusted;
-
(C2)
The next parameter set p(2) is determined by p(1), with the parameter corresponding to the second entry of m adjusted; and
-
(CN)
The last parameter set of the trajectory p(N) is determined by p(N−1), with the parameter corresponding to the last entry of m adjusted.
By using this parameter sampling strategy, the number of parameter sets in use is reduced from 2NK to (N + 1) K. This design was suggested by Morris (16).
For generating the trajectories, a MATLAB (Ver. 2012a, The MathWorks, Natick, MA) code was employed from the MATLAB Toolbox (21).
The proper elementary effect per parameter is calculated subsequently based on K single values. Because the mean of the values μi may prove misleading due to cancellation of effects (22), it is suggested to use the mean of the absolute single values,
| (3) |
where K is the number of trajectories and EEi(j) is the elementary effect of parameter i within the jth trajectory, and μi* is the sensitivity measure of the ith parameter.
We used K = 20N trajectories in all of our elementary effect studies. Therefore, the total number of parameter sets equals 20N (N + 1).
Analysis of FRAP Modeling and Acquisition
The performance of the simulations was tested successfully against our recently described analytical solution of the FRAP recovery curve (18). In all simulations performed the relative error between simulation and analytical solution was randomly distributed around zero and below 0.5% (see Fig. 1), demonstrating the reliable performance of the implemented algorithms. The same was observed for all other models (described in Mai et al. (18)), reaction schemes, initial conditions, and parameter sets (data not shown).
Because modeling assumptions are often only simplifications of the reality, we determined the impact of variations in these assumptions by varying corresponding model parameters. The model parameters were adapted by using the Morris method. The elementary effects were then calculated to gain a sensitivity measure.
The following three conditions were investigated in detail:
-
1.
Initial condition. What is the most appropriate model description for the fluorescence distribution immediately after the bleach? We addressed the question which of the simplified initial distributions describes the Gaussian profile best, and whether this simplification can be generalized (i.e., for arbitrary reaction diffusion parameters).
-
2.
Boundary condition. Do we need to restrict movement possibilities of the fluorophores in our models? To study this issue in more detail, we investigated the influence of the chosen boundary condition on the parameter inversion outcome.
-
3.
Geometry. It seems likely that the geometry of the bleached compartment has a considerable impact on inverted parameters. As a generalized approach, we sampled the whole parameter space using real cell geometries as a bleaching compartment.
Other factors are also known to influence the analysis and acquisition of FRAP data (23–28). Two of these cases considering normal diffusion, while neglecting sub- or superdiffusion and the simplification of three-dimensional processes by two-dimensional projections, were investigated in addition to Conditions 1–3. Corresponding results can be found in the Supporting Material. In contrast to the simplification of anomalous diffusion we employed, many studies have investigated the influence of internal boundaries in a more explicit way by using geometries of real cellular structures extracted from microscopy or tomography data (25,26,29). In this study, we focus on the general impact of sub- and superdiffusion. Whereas our approach can also be extended to determine the impact of real cellular boundaries, the simplified strategy will yield a reliable approximation of the general impact of heterogeneous environments.
Using FRAP simulations, we aim to identify the most influential (i.e., sensitive) factors on the outcome of a FRAP experiment. These results are essential for an optimized experimental setup and for assessing whether determined reaction diffusion parameters are reliable.
Influence of initial distribution inside the bleaching spot
The bleaching spot profile observed directly after bleaching corresponds to a Gaussian distribution, which cannot be described analytically in most cases. Nevertheless, methods have been described of how to adapt the initial Gaussian condition to make calculating an analytical solution possible. The initial fluorescence intensity profile in the bleaching spot is simplified either by a constant or adjusted constant (19) bleaching profile, or, in the most simplified way, the initial fluorescence intensity (I0) is considered to be I0 = 0 (10). We investigated whether these different initial conditions (ICs) are an appropriate approximation of the initial fluorescence distribution.
We started by using the specific parameter set IA (Tables 1 and 2) for the comparison of three different initial conditions as depicted in Fig. 2. These values were used to adjust the initial value θ and the radius R (see the Supporting Material for a detailed description). Simulations with these particular parameters led to a recovery adequately approximating the curve of the Gaussian IC only if an adjusted constant initial value θ (adapted radius R) were used, while the constant IC led to pronounced discrepancies between the recovery curves (Fig. 2). To prove that these results are not only valid for this specific parameter set, the elementary effects were calculated for all the reaction-diffusion and experimental setup parameters (parameter ranges used for simulation are IB; see Tables 1 and 2).
Table 2.
Experimental parameter values and ranges
| Bleaching spot (a, σ, r0) or (θ, r) | Position spot (d, R) or (dM) | b | |
|---|---|---|---|
| IA | 0.8, 1.2, 1 | — | — |
| IB | [0.1, 0.9], [0.1, 2], [0.5, 2.5] | — | — |
| IIA1 | 0.1, 2 | 1.8, 4 | 0 |
| IIA2 | 0.1, 2 | 1.8, 4 | 1 |
| IIB1 | [0.1, 0.9], [0.1, 0.9] | [0, 3], [4, 10] | [0, 1] |
| IIB2 | [0.55, 0.71], [1.74, 2.18] | [0, 3], [4, 10] | [0, 1] |
| IIIA1 | 0.1, 1 | 14.23 | 0 |
| IIIA2 | 0.1, 1 | 8.64 | 0 |
| IIIA3 | 0.1, 1 | 12.69 | 0 |
| IIIA4 | 0.1, 1 | 6.05 | 0 |
| IIIB | [0.55, 0.71], [1.74, 2.18] | [7.5, 14.25] | 0 |
Experimental parameter values and ranges used for Monte Carlo simulations. For bleaching profile, either a Gaussian distribution is chosen (bleaching level a, standard deviation σ, and radius r0) or an adjusted constant profile (bleaching level θ and adjusted radius r) is chosen. The position of the bleaching spot is specified by the distance between the center of the bleaching spot and a circular compartment d and a radius R of this circular compartment or a mean (average) distance to a complex compartment geometry dM. The kind of boundary condition is set by b.
Figure 2.
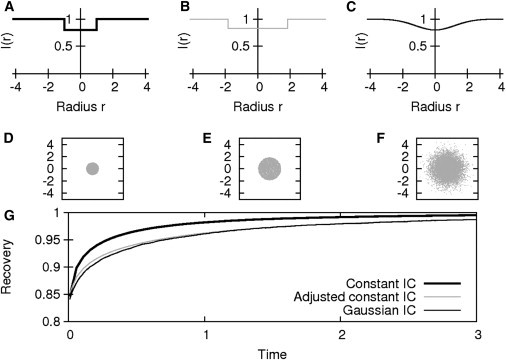
Influence of different types of initial condition (IC). (A–C) Bleaching spot profiles. (D–F) Initial distribution of bleached particles. (A and D) Constant IC. (B and E) Adjusted constant IC. (C and F) Gaussian IC using parameter set (IA), and (G) resulting FRAP recovery curves.
A total of 1120 (= 20 N(N + 1)) parameter sets were used to simulate FRAP curves considering all four different ICs (Gaussian profile, zero initial profile, constant profile, and adjusted constant profile). The elementary effects were calculated as differences to the Gaussian IC and were used to identify the parameters responsible for the deviation. The results as depicted in Fig. 3 show that the adjusted constant IC performs best over the whole parameter range, suggesting that it represents the most appropriate simplification of the initial bleaching profile. The elementary effects of the other two ICs are significantly larger for all parameters investigated.
Figure 3.
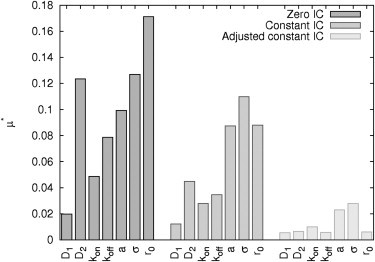
Influence of different parameters on mean absolute error between Gaussian IC versus simplified ICs. Elementary effects μ* of reaction-diffusion parameters (D1, D2, kon, koff) and the experimental setup (depth a and variance σ of Gaussian profile and radius of spot r0) using parameter ranges (IB).
Interestingly, the most sensitive parameters of the adjusted constant IC are the experimental parameters a and σ describing the characteristics of the Gaussian profile (i.e., depth a and variance σ). Consequently, it should be taking care of a comparable bleaching profile over all FRAP experiments analyzed.
Our simulations showed that an adjusted constant IC with the corresponding analytical solution is an appropriate approximation of the initial Gaussian distribution.
Influence of boundary condition
In typical FRAP models, the bleached compartment is considered to be infinite, allowing the observed molecules to distribute evenly across all membranes (boundary). This flow boundary condition usually does not apply to real cellular environments.
That the boundary condition indeed has an impact on the model outcome has already been shown (12,30) for selected parameter sets. However, to determine whether this is a general effect over different parameter ranges, we performed simulations using different boundary conditions and determined their effect on the parameter inversion outcome.
We started by running simulations with specific parameter sets IIA1 and IIA2 (Tables 1 and 2) in an artificial geometry. A circular geometry, exemplifying an arbitrary membrane enclosed cellular structure, was used as a simulation domain with either a flow boundary condition (b = 1; i.e., particles are allowed to cross the membrane without hindrance), or with a no-flow boundary condition (b = 0; i.e., the particles are restricted to the membrane enclosed domain).
The final distribution of particles simulated and the resulting averaged recovery curves are depicted in Fig. 4. It seems obvious that the simulations using this specific parameter set attach great importance to the boundary condition chosen.
Figure 4.
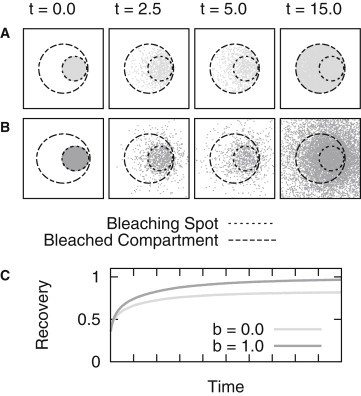
Influence of the chosen boundary condition on the FRAP recovery curve. Results are shown for simulations in a circular geometry with a bleaching spot positioned at the edge of the domain. (A, upper panel) Distributions of bleached particles considering a no-flow boundary are depicted (parameter set IIA1). (B, lower panel) Here, the no-flow boundary condition was omitted (parameter set IIA2). (C) Corresponding recovery curves.
The elementary effects were determined to assess whether or not this is a general outcome. All simulations were run employing the adjusted initial condition as we showed it to be the most appropriate approximation of the Gaussian profile. The parameter ranges used for the Monte Carlo simulations are IIB1 (Tables 1 and 2).
A total of 1800 (= 20 N (N + 1)) parameter sets were used to simulate the according FRAP curves and calculate the elementary effects based on the absolute distance between two recovery curves. The results as shown in Fig. 5 (black bars) are particularly interesting in two aspects: The most sensitive factors are θ and r describing the initial profile while b, the parameter characterizing the probability of particles crossing a boundary, is highly insensitive.
Figure 5.
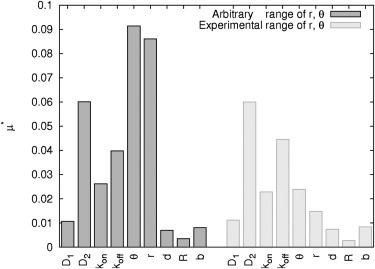
Effect of boundary condition. Elementary effects μ* of reaction-diffusion parameters (D1, D2, kon, koff) and experimental setup: depth θ and adjusted radius r of bleaching spot, distance between center compartment and center spot d, radius R of circular compartment and probability allowing particles crossing the membrane b (parameter ranges IIB1 and IIB2).
We wondered whether the insensitivity of b might be due to the broad range for θ and r chosen for the previous elementary effect analysis. We already learned while studying the influence on the initial condition that the initial profile should be kept constant during the experiments. Therefore, we restricted the range of θ and r to values obtained in real FRAP experiments (AhR-GFP bleached within the cytoplasm of Hepa-1c1c7 cells; see parameter ranges IIB2 in Tables 1 and 2). Simulations were run again with 1800 parameter sets where only the values of θ and r were adapted according to the restricted parameter ranges. Simulation results are depicted in Fig. 5 (gray bars). Limiting the parameter ranges of θ and r has no effect on the elementary effect of b.
Although our initial simulation using a single specific parameter set alleges an important role of the boundary condition chosen, our global analysis of arbitrary and experimental parameter ranges disproves this observation. In conclusion, these findings suggest that the boundary condition chosen has only a marginal effect on the inverted reaction diffusion parameters. Furthermore, inversion of a fast diffusion coefficient (D1) is highly unreliable, because the experimental parameters (θ and r) are more sensitive and therefore have an even greater impact on the FRAP recovery curve than the parameter of interest. The goal would be to decrease the ranges of the experimental parameters until their elementary effect is lower than that of each reaction-diffusion parameter.
Influence of bleaching spot position
In a setup similar to that described above for the boundary condition, the significance of the bleaching spot position for the FRAP recovery outcome was assessed. A cytoplasmic geometry was reconstructed from microscopy images using NeuRA2 (31,32) and simulations were performed at four different bleaching spot positions using 400 time steps to simulate 20 time units (Fig. 6 A). Recoveries of two different fractions of particles were examined using the parameterization IIIA (Tables 1 and 2).
Figure 6.
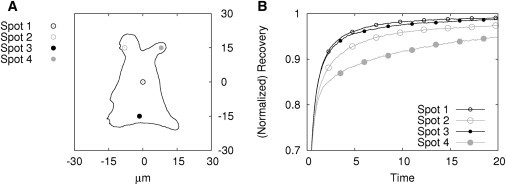
Influence of the bleaching spot location on the FRAP recovery. (A) Cytoplasmic geometry with four different positions of the bleaching spot. (B) Simulation results (recovery curves; parameter sets IIIA).
To find a reference recovery curve for comparison, we studied the particle distribution within the geometry at the simulated time steps (see the Supporting Material). A homogeneous distribution of particles was only observed for the central position of the bleaching spot (Fig. 6, Spot 1). Therefore, the corresponding recovery curve was set as a reference.
In these four examples, an influence of the bleaching spot position on the recovery curve is only apparent in regions of hindered diffusion (Fig. 6, Spots 2 and 4). Interestingly, a position next to the boundary of the geometry where the diffusion can take place unhindered to at least one half-plane (Fig. 6, Spot 3) has only a negligible influence on the recovery curve. We can then conclude that bleaching spots should not be positioned in regions like the cell edge, where protrusions could restrict the diffusion.
To prove that these observations are true not only for the single specific setup just presented but for the whole parameter range, the elementary effects were determined. Our previous results made obvious that the variations in experimental parameters should be minimized. Therefore, simulations were performed with limited, experimentally deduced, parameter ranges for r and θ (parameter ranges IIIB, Tables 1 and 2) to reliably assess the sensitivity of the reaction-diffusion parameters related to the bleaching spot position.
To address the relative position of the bleaching spot to the compartment boundary, we introduce a new parameter dM, which represents the mean distance to the periphery. The value dM is calculated as the mean length of 60 line segments from the bleaching spot center to the geometry boundary. This distance measure yields small values for positions in protrusions of a geometry and comparatively large values for those near a half-plane (Fig. 6, Spot 3) and in the center of the geometry (Fig. 6, Spot 1). The distribution of the distance-measure dM within the cytoplasmic geometry can be found in the Supporting Material. The parameter dM was varied in a range according to its distribution. A total of 1120 parameter sets (= 20 N (N + 1)) were used to simulate the according FRAP curves and calculate the elementary effects based on the absolute distance between two curves.
The analysis showed that dM does have a significant impact on the recovery—one that is even higher than that of the other experimental parameters (θ, r). Because the sensitivity of a parameter is directly related to the corresponding parameter range, limiting this range increases parameter certainty (see Section S3.2 in the Supporting Material). Therefore, the variation of dM has to be narrowed to achieve the overall goal of a reliable parameter inversion for diffusion and reaction processes. Although this seems hard to accomplish, large variations of dM can only appear if spot positions in diverse parts of the geometry are used for the bleaching experiments. Performing the experiments in comparable regions of the geometry is particularly important, as it is hard to calculate the uncertainty (i.e., parameter range) of this parameter in retrospect; information about the relative position of the bleaching spot and the cellular boundaries is limited.
Discussion
Intracellular reaction-diffusion parameters are commonly inverted from FRAP data. Although performing such experiments is facilitated by implementation of FRAP acquisition tools on commercially available microscopes, some aspects still have to be considered. Either the experimental setup or the subsequent analysis can contribute to misleading data interpretation, which has already been shown by several groups (19,23–26,30). All these studies focused on specific parameter sets. However, we propose a global approach employing Monte Carlo-based reaction-diffusion simulations coupled with a sensitivity measure based on elementary effects. Calculating elementary effects allows us to deduce the general influence of a parameter, obviating a bias by choosing a nonrepresentative parameter set.
The initial condition (IC), i.e., the initial fluorescence distribution characterized by the depth and the width of the Gaussian profile, was identified as a main influencing factor on the shape of the recovery curve. Variations in this initial distribution led to an uncertainty in reaction-diffusion parameter inversion. This issue can be addressed first of all by using identical settings in a set of FRAP experiments, which is usually taking care of. However, even accurate data acquisition can lead to diverse bleaching profiles. Concluding from our study an a posteriori outlier selection would be advisable to assure the comparability of the initial fluorescence distribution.
Because an analytical solution is not available for a Gaussian initial profile, parameter inversion models rely on an approximated IC. Our comparison showed that the adjusted constant IC is not only an adequate approximation of the Gaussian profile but also outperformed all other available ICs.
Although in cellular systems various mechanisms of membrane transport exist (i.e., boundary conditions of the system), analytical models used for parameter inversion of FRAP data only consider unhindered membrane passage. Unexpectedly, variations in transport mechanism indeed only had a minor impact on the recovery curve, indicating that such models can be used for data analysis without concern.
Cellular geometries can be very diverse with respect to the domain available for an unhindered diffusion. Therefore, positioning of the bleaching spot might have an considerable impact on the FRAP recovery. Our simulations showed that only in exceptional cases, like bleaching in cell edge protrusions, the spot position has a perceivable influence. Nevertheless, such positions should be avoided during data acquisition—especially because it is not possible to retrace the position of the bleaching spot relative to the compartment geometry from the generated imaging data. Hence, an a posteriori outlier selection cannot be performed as proposed for the initial distribution. Neglecting a priori considerations for bleaching spot positioning would increase the parameter uncertainty.
Overall, the parameters describing the initial bleaching profile, i.e., the bleaching efficiency and the size of the bleached region, were among the most sensitive factors in all cases investigated (Fig. 7). This underlines the importance of a consistent experimental setup together with an a posteriori selection of inconsistent measurements. Apart from these experimental aspects, a bleaching spot position avoiding cell protrusions is recommended. Surprisingly, our study showed that an exact knowledge of the underlying membrane transport mechanisms is not essential for an accurate data analysis.
Figure 7.
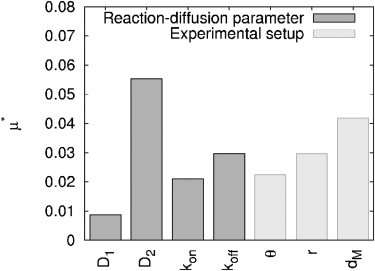
Effect of bleaching spot position. Elementary effects μ* of reaction-diffusion parameters (D1, D2, kon, koff) and experimental setup (depth θ and adjusted radius r of bleaching spot as well as median distance dM of bleaching spot center to compartment’s boundary) in real geometry (parameter ranges IIIB).
In conclusion, our work shows that elementary effects are a valuable tool in assessing parameter influences. We demonstrate that using only specific parameter sets can lead to contradictory results compared to the global elementary effects. Therefore, conducting a sensitivity analysis is highly valuable not only in studying FRAP data but also in studying intracellular processes in general.
Acknowledgments
We are deeply indebted to Matthias Cuntz (Helmholtz Centre for Environmental Research, Leipzig, Germany) for critical comments and helpful discussion.
J.M. was supported by the Helmholtz Impulse and Networking Fund through the Helmholtz Interdisciplinary Graduate School for Environmental Research (HIGRADE). Note that this publication was based on studies performed as part of our project “From Contaminant Molecules to Cellular Response: System Quantification and Predictive Model Development”, which was funded by the Helmholtz Alliance on Systems Biology.
Supporting Material
References
- 1.Phair R.D., Gorski S.A., Misteli T. Measurement of dynamic protein binding to chromatin in vivo, using photobleaching microscopy. Methods Enzymol. 2004;375:393–414. doi: 10.1016/s0076-6879(03)75025-3. [DOI] [PubMed] [Google Scholar]
- 2.Phair R.D., Scaffidi P., Misteli T. Global nature of dynamic protein-chromatin interactions in vivo: three-dimensional genome scanning and dynamic interaction networks of chromatin proteins. Mol. Cell. Biol. 2004;24:6393–6402. doi: 10.1128/MCB.24.14.6393-6402.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Köster M., Frahm T., Hauser H. Nucleocytoplasmic shuttling revealed by FRAP and FLIP technologies. Curr. Opin. Biotechnol. 2005;16:28–34. doi: 10.1016/j.copbio.2004.11.002. [DOI] [PubMed] [Google Scholar]
- 4.Braga J., McNally J.G., Carmo-Fonseca M. A reaction-diffusion model to study RNA motion by quantitative fluorescence recovery after photobleaching. Biophys. J. 2007;92:2694–2703. doi: 10.1529/biophysj.106.096693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Carrero G., Crawford E., Hendzel M.J. Quantification of protein-protein and protein-DNA interactions in vivo, using fluorescence recovery after photobleaching. Methods Enzymol. 2004;375:415–442. doi: 10.1016/s0076-6879(03)75026-5. [DOI] [PubMed] [Google Scholar]
- 6.Stavreva D.A., McNally J.G. Fluorescence recovery after photobleaching (FRAP) methods for visualizing protein dynamics in living mammalian cell nuclei. Methods Enzymol. 2004;375:443–455. doi: 10.1016/s0076-6879(03)75027-7. [DOI] [PubMed] [Google Scholar]
- 7.Giese B., Au-Yeung C.-K., Müller-Newen G. Long term association of the cytokine receptor gp130 and the Janus kinase Jak1 revealed by FRAP analysis. J. Biol. Chem. 2003;278:39205–39213. doi: 10.1074/jbc.M303347200. [DOI] [PubMed] [Google Scholar]
- 8.Howell B.J., Hoffman D.B., Salmon E.D. Visualization of Mad2 dynamics at kinetochores, along spindle fibers, and at spindle poles in living cells. J. Cell Biol. 2000;150:1233–1250. doi: 10.1083/jcb.150.6.1233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Howell B.J., Moree B., Salmon E.D. Spindle checkpoint protein dynamics at kinetochores in living cells. Curr. Biol. 2004;14:953–964. doi: 10.1016/j.cub.2004.05.053. [DOI] [PubMed] [Google Scholar]
- 10.Sprague B.L., Pego R.L., McNally J.G. Analysis of binding reactions by fluorescence recovery after photobleaching. Biophys. J. 2004;86:3473–3495. doi: 10.1529/biophysj.103.026765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Carrero G., Crawford E., de Vries G. Characterizing fluorescence recovery curves for nuclear proteins undergoing binding events. Bull. Math. Biol. 2004;66:1515–1545. doi: 10.1016/j.bulm.2004.02.005. [DOI] [PubMed] [Google Scholar]
- 12.Carrero G., McDonald D., Hendzel M.J. Using FRAP and mathematical modeling to determine the in vivo kinetics of nuclear proteins. Methods. 2003;29:14–28. doi: 10.1016/s1046-2023(02)00288-8. [DOI] [PubMed] [Google Scholar]
- 13.Reits E.A., Neefjes J.J. From fixed to FRAP: measuring protein mobility and activity in living cells. Nat. Cell Biol. 2001;3:E145–E147. doi: 10.1038/35078615. [DOI] [PubMed] [Google Scholar]
- 14.Houtsmuller A.B., Vermeulen W. Macromolecular dynamics in living cell nuclei revealed by fluorescence redistribution after photobleaching. Histochem. Cell Biol. 2001;115:13–21. doi: 10.1007/s004180000234. [DOI] [PubMed] [Google Scholar]
- 15.White J., Stelzer E. Photobleaching GFP reveals protein dynamics inside live cells. Trends Cell Biol. 1999;9:61–65. doi: 10.1016/s0962-8924(98)01433-0. [DOI] [PubMed] [Google Scholar]
- 16.Morris M.D. Factorial sampling plans for preliminary computational experiments. Technometrics. 1991;33:161–174. [Google Scholar]
- 17.Saltelli A., Ratto M., Tarantola S. John Wiley & Sons; New York: 2008. Global Sensitivity Analysis. The Primer. [Google Scholar]
- 18.Mai J., Trump S., Attinger S. Are assumptions about the model type necessary in reaction-diffusion modeling? A FRAP application. Biophys. J. 2011;100:1178–1188. doi: 10.1016/j.bpj.2011.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hinow P., Rogers C.E., DiBenedetto E. The DNA binding activity of p53 displays reaction-diffusion kinetics. Biophys. J. 2006;91:330–342. doi: 10.1529/biophysj.105.078303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mueller F., Wach P., McNally J.G. Evidence for a common mode of transcription factor interaction with chromatin as revealed by improved quantitative fluorescence recovery after photobleaching. Biophys. J. 2008;94:3323–3339. doi: 10.1529/biophysj.107.123182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ekstrom, P.E. 2005. Eikos- A Simulation Toolbox for Sensitivity Analysis. Global Sensitivity Analysis (software). The European Commission Joint Research Center, Ispra, Italy. http://sensitivity-analysis.jrc.ec.europa.eu.
- 22.Campolongo F., Cariboni J., Saltelli A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007;22:1509–1518. [Google Scholar]
- 23.Weiss M. Challenges and artifacts in quantitative photobleaching experiments. Traffic. 2004;5:662–671. doi: 10.1111/j.1600-0854.2004.00215.x. [DOI] [PubMed] [Google Scholar]
- 24.Olveczky B.P., Verkman A.S. Monte Carlo analysis of obstructed diffusion in three dimensions: application to molecular diffusion in organelles. Biophys. J. 1998;74:2722–2730. doi: 10.1016/S0006-3495(98)77978-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sbalzarini I.F., Mezzacasa A., Koumoutsakos P. Effects of organelle shape on fluorescence recovery after photobleaching. Biophys. J. 2005;89:1482–1492. doi: 10.1529/biophysj.104.057885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sbalzarini I.F., Hayer A., Koumoutsakos P. Simulations of (an)isotropic diffusion on curved biological surfaces. Biophys. J. 2006;90:878–885. doi: 10.1529/biophysj.105.073809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Siggia E.D., Lippincott-Schwartz J., Bekiranov S. Diffusion in inhomogeneous media: theory and simulations applied to whole cell photobleach recovery. Biophys. J. 2000;79:1761–1770. doi: 10.1016/S0006-3495(00)76428-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Saxton M.J. Anomalous subdiffusion in fluorescence photobleaching recovery: a Monte Carlo study. Biophys. J. 2001;81:2226–2240. doi: 10.1016/S0006-3495(01)75870-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Koumoutsakos P. Multiscale flow simulations using particles. Annu. Rev. Fluid Mech. 2005;37:457–487. [Google Scholar]
- 30.Angelides K.J., Elmer L.W., Elson E. Distribution and lateral mobility of voltage-dependent sodium channels in neurons. J. Cell Biol. 1988;106:1911–1925. doi: 10.1083/jcb.106.6.1911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Broser P.J., Schulte R., Wittum G. Nonlinear anisotropic diffusion filtering of three-dimensional image data from two-photon microscopy. J. Biomed. Opt. 2004;9:1253–1264. doi: 10.1117/1.1806832. [DOI] [PubMed] [Google Scholar]
- 32.Jungblut D., Queisser G., Wittum G. Inertia based filtering of high resolution images using a GPU cluster. Comp. Vis. Sci. 2011;14:181–186. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


