Abstract
This article investigates the dynamics of an important bacterial pathogen, Xylella fastidiosa, within artificial plant xylem. The bacterium is the causative agent of a variety of diseases that strike fruit-bearing plants including Pierce’s disease of grapevine. Biofilm colonization within microfluidic chambers was visualized in a laboratory setting, showing robust, regular spatial patterning. We also develop a mathematical model, based on a multiphase approach that is able to capture the spacing of the pattern and points to the role of the exopolymeric substance as the main source of control of the pattern dynamics. We concentrate on estimating the attachment/detachment processes within the chamber because these are two mechanisms that have the potential to be engineered by applying various chemicals to prevent or treat the disease.
Introduction
The bacterial pathogen Xylella fastidiosa is responsible for a variety of diseases affecting economically important agricultural crops such as grapevines, citrus, peach, and blueberries among others (1,2). The bacteria colonize the plant xylem vessels, eventually forming a biofilm, which is believed to be responsible for obstructing passage of water and nutrients to the aerial parts of the plant. The disease severely reduces the plant harvest, eventually killing the plants because there is no practical cure once the plant becomes infected. The bacterium is a serious threat to the wine industry in the US, because it is the causal agent of Pierce’s disease affecting wine grapes (1). The economic costs are enormous, affecting the multi-billion dollar wine industry in California and other states (3). Pierce’s disease and other diseases caused by X. fastidiosa are found throughout the Southern US in states from California to Florida, including Texas, New Mexico, Alabama, Georgia, and North and South Carolina.
Although the impacts of the disease are well documented and tremendous efforts have been made in controlling the insect vector that transmits the bacterium, very little is understood about the internal plant colonization. Understanding the development and dynamics of the biofilm formation will help develop methods to prevent or treat the infection within the plant. The goal of this investigation is to develop and analyze a theoretical model of the biofilm dynamics within artificial plant xylem.
We base our model on experimental studies that introduce bacteria into microfluidic chambers along with plant sap as the growth media. Microfluidic channels are used as artificial xylem vessels to reproduce phenomena occurring inside the plant, but with the advantage of allowing real-time microscopic observations. As the bacteria attach to the surface of the chambers, typical biofilm formation events are initiated (including phenotypic changes from planktonic to biofilm-forming life-styles (4)). As the biofilm is developing, sticky substances known as exopolymeric substances (EPS) are secreted by the bacterium and form part of a matrix where cells are protected from environmental stresses (4). These biofilms composed of bacterial cells and matrix are arranged in three-dimensional structures that resemble mountains and valleys. As the biofilm grows, more of the exopolymeric glue is produced. Eventually, striking patterns emerge within the chamber (see Fig. 1). The images display a relatively uniform pattern of holes and channels similar to, but phenomenologically distinct from, convection cells.
Figure 1.

Experimental view of the pattern formed within the artificial channel. The vertical scale is ∼80 μm. (Dark regions) Bacterial/biomass; the flow is from left to right.
The mathematical model developed below is derived using a multiphase framework that distinguishes several phases of the biofilm/fluid system. Because free bacteria are fed into the system within plant sap we must account for 1), fluid dynamics; 2), free bacteria; 3), bound bacteria; and 4), EPS. Free and bound bacteria behave very differently, although these two phases interact through attachment/detachment processes. Unbound bacteria move within the fluid phase, whereas bound bacteria are locked within the EPS phase (neither of which move appreciably). Therefore, the most general model has four material phases. In addition, the phase momenta are different because the fluid moves throughout the system, whereas the biofilm is relatively immobile and exerts a drag on the fluid. In the model given below, we derive equations that govern the dynamics of the volume fractions of each phase and the accompanying momentum equations.
Background
Multiphase methods have been used to model biofilm dynamics for several years (5–9). Each of these have treated the biofilm as a mixture between a fluid and networked solid. The main variations have to do with the treatment of the dynamical forces that are allowed. For example, in Cogan and Keener (5), the fluid motion is neglected and the focus is on biofilm production and redistribution whereas Zhang et al. (8) focuses on the effect of different biofilm material properties.
Initially, multiphase models were introduced as a model of biofilms to account for the effect of biomass redistribution and the interaction between the developed biofilm and the external fluid dynamics in a flow-cell geometry (i.e., dynamics within a two-dimensional tube). In Cogan and Keener (5) and Klapper and Dockery (7), the interaction between biomass production and the subsequent osmotic swelling played a dominant role. Differential growth that occurs due to gradients in nutrient leads to differential osmotic forces, which eventually induces a fingering-type instability that seems to play a role in the spatial patterning observed in experimental biofilms.
Later, Cogan and Keener (6) focused on the interplay between biofilm motion induced by the external fluid motion and the osmotic pressure. For a channel filled with a biofilm mixture that is forced to move by a pressure gradient, the network is pushed toward the sides of the channel. This motion is resisted by increasing osmotic pressure that tends to swell the network and resist the compression. A balance is eventually reached and a new steady distribution is reached that has a biofilm-free region in the center of the channel.
In Anguige et al. (9), the authors consider a different physical domain, and study the spread of a one-dimensional biofilm. They focus on a detailed model of the upregulation of EPS production via a quorum-sensing signal while neglecting the effect of osmotic pressures.
There are several new aspects of the multiphase framework that are explored here. One important contribution is expanding the biofilm compartment from a networked solid to distinct bacteria and polymer components. Along with the free bacterial phase, the attached, biofilm bacteria are a necessary component of this study because the biofilm is substantially affected by the addition of free bacteria (and the subsequent transient attachment to the polymer network). Although expanding the model allows for a more detailed treatment of the kinetics, a four-phase model requires substantial alterations in the numerical methods that we use.
In this study, we also neglect the role of the osmotic pressure so that we can focus on the interaction between the free and attached bacteria. This interaction seems to play a dominant role in the patterns that are observed although we are investigating the role of calcium experimentally (10). To our knowledge, there have been no mathematical models of Pierce’s disease and we are able to provide a model that captures one of the earliest and most distinctive biofilm processes exhibited by the bacterium. Thus, the model is formulated to focus on understanding the impact of adding or removing mineral elements to treat and/or prevent the disease progression without the use of antibiotics.
We make some a priori assumptions that simplify the model. The two most important assumptions focus on the momentum of the bacterial and EPS phases. As the free bacteria are transported by the fluid, they also use twitching motility to control their direction (11). This leads to both random and directed motility. For this article, we ignore the directed motility and assume that the free bacteria move with the same velocity as the fluid with additional random diffusion. From observations, it is clear that some bacteria move upstream, counter to the fluid motion; however, the cues that the bacteria are responding to are unknown and the density of bacteria that move against the flow is apparently much less than the bulk of the free bacteria. Likewise, even though the fluid exerts force on the biofilm (EPS and bound bacterial aggregate), we assume that both of these phases do not advect. This allows us to consider only one momentum equation to determine the fluid velocity. These assumptions are also consistent with the scales of the motion that are observed in the experiments.
The next two sections describe the experimental methods and mathematical model in more detail. These sections are followed by a section describing the results of our analysis including the dispersion relation and nonlinear, numerical studies. Our results indicate that the model captures the dynamics of the developing biofilm pattern; however, there are several aspects of the model that are not addressed. We discuss these in the final section.
Experimental Methods
Microfluidic chamber experiments using sap as growth media
Plant xylem fluid (sap) was collected from Vitis vinifera cv. Chardonnay grapevines grown near Geneva, New York, in April 2008, using a protocol previously described in Zaini et al. (12). Briefly, grapevines were cut and the xylem sap fluid was collected into 50-mL conical tubes for 1–2 h. Collected sap was brought back to the laboratory, filter-sterilized using a 0.22 μm-membrane filter, and frozen at −80°C for further use. After thawing, the collected sap was used as bacterial growth media inside microfluidic chambers. The fabrication of the microfluidic chambers was performed as previously described in De La Fuente et al. (13).
A two-parallel-channel chamber design was used for the experiments (80-μm wide by 3.7-cm long by 50-μm deep). Each channel has two inlets to allow the separate entry of media and bacteria and an outlet to allow media to flow out the other end. Xylella fastidiosa bacterial suspensions were introduced into the microfluidic chamber through tubing connected to the chamber as previously described in De La Fuente et al. (13). The media flow inside the chamber was controlled by an automated syringe pump (Pico Plus; Harvard Apparatus, Holliston, MA) and kept constant at 0.20 μL/min for the duration of the experiment. Microfluidic chambers were mounted onto a model No. IMT-2 microscope (Olympus, Melville, NY) and observed using 40× phase-contrast optics. Time-lapse images were recorded every 30 s with a SPOT-RT digital camera (Diagnostic Instruments, Sterling Heights, MI) controlled with MetaMorph Image software (Universal Imaging, Downington, PA).
To acclimate bacterial cells to grow in sap, X. fastidiosa cells were first grown in 8:2 mixture of sap and PD2 (14) media. After four days the media was switched to 9:1 sap:PD2 mixture for two days, and after that time full-strength sap was used.
Bacterial growth and movement was observed after the initial 3–4 days of incubation in mixtures of PD2 and sap. Although we could not observe bacterial growth when cells were incubated directly in pure sap (the acclimation period by incubation in different dilutions of sap before exposing them to pure sap) resulted in normal growth and movement. X. fastidiosa exhibited different growth habits depending on the culture media used. When grown in PD2, X. fastidiosa develops cell aggregates by 7–10 days as observed previously in De La Fuente et al. (15), whereas in sap X. fastidiosa growth occurred as a lawn of cells (closer to a standard biofilm). The formation of biofilm as thick structures was observed after 8–10 days of incubation. Growth of X. fastidiosa in sap provides a more natural environment in the microfluidic devices that allows a biofilm formation process resembling what occurs in nature inside the host plants, therefore it is a more accurate experimental setting for the mathematical studies presented here.
Model
The model that we derive uses a multiphase framework. Multiphase models have been used for a variety of applications including tumor growth, cell blebbing, and biofilm dynamics (5,16). All multiphase models assume that the material within a domain consists of phases that collectively fill all of the space. Typically conservation laws describe the governing dynamics. In particular, each phase is characterized with a volume fraction and a momentum. The volume fractions of all phases sum to one because there are no voids. This is often termed the saturation condition (16). As long as the densities of all the phases are equal, density is equivalent to volume, so conservation of volume is equivalent to conservation of mass. We denote the volume fractions of the phases as ϕf, ϕb, ϕn,EPS, and ϕn,b for the fluid, free bacteria, EPS, and bound bacterial phases, respectively. The notation ϕn* indicates that this phase is associated with the networked or biofilm phase. The associated velocities are denoted u*. We are restricting our analysis to one dimension even though the model is easily generalized to multiple dimensions. As noted above, we assume that the velocity of the free bacteria is equivalent to the fluid velocity so ub ≡ uf and we assume that un,EPS ≡ un,b ≡ 0.
Conservation of volume
The free bacteria are advected by the fluid, transiently attach to the developing biofilm, reproduce, and randomly diffuse. Following Berg (17), we model the random motility of the free bacteria as a diffusional process. Because X. fastidiosa does not swim and only moves via type IV-pili twitching motility (11), its speed (and hence its diffusion) is much less than that observed for flagellated bacteria such as Escherichia coli.
Rather than introduce a specific nutrient, we model cell growth using a logistic term. This is a relatively standard method used for bacterial growth when the details of nutrient dynamics are neglected (18).
The attachment/detachment processes are more novel although there are similarities with the model of bacterial veils described in Cogan and Wolgemuth (19,20). We assume that bound bacteria may detach from the biofilm network at a rate α1, whereas the free bacteria attach at a rate α2. However, it is clear that the EPS network plays a substantial role in the attachment/detachment process. In particular, we assume that the detachment rate decays as more polymer is produced by the biofilm. Thus the detachment term is given as
Although other forms of the detachment term lead to nontrivial dispersion curves, unless the decay of the detachment is quite abrupt as EPS is produced, we were unable to find any parameter sets that matched to observed scales. In fact, our studies indicate that biofilms formed by X. fastidiosa are very sensitive to the EPS concentration, which is in accord with a variety of studies that show that free bacteria are readily attached to biofilms growing within grapevine (21). A sketch of the detachment term is shown in Fig. 2. Together we denote the mass transfer, growth, and diffusion terms as Jb.
Figure 2.
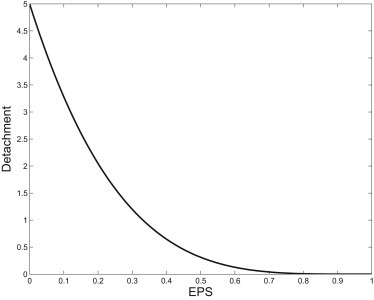
A sketch of the detachment decline indicating the rate of decay of detachment as a function of EPS.
Our governing equation for the free bacterial volume fraction is
| (1) |
The bound bacteria and the EPS are not advected; however, the bound bacteria are influenced by attachment/detachment processes and growth whereas EPS is produced by bound bacteria and decays at a constant rate. We also allow the network to diffuse at a rate that is much smaller than the diffusion rate of the free bacteria. Although the diffusion of the biofilm components are very small and do not change the overall results shown below, the addition simplifies the numerical methods. The governing equations for the biofilm-associated phases are
| (2) |
| (3) |
where c1 and c2 denote the production and decay of polymer, respectively. There are no advection terms on the left-hand-side because the biofilm velocity is assumed to be zero.
The equation governing the fluid volume fraction is
| (4) |
where Jf represents the interphase transfer terms. There are several choices that can be made for Jf, depending on the physical situation. Here, the saturation condition
implies that
We then sum Eqs. 1–4 and obtain an incompressibility equation,
| (5) |
The entire material is incompressible so any net production or decay of the bacterial and EPS phases must be balanced by uptake or production of fluid. Mathematically, this implies that
Conservation of momentum
Because the fluid and the free bacteria are the only phases that are in motion and we assume that the velocities are equal, we only need one governing equation. This is derived from conservation of momentum. Because the scaling within the microchannel implies that the inertial forces are negligible compared to the other forces, the momentum equation is a balance of forces. We include forces from internal fluid viscosity, forces from gradients in hydrostatic pressure, and resistive forces from the drag between the fluid and the fixed biofilm. This is quite similar to other multiphase models of biofilms (5) and yields an equation for the fluid velocity:
| (6) |
The first term is the viscous stress tensor in one dimension, with dynamic viscosity coefficient μf. The hydrostatic pressure is denoted P and the drag between the fluid and the biofilm is proportional to the fluid velocity, with drag coefficient . This ensures that the drag force disappears if there is either no fluid or no biofilm. This equation is sometimes referred to as a Brinkman equation and is a mixture of Stokes flow (balance of viscous forces and pressure) and Darcy flow (balance between pressure forces and drag forces).
Xylella fastidiosa uses twitching motility and the diffusion coefficient has not yet been estimated; however, it is clear that this bacterium moves slower than other, flagellated bacteria whose diffusion coefficients are ∼106 μm2/h. We estimate that Db ≈ 105 μm/h. Using the approximate flow velocity within the chamber, , as a reference velocity, as a reference length scale, and as a reference timescale, we obtain the nondimensional forms of the equations (after dropping the hats and returning to the previous notation)
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
Specific nondimensional parameters are given in Table 1. All parameters are dimensionless. We estimate the attachment/detachment parameters by fitting the scale of the spatial pattern. The bacterial kinetics (growth rates and carrying capacities) are estimated from observations in Characklis and Marshall (22).
Table 1.
Parameters used in the Simulations
| Parameters (nondimensional) | Symbol | Values | Source |
|---|---|---|---|
| Detachment rate | α1 | 5 | Assumed |
| Attachment rate | α2 | 2 | Assumed |
| Diffusion rate (free) | Db | 0.0003 | Assumed |
| Growth rate (free) | rb | 0.2 | (22) |
| Carrying capacity (free) | Kb | 0.1 | (22) |
| Diffusion rate (bound) | Dn,b | 1.5 × 10−5 | Assumed |
| Growth rate (bound) | Rn,b | 0.02 | (22) |
| Carrying capacity (bound) | Kn,b | 0.01 | (22) |
| EPS production rate | c1 | 5 | Assumed |
| EPS degradation rate | c2 | 1 | Assumed |
| Diffusion rate (EPS) | Dn,EPS | 1.5 × 10−5 | Assumed |
| Drag rate | κ | 5 | Assumed |
| Steady velocity | 0.1 | Assumed |
Results
We use two strategies to understand the dynamics of the governing nonlinear system derived above. The first is to note that there are uniform, equilibrium solutions. All that is required is that uf and P are constant and the right-hand sides of Eqs. 7–10 are zero while satisfying Eq. 12. Specifically, we solve
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
for the steady states , , , and .
This does not specify the uniform velocity, . This value was assumed to be ∼10% of the velocity in the clear chamber.
We then expand the solutions as
where Φ*, U, and Q are constants and . The solutions are substituted into the Eqs. 7–12 and retain only the linear terns. This yields a linear system of equations of the form Av = 0 for the amplitudes of the perturbations . The determinant of A must be zero to have nontrivial perturbations. This yields the dispersion relation between the growth rate, λ, and the wavenumber of the perturbation, k.
Solving this relation for λ(k), we find that perturbations grow if the maximum value of Im(λ) > 0 and decay if Im(λ) < 0. Although the dispersion curve is quite ungainly to write explicitly, it is easily determined for fixed parameters. Fig. 3 shows the dispersion curve for different values of the detachment rate, α1. This shows a typical instability where diffusion stabilizes the steady state to high-frequency perturbations and there is a unique, maximally unstable mode. More importantly, when the α1 = 5, the maximally unstable mode is in good agreement with the wavelength of the pattern observed in Fig. 1. We see that the maximally unstable mode is ∼12, which corresponds to a wavelength of ∼12 μm—which is well within the range of the apparent spacing in the experiments. The latter estimate was obtained by simple Fourier transform image processing.
Figure 3.
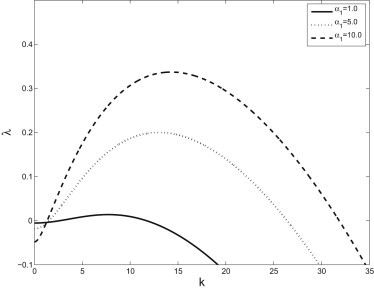
The dispersion curve, λ(k) for varying values of detachment rate. Other parameters are given in Table 1.
We only explore the behavior for varying detachment rates numerically because our initial study focuses on this component; however, we also show the dispersion curves for varying attachment rates and free-bacterial growth rates for comparison. Note that attachment and detachment have opposite effects on the location of the peak of the dispersion curves—that is, increasing α1 tends to increase the wavelength of the pattern while increasing α2 tends to decrease the wavelength. We are currently performing experiments that consider the role of calcium in the pattern formation process. Because calcium affects the binding rates, we expect to be able to use the future experiments to more fully explore the behavior of the system.
To further investigate the nonlinear dynamics of the pattern formation, we solve the equations numerically using a multigrid preconditioner for a Krylov subspace method. We use Vanka box relaxation for the smoother and first-order upwinding for the advection and implicit Euler for the diffusional components. This method is based on methods described in detail in Wright et al. (23) (see Figs. 4 and 5).
Figure 4.
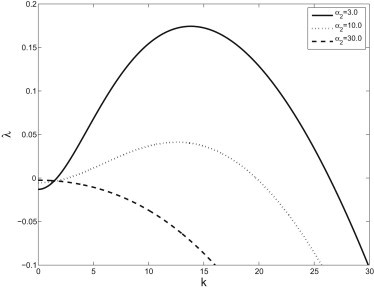
The dispersion curve, λ(k) for varying values of attachment rates. Other parameters are given in Table 1.
Figure 5.
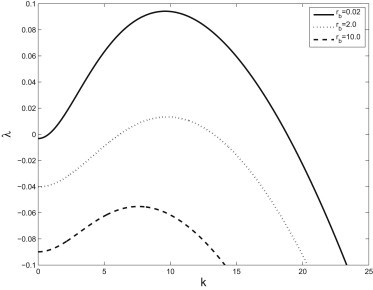
The dispersion curve, λ(k) for varying values of free bacterial growth. Other parameters are given in Table 1. We see that this primarily affects the magnitude of the instability rather than the spatial frequency.
We show snapshots of the dynamics in Figs. 6 and 7. The first shows the competition between two modes that are in the unstable regime predicted by the linear theory. The maximally unstable mode outgrows the other unstable mode. The second shows the maximally unstable mode alone. These numerical simulations indicate that the dispersion curve is capturing the dominant behavior of the system. To test a more complete view of the interaction between the excited modes, we also considered a random perturbation to the volume fractions—we see again that the high wavenumber modes decay, leaving an apparent dominant mode that is quite close to the maximally unstable mode predicted by the linear theory (see Fig. 8).
Figure 6.
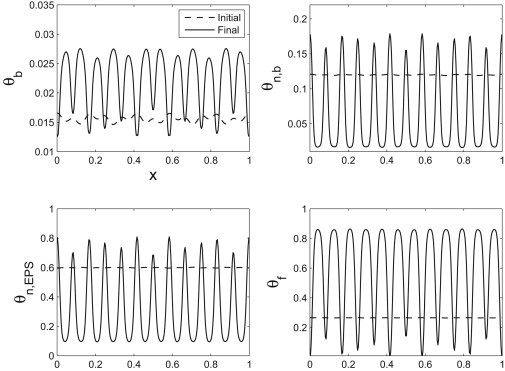
The initial and final volume fractions showing the competition between two unstable modes (5,12). The most unstable mode is 12 and eventually outpaces the smaller frequency perturbation.
Figure 7.
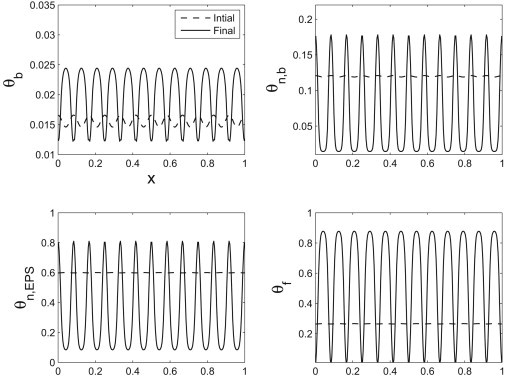
The initial and final volume fractions for a single wavelength perturbation showing the development of a regular pattern.
Figure 8.
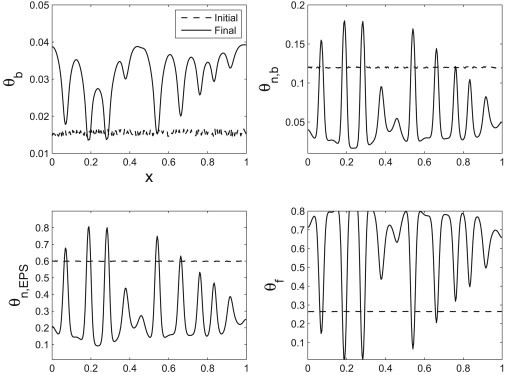
The steady states have been perturbed with a random perturbation. The high wavenumber components decay quite quickly. Lower modes are unstable, with the maximally unstable mode dominating.
We remark that, although the exponent of the detachment decay can be changed, the nonlinear dynamics are unphysical if the exponent is too low. In particular, we find the development of localized singularities where one of the volume fractions becomes negative. Presumably this is because we are missing physical representation for the motion of the biofilm; possibly the osmotic pressure plays a role in regularizing the system. In this regard, the model is not complete. However, evidence that we are capturing the important physical patterning indicates that the primary physics is accurately incorporated.
Discussion
We have developed a model of the dynamics of a developing pattern observed in an economically important pathogen that yields excellent agreement with experimental observations within artificial xylem. The model consists of six nonlinear PDE’s that govern the growth, mass transfer, and fluid dynamics of a bacterial population. This extends the concept of a multiphase model to incorporate four phases. We have also extended numerical methods for simpler multiphase models to a more biologically relevant situation.
Our analysis focuses on the role of detachment and attachment processes in the pattern formation process. In particular, our results indicate that the rate of detachment of bacteria from the biofilm plays an important role in controlling the spatial scale of the observed patterns. We argue that the bacteria are sensitive to the presence of EPS and that as the EPS concentration increases, there is a subsequent decrease in detachment of bacteria, leading to the observed patterns. If the decrease in detachment (as a function of EPS) is too slow, our model is unable to capture the correct spatial scale. Because attachment and detachment can be altered experimentally by the addition of calcium or other cross-linking agents, our initial study has focused on this component.
Although the model is capable of predicting observable patterns, that is not the main purpose of the model, but rather a validation of the model development. There are two particular directions that we are currently pursuing to extend our results: First, there is the obvious extension to two dimensions. It is not clear whether the spatial singularities that were seen for slower detachment decay are overly pronounced in one dimension because a two-dimensional system would allow for the fluid to escape around blockages. Second, we are investigating the role of the biofilm colonization in the bulk fluid motion within the xylem. As of this writing, there is some dispute regarding the effect of the biofilm on the plant’s fluid transport abilities. We believe that this model can address this.
Although the diffusion of X. fastidiosa has not been measured and it is possible that we are overestimating this rate, our results are quite robust in terms of being able to capture the observed scale. We are able to compensate for decreased diffusion by a decrease in the steady-flow rate. With the exception of the detachment terms, there is a relatively large parameter set that can recover the pattern scale that is observed. We do not regard our study as adequate to validate all the estimates that we use; however, we have concluded that the attachment and detachment processes are fundamentally important, which indicates a direction for future investigations that focus on disease control methods.
This also leads to questions regarding some of the simplifications that we have assumed. Although the biofilm does not move nearly as much as the fluid, it is not truly stationary. Previous multiphase models of biofilms have allowed (or focused on) the motion of the biofilm in response to fluid forces and osmotic pressures (6,7). Extending our model to include these extra forces will also help incorporate novel treatment strategies that use specific ions to alter the biofilm dynamics (10).
Acknowledgments
N.G.C. was supported by National Science Foundation grant No. DMS-1122378 and L.D.L.F. was supported by National Science Foundation grant No. DMS-1122343.
References
- 1.Purcell A.H., Hopkins D.L. Fastidious xylem-limited bacterial plant pathogens. Annu. Rev. Phytopathol. 1996;34:131–151. doi: 10.1146/annurev.phyto.34.1.131. [DOI] [PubMed] [Google Scholar]
- 2.Chatterjee S., Almeida R.P., Lindow S. Living in two worlds: the plant and insect lifestyles of Xylella fastidiosa. Annu. Rev. Phytopathol. 2008;46:243–271. doi: 10.1146/annurev.phyto.45.062806.094342. [DOI] [PubMed] [Google Scholar]
- 3.Brown C., Lynch L., Zilberman D. The economics of controlling insect-transmitted plant diseases. Am. J. Agric. Econ. 2002;84:279–291. [Google Scholar]
- 4.Stoodley P., Sauer K., Costerton J.W. Biofilms as complex differentiated communities. Annu. Rev. Microbiol. 2002;56:187–209. doi: 10.1146/annurev.micro.56.012302.160705. [DOI] [PubMed] [Google Scholar]
- 5.Cogan N.G., Keener J.P. The role of the biofilm matrix in structural development. Math. Med. Biol. 2004;21:147–166. doi: 10.1093/imammb/21.2.147. [DOI] [PubMed] [Google Scholar]
- 6.Cogan N., Keener J. Channel formation in gels. SIAM J. Appl. Math. 2005;65:1839–1854. [Google Scholar]
- 7.Klapper I., Dockery J. Role of cohesion in the material description of biofilms. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;74:031902. doi: 10.1103/PhysRevE.74.031902. [DOI] [PubMed] [Google Scholar]
- 8.Zhang T., Cogan N., Wang Q. Phase-field models for biofilms. II. 2-D numerical simulations of biofilm-flow interaction. Comm. Comput. Phys. 2008;4:72–101. [Google Scholar]
- 9.Anguige K., King J.R., Ward J.P. A multi-phase mathematical model of quorum sensing in a maturing Pseudomonas aeruginosa biofilm. Math. Biosci. 2006;203:240–276. doi: 10.1016/j.mbs.2006.05.009. [DOI] [PubMed] [Google Scholar]
- 10.Cruz L., Cobine P., Fuente L. De La. Calcium increases Xylella fastidiosa surface attachment, biofilm formation, and twitching motility. Appl. Environ. Microbiol. 2012;78:1321–1331. doi: 10.1128/AEM.06501-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Meng Y., Li Y., Hoch H.C. Upstream migration of Xylella fastidiosa via pilus-driven twitching motility. J. Bacteriol. 2005;187:5560–5567. doi: 10.1128/JB.187.16.5560-5567.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zaini P.A., De La Fuente L., Burr T.J. Grapevine xylem sap enhances biofilm development by Xylella fastidiosa. FEMS Microbiol. Lett. 2009;295:129–134. doi: 10.1111/j.1574-6968.2009.01597.x. [DOI] [PubMed] [Google Scholar]
- 13.De La Fuente L., Montanes E., Wu M. Assessing adhesion forces of type I and type IV pili of Xylella fastidiosa bacteria by use of a microfluidic flow chamber. Appl. Environ. Microbiol. 2007;73:2690–2696. doi: 10.1128/AEM.02649-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Davis M., Purcell A., Thomson S. Isolation media for the Pierce’s disease bacterium. Phytopathology. 1980;70:425–429. [Google Scholar]
- 15.De La Fuente L., Burr T.J., Hoch H.C. Autoaggregation of Xylella fastidiosa cells is influenced by type I and type IV pili. Appl. Environ. Microbiol. 2008;74:5579–5582. doi: 10.1128/AEM.00995-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cogan N., Guy R. Multiphase flow models of biogels from crawling cells to bacterial biofilms. HFSP J. 2010;4:11–25. doi: 10.2976/1.3291142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Berg H. Princeton University Press; Princeton, NJ: 1993. Random Walks in Biology. [Google Scholar]
- 18.Murray J. Springer; New York: 2002. Mathematical Biology, Vol. 1. An Introduction. [Google Scholar]
- 19.Cogan N.G., Wolgemuth C.W. Pattern formation by bacteria-driven flow. Biophys. J. 2005;88:2525–2529. doi: 10.1529/biophysj.104.053348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cogan N.G., Wolgemuth C.W. Two-dimensional patterns in bacterial veils arise from self-generated, three-dimensional fluid flows. Bull. Math. Biol. 2011;73:212–229. doi: 10.1007/s11538-010-9536-1. [DOI] [PubMed] [Google Scholar]
- 21.Gambetta G.A., Fei J., Matthews M.A. Leaf scorch symptoms are not correlated with bacterial populations during Pierce’s disease. J. Exp. Bot. 2007;58:4037–4046. doi: 10.1093/jxb/erm260. [DOI] [PubMed] [Google Scholar]
- 22.Characklis W., Marshall K., editors. Biofilms. Wiley and Sons; New York: 1990. [Google Scholar]
- 23.Wright G., Guy R., Fogelson A. An efficient and robust method for simulating two-phase gel dynamics. SIAM J. Sci. Comput. 2008;30:2535–2565. [Google Scholar]


