The Nested Structure of Cancer Symptoms: Implications for Analyzing Co-occurrence and Managing Symptoms

Summary

Objective

Although many cancer patients experience multiple concurrent symptoms, most studies have either focused on the analysis of single symptoms, or have used methods such as factor analysis that make a priori assumptions about how the data is structured. This article addresses both limitations by first visually exploring the data to identify patterns in the co-occurrence of multiple symptoms, and then using those insights to select and develop quantitative measures to analyze and validate the results.

Methods

We used networks to visualize how 665 cancer patients reported 18 symptoms, and then quantitatively analyzed the observed patterns using degree of symptom overlap between patients, degree of symptom clustering using network modularity, clustering of symptoms based on agglomerative hierarchical clustering, and degree of nestedness of the symptoms based on the most frequently co-occurring symptoms for different sizes of symptom sets. These results were validated by assessing the statistical significance of the quantitative measures through comparison with random networks of the same size and distribution.

Results

The cancer symptoms tended to co-occur in a nested structure, where there was a small set of symptoms that co-occurred in many patients, and progressively larger sets of symptoms that co-occurred among a few patients.

Conclusions

These results suggest that cancer symptoms co-occur in a nested pattern as opposed to distinct clusters, thereby demonstrating the value of exploratory network analyses to reveal complex relationships between patients and symptoms. The research also extends methods for exploring symptom co-occurrence, including methods for quantifying the degree of symptom overlap and for examining nested co-occurrence in co-occurrence data. Finally, the analysis also suggested implications for the design of systems that assist in symptom assessment and management. The main limitation of the study was that only one dataset was considered, and future studies should attempt to replicate the results in new data.

1. Introduction

Although cancer patients experience on average between 11-13 symptoms [1], most research has focused on the etiology, progression, and treatment of single symptoms. Furthermore, because of the additive impact of multiple symptoms, patients with many co-occurring symptoms generally fare worse than those who have only a few [2-8]. Understanding how symptoms co-occur in patients can therefore lead to more efficient assessment and management of symptoms, and significantly improve the overall function and quality of life for cancer patients [9].

To address this need, recent research has used data reduction methods such as factor analysis [10] and hierarchical clustering [10] to identify symptom clusters in different granularities of data. For example, hierarchical cluster analysis was used to identify a cluster of five symptoms (e.g., hot flashes) in menopausal women with breast cancer [11], and factor analysis was used to identify three clusters of symptoms across patients of all types of cancer [12]. While these early studies have made important inroads into identifying symptom clusters, researchers have admitted that such methods produce results that are inherently unverifiable [11]. For example, there is no commonly accepted method to select cut-off points in a dendrogram (generated by hierarchical clustering [10]) to identify disjoint clusters. More importantly, these methods are based on a priori assumptions about the existence of disjoint symptom clusters, potentially masking more complex relationships in the data.

Inspired by the importance of symptom cluster research, but concerned about the a priori assumptions in current methods about the structure of clusters in the data, we used a network layout algorithm to first visualize the complex relationship between cancer patients and symptoms. This approach enabled us to visually inspect the data, with minimal assumptions about the underlying structure of symptom co-occurrence in the data. For example, networks enable the identification of multiple structures (e.g., hierarchical, disjoint, overlapping, nested) in a single representation, and therefore can guide the selection of cluster analysis methods that are designed to analyze only specific types of structures. Using the visual observations from the networks, we therefore selected and developed the appropriate quantitative methods to verify the nature of the co-occurrence. Such a multi-method approach helped us to arrive at a new understanding of how symptoms co-occur across cancer patients, with insights about the treatment and management of co-occurring symptoms.

We begin with an overview of the relevant clinical literature referred to as “symptom cluster research.” Next, we present how the current literature motivated our research question, followed by a description of the data, and how we used a combination of network visualizations and quantitative methods to address that research question. The results of the analyses were then used to explore implications for the design of decision-support systems and methods to understand symptom co-occurrence. We conclude with a description of our future research in using networks and associated quantitative methods to understand patient factors associated with symptom clusters, and their implications for symptom management and treatment.

2. Background on Symptom Co-Occurrence

2.1 Current Research on Identifying Symptom Clusters

The research topic of symptoms clusters was first introduced by Dodd et al., [13] to bring attention to the fact that although many patients experience multiple co-occurring symptoms, most research in symptom management had until then focused on the etiology and treatment of single symptoms. They proposed the following working definition of a symptom cluster: “When three or more concurrent symptoms (e.g., pain, fatigue, and sleep disturbances, or nausea, vomiting, and poor appetite) are related to each other, they are called a symptom cluster.” [13]. Since then there have been other definitions proposed including two or more concurrent symptoms [14], but currently there is no resolution on the definition of a symptom cluster [1].

Despite the lack of agreement on the definition of a symptom cluster, there has been active research in identifying them in different patient-symptom databases. Most of the symptom cluster research has been in cancer [1, 15], although the approach is increasingly being used to analyze non-cancer conditions such as myocardial infarction [16], and fibromyalgia [17]. A recent review of the literature on cancer symptom cluster research [1] identified two classes of studies: (1) analysis of symptom clusters across all types of cancers pooled together, and (2) analysis of symptom clusters in specific cancers such as breast cancer. Within each class of studies there was considerable variability in the number of patients, the instruments used to identify symptoms, and the methods used. For example, Walsh and Rybicki [18] analyzed 922 cancer patients with different cancers using a 38-item symptom checklist. The data were analyzed using agglomerative hierarchical cluster analysis, which helped to identify 7 different symptom clusters. In contrast, Chen and Tseng [12] analyzed 151 cancer patients using the MD Anderson Symptom Inventory [19]. The data were analyzed using factor analysis which helped to identify two symptom clusters. Across the studies, the only common symptom cluster was nausea and vomiting, with high variability in the rest of the symptom clusters identified.

A similar variability in data collection, analysis methods and resulting symptom clusters occurs in the analysis of specific cancers such as breast cancer [11], and lung cancer [20]. To date, the research in specific cancer sites has not identified any common clusters across studies [1]. Symptom cluster research is therefore clearly in its early stages, and while there is considerable interest in identifying symptom clusters, there is neither consensus on the definition of symptom clusters, data collection methods, analytic approaches, nor resulting clusters [21-23].

2.2 Current Methods Used to Analyze Symptom Co-Occurrence

Although a consensus on definitions and data collection methods is crucial for symptom cluster research to move forward, we focus here only on the methods for identifying symptom clusters. As stated by two reviews of the symptom cluster literature [1, 15], researchers have used two main methods to analyze symptoms clusters: (1) agglomerative hierarchical clustering, and (2) factor analysis. The first approach can be used to either cluster symptoms based on how they co-occur across patients, or to cluster patients based on how they share symptoms. The method entails first generating a dendrogram (a hierarchy of symptoms or patients) based on how frequently the symptoms co-occur across patients or how patients are similar based on their symptoms. The resulting dendrogram is then visually inspected to determine a cut through the hierarchy to define disjoint clusters. Hierarchical clustering is highly dependent on the choice of dissimilarity and linkage measures, and the agglomerative nature of the algorithm makes it very sensitive to small variations in the data [24]. Furthermore, there is no commonly accepted method to determine the cut through a dendrogram, or whether a cut is even appropriate. Given these methodological issues, other methods (visual or quantitative) should be used to confirm the findings.

The second approach that is commonly used to identify symptom clusters is factor analysis [10]. This method predicts a set of latent factors that explain the covariance among a set of symptoms. For example, if two symptoms frequently co-occur together across patients, those two symptoms will be collapsed into a latent factor, with a significance value that denotes the amount of the covariance that can be explained by that factor. The resulting latent factors therefore help to identify the symptom clusters. Similar to hierarchical cluster analysis, factor analysis is also a data exploration method which can be used for a wide range of applications to reduce data. However, factor analysis used in the above way assumes that the underlying data has disjoint clusters, and is therefore biased to find such types of structures in the data.

We believe that while both these methods are powerful, they should be used and interpreted carefully so that they do not introduce biases in the analysis of symptom clusters. To avoid these problems, we decided to use network visualizations as a way to first visually analyze the data to determine how symptoms might be structured, and only then use data reduction methods with the appropriate biases to quantitatively analyze the data. Furthermore, because there is no consensus in the definition of the term “symptom clusters” (which to us inherently suggests non-overlapping groups of symptoms), we use the term “symptom co-occurrence” to keep open the possibility of more complex organizations of symptoms than what is currently expected when using the term “cluster”. For example, the symptoms might co-occur randomly, or uniformly across patients, both of which are valid co-occurrence patterns but which lack clusters.

3. Method

Based on the above motivations, our research began with the question: How do symptoms co-occur across cancer patients? To address this research question, we made critical decisions regarding data selection and data analysis as discussed below.

3.1 Data Selection

We conducted a secondary analysis on data collected in a published study on cancer symptom management [25]. The data consisted of 671 cancer patients who were 21 years of age or older, have a solid tumor cancer or non-Hodgkins lymphoma, were undergoing chemotherapy, and spoke and read English. The patients reported eighteen symptoms using the M.D. Anderson Symptom Inventory [19] which measures symptom severity ranging from zero (not present) to ten (worst imaginable), with symptom management advice given to patients whose symptom severity was greater or equal to four on any given symptom. Six patients did not report any symptom severity values and therefore were dropped from the analysis, resulting in a total of 665 patients. The patients varied on a number of disease and demographic variables including type and stage of cancer, sex and age (see Table I for descriptive statistics of the dataset). Similar to several studies [12], the focus of our study was to analyze how symptoms co-occurred across all 665 patients at baseline (i.e., prior to any interventions) and to use insights from that analysis for partitioning of the data based on cancer type and symptom severity.

Table I.

Patient Demographics

Cancer Type	Number of patients (percentage of total patients [rounded])	Sex		Cancer Stage			Age
		Male	Female	Early	Late	Missing Data	<36	36-70	>70	Missing Data
Breast	231(35%)	0	231	53	176	2	11	206	14	0
Lung (non-small)	112(17%)	58	54	13	99	0	1	87	24	0
Colon	79(12%)	26	53	9	70	0	5	64	9	1
GU	51(8%)	44	7	2	49	0	2	32	17	0
Gynecological	47(7%)	0	47	6	41	0	2	39	6	0
Non-Hodgkins	38(6%)	19	19	6	31	1	2	26	10	0
Gastrointestinal	32(5%)	21	11	0	30	2	0	29	3	0
Lung (small cell)	27(4%)	5	22	0	27	0	0	20	7	0
Pancreas	21(3%)	14	7	2	19	0	0	15	6	0
Other	19(3%)	11	8	2	16	1	0	18	1	0
Mesothelioma	8(1%)	4	4	2	6	0	0	8	0	0
Total	665(100%)	202	463	95	564	6	23	544	97	1

3.2 Data Analysis

Our analysis consisted of two steps. (1) Exploratory visual analysis using network visualizations. (2) Quantitative analysis of visual patterns by selecting appropriate existing methods, and developing new ones when the existing methods did not suffice. The results of these analyses were validated by assessing the statistical significance of the quantitative measures through comparison with random permutations of the networks of the same size and distribution. The overall methodology is therefore to visually inspect the data to determine the nature of the symptom co-occurrence, before selecting quantitative methods to analyze the observed patterns.

3.2.1 Exploratory Visual Analysis

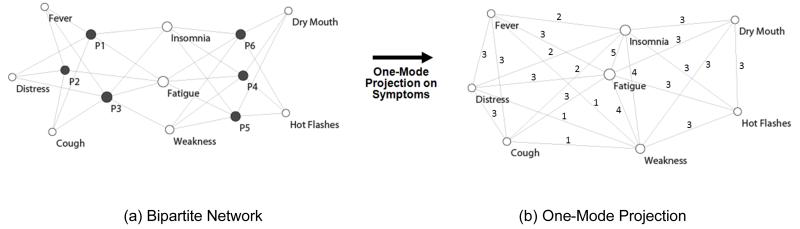
Networks are increasingly being used to analyze a wide range of phenomena, such as how diseases relate to genes [26], how diseases spread through a social network [27], and how information is scattered across web pages [28]. A network is a collection of nodes joined in pairs by edges; nodes represent one or more types of entities (e.g., patients or symptoms), and edges connecting pairs of nodes represent a specific relationship between the entities (e.g., a patient has reported a symptom). Figure 1a shows a sample bipartite network (where there are two classes of nodes, and edges exist only between different classes of nodes) of patients and their symptoms.

Figure 1.

A sample patient-symptom bipartite network (a) showing patients as black nodes, and symptoms as white nodes. The size of a node represents the number of edges that are connected to it. Therefore the Fatigue node in the center is large because many patients have that symptom. Bipartite networks can be reduced to analyze how symptoms co-occur using a method called a one-mode projection (b). Here the nodes represent symptoms, and the edges represent one or more times that the connected symptoms co-occur in a patient.

As shown in Figure 1a, the sample bipartite network visually represents the explicit relationships between the six patients and eight symptoms. In this network, the black nodes represent patients, the white nodes represent symptoms, and the size of a node is proportional to its degree (number of edges that connect to that node). For example, Fatigue is the most commonly occurring symptom with six edges each connected to a patient. In contrast, Dry Mouth is less common with only three edges, and located off-center close to the patients to which it is connected.

Network layout algorithms have two advantages for analyzing complex relationships. (1) They do not require a priori assumptions about the structure of clusters within the data, such as the hierarchical assumption of hierarchical clustering, or subspace model of factor analysis. Instead, by using a simple pair-wise representation of nodes and edges, network layouts enable the identification of multiple structures (e.g., hierarchical, disjoint, overlapping, nested) in a single representation [29]. (2) They can be visualized and analyzed using a set of network algorithms to reveal global regularities in the data. For example, Figure 1a shows how a force-directed layout algorithm [30] helps to visualize the relationship between patients and symptoms. The algorithm pulls together nodes that are tightly connected to each other, and pushes apart nodes that are not.

As shown, the result is that patients that have similar symptoms (e.g., P1, P2, and P3 in Figure 1a) are placed close to each other, and close to their symptoms (e.g., Fever). The layouts were created using Pajek [31] (version 1.24). While this layout depends on the force-directed assumption and its implementation, we view such algorithms as less biased for data exploration, because they do not impose a particular cluster structure on the data.

Our analysis first considered an un-weighted network, with edges indicating symptom prevalence at any severity (see later section on replication that takes severity into consideration when analyzing the network). In addition, nodes were colored to represent disease type (e.g., black nodes represent breast cancer patients).

To understand the structure of symptom co-occurrence, we transformed the bipartite network using a standard network reduction method called a one-mode projection [26]. As shown in Figure 1b, all patient nodes were removed, an edge was placed between two symptoms if they co-occurred in one or more patients, with a number (called the edge weight) denoting the frequency of the symptom co-occurrence. This network therefore showed the frequency with which pairs of symptoms co-occurred across patients.

3.2.2 Quantitative Analysis

We used two existing (modularity and hierarchical clustering) and two novel (degree of symptom overlap and co-occurrence block diagram) quantitative methods to analyze the patterns of symptom co-occurrence suggested by the network visualizations. The choice of these methods was the direct result of visual patterns observed from the bipartite and one-mode networks described above.

Each method computes a numerical measure that quantifies some aspect of the network, and the significance of this measure is determined by comparison to random permutations of the networks. Comparison to random permutations of an observed network is a standard approach in network science to test the validity of a quantitative pattern identified in the real data [26]. Random networks are generated by random reassignment of network edges while preserving the total number of edges and nodes observed in the original network. For all methods except modularity (which is a measure that incorporates comparison to random networks), we calculated a p-value as the fraction of times the random network’s measure was more extreme (larger or smaller, depending on the method) than that of the observed network. To ensure that our results were not caused merely by the prevalence of the symptoms (e.g., if two symptoms occur frequently, there is a high probability they will also co-occur), we also preserved symptom degree distribution when generating the random networks for agglomerative hierarchical clustering, and for the block diagram.

1. Degree of Symptom Overlap across Patients

To quantitatively analyze the observed overlap of symptoms across patients, we plotted the mean number of patients sharing symptom sets of different sizes. More precisely, for each number k ranging from one to the total number of symptoms, we generated a random k-tuple of symptoms, and calculated the number of patients in which at least those k symptoms co-occur. By averaging over the random choice of symptoms, we obtain a smooth curve. We then calculated the area under this curve as a measure of how many patients on average share a progressively increasing number of symptoms. Comparison of this area (which we call degree of symptom overlap) to random networks was done to reveal whether the symptom overlap was greater or less than what could be expected to occur by random chance.

2. Modularity

To assess the degree of clustering in the network, we used the RGraph algorithm [32] which attempts to partition a bipartite network into clusters (or modules) by optimizing modularity. The modularity of a partition is defined as the number of edges falling within clusters, minus the expected number of such edges in a network of the same size with randomly reassigned edges. Modularity values range from −1 to +1, where high values (>0.3) represent significantly more edges within clusters compared to random networks of the same size, zero represents no difference compared to random networks, and negative values represent fewer edges within clusters compared to random networks.

As discussed by the authors [32], the algorithm uses simulated annealing to optimize modularity, and takes as input a cooling factor and an iteration factor. These parameters determine tradeoffs between accuracy and computational efficiency. The values for these parameters were set to those suggested by the authors [32] in their instructions to use the algorithm, with an emphasis on accuracy (cooling factor [c]=0.999, iteration factor [f]=1).

3. Agglomerative Hierarchical Clustering

We used agglomerative hierarchical clustering to test if the symptoms were nested. By nested we mean that given a symptom ranking (e.g., from most common to least common), they are considered nested if a patient that exhibits a particular symptom in that list (e.g., the fifth ranked symptom), then that patient is highly likely to have all symptoms of higher rank (i.e., symptoms of rank one, two, three, and four). In addition, if a patient does not exhibit a particular symptom (e.g., the fifth ranked symptom), then that patient is highly likely to not have symptoms of lower rank (i.e., symptoms of rank six, seven, etc.). Intuitively, the symptoms are nested if, whenever a patient has a symptom, then that patient tends to have all other symptoms that are more prevalent in the data.

To test for nestedness, we used agglomerative hierarchical clustering with the Jaccard dissimilarity measure and Ward2 linkage criteria [10]. The Jaccard dissimilarity measure between two symptoms is one minus the ratio of the number of patients experiencing both symptoms to the number of patients experiencing either symptom [33]. The algorithms starts with each symptom as a singleton cluster, and recursively merges clusters based on minimum similarity, where dissimilarity is extended from symptoms to sets of symptoms using the linkage.

The dendrogram is often used to impose a clustering by thresholding at a certain level. However, there is no clear level at which to threshold. Instead, we use the following more systematic approach to assess whether the symptom co-occurrence follows a nested structure. We calculated the minimum number of edits it would take to transform the dendrogram generated from the real data, into a perfectly nested dendrogram (that is, a dendrogram whose depth is one minus the number of symptoms). The significance of this measure was determined by comparison to 1000 random networks, where the size and symptom degree distribution were preserved.

4. Co-occurrence Block Diagram

A limitation of the hierarchical clustering is that the agglomerative algorithm does not guarantee an optimal solution. This is because it aggregates sets of symptoms in incremental steps, and therefore the sets identified at any level of the dendrogram are not necessarily globally optimal.

Because we wished to understand the explicit relationship of how each symptom was related to the rest of the symptoms based on their co-occurrence across patients, we developed an exhaustive algorithm to create a block diagram of symptom co-occurrences. The rows in the block diagram represent the most frequent co-occurring symptom sets of different sizes, and the columns represent an ordered list of symptoms based on the frequency of their co-occurrence (explained below). This block diagram was generated by the following method:

1. Exhaustively identified all co-occurring symptom sets of different sizes. In other words we identified all co-occurring symptom sets of size one, two, three, … maximum number of co-occurring symptoms (which was sixteen).

2. Selected the most frequent symptom set for each set size generated in the above step. For example, the most frequent co-occurring set size of three was Fatigue, Insomnia, and Weakness. When there were two or more equally frequent sets, then a conservative approach was taken by selecting the one that least matched the symptom members of the last symptom set size.

3. Progressively added new symptoms to the columns in the block diagram for each additional row. For example, the most frequently co-occurring set size of four was Fatigue, Insomnia, Weakness, and Distress. Therefore, Distress was added to the fourth column of the block diagram.

4. Cells in the block diagram were colored black to indicate the symptoms comprising each co-occurring set. For example, the most frequent symptom set size of seven did not contain Pain, which was present in the most frequent set size of six. Therefore the respective cell in the Block Diagram was not colored black. To understand the role of symptom severity, we redid the above analyses with severity scores at greater or equal to four.

We used the block diagram to assess whether the symptoms co-occurred in a nested structure. If the pattern from left to right is a uniformly descending staircase pattern, then the symptoms are perfectly nested. However, if there are gaps in the perfectly staircase pattern, then the degree of nestedness is based on how many cells are out of place from a perfectly nested pattern. In particular, we calculated the number of edits needed in the block diagram to make it perfectly nested, where an edit is defined to be the operation of swapping two consecutive boxes on the same row. To test the significance of the degree of nestedness, we compared it to the same measure generated from 1000 random networks of the same size and symptom degree distribution.

5. Replication of Results in Subsets of the Data

To test whether the overall results changed if we considered only high symptom severity, or cancer type, we replicated two key analyses in subsets of the data. This was done by analyzing modularity and nestedness on a network which only had symptom severity greater or equal to four (the threshold for interventions to occur), and then on three of the most frequent cancers: breast (n=231), lung (n=112), and colon cancer (n=79).

4. Results

The analysis of the cancer data revealed three distinct patterns. For each of the three patterns we describe the results of the exploratory visual analysis, and the results of the quantitative analysis including their validation.

4.1 High Overlap of Symptoms across Patients

Visual Analysis

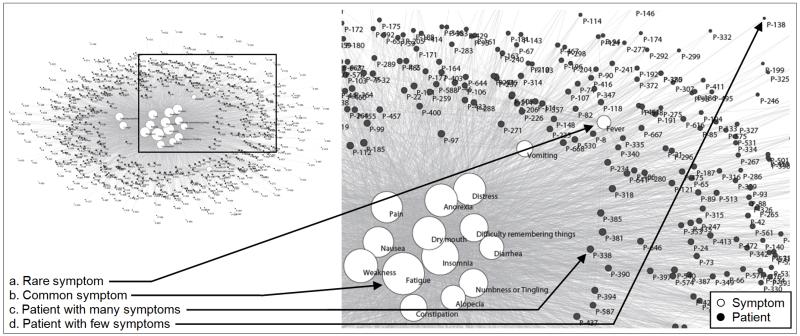
As shown in Figure 2, the patients form a ring around the eighteen symptoms in the center. Patients close to the inner set of symptoms tend to have many symptoms compared to patients in the outer ring. For example, the patient P-338 (c) has sixteen symptoms, whereas the patient P-138 (d) has only one symptom. This network topology where there are many high degree patients (with respect to the total number of symptoms) in the ring connecting to a small number of high degree symptoms in the center, suggests a high overlap in the number of symptoms for most patients (resulting in a gray mass of indistinguishable edges).

Figure 2.

A patient-symptom bipartite network in the top left (where edges represent symptom severity at any level) visually shows the high overlap of 18 symptoms (white nodes) across 665 patients (black nodes). This high overlap results in a large cluster of symptoms in the center of the network, and a few symptoms that are off center (shown in more detail in the inset). The size of the nodes is proportional to the edges that connect to them. Therefore common symptoms have large nodes, whereas rare symptoms have smaller nodes. The patients that have many symptoms are closer to the center and closer to their symptoms. The above layout was automatically generated by the Fruchterman Reingold algorithm [30]. Please see supplementary figure S1 for the same network where the patient nodes are colored by each patient’s type of cancer revealing that there exists no clustering of patients based on cancer type.

Quantitative Analysis

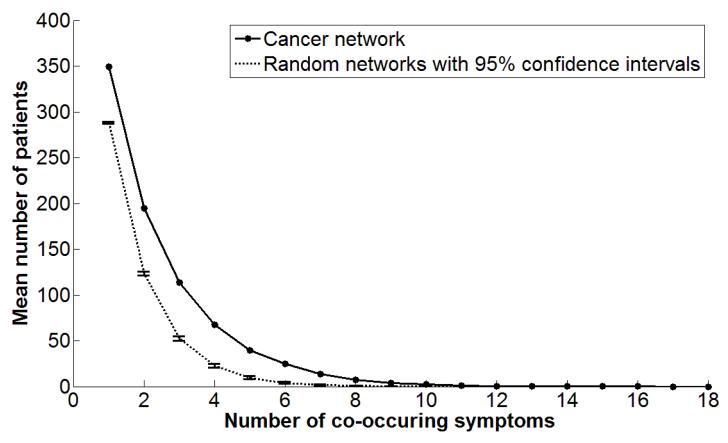
The above pattern of high overlap was quantitatively analyzed by plotting the mean number patients sharing symptom sets of different sizes. As shown by the solid curve in Figure 3, a high proportion of patients (80.41%) as measured by the area under the curve, share between one and three symptoms, and a diminishing number of patients share a higher number of symptoms.

Figure 3.

The mean number of patients who share different numbers of symptoms shows that many patients share between 1-3 symptoms, and a decreasing number of patients share more than 3 symptoms. The area under the curve is significantly different from the same curve generated from 1000 random networks of the same size (shown with 95% confidence intervals).

The area under this curve quantifies the degree of overlap. The degree of overlap (817.67) in the cancer network is significantly higher (p<.01) compared to the mean degree of overlap (504.08) of 1000 random networks of the same size. This result suggests that the high overlap of symptoms in the cancer network is not a random occurrence, and therefore a valid pattern of symptom co-occurrence.

4.2 Absence of Symptom Clusters

Visual Analysis

Figure 2 shows the absence of patient, symptom, or patient-symptom clusters. Most of the symptoms are clumped in the center, and the patients and cancer types are evenly distributed around the symptoms. This absence of distinct multiple clusters of symptoms was unexpected, as most of the literature on symptom clusters has hypothesized the presence of distinct symptom clusters in cancer. Futhermore, when we colored the patient nodes by cancer type (see online supplementary Figure S1), there were no patient clusters based on cancer type.

Quantitative Analysis

To quantitatively confirm the absence of symptom clusters, we used the well-known network measure called modularity, as implemented by the RGraph algorithm [32]. The modularity was extremely low at 0.067, indicating that the symptoms exhibit no significant clustering.

4.3 The Nested Structure of Symptom Co-Occurrence

Visual Analysis

As shown in Figure 2, there is a wide range in the degree of the symptoms. There are fifteen commonly-occurring symptoms in the center of the network, and three less common symptoms off center. For example, Fatigue (b) is the most commonly occurring symptom with edges to 602 of the 665 total patients. In contrast, Fever (a) is off-center with only 64 edges. This pattern of connections results in a high mean and standard deviation in symptom degree (Mean=287.61, SD=132.68), with overall low modularity or absence of distinct clusters.

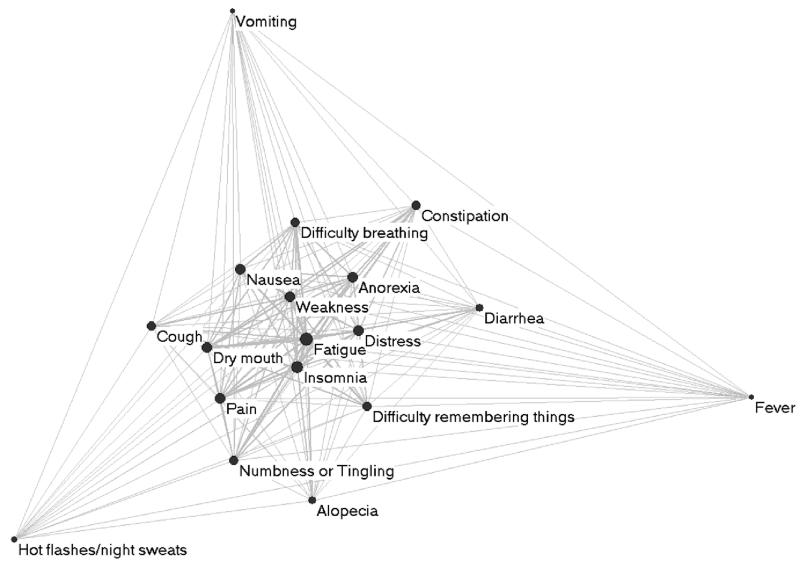
The absence of distinct clusters suggests that the symptoms are nested. To further probe this observation, we analyzed the one-mode projection on symptoms (designed to show how symptoms co-occur). Figure 4 shows the pair-wise relationship between symptoms, where the edge weight between two nodes denotes how many times the connected symptoms co-occurred across patients. As shown, the one-mode projection has a core-periphery topology which suggests a nested structure (a specific form of hierarchy). For example, Fatigue and Insomnia are in the center of the network because they co-occur most frequently with each other (442 times). However, they co-occur with progressively diminishing frequency with symptoms that are further and further away from the core (e.g., Fatigue co-occurs with Nausea only 308 times) and very infrequently with symptoms at the periphery (e.g., Fatigue co-occurs with Fever only 63 times).

Figure 4.

The one-mode projection on symptoms of the bipartite network (shown in Figure 1), reveals how pairs of symptoms co-occur across patients. The edge thickness is proportional to the number of times two symptoms co-occur in a patient. Highly co-occurring symptom are pulled together, and because of the nested structure, have also been pulled to the center.

Quantitative Analysis

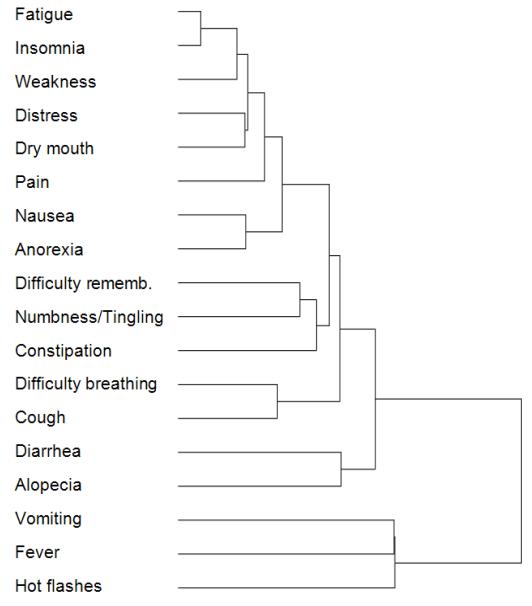
The above nested structure of symptoms was first quantitatively analyzed using hierarchical clustering. As shown in Figure 5, the depth of the resulting dendrogram is nine. Furthermore, although we could select an arbitrary cut-off point to identify disjoint clusters, there is actually no natural break in the dendrogram to reliably determine such clusters. This confirms the results of our earlier modularity analysis which found that there appears to be an absence of distinct symptom clusters in the data. In addition, the number of edits needed to transform the actual dendrogram to a perfectly nested dendrogram was eight.

Figure 5.

A dendrogram generated by the agglomerative hierarchical clustering method suggests the nested structure of symptom co-occurrence.

The above tree depth and number of edits for the network were compared against dendrograms generated from 1000 random networks of the same size and symptom degree distribution. The mean tree depth of the random networks was six, and the mean number of edits to transform the random networks to perfectly nested networks was eleven. The results revealed that the probability of the nested structure of cancer symptoms occurring by chance was less than 0.1 percent (p < 0.001).

Unfortunately, the one-mode projection and the hierarchical cluster analysis both have inherent limitations in revealing the explicit members of the nested structure: The one-mode projection is limited in that it can only show the pair-wise associations and therefore conceals how groups of symptoms co-occur; the agglomerative nature of the dendrogram conceals globally optimal co-occurrence frequencies.

To address the above limitations, we analyzed the symptom co-occurrence data using the co-occurrence block diagram. As shown in Figure 6, the block diagram lists the most frequently co-occurring symptoms, ranging from one to the maximum set size of sixteen co-occurring symptoms. With the exception of set sizes seven, eleven, and fourteen, the most frequently occurring symptom sets are a proper subset of the next larger set size. The degree of nestedness (number of edits required for a perfectly nested pattern) = fifteen, which was significantly less than the mean degree of nestedness of 1000 random networks that preserved the size and symptom degree distribution of the original network (mean = 228.4, p < 0.001). The analysis therefore explicitly revealed the strongly nested nature of symptom co-occurrence, which was significant.

Figure 6.

A block diagram showing the most frequently co-occurring symptoms for each size of symptom set. With the exception of set sizes 7, 11, and 14, the symptoms follow a strongly nested pattern.

4.4 Replication of Results in Subsets of the Data

Partitioning Data Based on Symptom Severity

As described in the Data Selection section, an important symptom severity threshold was greater than or equal to four, at which level tailored symptom management advice was given to the patients. We therefore removed all edges in the network that were below four, and repeated two key quantitative analyses on the resulting network: (1) modularity (to test if there existed symptom clusters), and (2) the degree of nestedness using the block diagram (to test for nestedness).

Modularity for the new network (with severity greater than or equal to four) was extremely low at 0.078. Therefore, similar to the network which did not take into consideration symptom severity, there was also strong evidence for the absence of symptom clusters when taking into account symptom severity. Furthermore, for the new network, the degree of nestedness was high at 59 edits required to achieve perfect nesting, versus a mean of 282.78 edits required for 1000 random networks (that preserved the size and symptom degree distribution of the original network) to achieve perfect nesting. These results were significant (p < 0.001).

Partitioning Data Based on Cancer Type

As shown in Table II, the dataset contained eleven different cancer types. We therefore analyzed whether the patterns observed in the pooled analysis changed when the different cancer types were analyzed individually. We extracted the three most frequent cancer subtypes, namely breast (n=231), lung (n=112), and colon cancer (n=79), and repeated the analysis of modularity and degree of nestedness. As shown in Table II, there was very low modularity for each cancer type, suggesting the absence of symptom clusters, and significantly high nestedness instead.

Table II.

The modularity and degree of nestedness for the top three most frequent cancer types in the dataset. In all cases the modularity is very low (indicating that there exists no symptom clusters), and significantly higher degree of nestedness compared to 1000 random networks of the same size and symptom degree distribution.

Cancer Type (number of patients)	Modularity	Degree of Nestedness
		Number of edits required for block diagram (generated from the real network) to be perfectly nested	Mean number of edits required for block diagrams (generated from 1000 random networks) to be perfectly nested	Significant difference between real network and random networks
Breast (n=231)	0.068	17	232.5	p=0
Lung (n=112)	0.072	66	204.6	p=0.007
Colon (n=79)	0.074	58	235.9	p=0

5. Discussion

Based on the clinical literature, we expected that our analysis would identify distinct symptom clusters. Distinct clusters occur infrequently in random networks [26] and hence their occurrence would have been highly indicative of a meaningful underlying process. However, we found no such clusters. This result was replicated when taking into account symptom severity, in addition to specific cancer type. Fortunately, our seemingly null results led us to probe deeper into the structure of co-occurring symptoms using multiple methods, starting with visualizations and analyzing those observations through existing and new quantitative methods. This exploratory process led us to the conclusion that symptoms co-occur in a nested pattern rather than in distinct clusters. Furthermore, the comparison of the results with equivalent random networks led us to conclude that cancer symptom co-occurrence is more complex than we originally expected, but not random as we subsequently feared.

We believe that our overall methodology could address the variability in methods currently used to analyze symptom clusters [1]. By first visually analyzing their data, researchers could decide on which quantitative method is the most appropriate for analyzing patterns of symptom co-occurrence in their data, and therefore achieve a more systematic methodology for analyzing symptom co-occurrence.

5.1 Limitations

The limitation of the overall study was that we considered only one dataset to analyze patterns in cancer symptomatology. Future studies should apply the same methods described in this article to test whether the nested pattern of symptom co-occurrence is also present using similar data from another population¹.

Another limitation of our work is that the block diagram used to measure degree of nestedness requires an exhaustive search for the most frequent symptom combinations for each set size, a technique which is feasible only in datasets with relatively few symptoms. Our ongoing research addresses computationally efficient algorithms to generate block diagrams regardless of the number of symptoms. Until this work is completed, the existing block diagram approach can be used to complement existing methods such as hierarchical clustering, rather than to replace them.

5.2 Implications for Clinical Practice and Research

Our findings have implications for both clinical practice and future research. Currently cancer patients undergoing chemotherapy are screened for upwards of eighteen symptoms during clinic visits [34-36]. As these patients are already burdened with the stress of therapy, efficient means for assessing symptoms are needed not only during office visits, but also at home where there is increasing interest in using telephonic or web-based symptom monitoring [37, 38].

The absence of disjoint symptom clusters precludes an approach of asking a few questions to eliminate candidate symptom clusters. Instead, the nested pattern of symptom co-occurrence suggests new approaches for developing computational systems for rapid symptom assessment. For example, to efficiently identify all severe symptoms, a system could initially present a list of common symptoms ranked by frequency or severity. Each time a symptom is selected, the remaining symptoms are re-ranked based on their co-occurrence in the data with the already selected symptoms. For example, a patient presenting Fatigue with Insomnia may next be asked about Weakness, while a patient presenting Fatigue without Insomnia may next be asked about Dry Mouth as the latter most frequently co-occurs in patients with Fatigue but not Insomnia. Such a process should save time and reduce excess burden on the patient by obtaining a complete picture of the patient’s symptoms through a small set of targeted questions.

The nested structure of cancer symptoms also suggests that the underlying biochemical mechanism in chemotherapy may involve a single mediator which causes additional symptoms as its concentration increases. Alternatively, it may involve a chain reaction where each intermediate state causes another symptom. Future research will need to confirm our results, and test such emergent hypotheses. Additionally, the results imply that symptom cluster researchers can avoid biasing their results by (1) visualizing their data to develop hypotheses about the underlying structure of symptom co-occurrence, (2) selecting appropriate multiple methods to verify observations realizing the limitations of single methods, and (3) developing new methods if current methods do not suffice.

6. Conclusions and Future Research

Inspired by the research on symptom clusters, but concerned by the limitations of using methods with a priori assumptions about the structure of clusters in the data, we used networks to visually analyze how symptoms co-occurred across cancer patients. These observations were then quantitatively analyzed through carefully selected existing and novel methods, and compared against random permutations of the network. Although the results consistently showed the absence of multiple distinct symptom clusters, the multi-method approach revealed a strongly nested structure of symptom co-occurrence, where a small set of symptoms co-occurred in many patients, and a progressively larger set of symptoms co-occurred with a decreasing number of patients. This result reveals a more complex co-occurrence organization of symptoms across patients than previously reported. The result also suggests that a computational approach designed carefully to fit into current work practice could limit the questions clinicians need to ask patients in order to obtain a complete picture of their symptoms.

Because symptoms can be caused by a number of factors that change over time including the disease itself, co-morbid conditions, treatment, and other symptoms, our future research aims to use networks in combination with quantitative methods to probe deeper into this large number of variables. Our aim is to help clinicians accurately identify, predict, and treat co-occurring symptoms, with the ultimate goal of improving compliance with therapy, and the overall quality of life for cancer patients.

Supplementary Material

supplementary material

Figure S1. The patient-symptom bipartite network (similar to the one shown in Figure 2) shows how 18 symptoms (white nodes) co-occur across 665 patients (colored by each patient’s type of cancer). The layout suggests that there exist no distinct clusters of patients based on cancer type.