Abstract
Early and accurate prediction of tissue outcome is essential to the clinical decision-making process in acute ischemic stroke. We present a quantitative predictive model of tissue fate that combines regional imaging features available after onset. A key component is the use of cuboids randomly sampled during the learning process. Models trained with time-to-maximum feature (Tmax) computed from perfusion weighted images (PWI) are compared to the ones obtained from the apparent diffusion coefficient (ADC). The prediction task is formalized as a regression problem where the inputs are the local cuboids extracted from Tmax or ADC images at onset, and the output is the segmented FLAIR intensity of the tissue 4 days after intervention. Experiments on 25 acute stroke patients demonstrate the effectiveness of the proposed approach in predicting tissue fate. Results on our dataset show the superiority of the regional model vs. a single-voxel-based approach, indicate that PWI regional models outperform ADC models, and demonstrates that a nonlinear regression model significantly improves the results in comparison to a linear model.
Keywords: Brain ischemia, Acute stroke diagnostic, Prediction, Stroke, Regional, Perfusion weighted images, Lesion growth
INTRODUCTION
Stroke is a leading cause of death and a major cause of long term disabilities throughout the world. Recovery can be achieved if recanalization of the occluded vessel occurs early on. Available therapeutic strategies are associated with specific risks that need to be counterbalanced with possible benefits. For example, tPA increases the chances of hemorrhage and has to be applied early after symptoms onset. While clinical trials have established safety time windows, they reflect an average from a heterogeneous population. Some patients may be unnecessarily excluded and potentially miss a treatment opportunity. Therefore, there is a need for a better utilization of available imaging data to predict tissue outcome to quantify the potential benefits of an intervention and offer a personalized treatment.
Lesion growth in ischemic stroke is known to be a dynamic process that evolves spatially over time due to regional hemodynamic compromise. Without successful treatment, the core of the lesion may expand to nearby tissue. Consequently, a healthy voxel surrounded by wounded tissue at early stages is more likely to become irreversibly damaged. Based on this observation, we hypothesize in this study that the regional distribution of image intensities surrounding a voxel at early stages may capture characteristics about the dynamic of growth of the lesion and be predictive of tissue outcome.
Several quantitative models of tissue fate have recently been studied. They are typically built by mapping each voxel intensity at onset to the observed tissue fate, as measured in Fluid Attenuated Inversion Recovery (FLAIR) images several days after intervention. Wu et al.22,23 evaluated a generalized linear model (GLM) based on diffusion (DWI) and perfusion-weighted (PWI) magnetic resonance imaging (MRI) on 14 patients. Rose et al.14 used Gaussian models trained on multiple parameters (DWI, cerebral blood flow (CBF), cerebral blood volume (CBV), mean transit time (MTT)) to predict tissue outcome on 19 patients. Other studies were performed based on logistic regression,24 on ISODATA clustering18 applied to apparent diffusion coefficient (ADC) and CBF. The time-to-maximum (Tmax) parameters has also demonstrated its predictive power for tissue outcome.12,13 It has been shown to predict actual CBF more accurately than MTT.13 These studies were essentially performed by considering each voxel independently. Only a few approaches have implicitly integrated regional information by exploiting spatial correlation between voxels,11 using a prior map of spatial frequency-of-infarct,17 and Neural Networks.8 These studies have demonstrated signs of improvement in comparison to single-voxel-based models. Our previous work15 has shown a similar trend for MTT, time-to-peak (TTP), and Tmax parameters. However, our study was preliminary; the dataset was limited in size (7 patients), results were reported in terms of relative regression error, and no measure of significance was estimated.
This paper is inspired by these findings and introduces a regional predictive model of tissue fate that combines the information available at onset in terms of FLAIR images with either Tmax, or ADC to predict the tissue outcome 4 days after intervention. The proposed model allows us to study the impact of a regional model on tissue fate prediction (i.e., our main hypothesis). The framework relies on a regression model that is trained on a set of images with known outcome. Once the model has been trained, it can be used to predict the tissue fate, in terms of followup FLAIR intensity, on new cases. Our long term goal is to provide such predictions together with onset images to clinicians during the clinical decision making process.
From a technical perspective, the model has two main contributions: (a) First, the regional distribution among neighboring voxels is captured by the use of cuboids (Fig. 1). During learning, pairs of cuboids are sampled at similar locations in FLAIR and either Tmax or ADC images, and combined into a single input vector for the predictive model. In the case of acute stroke, abnormal Tmax values may indicate hypoperfusion and poor collateral supply. However, the exact physiological meaning of Tmax is complex because the observed delay may originate from various other causes.4 ADC allows to detect early and acute ischemic changes. It was chosen over DWI because it shows a minor difference between white matter and grey matter.
FIGURE 1.

Illustration of a pair of cuboids extracted at the same location in FLAIR and Tmax images (extracted from PWI images) and used by the regression model to predict the tissue outcome in terms of FLAIR intensity.
The output of the model is the survival outcome extracted 4 days after a successful intervention from segmented FLAIR images, the gold standard to depict irreversible lesions. (b) The second contribution is to exploit kernel spectral regression (SR-KDA)12 to infer the relation between cuboids extracted at onset and the tissue fate. SR-KDA has been shown in the literature and our previous works16 to successfully capture nonlinear relationships in a wide variety of problems. The performance of SR-KDA was at least on par with state-of-the-art techniques such as Support Vector Machines (SVM), Adaptive Boosting (AdaBoost), and decision trees while offering more efficient training of the model. To the best of our knowledge, however, it has never been used in the context of Stroke.
METHODS
Patients, and MRI Data Acquisition
Patients in this study were identified with symptoms of ischemic stroke and admitted at the University of California-Los Angeles Medical Center. The use of this data was approved by the local Institutional Review Board. Inclusion criteria for this study included: (1) diagnosis of acute stroke due to occlusion of the middle cerebral artery (MCA), (2) admission to ICU within 6 h of last known well time, (3) MRI (including ADC and PWI) of the brain performed before recanalization therapy and 4 days later, (4) absence of hemorrhage. A total of 25 patients (mean age, 56 ± 21 years; age range, 27–89; 15 women; average NIHSS of 14 ± 6.3; 18 hypertensive; six obese; nine smokers) satisfied the above criteria. All patients had the revascularization success determined using the Thrombolysis in Cerebral Infarction (TICI) scale: TICI Score 3, 2b, and 2a in 5, 7, and 13 patients, respectively. 17 patients were administred with IV-Tpa and all were treated with Mechanical Embolus Removal in Cerebral Ischemia (MERCI) devices.21 The median time from symptom onset to baseline MRI was 4h38 (IQR 1h43, 5h39), and to followup MRI was 4 days 13h30 (IQR 3 days 15h08, 4 days 22h17). Median time from onset to intervention was 6h20 (IQR 1h59, 8h30). Average lesion size at onset was 10.35 ± 13.1 and 43.6 ± 18.2 cm3 at followup.
All patients underwent MRI using a 1.5 Tesla echo planar MR imaging scanner (Siemens Medical Systems). This study is based on the analysis of Tmax, ADC, and FLAIR images. The MR-PWI scanning was performed with a timed contrast-bolus passage technique (0.1 mg/kg contrast administered intravenously at a rate of 5 cm3/s), with a repetition time (TR) range of 1770 to 2890 ms, and average echo time (TE) of 44 ± 10.4. Pixel dimension varies from 0.859 × 0.859 × 6 to 1.875 × 1.875 × 7 mm. ADC was acquired with b values of 1000 s/mm2 and range values of TR and TE, of 3500–6000 and 78–118 ms, respectively. Pixel dimension on ADC images varies from 0.9375 × 0.9375 × 7 to 0.859 × 0.859 × 7 mm. The FLAIR sequence has a TR ranging from 7000 to 1,0000 ms; a TE ranging from 82 to 123 ms; and an inversion time (TI) ranging from 2400 to 2500 ms. Pixel dimension on FLAIR images was 0.859 × 0.859 × 7 mm.
Image Preprocessing
Automatic Brain Volume Segmentation
The skull and non-brain tissue is removed from FLAIR images using the FSL Brain Extraction Tool (BET).20 BET estimates an intensity threshold to discriminate between brain/non-brain voxels. Then, it determines the center of gravity of the head, defines a sphere based on the center of gravity of the volume, and finally deforms it toward the brain surface.
FLAIR Image Normalization
Because FLAIR images were acquired with different settings and originated from different patients, their intensity value was not directly comparable. To allow for inter-patient comparisons, FLAIR images were normalized with respect to the average intensities within the contralateral white matter. The normal-appearing white matter was delineated manually by an experienced researcher for both onset and follow-up brain volumes.
Tmax Features
Tmax was extracted from PWI images with a software developed in our imaging laboratory, the Stroke Cerebral Analysis (SCAN) package. The tissue contrast agent concentration C(t) can be expressed as a convolution of the arterial input function (AIF) identified from the contralateral MCA and the residue function R(t),4 C(t) = CBF × (AIF(t) ⊗ R(t)). The AIF was estimated from manually selected voxels using a gamma variate fit. The residue function is obtained by deconvolution, and the time to its maximum value is used to specify Tmax. Therefore, Tmax is the arrival delay between the AIF and C(t).
Image Registration
Registration between FLAIR, ADC, and Tmax images is necessary because the outcome of an extracted cuboid, measured as a voxel value in the followup image, has to correspond to the same anatomical location in the different volumes. Co-registration was performed for each patient independently. Because the intensity of FLAIR images may present large variations between onset and followup due to changes in the tissue perfusion caused by the stroke, several attempts to use automatic image registration methods failed to accurately align the volumes. Instead, we developed a semi-automatic registration software in Matlab that utilized five landmark points placed manually at specific anatomical locations (center, plus four main cardinal directions) on the slice of the brain that had the largest ventricular area. An affine projection was applied to project the followup FLAIR and acute Tmax on the original FLAIR volume.
Ground Truth
During evaluation, the prediction task will be posed as a classification problem where each voxel will be predicted as infarcted or not. To obtain this binary groundtruth, a semi-automatic segmentation of infarcts was performed on FLAIR images by an expert in neurology who was asked to delineate infarcts, comparing the infarcted hemisphere with the contralateral hemisphere if needed. The expert was only presented FLAIR images and was blinded to ADC, Tmax, and predicted images. Outlining was performed with the help of the commercially available medical imaging software 3D Doctor (http://www.ablesw.com/) that uses connectivity during the segmentation process. Outlier regions were manually identified and removed. The voxels falling in the infarct were labelled as 1, while the rest of the volume was marked as 0.
Cuboid Sampling
For training, we exploit a set of FLAIR images F at onset, their corresponding co-registered Tmax or ADC feature map M, and followup FLAIR images F’. The dataset {X, Y} used to train and to evaluate the predictive model is created by extracting cuboids of fixed size w × l × d among onset images with their corresponding outcome. Each cuboid is described by its raw voxel values, yielding an input vector of s = w × l × d numerical attributes. Our method extracts a large number of cuboids at random positions from training images. In practice, given a sampled location {i, j, k}, we extract a cuboid cF in the acute FLAIR image at F(i, j, k) and a corresponding cuboid cM in the Tmax or ADC map at M(i, j, k).
For efficient correspondence of similar cuboids across patients,10 it is desirable to obtain cuboids that are invariant to rotations. As illustrated in Fig. 2, rotation invariance is especially useful when considering cuboids that are equidistant to a lesion core but located at different directions. If no rotational normalization is performed, the cuboids have a lower similarity (i.e., larger voxel-by-voxel distance). Although the presence of intraparenchymal gradient in images reflects local pressure differences that may be influential of lesion growth, the motivation of using gradient in this study is computational. We aim at presenting the classifier with consistent, comparable examples, so that it can use the available regional information optimally. For these reasons, the cuboids are normalized with respect to the direction θ of the image gradient2 using Lanczos interpolation,7
| (1) |
| (2) |
where are the Gaussian derivatives in X and Y directions, computed from the acute FLAIR image F and input image M,
| (3) |
| (4) |
where is a 2D isotropic Gaussian filter with standard deviation σ = 3 in our experiments. The two cuboids are merged into a single, multi-modal cuboid x = {cF’,cM’} that corresponds to the concatenation of the cuboids extracted at the same location in the different volumes. Each multi-modal cuboid x is then labeled with the intensity y of the central voxel in the corresponding follow-up FLAIR image y = F’(i,j,k). The dataset consists of the set of multi-modal cuboids x ∈ X and their corresponding outputs y ∈ Y that represent the followup FLAIR intensities.
FIGURE 2.

Illustration of the orientation normalization of cuboids extracted from a Tmax image at two different locations (A, B). While the two raw cuboids have a low similarity (red) if they are compared using a voxel-by-voxel distance, they can be more easily matched by the model if they are rotationally normalized with respect to the local gradient.
Regression-Based Predictive Model
Our predictive model takes the form a regression model y = f(x) that maps the tissue outcome y ∈ Y as a function of the multi-modal cuboid x ∈ X extracted at the same location. In this study, a comparative analysis will be provided between multi-linear regression,5 and kernel spectral regression (SR-KDA)3 which is described below.
Kernel Spectral Regression
SR-KDA3 is a recently proposed method to solve kernel discriminant analysis (KDA) problems efficiently. It poses the discriminant analysis as a regularized regression problem. SR-KDA projects input data X onto a high-dimensional space via a Gaussian kernel K,
| (5) |
where σ is the user-specified standard deviation of the kernel.
SR-KDA estimates the mapping using a Cholesky decomposition from the regularized positive definite matrix K to obtain vector α,
| (6) |
| (7) |
where I is the identity matrix and δ > 0 the regularization parameter. When a new multi-modal cuboid, xnew, is extracted from a new image, the FLAIR intensity at followup, , is predicted using
| (8) |
| (9) |
where k is the vector resulting from the kernel projection of xnew into the kernel space using training data X.
Experimental Setup
The proposed experiments are designed to answer the following questions: Do the neighboring voxels help predict the outcome of the tissue at a specific voxel? If so, what is the optimal size of this neighborhood for Tmax and ADC images? Can it be captured by a linear model? Specifically, these questions will be addressed by evaluating the tissue fate prediction accuracy of the multiple linear regression (LIN) and kernel spectral regression (SR-KDA) (“Kernel Spectral Regression” section) on our dataset (“Patients, and MRI Data Acquisition” section). The problem is posed as a classification task where the output corresponds to the segmented FLAIR at followup (“Ground Truth” section)
Training of the regression models is performed from a set of training samples that, in the ideal case, should be uniformly distributed throughout the data space. However, this is not the case for most of the stroke patients where the brain volume contains a larger number of healthy voxels. A recent study9 has shown that an unequal number of infarcted and noninfarcted voxels can negatively impact the overall performance of the system. Following the methods of the study, we perform a random sampling on the input cuboids so that an equal number of infarcted and noninfarcted cuboids are present in the training set. The number of training samples for each slice was set to a maximum of 85 cuboids of class 0 and 85 cuboids of class 1. In theory, this could create a large dataset of 170 × nbSlice × nbCases training samples. In practice, however, we reduce the size of the dataset during the extraction process such that the number of extracted cuboids for a slice is equal to the minimum number of occurrence of either class (0 or 1). For example, if only 10 voxels are infarcted (class 1) on the followup of one slice, only 10 cuboids will be extracted for class 1 as well as 10 other cuboids for class 0. This procedure has the advantage of speeding up the cuboid extraction process and generates less than 10,000 training samples equally distributed between the two classes.
Cuboid Size
We evaluate the accuracy of the LIN and SR-KDA regression methods to predict tissue fate for different sizes of cuboids. For each cuboid size and regression method, two predictive models are trained, one for each type of image: Tmax and ADC. The models are evaluated using a leave-one-patient-out crossvalidation so that the data from the patient evaluated is excluded from the training set. In this experiment, cuboids are symmetric; w, l have the same length (“Cuboid Sampling” section). The tested sizes1 spanned from 1 × 1 to 23 × 23. Because the image resolution varies across the dataset, the cuboid size is set relative to a resolution of 1 × 1 mm per voxel. During the leave-one-out crossvalidation, the Area Under the Curve (AUC) is computed from the ROC curve for each patient. The average AUC and standard deviation across patients are calculated and used as measure of performance. The parameters σ, δ of SR-KDA were optimized at each iteration of the leave-one-out procedure by running another leave-one-out cross-validation excluding the patient to be tested at the current iteration.
In addition to reporting the AUC values, a global ROC curve was generated for each combination of input image (Tmax, ADC) and regression model (SR-KDA, LIN). For fair comparison, the cuboid size of each combination was the one that led to the best accuracy in the previous experiment (15 × 15 for Tmax + SR-KDA, 13 × 13 for ADC + SR-KDA, 7 × 7 for Tmax + LIN, 5 × 5 for ADC + LIN), as reported in Fig. 3. The results obtained by the regional methods were also compared to the accuracy of single-voxel-based models. To generate a global ROC curve, predictions are first computed for each specific patient i during the crossvalidation. Then, all the prediction vectors are concatenated into a single vector , and the global ROC curve is computed from the data of all patients .
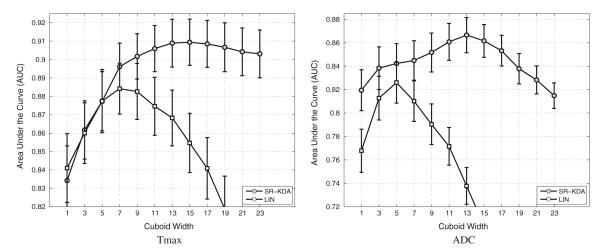
FIGURE 3.
Effect of the cuboid size on the average AUC using SR-KDA regression model for Tmax (left) and ADC (right) images. Results are reported after a leave-one-patient-out crossvalidation.
McNemar and DeLong Significance Tests
Although differences in AUCs can be used to rank different models, they may not be statistically significant. A McNemar’s test19 is used to verify if the difference between LIN and SR-KDA and between regional and single-voxel-based models are statistically significant for the two types of images. McNemar’s test, which is based on a Fisher-test with one degree of freedom, is a useful tool in determining if two methods have comparable error rates.
McNemar’s test is applied to determine if two hypotheses of this paper are supported by a statistical significance test. First, we verify that the improvement in performance obtained by the regional cuboids vs. a single voxel is significant. To do so, the McNemar’s test is performed between the models obtained using SR-KDA with 15 × 15 cuboids and SR-KDA with a single voxel 1 × 1. We repeat a similar test for the ADC images where the cuboid sizes 5 × 5 and 1 × 1 were compared. For the second test, we verify that the improvements obtained by a nonlinear (SR-KDA) vs. a linear (LIN) regression model are significant as well for the Tmax and ADC images. The McNemar’s test is performed between the models obtained using SR-KDA with 15 × 15 cuboids and LIN with size 7 × 7 for Tmax images, and SR-KDA with 13 × 13 cuboids and LIN with size 5 × 5 on ADC images.
In addition to McNemar’s test, we perform a significance test directly between the ROC curves computed using the different models (SR-KDA, LIN, regional, single-voxel) using DeLong et al.6 method. For each method, we also report the standard error and the confidence interval associated with the ROC curves using a binomial exact test. Statistical tests were performed with help of the commercially available software MedCalc (http://www.medcalc.org/).
RESULTS
The average AUCs after a leave-one-patient-out crossvalidation for an increased cuboid size are reported in Fig. 3. The value of the AUC can be interpreted as the probability of correct classification for a randomly selected pair of positive and negative samples. Usually, any AUC result above 90% is considered as excellent.
SR-KDA reaches an accuracy of 90.9 ± 1.1 at a size of 15 × 15 on Tmax, and 86.7 ± 1.5 at its best for a size of 13 × 13 on ADC images. These results suggest that the tissue outcome is very well predicted from Tmax images. The optimal cuboid size is different for the two types of images, but both perform better than single-voxel-based models; from 83.5 ± 1.8 to 90.9 ± 1.1 for Tmax, from 81.9 ± 1.5 to 86.7 ± 1.5 for ADC. These results validate the hypothesis that a regional approach, which takes into account neighboring voxels, greatly improves the prediction accuracy regardless the type of image used. After reaching the optimal size, the results based on Tmax still remain over an average AUC of 90, while the models based on ADC show a sharper decrease. It is not clear however if the optimal size depends on the number of training cases available. It could be argued that as the cuboid size increases, so does the complexity of the associated model, and so does the number of examples necessary to train the model. It is possible that as the number of available examples increases, improved performance could be obtained at even larger cuboid sizes.
The linear model reaches a maximum of 88.4 ± 1.4 for Tmax at size 7 × 7, and 82.6 ± 1.8 at size 5 × 5 for ADC. These results seem to indicate that a nonlinear model is necessary to fully capture the complexity of the spatial distribution of the intensity. Unlike models trained using SR-KDA, the performance of linear models decreases rapidly once the optimal size is reached. A possible reason for this decrease is that the irrelevant, noisy information included in the data may increase with respect to the cuboid size and may therefore disrupts the training of the model. Linear models are known to be affected by outliers.
We didn’t observe any significant improvements by concatenating Tmax with ADC cuboids within the same model. This may be due to the difference in regularization required for each type of cuboid. Another reason is that the number of training samples may be too low for the classifier to be able to identify the predictive link between ADC + Tmax and outcome.
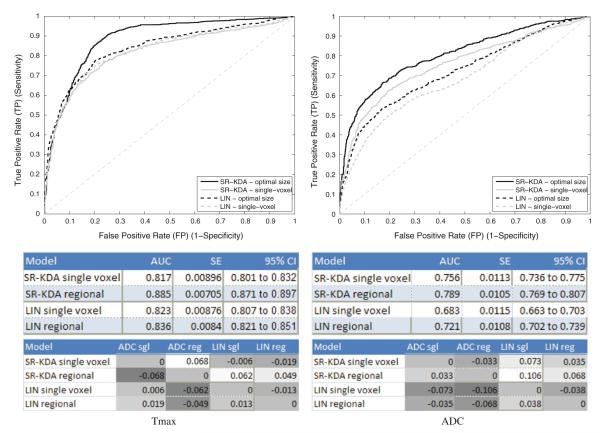
Global ROC curves that illustrate the results in terms of true positive and false positive rates are depicted in Fig. 4. The ROC curves produced by SR-KDA and LIN models for Tmax are shown on the left, and the ROCs for the ADC are displayed on the right. Each curve is labelled as “optimal size” or “single-voxel” depending if a regional model is trained with the size that led to the best results in the previous experiments (Fig. 3). Two tables are shown under each plot to report the AUC, standard error, and 95% confidence interval (CI) for each curve. It can be observed that the AUC of globally computed ROC curves is lower that the average AUC computed from individual ROCs (Fig. 3). This can be explained by a shift of the predictions at the patient level. For example, if an image is imperfectly normalized such that all the FLAIR input values in the image are slightly shifted, it may lead to predictions that are also slightly shifted. While this phenomenon may not affect the AUC computed at the patient level, because the difference between the two classes of voxels remain the same across a single image, it will impact on the computation of the global ROC curve (as reported in Fig. 4) because the predicted samples of all the patients are used at the same time to construct the ROC.
FIGURE 4.
Receiver operating characteristic (ROC) curve for Tmax (left), and ADC (right). Regional results are produced using the cuboid size that led to the best average AUC for each modality (as reported in Fig. 3).
Despite the global decrease in performance that affects all the methods, the results still indicate that regional models trained with SR-KDA outperform single-voxel-based models, from 81 to 88 for Tmax and from 75 to 79 for ADC images. The middle table reports the confidence intervals. It indicates that for SR-KDA there is no or little overlap between them which is reflected by the DeLong’s test that found differences between single-voxel and regional models significant (with p-values <0.0001) for both types of images. Please note that the relative differences in AUC for each method is reported in the bottom table.
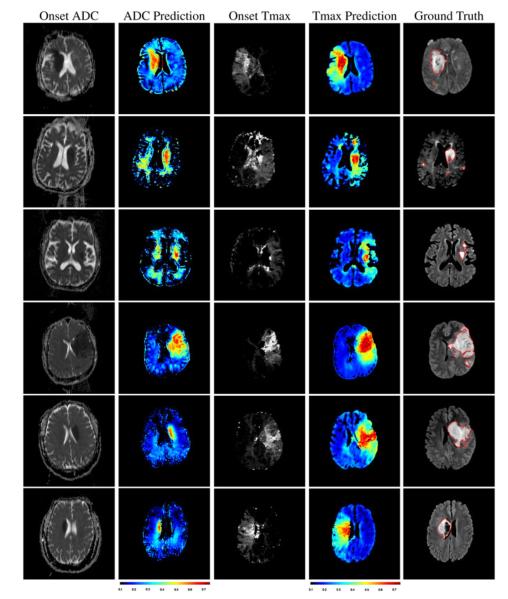
The similarity between the prediction and the actual outcome of the brain tissue can be visualized in Fig. 5 on arbitrary slices. Illustrated cases were chosen to reflect the variability in outcomes observed across our dataset. Rows 2, 3, 6 depict three cases that had a significantly smaller final lesion size than the other three cases. The columns respectively correspond to ADC at onset, day 4 predictions from ADC, Tmax at onset, day 4 predictions from Tmax, and the outlined ground truth depicted by red contours on FLAIR images at day 4. The predictions were obtained from the SR-KDA model trained using a leave-one-out crossvalidation with cuboid size of 15 × 15 × 1 for Tmax, and 13 × 13 × 1 for ADC. It can be observed than predictions based on ADC tend to underestimate the final size of the lesion. Regional predictions based on Tmax better match the final area, and are not affected but the noisy voxels that are present in source Tmax images. It can also be seen in rows 1, 4, 5, 6 that the growth of lesion may have been associated with a deformation and shift of the tissue which makes the prediction on those cases even more challenging.
FIGURE 5.
ADC (col. 1) and Tmax perfusion at onset (col. 3) are illustrated with the corresponding prediction of the models (col. 2) and (col. 4) for six patients. During our evaluation, predictions were compared to the ground truth (col. 5, red contours) manually outlined in followup FLAIR at day 4. Regional predictions based on ADC images tend to underestimate the final infarct. Predictions based on Tmax tend to better match the final extent of the infarct.
McNemar Test
Significance results of the McNemar’s test are summarized in Table 1. With a 95% confidence interval and one degree of freedom, two methods are considered significantly different if the value χ2 is above 3.8414. For the test between regional vs. single-voxel-based models (first two rows) McNemar’s values are 46.75, 45.02 for Tmax and ADC, respectively. Both are considered significant because they are over 3.8414. For the test between LIN and SR-KDA methods, McNemar’s values are 18.81, 15.46 for group Tmax and ADC, respectively, and their difference can also be considered significant. All the p-values for these NcNemar’s values were below 0.0001.
TABLE 1.
Results of McNemar’s test to measure the significance of using regional vs. single-voxel-based models using Tmax and ADC images.
| Test | McNemar |
|---|---|
| Tmax—SR-KDA 15 × 15 vs. SR-KDA 1 × 1 | 46.75 |
| Tmax—SR-KDA 15 × 15 vs. LIN 7 × 7 | 33.95 |
| ADC—SR-KDA 13 × 13 vs. SR-KDA 1 × 1 | 18.81 |
| ADC—SR-KDA 13 × 13 vs. LIN 5 × 5 | 15.46 |
Computational Performance
The predictive model was implemented in Matlab and executed on a Dell Optiplex 760 desktop computer equipped with an Intel Core2 Duo CPU cadenced at 3.33 GHz. The training of the predictive model, excluding image normalization, volume registration, and ground truth selection took approximately 10 min for 10 × 10 cuboids, while the prediction on an entire volume took less than 1 min and tend to increase proportionally with the size of the cuboids.
DISCUSSION
The prediction of brain tissue fate in ischemic stroke, and by extension the identification of salvageable tissue, is a challenging problem that holds useful information for the clinician during the decision making process. Ultimately, automatic tissue fate predictive models could help us understand the underlying mechanisms of lesion growth. These mechanisms are complex, as they depend on a wide variety of factors such as: quality of blood perfusion to the area, quality of collaterals, energy delivery, age and medical history of the patient, etc. Integrating all these elements within a unified predictive model is the long-term goal of our research.
In this paper, we have described a generic framework to predict the likely outcome of brain tissue in ischemic stroke patients. This approach is based on Tmax or ADC, and FLAIR images extracted at onset. Although regional models were trained on a rather small dataset, our experimental results have validated the method by improving those obtained by linear and single-voxel-based approaches. The good performances demonstrated by the system may be explained by the following reasons:
Regional
The use of cuboids significantly improves a single-voxel-based approach. From a technical perspective, a possible explanation of this improvement is that cuboids implicitly represent the regional distribution of intensity and correlation among voxels and are more robust to noise. From a physiological point of view, it appears that the distribution of the delay (Tmax), observed in the immediate surrounding of the voxel to be predicted, holds specific features that are predictive of outcome (and by extension reversal of Tmax abnormalities).
Nonlinear
SR-KDA improves the prediction accuracy in comparison with a linear regression approach. A possible explanation for this difference is that the relation between the multi-modal cuboids extracted at onset and the followup FLAIR intensity is not a linear one, and it is therefore better captured by a nonlinear model such as SR-KDA. A consequence of this results, is that a threshold-based approach is not optimal for prediction. Because machine learning algorithms can identify complex rules to map regional features to outcome, they are certainly a promising direction to pursue.
Randomness
Efficiently exploiting the millions of cuboids available in the training set is a complex task. To obtain a representative training set, we randomly sample cuboids across images so that a similar number of cuboids is sampled for each outcome (infarcted or not). Such a solution should allow us to train models with a potentially much larger, and thus more representative, balanced dataset.
In principle, even after normalization, FLAIR (as well as Tmax and ADC) images are not necessarily comparable between patients. However, in practice, the “leave-one-patient-out” approach excludes all the data of the patient to be evaluated from the training set, and therefore, solely relies on the other patients to make predictions. Results obtained in terms of average AUC show that after normalization, infarcted and non-infarcted tissue can with a reasonable confidence be predicted across patients in our dataset.
It should be acknowledged that before integration of the model in the stroke imaging protocol, a multi-center evaluation of the proposed regional model should be performed to validate the results on a more representative set of cases. A limitation of this study is to include data with various degree of recanalization (TICI scores from 2a to 3). A regional predictive model should be trained for each TICI recanalization score (0, 1, 2a, 2b, 3) separately. During diagnostic, predicted images could help clinicians to visualize the likely benefits of the intervention and the dependency to the degree of recanalization. It would also be beneficial to build a serial predictive model that could be updated using a measure of reperfusion obtained after the intervention. Reperfusion is known to be a determining factor of lesion growth.
While a correct prediction indicates that the relation between the input region and the outcome of the tissue can be captured by the model, prediction errors may originate from several technical approximations. The co-registration of images is a critical step of the framework. Slight errors in the image alignment may easily affect the model because wrongly labelled cuboids would be included in the training set. It is clear that the co-registration technique used in this study (five landmark points and an affine transform) could be improved using a nonlinear registration technique that would be robust to the deformation and appearance changes due to the lesion growth. Another possible cause of error is due to the distortion in the Echo Planar Imaging (EPI) based measurements that was not taken into account in this study. The computation of Tmax which was based on the manual selection of the AIF is also subject to errors that may affect the results. Automatic and precise estimation of the AIF would be desirable.
The regional distribution of the intensity was extracted with cuboids. Other shapes and layout could be considered (such as circular or fovea regions1) and learned in a discriminative fashion depending on the affected area to obtain a better description of the neighborhood. In addition, we used raw image values to describe each cuboid. Histogram-based approaches and other local image descriptors10 have been shown to offer better performance than raw voxel values on a wide variety of imaging applications, and could be investigated in the context of stroke.
The current study was focused on patients with MCA occlusion only. It would be interesting to evaluate the regional model on other stroke locations as well. Other applications of the regional model may include prediction of hemorrhagic transformation (HT) from other types of input images.
The predictive model introduced in this study is not linked to a specific type of input images. For example, other parameters extracted from PWI images could be used as input to the model in addition to the one used in the study. While Tmax performed consistently better than ADC on our dataset, further work is needed to evaluate if the combination of the two parameters within a regional model can improve the overall prediction accuracy.
CONCLUSION
The main result of this study is to demonstrate that regional models significantly improve the prediction of tissue fate when applied on Tmax and ADC images at onset. While the predictive power of regional model has also been observed in our experiments using linear models, a nonlinear model seems necessary to fully capture the relation between the regional imaging features of a voxel and its outcome. There is, however, a margin for improvement by taking into account additional physiological parameters (e.g., reperfusion, collateral flow), other types of images (e.g., CBV, MTT, …), serial data, and multi-center data. The framework developed in this study should help us to further study the factors of lesion growth in a quantitative fashion and ultimately provide the clinician with reliable prediction of tissue fate.
ACKNOWLEDGMENTS
This work was partially supported by the National Natural Science Foundation of China (NSFC) to F.S., grant number 31050110122. D.L. was partially supported by NIH/NINDS K23NS054084, P50NS044378, K24NS072272.
Footnotes
The low sagittal resolution (≥7 mm per voxel) of PWI images did not allow us to test the z-size of the cuboid which was set to 1 slice.
REFERENCES
- 1.Brown M, Hua G, Winder S. Discriminative learning of local image descriptors. IEEE Trans. Pattern Anal. Mach. Intell. 2011;33(1):43–57. doi: 10.1109/TPAMI.2010.54. [DOI] [PubMed] [Google Scholar]
- 2.Brown M, Szeliski R, Winder S. Multi-image matching using multi-scale oriented patches. CVPR. 2005;1:510–517. [Google Scholar]
- 3.Cai D, He X, Han J. Spectral regression for efficient regularized subspace learning. ICCV. 2007 [Google Scholar]
- 4.Calamante F, Christensen S, Desmond PM, Ostergaard L, Davis SM, Connelly A. The physiological significance of the time-to-maximum (Tmax) parameter in perfusion MRI. Stroke. 2010;41:1169–1174. doi: 10.1161/STROKEAHA.110.580670. [DOI] [PubMed] [Google Scholar]
- 5.Chatterjee S, Hadi AS. Influential observations, high leverage points and outliers in linear regression. Stat. Sci. 1986;1:379–393. [Google Scholar]
- 6.DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44:837–845. [PubMed] [Google Scholar]
- 7.Duchon CE. Lanczos filtering in one and two dimensions. J. Appl. Meteorol. 1979;18(8):1016–1022. [Google Scholar]
- 8.Huang S, Shen Q, Duong TQ. Artificial neural network prediction of ischemic tissue fate in acute stroke imaging. J. Cereb. Blood Flow Metab. 2010;39:1661–1670. doi: 10.1038/jcbfm.2010.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jonsdottir K, Ostergaard L, Mouridsen K. Predicting tissue outcome from acute stroke magnetic resonance imaging: improving model performance by optimal sampling of training data. Stroke. 2009;40:3006–3011. doi: 10.1161/STROKEAHA.109.552216. [DOI] [PubMed] [Google Scholar]
- 10.Mikolajczyk K, Schmid C. A performance evaluation of local descriptors. IEEE Trans. Pattern Anal. Mach. Intell. 2005;27:1615–1630. doi: 10.1109/TPAMI.2005.188. [DOI] [PubMed] [Google Scholar]
- 11.Nguyen V, Pien H, Menenzes N, Lopez C, Melinosky C, Wu O, Sorensen A, Cooperman G, Ay H, Koroshetz W, Liu Y, Nuutinen J, Aronen H, Karonen J. Stroke tissue outcome prediction using a spatially-correlated model. PPIC. 2008 [Google Scholar]
- 12.Olivot J, Mlynash M, Thijs V, Purushotham A, Kemp S, Lansberg M, Wechsler L, Gold G, Bammer R, Marks M, Albers G. Geography, structure, and evolution of diffusion and perfusion lesions in Diffusion and perfusion imaging Evaluation For Understanding Stroke Evolution (DEFUSE) Stroke. 2009;40(10):3245–3251. doi: 10.1161/STROKEAHA.109.558635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Olivot JM, Mlynash M, Zaharchuk G, Straka M, Bammer R, Schwartz N, Lansberg MG, Moseley ME, Albers GW. Perfusion MRI (Tmax and MTT) correlation with xenon CT cerebral blood flow in stroke patients. Neurology. 2009;72:1140–1145. doi: 10.1212/01.wnl.0000345372.49233.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rose S, Chalk J, Griffin M, Janke A, Chen F, McLachan G, Peel D, Zelaya F, Markus H, Jones D, Simmons A, O’Sullivan M, Jarosz J, Strugnell W, Doddrell D, Semple J. MRI based diffusion and perfusion predictive model to estimate stroke evolution. JMRI. 2001;19(8):1043–1053. doi: 10.1016/s0730-725x(01)00435-0. [DOI] [PubMed] [Google Scholar]
- 15.Scalzo F, Hao Q, Alger J, Hu X, Liebeskind D. Tissue fate prediction in acute ischemic stroke using cuboid models. ISVC. 2010;6454:292–301. [Google Scholar]
- 16.Scalzo F, Xu P, Asgari S, Bergsneider M, Hu X. Regression analysis for peak designation in pulsatile pressure signals. Med. Biol. Eng. Comput. 2009;47:967–977. doi: 10.1007/s11517-009-0505-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shen Q, Duong T. Quantitative prediction of ischemic stroke tissue fate. NMR Biomed. 2008;21:839–848. doi: 10.1002/nbm.1264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shen Q, Ren H, Fisher M, Duong T. Statistical prediction of tissue fate in acute ischemic brain injury. J. Cereb. Blood Flow Metab. 2005;25:1336–1345. doi: 10.1038/sj.jcbfm.9600126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Siegel S, Castellan N. Nonparametric Statistics for the Behavioral Sciences. 2nd ed McGraw–Hill, Inc.; Boston: 1988. [Google Scholar]
- 20.Smith S. Fast robust automated brain extraction. Hum. Brain Mapp. 2002;17(3):143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Smith WS, Sung G, Saver J, Budzik R, Duckwiler G, Liebeskind DS, et al. Mechanical thrombectomy for acute ischemic stroke: final results of the Multi MERCI trial. Stroke. 2008;39:1205–1212. doi: 10.1161/STROKEAHA.107.497115. [DOI] [PubMed] [Google Scholar]
- 22.Wu O, Koroshetz W, Ostergaard L, Buonanno F, Copen W, Gonzalez R, Rordorf G, Rosen B, Schwamm L, Weisskoff R, Sorensen A. Predicting tissue outcome in acute human cerebral ischemia using combined diffusion- and perfusion-weighted MR imaging. Stroke. 2001;32(4):933–942. doi: 10.1161/01.str.32.4.933. [DOI] [PubMed] [Google Scholar]
- 23.Wu O, Sumii T, Asahi M, Sasamata M, Ostergaard L, Rosen B, Lo E, Dijkhuizen R. Infarct prediction and treatment assessment with MRI-based algorithms in experimental stroke models. J. Cereb. Blood Flow Metab. 2007;27:196–204. doi: 10.1038/sj.jcbfm.9600328. [DOI] [PubMed] [Google Scholar]
- 24.Yoo AJ, Barak ER, Copen WA, Kamalian S, Gharai LR, Pervez MA, Schwamm LH, Gonzalez RG, Schaefer PW. Combining acute diffusion-weighted imaging and mean transmit time lesion volumes with NI-HSSS improves the prediction of acute stroke outcome. Stroke. 2010;41:1728–1735. doi: 10.1161/STROKEAHA.110.582874. [DOI] [PubMed] [Google Scholar]