Non-local statistical label fusion for multi-atlas segmentation

Abstract

Multi-atlas segmentation provides a general purpose, fully-automated approach for transferring spatial information from an existing dataset (“atlases”) to a previously unseen context (“target”) through image registration. The method to resolve voxelwise label conflicts between the registered atlases (“label fusion”) has a substantial impact on segmentation quality. Ideally, statistical fusion algorithms (e.g., STAPLE) would result in accurate segmentations as they provide a framework to elegantly integrate models of rater performance. The accuracy of statistical fusion hinges upon accurately modeling the underlying process of how raters err. Despite success on human raters, current approaches inaccurately model multi-atlas behavior as they fail to seamlessly incorporate exogenous intensity information into the estimation process. As a result, locally weighted voting algorithms represent the de facto standard fusion approach in clinical applications. Moreover, regardless of the approach, fusion algorithms are generally dependent upon large atlas sets and highly accurate registration as they implicitly assume that the registered atlases form a collectively unbiased representation of the target. Herein, we propose a novel statistical fusion algorithm, Non-Local STAPLE (NLS). NLS reformulates the STAPLE framework from a non-local means perspective in order to learn what label an atlas would have observed, given perfect correspondence. Through this reformulation, NLS (1) seamlessly integrates intensity into the estimation process, (2) provides a theoretically consistent model of multi-atlas observation error, and (3) largely diminishes the need for large atlas sets and very high-quality registrations. We assess the sensitivity and optimality of the approach and demonstrate significant improvement in two empirical multi-atlas experiments.

1. Introduction

Segmentation of anatomical structures on medical images is essential for scientific inquiry into the complex relationships between biological structure and function as well as clinical diagnosis, treatment, and assessment. The long-held “gold standard” for highly robust segmentation has been through expert manual delineation (Crespo-Facorro et al., 1999; Tsang et al., 2008). Yet, manual delineation is extremely resource consuming and plagued by inter- and intra-rater variability (e.g., 10–20% by volume (Ashton et al., 2003; Joe et al., 1999)). Alternatively, fully-automated algorithms often result in robust and accurate estimations for specific classes of problems (e.g., brain-tissue classification (Cocosco et al., 2003; Van Leemput et al., 1999; Wells III et al., 1996), optic nerve segmentation (Noble and Dawant, 2011)). Unfortunately, the success of automated techniques is often dependent upon the application, modality, and image quality (Fischl et al., 2002; Heckemann et al., 2006; Rohlfing et al., 2004a; Yeo et al., 2008).

Atlas-based segmentation methods form a middle-ground between fully-manual and fully-automatic segmentation approaches (Collins et al., 1995; Gee et al., 1993). In atlas-based models, spatial information is transferred from an existing dataset (labeled atlas) to a previously unseen context (target) through deformable registration. Proposed extensions enable the summary of multiple atlases into a common coordinate system by constructing (1) unbiased average atlases (Guimond et al., 2000; Joshi et al., 2004) and (2) target-specific atlases (Commowick et al., 2009; Ericsson et al., 2008). Yet, the accuracy of single-atlas based methods is limited due to the bias concerns and lack of correspondence to the target (Ashburner and Friston, 2005; Han and Fischl, 2007). Thus, an alternative strategy that independently utilizes multiple atlases (i.e., multi-atlas segmentation) has come to represent the de facto standard baseline for atlas techniques. In multi-atlas segmentation (Heckemann et al., 2006; Rohlfing et al., 2004b), multiple atlases are separately registered to the target and the voxelwise label conflicts between the registered atlases are resolved using label fusion.

Perhaps surprisingly, a majority vote, the simplest fusion strategy, has been shown to result in highly robust segmentations (Aljabar et al., 2009; Heckemann et al., 2006; Rohlfing et al., 2004a; Rohlfing and Maurer, 2007). More recently, weighted voting strategies that use global (Artaechevarria et al., 2009; Chen et al., 2012), local (Isgum et al., 2009; Sabuncu et al., 2010; Wang et al., 2011), semi-local (Sabuncu et al., 2010; Wang et al., 2012), and non-local (Coupé et al., 2011) intensity similarity metrics have demonstrated consistent improvement in segmentation accuracy. Particularly for neurological applications, highly local weights have provided the most consistent results in segmentation quality (Artaechevarria et al., 2009; Sabuncu et al., 2010).

In contrast to ad hoc voting, statistical fusion strategies (e.g., Simultaneous Truth and Performance Level Estimation, STAPLE (Warfield et al., 2004)) directly integrate a stochastic model of rater behavior into the estimation process. Despite elegant theory and success on human raters, applications to the multi-atlas context have proven problematic (Asman and Landman, 2011a; Sabuncu et al., 2010; Wang et al., 2011, 2012). In response, a myriad of advancements to the STAPLE framework have been proposed to account for (1) spatially varying task difficulty (Asman and Landman, 2011b; Rohlfing et al., 2004b), (2) spatially varying rater performance (Asman and Landman, 2011a, 2012a; Commowick et al., 2012; Weisenfeld and Warfield, 2011), and (3) instabilities in the rater performance level parameters (Commowick and Warfield, 2010; Landman et al., 2011b). Yet, these advanced techniques remain inherently models of human observation error as they fail to directly incorporate the image intensity differences between the atlases and the target. Moreover, initial attempts to incorporate intensity into the STAPLE framework have relied upon ad hoc extensions that simply ignore voxels based upon a priori similarity measures (Cardoso et al., 2011; Weisenfeld and Warfield, 2011).

Regardless of the approach, label fusion models have consistently made an implicit assumption that the use of multiple atlases results in a voxelwise, collectively unbiased representation of the target. This assumption is manifested through the fact that nearly all fusion algorithms determine the optimal label using only directly corresponding intensity and label information. Ergo, multi-atlas methods are generally dependent upon highly accurate registration and the use of large numbers of atlases. We are left with several problems in multi-atlas segmentation: (1) a dependence on large-scale, high-quality registrations, (2) voting-based algorithms lack the theoretical underpinning of statistical fusion observation models and (3) statistical fusion algorithms fail to incorporate intensity information. Thus, previous approaches have failed to accurately model the stochastic process of registered atlas observation error.

Meanwhile, a relatively new framework in the field of image analysis, non-local means, has gained momentum in terms of quantifying complex image characteristics (e.g., noise structure, spatially varying correspondence). In non-local means, images are deconstructed into a collection of small volumetric patches and the similarity or correspondence between these patches is quantified to learn the underlying image structure (Buades et al., 2005). The non-local means framework has emerged in the context of image de-noising (Buades et al., 2005; Coupé et al., 2006; Kervrann et al., 2007; Liu et al., 2008; Manjón et al., 2008; Van De Ville and Kocher, 2009). However, more recent work has demonstrated the applicability of non-local means to new applications such as synthesizing image contrast (Roy et al., 2010a), in-painting (Sun and Tappen, 2011), and image segmentation (Coupé et al., 2011; Roy et al., 2010b).

Herein, we propose a novel statistical fusion algorithm (Non-Local STAPLE – NLS) that reformulates the STAPLE framework from a non-local means perspective. NLS models the registered atlases as collections of volumetric patches containing both intensity and label information and uses the non-local criteria (Buades et al., 2005; Coupé et al., 2011) to resolve imperfect correspondence. Through this reformulation, we seamlessly integrate exogenous intensity information into the estimation process to provide a theoretically consistent model of multi-atlas observation error. NLS provides a model in which we learn which label each atlas would have observed given perfect correspondence with the target. This presentation is an extension and generalization of a recently published conference paper (Asman and Landman, 2012b). Herein, we provide additional examples, derivations and insights that were not part of the original conference publication.

In this manuscript, we begin by deriving the theoretical basis and the parameters for initialization and convergence governing NLS. Next, we demonstrate significant improvement over the state-of-the-art fusion algorithms on two distinct datasets: (1) computed tomography (CT) images for thyroid segmentation and (2) structural magnetic resonance (MR) images for whole-brain segmentation. For whole-brain segmentation, we demonstrate that NLS dramatically lessens the need for large-scale and highly accurate non-rigid registration. Lastly, we provide insight into the sensitivity of NLS to the various model parameters, assess the optimality of the algorithm, and provide a comparison to a direct application of non-local voting.

2. Theory

The following presentation provides the theoretical model governing NLS in the commonly used Expectation–Maximization (EM) framework (Dempster et al., 1977). For clarity and consistency, the notation closely follows the presentation of the original STAPLE algorithm (Warfield et al., 2004).

2.1. Problem definition

Consider a target gray-level image represented as a vector, I ∈ ℝ^N×1. Let T ∈ L^N×1 be the latent representation of the true target segmentation, where L = {0, …,L − 1} is the set of possible labels that can be assigned to a given voxel. Consider a collection of R registered atlases with associated intensity values, A ∈ ℝ^N×R, and label decisions, D ε L^N×R. Let θ ∈ ℝ^R×L×L parameterize the performance level of raters (registered atlases). Each element of θ, θ_js′s, represents the probability that rater j observes label s′ given that the true label is s at a given target voxel and the corresponding voxel on the associated atlas—i.e., θ_js′s ≡ f (D_i^*j = s′, A_j|T_i = s, I_i, θ_js′s), where i^* is the voxel on atlas j that corresponds to target voxel i. Throughout, the index variables i, i^* and i′ will be used to iterate over the voxels, s and s′ over the labels, and j over the registered atlases.

2.2. The non-local STAPLE algorithm

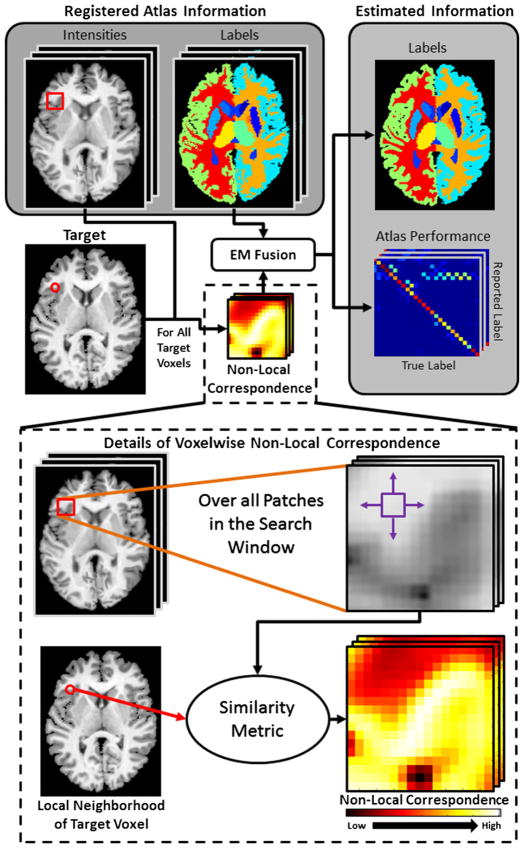
As with other statistical fusion algorithms, NLS uses EM to estimate the true (latent) segmentation based on the target intensities, atlas information, and the rater performance level parameters (see Fig. 1 for a graphical summary of NLS). In traditional EM terminology, the underlying voxelwise label probabilities represent the hidden data that we are estimating, and the performance level parameters, θ, represent the hidden model parameters that help determine the optimal solution for the target segmentation. The estimation of these parameters is accomplished by iterating between the E-step (i.e., the estimation of the voxelwise label probabilities) and the M-step (i.e., the estimation of the performance level parameters that maximize the expected value of the conditional log likelihood function). Before presenting the derivation of our EM-based approach, we define our non-local correspondence model, and an approximation of the performance level parameters that provides a technique for deriving the algorithm.

Fig. 1.

Flowchart of the Non-Local STAPLE (NLS) algorithm. NLS integrates a non-local correspondence model (using the atlas-target intensity relationships) into the estimation process. Point-wise correspondence is constructed in a traditional non-local means approach.

2.3. Non-local correspondence model

In order to reformulate the traditional STAPLE model of rater behavior from a non-local means perspective, we need to define an appropriate non-local correspondence model. Given a voxel on the target image, i, this correspondence model provides a technique for determining the corresponding voxel on a given atlas, i^*. In our model, there are two primary components that are required to define the non-local correspondence: (1) the intensity similarity model between a given atlas voxel and the target voxel of interest, and (2) the spatial compatibility between two voxel locations in the common target image coordinate system.

First, there are several options that could be used to define the intensity similarity between a given atlas voxel and the target voxel (e.g., correlation coefficient (Cardoso et al., 2011), mutual information (Artaechevarria et al., 2009), Gaussian intensity difference (Sabuncu et al., 2010)). Herein, we use a Gaussian difference model, which, assuming proper intensity normalization, has been shown to be highly successful, particularly on neurological applications (Asman and Landman, 2012c; Coupé et al., 2006; Sabuncu et al., 2010).

Second, we need to define a metric for the spatial compatibility between a given atlas voxel and the target voxel in image space. Traditional non-local means algorithms for image de-noising (Buades et al., 2005; Coupé et al., 2006; Kervrann et al., 2007; Manjón et al., 2008) weight all voxels equally, regardless of the distance between the voxels in image space. However, in order to translate non-local means to segmentation-based applications, limited search regions are typically defined in order to prevent confusion between structures with similar intensity profiles (Coupé et al., 2011; Roy et al., 2010b). Here, we employ a Gaussian window-based model so that highly local voxels are more highly weighted. This reflects our desire to estimate that the underlying corresponding voxel i^* is both similar to the target voxel and, due to the registration process, generally close in terms of the target image coordinate system.

Together, we define the probability of correspondence between an atlas voxel and the given target voxel (i.e., f (A_i′j|I_i)) to be the product of two Gaussian distributions.

$$f(A_{i^{\prime }j}\mid I_i)\equiv {\alpha }_{{ji}^{\prime }i}=\frac{1}{Z_{\alpha }}exp\left(-\frac{{\left|\right|\wp (A_{i^{\prime }j})-\wp (I_i)\left|\right|}_2^2}{2{\sigma }_i^2}\right)exp\left(-\frac{{\mathcal{E}}_{{ii}^{\prime }}^2}{2{\sigma }_d^2}\right)$$ (1)

where the first distribution is the intensity similarity model, the second distribution is the spatial compatibility model, and Z_α is a partition function. In the intensity similarity model, ℘ (·)is the set of intensities in the patch neighborhood of a given intensity location and σ_i is the standard deviation of the assumed distribution. In the spatial compatibility model, ε_ii′ is the Euclidean distance between voxels i and i′ in image space and σ_d is the corresponding standard deviation.

Lastly, the partition function, Z_α enforces the constraint that

$$\sum _{i^{\prime }\in \mathcal{N}(i)}{\alpha }_{{ji}^{\prime }i}=1$$ (2)

where (i) is the set of voxels in the search neighborhood of a given target voxel. Through this constraint, α_ji′i can be directly interpreted as the probability that voxel i′ on atlas j is the latent corresponding voxel, i^*, to a given target voxel i.

2.4. Approximation of the latent performance level parameters

The following derivation of NLS hinges upon knowledge of the voxel i^* on atlas j that directly corresponds to voxel i on the target image. If the directly corresponding voxel was known, then the ideal non-local correspondence model would be known and we could ignore the intensity relationships to use a typical definition of the underlying performance level parameters.

$$f(D_{i^{\ast }j}=s^{\prime },A_j\mid T_i=s,I_i,{\theta }_{{js}^{\prime }s})=f(D_{i^{\ast }j}=s^{\prime }\mid T_i=s,{\theta }_{{js}^{\prime }s})\equiv {\theta }_{{js}^{\prime }s}$$ (3)

Unfortunately, this corresponding voxel, i^*, is unknown and we are forced to approximate it using the previously defined non-local correspondence model. Using the model in Eq. (1), we can approximate this relationship by taking the expected value of f (D_i^*j = s′, A_j|T_i = s, I_i, θ_js′s) across the atlas image. Using an assumption of conditional independence between the labels and intensity, we approximate the desired density function

$$\begin{array}{l}f(D_{i^{\ast }j}=s^{\prime },A_j\mid T_i=s,I_i,{\theta }_{{js}^{\prime }s})\approx E[f(D_j,A_j\mid T_i=s,I_i,{\theta }_{js})]\\ =E[f(D_j\mid T_i=s,{\theta }_{js})f(A_j\mid I_i)]=\sum _{i^{\prime }\in \mathcal{N}(i)}f(D_{i^{\prime }j}=s^{\prime }\mid T_i\\ =s,{\theta }_{{js}^{\prime }s})f(A_{i^{\prime }j}\mid I_i)=\sum _{i^{\prime }\in \mathcal{N}(i)}{\theta }_{{js}^{\prime }s}{\alpha }_{{ji}^{\prime }i}\end{array}$$ (4)

where (i) is the set of voxels in the search neighborhood of voxel i, and α_ji′i is the previously defined non-local correspondence model (Eq. (1)).

As in Sabuncu et al. (2010), we assume conditional independence between the labels and intensity, which seemingly neglects their complex relationships. However, our assumption is that the information gained from inclusion of the atlas intensity is related to understanding the lack of local correspondence between the target and the atlas, which, through the estimation process, indirectly models the complex label-intensity relationships.

Additionally, it is important to note that this model of the performance level parameters is inherently an approximation based upon an assumed a priori distribution (Eq. (1)) governing the non-local correspondence between the target and the atlases. Ideally, the non-local correspondence parameters would be treated as additional model parameters that are iteratively updated in the M-step of the subsequent EM algorithm. Unfortunately, there are two primary limitations that prevent the construction of this type of idealized model. First, this model makes solving the M-step of the algorithm mathematically difficult as we would be forced to simultaneously estimate the raters’ performance and the voxel(s) that represent the true underlying correspondence. Second, it dramatically increases the number of parameters that we would be attempting to estimate. To illustrate, given a non-local search neighborhood consisting of K voxels, the number of augmented model parameters would be approximately K × N × R which leaves an underdetermined system given the amount of data that is available to estimate these parameters. Regardless, despite these limitations, the proposed model approximation captures many of the same benefits that would likely be achieved assuming the “ideal” approach were possible to construct.

2.5. E-step: estimation of the voxelwise label probabilities

Let W ∈ ℝ^L×N, where $W_{si}^{(k)}$ represents the probability that the true label associated with voxel i is label s at iteration k of the algorithm given the provided information and model parameters

$$W_{si}^{(k)}\equiv f(T_i=s\mid D,A,I,{\theta }^{(k)})$$ (5)

Using a Bayesian expansion and the assumed conditional independence between the registered atlas observations, Eq. (5) can be rewritten as

$$W_{si}^{(k)}=\frac{f(T_i=s){\prod }_{j}f\left(D_{i^{\ast }j}=s^{\prime },A_j\mid T_i=s,I_i,{\theta }_{{js}^{\prime }s}^{(k)}\right)}{{\sum }_{n}f(T_i=n){\prod }_{j}f\left(D_{i^{\ast }j}=s^{\prime },A_j\mid T_i=n,I_i,{\theta }_{{js}^{\prime }n}^{(k)}\right)}$$ (6)

where f(T_i = s) is a voxelwise a priori distribution of the underlying segmentation, and D_i^*j is the label decision by atlas j at the atlas image voxel i* that corresponds to voxel i on the target image. Note that the denominator of Eq. (6) is simply the solution for the partition function that enables W to be a valid probability mass function (i.e., Σ_sW_si = 1).

As previously noted, we do not know the corresponding atlas voxel. Thus, using the non-local correspondence model (Eq. (1)) and the provided approximation (Eq. (4)), we can approximate the final solution for the voxelwise label probabilities

$$W_{si}^{(k)}=\frac{f(T_i=s){\prod }_j{\sum }_{i^{\prime }\in \mathcal{N}(i)}{\theta }_{{js}^{\prime }s}^{(k)}{\alpha }_{{ji}^{\prime }i}}{{\sum }_{n}f(T_i=n){\prod }_j{\sum }_{i^{\prime }\in \mathcal{N}(i)}{\theta }_{{js}^{\prime }n}^{(k)}{\alpha }_{{ji}^{\prime }i}}$$ (7)

where, it is assumed that D_i′j = s′.

2.6. M-step: estimation of the performance level parameters

The estimate of the performance level parameters (M-step) is obtained by finding the parameters that maximize the expected value of the conditional log likelihood function (i.e., using the result in Eq. (7)).

$$\begin{array}{l}{\theta }_j^{(k+1)}=arg{max}_{{\theta }_j}\sum _{i}E\left[lnf\left(D_{i^{\ast }j}=s^{\prime },A_j\mid T_i=s,I_i,{\theta }_{{js}^{\prime }s}^{(k)}\right)\mid D,A,I,{\theta }^{(k)}\right]\\ =arg{max}_{{\theta }_j}\sum _i\sum _s{W}_{si}^{(k)}lnf\left(D_{i^{\ast }j}=s^{\prime },A_j\mid T_i=s,I_i,{\theta }_j^{(k)}\right)\end{array}$$ (8)

Noting the constraint that each row of the rater performance level parameters must sum to unity to be a valid probability mass function (i.e., ${\sum }_{s^{\prime }}{\theta }_{{js}^{\prime }s}^{(k)}=1$), we can maximize the performance level parameters for each element by using a Lagrange Multiplier (λ) (Bellman, 1956) to formulate the constrained optimization problem. Following this procedure, we obtain

$$\begin{array}{l}0=\frac{\partial }{\partial {\theta }_{{js}^{\prime }s}}\left[\sum _i\sum _s{W}_{si}^{(k)}ln\left(f\left(D_{i^{\ast }j}=s^{\prime },A_j\mid T_i=s,I_i,{\theta }_j^{(k)}\right)\right)+\lambda \sum _{s^{\prime }}{\theta }_{{js}^{\prime }s}\right]\\ 0=\sum _i{W}_{si}^{(k)}\frac{\frac{\partial }{\partial {\theta }_{{js}^{\prime }s}}\left[f\left(D_{i^{\ast }j}=s^{\prime },A_j\mid T_i=s,I_i,{\theta }_j^{(k)}\right)\right]}{f\left(D_{i^{\ast }j}=s^{\prime },A_j\mid T_i=s,I_i,{\theta }_j^{(k)}\right)}+\lambda \end{array}$$ (9)

However, in order to solve for θ _js′s we have to utilize the approximation presented in Eq. (4). The density function of interest, $f\left(D_{i^{\ast }j}=s^{\prime },A_j\mid T_i=s,I_i,{\theta }_j^{(k)}\right)$, appears in both the numerator and the denominator. In the denominator, we see the exact density function that we are trying to maximize; thus, we substitute the direct definition of the performance level parameters presented in Eq. (3). In the numerator, however, we need to take the derivative of this density function with respect to the current element of the performance level parameters (and the dependence structure is not apparent in Eq. (3)). To capture the inherent noise and lack of local correspondence between the target and the atlases, we use the approximation of this density function (i.e., Eq. (4)) in the numerator. Using these substitutions and some straightforward algebraic manipulation we obtain

$$\begin{array}{l}0=\frac{{\sum }_i{W}_{ni}^{(k)}\frac{\partial }{\partial {\theta }_{{js}^{\prime }s}}\left[{\sum }_{i^{\prime }\in \mathcal{N}(i)}{\theta }_{{js}^{\prime }s}^{(k)}{\alpha }_{{ji}^{\prime }i}\right]}{{\theta }_{{js}^{\prime }s}}+\lambda \\ 0=\frac{{\sum }_i{W}_{ni}^{(k)}\frac{\partial }{\partial {\theta }_{{js}^{\prime }s}}\left[{\sum }_{s^{\prime }}{\sum }_{i^{\prime }\in \mathcal{N}(i):D_{i^{\prime }j}=s^{\prime }}{\theta }_{{js}^{\prime }s}^{(k)}{\alpha }_{{ji}^{\prime }i}\right]}{{\theta }_{{js}^{\prime }s}}+\lambda \\ 0=\frac{{\sum }_i{W}_{ni}^{(k)}{\sum }_{i^{\prime }\in \mathcal{N}(i):D_{i^{\prime }j}=s^{\prime }}{\alpha }_{{ji}^{\prime }i}}{{\theta }_{{js}^{\prime }s}}+\lambda \\ {\theta }_{{js}^{\prime }s}=\frac{{\sum }_i{W}_{ni}^{(k)}{\sum }_{i^{\prime }\in \mathcal{N}(i):D_{i^{\prime }j}=s^{\prime }}{\alpha }_{{ji}^{\prime }i}}{-\lambda }\end{array}$$ (10)

Finally, solving for the Lagrange Multiplier leaves the final solution for each element of the performance level parameters

$${\theta }_{{js}^{\prime }s}^{(k+1)}=\frac{{\sum }_i\left({\sum }_{i^{\prime }\in {\mathcal{N}}_s(i):D_{i^{\prime }j}=s^{\prime }}{\alpha }_{{ji}^{\prime }i}\right)W_{si}^{(k)}}{{\sum }_i{W}_{si}^{(k)}}$$ (11)

2.7. Initialization, model parameters, and detection of convergence

As with all of the algorithms that have been presented in the STAPLE family, NLS can be initialized using either an initial estimate of the performance level parameters or the voxelwise label probabilities. For all of the presented experiments, NLS was initialized with performance parameters equal to 0.95 along the diagonal and randomly setting the off-diagonal elements to fulfill the required constraints. Note that initializing NLS in this way is essentially the same as initializing the voxelwise label probabilities to that of a majority vote.

For all presented experiments, the voxelwise label prior, f(T_i = s), was initialized using the label probabilities from a “weak” log-odds majority vote (i.e., decay coefficient set to 0.5 voxels) (Sabuncu et al., 2010). We found that initializing in this manner provided enough spatial information for NLS to consistently converge to a desired optimum, without being too spatially restrictive. Alternative approaches could be to (1) initialize using a global prior (i.e., the same probabilities for every voxel), or (2) use the output of another segmentation algorithm.

There are several parameters in the non-local correspondence model that need to be set in order to efficiently utilize NLS. First, there are two neighborhood parameters that need to be initialized: the search neighborhood, 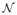(i), and the patch neighborhood, ℘ (·). Both of these parameters are functions of the input data (e.g., the resolution of the images, the quality of registration). For all of the presented experiments we used a search neighborhood of size 11 × 11 × 11 voxels centered at the target voxel of interest. We found that inter-subject registrations were of a high enough quality that a search neighborhood of this size was able to consistently capture the underlying non-local correspondence. For the patch neighborhood, several potential sizes are considered (all of which are centered at the voxel of interest) and the benefits and detriments of varying this value are discussed later in this manuscript. The two standard deviation parameters that need to be set are σ_i and σ_d, which control the impact of the intensity difference and the Euclidean distance-based decay, respectively. In general, σ_i is a function of the intensity normalization process and, thus, spread of intensity values. The parameter σ_d can be thought of as a proxy for the search neighborhood. Unless otherwise noted, these values were set to 0.1 and 2, for σ_i and σ_d, respectively. These “default” values were obtained during the coding implementation of the proposed algorithm and were tested on a single whole-brain volume in order to obtain reasonable results. Note that this is a non-ideal approach for determining these parameters as it (1) slightly biases the presentation of results, and (2) does not guarantee the optimality of the parameters (as indicated in Fig. 8). For future applications, where distinct and independent testing and training data are available, it would be more appropriate to determine the optimal parameter values using the training data only (i.e., the available atlases).

Fig. 8.

Sensitivity to NLS model parameters. The sensitivity of NLS to σ_i (A) and σ_d (B) demonstrate degraded performance for values that are either too small or too large. Regardless, consistent improvement over a locally weighted vote is achieved. Gray outlines indicate the values used in the previously presented experiments. The qualitative results demonstrate the benefits and detriments of optimal and sub-optimal model parameter values.

Convergence of NLS was detected by monitoring the change in the performance level parameters between consecutive iterations. As with the original STAPLE algorithm, we considered the algorithm to have converged when the average change in the on-diagonal elements of the performance level parameters fell below 10⁻⁴. For all presented experiments, convergence occurred in fewer than 10 iterations.

Lastly, while not necessarily a model parameter, “consensus voxels” (i.e., voxels where all raters agree) were ignored during the estimation process. Due to the non-local nature of the algorithm, consensus voxels were determined in two subsequent steps. First, an initial “consensus voxels” estimate was obtained by finding all voxels for which max_s f(T_i = s) > 0.95. Second, this initial estimate was post-processed to include a safety margin around the estimated non-consensus voxels that is defined by the search neighborhood (i.e., all voxels within the search neighborhood of a non-consensus voxel were determined to be non-consensus as well). This accomplishes two tasks: (1) it improves the runtime of the algorithm and (2) it prevents the performance level parameters from being unnecessarily biased due to the inclusion of highly “consensus” regions (Asman and Landman, 2011b; Rohlfing et al., 2004b).

3. Methods and results

An implementation of the Non-Local STAPLE algorithm is available as part of the Java Image Science Toolkit (JIST, www.nitrc.org/projects/jist).

3.1. Baseline algorithms

Our first baseline algorithm is a log-odds majority vote (MV) (Sabuncu et al., 2010). For all presented experiments the decay coefficient was set to unity, as suggested in (Sabuncu et al., 2010). Our second baseline is a locally weighted vote (LWV) (Artaechevarria et al., 2009; Isgum et al., 2009; Sabuncu et al., 2010). LWV procedures have come to represent the state-of-the-art fusion strategy as they provide consistent improvement over both MV and globally-weighted approaches. The implementation presented here is the same as suggested in Sabuncu et al. (2010). Note that a LWV has a parameter that is essentially identical to the σ_i parameter in NLS (see Eq. (1)). For fairness of comparison, this parameter was initialized to the same value (herein, 0.1) for both algorithms. Our next baseline is the original STAPLE algorithm (Warfield et al., 2004). Due to the amount of overlap between STAPLE and NLS the same parameter values were used when applicable. Thus, the algorithms were equivalently initialized, the same values were used for the voxelwise label prior, f(T_i = s), “consensus voxels” were ignored using the same discriminant criteria, and convergence was detected using the same threshold.

Our last baseline algorithm is Spatial STAPLE (Asman and Landman, 2011a, 2012a; Commowick et al., 2012). Spatial STAPLE represents an extension to the traditional STAPLE framework that allows for the estimation of a smooth spatially-varying performance level field instead of global performance level parameters and has been shown to provide robust and accurate multi-atlas segmentations. Where applicable, Spatial STAPLE was utilized using identical parameters to NLS and STAPLE. In addition, the performance level parameters were calculated on a voxelwise basis using a half-window size of 10 mm in all cardinal directions. Note that Spatial STAPLE is very similar to another recently proposed algorithm – Local STAPLE MAP (Commowick et al., 2012). The primary difference is the way in which the performance level parameters are kept stable. Here, Spatial STAPLE uses a non-parametric distribution governed by an initial estimate from the original STAPLE algorithm as opposed to the parametric beta distribution that is proposed in Local STAPLE MAP. Investigation into the optimal way to maintain performance level stability is outside of the scope of this manuscript.

3.2. Motivating simulation

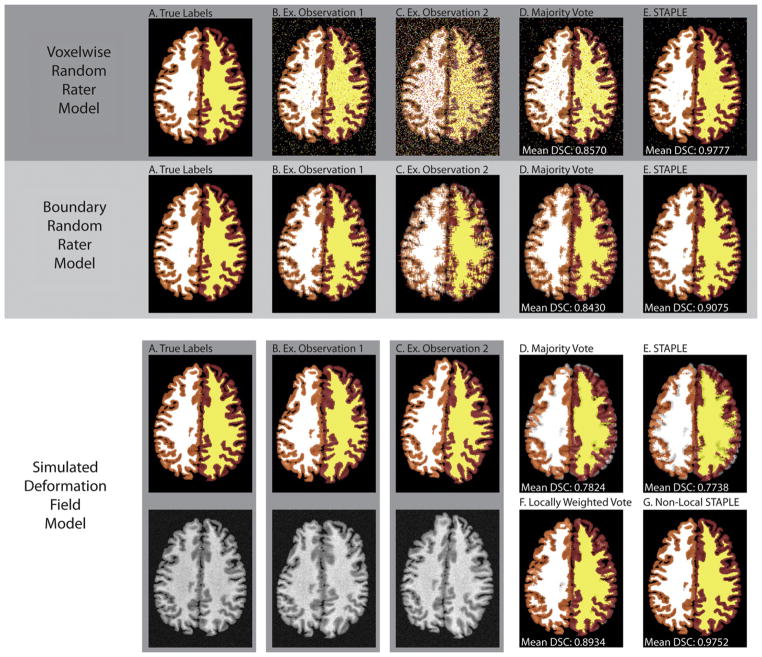
Before presenting the empirical results, we present a toy simulation to demonstrate the limitations of the traditional STAPLE model of rater behavior (Fig. 2). A single 2D slice (144 × 191 voxels) from a manually labeled whole-brain dataset was used as the basis for the presented simulation models (see the “Empirical Evaluation” section for details on the dataset). The presented slice has four non-background labels (left/right cerebral gray matter and left/right cerebral white matter) and the accuracy of the presented algorithms is presented in terms of the mean Dice Similarity Coefficient (Dice, 1945) across these labels. For each presented example, eight label observations were simulated per fusion estimate. In Fig. 2 we present three different models of rater observation behavior:

Fig. 2.

Simulated models of rater behavior and their impact on fusion performance. The first two examples present traditional models of human observation behavior, and, for both models, STAPLE substantially outperforms a majority voting based approach. In contrast, the third example simulates a typical multi-atlas observation model. In this case, STAPLE is outperformed by a majority vote. Additionally, the multi-atlas fusion approaches that utilize the target-atlas intensity relationships (e.g., locally weighted vote and the proposed Non-Local STAPLE) provide substantial improvement.

• The first observation model represents a “voxelwise random rater model” (Asman and Landman, 2011b; Landman et al., 2011b; Warfield et al., 2004) in which simulated confusion matrices are constructed for each rater. Simulated observations are generated through Monte Carlo sampling of these confusion matrices given the true segmentation. Here, confusion matrices were randomly constructed with constant on-diagonal values linearly distributed between 0.5 and 0.9.

• The second observation model represents a “boundary random rater model” (Asman and Landman, 2011a,b; Landman et al., 2011a,b) in which the boundary voxels on the true segmentation are randomly shifted. The shift amount was randomly sampled from a zero-mean Gaussian distribution that is unique to each rater. The standard deviation values of these distributions were linearly distributed between 0.5 and 2.

• The last observation model represents a “simulated deformation field model” in which simulated deformation fields are applied to the true labels by sampling a sixth-order Chebyshev polynomial with random coefficients unique to each rater. These coefficients were randomly sampled from a zero-mean Gaussian distribution with standard deviation equal to unity.

The first two examples are typical simulated models of human rater observation behavior, and, in both cases, STAPLE provides substantial improvement over a MV. To contrast, the third example simulates a typical multi-atlas observation model, in which random deformations are applied to a target image. In this case, STAPLE is slightly outperformed by a MV, which highlights the lack of applicability of STAPLE’s observations model to a multi-atlas context. Additionally, using the intensity images of the simulated “atlases” in the third simulation model, we show that a LWV and NLS provide substantial improvement over the traditional “human rater” fusion models (i.e., MV and STAPLE) that ignore the target-atlas intensity relationships.

3.3. Empirical evaluation

We consider two distinct empirical datasets. Our first dataset is a collection of 15 CT head and neck atlases used for thyroid segmentation. The images used in this experiment were collected from consenting patients who underwent intensity-modulated radiation therapy. The patients were injected with 80 mL of Optiray 320, a 68% iversol-based nonionic contrast agent. Each image has a voxel size of 1 × 1 × 3mm³. The expert labels were obtained from a local expert radiologist and verified by multiple experienced human raters. Note that 5 of the 15 patients in this data set underwent a surgical procedure that split their thyroid into two distinct sections.

Our second dataset is a collection of 15 Magnetic Resonance (MR) images of the brain as part of the Open Access Series of Imaging Studies (OASIS) (Marcus et al., 2007) dataset. This data was expertly labeled courtesy of Neuromorphometrics, Inc. (Somerville, MA) and provided under a non-disclosure agreement. A refined dataset (using the OASIS brains and a subtly revised labeling protocol) has recently been made available as part of the MICCAI 2012 workshop on multi-atlas labeling. This data is available at the following URL: https://masi.vuse.vanderbilt.edu/workshop2012/ or directly from Neuromorphometrics. For each atlas, a collection of 26 labels (including background) were considered: ranging from large structures (e.g., cortical gray matter) to smaller deep brain structures (see Fig. 5 for a list of all labels). Note that all of the cortical surface labels were combined to form left and right cortical gray matter labels. All images are 1 mm isotropic resolution and, for ease of analysis, the brain region was extracted.

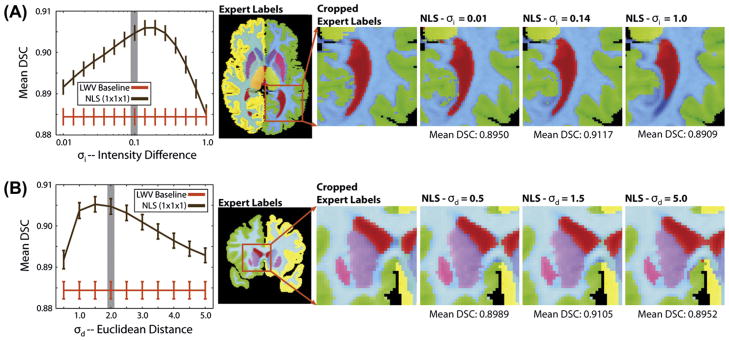
Fig. 5.

Per-label accuracy comparison on the whole-brain segmentation problem using a pairwise non-rigid registration procedure. NLS provides consistent improvement over locally weighted voting. In this case, NLS using a single voxel patch neighborhood consistently outperformed a larger (3 × 3 × 3) patch neighborhood.

Note that, while all baseline algorithms were considered, the STAPLE results are not shown for the whole-brain segmentation problem as it has been demonstrated to be consistently outperformed by a LWV for whole-brain segmentation (Artaechevarria et al., 2009; Asman and Landman, 2011a; Isgum et al., 2009; Sabuncu et al., 2010). Nevertheless, the MV results are shown in order to provide a reference baseline for registration performance and segmentation accuracy.

3.4. Pre-processing and analysis

All pairwise registrations were performed using an initial affine registration (Jenkinson and Smith, 2001), and, when noted, all pairwise non-rigid registrations were performed using the Vectorized Adaptive Bases Registration Algorithm (VABRA) (Rohde et al., 2003). After registration, the images were (1) cropped so that excess background was removed, and (2) intensity normalized such that the 25th and 75th percentiles of the range of the non-background intensity values were set to 0 and 1, respectively. Quantitative accuracy was assessed using the Dice Similarity Coefficient (DSC) (Dice, 1945), Hausdorff distance (Huttenlocher et al., 1993), and mean surface distance. The surface distance metrics were computed unidirectionally in terms of the distance from the expert labels to the estimated segmentation.

3.5. Thyroid segmentation results

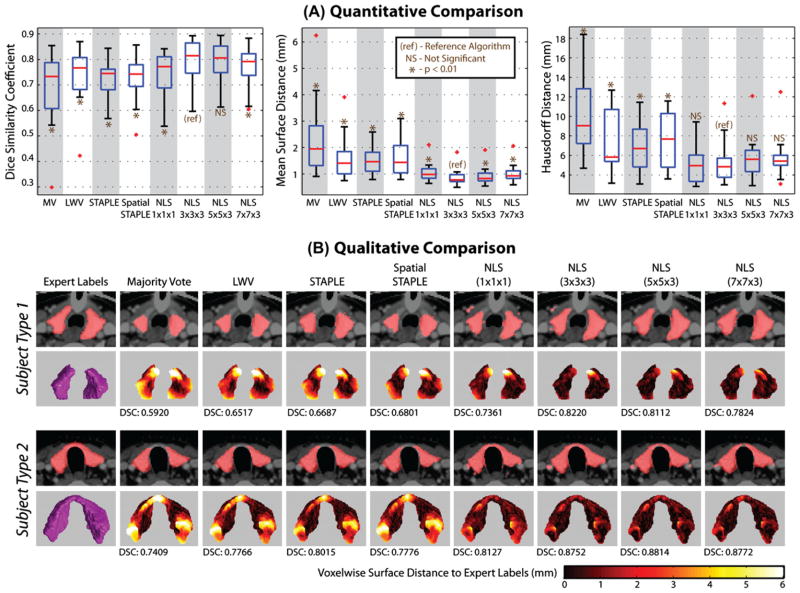
Our first experiment analyzes the fusion accuracy for segmentation of the thyroid. In addition to the benchmarks, NLS was run using various patch neighborhood, ℘ (·), sizes (1 × 1 × 1, 3 × 3 × 3, 5 × 5 × 3, and 7 × 7 × 3 voxels), all of which were centered at the voxel of interest. Due to the slice thickness of 3 mm, the third dimension of the patch neighborhoods were not increased beyond three voxels. We performed a leave-one-out cross-validation experiment (i.e., 14 atlases per segmentation estimate) to assess fusion accuracy. The results of this experiment are presented in Fig. 3.

Fig. 3.

Results of the empirical multi-atlas segmentation of the thyroid. The quantitative results (A) show that NLS provides significant improvement in terms of the DSC, Hausdorff distance, and mean surface distance, with a 3 × 3 × 3 patch neighborhood as the most consistent performer. The qualitative results (B) support the quantitative improvement and demonstrate that NLS provides substantial improvement in shape, boundary, and point-wise surface distance error. Note that “Subject Type 1” underwent a surgery to surgically bisect the thyroid.

The quantitative results, in terms of the spread across the 15 atlases, can be seen in Fig. 3A. The NLS based approaches provide significant improvement (p < 0.01, paired t-test) over all of the considered baseline algorithms in terms of the DSC, Hausdorff distance and mean surface distance. NLS using a 3 × 3 × 3 (voxels) patch neighborhood size was the most consistent performer as it significantly outperformed (p < 0.01, paired t-test) the other NLS based approaches in terms of the DSC and the mean surface distance. The median DSC performance was improved by 0.05 over a LWV and 0.08 over STAPLE. Only the NLS based approaches achieved submillimetric accuracy in terms of the mean surface distance between the expert labels and the segmentation estimates. Additionally, NLS using a 3 × 3 × 3 (voxels) patch neighborhood provided over 1 mm improvement over a LWV and over 2 mm improvement over STAPLE and Spatial STAPLE in terms of the Hausdorff distance.

Qualitative results are presented in Fig. 3B, where, for all considered algorithms a representative slice and a 3D rendering of the point-wise surface distance error is presented. Example results are presented for a representative patient that underwent a surgery to bisect the thyroid (subject type 1) and a representative subject that did not (subject type 2). The segmentations from NLS are all qualitatively superior to the other baseline algorithms as they more accurately estimated the underlying shape and size and resulted in substantial reductions in point-wise surface distance error. For small patch neighborhoods (e.g., 1 × 1 × 1 – a single voxel) it is evident that high quality boundaries are estimated, but “speckle noise” is more likely to be apparent. Alternatively, for larger windows, estimations are smoother but sacrifice the high quality boundary estimation. Note that only the NLS based approaches correctly estimated the connected topography of the second subject.

3.6. Whole-brain segmentation results

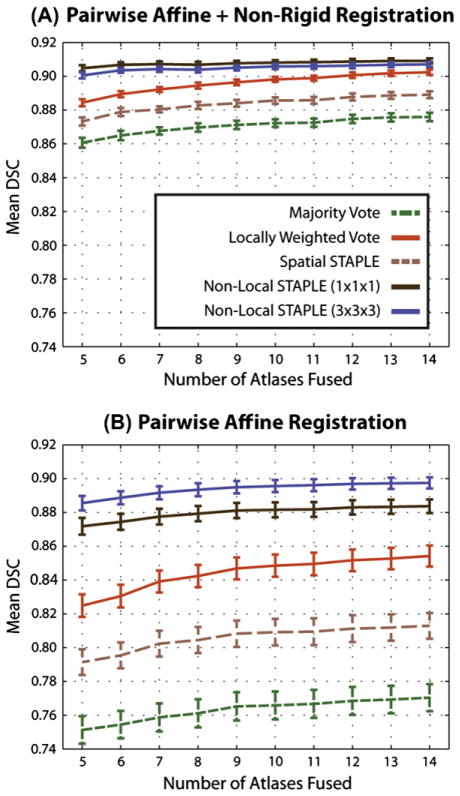
Our second experiment analyzes fusion accuracy for whole-brain segmentation. For this experiment, NLS was run using both 1 × 1 × 1 (voxel) and 3 × 3 × 3 (voxel) patch neighborhoods. The results of this experiment are presented using a pairwise non-rigid registration procedure and a pairwise affine registration procedure. For both registration procedures, the overall accuracy (in terms of mean DSC) was assessed using a cross-validation experiment with between 5 and 14 atlases per target. Additionally, the per-label accuracy was assessed using five atlases per target.

The results of the overall accuracy comparison for both registration procedures are summarized in Fig. 4. The results indicate that, for both the pairwise non-rigid registration (Fig. 4A) and the pairwise affine registration (Fig. 4B), NLS demonstrates significant improvement (p < 0.001, paired t-test) over MV, LWV and Spatial STAPLE regardless of the number of atlases fused. For the non-rigid registration, NLS using a single voxel patch neighborhood provided a small, yet consistent, improvement over the larger 3 × 3 × 3 (voxels) patch neighborhood. Interestingly, the opposite was true for the affine registration, where the larger neighborhood provided consistent improvement over the single voxel neighborhood. This difference indicates the importance of using larger patch neighborhoods when the quality of registration is diminished, and the expected correspondence is highly non-local. Additionally, for both registration procedures, NLS using only five atlases exhibited significant improvement (p < 0.05) over a LWV using all 14 available atlases. Note that, unlike (Commowick et al., 2012), Spatial STAPLE is consistently outperformed by a LWV. This disparity is primarily due to the fact that the structures presented here are highly dependent upon their intensity characteristics. In (Commowick et al., 2012), they focus on cortical segmentation – a problem in which intensity information provides little benefit in terms of distinguishing between adjacent labels.

Fig. 4.

Overall accuracy, in terms of mean DSC, comparison for whole-brain segmentation. For both pairwise non-rigid and pairwise affine registration procedures, NLS provides significant improvement over traditional fusion approaches.

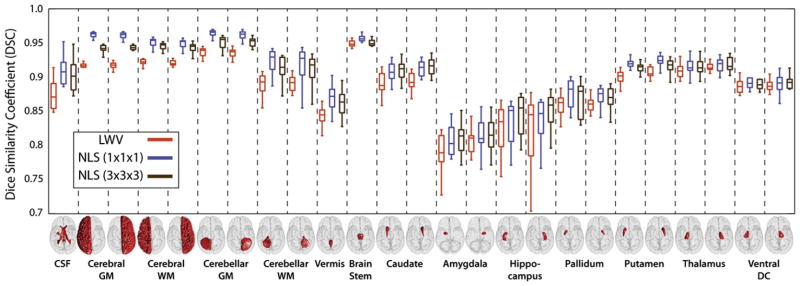
The per-label results for the non-rigid (Fig. 5) and affine (Fig. 6) registration procedures demonstrate consistent improvement over a LWV regardless of label size, location and shape. For the non-rigid results, NLS using a single voxel patch neighborhood resulted in significantly superior (p < 0.05) results over LWV on 23 out of 25 labels and for 16 out of 25 labels over NLS using a 3 × 3 × 3 (voxels) patch neighborhood. For the affine results, NLS using a 3 × 3 × 3 (voxels) patch neighborhood resulted in significant improvement (p < 0.05) over LWV on all considered labels and for 20 out of 25 labels over NLS using a single voxel patch neighborhood. For both registration procedures, none of the baseline algorithms were significantly superior to either NLS approach for any label.

Fig. 6.

Per-label accuracy comparison on the whole-brain segmentation problem using a pairwise affine registration procedure. As in Fig. 5, NLS provides consistent improvement over locally weighted voting. In this case, NLS using a larger (3 × 3 × 3) patch neighborhood consistently outperformed a single voxel patch neighborhood.

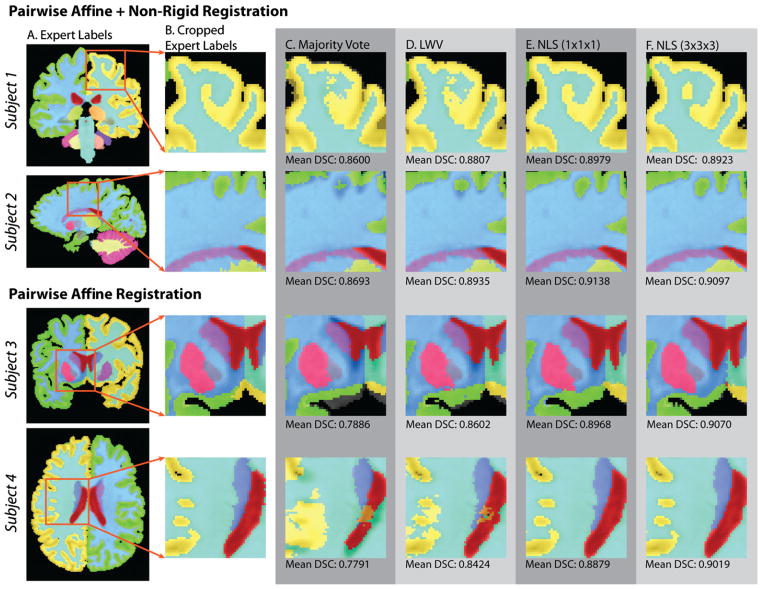
The qualitative results (Fig. 7) support the quantitative improvement exhibited by NLS over previous algorithms (Figs. 4–6). Fig. 7 shows four different subjects (two for non-rigid and two for affine) with the associated expert labels and cropped estimates from the considered baseline algorithms using 5 atlases per estimate. Spatial STAPLE is not shown as it was consistently outperformed by LWV for all considered target images. For reference, MV estimates are provided in order to provide important insight into the quality of the registration. For each presented estimate, the mean DSC value on the presented subject is available below the image. Each example demonstrates the type of improvement exhibited by NLS over voting-based algorithms. NLS provides consistent improvement in terms of shape, size and location of the various labels. Additionally, through the process of finding non-local correspondence, NLS results in segmentation estimates that are qualitatively more consistent in terms of the associated intensity profile, and less dependent upon using high-quality non-rigid registration with large numbers of atlases.

Fig. 7.

Qualitative comparison between the various fusion algorithms for whole-brain segmentation using 5 atlases. For both registration procedures, the qualitative results support the quantitative improvement demonstrated by NLS in Figs. 4–6. The NLS results are qualitatively superior to alternative voting-based procedures in terms of overall shape, size, location and appearance. Note that the mean DSC labels indicate the mean observed DSC for all labels for the corresponding subject (row) and algorithm (column).

3.7. Sensitivity to model parameters

The sensitivity of an algorithm to the model parameters plays a critical role in determining the robustness and applicability of the approach to new problem spaces. The sensitivity of NLS to patch window sizes, quality of registration, and the number of atlases has been presented throughout Figs. 3–7. Here, we assess the sensitivity of NLS to the two standard deviation parameters, σ_i and σ_d (see Eq. (1)). First, σ_i is the standard deviation of the Gaussian intensity difference model and controls how selective the non-local approach is in determining the correspondence between the various voxels. Second, σ_d is the standard deviation of the Gaussian distance model and it weights voxels based upon their distance to the current target voxel of interest. The parameter σ_d can be thought of as a proxy for the size of the search neighborhood (i.e., as the value of σ_d decreases the impact of the extreme elements in the search neighborhood approaches zero). Note, due to this relationship, alternative values for the search neighborhood are not considered. Here, we utilize NLS with a single voxel patch neighborhood on the non-rigidly registered whole-brain data set. Unless the parameter values are being explicitly modified, the previously discussed default parameter values are used.

The results of this sensitivity test (Fig. 8) demonstrate that NLS is not particularly sensitive to the standard deviation parameters, and continues to exhibit consistent improvement over LWV across a large range of parameter values. Fig. 8A demonstrates the NLS sensitivity to the σ_i parameter with associated qualitative estimates for various parameter values shown to the right. For values of σ_i that are too small, NLS results in noisy estimates that contain undesired “holes” in the segmentation. On the other hand, large values result in segmentations that are overly smooth and fail to accurately model the underlying intensity profile. While not shown, one important case for this parameter is when σ_i = ∞ (i.e., ignoring intensity characteristics and only incorporating registration uncertainty via spatial locality). If we set σ_i to ∞ then the algorithm converges to a mean overall accuracy of 0.8746 – an accuracy level statistically indistinguishable from Spatial STAPLE. This provides two important insights (1): it highlights the need of incorporating intensity information into the estimation framework for this particular application, and (2) it demonstrates that, despite using global performance level parameters, NLS is able to overcome some of the inherent registration uncertainty without directly utilizing the image intensity characteristics. Fig. 8B shows the sensitivity to the σ_d parameter. In this case, values that are too small cause NLS to use too few voxels to capture the non-local correspondence between the atlases and the target. Values that are too high result in the inclusion of regions of the image that are not anatomically indicative of the label of interest. The gray bars on Fig. 8 indicate the default values used in the previous experiments.

3.8. Model optimality

Like STAPLE, NLS is derived in an EM framework in which parameters are iteratively computed in order to estimate the optimal solution for the underlying segmentation. While EM algorithms are guaranteed to converge to a local optimum, convergence to a global optimum is not guaranteed. Thus, it is important to assess the ability of NLS to converge to a reasonable local optimum. Given the true segmentation and a provided nonlocal correspondence model, it is straightforward to calculate the globally ideal performance level parameters for NLS by replacing the voxelwise label probabilities (i.e., W_si) with the true segmentation in Eq. (11)

$${\theta }_{{js}^{\prime }s}^{\ast }=\frac{{\sum }_i\left({\sum }_{i^{\prime }\in {\mathcal{N}}_s(i):D_{i^{\prime }j}=s^{\prime }}{\alpha }_{{ji}^{\prime }i}\right)\delta (T_i,s)}{{\sum }_i\delta (T_i,S)}$$ (12)

where ${\theta }_{{js}^{\prime }s}^{\ast }$ represents the globally ideal performance level parameters, T_i is the true segmentation at voxel i and, δ(T_i, s) is the Kronecker delta function which is equal 1 if T_i = s and 0 otherwise. For the traditional STAPLE model, the globally ideal performance level parameters can be calculated in a similar manner:

$${\theta }_{{js}^{\prime }s}^{\ast }=\frac{{\sum }_{i:D_{ij}=s^{\prime }}\delta (T_i,s)}{{\sum }_i\delta (T_i,s)}$$ (13)

Here, for both STAPLE and NLS, we compare the results of the converged algorithm to the results of the algorithm using the globally ideal performance level parameters. We enumerate ideal STAPLE and ideal NLS to indicate the results of the algorithms using the globally ideal performance level parameters. We assess the results across the 15 whole-brain images using five non-rigidly registered atlases per estimate and a single voxel patch neighborhood.

The results of this experiment (Fig. 9) demonstrate multiple important concepts. The converged NLS estimate is nearly identical to the accuracy of the ideal NLS estimate, which is an indication that, despite using only five atlases, NLS is able to converge to an estimate that is very close to the global optimum. To contrast, the converged STAPLE estimate is significantly lower than the ideal STAPLE estimate, which indicates a strong need for using larger numbers of atlases. Additionally, the ideal STAPLE estimate is only slightly better than the MV estimate. Thus, regardless of converging to the global optimum or not, the STAPLE model of rater behavior does not accurately model the observation behavior exhibited in this multi-atlas context. While perhaps surprising, these results are supported by the literature, where, even when large numbers of atlases are used (i.e., the probability of converging to global optimum is increased), STAPLE is, at best, slightly better than a MV in a multi-atlas context (Artaechevarria et al., 2009; Asman and Landman, 2011a; Sabuncu et al., 2010; Wang et al., 2011).

Fig. 9.

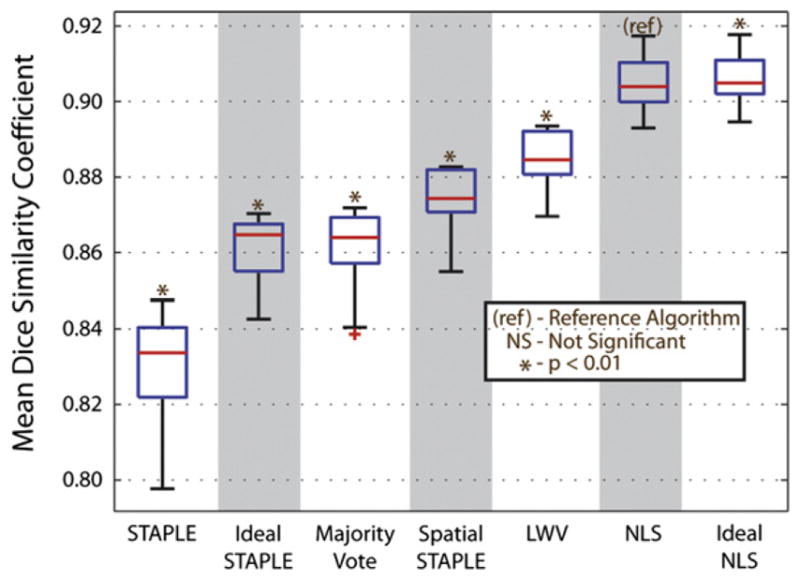
Assessment of the model optimality of the NLS approach. The results using ideal STAPLE and ideal NLS represent the estimates using the globally ideal performance level parameters with 5 atlases per estimate. NLS consistently converged to an estimate that is very close to “ideal” NLS (i.e., the global optimum). On the other hand, STAPLE consistently converged to a value significantly less than the global optimum. Additionally, the results of the “Ideal STAPLE” approach are only slightly better than a MV, which indicates the non-optimality of the traditional STAPLE observation model.

3.9. Comparison to non-local voting

Heretofore, we have limited our comparisons to the algorithms that represent the state-of-the art label fusion algorithms (i.e., the algorithms that are most commonly utilized in the label fusion literature). However, like NLS, recent techniques have been proposed that integrate a non-local correspondence model into a votingbased fusion approach (Coupé et al., 2011; Roy et al., 2010b). In order to more fully characterize the performance of NLS to premier segmentation approaches, we compare the results of NLS to a straightforward non-local voting-based procedure (Coupé et al., 2011) for the affine registration whole-brain segmentation problem using 5 atlases per target. For fairness of comparison, identical values were used for NLS and the non-local voting-based approach where applicable (i.e., search neighborhood set to 11 × 11 × 11 voxels, patch neighborhood set to 3 × 3 × 3 voxels, and σ_i set to 0.1).

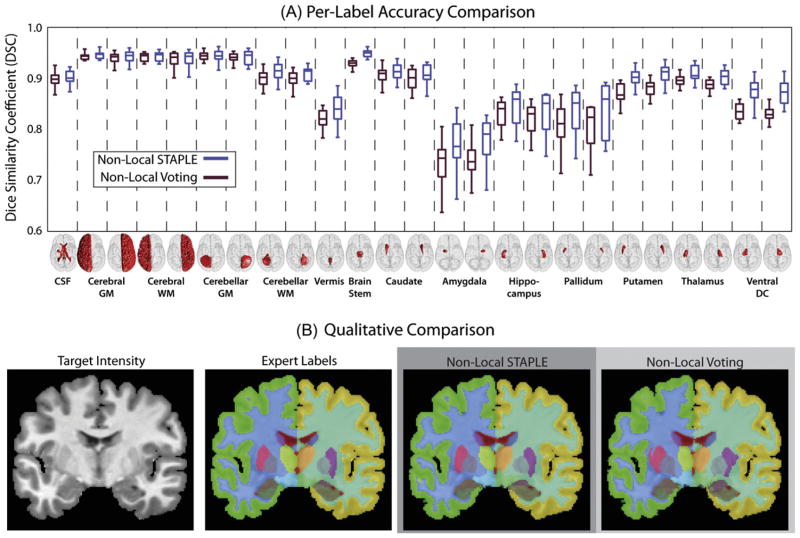
The results of this comparison (Fig. 10) indicate that NLS provides significant improvement over non-local voting approaches, particularly when estimating small and more complex deep brain structures. First, a per-label comparison (Fig. 10A) demonstrates that NLS provides significant improvement (p < 0.05, paired t-test) over the non-local voting approach on 18 out of the 25 considered labels. For the larger labels that are more easily distinguishable from the surrounding structures (e.g., CSF, cerebral/cerebellar white and gray matter), NLS and the non-local voting approaches are statistically indistinguishable. However, for the smaller, more complex deep-brain structures (e.g., hippocampus, thalamus, and putamen) NLS provides consistent and significant improvement. The qualitative results (Fig. 10B) support the quantitative improvement. Here, a representative example from the two approaches is visually presented and NLS is qualitatively superior to the non-local voting approach.

Fig. 10.

Comparison to non-local voting fusion. NLS provided consistent improvement over non-local voting, particularly for the smaller deep brain structures (A). NLS provided significant improvement on 18 of the 25 considered labels. Particularly for the smaller labels, the benefits of the proposed multi-atlas rater model are evident. The qualitative comparison (B) supports the per-label comparison and demonstrates the type of improvement achieved by NLS.

4. Discussion

Non-Local STAPLE represents the first statistical fusion algorithm that seamlessly incorporates intensity into the estimation process and creates a cohesive theoretical model specifically targeting registered atlas observation behavior. Additionally, NLS largely overcomes several of the current obstacles that plague multi-atlas segmentation including the need for high-quality non-rigid registration and large numbers of atlases. These goals are accomplished through the reformulation of the STAPLE algorithm from a non-local means perspective and the integration of the concept of non-local correspondence into the estimation process. Intriguingly, despite this reformulation, the interpretation of the NLS rater model remains straightforward. In words, using a model of non-local correspondence, NLS provides a weighted sum over the non-local search neighborhood to determine what labels would have been observed given perfect correspondence between the target and the atlases. Herein, we demonstrated superior performance over state-of-the-art fusion algorithms on two empirical datasets. For thyroid segmentation (Fig. 3), significant improvement was shown in terms of the DSC, Hausdorff distance, and mean surface distance. For whole-brain segmentation, significant improvement was demonstrated in terms of overall accuracy (Fig. 4), per-label accuracy (Figs. 5 and 6) and qualitative assessment (Fig. 7).

The sensitivity of the NLS approach was demonstrated with respect to the various model and multi-atlas parameters. In terms of the multi-atlas parameters, NLS is significantly less dependent upon the number of atlases (Fig. 4) and the quality of the registration (Figs. 4–7). In terms of the NLS model parameters, the size of the patch neighborhood seems to be particularly dependent upon the quality of registration. For both the thyroid (Fig. 3) and the pairwise affine whole-brain results (Fig. 6), where the registration is relatively poor compared to the non-rigid whole-brain registration, patch neighborhoods greater than a single voxel provided significant improvement over smaller patch neighborhoods. Additionally, NLS is fairly insensitive to the two standard deviation parameters in the non-local correspondence model, which further demonstrates the stability of the approach (Fig. 8). Lastly, and importantly, despite using only 5 atlases, NLS consistently converged to an estimate that is very close to the global optimum (Fig. 9). While not a definitive proof, this is a strong indication of the optimality of the NLS model of multi-atlas observation behavior.

While the primary focus of this paper is to investigate the theoretical advancements provided by NLS when compared to the state-of-the-art fusion algorithms, we also demonstrate significant improvement over a recently proposed non-local voting-based approach (Fig. 10). The results of this comparison highlight the benefits of the proposed framework. First, the observed performance increase by NLS is a strong indication that the proposed model of multi-atlas observation error accurately captures empirically observed atlas performance. Second, it indicates a need for the inclusion of a cohesive rater model into the estimation framework so that informed judgment can be made about the applicability of a given atlas to the label estimates, particularly when estimating the complex relationships between easily confused structures. Moreover, while NLS and non-local voting-based approaches similarly include non-local correspondence models, there are stark contrasts in the way in which these techniques estimate the underlying segmentation. In NLS, the non-local correspondence model is used to learn which label an atlas would have observed given perfect correspondence. As a result, all atlases have an equal opportunity to contribute at all considered voxels, and the quality of an atlas observation is captured by the rater performance parameters. To contrast, in non-local voting, atlases can be completely deweighted from the estimation process if their intensity characteristics are too different from the target intensity characteristics. As a result, non-local voting-based procedures are susceptible to being biased towards particular atlases and labels as they are more dependent upon accurate intensity normalization and highly representative atlas intensity profiles.

Despite the promise of the NLS fusion model, several questions still persist in order to understand the optimality of the algorithm. For example, the effect of using an alternative similarity metric (e.g., normalized correlation coefficient, mutual information) to the assumed Gaussian difference model presented here (Eq. (1)) needs to be investigated. Alternative similarity measures may dramatically lessen the potential impact of noise and the need for accurate intensity normalization between the target and the atlases. Additionally, the procedure for determining the optimal parameter values for a given problem remains primarily ad hoc. Statistically driven maximum likelihood and maximum a posteriori models to estimate the optimal parameter values through (1) the use of the training data, or (2) direct integration into the estimation model, would provide valuable advancements for the applicability of NLS to new problem spaces.

Herein, we have restricted our comparisons to algorithms that strictly perform a label fusion task. As a result, meta-analysis algorithms that (1) use the label fusion results as a prior for a more complex segmentation procedure (Gholipour et al., 2012; Lotjonen et al., 2010; Sdika, 2010), (2) append a Markov Random Field (MRF) to the estimation model (Sabuncu et al., 2010; Warfield et al., 2004), or (3) perform either global or local atlas pre-selection (Aljabar et al., 2009; Cardoso et al., 2011; Weisenfeld and Warfield, 2011) are not considered here. In general, these types of advancements provide practical, real-world benefits that are widely applicable to the field of label fusion and not necessarily specific to a particular fusion algorithm. As a result, we feel that inclusion of these types of approaches would only obfuscate the presentation of results. Nevertheless, these meta-analysis approaches could easily utilize the NLS fusion model and, potentially, see improved segmentation results. Further investigation into the applicability of NLS to these meta-analysis approaches (e.g., determination of an optimal MRF) is certainly warranted.

Additionally, other than Spatial STAPLE, notably absent from the list of considered baseline algorithms are some of the more recent advancements to the STAPLE algorithm. There are two primary reasons for not directly comparing to these extensions. First, it is straightforward to illustrate that NLS is a direct extension of the original STAPLE algorithm. NLS can be thought of as a family of algorithms governed by the non-local correspondence model. From this perspective, the original STAPLE algorithm can be seen as simply a special case of the proposed NLS framework. To illustrate, consider a non-local correspondence model where α_ji′i = 1 if and only if i = i′ and, otherwise, α_ji′i = 0. In this case, the E- and M-steps (Eqs. (7) and (11), respectively) simplify to the original STAPLE algorithm. Second, we propose that NLS is not mutually exclusive to these proposed advancements. For example, (1) incorporations of spatially varying performance level estimates (Asman and Landman, 2011a, 2012a; Commowick et al., 2012; Weisenfeld and Warfield, 2011), (2) capturing task difficulty through the augmentation of the E-step with “consensus levels” (Asman and Landman, 2011b), (3) locally ignoring atlas voxels based upon a priori intensity characteristics (Cardoso et al., 2011; Weisenfeld and Warfield, 2011), and (4) models for stabilizing the performance level parameters (Commowick and Warfield, 2010; Landman et al., 2011b) could all be seamlessly integrated into the NLS framework. In particular, the recent advancements that allow for local spatially-varying performance level parameters within the STAPLE framework (e.g., Spatial STAPLE and Local STAPLE MAP) represent fascinating potential improvements to the NLS framework. Despite the fact that NLS uses local intensity information in order to reformulate the rater performance model, it remains an inherently global approach as, like the original STAPLE algorithm, the performance level parameters describe global atlas performance. A reformulation of this type of approach to allow for both local intensity characteristics and local performance level parameters could potentially provide significant benefit in terms of overall accuracy and robustness. Continued investigation into the integration of the proposed STAPLE advancements represents fascinating avenues of continued research into rater performance model optimality.

Lastly, one problem with the current implementation of NLS is the excessive runtime. As the number of voxels, number of raters, number of labels, and size of the neighborhood parameters increase, so does the runtime of NLS. For relatively small datasets with minimal numbers of labels (e.g., the thyroid example), NLS typically converged in approximately one minute for a single 3 GHz CPU core with an implementation in Java. Yet, when applied to the multi-label whole-brain segmentation problem, NLS took upwards of 6 h to converge. Nevertheless, this algorithm is highly parallelizable, as each voxel can effectively be computed independently. Thus, a multi-core implementation or other advancements such as a graphics processing unit (GPU) implementation (Huang et al., 2009; Huhle et al., 2008), or other proposed non-local means optimizations (Coupé et al., 2006; Liu et al., 2008) should be applicable in this context.

5. Conclusions

We have derived and investigated Non-Local STAPLE, a new statistical fusion algorithm for multi-atlas segmentation. Through a reformulation from a non-local means perspective, NLS represents the first statistical fusion algorithm that (1) creates a cohesive theoretical model specifically targeting registered atlas observation behavior, and (2) seamlessly incorporates intensity into the core of the STAPLE estimation framework. As a result, NLS largely overcomes the need for high-quality non-rigid registration and large numbers of atlases. Herein, we have demonstrated significant improvement over state-of-the-art algorithms for both CT thyroid segmentation and MR whole-brain segmentation. Further, we have assessed the sensitivity of the approach to the quality of registration, the number of fused atlases, and the various non-local correspondence model parameters and shown that NLS is able to consistently converge to segmentations that are very close to the global optimum. Lastly, we have demonstrated that NLS provides significant improvement over recently proposed non-local voting- based fusion which further validates the usefulness of the proposed theoretically-consistent model of multi-atlas observation error.