Bayesian methods for meta-analysis of causal relationships estimated using genetic instrumental variables

Abstract

Genetic markers can be used as instrumental variables, in an analogous way to randomization in a clinical trial, to estimate the causal relationship between a phenotype and an outcome variable. Our purpose is to extend the existing methods for such Mendelian randomization studies to the context of multiple genetic markers measured in multiple studies, based on the analysis of individual participant data. First, for a single genetic marker in one study, we show that the usual ratio of coefficients approach can be reformulated as a regression with heterogeneous error in the explanatory variable. This can be implemented using a Bayesian approach, which is next extended to include multiple genetic markers. We then propose a hierarchical model for undertaking a meta-analysis of multiple studies, in which it is not necessary that the same genetic markers are measured in each study. This provides an overall estimate of the causal relationship between the phenotype and the outcome, and an assessment of its heterogeneity across studies. As an example, we estimate the causal relationship of blood concentrations of C-reactive protein on fibrinogen levels using data from 11 studies. These methods provide a flexible framework for efficient estimation of causal relationships derived from multiple studies. Issues discussed include weak instrument bias, analysis of binary outcome data such as disease risk, missing genetic data, and the use of haplotypes.

1. Introduction

In traditional observational epidemiological studies, associations between a risk factor or phenotype (X) and outcome (Y) are often biased by unmeasured confounders or reverse causation. Mendelian randomization [1] is a technique for using genetic markers (G) as instrumental variables (IV) to assess the true causal association without direct experiment. It uses the random allocation of genes at conception in an analogous way to treatment assignment in a randomized control trial [2]. By finding genetic markers associated with the levels of the phenotype, the different genotypes give rise to groups which, under certain assumptions, are randomly assigned and so are independent of measured and unmeasured confounders (U) and the effects of reverse causation. The assumptions underlying an IV analysis are depicted in the directed acyclic graph (DAG) in Figure 1. An IV is a variable G, which is [3]

Figure 1.

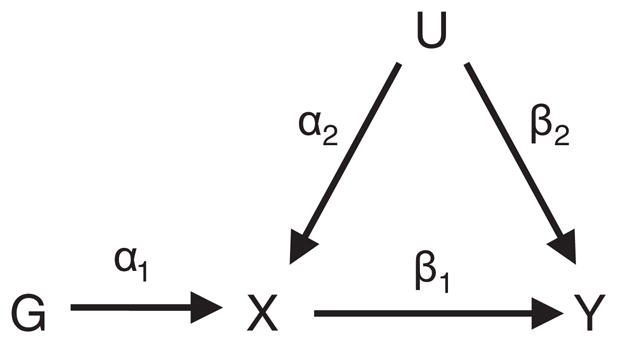
Directed acyclic graph (DAG) of the Mendelian randomization assumptions.

1. independent of any possible confounders (i.e. G⫫U),

2. associated with the phenotype (i.e. G¬⫫X), and

3. independent of the outcome given the phenotype and confounders (i.e. G⫫Y|X,U).

There are many ways in which these assumptions may be violated [4], some of which we return to in the discussion.

We consider the case where the outcome Y is continuous, and defer the issues relating to binary outcomes to the discussion. If the phenotype X and all confounders U are exactly measured, the causal association between X and Y (β₁ in Figure 1) can be estimated using standard multiple regression of Y on X and U. In a study where G, X, and Y are measured, but some confounders U are not, several IV-based methods are available to estimate the causal association between X and Y. The most basic, the ratio of coefficients method [3, 5], can be used when there is one instrument, for example a single nucleotide polymorphism (SNP), providing genetic information: either the SNP is dichotomized (for example by combining the heterozygous group with one of the homozygous groups; recessive or dominant model), or linearity is assumed according to the number of variant alleles (additive model). In the latter case, the causal association is estimated as the ratio of the regression coefficient of the outcome Y on the number of variant alleles of the SNP to the regression coefficient of the phenotype X on the number of variant alleles of the SNP [4]. As the regression coefficients are asymptotically normal, approximate confidence intervals for the ratio can be calculated using Fieller’s theorem [6] or the asymptotic variance can be estimated using a Taylor expansion [7]; the correlation between the two regression coefficients can be estimated by bootstrapping, but is often assumed to be zero since it is typically small [8].

The two-stage least-squares (2SLS) method [4] can be used for multiple, polychotomous SNPs in one study. Least-squares regression of the phenotype on the SNPs is used to obtain fitted values for the phenotype (X̂|G). Each SNP can be considered either as a continuous variable (per allele analysis) or as a factor with three levels (2df analysis). The effects of different SNPs can be combined additively; alternatively interactions can be included. The regression coefficient of the outcome Y on these fitted values for the phenotype is the estimate of the causal association. The point estimate from the 2SLS method performed per allele is equal to that from the ratio of coefficients method in the case of a linear effect of a single IV. If the uncertainty in the fitted values is ignored in the second-stage regression, the standard error of the estimate of the causal association will be underestimated, and so a correction is needed [9]. To define confidence limits, the asymptotic normal distribution of the 2SLS estimator is used.

Methods based on genetic IVs are now being extensively used in practice. For example, they have been used for estimating the causal relationship between blood concentrations of C-reactive protein (CRP) and insulin resistance [10], CRP and carotid intima-media thickness [11], and folate levels and coronary heart disease (CHD) [8]. A recurring problem is that the anticipated causal effects are only of moderate size, and the effects of genetic markers on the phenotype are typically small, so that IV techniques suffer from low power and poor precision. Typically, sample sizes of tens of thousands are required [12, 13]. Meta-analysis of results from different studies is therefore often necessary, but current meta-analysis methods are restricted to studies all measuring the same single dichotomous or trichotomous SNP [8, 14].

We seek here to extend these established methods: first to gain power by using evidence from multiple studies, second to synthesize evidence across studies that use different SNPs as instrumental variables, third to use multiple SNPs simultaneously [15], and finally to avoid the problems of ‘weak instruments’ [16]. IV-based estimates using a weak instrument, where the association between phenotype and the IV is not statistically strong, suffer bias in the direction of the original observational association and deviation from an asymptotic normal to a more heavy-tailed distribution [17]. The F-statistic from the regression of phenotype on SNPs is commonly used as a measure of instrument strength [18].

We first describe a Bayesian approach to the estimation of causal effects using individual data on genetic characteristics. We present the simple case of a single genetic marker in one study (Section 2), and extend this to an analysis of multiple genetic markers in one study (Section 3). A hierarchical model for meta-analysis is then developed (Section 4), which efficiently deals with different genetic markers measured in different studies and with heterogeneity between studies. The focus of this paper is on data from representative cross-sectional population studies; application to case-control studies is deferred to the discussion (Section 5).

2. A single genetic marker in one study

2.1. Conventional methods

We first consider the case of a single SNP in one study, where confounding causes the observational estimate of the association of phenotype and outcome to be different from the causal relationship. Let individual i have phenotype level x_i, outcome y_i, genotype g_i, taking a value in {0,1,2}, and unmeasured confounder u_i. We assume that all the confounders can be summarized by a single value u_i. Similar to Palmer et al. [19], we consider the model represented in Figure 1:

$$\begin{array}{l}{x}_i={\alpha }_0+{\alpha }_1{g}_i+{\alpha }_2{u}_i+{\epsilon }_{xi}\\ y_i={\beta }_0+{\beta }_1{x}_i+{\beta }_2{u}_i+{\epsilon }_{yi}\end{array}$$ (1)

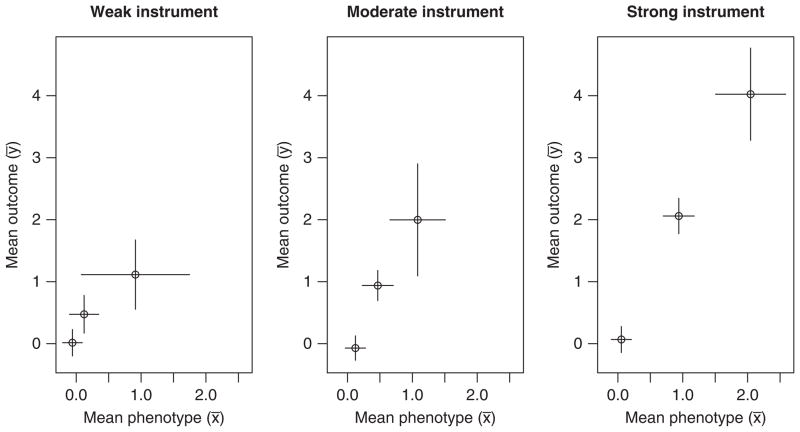
with $u_i~\text{N}(0,{\sigma }_u^2),{\epsilon }_{xi}~\text{N}(0,{\sigma }_1^2),{\epsilon }_{yi}~\text{N}(0,{\sigma }_2^2)$ independently. As an example, we simulate data for a sample of size 300, containing 12 individuals with g_i = 2, 96 with g_i = 1, and 192 with g_i = 0, corresponding to the Hardy–Weinberg equilibrium for a minor allele frequency of 20 per cent. We set the parameters $({\alpha }_0,{\alpha }_2,{\beta }_0,{\beta }_1,{\beta }_2,{\sigma }_u^2,{\sigma }_1^2,{\sigma }_2^2)=(0,1,0,2,-3,1,0.25,0.25)$, and consider the cases of a weak instrument (α₁ = 0.3, giving an expected F-value for the regression of X on G of 7), a moderate instrument (α₁ = 0.5, F-value 20) and a strong instrument (α₁ = 1, F-value 75). Figure 2 shows the simulated data grouped by genotype graphically.

Figure 2.

Graphs of mean outcome (ȳ) against mean phenotype (x̄) in three genetic groups for the weak, moderate, and strong instrument simulated examples of Section 2.1. Error bars are 95 per cent CIs for the means.

The observational estimates obtained by regressing Y on X (Table I) are far from the true causal association (β₁ = 2) as expected because of the strong negative confounding (U is positively related to X but negatively to Y). The IV-based ratio method (assuming zero correlation between coefficients) gives estimates compatible with β₁ = 2, but with a wide confidence interval in the case of the weak or moderate instrument.

Table I.

Causal parameter estimates and confidence/credible intervals using ratio, 2SLS, and the Bayesian methods compared with the observational estimate for the weak, moderate, and strong instrument simulated examples of Section 2.1.

	Estimate	95 per cent CI/CrI
Weak instrument—(F = 7)
Observational estimate	−0.358	−0.506, −0.210
Ratio method	1.637	0.563, 6.582
Bayesian method	1.496	0.536, 7.190
2SLS method	1.637	−0.126, 3.400
Moderate instrument—(F = 20)
Observational estimate	−0.251	−0.393, −0.109
Ratio method	2.555	1.481, 6.007
Bayesian method	2.417	1.473, 4.592
2SLS method	2.555	0.801, 4.309
Strong instrument—(F = 75)
Observational estimate	0.108	−0.061, 0.276
Ratio method	2.136	1.632, 2.906
Bayesian method	2.107	1.633, 2.817
2SLS method	2.136	1.469, 2.804

2.2. A Bayesian method

Estimating the causal parameter by the ratio method is equivalent to determining the gradients in Figure 2 [4]. We can reformulate the problem as one of linear regression with heterogeneous error in X. For each genotype value j = 0,1,2, we calculate the mean level of the phenotype x̄_j with its variance ${\sigma }_{xj}^2$ and mean outcome ȳ_j with its variance ${\sigma }_{yj}^2$. The model is

$$\begin{array}{l}{\overline{x}}_j~\text{N}({\xi }_j,{\sigma }_{xj}^2)\\ {\overline{y}}_j~\text{N}({\eta }_j,{\sigma }_{yj}^2)\\ {\eta }_j={\beta }_0+{\beta }_1{\xi }_j\end{array}$$ (2)

Thus, we assume that each observed mean phenotype x̄_j is from a normal distribution with unknown true mean ξ_j and known variance ${\sigma }_{xj}^2$, each observed mean outcome ȳ_j is from a normal distribution with unknown true mean η_j and known variance ${\sigma }_{yj}^2$, and there is a linear relationship between η and ξ. β₁ represents the increase in outcome for unit increase in true phenotype and is the parameter of interest.

To implement this model, we employ Bayesian analysis and Markov Chain Monte Carlo (MCMC) methods with the Gibbs sampling. This allows extension to more complicated situations, as in the next sections. We used vague priors (independent normals with zero mean and large variance of 100²) for the regression parameters and each ξ_j. We performed this analysis in WinBUGS [20] using 150 000 iterations, discarding the first 1000 as ‘burn-in’, employing different starting values to assess convergence of the posterior distribution and sensitivity analyses to show lack of dependence on the prior distributions. The posterior distributions shown in Figure 3 are non-normal, with a heavier tail toward larger values especially for the weaker instruments. For this reason, the posterior median of the distribution of β₁ is taken as the estimate of the causal association. Table I shows that the estimates and the intervals from this Bayesian group-based method are similar to those from the ratio method. Other simulated examples (not shown) also demonstrated similar results. The 2SLS per allele method gives the same estimates as the ratio method, but the intervals are symmetric and so deviate from the ratio and the Bayesian methods for the weaker instruments.

Figure 3.

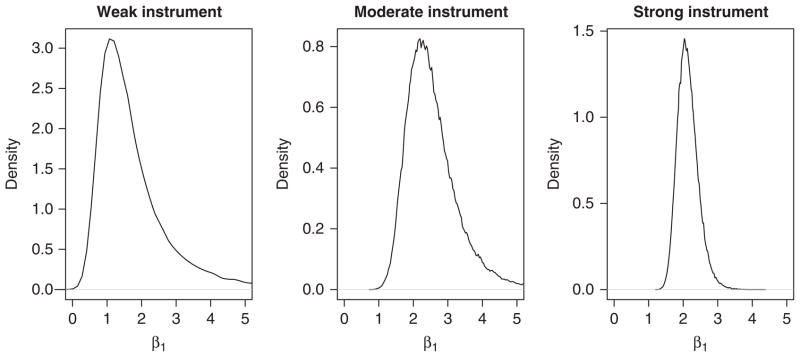
Kernel-smoothed density of posterior distribution of the causal parameter for the weak, moderate, and strong instrument simulated examples of Section 2.1 using the Bayesian method of Section 2.2.

This Bayesian method assumes that the variances ${\sigma }_{xj}^2$ and ${\sigma }_{yj}^2$ are known, whereas in fact they need to be estimated from the data, an issue which is addressed in the next section.

3. Multiple genetic markers in one study

3.1. Methods

If we have data in the study from more than one SNP then, provided they satisfy the IV assumptions above, all SNPs can be used simultaneously to divide the population into many subgroups. For each diallelic SNP, there are three genotypic categories, corresponding to 0, 1, or 2 variant alleles. For a data set with n diallelic SNPs, we have a maximum 3ⁿ categories, for each of which we can measure the mean phenotype and outcome, and examine the regression as in (2) above to estimate β₁, the causal association. In practice, fewer than the maximum number of genotypic groups will be observed, due to correlation between SNPs caused by linkage disequilibrium (LD).

If the number of groups is large, and so their sizes n_j are small, then the assumption of exact knowledge of ${\sigma }_{xj}^2$ and ${\sigma }_{yj}^2$ for each group is not appropriate. Indeed if n_j = 1, the group-specific variance cannot even be calculated. It is then preferable to base the analysis on the standard deviation in the whole population for the phenotype (σ_x) and the outcome (σ_y), using an individual-based model for phenotype and outcome. For each individual i in category j, we have

$$\begin{array}{l}{x}_{ij}~\text{N}({\xi }_j,{\sigma }_x^2)\\ y_{ij}~\text{N}({\eta }_j,{\sigma }_y^2)\\ {\eta }_j={\beta }_0+{\beta }_1{\xi }_j\end{array}$$ (3)

The observed phenotype and outcome for each individual are here modelled using normal distributions, although other distributions might be more appropriate for some applications. The information about ξ_j now depends on the population standard deviation for the phenotype as well as the size of the group. In the application below, vague Uniform[0,20] priors are used for σ_x and σ_y, whereas the other priors remain as before.

An alternative analysis is to assume a linear relationship between the phenotype and the number of variant alleles for each SNP, which is also additive across SNPs. If this structure is appropriate, the analysis should be more efficient as the correlation between similar genotypes is accounted for and fewer parameters are estimated. Then we use these modelled values in the second-stage regression. Writing G as the matrix of genotypes, so that G_ik is the number of variant alleles in SNP k for individual i, and α_k is the first-stage regression coefficients, then the model is

$$\begin{array}{l}{\xi }_i={\alpha }_0+\sum _k{\alpha }_k{G}_{ik}\\ x_i~\text{N}({\xi }_i,{\sigma }_x^2)\\ y_i~\text{N}({\eta }_i,{\sigma }_y^2)\\ {\eta }_i={\beta }_0+{\beta }_1{\xi }_i\end{array}$$ (4)

Independent vague N(0,100²) priors are now placed on the α_k rather than the ξ_i. The values of α_k depend, through feedback, on all the data including the outcome Y.

Models (3) and (4) are the equivalent of 2SLS in a Bayesian setting, except that there is feedback on the first-stage coefficients from the second-stage regression; the posterior distribution of the causal association parameter β₁ naturally incorporates the uncertainty in the first-stage regression, but with no assumption of asymptotic normality on its distribution.

3.2. Application to CRP and fibrinogen

CRP is an acute-phase protein produced by the liver as a part of the inflammation response pathway. Fibrinogen is a soluble blood plasma glycoprotein, which enables blood-clotting and is also associated with inflammation. The pathway of inflammation is not well understood, but is important as both CRP and fibrinogen are proposed as risk markers of CHD [13]. Furthermore, although CRP is associated with CHD risk, this association reduces on adjustment for various risk factors, and attenuates to near null on adjustment for fibrinogen [21]. It is important, therefore, to assess whether CRP causally affects levels of fibrinogen, since if so adjusting for fibrinogen would represent an overadjustment. The CRP gene has several common variations, which are associated with different blood concentrations of CRP. We use IV techniques to estimate the causal effect of CRP on fibrinogen. As CRP has a positively skewed distribution, we take its natural logarithm, and assume a linear relationship between fibrinogen and log_e(CRP). All SNPs used here as IVs are in the CRP regulatory gene on chromosome 1.

The Cardiovascular Health Study (CHS) [22] is an observational study of risk factors for cardiovascular disease in adults 65 years or older. We use cross-sectional baseline data for 4469 white subjects from this study, in which four diallelic SNPs relevant to CRP were measured: rs1205, rs1800947, rs1417938 and rs2808630. Each of these SNPs was found to be associated with CRP levels. We checked their associations with seven known CHD risk factors (age, body mass index, triglycerides, systolic blood pressure, total cholesterol, low- and high-density lipoproteins) for each SNP, and found no significant associations (P<0.05) out of the 28 examined. This suggests that the SNPs are valid instruments.

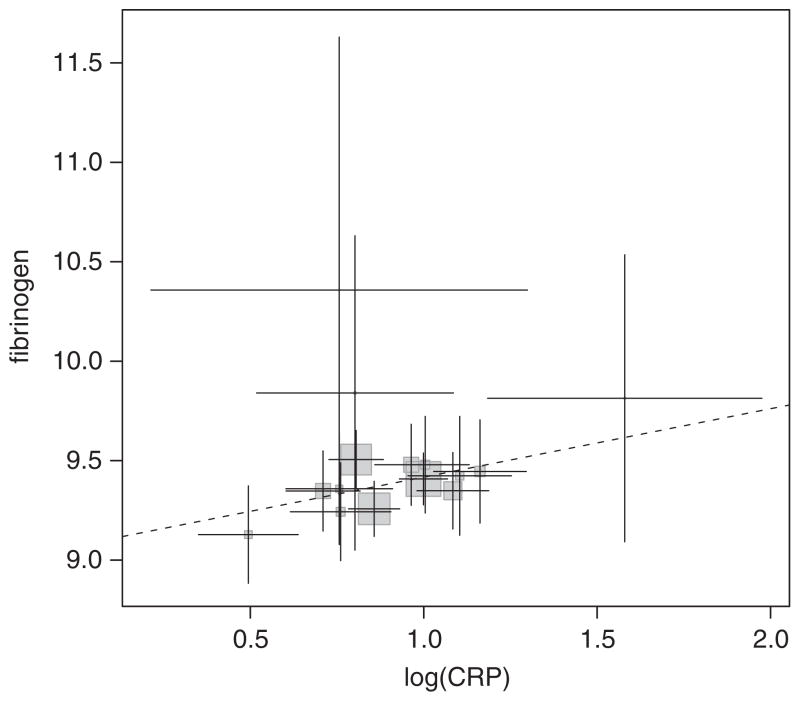
We used each of the techniques for estimating causal association mentioned above. The ratio method for each SNP separately is based on per allele regressions. For the 2SLS method, we use first a per allele model additive across SNPs and second a fully factorial version of the 2df model where each observed genotype is placed in a separate category. The 2SLS per allele model is equivalent to the structure-based Bayesian model (4) and the 2SLS factorial model is equivalent to the individual-based Bayesian model (3). When using the group-based regression (2), we excluded all genotypic groups with less than five subjects (14 subjects excluded, Figure 4). The individual-based (3), structure-based (4), ratio, and 2SLS analyses include all subjects. A sensitivity analysis was performed excluding from the 2SLS factorial and the Bayesian individual-based analyses all individuals from genotypic groups with less than five subjects. The observational increase in fibrinogen (μmol/l) per unit increase in log(CRP) is 0.937 (s.e. 0.024) and correlation between fibrinogen and log(CRP) is 0.501. The F_4,4464 statistic in the regression of log(CRP) on the SNPs additively per allele is 27.2, indicating that the instruments together are moderately strong, with a relative size bias less than 5 per cent [16, 23]. As we have used more IVs than we have phenotypes, we can perform an overidentification test. The Sargan test [24] is a test of the validity of the IV and linearity assumptions in the model. The test statistic is 7.15, which compared with a ${\chi }_3^2$ distribution gives a p-value of 0.067, meaning that the validity of the instruments is not rejected at the 5 per cent level.

Figure 4.

Plot of mean fibrinogen against mean log(CRP) in the Cardiovascular Health Study stratified by genotypic group. Error bars are 95 per cent CIs. Groups with less than five subjects omitted. The size of the shaded squares is proportional to the number of subjects in each group. The dashed line is the estimate of causal association from the group-based method without random effects.

The ratio method gives a different point estimate for each SNP, all of which are compatible with zero association (Table II). Using the 2SLS methods on all of the SNPs together, we obtain answers that synthesize all of the relevant data for each of the SNPs. The Bayesian methods give causal estimates consistent with the 2SLS estimates (Table II). The Bayesian structural-based and 2SLS per allele models give lower estimates of causal association than the other models, with 95 per cent CIs that include zero. The Bayesian credibility intervals are (appropriately) asymmetric, as no normal assumption has been made. The Bayesian structural-based and 2SLS per allele models give lower estimates of causal association than the other models. The Bayesian individual-based and the 2SLS factorial methods both give different results when individuals from small genotypic groups are excluded. This is due to weak instruments leading to a bias in the causal estimate in the direction of the confounded (observational) association [16]. We return to bias from weak instruments in the discussion.

Table II.

Comparison of the causal estimates of increase in fibrinogen (μmol/l) per unit increase in log_e(CRP) in the Cardiovascular Health Study.

	Estimate	95 per cent CI
Method
Ratio using rs1205	0.234	−0.169, 0.660
Ratio using rs1417938	−0.608	−1.581, 0.137
Ratio using rs1800947	0.203	−0.478, 0.940
Ratio using rs2808630	2.722	−∞, +∞
2SLS factorial using all SNPs	0.376	0.088, 0.665
2SLS factorial (excluding small groups)	0.280	−0.041, 0.601
2SLS per allele using all SNPs	0.200	−0.138, 0.538
Bayesian methods
Group-based (excluding small groups)	0.342	0.004, 0.698
Individual-based	0.389	0.049, 0.728
Individual (excluding small groups)	0.300	−0.045, 0.666
Structural-based	0.212	−0.157, 0.586

Ninety-five per cent confidence/credible interval (CI/CrI) are shown. Small groups are genotypic groups with less than five subjects.

4. Multiple genetic markers in multiple studies

4.1. Methods

The above framework leads naturally to a model for meta-analysis across multiple studies. Assumption (c) in Section 1 for IVs ensures that, in principle, the same parameter β₁ is being estimated regardless of how many and which SNPs are available in each study. This is because the outcome is independent of the IV given the phenotype (which is measured) and the confounders (which are averaged over). We thus propose a hierarchical model for β₁ estimated across multiple studies as follows. For a fixed-effect meta-analysis, we assume the same value of β₁ for each study. For a random-effects meta-analysis, we allow β_1m from study m to come from a distribution with mean β₁ and variance ψ². This acknowledges the possibility that the causal parameters are somewhat different across studies, as is plausible due to the influences of different population characteristics, but that they are expected to have generally similar values.

For the group-based regression (2), for group j in study m, a fixed-effect meta-analysis is

$$\begin{array}{l}{\overline{x}}_{jm}~\text{N}({\xi }_{jm},{\sigma }_{\mathit{xjm}}^2)\\ {\overline{y}}_{jm}~\text{N}({\eta }_{jm},{\sigma }_{\mathit{yjm}}^2)\\ {\eta }_{jm}={\beta }_{0m}+{\beta }_1{\xi }_{jm}\end{array}$$ (5)

Values for β_0m, the constant terms in the regression, will vary depending on the average level of outcome in the population in each study, and are thus given independent vague N(0,100²) priors for each study.

For a random-effect meta-analysis, the last line of (5) is replaced by

$$\begin{array}{l}{\eta }_{jm}={\beta }_{0m}+{\beta }_{1m}{\xi }_{jm}\\ {\beta }_{1m}~\text{N}({\beta }_1,{\psi }^2)\end{array}$$ (6)

We use a Uniform[0,20] prior for ψ in the example below.

These modifications to the simple group-based analysis (2) for a meta-analysis context can also be similarly made to the individual-based model (3), and to the structured model (4). For example, the full model using a structured model (4), assuming heterogeneity between studies, for individual i and SNP k = 1…K_m in study m is

$$\begin{array}{l}{\xi }_{im}={\alpha }_{0m}+\sum _{k=1}^{K_m}{\alpha }_{km}{G}_{\mathit{ikm}}\\ x_{im}~\text{N}({\xi }_{im},{\sigma }_{xm}^2)\\ y_{im}~\text{N}({\eta }_{im},{\sigma }_{ym}^2)\\ {\eta }_{im}={\beta }_{0m}+{\beta }_{1m}{\xi }_{im}\\ {\beta }_{1m}~\text{N}({\beta }_1,{\psi }^2)\end{array}$$ (7)

In this model, we assume that the first-stage regression coefficients α_km are unrelated in the different studies. An extra sophistication would be to assume that these coefficients are common or related when different studies involve the same set of SNPs. Example WinBUGS code is given in the appendix.

4.2. Application to CRP and fibrinogen

We give an example of meta-analysis of 11 studies [13] using the methods described. In addition to the CHS used in Section 3.2, we incorporate data from a further eight general population cohort studies: British Women’s Heart and Health Study (BWHHS), Copenhagen City Heart Study (CCHS), Copenhagen General Population Study (CGPS), English Longitudinal Study of Ageing (ELSA), Framingham Health Study (FRAM), Northwick Park Heart Study II (NPHS2), Rotterdam Study (ROTT), and Whitehall II Study (W2). In each of these, the analyses presented here are cross-sectional, based on the baseline measurements of CRP and fibrinogen. We also use data from two case-control studies, the Nurses’ Health Study (NHS) and Stockholm Heart Epidemiology Program (SHEEP), again with CRP and fibrinogen measured at baseline. We use the data from controls alone since these better represent cross-sectional population studies. Details of these studies are summarized in Table III.

Table III.

Summary of studies in meta-analysis of Section 4.2: SNPs measured, number of participants with complete genetic data, number of participants in genotypic groups of size less than 5 excluded from some analyses, F value with degrees of freedom (df), p-value from the Sargan test of overidentification from additive per allele regression of phenotype on SNPs used as IVs.

Study	SNPs used*	Participants	Excluded	F value	df	Overid p-value
BWHHS	g1, g3, g5	3188	7	16.7	(3, 3184)	0.638
CCHS	g1, g2, g4	7998	5	29.6	(3, 7994)	0.358
CGPS	g1, g2, g4	35 679	5	152.0	(3, 35675)	0.439
CHS	g1, g3, g5, g6	4469	15	27.2	(4, 4464)	0.067
ELSA	g1, g2, g4	4409	8	24.7	(3, 4405)	0.367
FRAM	g1, g2, g4	1575	4	10.0	(3, 1571)	0.447
NHS	g1, g6	414	0	13.2	(2, 411)	0.984
NPHS2	g1, g2, g4	2153	3	11.6	(3, 2149)	0.344
ROTT	g1, g2	2077	2	11.9	(2, 2074)	0.983
SHEEP	g1, g2, g4	1044	4	10.5	(3, 1040)	0.680
W2	g1, g2, g4	4354	5	21.5	(3, 4350)	0.469
Total		67 361	58

^*g1= rs1205, g2= rs1130864, g3= rs1417938, g4= rs3093077, g5= rs1800947, g6= rs2808630.

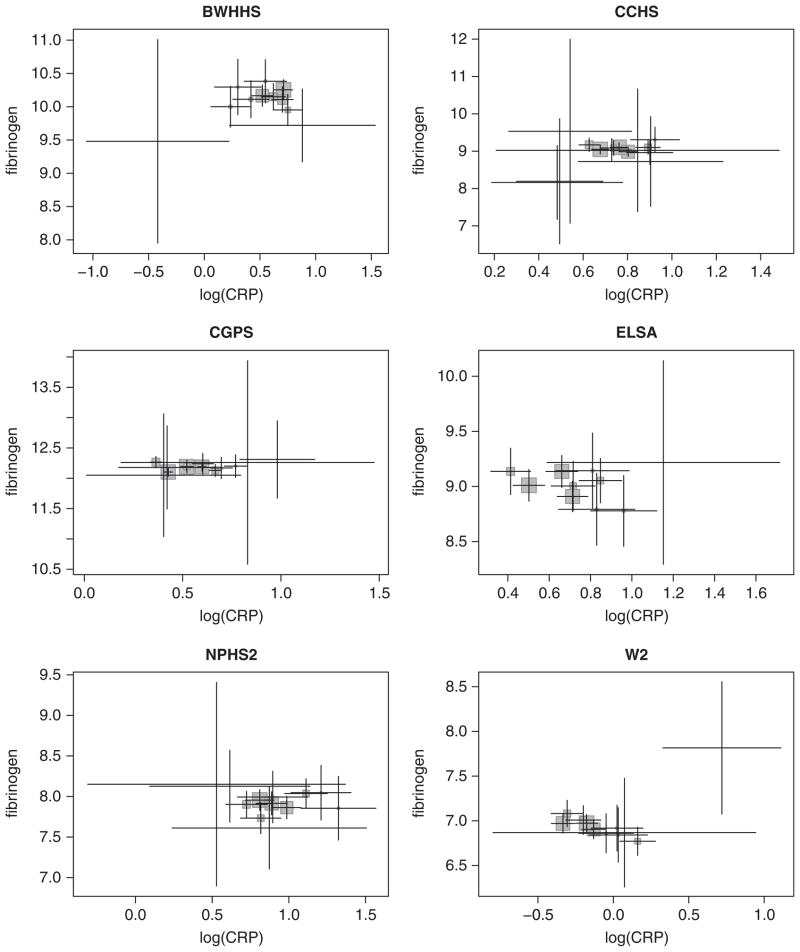
To avoid problems with weak instruments, we want to choose genetic instruments that together are strongly related to log(CRP). For this, the instrument was chosen to maintain the F statistic above 10 and to include sequentially, where available, each of SNPs rs1205, one of rs1130864 and rs1417938 (these SNPs are in complete LD), rs3093077, rs1800947, and rs2808630. In the meta-analysis we use between two and four SNPs as instruments in each study; the Sargan overidentification tests were satisfied (Table III). The choice of instruments here is not made a priori, as should ideally be the case, but pragmatically to exemplify the method. For comparison with the Bayesian methods, we use the study-specific 2SLS causal estimates and corresponding asymptotic standard errors in a standard two-step inverse variance weighted meta-analysis (using a moment estimator of the between-study variance in the case of random-effects meta-analysis). Mean log(CRP) and fibrinogen levels for the genotypic groups for six of the studies are shown in Figure 5.

Figure 5.

Plot of mean fibrinogen against mean log(CRP) for six studies from Section 4.2 stratified by genetic group. Error bars are 95 per cent CIs. Groups with less than five subjects omitted. The size of the shaded squares is proportional to the number of subjects in each group.

Table IV shows a causal association of log(CRP) on fibrinogen, which does not significantly differ from the null, except for the structural-based fixed-effect meta-analysis, which suggests a weak negative causal association. Groups of size less than 5 have been omitted in the 2SLS factorial, group-based and individual-based analyses. There is no clear preference for the random-effects models from the deviance information criterion (DIC) [25]. The DIC should only be used to compare between a fixed- or random-effect model, and not between models based on different data structures. Again, the structural-based models give lower estimates of causal association than the other methods.

Table IV.

Estimates of increase in fibrinogen (μmol/l) per unit increase in log_e(CRP), 95 per cent confidence/credible interval (CI/CrI), deviance information criterion (DIC) and heterogeneity parameter (ψ) in meta-analysis of 11 studies using 2SLS and the Bayesian methods. Genotypic groups with less than five individuals excluded from the 2SLS factorial, group-based and individual-based analyses.

Fixed-effect meta-analysis	Estimate	95 per cent CI/CrI	DIC*
2SLS factorial	−0.005	−0.139, 0.130
2SLS per allele	−0.086	−0.255, 0.082
Group-based	−0.008	−0.142, 0.125	−242.1
Individual-based	−0.036	−0.164, 0.090	500 692
Structural-based	−0.136	−0.276, −0.002	501 037
Random-effects meta-analysis	Estimate	95 per cent CI/CrI	DIC	ψ
2SLS factorial	−0.007	−0.151, 0.137		0.072
2SLS per allele	−0.086	−0.255, 0.082		0.000
Group-based	−0.017	−0.234, 0.177	−244.5	0.188
Individual-based	−0.039	−0.228, 0.153	500 692	0.155
Structural-based	−0.150	−0.365, 0.048	501 037	0.169

^*Note: DIC should be used to compare between a fixed- or random-effect model and not between models.

5. Discussion

In this paper, we have described a Bayesian approach to analysis of Mendelian randomization studies. We introduced the approach in a simple example of a confounded association with one IV. We extended the method to use multiple IVs, to use individual participant data and to incorporate an explicit, here additive, genetic model. We then show how this leads naturally to a meta-analysis, which can be performed even with heterogeneous genetic data. These methods have been applied in the estimation of the causal association of CRP levels on fibrinogen.

5.1. Bayesian methods in IV analysis

The Bayesian approach has similarities to the 2SLS method. In both, fitted values of phenotype are estimated for each genotypic group, which are then used in a regression of outcome on phenotype. In 2SLS, these fitted values are assumed to be precisely known in the second-stage regression, and a correction is made to the second-stage standard error to account for this using sandwich variance estimators. In the Bayesian framework, the fitted values of phenotype and outcome are estimated simultaneously, and the standard error in the causal parameter is directly estimated from the MCMC sampling process. This means that no assumption is made on the distribution of the causal parameter, giving appropriately sized standard errors and skew CIs. The Bayesian approach allows us to be explicit about the assumptions made. This gives us flexibility to determine the model according to what we believe is plausible without being limited to linear or normal assumptions.

Additionally, the Bayesian approach provides a framework to perform analyses that are not possible using 2SLS. These include meta-analysis in a single hierarchical model, imputation of missing data, use of haplotypes with uncertainty, and analysis of binary outcomes, each of which is discussed below. It also allows for more accurate inference when using instruments that are weak.

Bayesian methods have not been widely proposed for IV analyses or applied in the Mendelian randomization studies. Although Bayesian methods for IV analysis have been suggested in the econometrics literature [26, 27], their use is not common and differences between the fields mean that the methods cannot easily be translated into an epidemiological setting [28]. McKeigue et al. [29] have performed a Bayesian analysis in the single SNP and single study situation, but regarding the parameter of interest as the ‘ratio of the causal effect to crude [observational] effect’. We prefer to regard β₁, the causal association, as the parameter of interest.

5.2. Meta-analysis

Methods for meta-analysis of Mendelian randomization studies have not been extensively discussed, and have been restricted to studies measuring one identical SNP [8, 14, 30]. In applications, meta-analyses of studies have concentrated on testing for a causal effect, without accounting for the uncertainty in the estimated mean difference in phenotype values between genotypic groups [31, 32]. Where this uncertainty has been accounted for, confidence intervals for the causal association have been too wide to exclude a moderate causal association [33, 34]. Our proposed analysis thus extends this previous work in a number of ways: first by using a flexible Bayesian framework that eliminates the problems caused by non-normal causal estimates, second by presenting a coherent framework for estimation of the causal association using data from multiple studies, and third by allowing the use of different genetic markers in different studies.

An advantage of the Bayesian setting for meta-analysis is that the whole analysis can be performed in one step. This keeps each study distinct within the hierarchical model, only combining studies at the top level. This is more effective at dealing with heterogeneity, both statistical and in study design, than performing separate meta-analyses on each of the genotype–phenotype and genotype–outcome associations [8]. An alternative approach where the causal association estimate and its precision are estimated in each study, and these estimates are combined in a meta-analysis in a second stage, is not recommended for two reasons. First, the distribution of each causal estimate is not normal (especially if the instrument is not strong), and so the uncertainty is not well represented by its standard error, and second, some causal estimates from individual studies may have infinite variance. Examples of these problems are apparent in Figure 3 and Table II.

5.3. Weak instruments

A cause for concern in IV analysis is the bias created by using ‘weak instruments’, that is instruments not strongly associated with the phenotype. When several instruments are used, an instrument is strong if it explains sufficient variance in the phenotype given the other included instruments. Owing to the correlation between SNPs, an instrument that is strong on its own may not be strong when considered in addition to other instruments. As the number of instruments increases, if no more of the variation in the phenotype is explained, then the overall instrument becomes weaker and two problems occur. First, the theoretical bias of the IV estimator increases, due to the random correlation between the IVs and unmeasured confounders [35]. If the variation in the phenotype explained by confounders is relatively large compared with the variation in the phenotype caused by the IVs, then the instruments may model the variation in the confounders rather than the systematic variation from the genetic differences. This will give rise to a correlation between the confounders and the fitted phenotype values, which will lead to bias of the IV estimate in the direction of the confounded estimate [17, 23]. This bias affects all the methods considered: the ratio of coefficients method, 2SLS, and the proposed Bayesian method. Second, as the instruments weaken, the distribution of the causal estimate becomes heavy-tailed, leading to possible underestimation of the size of a test based on 2SLS [23], although recent work on modifying the 2SLS method has concentrated on improving properties of test size and confidence intervals with weak instruments [36, 37]. The Bayesian method has an advantage here, in that it makes no assumption of normality. The shape of the posterior distribution for the causal parameter β₁ reflects its true uncertainty.

An extreme case of weak instruments is where multiple instruments place each individual in their own separate genetic group. Then the IV estimate, derived from the regression as in Figure 2, is equal to the observational confounded estimate. The generally quoted advice that an instrument with F>10 is strong is an oversimplification [17]. A modified list of values for a version of the F statistic that limit bias and preserve test size due to Stock and Yogo [23] is quoted in the function ivreg2 in Stata [9].

Instruments should be specified in Mendelian randomization studies prior to data collection. When this is not possible, instruments should be chosen so as not to use those that give little additional strength to the G–X association. Overidentification tests, such as the Sargan or Basmann test [9] can be performed to test the validity of instruments. However, it should not be thought that an overidentification test is a cure-all: instruments that pass the test can still give estimates that suffer from bias. Sensitivity analyses, especially when the F statistic is below 10, should be performed using different instruments and models of genetic association with informally investigate heterogeneity of estimates indicating possible bias or violation of IV assumptions.

Although the individual-level model includes all of the participants, the inclusion of many small groups potentially weakens the instruments in the model and so increases bias. Small groups will not have enough participants for confounder levels to be assumed equal between groups. The structural model may then be preferred, and will be less biased and more efficient if the additive assumptions for the effects of genotype on phenotype are valid. Fewer parameters are estimated and groups with similar genotypes will have correlated estimated true levels of phenotype, which provides extra information in the analysis. In each of our analyses, the individual and the group-based models give more positive estimates of causal association than the structural-based model. This is due to greater bias in the direction of the observed association in the individual and the group-based models from weaker instruments with more degrees of freedom in the G–X association.

5.4. Missing data and haplotype assignment

If there are missing SNP data when applying the individual-based or group-based Bayesian models, and if we can assume that this missingness is not associated with any variable except possibly conditional on the genotype, then the pattern of missing data satisfies the IV assumptions. For each SNP, missing values can be included as a separate category when defining the subgroups. If there are missing genetic data when applying the structural model, we can impute the missing data M times using the correlation between SNPs with software such as fastPHASE [38]. These multiple imputations can then be included in the Bayesian model, for example using the WinBUGS function m~ dpick(1,M). Alternatively, if we believe that the variation in the phenotype is better explained by haplotypes than by genotypes, then we can use standard software to infer haplotypes [38] and instead use these haplotype assignments in a multiple imputation, with the true phenotype level as the sum of contributions from each haplotype [4].

5.5. Binary outcomes

The Bayesian group-level method can be applied to binary outcomes, such as disease events, using a normal approximation to the distribution of log-odds as the outcome. In this case, for example, ȳ_j and ${\sigma }_{yj}^2$ for genotype group j in model (2) are replaced by logit(p_j) and 1/n_1j + 1/n_2j, respectively, where p_j is the observed probability of the event in group j, n_1j the number of events, and n_2j the number of non-events. Alternatively, we can model the probability of an event directly using logistic regression. We replace the normal distribution of the outcome in each group in model (2) with a binomial distribution as follows:

$$\begin{array}{l}{n}_{1j}~\text{Binomlal}({\pi }_j,n_{1j}+n_{2j})\\ \text{logit}({\pi }_j)={\beta }_0+{\beta }_1{\xi }_j\end{array}$$ (8)

For an individual-level analysis of binary data, as in model (3), the outcome y_ij for individual i in genotype group j takes the value of 0 or 1. Then the first line in model (8) is replaced by y_ij ~ Binomial(π_j, 1). Similar adaptations for binary outcomes can be made to the meta-analysis models (5) and (7).

Such models for binary outcomes are valid for testing the causal hypothesis β₁ = 0. However, they do not provide unbiased estimators of a non-zero causal parameter [2], due to the non-collapsibility of the log-odds function over the distribution of the unknown confounders [39]. Alternative methods, including marginal structural models [40] and structural mean models [41], have been proposed for binary outcomes in a classical setting, but these do not provide consistent estimators either [42]. An alternative estimator, usually called the control variable approach, involves including the residuals from the first-stage regression of X on G into the second-stage regression of Y on X̂ [43]. This has been shown usually to reduce bias for IV analyses involving binary outcomes in the Mendelian randomization setting [19]. An alternative approach would be to use a relative risk model. This does not suffer the same problems of non-collapsibility and the parameter estimated from such an approach is the relevant causal parameter [2]. Application of these ideas and methods within our Bayesian model formulation needs investigation.

6. Conclusion

The validity of IV analyses relies on the assumptions specified in the introduction. These assumptions can only be partially verified from data, and there are a number of ways in which they may be violated for the Mendelian randomization studies [4]. Whereas the association between the genotypes and the measured confounders can be assessed, and checked that they are compatible with chance, associations with unmeasured confounders clearly cannot be checked. Potential correlations caused by LD between the SNPs of interest and other genetic variants, which act on the outcome through different biological pathways, would also violate the assumptions implicit in Figure 1. The argument against the existence of such pathways is usually biological rather than statistical. Finally it is difficult to rule out the possibility that a genetic mutation leads, through developmental compensation or canalization, to feedback regulation which affects the distribution of confounders. Thus, causal estimates derived from all IV analyses should be subject to the caveat that they rely on assumptions. Nevertheless, our proposed Bayesian method for meta-analysis of Mendelian randomization studies is a useful methodological advance. It should also find application in the context of the increasing number of consortia that are now collating the relevant genetic, phenotype, and outcome data from multiple studies [13].

Appendix A: WinBUGS code for random-effects meta-analysis of group-based model

model {
# prior for hierarchical causal estimate (parameter of interest)
 betatrue ~ dnorm(0, 0.000001)
# prior for standard deviation of individual study estimates
 betasd ~ dunif(0, 20)
 betatau <- pow(betasd, -2)
for(m in 1:S) { # S = number of studies
# prior for regression intercept parameter
  beta0[m] ~ dnorm(0, 0.000001)
# distribution of study-specific causal estimates
  beta[m] ~ dnorm(betatrue, betatau)
 for (j in 1:G[m]) { # G[m] = number of genetic subgroups in study m
# distribution of phenotype in subgroup j, study m
  x[j, m] ~ dnorm(xi[j, m], xtau[j, m])
# distribution of outcome in subgroup j, study m
  y[j, m] ~ dnorm(eta[j, m], ytau[j, m])
# prior for true value of phenotype in subgroup j, study m
  xi[j, m] ~ dnorm(0, 0.000001)
# linear model of true outcome on true phenotype
  eta[j, m] <- beta0[m] + beta[m] * xi[j, m]
  }
 }
}

Appendix B: WinBUGS code for fixed-effect meta-analysis of structure-based model

model {
# prior for fixed causal estimate (parameter of interest)
 beta ~ dnorm(0, 0.000001)
for(m in 1:S) {
# prior for regression intercept parameter
 beta0[m] ~ dnorm(0, 0.000001)
 alpha0[m] ~ dnorm(0, 0.000001)
# prior for study phenotype standard deviation
 xsd[m] ~ dunif(0, 20)
 xtau[m] <- pow(xsd[m], -2)
# prior for study outcome standard deviation
 ysd[m] ~ dunif(0, 100)
 ytau[m] <- pow(ysd[m], -2)
 for(k in 1:G[m]) { # G[m] = number of genes in study m
# prior for gene-phenotype regression parameters
  alpha[k, m] ~ dnorm(0, 0.000001)
  }
 for (i in 1:N[m]) { # N[m] = number of individuals in study m
# linear model of true phenotype on genes
  xi[i, m] <- inprod(alpha[1:G[m], m], gene[i, 1:G[m], m]) + alpha0[m]
# distribution of phenotype in individual i, study m
  x[i, m] ~ dnorm(xi[i, m], xtau[m])
# distribution of outcome in individual i, study m
  y[i, m] ~ dnorm(eta[i, m], ytau[m])
  eta[i, m] <- beta0[m] + beta * xi[i, m]
  }
 }
}