Improved Analysis for Determining Diffusion Coefficients from Short Single-Molecule Trajectories with Photoblinking

Abstract

Two Maximum Likelihood Estimation (MLE) methods were developed for optimizing the analysis of single-molecule trajectories that include phenomena such as experimental noise, photoblinking, photobleaching, and translation or rotation out of the collection plane. In particular, short, single-molecule trajectories with photoblinking were studied, and our method was compared with existing analytical techniques applied to simulated data. The optimal method for various experimental cases was established, and the optimized MLE method was applied to a real experimental system: single-molecule diffusion of fluorescent molecular machines known as nanocars.

Introduction

Multiple molecule tracking has become a valuable and widely used technique in diverse fields, including in vitro cell biology,^1-4 in vivo dynamics,⁵ microrheology,^{6, 7} as well as surface and interface dynamics.^8-14 Computer automated tracking has made simultaneous extraction of multiple molecule trajectories from video frames an efficient, low-cost technique. However, the method of analyzing single-molecule trajectories is an area of contention.^{6, 15-21}

The simplest and most commonly used technique is mean square displacement (MSD) analysis. The MSD is computed for all possible time lags. The diffusion coefficient is proportional to the slope of the linear fitted MSD vs. time lag plot and can be calculated using Einstein’s equation: <r²>=4Dt. In practice, the stochastic nature of diffusion, the collection process, and various other factors compromise the value of this technique. Recent progress has brought the MSD analysis technique into maturity.^{6, 15, 16} By correctly considering noise sources and their statistical implications, Michalet’s optimized least-square fit technique (OLSF) and Berglund’s maximum likelihood estimator (MLE) were shown to effectively reach the theoretical limit of relative standard deviation (RSD) as predicted by Fisher information theory.²² However, the collection and analysis of experimental data can be more complicated due to several factors. For long trajectories, molecules can undergo anomalous diffusion^23-26 or confined diffusion.^{26, 27} In other cases, the optimal trajectory length can be ended by fluorescence blinking and bleaching^{8, 28}or out of focus motion.^{26, 29, 30} Additionally, both short and long trajectories can contain brief lapses in molecule’s location due to photoblinking. For data analysis, a photoblinking event results in disparities in the time lag of affected displacements. How these optimized methods²² apply to suboptimal experimental conditions mentioned above is still an open question. In this work, we will focus on finding the best method to analyze short trajectories containing 20 or less measured displacements with photoblinking.

Statistically, the RSD of the diffusion coefficient increases as the trajectory length decreases. Analysis of experimental data with varying signal-to-noise ratios results in either over- or underestimation of the actual diffusion coefficient. As a consequence, the analyzed diffusion coefficient from experimental data is always biased relative to the true diffusion coefficient.

Photoblinking also prohibits the use of a general method to calculate the diffusion coefficient. For example, in trajectories where photoblinking occurs, the second MSD point may be more accurate than the first. Because of this, application of OLSF becomes problematic when deciding which MSD points should be used for fitting.²² How can accurate information be extracted from short trajectories with photoblinking when further experimental optimization is not feasible?

In order to answer this question, we have derived two maximum likelihood estimators, MLE (1) and MLE (2), to analyze short trajectories with photoblinking based on Berglund’s work.¹⁵ Two different methods are required to properly analyze trajectories with different noise levels. We apply these methods to single-molecule trajectories and build a model to test and characterize the analysis methods and draw the conclusions.

This article is organized as follows. In the methods section, we present the theoretical groundwork for the two MLE methods used for trajectories with photoblinking. In the results and discussion section, we first study the influence of photoblinking on the RSD and root-mean-square deviation (RMSD) of diffusion coefficients calculated by MLE (1), MLE (2), and OLSF²² methods; then, we determine which method is appropriate for different noise and photoblinking levels. Finally, we test our analysis on real single-molecule trajectories that possess photoblinking.

Methods

Based on previous work,^{15, 22} we first derive two likelihood functions that are applied to noise-free and noisy trajectories. Both are written for the one-dimensional case; the corresponding likelihood functions for cases of more than one dimension are simply linear combinations of the log likelihood function for each dimension. Because most single-molecule tracking data are two-dimensional, later analysis will compare the performance of the MLEs in two dimensions.

In cases of noise-free data, all measured displacements are independent of one another. As a result, the likelihood function is simply the product of the distribution function of each displacement. The distribution function for Brownian motion is:³¹

$$P({\Delta }_i,n_i\mathit{dt})=\frac{1}{\sqrt{4\pi {\mathit{Dn}}_i\mathit{dt}}}\exp (-\frac{{\Delta }_i^2}{4{\mathit{Dn}}_i\mathit{dt}}),$$ (1)

where Δ_i is i^th displacement, dt is the time lag between frames, n_i is the frame number, and D is the diffusion coefficient. The value of n_i is one for displacements without recorded photoblinking. When photoblinking causes the recording of a molecule’s location to lapse for k frames, n_i takes the value k+1. For simulated trajectories, the duration of photoblinking could be arbitrarily long and this is in principle similar to experimental data; when analyzing experimental data however, the short trajectories and the positive re-identification of the molecule after a photoblinking event in the automated tracking algorithm typically limits the duration of photoblinking to one frame.⁸ The second moment of the probability distribution generates Einstein’s equation:³¹

$$<{\Delta }_i^2>=2{\mathit{Dn}}_i\mathit{dt},$$ (2)

The corresponding log likelihood function is:

$$L\left(\Delta \right)=\log \left\{\prod _i\frac{1}{\sqrt{4\pi {\mathit{Dn}}_i\mathit{dt}}}\exp \right(-\frac{{\Delta }_i^2}{4{\mathit{Dn}}_i\mathit{dt}}\left)\right\}=\sum _i\log \left\{\frac{1}{\sqrt{4\pi {\mathit{Dn}}_i\mathit{dt}}}\exp \right(-\frac{{\Delta }_i^2}{4{\mathit{Dn}}_i\mathit{dt}}\left)\right\}.$$ (3)

When n_i is identical for each measured displacement, this equation is identical to the likelihood function in Reference 17. For the two-dimensional case, L_2d (Δ) = L(Δ_x) + L(Δ_y). Generally, the diffusion coefficient is given by:

$$D=\frac{\sum _{i=1}^N{\Delta }_i^2∕n_i}{2\mathit{Ndt}},$$ (4)

where N is the number of measured displacements. We call this maximum likelihood estimator MLE (1) in this work.

Two kinds of uncertainty related to the molecule’s location should be considered: noise and motion blur.^{15, 16} Noise is related to the pixel size, signal intensity, and noise source;¹⁶ motion blur is due to finite camera integration time.¹⁵ Both uncertainties have been discussed at length by several authors.^{6, 15-17, 32-36} These two factors broaden a molecule’s location into a Gaussian probability distribution with variances σ² and 2DRdt for noise and motion blur, respectively. σ² is the static localization uncertainty¹⁵ and R is the motion blur coefficient.¹⁶ We define reduced square localization error x as x = σ²/(Ddt).²² When trajectories possess uncertainties in molecule’s location, MLE (1) is a biased estimator because the estimated diffusion coefficient is equal to the true diffusion coefficient plus the contribution from the uncertainties.

If noise and motion blur are considered, the measured displacements are no longer independent of one another. Using the same approach outlined in Berglund’s work,¹⁵ we have the following covariance matrix:

$$\begin{array}{cc}\hfill <{\Delta }_k{\Delta }_k>=& 2{\mathit{Dn}}_k\mathit{dt}-2(2\mathit{DRdt}-{\sigma }^2)={\alpha }_k\hfill \\ \hfill <{\Delta }_{k\pm 1}{\Delta }_k>& =2\mathit{DRdt}-{\sigma }^2=\beta \hfill \\ \hfill <{\Delta }_k{\Delta }_j>=& 0\text{otherwise}.\hfill \end{array}$$ (5)

In principle, we can decouple the measured displacements using an orthogonal matrix A:

$$<A\Delta {\left(A\Delta \right)}^T>=A<\Delta {\Delta }^T>A^T=\Lambda =\left[\begin{array}{cccc}\hfill {\lambda }_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\lambda }_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda }_{N-1}\hfill \end{array}\right],$$ (6)

where ʌ is a diagonal matrix and λ_i is a linear combination of D and σ². Because the new displacements AΔ are independent and have the same distribution function with different time lags, we can use the log likelihood function (Eq. 3) to obtain the log likelihood function that considers noise and motion blur:

$$\begin{array}{cc}\hfill & L\left(\Delta \right)=\log \left\{\prod _i\frac{1}{\sqrt{2\pi {\lambda }_i}}\exp \right(-\frac{{\left(A\Delta \right)}_i^2}{2{\lambda }_i}\left)\right\}\hfill \\ \hfill & =-\frac{1}{2}\log \mid \Lambda \mid -\frac{1}{2}{\left(A\Delta \right)}^T{\Lambda }^{-1}\left(A\Delta \right)=-\frac{1}{2}\log \mid \Sigma \mid -\frac{1}{2}{\Delta }^T{\Sigma }^{-1}\Delta ,\hfill \end{array}$$ (7)

where:

$$\begin{array}{cc}\hfill & {\left(\Sigma \right)}_{\mathit{ij}}={\left(A^{-1}\Lambda A\right)}_{i,j}=<{\Delta }_i{\Delta }_j>\hfill \\ \hfill & =[2{\mathit{Dn}}_i\mathit{dt}-2(2\mathit{DRdt}-{\sigma }^2\left)\right]{\delta }_{i,j}+[2\mathit{DRdt}-{\sigma }^2]{\delta }_{i,j\pm 1}\hfill \\ \hfill & ={\alpha }_i{\delta }_{i,j}+\beta {\delta }_{i,j\pm 1},\hfill \end{array}$$ (8)

The expression for the likelihood function (Eq. 7) is almost the same as Berglund’s likelihood function;¹⁵ however, time lags of measured displacements are not identical in the covariance matrix σ. We call this maximum likelihood estimator MLE (2). The displacements and corresponding time lags need to be extracted from the trajectories with photoblinking and then used in Eq. 7 to find the most likely diffusion coefficient. Notice that, when R = 0 and σ² = 0, the log likelihood function (Eq. 7) becomes the log likelihood function described by MLE (1). The diffusion coefficient estimated by MLE (2) equals the true diffusion coefficient, making MLE (2) an unbiased estimator.

The approximation method for the log likelihood function presented in Reference 15 is not applicable here because the time lags are not necessarily identical. However, for short trajectories, the use of the exact log likelihood function (Eq. 7) is no longer computationally prohibitive and may be directly used. Unless otherwise noted, all conclusions in this work are only for short trajectories. We will limit our discussion to situations when R = 0. Because (2DRdt – σ²) can be replaced by σ’², conclusions in this work can be easily derived for other cases of R.

Results and discussion

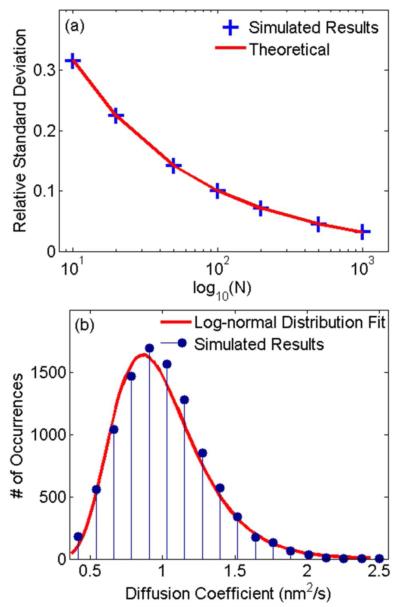
For noise-free data, the smallest RSD of the diffusion coefficient depends only on the number of measured displacements of each trajectory and is not directly influenced by the photoblinking level. The photoblinking level of a trajectory is defined as the number of frames with photoblinking over the total number of frames. Previous work^{15, 17} has shown that the smallest RSD for trajectories with N displacements is equal to $\sqrt{1∕N}$ when there is neither noise nor photoblinking. In these situations, the measured displacements are independent of one another, and the time lag for each displacement is identical. The simulated results in Figure 1a show that, even when considering photoblinking, the RSD calculated using MLE (1) is still equal to $\sqrt{1∕N}$. In other words, the RSD is not influenced if the time lag for each measured displacement is different as long as those measured displacements are independent of one another. Each simulated point uses 10,000 simulated trajectories with a photoblinking level of 0.3, where the photoblinking level is defined as the number of blinking frames over the number of total frames. Simulations using photoblinking levels of 0.1 and 0.5 produced the same results (data not shown). Figure 1b shows that the distribution of the calculated diffusion coefficient is still log-normal^{37, 38} even with photoblinking. However, the influence of photoblinking becomes more complicated when considering noise.

Figure 1.

The influence of photoblinking on noise-free data. (a) Simulated results (data points) show that the RSD equals $\sqrt{1∕N}$ for different number of displacements N, perfectly matching the RSD predicted by Fisher information theory (line).^{15, 17} (b) The distribution of diffusion coefficients for trajectories of N = 20 (data points), fitted with log-normal distribution (line).³⁸ There is only minor difference between the simulated distribution and the fit. The result signifies that photoblinking does not influence the log-normal distribution of the diffusion coefficient.

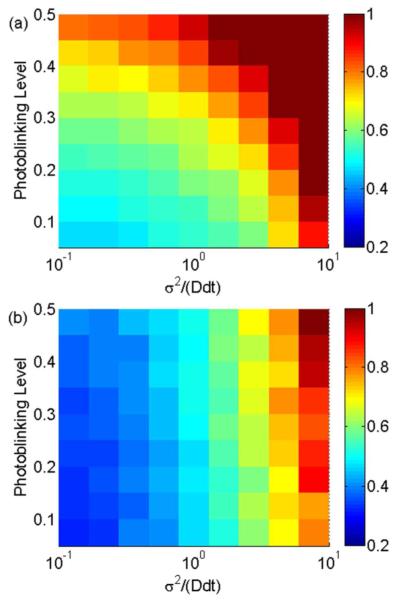
When considering data with noise present, OLSF²² quickly fails as the photoblinking level increases. Because photoblinking is stochastic in both number and position, OLSF cannot accurately determine how many MSD points to fit. The detriment of photoblinking to the accuracy of MLE (2) is considerably less severe. MLE (2) is still able to provide the most likely diffusion coefficient because it uses all of the measured displacements. Figures 2a and 2b show the RSD calculated by OLSF and MLE (2). As photoblinking levels increase, the RSD calculated with OLSF increases very quickly, while the RSD of MLE is less affected. Notice these results are only for short trajectories where N ≤ 20, which are typical trajectory lengths when photobleaching is present. For longer trajectories, the approximation method in Reference 8 is impossible due to photoblinking, and using this method becomes numerically inconvenient or even impossible. In those cases, OLSF may be a better choice. Even for short trajectories, MLE (2) is not always the best choice.

Figure 2.

The RSD (color scale) calculated with (a) OLSF and (b) MLE (2) as it varies with reduced square localization error x and photoblinking level. The length of the simulated trajectories is 20. The same color scale is used for both figures for comparison. (a) The results from OLSF. For data with photoblinking, the results of this method are generally less accurate than the results of MLE (2). In addition, the accuracy of OLSF decreases rapidly as the photoblinking level increases. (b) The results from MLE (2). This method is less influenced by photoblinking.

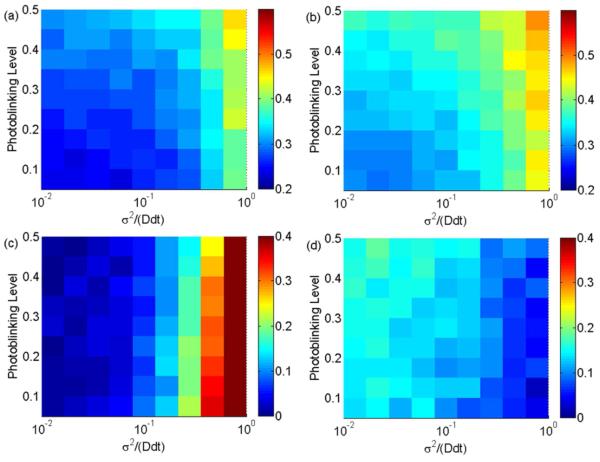
Results in Figure 3 show that when x = σ²/(Ddt) > 0.1, MLE (2) is unbiased; however, when x = σ²/(Ddt) < 0.1, MLE (2) is heavily biased. In this situation, it is better to use the biased MLE (1). Figures 3a and 3b illustrate that the RSD of MLE (1) is slightly lower than the RSD of MLE (2) for small noise levels. When x < 0.1, the former is about 0.1 smaller than the latter; when x > 0.1, their difference diminishes. Both RSDs increase as x and the photoblinking level increase. Figures 3c and 3d show that, for x < 0.1, the RMSD of MLE (1) is less biased than MLE (2). As seen in Figure 3c, the RMSD of MLE (1) increases as x increases because the bias of estimated diffusion coefficients is directly proportional to the uncertainties. Here, the influence of the photoblinking level is not obvious. Conversely, the RMSD of MLE (2) decreases as x increases (Figure 3d). When x < 0.1, the RMSD of MLE (2) is larger than 0.1while the RMSD of MLE (1) is negligible. This is because MLE (2) forces the diffusion coefficient and static localization uncertainty to be positive in value. As a result, the estimated diffusion coefficient is biased if the true diffusion coefficient is one order of magnitude smaller than the static localization uncertainty. This artifact causes MLE (2) to be biased when x < 0.1, as shown in Figures 3c and 3d.

Figure 3.

The RSD (top) and the RMSD (bottom) of MLE (1) (left) and MLE (2) (right) as they vary with reduced square localization error x and photoblinking level. The length of the simulated trajectories is 20. (a) The RSD of MLE (1). (b) The RSD of MLE (2). The same color scale is used in (a) and (b) for direct comparison. For x < 1, the RSD of MLE (1) is slightly smaller than the RSD of MLE (2) by about 0.1. (c) The RMSD of MLE (1). (d) The RMSD of MLE (2). The same color scale is used in (c) and (d) for direct comparison. For x < 0.1, the RMSD of MLE (1) is larger than 0.1 while the RMSD of MLE (2) is negligible; after x > 0.1, the RMSD of MLE (2) is negligible while the RMSD of MLE (1) increases rapidly.

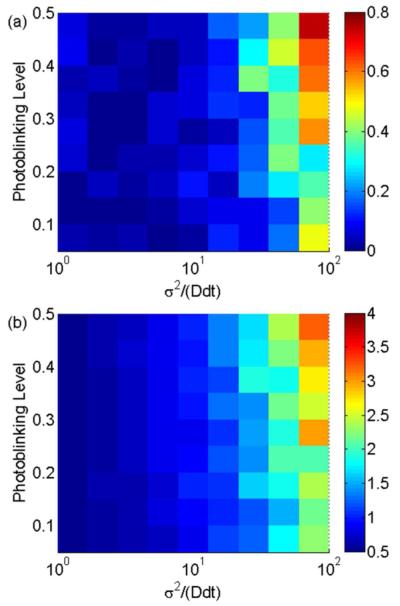
When x = σ²/(Ddt) > 10, the diffusion coefficient calculated by MLE (2) is highly biased, and no reliable conclusions about the diffusion coefficient can be made. Figures 4a and 4b demonstrate that the RMSD and the RSD of MLE (2) rapidly increase when x > 10. When x < 10, the RMSD of MLE (2) is negligible, and the RSD of MLE (2) increases slowly. When x > 10 (especially when x > 30), MLE (2) fails to accurately calculate the diffusion coefficient. In this case, the RMSD could be as large as the diffusion coefficient, and the RSD might be several times larger. This behavior occurs because D and σ² are not orthogonal in MLE (2),¹⁵ so the RSD of one influences the accuracy of the other. Therefore, for short trajectories, MLE (2) is unbiased only when D and σ² are different by less than one order of magnitude.

Figure 4.

The RMSD (a) and the RSD (b) of MLE (2) as they vary with reduced square localization error x and photoblinking level. The length of the simulated trajectories is 20. Both the RMSD and the RSD increase quickly with x for x > 10.

These results suggest how one should design experiments, analyze data, and make conclusions. Ideally, experiments should be designed in a way to minimize reduced square localization error x and extend the length of the trajectories. On average, the lifetime of a fluorescent molecule before it photobleaches into dark state is fixed in ambient conditions so that increasing the time lag between frames will increase the average displacement without changing the noise related to the uncertainty of the molecule’s location. However, identifying each molecule between frames becomes problematic when the time lag is significantly increased. If further experimental optimization is not an option, determination of the best analysis method becomes critical. Experimentally, noise can be estimated based on the pixel size, signal-to-background ratio of the point spread function (PSF), and the shot noise.^{16, 39, 40} For samples undergoing fast diffusion with an estimated noise at least one order of magnitude smaller than the average displacement, MLE (1), though biased, should be adopted to give an accurate estimation of the diffusion coefficient. A simple experimental example of the applicability of MLE (1) is shown in the Supporting Information. Alternatively, if the estimated noise is comparable with the average displacement, the unbiased MLE (2) should be used to give a strong estimation of the diffusion coefficient. However, if the noise is much larger than the averaged displacement, the positions of the molecules are extremely blurred. The calculated diffusion coefficient may therefore be several times or even several orders of magnitude different from the true diffusion coefficient, so no definite conclusions can be made.

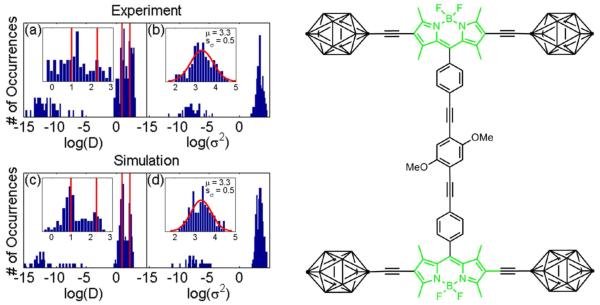
Although we have defined the optimal estimators for different cases in terms of noise level, recovering information from short trajectories with photoblinking is often not straightforward. As an example, we have analyzed experimental trajectories of single molecule diffusion. We selected single fluorescent molecules, which were designed to roll over a surface and have been termed nanocars.^{8, 28, 41, 42} The structure of the nanocar in this study is shown in Figure 5.⁴¹ Trajectories of single nanocars are typically short and possess photoblinking. An additional complication arises from the fact that no sample is 100% pure, and thus the observed single molecule fluorescence occurs from two sub-classes: those that are moving and presumed to be true ‘nanocars’, and those that are not moving and presumed to be either single fluorophores or nanocars with non-symmetrical wheel functionalization. Previous analysis^{41, 42} required the manual classification of ‘moving’ and ‘non-moving’ molecules, and separate transport analysis.

Figure 5.

Analysis of single nanocar diffusion. The chemical structure of the nanocar is shown on the right.⁴¹ (a), (b) The distribution of log(D) and log(σ²) obtained from experimental nanocar trajectories. The insets show the resulting distributions after removing trajectories that yield underestimated values in log(D) or log(σ²) due to statistical fluctuations. (c), (d) The distribution of log(D) and log(σ²) of 200 simulated trajectories. 30% of the simulated molecules undergo diffusion with D = 2×10² nm²/s, while the remaining molecules diffuse with D of 1×10 nm²/s. The insets show the resulting distributions after removing trajectories that yield underestimated values in log(D) or log(σ²). The red lines in (a) and (c) and their insets correspond to D = 1×10 nm²/s and D = 2×10² nm²/s. The red lines in the inserts of (b) and (d) represent a normal distribution with μ = 3.3 and s_σ = 0.5.

In the current analysis, nanocar trajectories including photoblinking events are compiled by searching for the absent molecules in frames following the photoblinking and connecting the pre- and post-photoblinking positions. The trajectory is terminated if no corresponding molecule can be clearly defined after the photoblinking event.⁸ The time lag between frames is 30 s. On average, a trajectory has 10 displacements and a photoblinking level of 0.1. More details of these experiments are discussed in References 8, 28, 41, and 42. The estimated x is larger than 1 in these experiments. Therefore, according to our algorithm for choosing the best analysis method, MLE (2) is more appropriate. MLE (1) results in an extremely biased distribution in D (not shown), but as mentioned earlier, MLE (1) is not appropriate for such noisy data. After directly applying MLE (2) to the trajectories, we obtain the distributions of log(D) and log(σ²) shown in Figures 5a and 5b, respectively. Notice that from the diagonal elements in Σ, 2Dn_kdt+2σ², the contributions of D and σ² are coupled. Because we are dealing with the statistics of short trajectories, under-sampling can result when the length of the trajectory is small, and the standard deviations of D and σ² are relatively large. These under-sampled values correspond to rare cases in which σ² is more than one order larger than Ddt, and yield values of D that are orders of magnitude smaller than expected for even a stationary analyte. These values do not imply anything about the corresponding analytes’ motion or lack thereof, but are instead due to insufficient temporal sampling. This has been verified by simulations shown in Figure 5c and 5d, which will be discussed in detail later. Hence, trajectories with estimated Ddt/σ² > 10⁴ and Ddt/σ² < 10⁴, which correspond to values for log(D) smaller than −5 (D < 10⁻⁵ nm²/s) in Figure 5a and values for log(σ²) smaller 0 (σ² < 1 nm²) in Figure 5b can and should be automatically excluded from MLE analysis. The resulting distributions of log(D) and log(σ²) are shown in the insets of Figures 5a and 5b. Because the underestimated values for either log(D) or log(σ²) have corresponding values that fall within the main distribution, these values also have to be removed as the entire trajectory is deleted from the set of data. Hence, the distributions in the insets do not simply present magnified views of the original distributions. The validity of this procedure is justified in more detail below.

The presence of two groups of nanocars becomes obvious after removing the biased log(D) values. Stationary nanocars with D of about 1×10 nm²/s and nanocars in motion with D of about 2×10² nm²/s can clearly be identified in the inset of Figure 5a (as also indicated by the red lines). The log(σ²) values now display a normal distribution with a mean value of μ = 3.3 and standard deviation of s_σ = 0.5. The mean value of σ² is ~3×10³ nm². The bimodal distribution of D agrees with the previous work, which distinguished the stationary nanocars from moving nanocars based on the displacement of the nanocars compared to the localization error of the PSF.^{41, 42} The diffusion coefficient (D = 2 × 10² nm²/s) estimated from MLE (2) and the analysis procedure demonstrated above also agree with the previously published result (D = 2.4 × 10² nm²/s), which used a squared-displacement analysis.^41,42 The small deviation between these calculated diffusion constants is likely due to the empirical criterion used before, which subjectively excludes some slow moving nanocars. Our analysis procedure presented here based on MLE (2) only rejects the trajectories that contain large statistical noise without requiring an a priori threshold regarding the minimum displacements of the nanocars. The advantage of the proposed method over the previous analysis is that our proposed method is statistically robust and objective in terms of a pre-selection for acceptable trajectories, in contrast to the manual selection procedure used in previous analysis.^{41, 42}

To verify our analysis procedure, we simulated 200 trajectories with parameters mirroring the nanocar experiments. 30% of the trajectories undergo diffusion with D = 2×10² nm²/s, while the remaining molecules diffuse with D = 1×10 nm²/s as indicated by the read lines in Figure 5c. The time lag dt is 30 s, and log(σ²) is a normal distribution with a mean of μ = 3.3 and a standard deviation of s_σ = 0.5. The length of each trajectory is randomly generated to fall within 5 to 15 steps, and each position has a 0.1 probability to be blank in order to mimic photoblinking. As seen in Figures 5c and 5d, the simulated distributions of log(D) and log(σ²) are very similar to those obtained from the experimental trajectories (5a and 5b), including values that are underestimated because of the added noise. If the noise is removed from the initially simulated trajectories, most of these values would be absent, which further justifies our procedure of removing them from the final distribution as they purely stem from statistical fluctuations. The resulting distributions after removal of these data points are shown in the insets of Figures 5c and 5d. The simulated distributions match those obtained from the experimental trajectories very well. The validity of our objective analysis approach is therefore justified, along with its advantages in terms of objectivity and convenience.

Conclusions

We have theoretically derived two maximum likelihood estimators, MLE (1) and MLE (2), to analyze short trajectories with photoblinking. We have shown that MLE (1) achieves nearly ideal accuracy in estimating D under small noise level (x < 0.1), and that MLE (2) is the best estimator we know for short trajectories with photoblinking in medium and large noise levels (x > 0.1). Their accuracies were compared to the theoretical limit without noise and OLSF with noise. By investigating experimental parameters such as length of trajectories, photoblinking level, signal-to-noise ratio, the most applicable analysis method can be determined based on the discussion in this work. Finally, we have applied these methods to experimentally acquired single-molecule trajectories with photoblinking and verified their validity via additional simulations.

In future work, more complicated systems with time variable localization uncertainty and time-dependent diffusion coefficients will be studied by including more information in the likelihood function and integrating local MSD analysis.⁴³ Recently, sub-diffusion in biological systems has been frequently observed and studied,^{30, 44, 45} but the associated physical mechanisms are still not well characterized. However, sub-diffusion can be described by continuous time random walk at short time-scale and modeled by fractional Brownian motion at long time-scale.⁴⁵ Since Brownian motion is a special case of fractional Brownian motion, we are investigating extending this likelihood function to study sub-diffusion.