Possibility of Atherosclerosis in an Arterial Bifurcation Model

Abstract

Introduction

Arterial bifurcations are susceptible locations for formation of atherosclerotic plaques. In the present study, steady blood flow is investigated in a bifurcation model with a non-planar branch.

Methods

The influence of different bifurcation angles and non-planar branch is demonstrated on wall shear stress (WSS) distribution using three-dimensional Navier–Stokes equations.

Results

The WSS values are low in two locations at the top and bottom walls of the mother vessels just before the bifurcation, especially for higher bifurcation angles. These regions approach the apex of bifurcation with decreasing the bifurcation angle. The WSS magnitudes approach near to zero at the outer side of bifurcation plane and these locations are separation-prone. By increasing the bifurcation angle, the minimum WSS decreases at the outer side of bifurcation plane but low WSS region squeezes. WSS peaks exist on the inner side of bifurcation plane near the entry section of daughter vessels and these initial peaks drop as bifurcation angle is increased.

Conclusion

It is concluded that the non-planarity of the daughter vessel lowers the minimum WSS at the outer side of bifurcation and increases the maximum WSS at the inner side. So it seems that the formation of atherosclerotic plaques at bifurcation region in direction of non-planar daughter vessel is more risky.

Introduction

Atherosclerosis is a disease of the arteries characterized by the deposition of plaques of fatty material on their inner walls and usually occurs at bifurcation, branching regions and high curvature of vessels. Cholesterol is a component of blood plasma which is transferred from one point to another in the form of solid particles as they are not soluble in blood. The collection of cholesterol components with calcium and some proteins are of high possibility in the places where shear stress is low or a circulatory flow exists (Delfino et al. 1997). There are three risk factors for the development of the atherosclerotic plaques which include low shear stress region, high vessel pressure distribution, and high particle residence time in the region of the atherosclerosis (Araim et al. 2005, Wang et al. 2002).

Recently, researchers have performed a lot of work on blood flow in order to disclose the reason of the atherosclerosis theoretically (Sarkar et al. 1998) and experimentally (Zhao et al. 2000, Ding et al. 2001). Caro et al. (1996) and Lu et al. (2002) investigated the effect of non-planarity of the vessel on flow parameters and wall shear stresses in steady state condition. Chakravarty and Sen (2006) simulated two-dimensional unsteady flow in blocked bifurcations. Chen and Lu (2004, 2006) investigated numerically the non-Newtonian blood in steady and pulsatile condition through a three-dimensional model for a bifurcation with non-planar branch. Gijsen et al. (1999, 1999) modeled blood flow by finite element method in a carotid bifurcation after a laboratory study. They compared Newtonian and non-Newtonian treatment and showed that non-Newtonian model agrees more by the experimental results. Stroud et al. (2002) simulated steady blood flow in a bifurcation in the presence of a blockage at different Reynolds numbers. They used two turbulent models in blocked place to simulate caused vortices. Van de Vosse et al. showed the axial velocity changes under the effect of secondary flow in an uneven vessel (Van de Vosse et al. 1989, Bovendeerd et al. 1987). Results of Hofer et al. (1996), Liu (2007), Santamarina et al. (1998), Weydahl and Moore (2001), Lee et al. (2001), Lu et al. (2002), Shipkowitz et al. (1998) depicted that the circulation and secondary flow in complex geometries and multi-branch increase the possible onset and enhancement stenosis because of their effect on velocity profiles and wall shear stresses.

In this study, the chance of blockage is compared at different bifurcation angles under steady-state conditions and the influence of non-planar branch is demonstrated on shear stress distribution at bifurcation region using three-dimensional Navier–Stokes equations.

Problem formulation

Geometric model

In this paper, the model of Lu et al. (Lu et al. 2002, Chen and Lu, 2004, 2006) for bifurcation with a non-planar branch is studied. In this model, all the vessels are of the same diameter D, where mother vessel’s length is 3D before bifurcation. The mother vessel is divided into daughter vessels in bifurcation place. In main model, there are two daughter vessels of 90˚ angle toward each other which is changed into 60˚ and 75˚ to consider the effect of bifurcation angle on flow properties. One daughter vessel is straight planar 1.5D along the axial and then undergoes 45˚ bending with a radius of 4D before it straightens up for a further length of 4D. This complex includes non-planar branch. The other daughter vessel is straight with a length of 8D after bifurcation. This bifurcation model is shown in Fig. 1.

Fig. 1.

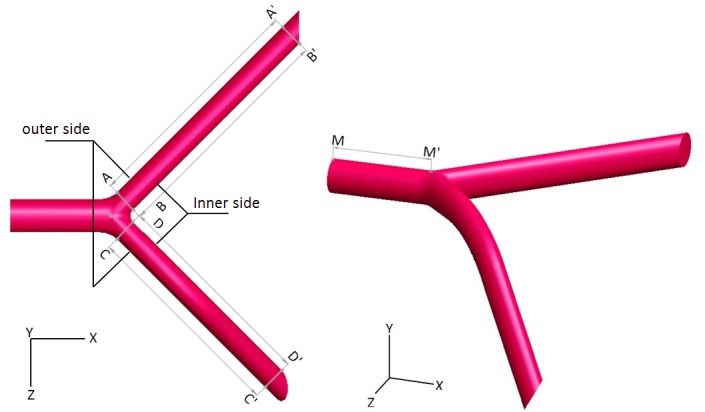
Bifurcation model with planar and non-planar branches.

Governing equations

Considering blood as incompressible and Newtonian fluid, the Navier–Stokes equations are expressed as follows:

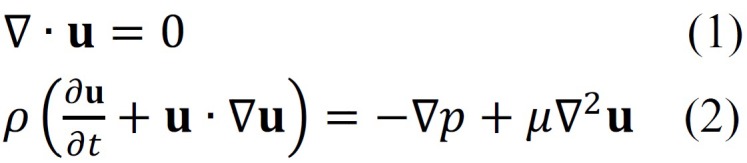
Where U denotes velocity vector, r density, p pressure, and µ dynamic viscosity.

Boundary conditions

At the inlet of the mother vessel, Womersley velocity profiles are imposed with average velocity of 0.2 m/s (Re=360). The blood density was taken 1050kg/m³ and viscosity 0.0035 Pa/s (Liu 2007).

A constant pressure and a zero axial velocity gradient are used at the exit of each daughter vessel. The no-slip boundary condition is used at the rigid vessel wall. The governing equations are solved by using a finite element method based on the fractional-step velocity correction (Lu et al. 2002, Chen and Lu 2004, 2006, Kovacs and Kawahara 1991).

The Galerkin weighted residual method (Kovacs and Kawahara 1991) is used for spatial discretization of the finite element. The computational domains are subdivided in to non-uniformly grid of 262544, 276520 and 286469 quadratic tetrahedral elements for 90˚, 75˚ and 60˚ bifurcation angle models, respectively. The grids are much denser in the near wall areas where detailed flow parameters are important and high variable gradients are expected.

Numerical results

The presentation of results concentrates on the wall shear stress (WSS) distributions along generating lines on vessels (Fig. 1.) for three bifurcation angles and is shown in Fig. 2. In all the cases, horizontal axis indicates the position on generating lines with respect to the exit of the mother vessel at the point of bifurcation. The negative values on horizontal axis show the positions of generating lines on mother vessel.

Fig. 2.

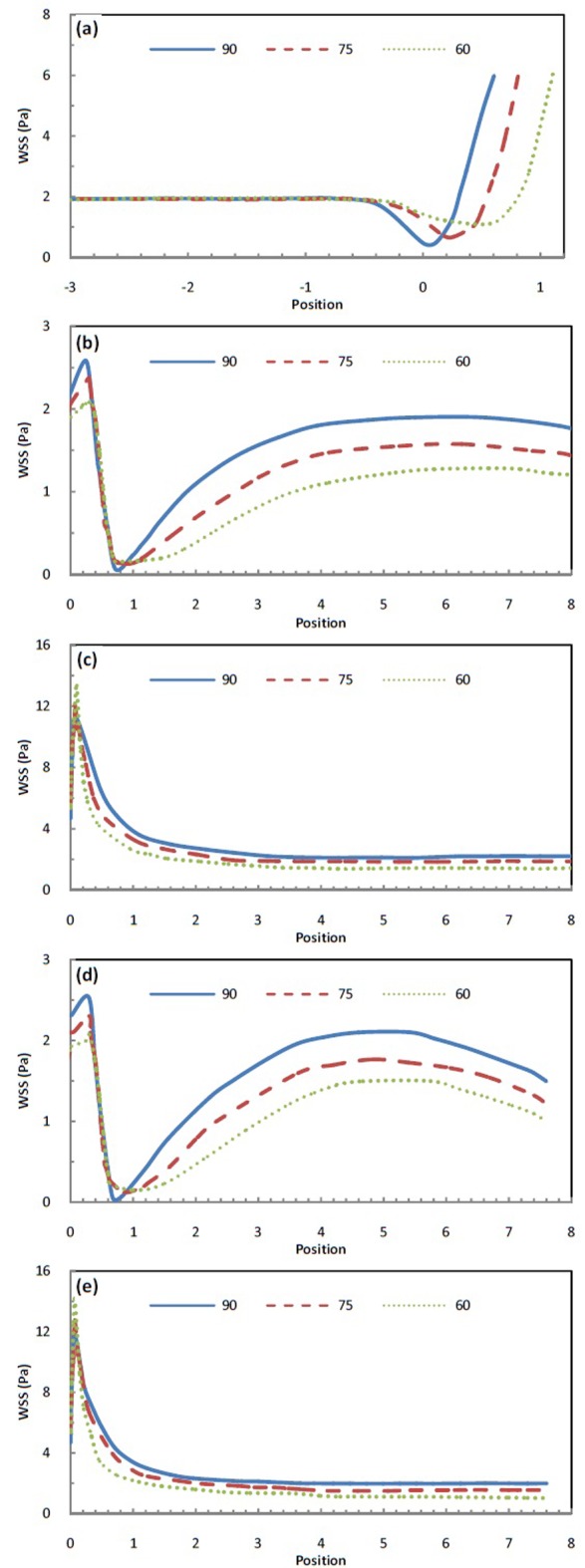
Fig. 2. Distributions of WSS along generating lines on the vessels for three bifurcation angles: a) M-M’; b) A-A’; c) B-B’; d) C-C’; e) D-D’.

The comparison of the results illustrates the influences of the bifurcation angle and non-planar daughter vessel on WSS distributions on vessels. As shown in Fig. 2 (a), WSS decreases at bifurcation region along line M-M’. The decrease is more remarkable for 90˚ bifurcation angle. Also, this decrease of WSS for the case of 60˚ bifurcation angle happens closer to the apex of bifurcation comparing to the other cases.

At the outer side of the bifurcation plane, along lines A-A’ and C-C’ in Fig. 2(b,d), WSSs decrease considerably. Increasing bifurcation angle, position of the minimum WSS along lines A-A’ and C-C’ comes closer to the entry section of daughter vessels. After these drops, the WSSs increase specially for lager bifurcation angles and become stable. Comparison of the minimum WSSs along planar and non-planar branches for different cases, summarized in Table 1, illustrates that the case with 90˚ bifurcation angle has the least amongst the others and the minimum values along non-planar branch are lower than those along planar one for all the models.

Table 1. The minimum and maximum values of WSS on vessels for three bifurcation angles at Re=360 .

זmax (Pa)	זmin (Pa)	Bifurcation angle
Non-planar branch	Planar branch	Non-planar branch	Planar branch
14.2178	13.3405	0.1475	0.1543	60˚
12.7634	12.1564	0.1212	0.1293	75˚
11.9835	11.2391	0.0454	0.0624	90˚

At the inner side of the bifurcation plane, along lines B-B’ and D-D’ in Fig. 2 (c, e), immediately after the stagnation region at apex of bifurcation, WSS increases considerably up to maximum values. But, this initial peak drops faster for lower bifurcation angles, as we move away from the bifurcation region, resulting in higher values of WSS at higher bifurcation angle. By comparing the maximum values of WSS along planar and non-planar branches listed in Table 1 for three bifurcation angles, it is concluded that the WSS peak for the case of 60˚ bifurcation angle is larger than that of the others and the maximum values along non-planar branch are higher than those along planar one for all the models.

Conclusion

The risk for atherosclerotic disease is related to the WSS on vessels wall and it has believed that the atherosclerotic plaques form in the regions of low WSS. Bifurcation regions are susceptible locations to the development of intimal thickenings. In this study, three bifurcation models with a non-planar daughter vessel were analyzed numerically and WSS distributions along generating lines were illustrated for different bifurcation models.

The WSS values are low in two locations at the top and bottom walls of the mother vessel just before the bifurcation. These regions approach to the apex of bifurcation with decreasing the bifurcation angle. This is due to the existence of the stagnation regions of dividing surface and is more considerable for high bifurcation angles. The WSS magnitudes approach near to zero at the outer side of bifurcation plane, vicinity of points A and C, especially for higher bifurcation angles and these locations are separation-prone. By increasing the bifurcation angle, low WSS region squeezes and the location of minimum WSS approaches to the entry section of bifurcation. Therefore, it is not possible to clearly conclude that which bifurcation angles favor the development of atherosclerotic lesions. WSS peaks exist on the inner side of bifurcation plane near the entry section of daughter vessels and these peaks drop as bifurcation angle increases. It is understood (achieved) that the non-planarity of the daughter vessel has an important influence on the WSS profiles at bifurcation region; it lowers the minimum WSS at the outer side of bifurcation and increases the maximum WSS at inner side. This is due to the fact that the non-planarity in the daughter vessel swerves the flow from the outer side to the inner side of the bifurcation at the side of non-planar branch. So, it seems that the formation of a separation region and atherosclerotic plaques at the outer side of bifurcation plane is more risky at the side of non-planar daughter vessel.

Ethical Issues

None to be declared.

Conflict of interests

The authors declare no conflict of interests.