Recursive Feature Elimination for Brain Tumor Classification using Desorption Electrospray Ionization Mass Spectrometry Imaging

Abstract

The metabolism and composition of lipids is of increasing interest for understanding and detecting disease processes. Lipid signatures of tumor type and grade have been demonstrated using magnetic resonance spectroscopy. Clinical management and ultimate prognosis of brain tumors depend largely on the tumor type, subtype, and grade. Mass spectrometry, a well-known analytical technique used to identify molecules in a given sample based on their mass, can significantly improve the problem of tumor type classification. This work focuses on the problem of identifying lipid features to use as input for classification. Feature selection could result in improvements in classifier performance, discovery of biomarkers, improved data interpretation, and patient treatment.

I. Introduction

There are approximately 21,000 new cases of brain and spinal cancer diagnosed in the United States each year, and the overall five-year survival rate is estimated to be 34% [1]. For some types of brain cancer, however, the median survival is less than two years [2], [3]. Clinical management and ultimate prognosis depend largely on the tumor type, subtype, and grade as evaluated by magnetic resonance imaging (MRI) and tissue histopathology when available. Biopsied or resected tumor tissue is classified based on the type or subtype of progenitor cells promoting neoplastic growth, and into risk grades II, III, and IV, based on characteristic features of malignant proliferation [4], [5]. In this work we focus on the subtypes astrocytoma and oligodendroglioma which present morphological features of respectively astrocytes and oligodendrocytes of the glial cell family in the brain. The survival profile of these subtypes varies greatly, with astrocytoma presenting a higher risk of malignancy as compared to oligodendrogliomas [1], thus differentiation between these subtypes is of significance to both direct patient care and research to improve treatments.

The metabolism and composition of lipids is of increasing interest for understanding and detecting disease processes [6]. Lipid signatures of tumor type and grade have been demonstrated using magnetic resonance spectroscopy [7], [8]. In many gliomas, the phosphatidylinositol lipid pathway is an important factor in cell growth due to mutation-driven increases in the PI3 kinase enzyme activity, which impedes normal apoptosis - mechanism of cell death.

Mass spectrometry (MS) is a well-known analytical technique used to identify molecules in a given sample based on their mass. The analysis of the sample involves two main steps: i) ionization, and ii) mass analysis. There are a number of different ionization techniques, including matrix-assisted laser desorption ionization (MALDI), and more recently, desorption electrospray ionization (DESI). In MALDI-MS, the sample is coated with a matrix, a light-absorbing organic acid with low molecular weight. The ionization mechanism in MALDI involves shooting an ultraviolet or infrared laser beam to the compound. The matrix enhances the desorption and ionization by absorbing the energy from the laser and producing charged molecules, which in turn are analyzed by the mass analyzer. The output of the mass spectrometer is a spectrum indicating the mass-to-charge ratio (m/z) of the molecule on the x-axis and its associated detected relative abundance on the y-axis.

While MALDI-MS is capable of identifying molecules with higher m/z values, the sample preparation limits its translation to “real-time” application. In DESI-MS, the ionization involves targeting the sample with a stream of charged solvent droplets. The analyte (i.e., the sample to be analyzed) molecules are taken up by the charged solvent and are analyzed by the mass analyzer. DESI-MS is used to analyze molecules with lower weights including lipids. However, unlike MALDI-MS, where the desorption and ionization are performed in the vacuum and involves sample preparation, in DESI-MS the surface ions are produced in ambient conditions requiring no sample preparation. This property of DESI-MS could be extremely useful in clinical applications, specifically during surgery, where it is critical to analyze samples for specific biomarkers (e.g., possible traces of cancer). In [9], authors discuss the application of DESI-MS for intraoperative analysis of tumors for neurosurgery.

In mass spectrometry imaging, the sample is moved in the x-y plane in the ionization source, and hence, can analyze specific regions in the sample referred to as pixels. Note that each pixel from the sample corresponds to a spectrum indicating the relative abundance of different molecules in the region defined by the pixel. In contrast to profiling molecular distribution of tissue extracts, in mass spectrometry imaging the morphological features in the tissue is preserved allowing for visual comparison between the chemical composition of the tissue and the heterogeneity and the infiltration levels within the tissue.

Mass spectrometry and machine-learning have been used for assessment of cancers from other organs as well as brain cancer. Ovarian cancer was correctly predicted from serum samples analyzed with MS using classifiers based on peak-probability and support vector machines [10], [11]. Prostate samples have also been distinguished by similar techniques [12]. In our previous work, we have used matrix assisted laser desorption ionization MS (MALDI-MS) to classify progression of meningioma [13]. With a similar approach, post-operative DESI-MS analysis showed utility to discriminate gliomas along several axes of the histopathological criteria used to assess tumor severity, namely type and grade [14], [15].

This work focuses on the problem of identifying lipid features to use as input for classification. Specifically, we consider the feature selection problem for the classification of astrocytoma and oligodendroglioma samples using their mass spectrum. Feature selection could result in improvements in classifier performance as well as in discovery of biomarkers and improved interpretation of biological data. In the case of tumor subtype classification, biomarker discovery allows for an improved diagnosis and treatment.

II. Classification and Feature Selection

In this section, we briefly review the support vector machine (SVM) algorithm and a feature selection framework which is closely related to SVM.

A. Support Vector Machine Algorithm

The support vector machine algorithm [16] is a sparse kernel algorithm used in classification and regression problems. Here, we will briefly discuss the SVM framework for the two-class classification problem. Let the training set be given by x₁, x₂, … , x_N, with target values given by z₁, z₂, … , z_N, respectively, where $x_n\in {\mathbb{R}}^D$ and z_n ∈ {−1, 1}, n = 1, 2, … , N. Moreover, assume that this training set is linearly separable in a feature space ${\mathbb{R}}^M$ defined by the transformation $\varphi :{\mathbb{R}}^D\to {\mathbb{R}}^M$; that is, there exists a linear decision boundary in the feature space separating the two classes.

To classify a new data point $x\in {\mathbb{R}}^D$ by predicting its target value z define

$$y\left(x\right)\triangleq w^{\mathrm{T}}\varphi \left(x\right)+b,$$ (1)

where $w\in {\mathbb{R}}^M$ is a weight vector and $b\in \mathbb{R}$ is a bias parameter. This representation can be rewritten in terms of a kernel function as $y\left(x\right)={\sum }_{n=1}^N{a}_n{z}_{n}k(x,x_n)+b$, where a_n, n = 1, 2, … , N, and b are parameters determined by the training set x_n and z_n, n = 1, 2, … , N, and k(·, ·) is the kernel function. The sign of the function y(x) determines the class of x. More specifically, for a new data point x, the target value is given by z = sgn(y(x)), where sgn $y\triangleq \frac{y}{\mid y\mid }$, y ≠ 0, and sgn(0) ≜ 0. In the SVM approach the parameters w and b are chosen such that the margin, that is, the minimum distance between the decision boundary and the data points, is maximized. Hence, only a subset of the training data (i.e., support vectors) is used to determine the decision boundary. It can be shown that the solution to the SVM problem results in a convex optimization problem, and hence, a global optimum is guaranteed.

In the case where there is an overlap between the two data classes, the SVM algorithm can be modified by allowing misclassification of data points. In this case the margin is maximized while penalizing misclassified points. Such a trade-off is controlled by a positive complexity parameter C, which is determined using a hold-out method such as cross-validation [16].

B. Recursive Feature Elimination

In this section, we briefly review a feature selection algorithm referred to as recursive feature elimination (RFE) which is based on the SVM algorithm. Although the RFE framework can be applied to SVM with a nonlinear kernel [17], here, we consider the SVM algorithm with a linear kernel.

As discussed above, each data point x resides in a high dimensional feature space ${\mathbb{R}}^D$, D ⪢ 1. However, in studying biological data one observes a high degree of correlation among the components of x. In addition, x could contain components that do not contribute to the classification problem and can be regarded as noise (i.e., uninformative features). Hence, it is desirable to select a subset of components in ${\mathbb{R}}^D$ and exclusively use them for data classification. The process of selecting a subset of components in the feature space is referred to as feature selection. Feature selection could result in improvements in classifier performance as well as in discovery of biomarkers and improved data interpretation for biological data. In the case of tumor subtype classification, biomarker discovery allows for an improved diagnosis and treatment.

The feature selection problem for high dimensional data is challenging. Using an exhaustive search method to identify the optimal set of features subject to some model selection criterion is computationally infeasible for high dimensional feature spaces. In a framework proposed in [17], SVM is used for feature selection by iteratively removing features (i.e., components in the feature space) that are least informative for classification. Specifically, let w = [w₁, … , w_D]^T denote the weight vector in (1) identified by training the SVM on the training set as discussed in Section II-A. In the RFE framework, we define the feature index set ${\mathcal{S}}_1\triangleq \{1,\cdots ,D\}$, identify components which play the “weakest” role in the SVM classification and recursively eliminate features and the corresponding components in the feature space from the data. Specifically, in iteration k, the component $i_k\triangleq {\mathrm{argmin}}_{i\in {\mathcal{S}}_k}{w}_i^2$ is eliminated from the feature space, where ${\mathcal{S}}_k$ is the feature index set in iteration k. In the next iteration, the SVM algorithm is re-trained on the modified training set and the process described above is repeated. This process can be repeated until all features in the feature space are eliminated or some termination criterion is met. See [17] for a detailed discussion.

III. Feature Selection using the Recursive Feature Elimination Framework

In this section, we apply the RFE framework discussed in Section II-B to the problem of classification of two glioma subtypes, namely, astrocytoma and oligodendroglioma. The data were collected from research subjects under approved local Institutional Review Board protocol at the Brigham and Women’s Hospital, Boston, MA. In this study, 29 glioma samples were acquired from multiple research subjects, with samples of astrocytomas and oligodendrogliomas and from different grades between II to IV. Here, the term “sample” refers to one piece of resected tissue and all the spectra acquired from it.

A. Preprocessing of DESI Mass Spectra

Each spectrum contains numerous peaks each corresponding to a specific molecule or a set of molecules. However, before using the spectra to classify tumor samples into two different subtypes, preprocessing steps are necessary. First, each spectrum is denoised using the undecimated wavelet transform (UDWT). Then, the baseline artifact is estimated and removed in the denoised signal [18].

Next, in the normalization step, individual spectra are rescaled such that the area under the curve (also referred to as total ion current) for all spectra correspond to some fixed constant value. In the peak detection stage, peaks are identified by locating local maxima in the denoised and normalized spectra. The peaks indicate the presence of a molecule or a fraction of the molecule in the region of the sample corresponding to the spectrum, where its identity can be determined by the m/z ratio. We used MATLAB Bioinformatic Toolbox for preprocessing of spectra. See [18-20] for a detailed discussion.

B. Peak Matching

Next, we discuss a feature extraction framework for mass spectrometry data which is also referred to as peak matching or binning. As discussed earlier, the m/z ratio of each detected peak in a spectrum indicates the presence of a molecule or a fraction of a molecule in the region of the sample corresponding to the spectrum. However, the fact that the mass spectrometer introduces a measurement error m_error introduces small shifts in the location of the peaks in different spectra. As a result, prior to any form of analysis involving a set of spectra, the peaks in different spectra corresponding to the same molecule (with the same m/z value) need to be matched.

In a standard technique in mass spectrometry data analysis, the entire range of m/z ratios is partitioned into a set of “bins” (each defined by an interval), where each bin is associated with a unique molecule (or a fraction of a molecule) with a given m/z ratio. Once the bins are identified, each spectrum is revisited, and based on the m/z ratio of each individual peak, the peak is assigned to one of the bins. Peaks corresponding to the same bin are assumed to be associated with the same molecule [18], [21]. This procedure can be regarded as a feature extraction technique, where the bins serve as features allowing peaks across different spectra to be analyzed.

Here, we follow the mass clustering framework introduced in [21] to identify the bins of variable size. The mass clustering framework in [21], which is essentially a variation of the centroid linkage hierarchical clustering algorithm [22], considers each bin as a cluster of points, that is, a set of m/z ratios. The algorithm starts by considering singleton clusters (each m/z ratio is a cluster). Next, in each iteration, new clusters are formed by merging clusters with minimum inter-cluster distance. See [22] for a detailed discussion. Note that contrary to the distance function given in [21], where the measurement error is a function of the measured mass, we use an absolute measure of distance to define the mass distance function. This is due to the fact that the mass analyzer used in this study has a measurement error approximated to be constant for the m/z range between 200.08 and 1000.

C. Identified Features

Next, we apply the RFE framework presented in Section II-B to the classification problem involving two glioma subtypes, namely, astrocytoma and oligodendroglioma. Here, we perform feature selection and concurrently evaluate the classifier’s performance. In order to assess the performance of the SVM classifier, a k-fold cross-validation method is used [22]. Specifically, the collection of all available samples is partition into k subsets. The SVM classifier is trained on k − 1 subsets and tested on the remaining subset. This process is repeated k times so that the classifier is tested on all available partitions. In each run of cross-validation, the RFE is applied to the training set.

For the mass spectrometry data set a total of 821 bins of size less than 1 m/z were identified, that is, each spectrum resides in a 821-dimensional space. The average accuracy for the classification of astrocytoma and oligodendroglioma mass spectrometry samples using an SVM classifier with a linear kernel is given in Figure 1, where we used a 4-fold cross-validation. We notice in Figure 1 that the classifier performance starts degrading at iteration 680 of the RFE framework. Note that the set of selected features by the RFE framework is not necessarily the same in each run of cross-validation. The set of features retained by the RFE framework in iteration 680 for all 4 cross-validation runs was chosen for further analysis.

Fig. 1.

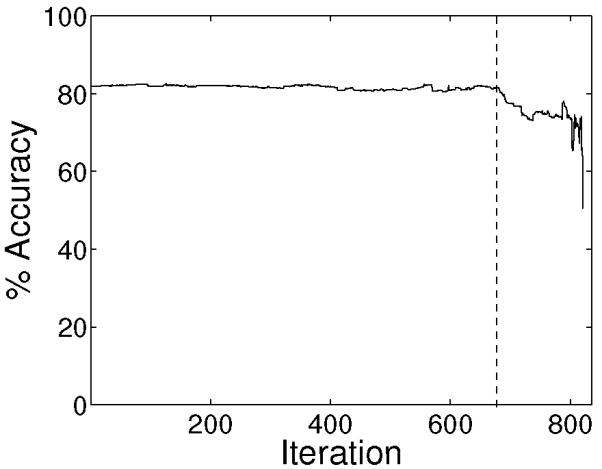
Average classification accuracy of the SVM classifier.

In order to identify significant features, a histogram of the selected features (i.e., m/z values) for all 4 runs of cross-validation is computed. The histogram is given in Figure 2 and a list of m/z values which have appeared at least 3 times (out of 4 possible appearances) is given in Table II.

Fig. 2.

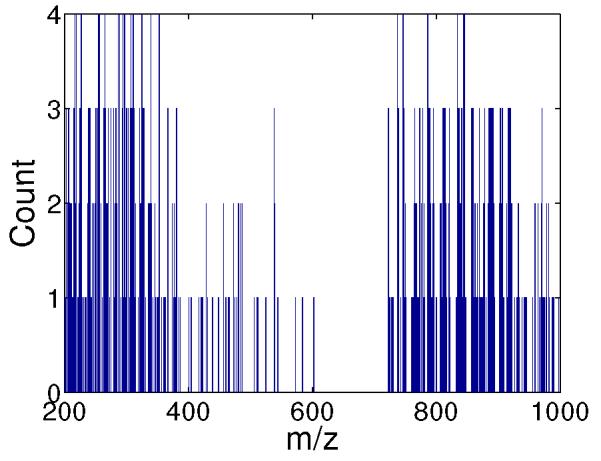
Histogram of the selected features identified by the RFE framework.

TABLE II. Selected m/z values identified by the RFE framework.

203	264.1	303.2	381.1	778.3	814.3	869.7	892.7
207.1	266.3	306.3	538.6	787.3	821.4	878.7	903.7
215.3	271.1	309.3	722.7	788.5	835.3	885.6	906.7
225.2	275.1	312.5	723.7	789.5	836.7	886.6	907.7
239.2	279.3	321.2	738.7	790.4	837.6	887.7	916.7
241.3	283.4	326.3	739.7	795.3	840.7	888.7	917.7
251.1	293.3	327.3	748.7	810.4	841.7	889.7	918.7
253.4	300.1	328.3	765.7	812.5	857.7	890.7	920.7
263.1	301.1	367.1	773.6	813.3	859.7	891.7	970.7

D. Discussion

In this section, we underline the significance of the features selected in the classification problem involving astrocytomas and oligodendrogliomas from a biochemical perspective. Under the experimental DESI mass spectrometry conditions used for tissue analysis, the majority of the molecules extracted and detected constituted of free fatty acids, corresponding dimers, and lipids. In previous work, we identified some lipids that discriminated astrocytoma grades by qualitative assessment of imaging spectra, but the approach was limited for the assessment of glioma subtype [14]. The general observation was that sulfatides appeared to have discrimination power as they were typically observed from astrocytomas and absent in oligodendriogliomas, but their absence from astrocytomas grade IV prevented us from drawing such conclusions.

In a follow-up study [15], we observed that the lipid profile of a grade III astrocytoma contains lipid species of all glycerophosphoserines (PS), glycerophosphoinositols (PI), and sulfatides (ST) classes, whereas the grade III oligodendroglioma shows a distinct profile of lipid species with PS(40:4) m/z 838.3, and PI(38:4) m/z 885.5 present at much higher relative abundances than observed in the pure astrocytoma. Using a combination of in-house programs and commercial software solution (ClinProTools), we were able to classify subtypes of gliomas using SVM, but have found considerable limitations in data pre-processing workflow and feature selection. The approach presented in this paper provides a solution to this problem by providing a framework to systematically select relevant features for classification.

TABLE I. Recursive Feature Elimination.