Automated, Foot-Bone Registration Using Subdivision-Embedded Atlases for Spatial Mapping of Bone Mineral Density

Abstract

We present an atlas-based registration method for bones segmented from quantitative computed tomography (QCT) scans, with the goal of mapping their interior bone mineral densities (BMDs) volumetrically. We introduce a new type of deformable atlas, called subdivision-embedded atlas, which consists of a control grid represented as a tetrahedral subdivision mesh and a template bone surface embedded within the grid. Compared to a typical lattice-based deformation grid, the subdivision control grid possesses a relatively small degree of freedom tailored to the shape of the bone, which allows efficient fitting onto subjects. Compared with previous subdivision atlases, the novelty of our atlas lies in the addition of the embedded template surface, which further increases the accuracy of the fitting. Using this new atlas representation, we developed an efficient and fully automated pipeline for registering atlases of 12 tarsal and metatarsal bones to a segmented QCT scan of a human foot. Our evaluation shows that the mapping of BMD enabled by the registration is consistent for bones in repeated scans, and the regional BMD automatically computed from the mapping is not significantly different from expert annotations. The results suggest that our improved subdivision-based registration method is a reliable, efficient way to replace manual labor for measuring regional BMD in foot bones in QCT scans.

Background

Bone mineral density (BMD), measured as the amount of calcium hydroxyapatite per unit volume, is an important indicator of bone health [1]. The three-dimensional (3D) BMD within a bone can be captured using quantitative computed tomography (QCT), which offers per-voxel BMD measures [2]. Comparing the BMD over localized regions (e.g., region of the bone near the joint) between scans at different time points or from different individuals can potentially provide clinically valuable information. For example, a drop in BMD in a bone region over time may predict future fractures within that region [3]. Also, within a specific region, differences in BMD between a patient and a healthy individual may be indicative of disease.

The key to performing such spatial comparison is establishing a mapping between the interior (i.e., 3D space bounded by the surface) of two bones in QCT scans. While there are tools that can accurately segment individual bones in QCT images [4], obtaining interior mapping between bones is challenging for two reasons. First, the shape of the bone can change over time and (more drastically) varies among different subjects in a non-rigid manner, and currently there is no known physical model for bone shape variation. Second, the BMD can change regionally within a bone over time, and such changes may or may not correspond to the change of the anatomical shape. In other words, BMD computed from QCT scans cannot be used as a guide for computing the spatial mapping of bone interiors.

There is a rich literature on non-rigid registration methods (see for example extensive surveys in citations [5–7]). These methods typically compute over the source image a displacement field that achieves some fitting objective while minimizing some energy formulation. When BMDs, which are computed from Hounsfield Units and displayed as image intensities, in source and target images are well-correlated, an intensity-based metric such as mutual information [8] can be used as the fitting objective. However, as discussed above, such metrics are not suitable for registering bones in QCT scans. Since the segmented bone surfaces can be easily obtained [4], we choose the fitting objective as the Euclidean distance between the registered source and target surfaces [9]. For warping anatomical structures, a variety of energy formulations have been proposed, such as thin-plate splines [10], elasticity [11], strain energy [12], fluid dynamics [13], and diffusion energy [14]. In this work, we adopt a linear energy formulation that is similar to thin-plate splines and penalizes locally non-affine transformations [15].

The computation of the displacement field is determined largely by the way in which the field is represented. While the displacement can be computed for each and every voxel in the source image, the computational cost of such computation is high due to the extremely large number of degrees of freedom. A much more efficient choice is to compute the displacements only at the grid points of a sparse lattice, and obtain the displacement at an individual voxel by blending the displacements at the lattice points, for example using B-spline basis functions [16]. While the lattice-based approach has a drastically reduced number of degrees of freedom, the volumetric lattice in practice still needs hundreds or even thousands of grid points to capture the deformation of a flexible anatomical structure (e.g., a lattice with 10 points in each dimension has 1,000 grid points). More recently, subdivision meshes [17] have emerged as an even more efficient way to represent the displacement field. Unlike volumetric lattices that are limited by a regular Cartesian structure, the control grid of a subdivision atlas can assume arbitrary topology, allowing the warping to be captured with a small number (typically several tens) of control points. To use subdivision meshes in registering anatomical images, an atlas is constructed from a reference anatomical structure and is subsequently registered onto target images. The subdivision atlases have been used in registering both 2D [18] and 3D [15, 19] biomedical images.

An inherent drawback of existing subdivision atlases is that they are limited to anatomical structures with a smooth, “blobby” boundary. Representing shapes with rich boundary details (e.g., foot bones) using subdivision atlases can result in larger errors in fitting the target boundary. This is due to the lack of geometric details on the atlas, and not due to the lack of flexibility in the deformation control. In this paper, we present an improved atlas representation, called subdivision-embedded atlases, which inherits the compact structure of previous subdivision atlases but is capable of accurately capturing the geometry of anatomical shapes with rich boundary features.

Using the new atlas representation, we created atlases for all 12 tarsal and metatarsal human foot bones, whose BMD measures are important for assessing the bone-related impairments due to diabetes mellitus and peripheral neuropathy [19]. We designed an efficient and fully automatic pipeline for registering all 12 bones in a segmented QCT scan to their respective atlases, which allows spatial mapping of BMD between the interior of these bones from different subjects and scanned at different time points. To the best of our knowledge, this is the first unsupervised method for registering all mid- and hind- foot bones from segmented QCT scans.

The efficiency and accuracy of our method is evaluated using a suite of segmented QCT scans. Registering all 12 bone atlases finished within minutes for each scan. The evaluation shows that registering the atlases in our improved representation gives lower error in fitting the boundary surface of a target bone than registering the previous subdivision atlases. We also showed that our spatial BMD mapping is consistent for bones in repeated scans and agrees with manual measurements by experts over user-specified volumes-of-interest (VOIs).

Methods

Atlas Representation

Subdivision Atlases

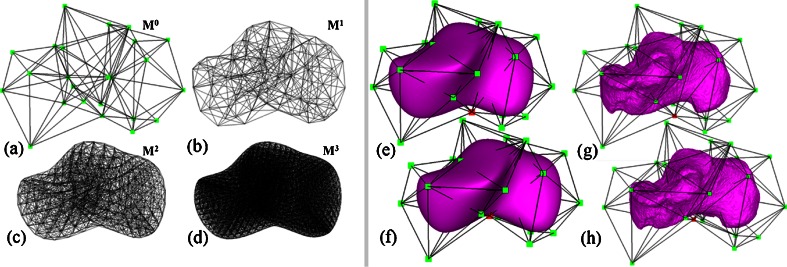
Subdivision is a modeling technique widely used in geometric design [20]. Starting from a coarse initial mesh M⁰ consisting of polygonal or polyhedral cells, subdivision generates a sequence of smoother meshes with finer cells M¹, M², M³… that approach some limit shape M^∞. Various subdivision algorithms have been proposed for different kinds of meshes. For modeling anatomical structures in 3D, we consider the tetrahedral subdivision scheme of Schaeffer et al. [21]. Given an initial mesh consisting of tetrahedral cells of arbitrary topology (Fig. 1a), this algorithm yields smoothly subdivided meshes M^k consisting of both tetrahedral and octahedral cells (Fig. 1b–d).

Fig. 1.

Left A tetrahedral subdivision mesh after 0, 1, 2, and 3 iterations of subdivision (a–d). Right: the subdivision atlas of the calcaneus (e) consisting solely of a subdivision mesh, the subdivision-embedded atlas (g) consisting of a subdivision mesh and a template surface (purple), and the deformed atlases (f, h) after dislocating a single vertex (red) in the coarse subdivision mesh

Subdivision has been applied for deformable registration of anatomical structures (see the review by Ju et al. [15]). In these methods, an atlas of an anatomical structure is constructed as some coarse mesh M⁰ so that the exterior of the subdivided mesh M^k at a sufficiently high level k (e.g., 5) fits the boundary of a template structure. As an example, Fig. 1e is an atlas of the calcaneus represented as a tetrahedral subdivision mesh, showing M⁰ in wireframe and the exterior of M^k as a shaded surface. The key motivation of using subdivision is that the deformation of the subdivided mesh M^k is controlled by the displacement of the vertices in the coarse mesh M⁰ in a simple, linear fashion. Each vertex v in M^k can be represented by a linear combination of vertices in M⁰. The coefficients in this linear combination are called the mask of v, which can be computed entirely by the topological structure of M⁰ and are independent of the locations of vertices in M⁰ [15]. After the vertices in M⁰ are displaced, the deformed location of v can be simply computed by multiplying its mask with the new vertex locations in M⁰. Figure 1f demonstrates the deformed subdivided mesh M^k after one of the control vertices (colored red) is dislocated. To register the atlas onto a target structure, a least-squares system can be set up to compute a deformed coarse mesh 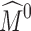such that the exterior vertices of the subdivided mesh 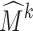fit the boundary surface of the target structure and that the interior of the atlas is warped with low distortion. Registering the atlas onto multiple target structures establishes a common anatomy-based coordinate frame within each structure (as defined by the polyhedral cells in the deformed 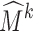), which allows mapping of spatial data among these structures.

An inherent drawback of subdivision atlases is that they exhibit an overly smooth shape and often cannot represent anatomical structures with rich geometric features on the boundary. For example, the smooth exterior of the subdivided atlas M^k in Fig. 1e does a poor job of capturing some of the key bony prominences and articular indentations on the calcaneus shown in Fig. 1g. Such a “blobby”-looking exterior cannot be accurately registered to a target calcaneus surface, and this in turn results in errors in interior mapping. This drawback has limited the application of subdivision atlases to those structures with smooth boundary shapes, such as the mouse brain [18] and the metatarsal bones (which have smoother exteriors than tarsal bones like the calcaneus) [19]. Note that an accurate registration of the boundary is particularly important for mapping bone BMD, since the BMD is most concentrated near the bone surface in the cortical shell. Although the overly smooth appearance of subdivision atlases can be alleviated by using a more complex coarse mesh 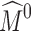, this choice is undesirable as the increased complexity of the atlas leads to increased difficulty in constructing the atlas (which is typically done by hand) as well as a higher computational cost for registration.

Subdivision-embedded Atlases

To accurately capture boundary details without adding complexity to the subdivision mesh, we propose a hybrid atlas representation called a subdivision-embedded atlas. As in subdivision atlases, a coarse mesh M⁰ is used for controlling the deformations of the volume enclosed by the subdivided mesh M^k. Instead of using the exterior of M^k to model the boundary of the anatomical structure, we use an additional triangular mesh (called the template surface) constructed from the boundary surface of the template structure. An example atlas for the calcaneus is shown in Fig. 1g, where M⁰ is drawn in wireframe and the embedded template surface is shaded. Note that, compared with the subdivision atlas shown in Fig. 1e, the subdivision-embedded atlas exactly captures the surface geometry of the bone without increasing the complexity of the coarse mesh M⁰. As a consequence, registering the subdivision-embedded atlas to a target bone results in a more accurate fitting of the bone surface without increasing the computational complexity.

The template surface can be warped by manipulating the coarse mesh M⁰ in a similar way to how the subdivided mesh M^k is deformed. Specifically, we represent each vertex v of the template surface as a linear combination of locations of the vertices in M⁰. The coefficients of such a linear combination are called the mask of v, and are computed by barycentric interpolation of the masks associated with the vertices of the tetrahedral or octahedral cell in M^k that encloses v. For computing the barycentric interpolation, we use mean value coordinates, which offer robust, smooth interpolation over any polyhedral shape [22]. After deforming the coarse mesh M⁰, the new location of v is determined by multiplying its mask to the deformed locations of control vertices in M⁰. Figure 1h shows an example of template surface deformation by dislocating one control vertex (colored in red).

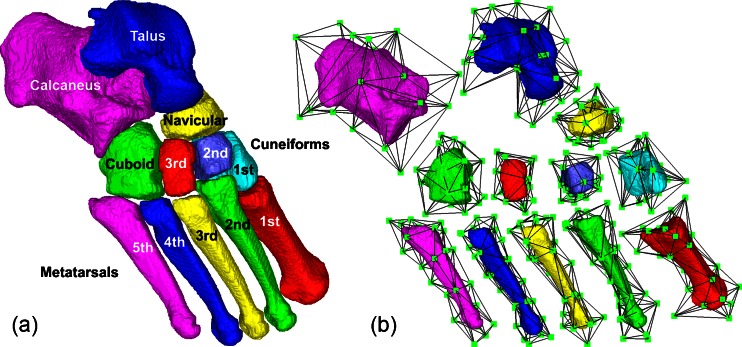
We create one atlas for each of the seven tarsal bones (first through third cuneiforms, cuboid, navicular, talus, and calcaneus) and five metatarsal bones in the human foot from a user-chosen segmented QCT scan (see Fig. 2). For each bone, we first create the template surface by extracting a triangulated boundary of the segmented bone using marching cubes [23] and smoothing the surface with Laplacian-based fairing [24] (Fig. 2a). To create the coarse mesh M⁰, we first decimate the template surface down to a small number of triangles using quadratic-error-based simplification [25]. The simplified triangular surface is inflated from the centroid of the template by 5% to form the exterior triangles of M⁰, so that the subdivided mesh M^k completely encloses the template surface. Finally, we create the interior tetrahedra of M⁰ by manually placing a couple of interior vertices and connecting them to the exterior triangles (Fig. 2b).

Fig. 2.

Template surfaces for 12 tarsal and metatarsal bones (a) and the subdivision-embedded atlas for each bone (b)

Atlas Registration

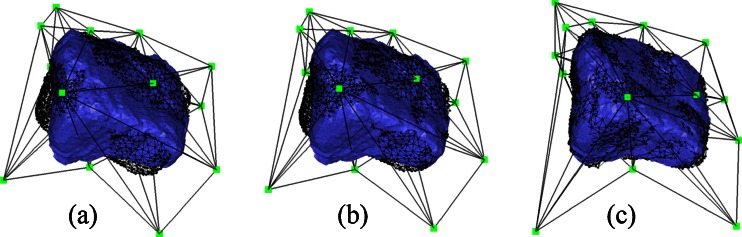
To compare BMD interior to bones in different scans, we need to register the atlas onto the segmented bones in each scan. To register a subdivision-embedded atlas onto a target structure, we displace the vertices of M⁰ so that the deformed template surface fits the boundary of the target (called the target surface) by a low-distortion warp. Our method extends the registration pipeline for subdivision atlases by Ju et al. [15] to use our new subdivision-embedded atlases. The pipeline consists of a rigid alignment stage and a non-rigid deformation stage. We will explain these two stages next and use a second cuneiform as an example to illustrate the effect of each stage in Fig. 3. Similar to subdivision atlases, registering a subdivision-embedded atlas onto multiple target structures allows mapping of the interior of these structures using the common coordinate frame defined by the polyhedral cells in the deformed atlases.

Fig. 3.

Registering the atlas of a second cuneiform onto a target surface (the atlas is shown in black wire frame and the target surface is shown in blue): after PCA-based rigid alignment (a), after ICP-based rigid alignment (b), and after non-rigid deformation (c)

Rigid Alignment

The target surface is created in the same way as the template surface from the segmentation. An initial alignment between the atlas and the target surface is achieved using translations and rotations by aligning their centroids and principle axes that are obtained by principle component analysis (PCA). For robust results, the centroids and the axes are computed using all interior voxels in the segmented template and target bones, instead of using only vertices on their boundary surfaces. Since some bones (e.g., the cuneiforms) exhibit spherical shapes, the PCA-based alignment may not give satisfactory results (e.g., Fig. 3a). We improve the alignment using iterative closest point (ICP) registration. During each iteration, the atlas is transformed by the best rigid-body transformation (in the least-squares sense) that brings each vertex on the template surface into alignment with its closest point on the target surface. Such transformation can be computed using singular-value decompositions. The process terminates if the displacement of the template vertices between two iterations falls beneath a user-provided threshold. The ICP-based improvement brings the template surface into close alignment with the target surface (e.g., Fig. 3b).

Non-rigid Deformation

To further account for local shape variations between the template and target structures, we next compute a flexible warp of the atlas as displacements of the vertices in the coarse subdivision mesh M⁰. Denoting the vertex positions in M⁰ after rigid alignment as X. Our goal is to compute new positions 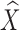that minimize the combined energy,

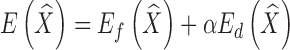where 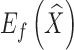measures the fitting error between the deformed template surface and the target surface, 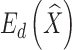measures the distortion in the deformation, and α is a balancing weight. The fitting error is defined as

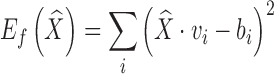where v_i is the stored mask of the ith vertex on the template surface (and hence 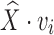is the deformed location of the vertex), and b_i is the location of the closest point on the target surface to that vertex prior to deformation. We follow the approach in [15] to define the distortion as the amount of non-affine deformation (i.e., deformations that cannot be represented as a combination of translations, rotations, scalings, and shearings) of each pair of cells in the subdivided mesh M^l for a chosen level l (e.g., 2). Consider a tetrahedralized M^l where each octahedron is divided into eight tetrahedra by its centroid, the distortion term is a summation over all pairs of tetrahedra {p_i, p_s, p_t, p_r}, and {p_j, p_s, p_t, p_r} in the resulting tetrahedral mesh that share a common triangle {p_s, p_t, p_r}:

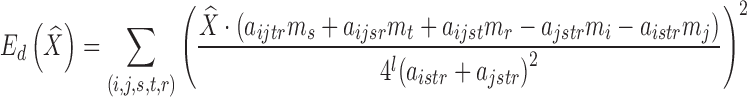Here, a_istr denotes the unsigned volume of the tetrahedron formed by {p_i, p_s, p_t, p_r} in the un-deformed mesh, and m_i denotes the mask of the vertex p_i. Note that both terms E_f, E_d are quadratic in the variables 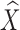, and hence minimizing the combined energy E is a least-squares problem that can be solved by a linear system of equations. An example result is shown in Fig. 3c.

BMD Mapping

We mark each tetrahedral or octahedral cell in the un-deformed mesh M^k as interior if all vertices of the cell belong to some voxel of the segmented template. After registering the atlas to the target bone, we compute at each deformed interior cell of 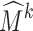the tri-linearly interpolated intensity (in Hounsfield Units) of the QCT volume at the centroid location of the cell. The value at each cell can then be compared with that mapped from another target bone. In this way, the atlas acts as a common coordinate system for comparing regional BMD from different scans.

Evaluation Method

Test Data

The QCT images from nine young healthy adult subjects were used in this study. The healthy subjects were recruited from the Washington University staff and student population. The subject demographics for the five males and four females are given in Table 1. Two repeated scans over a short interval (within approximately 30 min) were acquired for both feet of each subject, amounting to a total of 36 foot scans. The 12 foot bones were segmented from each scan. We chose one of the 36 scans, called the template scan, to construct the twelve bone atlases (as shown in Fig. 2), which were automatically registered to the other 35 scans.

Table 1.

Subject demographics. The table reports mean and standard deviation (in parenthesis) of age, height (in centimeters) and weight (in kilograms) of the nine subjects who participated in our evaluation

	Number	Age	Height	Weight
Male	5	26(3)	176(5)	87(18)
Female	4	26(5)	171(9)	70(11)

The complete details for acquiring the QCT images with the image processing and segmentation methods have been previously published [4, 26, 27], but we provide a brief description. Each subject was supine on the spiral CT scanner table. The images of the foot from the toes to above the talus were acquired with a Siemens Definition 64-Slice CT dual-source scanner (Siemens Medical Systems, Inc, Malvern, PA, USA) using only a single radiation source. The middle of each foot was placed approximately in the iso-center of the scan volume since the table was positioned at approximately 120 mm down from the rotation center (iso-center). The right foot was positioned at approximately 45° relative to the table surface and scanned first. Then the left foot was positioned and scanned. The right and left foot scans were repeated for a total of four foot scans per patient. The CT parameters used to acquire the images were: 38.4-mm table increment per gantry rotation (64 slices × 0.6 mm collimation = 38.4 mm), 220 mAs, 120 kVp, pitch of 1, rotation time of 0.5 s, and a 512 × 512 matrix. The Siemens’ B70f kernel was used to reconstruct CT images with a 0.6-mm slice thickness (no gaps between slices).

Analyze software [28, 29] was used to convert the CT DICOM images to Analyze 7.5 formatted files. With Java software running in ImageJ 1.40g, edge detection methods [19, 26, 30] were used to determine the edges of the bones within the soft tissue [31]. Graph-cut methods [4, 26] were used to segment each bone individually once the edges of the bones were determined. The BMD at each voxel was determined from a calibration phantom (QCT-Bone Mineral Phantom, Image Analysis, Inc., Columbia, KY) [19, 27].

Evaluation Metrics

Atlas registration is evaluated in three ways. First, we evaluate the accuracy of fitting the target bone surfaces using our subdivision-embedded atlases, and compare it with the accuracy using the previous subdivision atlases [15, 19]. We constructed subdivision atlases for the 12 bones by taking the coarse mesh M⁰ in each of our 12 subdivision-embedded atlases. These 12 bone atlases from one scan were registered to the 35 scans using the pipeline described in [15]. The fitting accuracy of both techniques (subdivision-embedded atlas vs. subdivision atlas) is measured using two metrics, the two-sided Hausdorff distance and the mean distance. The two-sided Hausdorff distance computes the maximum shortest distance from a vertex on one surface to any vertex on the other surface. The mean distance computes the mean of shortest distances over all vertices on two surfaces. The Hausdorff and mean distances capture respectively the worst and average deviation between two surfaces. The two metrics are evaluated between the target bone surface and the deformed template surface (for subdivision-embedded atlases) or the deformed exterior surface of the subdivision mesh (for subdivision atlases). Multivariate repeated measures analysis of variance was performed to determine if there is a significant difference between the two techniques in terms of these metrics.

With the lack of ground-truth of how the interior of two bones are mapped, we evaluate the quality of BMD mapping created by our registration in two ways. First, we assess its consistency in mapping bones segmented from two repeated scans of the same foot. Due to changes in positioning during imaging, the two scans generally do not align when they are superimposed. Ideally, after atlas registration, the BMD mapped from both scans onto the same atlas cell should be identical. We compute the difference between the two mappings as the root mean squared deviation (RMSD) of the mapped values over all atlas cells, normalized by the difference between the maximum and minimum Hounsfield Unit values in the first scan.

Second, we compare BMD measurements in VOIs produced by our mapping method with those created by expert annotations. We examined the second metatarsal, a cylindrical bone consisting of three parts, head, shaft, and base, which we consider as VOIs. We took 18 scans, the first of each pair of repeated scans (including the template scan). We numbered the bones in these scans 1 through 18, with the 18th bone being the template scan. A human expert was asked to place two cutting planes along the bone axis in each scan to define the three VOIs. The expert did three trials for each bone. For each trial, the expert was blinded with regard to the VOIs defined in previous trials. Hence, for each VOI i on each bone j, we obtained three Hounsfield Unit values based on the three human trials, noted as H¹_i,j, H²_i,j, H³_i,j for i = 1,2,3 and j = 1,…,18. We also registered the atlas (created from the 18th bone) to the 17 non-template scans, and obtained three Hounsfield Unit values for each VOI i in each bone j using only the three VOI definitions on the template bone. The average of these three values was used as the atlas-based measurement, noted as A_i,j for i = 1,2,3 and j = 1,…,17. Multivariate repeated measures analysis of variance was used to determine if there is a significant difference among the three human-based measurements (H¹_i,j, H²_i,j, H³_i,j) and the atlas-based measurement (A_i,j) over all VOIs and bones.

Results

All experiments were performed on a consumer PC with 2.4 GHz CPU and 2 GB of memory. After the initial process of bone segmentation, surface generation, and atlas construction, registering the atlases onto the bone surfaces was completely automated and took less than 3 min for each scan.

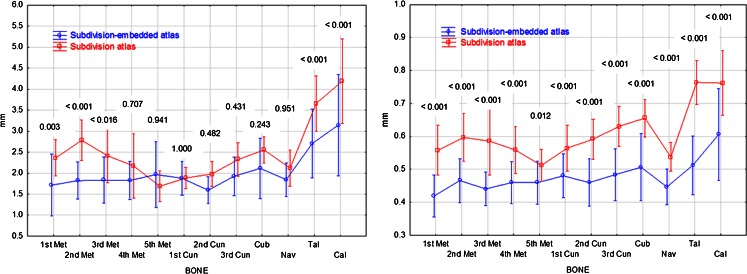
Figure 4 reports the Hausdorff distances and mean distances, measured in millimeter, between the target bone surfaces and the deformed surfaces of the subdivision-embedded atlases (blue lines) or the subdivision atlases (red lines) for each bone over all 35 scans. The vertical bars are 95% confidence intervals. For each bone, the Tukey honestly significant difference (HSD) p values for the comparison of the two methods using multivariate repeated measures analysis of variance are shown above the vertical lines. Based on the analysis, the Hausdorff distances for subdivision-embedded atlases were lower than subdivision atlases for the first, second, and third metatarsals, talus, and calcaneus (Tukey HSD p < 0.016). For mean distances, the values for subdivision-embedded atlases were lower than subdivision atlases for all bones (Tukey HSD p ≤ 0.012).

Fig. 4.

Plots of Hausdorff and mean distances for each bone for the subdivision-embedded atlas and subdivision atlas methods. Vertical lines are 95% confidence intervals. For each bone, the Tukey honestly significant difference p value for the comparison of the two methods is shown above the interval lines

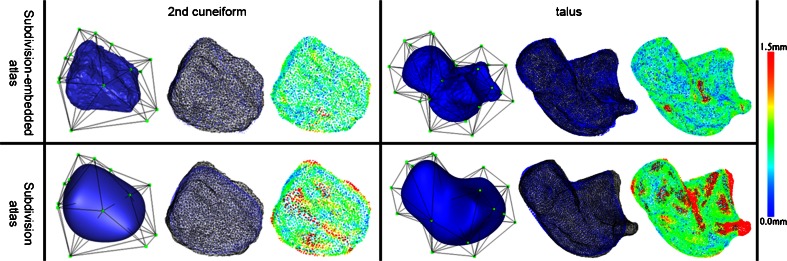
Figure 5 visually compares the fitting accuracy between the two techniques on the second cuneiform and talus. Note that traditional subdivision atlases (Fig. 5c,d) cannot accurately fit to the local bony prominences and articular indentations of the target surfaces, whereas the subdivision-embedded atlases (Fig. 5a,b) are able to fit those areas with much less error due to the use of the geometrically rich template surface.

Fig. 5.

Comparing the registration of subdivision-embedded atlases (top) and subdivision atlases (bottom) on second cuneiform (left) and talus (right). The three pictures in each table cell show, from left to right, the original un-deformed atlas, deformed atlas surface (blue dots) with the target surface (black wire), and the target surface where each point is colored by its shortest distance to the deformed atlas surface. The color legend is shown to the right

Figure 6 reports the difference between BMD mappings of each pair of repeated scans. The normalized RMSDs for all 18 pairs of scans are shown in this box plot, where each bar marks the minimum, lower quartile, median, upper quartile, and maximum of the 18 values for each bone. In most cases, the RMSD deviation between the two mappings is within 4% of the in-bone BMD variation, and is within 6% in all cases.

Fig. 6.

Box plot of normalized RMSD between mapped BMD in 18 pairs of repeated scans over each bone

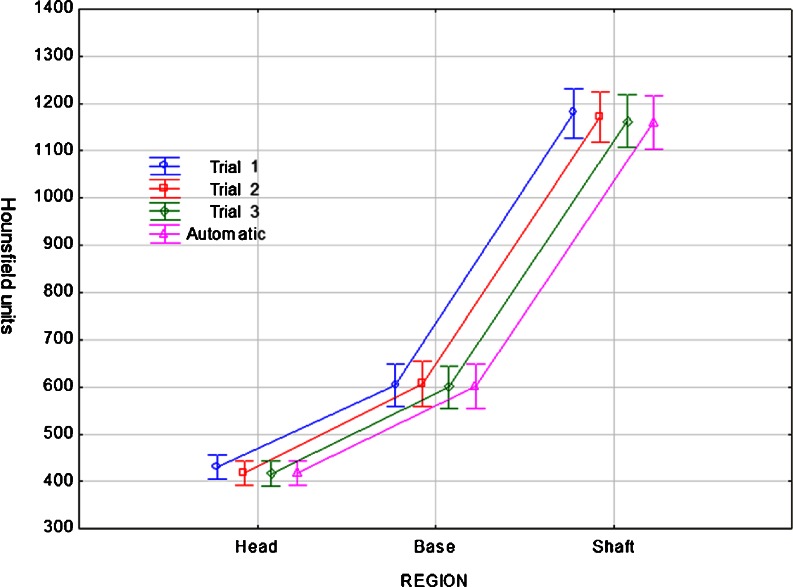
Figure 7 reports the regional BMD, measured in Hounsfield units, using human annotations (“Trial 1, 2, 3”) and atlas registration (“Automatic”) for each VOI (head, base and shaft) over all 17 second metatarsals. The vertical bars are 95% confidence intervals. Using multivariate repeated measures analysis of variance, we found that, for the head VOI, Trial 1 resulted in higher Hounsfield Unit values than the other methods (Tukey HSD p ≤ 0.035). For the base VOI, no difference was demonstrated between methods (p ≥ 0.765). For the shaft VOI, Trial 1 resulted in higher values than Trial 3 and Automatic methods (p ≤ 0.001). In sum, there is no significant difference between the atlas-based regional measurements and those based on human annotations. Note that the definitions of VOI by the same expert in different trials can exhibit large variation, as shown in Fig. 8 for subject 16. On the other hand, the automated atlas-based method produces repeatable measurements.

Fig. 7.

Plots of regional BMD measured by human annotations and atlas registration for each VOI (head, base and shaft) of the second metatarsal over 17 scans. Vertical lines are 95% confidence intervals

Fig. 8.

VOI definitions annotated by a human expert in three trials on the second metatarsal bones in two different subjects. The VOIs are defined by planar boundaries selected by the expert using an interactive in-house software. The intersection curves of these planes with the bone surface are drawn in different color for each trial. Note that large deviation of the planes among the trials in Subject 16

Discussion

The primary application of our bone registration technique is to perform quantitative measurements in an efficient and non-subjective way. While human experts are equipped with tremendous domain knowledge and powerful visual perception skills, they cannot always make judgments consistently and bias always exists. The atlas-based mapping allows user-provided annotations on the template bone to be automatically and consistently “transferred” onto target surfaces. Our method can also be used to transfer from the template to target bones other types of annotations, such as surface landmarks, interior landmarks, and bone orientations. This would enable a range of geometric measurements to be automated.

Our registration method assumes the target boundary has similar geometric features as those of the template surface. While such similarity is observed in our testing suite made up of bone scans of healthy feet, bones from patients with severe foot deformities may exhibit significant variation in boundary geometry and even loss of large bone regions, in which case the proposed method would not be able to register as accurately or consistently as reported here. Moreover, it is questionable what constitutes a good spatial mapping between severely deformed or fractured bones.

As the target bone surface is pre-processed with Laplacian-based fairing [24] prior to being fitted by the atlas, our registration method is not sensitive to small variations in segmentation. Such robustness can be seen in the consistency of BMD mapping between the same bones in repeated scans (the same bone has different segmentation in the two scans due to the change in position and orientation). However, large errors in segmentation, such as missing or adding a significant bone volume, could potentially affect the registration as much as bones with sever deformities do. The graph-cut based segmentation method we used in our pipeline [4] is a semi-automated routine that has been shown to be both highly consistent with human annotation [4] and reliable among individual operators [26].

We constructed the atlas from an arbitrarily selected healthy subject in our experiments. When working with a particular group of subjects, selecting one whose bone shape is representative of that group would yield more accurate results. Alternatively, an average foot can be constructed by statistical method such as [32] and used for constructing the atlases.

Like previous subdivision-based approaches [15, 19], our registration method makes the assumption that the interior of the bone mostly likely undergoes a locally affine (i.e., linear) warping between two time points or between two different subjects. Although seemingly artificial, the assumption is supported by our evaluation results in terms of consistency and accuracy on healthy foot bones. As part of the future work, we would like to explore the use of non-linear energy formulations, such as elasticity and strain energy, in the context of subdivision-embedded atlases and compare these results with those using our energy formulation. We would also like to explore how correspondences of surface features (e.g., ridges and corners) [33] can be incorporated in our matching framework to further improve the accuracy of boundary fitting.

Conclusion

We proposed a novel atlas representation (subdivision-embedded atlases) and applied it for deformable spatial mapping of segmented foot bones from QCT scans. Compared with existing subdivision atlases, the new atlases capture detailed boundary geometry of anatomical structures while maintaining a coarse control grid for efficient deformation. Our experiments indicated that the method offers a reliable, efficient alternative to human annotations for measuring regional BMD in QCT scans of foot bones.