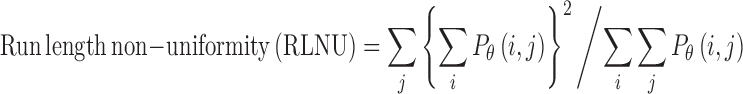Abstract
Among gynecological malignancies, ovarian cancer is the most frequent cause of death. Image mining algorithms have been predominantly used to give the physicians a more objective, fast, and accurate second opinion on the initial diagnosis made from medical images. The objective of this work is to develop an adjunct computer-aided diagnostic technique that uses 3D ultrasound images of the ovary to accurately characterize and classify benign and malignant ovarian tumors. In this algorithm, we first extract features based on the textural changes and higher-order spectra information. The significant features are then selected and used to train and evaluate the decision tree (DT) classifier. The proposed technique was validated using 1,000 benign and 1,000 malignant images, obtained from ten patients with benign and ten with malignant disease, respectively. On evaluating the classifier with tenfold stratified cross validation, the DT classifier presented a high accuracy of 97 %, sensitivity of 94.3 %, and specificity of 99.7 %. This high accuracy was achieved because of the use of the novel combination of the four features which adequately quantify the subtle changes and the nonlinearities in the pixel intensity variations. The rules output by the DT classifier are comprehensible to the end-user and, hence, allow the physicians to more confidently accept the results. The preliminary results show that the features are discriminative enough to yield good accuracy. Moreover, the proposed technique is completely automated, accurate, and can be easily written as a software application for use in any computer.
Keywords: Ovarian tumor, Texture features, Higher-order spectra, Characterization, Classification, Computer-aided diagnosis
Introduction
In 2011, in the United States, it is estimated that 21,990 new cases will be diagnosed with and 15,460 women would die of ovarian cancer [1]. Ultrasonography and the determination of the levels of a tumor marker called cancer-antigen 125 (CA125) are currently the most commonly used techniques for detecting ovarian cancer. In the case of ultrasonography, the ultrasonographers and radiologists visually inspect the acquired ultrasound images for any subtle changes that differentiate the benign and malignant tumors. Even though this is currently the most common practice, the accuracy and reproducibility of the visual interpretations are most often dependent on the skill of the observer. In the case of evaluation based on serum CA125, this marker has been found to be elevated only in 50 % of stage 1 cancers [2]. Furthermore, CA125 can also be raised in other malignancies such as uterine and pancreatic, and sometimes in many benign conditions such as fibroids, endometriosis, pelvic inflammatory disease, and benign ovarian cysts [3]. Menon et al. [4] examined women with elevated CA125 levels and observed that the ultrasound parameters result in varying sensitivity ranging from 84 % to l00 %, with a specificity of 97 %, but only a positive predictive value (PPV) of 37.2 %. Other modalities such as computerized tomography, magnetic resonance imaging, and radioimmunoscintigraphy are limited by one or more of these factors: cost, device availability, and radiation exposure. Moreover, preoperative determination of whether an ovarian tumor is malignant or benign, especially when the tumor has both solid and cystic components, has been found to be difficult [5]. Because ultrasound findings of ovarian masses may be inconclusive, on occasion, subsequent surgical removal of the ovary may show that the mass is benign. Such unnecessary procedures not only increase healthcare cost and time but also increase patient anxiety. Owing to the indicated limitations, it is evident that either one of the following solutions are warranted: (a) a stand-alone accurate tumor diagnostic modality; (b) a multi-modality-based standardized diagnostic protocol that reliably differentiates benign and malignant tumors; (c) an adjunct diagnostic modality/technique that accurately classifies the tumors and therefore gives a valuable second opinion to doctors in order to decide further diagnostic protocol for the patient.
The key objective of our work is to develop one such adjunct technique for ovarian tumor classification. Medical data mining has become an increasingly popular field of science over the past few decades. Computer-aided diagnostic (CAD) techniques developed using data mining framework generally follow these steps: (1) image pre-processing to remove noise; (2) extraction of representative features that quantify the changes in the images (also called the feature extraction phase); (3) selection of significant features (also called the feature selection phase); (4) classification phase wherein classifiers are built and evaluated using the selected features. Thus, CAD-based techniques can prove to be excellent adjunct techniques, especially for real-time mass screening, because of their ease of use, speed, non-invasiveness, cost-effectiveness, and reliability. Therefore, we have developed a CAD technique that can help the doctors in deciding if the primary diagnosis of whether the tumor is benign or malignant is correct and thus can allow the physicians to make a more confident call with respect to the subsequent treatment protocol.
In the area of ovarian disease management, CAD techniques have been used for automatic follicle segmentation in order to better understand ovarian follicle dynamics [6, 7], for polycystic ovary syndrome detection [8], ovarian cyst classification [9], and ovarian ultrasound image retrieval [10]. There are very few studies in the application of CAD for ovarian cancer detection. Most of these studies use features based on (a) blood test results [11], (b) mass spectrometry (MS) data [12–16], and (c) ultrasound images [17–21]. Such MS-based classification studies are affected by the curse of dimensionality [22] as they have to process a high-dimensional feature set obtained from a small sample size. Moreover, the MS equipment is expensive and not available in most developing and under-developed countries. Therefore, in our work, we have proposed the use of images acquired using the commonly available and low-cost ultrasound modality.
Compared with 2D ultrasonography, a 3D ultrasonography approach allows for more objective and quantitative documentation of the morphological characteristics of benign and malignant tumors [23]. Studies have shown that the selective use of 3D ultrasonography and power Doppler ultrasound can improve the diagnostic accuracy of ovarian tumors [24, 25]. Therefore, we have used 3D transvaginal ultrasonography for acquisition of the 2D images used in this work.
Materials and Methods
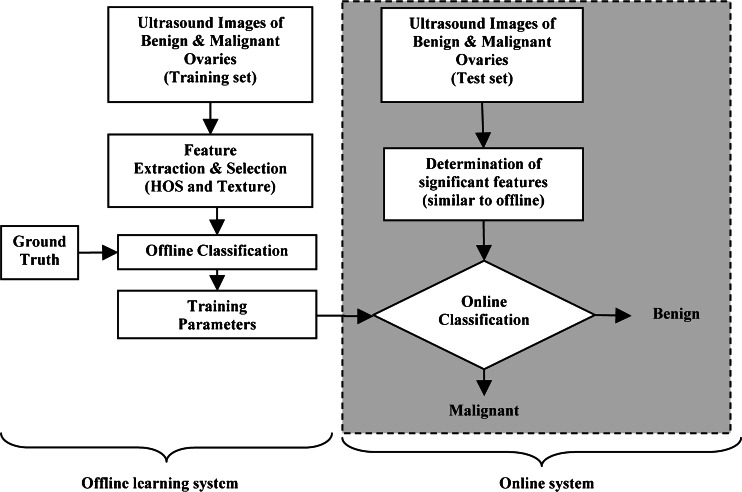
Figure 1 depicts the block diagram of the proposed real-time image mining CAD technique. It consists of an online classification system (shown on the right side of Fig. 1) which processes an incoming patient’s test image. This online system predicts the class label (benign or malignant) based on the transformation of the online grayscale feature vector by the training parameters determined by an off-line learning system (shown on the left side of Fig. 1). The off-line classification system is composed of a classification phase which produces the training parameters using the combination of grayscale off-line training features and the respective off-line ground truth training class labels (0/1 for benign/malignant). The grayscale features for online or off-line training are obtained using the same protocol for feature extraction: texture features and the higher-order spectra (HOS) features. Significant features among the extracted ones are selected using the t test. We evaluated the decision tree (DT) classifier. The above CAD system was developed using an image database that is split into a training set and a test set. The training set images were used to develop the DT classifier. The built classifier was evaluated using the test set. For evaluation, we used a k-fold cross-validation protocol. The predicted class labels of the test images and the corresponding ground truth labels (0/1) are compared to determine the performance measures of the system such as sensitivity, specificity, accuracy, and PPV.
Fig. 1.
Block diagram of the proposed system for ovarian tumor characterization and classification; the blocks outside the shaded rounded rectangular box represent the flow of offline training system, and the blocks within the box represent the online real-time system
In this section, we describe in detail the image acquisition procedure and the various techniques used for feature extraction and selection and classification.
Patients and Image Acquisition
Twenty women (age, 29–74 years; mean ± SD = 49.5 ± 13.48) were recruited for this study. The study was approved by the institutional review board. The procedure was explained to each subject, and informed consent was obtained. Among these 20 women, 11 were premenopausal and nine were post-menopausal. All these patients were consecutively selected during pre-surgical evaluation by one of the authors of this paper (blinded for peer review). Patients with no anatomopathological evaluation were excluded from the study. Biopsies indicated that, among the 20 patients, ten had malignancy in their ovaries and ten had benign conditions. Post-operative histology results indicated that the benign neoplasms were: five endometriomas, two mucinous cystadenoma, one cystic teratoma, one pyosalpinx, and one serous cyst. The malignant neoplasms were: three primary ovarian cancers (undifferentiated carcinomas), three borderline malignant tumors, one Krukenberg cancer, one serous cystadenocarcinoma, one serous carcinoma, and one carcinosarcoma. All patients were evaluated by 3D-transvaginal ultrasonography using a Voluson-I (GE Medical Systems) according to a predefined scanning protocol using 6.5 MHz probe frequency (Thermal Index, 0.6 and Mechanical Index, 0.8). A 3D volume of the whole ovary was obtained. The acquired 3D volumes were stored on a hard disk (Sonoview™, GE Medical Systems). Volume acquisition time ranged from 2 to 6 s depending on the size of the volume box. In cases where a given adnexal mass contained more than one solid area and, hence, had more than one volume stored, only the volume best visualizing the mass was chosen for further analysis. Figure 2 shows typical ultrasound images of benign and malignant classes. We chose the middle 100 images from each volume from each subject. Thus, the evaluated database consisted of 1,000 benign images and 1,000 malignant images.
Fig. 2.
Ultrasound images of the ovary: (B1–B2) benign conditions (M1–M2) malignant tumors. B1: histology: endometrioma; echo: characteristic diffuse, low-level echoes of the endometrioma giving a solid appearance. B2: histology: endometrioma; echo: characteristic diffuse, low-level echoes of the endometrioma giving a solid appearance. M1: histology: borderline malignant tumor; echo: multiloculate echo-pattern with multiple thick septa. M2: histology: serous carcinoma; echo: homogenous hyperechogen
Feature Extraction
Feature extraction is one of the most important steps in an automated CAD system. It was observed that the type of tumor (tumor-like lesions, benign, tumors of low malignant potential, and malignant) was correlated with lesion diameter, with larger tumors more likely to be malignant [26]. Moreover, there are several morphological changes in the benign and malignant ultrasound images [27, 28]. Usually, the histopathologic cytoarchitecture of malignant tumors is different from benign neoplasm with several areas having intra-tumoral necrosis [29]. These changes in lesion diameter and cytoarchitecture variations manifest as non-linear changes in the texture of the acquired ultrasound images. Therefore, in this work, we have extracted features based on the textural changes in the image and also non-linear features based on the higher-order spectra information. In this section, we describe these features in detail.
Texture Features
Texture features measure the smoothness, coarseness, and regularity of pixels in an image. The extracted texture descriptors quantify the mutual relationship among intensity values of neighboring pixels repeated over an area larger than the size of the relationship [30, 31]. There are several texture descriptors available in the literature [31]. We have chosen the following features:
-
Deviation
Let f(i), where (i = 1,2,…n) be the number of points whose intensity is i in the image and Ax be the area of the image. The occurrence probability of intensity i in the image is given by: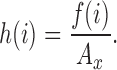 The standard deviation is given by
The standard deviation is given by
where μ = mean of intensities.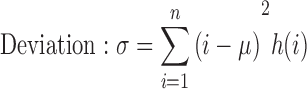
1 -
Fractal Dimension (FD)
Theoretically, shapes of fractal objects remain invariant under successive magnification or shrinking of objects. Since texture is usually a scale-dependent measure [32], using fractal descriptors can alleviate this dependency. A basic parameter of a fractal set is called the fractal dimension (FD). FD indicates the roughness or irregularity in the pixel intensities of the image. Visual inspection of the benign and malignant images in Fig. 2 shows that there are differences in the regularity of pixel intensities in both classes. We have hence used FD as a measure to quantify this irregularity. The larger the FD value, the rougher the appearance of the image. Consider a surface S in Euclidean n-space. This surface is self-similar if it is the union of Nr non-overlapping copies of itself scaled up or down by a factor of r. Mathematically, FD is computed [33, 34] using the following formula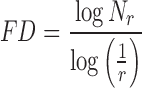
2 In this work, we used the modified differential box counting with sequential algorithm to calculate FD [34]. The input of the algorithm is the gray-scale image where the grid size is in the power of 2 for efficient computation. Maximum and minimum intensities for each (2 × 2) box are obtained to sum their difference, which gives the M and r by
where M = min(R,C), s is the scale factor, R and C are the number of rows and columns, respectively. When the grid size gets doubled, R and C reduce to half of their original value and above procedure is repeated iteratively until max(R,C) is greater than 2. Linear regression model is used to fit the line from plot log(Nr) versus log(1/r) and the slope gives the FD as: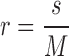
3 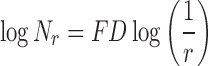
4 -
Gray Level Co-occurrence Matrix (GLCM)
The elements of a gray level co-occurrence matrix (GLCM) are made up of the relative number of times the gray level pair (a, b) occurs when pixels are separated by the distance (a,b) = (1, 0). The GLCM of an m × n image can be defined by [35]
where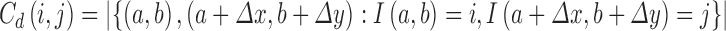
5 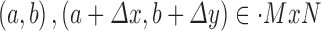 ,
, 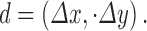
 denotes the cardinality of a set. The probability of a pixel with a grey level value i having a pixel with a gray level value j at a
denotes the cardinality of a set. The probability of a pixel with a grey level value i having a pixel with a gray level value j at a 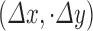 distance away in an image is
distance away in an image is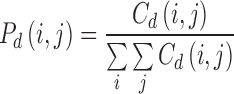
6 We calculated the following features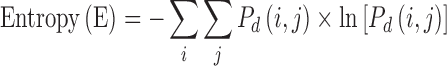
7 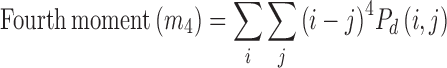
8 -
Run Length Matrix
Higher-Order Spectra (HOS)
Second order statistics can adequately describe minimum-phase systems only. Therefore, in many practical cases, higher-order correlations of a signal have to be studied to extract information on the phase and nonlinearities present in the signal [38–41]. Higher-order statistics denote higher-order moments (order greater than 2) and non-linear combinations of higher-order moments, called the higher-order cumulants. In the case of a Gaussian process, all cumulant moments of order greater than 2 are 0. Therefore, such cumulants can be used to evaluate how much a process deviates from Gaussian behavior. Prior to the extraction of HOS-based features, the pre-processed images are first subjected to Radon transform [42]. This transform determines the line integrals along many parallel paths in the image from different angles θ by rotating the image around its center. Hence, the intensities of the pixels along these lines are projected into points in the resultant transformed signal. Thus, the Radon transform converts a 2D image into a 1D signal at various angles in order to enable calculation of HOS features. This 1D signal is then used to determined the bispectrum, B(f1,f2), which is a complex valued product of three Fourier coefficients given by
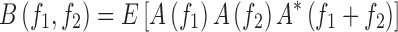 |
10 |
where A(f) is the Fourier transform of a segment (or windowed portion) of a single realization of the random signal a(nT), n is an integer index, T is the sampling interval, and E[.] stands for the expectation operation. A*(f1 + f2) is the conjugate at frequency (f1 + f2). The function exhibits symmetry and is computed in the non-redundant/principal domain region Ω as shown in Fig. 3. We calculated the H parameters that are related to the moments of bispectrum. The sum of logarithmic amplitudes of bispectrum H1 is
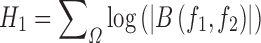 |
11 |
Fig. 3.
Principal domain region (Ω) used for the computation of the bispectrum for real signals
The weighted center of bispectrum (WCOB) is given by
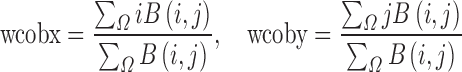 |
12 |
where i and j are frequency bin index in the non-redundant region.
We extracted H1 and two weighted center of bispectrum features for every 1° of Radon transform between 0 and 180°. Thus, the total number of extracted features would be 724 (181 × 3). To summarize, the following are the steps to calculate the HOS features from the ultrasound image [36]: (1) The original image is first converted to 1D signal at every 1° angle using Radon transform. (2) The 256 point FFT is performed with 128 points overlapping to maintain the continuity. (3) The bispectrum of each Fourier spectrum is computed using the Eq. 9. Similarly, the bispectrum is determined for every 256 samples. (4) The average of all these bispectra gives one bispectrum for every ultrasound image. (5) From this average bispectrum, the moments of bispectrum and weighted center of bispectrum features given in Eqs. 11 and 12 are calculated.
Feature Selection
After the feature extraction process, there were a total of 729 features (five texture-based and 724 HOS-based). Most of these features would be redundant in information they retain, and using them to build classifiers would result in the curse of dimensionality problem [22] and over-fitting of classifiers. Therefore, feature selection is done to ensure that only unique and informative features are retained. In this work, we have used Student’s t test [43] to select significant features. Here, a t statistic, which is the ratio of difference between the means of the feature for two classes to the standard error between class means, is first calculated, and then the corresponding p value is calculated. A p value that is less than 0.01 or 0.05 indicates that the means of the feature are statistically significantly different for the two classes, and hence, the feature is very discriminating. On applying the t test, we found that many features had a p value less than 0.01. However, on evaluating several combinations of these significant features in the classifier, we found that only the four features listed in Table 1 presented the highest accuracy. Therefore, the entire dataset is now represented by a set of these four features for every patient.
Table 1.
Significant features that had a p value < 0.01 and their ranges (mean ± standard deviation) for benign and malignant classes
| Feature | Benign | Malignant | p value |
|---|---|---|---|
| FD | 2.31 ± 3.939E-02 | 2.32 ± 2.715E-02 | <0.0001 |
| Σ | 60.7 ± 12.5 | 54.5 ± 6.88 | <0.0001 |
| m4 | 3.05 ± 0.651 | 3.25 ± 0.674 | <0.0001 |
| E | 4.36 ± 0.677 | 4.28 ± 0.594 | 0.007 |
| RLNU | 344 ± 113 | 358 ± 64.1 | 0.0006 |
| wcobx (20°) | 7.19 ± 1.81 | 6.46 ± 2.26 | <0.0001 |
| H1 (80°) | 52,120 ± 3.613E + 03 | 49,770 ± 3.023E + 03 | <0.0001 |
| wcoby (90°) | 2.92 ± 0.593 | 2.49 ± 0.281 | <0.0001 |
Classifier Used
In the case of DTs, the input features are used to construct a tree, and then a set of rules for the different classes are derived from the tree [44]. These rules are used for determining the class of an incoming new image.
Classification Process
Usually in classification, the hold-out technique wherein a part (mostly 70 %) of the acquired dataset is used for training the classifier and the remaining samples are used for evaluating the performance of the classifier. However, the performance measures obtained using this technique may depend on which samples are in the training set and which are in the test set, and hence, the final resultant performance measures may be significantly different depending on how the split is made. In order to get robust results, we have adopted stratified k-fold cross-validation technique as the preferred data resampling technique in this work. In this technique, the dataset is randomly split into k equal folds, each fold containing the same ratio of non-repetitive samples from both the classes. In iteration 1, (k − 1) folds of data are used to train the classifier, and the remaining one fold is used to test the classifiers and to obtain the performance measures. This procedure is repeated for (k – 1) more times by using a different test set each time. The averages of the performance metrics obtained in all the iterations are reported as the overall performance metrics. In this work, k was taken as 10. Due to this iterative technique, the trained classifier will be more robust. Jackknifing, similar to onefold cross-validation method, instead of estimating the performance metrics over all the folds like in k-fold cross-validation, we compute and study the bias of some statistic of interest in each fold of the data. In this work, we are interested in the generalization capability of the classifier, and hence, we used k-fold cross-validation method.
Performance Measures
Sensitivity, specificity, positive predictive value, and accuracy were calculated to evaluate the performance of the classifiers. True negative (TN) is the number of benign samples identified as benign. True positive (TP) is the number of malignant images identified as malignant. The number of malignant samples detected as benign is quantified by the false-negative (FN) measure. False-positive (FP) is the number of benign samples identified as malignant. Sensitivity, which is the proportion of actual positives (malignant cases) which are correctly identified, is calculated as TP/(TP + FN), and specificity, which is the proportion of actual negatives (benign cases) which are correctly identified, is determined as TN/(TN + FP). PPV, which is the ratio of true positives to combined true- and false-positives, is calculated as TP/(TP + FP), and accuracy, which is the ratio of the number of correctly classified samples to the total number of samples, is calculated as 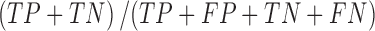 .
.
Results
Selected Features
Table 1 presents the mean ± standard deviation (SD) values of the selected features for both the benign and malignant classes. The low p value indicates that the listed features are significant. Even though the means of the features between the two classes appear to be close-valued in Table 1, the t test does not determine the significance based on the overall mean values. As previously indicated, the t test judges the difference between their means relative to the spread or variability of their data. In this perspective, the listed features were found to be significant.
Classification Results
Since tenfold cross-validation was employed, during each of the ten iterations, 900 images from each class (a total of 1,800 images) were used for building the classifier, and the remaining 100 images from each class (a total of 200 images) were used for testing and for determining the performance metrics. The averages of the performance measures obtained in the ten folds are reported in Table 2. It is evident that the simple decision tree classifier presented the high accuracy of 97 %, sensitivity of 94.3 %, and specificity of 99.7 %. The advantage of the DT classifier over the other classifiers is that this classifier uses rules to classify a new image. These rules are comprehensible to the end-user and, hence, allow the physicians to more confidently accept the result from the classifier. This is not the case with classifiers such as the artificial neural networks which, in most cases, behave like black boxes by not being transparent in the way in which they determine the class label.
Table 2.
Performance measures obtained using the DT classifier
| Classifier | TN | FN | TP | FP | Accuracy (%) | PPV (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|---|---|---|---|---|
| DT | 100 | 6 | 94 | 0 | 97 | 99.7 | 94.3 | 99.7 |
TN true-negative, FN false-negative, TP true-positive, FP false-positive
Discussion
There are very few CAD-based studies in the field of ovarian tumor classification. Age and results of 30 blood tests were used as features in a multi-layer perceptron classifier in order to classify the patient into one of the three classes, namely, benign, early stage, and late-stage cancers. On testing 55 cases, an accuracy of 92.9 % was recorded [11]. Assareh et al. [12] selected three significant biomarkers among the high dimensional input data from protein mass spectra and used them in two fuzzy linguistic rules. On using these rules for classification, they have reported a classification accuracy of 100 % for one dataset (91 controls, 162 cancers) and 86.36 % for another dataset (100 normal, 16 benign, 100 cancers). The limitation of this study was the use of hold-out technique for data resampling. As indicated earlier, hold-out technique generally results in less robust results due to the dependence of the dataset split made for selecting training and test sets. On using a complementary fuzzy neural network on a DNA microarray gene expression dataset (24 normal, 30 cancers), Tan et al. [13] reported an accuracy of 84.72 % using nine features. In another mass spectra-based study, binary images were first modeled based on the proteomic mass spectrum data from 100 normal and 100 cancers. On evaluation using these models, an accuracy of 96.5 % was obtained [14]. Tang et al. [15] proposed a novel approach for dimensionality reduction in mass spectrometry data and tested it using high-resolution SELDI-TOF data for ovarian cancer (95 normal, 121 cancers). Four statistical moments were used in a kernel partial least-squares classifier and sensitivity of 99.5 %, specificity of 99.16 %, and accuracy of 99.35 % were achieved. Petricoin et al. [16] used a genetic algorithm with self-organizing cluster analysis for detecting ovarian cancer. They used spectra derived from analysis of serum from 50 normal women and 50 patients with ovarian cancer to identify a proteomic pattern that completely discriminated cancer from normal conditions. They identified pattern was used to evaluate 50 malignant and 66 benign conditions. A sensitivity of 100 % and specificity of 95 % was observed. Even though the accuracies obtained using MS data are high, the use of these techniques is limited by the availability and cost of the necessary equipment for data analysis.
Tailor et al. [17] used variables such as age, menopausal status, maximum tumor diameter, tumor volume, locularity, the presence of papillary projections, the presence of random echogenicity, the presence of analyzable blood flow velocity waveforms, the peak systolic velocity, time-averaged maximum velocity, the pulsatility index, and resistance index obtained from 52 benign and 15 malignant transvaginal B-mode ultrasonography images. Using a variant of the back-propagation method, they obtained a sensitivity and specificity of 100 % and 98.1 %. Bruning et al. [18] developed a knowledge-based system called ADNEXPERT that used histopathologic and sonographic data for computer-assisted ultrasound diagnosis of adnexal tumors. On evaluation using 69 new adnexal tumor cases, ADNEXPERT achieved an accuracy of 71 %. Biagiotti et al. [19] used variables such as age, papillary projections, random echogenicity, peak systolic velocity, and resistance index obtained from 175 benign and 51 malignant transvaginal B-mode ultrasonography images. Using a three-layer back-propagation network, they obtained 96 % sensitivity. All these three studies [17–19] used features based on evaluations made by the operator, and hence, these features may be subjective in nature. Zimmer et al. [20] proposed an automatic analysis of the B-mode ultrasound images by quantification of grey-level intensity variations (mean, standard deviation, etc.). Using a segmented region of interest, their algorithm classified the tumour into three main categories (cyst, solid, and semi-solid) and obtained a low accuracy of 70 % for tumors containing solid portions. Lucidarme et al. [21] used the Ovarian HistoScanning (Advanced Medical Diagnostics, Waterloo, Belgium) technique for tumor classification. This technique registered 98 % sensitivity, 88 % specificity, and 91.73 % accuracy. HistoScanning is an automatic scoring system based on the quantification of tissue disorganization induced by malignant processes in backscattered ultrasound waves before image processing. Recently, we extracted texture features based on local binary patterns and Laws texture energy and used them to build and train a support vector machine classifier. On evaluating 1,000 benign and 1,000 malignant images using the developed system, we obtained a high accuracy of 99.9 % [45]. We tested only texture features in Acharya et al. [45] whereas we evaluated a novel combination of HOS and texture features in this present study.
Our study is along the lines of Zimmer et al. [20] wherein we have quantified the grey-level intensity variations in the ultrasound images using texture and HOS-based features. Zimmer et al. [20] employed segmentation algorithms to determine the region of interest (ROI) of the ovarian mass in B-mode ultrasound images. In our technique, we use the whole 2D image and not any segmented portions. We have taken the Radon transform for every 1° circularly around the image to acquire all the possible information within the image. Our results show that all the four selected nonlinear features have unique ranges (with low p values). The structural features outside the lesion like noise or other changes do not contribute to our results because nonlinear features like HOS are robust to noise and capture the nonlinear interaction of the pixels in the frequency domain and also capture phase coupling. Therefore, the changes outside the lesion do not influence our features or classification results. Using the DT classifier, we have achieved a high accuracy of 97 % due to the use of the novel combination of the four features in the classifier. The time taken to obtain the diagnosis prediction was less than 1 min. Our proposed algorithm has the following features:
The proposed system uses the whole ultrasound image (not any specific ROI), automatically extracts features and uses them in the DT classifier to predict the class (benign/malignant) of the patient. Since no user-interaction is necessary, the end results are more objective and reproducible compared to manual interpretations of ultrasound images which can at times result in inter-observer variations.
Because of the use of the stratified cross-validation data resampling technique, the system is generalized to accurately predict the class of new ultrasound images, and hence, the proposed technique is robust.
Only four simple and easily determinable powerful features have to be calculated from the images for use in the classifiers. This significantly reduces the computational load and time. Unlike MS data, there is no need for complex techniques for dimensionality reduction.
Since we use images acquired using commonly available and affordable ultrasound modality, there is no additional cost for image acquisition. Moreover, the algorithm can be easily written as a software application that can be installed and used in any radiologists’ or physicians’ office at no extra cost.
The physician has to just run the software on the acquired B-mode ultrasound images. The software does all the processing and outputs classified image after characterization of the tissue. Hence, there is no need for trained experts for running the software.
On the limitations side, the robustness of such CAD techniques depends on the determination of good features that well discriminate the classes, in this case, benign and malignant tumors. Moreover, for medical legal concerns, the radiologists have to store all CAD findings and images which increase digital storage requirements. When we use such CAD tools, we tend to rely on the CAD results, leading to a lower performance in detecting cancers than when we do not use CAD. Thus, using CAD may degrade human decision making. Hence, clinical success of such CAD tools depend on these tools having a high sensitivity and a reasonable specificity, and also good reproducibility of the results [46]. In this study, we have obtained a high sensitivity of 94.3 % and specificity of 99.7 %. However, we believe that there is more room for improvement in accuracy. Therefore, as part of our future studies, we intend to analyze other texture features to determine more discriminating features. Moreover, the clinical applicability of our proposed technique has to be established with more studies containing larger image databases from multi-ethnic groups. We also intend to extend the study protocol to 3D, wherein we would include the spatial information of the 3D slices taken from a single patient for analysis.
Conclusion
We have presented a CAD technique for ovarian tumor classification in this paper. A novel combination of four texture and HOS-based features that adequately quantify the non-linear changes in both benign and malignant ovarian ultrasound images was used to develop classifiers. Our study shows that the decision tree classifier is capable of classifying benign and malignant conditions with a high accuracy of 97 %, sensitivity of 94.3 %, and specificity of 99.7 %. The developed classifier is robust as it was evaluated with 1,000 benign and 1,000 malignant samples using tenfold stratified cross-validation. The preliminary results obtained using the system show that the features are discriminative enough to yield good classification accuracy of 97 %. Moreover, the CAD tool would be a more objective alternative to manual analysis of ultrasound images which might result in inter-observer variations. The system can be installed as a stand-alone software application in the physician’s office at no extra cost. However, the system has been tested only on 20 cases, and further clinical validation will be required to assess the diagnostic accuracy of proposed method.
Contributor Information
S. Vinitha Sree, Phone: +1-916-7495628, Email: vinitha.sree@gmail.com.
Jasjit S. Suri, Email: jsuri@comcast.net
References
- 1.NCI (National Cancer Institute) on ovarian cancer. Information website http://www.cancer.gov/cancertopics/types/ovarian. Accessed October 4, 2011
- 2.Bast RC, Jr, Badgwell D, Lu Z, et al. New tumor markers: CA125 and beyond. Int J Gynecol Cancer. 2005;15:274–281. doi: 10.1111/j.1525-1438.2005.00441.x. [DOI] [PubMed] [Google Scholar]
- 3.Zaidi SI. Fifty years of progress in gynecologic ultrasound. Int J Gynaecol Obstet. 2007;99:195–197. doi: 10.1016/j.ijgo.2007.08.002. [DOI] [PubMed] [Google Scholar]
- 4.Menon U, Talaat A, Rosenthal AN, et al. Performance of ultrasound as a second line test to serum CA125 in ovarian cancer screening. BJOG. 2000;107:165–169. doi: 10.1111/j.1471-0528.2000.tb11685.x. [DOI] [PubMed] [Google Scholar]
- 5.Kim KA, Park CM, Lee JH, et al. Benign ovarian tumors with solid and cystic components that mimic malignancy. AJR Am J Roentgenol. 2004;182:1259–1265. doi: 10.2214/ajr.182.5.1821259. [DOI] [PubMed] [Google Scholar]
- 6.Lenic M, Zazula D, Cigale, B: Segmentation of ovarian ultrasound images using single template cellular neural networks trained with support vector machines. In: Proceedings of 20th IEEE International Symposium on Computer-Based Medical Systems, 2007, 205–212
- 7.Hiremath PS, Tegnoor JR: Recognition of follicles in ultrasound images of ovaries using geometric features. In: Proceedings of International Conference on Biomedical and Pharmaceutical Engineering, 2009, 1–8
- 8.Deng Y, Wang Y, Chen P: Automated detection of polycystic ovary syndrome from ultrasound images. In: Proceedings of the 30th Annual International IEEE EMBS Conference, 2008, 4772–4775 [DOI] [PubMed]
- 9.Sohail ASM, Rahman MM, Bhattacharya P, Krishnamurthy S, Mudur SP: Retrieval and classification of ultrasound images of ovarian cysts combining texture features and histogram moments. In: IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 2010, 288–291
- 10.Sohail ASM, Bhattacharya P, Mudur SP, Krishnamurthy S: Selection of optimal texture descriptors for retrieving ultrasound medical images. In: IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 2011, 10–16
- 11.Renz C, Rajapakse JC, Razvi K, Liang SKC: Ovarian cancer classification with missing data. In: Proceedings of 9th International Conference on Neural Information Processing 2, 2002, 809–813
- 12.Assareh A, Moradi MH: Extracting efficient fuzzy if-then rules from mass spectra of blood samples to early diagnosis of ovarian cancer. In: IEEE Symposium on Computational Intelligence and Bioinformatics and Computational Biology, 2007, 502–506
- 13.Tan TZ, Quek C, Ng GS, Razvi K. Ovarian cancer diagnosis with complementary learning fuzzy neural network. Artif Intell Med. 2008;43:207–222. doi: 10.1016/j.artmed.2008.04.003. [DOI] [PubMed] [Google Scholar]
- 14.Meng H, Hong W, Song J, Wang L: Feature extraction and analysis of ovarian cancer proteomic mass spectra. In: 2nd International Conference on Bioinformatics and Biomedical Engineering, 2008, 668–671
- 15.Tang KL, Li TH, Xiong WW, Chen K. Ovarian cancer classification based on dimensionality reduction for SELDI-TOF data. BMC Bioinforma. 2010;11:109. doi: 10.1186/1471-2105-11-109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Petricoin F. Use of proteomic patterns serum to identify ovarian cancer. Lancet. 2002;359:572–577. doi: 10.1016/S0140-6736(02)07746-2. [DOI] [PubMed] [Google Scholar]
- 17.Tailor A, Jurkovic D, Bourne TH, Collins WP, Campbell S. Sonographic prediction of malignancy in adnexal masses using an artificial neural network. Br J Obstet Gynaecol. 1999;106:21–30. doi: 10.1111/j.1471-0528.1999.tb08080.x. [DOI] [PubMed] [Google Scholar]
- 18.Brüning J, Becker R, Entezami M, Loy V, Vonk R, Weitzel H, et al. Knowledge-based system ADNEXPERT to assist the sonographic diagnosis of adnexal tumors. Methods Inf Med. 1997;36:201–206. [PubMed] [Google Scholar]
- 19.Biagiotti R, Desii C, Vanzi E, Gacci G. Predicting ovarian malignancy: application of artificial neural networks to transvaginal and color Doppler flow US. Radiology. 1999;210:399–403. doi: 10.1148/radiology.210.2.r99fe18399. [DOI] [PubMed] [Google Scholar]
- 20.Zimmer Y, Tepper R, Akselrod S. An automatic approach for morphological analysis and malignancy evaluation of ovarian masses using B-scans. Ultrasound Med Biol. 2003;29:1561–1570. doi: 10.1016/j.ultrasmedbio.2003.08.013. [DOI] [PubMed] [Google Scholar]
- 21.Lucidarme O, Akakpo JP, Granberg S, et al. A new computer-aided diagnostic tool for non-invasive characterisation of malignant ovarian masses: results of a multicentre validation study. Eur Radiol. 2010;20:1822–1830. doi: 10.1007/s00330-010-1750-6. [DOI] [PubMed] [Google Scholar]
- 22.Bellman RE: Dynamic programming. Chemsford, MA: Courier Dover Publications, 2003
- 23.Hata T, Yanagihara T, Hayashi K, Yamashiro C, et al. Three-dimensional ultrasonographic evaluation of ovarian tumours: a preliminary study. Hum Reprod. 1999;14:858–861. doi: 10.1093/humrep/14.3.858. [DOI] [PubMed] [Google Scholar]
- 24.Laban M, Metawee H, Elyan A, Kamal M, Kamel M, Mansour G. Three-dimensional ultrasound and three-dimensional power Doppler in the assessment of ovarian tumors. Int J Gynaecol Obstet. 2007;99:201–205. doi: 10.1016/j.ijgo.2007.03.027. [DOI] [PubMed] [Google Scholar]
- 25.Cohen LS, Escobar PF, Scharm C, Glimco B, Fishman DA. Three-dimensional power Doppler ultrasound improves the diagnostic accuracy for ovarian cancer prediction. Gynecol Oncol. 2001;82:40–48. doi: 10.1006/gyno.2001.6253. [DOI] [PubMed] [Google Scholar]
- 26.Okugawa K, Hirakawa T, Fukushima K, Kamura T, Amada S, Nakano H. Relationship between age, histological type, and size of ovarian tumors. Int J Gynaecol Obstet. 2001;74:45–50. doi: 10.1016/S0020-7292(01)00406-4. [DOI] [PubMed] [Google Scholar]
- 27.Webb JAW. Ultrasound in ovarian carcinoma. In: Reznek R, editor. Cancer of the ovary. Cambridge: Cambridge University Press; 2006. pp. 94–111. [Google Scholar]
- 28.Guerriero S, Alcazar JL, Pascual MA, Ajossa S, Gerada M, Bargellini R, Virgilio B, Melis GB. Intraobserver and interobserver agreement of grayscale typical ultrasonographic patterns for the diagnosis of ovarian cancer. Ultrasound Med Biol. 2008;34:1711–1716. doi: 10.1016/j.ultrasmedbio.2008.04.007. [DOI] [PubMed] [Google Scholar]
- 29.Testa AC, Gaurilcikas A, Licameli A, Mancari R, Di Legge A, Malaggese M, Mascilini F, Zannoni GF, Scambia G, Ferrandina G. Sonographic features of primary ovarian fibrosarcoma: a report of two cases. Ultrasound Obstet Gynecol. 2009;33:112–115. doi: 10.1002/uog.6291. [DOI] [PubMed] [Google Scholar]
- 30.Park SB, Lee JW, Kim SK. Content-based image classification using a neural network. Pattern Recogn Lett. 2004;25:287–300. doi: 10.1016/j.patrec.2003.10.015. [DOI] [Google Scholar]
- 31.Gonzalez C, Woods RE: Digital image processing, New Jersey: Prentice Hall, 2001
- 32.Fortin C. Fractal dimension in the analysis of medical images. IEEE Eng Med Biol. 1992;11:65–71. doi: 10.1109/51.139039. [DOI] [Google Scholar]
- 33.Mandelbrot BB. The fractal geometry of nature. NY: WH Freeman Ed; 1982. [Google Scholar]
- 34.Biswas MK, Ghose T, Guha S, Biswas PK. Fractal dimension estimation for texture images: a parallel approach. Pattern Recogn Lett. 1998;19:309–313. doi: 10.1016/S0167-8655(98)00002-6. [DOI] [Google Scholar]
- 35.Haralick RM, Shanmugam K, Dinstein I. Textural features for image classification. IEEE Trans Syst Man Cybern. 1973;SMC-3:610–621. doi: 10.1109/TSMC.1973.4309314. [DOI] [Google Scholar]
- 36.Ramana KV, Ramamoorthy B. Statistical methods to compare the texture features of machined surfaces. Pattern Recognition. 1996;29:1447–1459. doi: 10.1016/0031-3203(96)00008-8. [DOI] [Google Scholar]
- 37.Galloway MM. Texture classification using gray level run length. Comput Graph Image Process. 1975;4:172–179. doi: 10.1016/S0146-664X(75)80008-6. [DOI] [Google Scholar]
- 38.Nikias C, Petropulu A: Higher-order spectral analysis, Englewood Cliffs, NJ: Prentice-Hall, 1997
- 39.Chua KC, Chandran V, Acharya UR, Lim C: Application of higher order spectra to identify epileptic EEG. J Med Syst 1–9, 2010. doi:10.1007/s10916-010-9433-z [DOI] [PubMed]
- 40.Acharya UR, Chua KC, Lim TC, Dorithy, Suri JS. Automatic identification of epileptic EEG signals using nonlinear parameters. J Med Mech Biol. 2009;9:539–553. doi: 10.1142/S0219519409003152. [DOI] [Google Scholar]
- 41.Chua KC, Chandran V, Acharya UR, Lim CM. Analysis of epileptic EEG signals using higher order spectra. J Med Eng Technol. 2009;33:42–50. doi: 10.1080/03091900701559408. [DOI] [PubMed] [Google Scholar]
- 42.Ramm A, Katsevich A: The Radon transform and local tomography. Boca Raton, FL: CRC Press, 1996
- 43.Box JF. Guinness, gosset, fisher, and small samples. Statist Sci. 1987;2:45–52. doi: 10.1214/ss/1177013437. [DOI] [Google Scholar]
- 44.Larose DT: Decision trees. In: Discovering knowledge in data: an introduction to data mining, New Jersey, USA: Wiley Interscience, 2004: 108–126
- 45.Acharya UR, Sree SV, Krishnan MM, Saba L, Molinari F, Guerriero S, Suri JS: Ovarian tumor characterization using 3D ultrasound. Technol Cancer Res Treat, 11:543-552;2012 [DOI] [PubMed]
- 46.Philpotts LE. Can computer-aided detection be detrimental to mammographic interpretation? Radiology. 2009;253(1):17–22. doi: 10.1148/radiol.2531090689. [DOI] [PubMed] [Google Scholar]