pH-sensitive residues in the p19 RNA silencing suppressor protein from carnation Italian ringspot virus affect siRNA binding stability

Abstract

Tombusviruses, such as Carnation Italian ringspot virus (CIRV), encode a protein homodimer called p19 that is capable of suppressing RNA silencing in their infected hosts by binding to and sequestering short-interfering RNA (siRNA) away from the RNA silencing pathway. P19 binding stability has been shown to be sensitive to changes in pH but the specific amino acid residues involved have remained unclear. Using constant pH molecular dynamics simulations, we have identified key pH-dependent residues that affect CIRV p19–siRNA binding stability at various pH ranges based on calculated changes in the free energy contribution from each titratable residue. At high pH, the deprotonation of Lys60, Lys67, Lys71, and Cys134 has the largest effect on the binding stability. Similarly, deprotonation of several acidic residues (Asp9, Glu12, Asp20, Glu35, and/or Glu41) at low pH results in a decrease in binding stability. At neutral pH, residues Glu17 and His132 provide a small increase in the binding stability and we find that the optimal pH range for siRNA binding is between 7.0 and 10.0. Overall, our findings further inform recent experiments and are in excellent agreement with data on the pH-dependent binding profile.

Introduction

RNA silencing (or RNA interference [RNAi])^1–3 is an evolutionarily conserved gene inactivation pathway in eukaryotes that involves the conversion of long double-stranded RNA (dsRNA) into 21–24 nucleotide-long short-interfering RNA (siRNA) or microRNA (miRNA) by DICER, an enzyme that is a part of the endoribonuclease family of proteins.⁴ These small RNAs are then separated into individual strands, incorporated into a multiprotein complex called RNA-induced silencing complex (RISC),⁵ and ultimately used to target the degradation of reasonably complementary messenger RNA (mRNA). In plants, RNA silencing has evolved into a mechanism that can respond to both endogenous and exogenous dsRNA, the latter of which helps to defend against transgenes, transposons, and infection by RNA viruses. As a result, Tombusviruses such as Tomato bushy stunt virus (TBSV) and Carnation Italian ringspot virus (CIRV) have evolved an elegant 19 kDa protein, aptly named p19, which is capable of suppressing RNA silencing in its host by binding to and sequestering siRNA from a RISC.^{6, 7}

X-ray structures of p19 bound to a 21 nucleotide (nt) siRNA have been crystallized from TBSV⁸ and CIRV.⁹ In both structures, p19 exists as a homodimer and is composed of five α-helices and four β-strands in each monomer (Fig. 1). Key tryptophan residues, shown experimentally and computationally to be crucial for siRNA recognition, form end-capping calipers around the RNA by stacking with the exposed terminal base pairs.^8–10 Three conserved lysine residues (Lys60, Lys67, and Lys71) found in the β-sheet–RNA interface form important sequence-independent interactions with the siRNA phosphate backbone.^{8, 9} Mutations of Lys60 and Lys71 to alanine in TBSV have displayed decreases in the lethal necrosis phenotype.^{11, 12} Recent experiments have also identified two cysteine residues that appear to be responsible for maintaining the overall structural integrity of the p19 protein as modifications of these cysteines (Cys110 and Cys134 in CIRV) resulted in a reduction of siRNA binding activity.^{13, 14}

Figure 1.

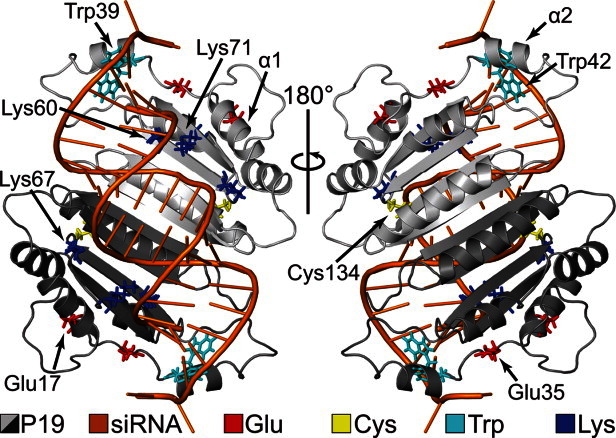
CIRV p19–siRNA complex. The complex has been rotated by 180° (PDBID: 1RPU).

Over the past few years, p19 has been used in several systems to suppress RNAi^15–22 and has also emerged as a valuable tool for characterizing small RNAs.^8,9,23–26 Furthermore, as environmental factors (e.g., acidity/alkalinity, salt concentration, water levels, etc.) can vary significantly across different plant hosts, it has become increasingly important to understand how the protein environment can affect the function of p19. Recent investigations using fluorescence detection assays have revealed that CIRV p19 has the most significant affinity for 21-nt siRNA in the pH range from 6.0 to 9.0.²⁷ More specifically, it was shown that p19–siRNA binding is dependent on three apparent pK_a values, 7.1, 8.0, and 10.6, that were hypothesized to correspond to one or more histidine, cysteine, and lysine residues, respectively. However, due to the limited resolution of the experiment, the identity of these ionizable residues has remained unknown. Therefore, it is necessary to consider alternative approaches.

Computational methods using molecular dynamics (MD) simulations an/or Monte Carlo (MC) sampling have been developed with considerable success for predicting protein pK_a values (see reviews^28–30). Often referred to as constant pH MD (CPHMD) simulations, the titration coordinate is typically implemented in either a discrete manner^31–43 where protonation states are modified with an MC step at some regular MD interval or using a continuous function^44–46 that describes the protonation state via the λ dynamics method developed by Brooks and coworkers.^47–49 Recent studies have shown that CPHMD is a reliable and robust method that is capable of predicting pK_a values in a variety of biomolecular systems.^50–56 Thus, to uncover the pH-dependent residues in the CIRV p19 protein involved in siRNA binding stability, we have carried out CPHMD simulations^44–46 of the p19 protein dimer in both holo (siRNA-bound) and apo (siRNA-free) forms and determined the pK_a values for all titratable residues. These results were then used to calculate the pH-dependent siRNA binding stability profile and corresponding pH-dissociation constant profile. Details of the conformational dynamics for important titratable residues at different pH conditions were also investigated and the results were compared with experiment.

Results

CPHMD simulation stability

CPHMD simulations ranging from pH 1 to 14 were performed for both apo and holo systems and the C_α-root-mean-square deviation (RMSD) relative to the crystal structure at different pHs is shown in Supporting Information Figure S1. In general, the apo simulations demonstrated larger average C_α-RMSDs than the holo simulations. The largest C_α-RMSD was ∼5.3 Å among all apo simulations (at pH 2) and ∼3.7 Å from all holo simulations (at pH 14). Visual inspection of the protein structure from the apo simulations revealed that the p19 core and RNA-binding interface (residues 55–152) were very stable. Instead, the elevated p19 C_α-RMSDs in the apo systems came from the increased dynamics of the α2-helix (residues 39–45) from both monomers (Fig. 1 and Supporting Information Fig. S2). In the holo system, α2 is connected to the N-terminal α1-helix (residues 9–17) by a long flexible linker (residues 18–38) and contains important tryptophan residues (Trp39 and Trp42) that form end-capping calipers around the terminal base pairs of the siRNA.⁹ In the apo simulations, these base stacking interactions are lost due to the absence of RNA which resulted in an increase in α2 dynamics and, to a lesser extent, α1 dynamics.

pK_a values calculated from holo and apo simulations

The pK_a values for each Glu, Asp, His, Cys, and Lys residue were obtained by fitting their simulated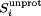 values (combined from both monomers) to the Henderson–Hasselbalch equation (see Materials and Methods section). The calculated results are summarized in Table I and Supporting Information Table S1.

Table I.

pK_aValues^aCalculated from CPHMD for the Holo and Apo States

Residue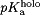
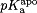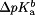Asp9	4.17	3.51	0.66
Glu12	5.29	4.30	1.00
Glu17	4.94	6.15	-1.20
Asp20	5.54	4.48	1.06
Asp34	3.56	2.41	1.15
Glu35	5.97	5.20	0.77
Glu41	4.75	4.24	0.51
Lys60	11.11	8.94	2.17
Lys67	11.43	10.26	1.18
Lys71	12.00	9.93	2.06
His132	5.76	6.39	-0.63
Cys134	10.93	10.05	0.88
Glu151	5.15	4.59	0.56

^aOnly pK_a values with 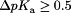are displayed. A full list pK_a values for all titratable residues is provided in Supporting Information Table S1.

^b .

Effects of pH on p19–siRNA binding

The net charge of both holo and apo p19 as a function of pH was determined from the computed pK_a values [Fig. 2(A)]. Overall, both systems became progressively more negative as the pH was increased until all 26 titratable residues were completely deprotonated. The apo form of the protein was found to be more negatively charged than the holo form except between pH 6 and 8 where the total charge of both forms of the protein was nearly the same. Substituting the pK_a values into the Wyman–Tanford linkage equation, we calculated the pH-dependent changes in the total binding stability ( ) as well as the individual contributions from each titratable residue [Figs. 2(B) and 3]. At pH > 9, the deprotonation of several conserved lysine residues (Lys60, Lys67, and Lys71) and a nonconserved cysteine residue (Cys134) led to a large destabilization in siRNA binding by about 14.0 kcal/mol. Upon deprotonation at 4 < pH < 6, several acidic residues (Asp9, Glu12, Asp20, Glu35, and Glu41) destabilized the protein–siRNA complex by ∼7 kcal/mol. Changes in the binding stability were smallest (<1.0 kcal/mol) between pH 6 and 8, which is consistent with the lack of difference in net charge between both apo and holo systems in the same pH range. Only deprotonation of Glu17 and His132 contributed significantly to stabilizing the siRNA-bound complex in this pH range.

Figure 2.

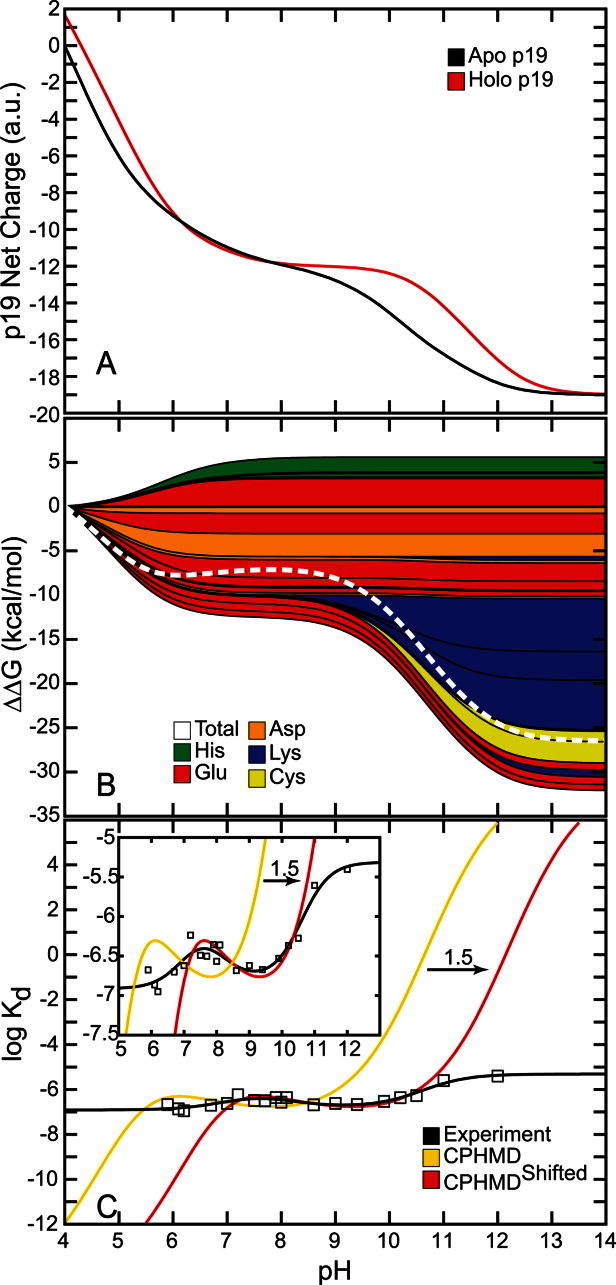
Effects of pH on p19–siRNA binding. (A) Net charge of the holo and apo p19. (B) Total binding stability (white) and per residue contributions to binding stability (colors). Positive values increase binding stability (i.e., favors holo form) while negative values destabilizes binding (i.e., favors apo form). (C) pH-dependent dissociation constant profiles compared with experiment. CPHMD^shifted (red) is identical to CPHMD (yellow) except that it is shifted to the right by 1.5 pH units for comparison with experiment (black).

Figure 2(C) shows the dissociation constant profile and a modified profile in comparison with the experimentally determined profile from Koukiekolo et al.²⁷ The unmodified log K_d profile showed minimal change over the last 5 ns of production simulation (see Supporting Information Fig. S3) and was in close agreement with the experimental profile. A much better match with experiment was achieved in the modified profile (CPHMD^shifted), which was shifted by 1.5 pH units relative to the unmodified profile [see Fig. 2(C) and inset].

pH-dependent conformational dynamics

Various pH-dependent intraprotein and protein–RNA interactions were assessed from the holo simulations (Fig. 4). Deprotonation of Lys60 and Lys67 showed a drastic decrease in Lys–RNA salt bridge formation [Supporting Information Fig. S2 and Fig. 4(A, B)]. However, Lys71, in its neutral form, only displayed a moderate decrease in Lys–RNA interactions [Fig. 4(C)]. Next, measuring the solvent accessible surface area (SASA) for the Cys134 sulfur atom revealed that its side chain was essentially buried when in its reduced form and was much more solvent exposed when negatively charged [Fig. 4(D)]. Upon ionization, Glu17 and Glu35 formed more stable salt bridges with Arg72 and Arg85, respectively [Supporting Information Fig. S2 and Fig. 4(E, F)]. Formation of the Glu35–Arg85 salt bridge also appears to stabilize the Trp39–RNA base stacking interactions but has little to no effect on Trp42–RNA interactions [Supporting Information Fig. S2 and Fig. 4(G, H)].

Figure 4.

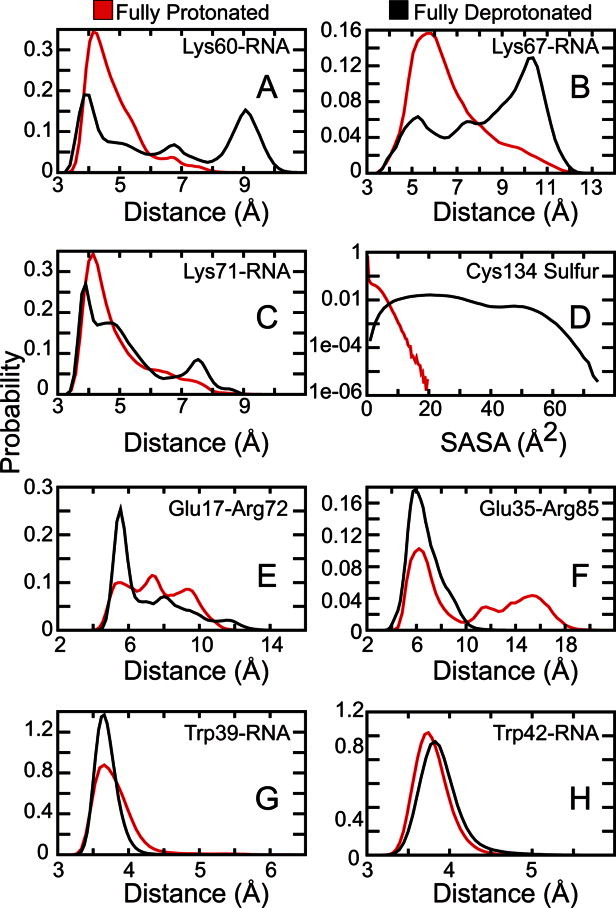
Conformational dynamics of key intraprotein and protein–RNA interactions. Lys–RNA and Glu–Arg distances correspond to salt bridge interactions. Trp–RNA distances and Cys SASA correspond to end-capping interactions and the solvent accessible surface area (SASA) for the cysteine sulfur atom, respectively. See Materials and Methods section for more detail.

Discussion

The primary goal of this study was to assess the overall p19–siRNA binding stability and to identify the important pH-sensitive residues that affect siRNA binding. Previously, Koukiekolo et al. hypothesized that p19–siRNA binding is dependent on the ionization of one or more histidine, cysteine, and lysine residues.²⁷ They determined this by fitting fluorescence data to an equation that represents the titration of three apparent pK_a values (found to be 7.1, 8.0, and 10.6) and then attributed these numbers to a particular type of residue based on each residue's reference pK_a value. However, the detailed resolution needed to pinpoint the residues associated with these experimental pK_a values is well beyond the capacity of their assays. Thus, using atomic-level resolution CPHMD simulations, we have computed pK_a values for 26 titratable residues from the p19 protein dimer in both holo and apo systems and compared our results with the current literature. As pointed out previously, the observed changes in the binding stability are likely the result of the deprotonation/protonation of titratable residues that interact with the siRNA and/or the result of local pH-sensitive changes that affect the structural integrity of the p19 protein.²⁷

Overall, the 14 holo and 14 apo CPHMD simulations showed remarkable stability in the p19 structure as demonstrated by their C_α-RMSD in different pH environments (Supporting Information Fig. S1). This structural stability is consistent with traditional explicit solvent MD simulations of CIRV p19 with fixed protonation states.¹⁰ The holo simulations displayed slightly lower C_α-RMSD values compared with the apo systems due to the presence of the siRNA. Visual inspection of the apo p19 simulations showed that the differences in RMSD were caused by the loss of Trp39/Trp42–RNA end-capping interactions which resulted in a significant increase in the α2-helix dynamics along with added mobility in the α1-helix (Fig. 1 and Supporting Information Fig. S2). The flexibility found in the N-terminal region of p19 is in line with a model where a negatively charged siRNA first binds to the positively charged p19 β-sheet surface and then the tryptophan residues act as calipers to measure the length of the bound dsRNA by stacking with the terminal base pairs.^{9, 10}

Using the pK_a values calculated from all 26 titratable residues in the holo and apo p19 simulations (Table I and Supporting Information Table S1), we computed the net charge of both p19 systems as well as the pH-dependent binding stability ( ) of the entire system and for each titratable residue [Fig. 2(A, B)]. > 0 increases binding stability while < 0 decreases binding stability. Overall, both systems became more negative as each titratable residue was deprotonated due to an increase in pH and, in general, the net charge of the holo system was more positive than the apo system [Fig. 2(A)]. This was expected as a more negative net charge would result in siRNA dissociation due to the charge–charge repulsion between the negatively charged siRNA and the protein in the holo system. Between pH 6 and pH 8, the total charge for both systems was nearly identical. It is also interesting to note that, with the exception of Cys134 (not conserved) and His132 (charged conserved as arginine), 11 of the 13 titratable residues found to contribute significantly to the binding stability (Table I) are well conserved across the Tombusvirus p19 family⁹ which generally implies some level of functional importance.

At pH > 9, the side chains of Lys60, Lys67, and Lys71 become neutralized and, as a result, their direct interactions with the negatively charged siRNA backbone are reduced [Figs. 3 and 4(A–C)]. Deprotonation of these three conserved residues has the largest destabilizing effect on siRNA binding as reflected in the 14.0 kcal/mol drop in free energy [Fig. 2(B)]. This is consistent with past mutations of Lys60 and Lys71 that resulted in decreases in the lethal necrosis phenotype.^{11, 12} Thus, we hypothesize that mutating one or more of these lysine residues to arginine, which has a much higher pK_a and therefore would remain positively charged, may help to increase the binding stability at higher pH ranges. In addition, Cys134 was found to be highly solvent exposed when it is deprotonated [Figs 3 and 4(D)]. Koukiekolo et al. suggested that the role of the cysteine amino acid is to preserve the structural integrity of the protein and that the deprotonation of cysteine (or other titratable residues) could lead to structural changes that could either destabilize the p19 dimer or the p19–siRNA complex.^13,14,27 From our simulations, we suggest that Cys134 becomes more solvent exposed to prevent having a buried charge that could affect the stability of the local p19 structure. Therefore, we proffer that mutation of Cys134 to its isosteric equivalent, serine, may be beneficial to the CIRV p19 binding affinity.

Figure 3.

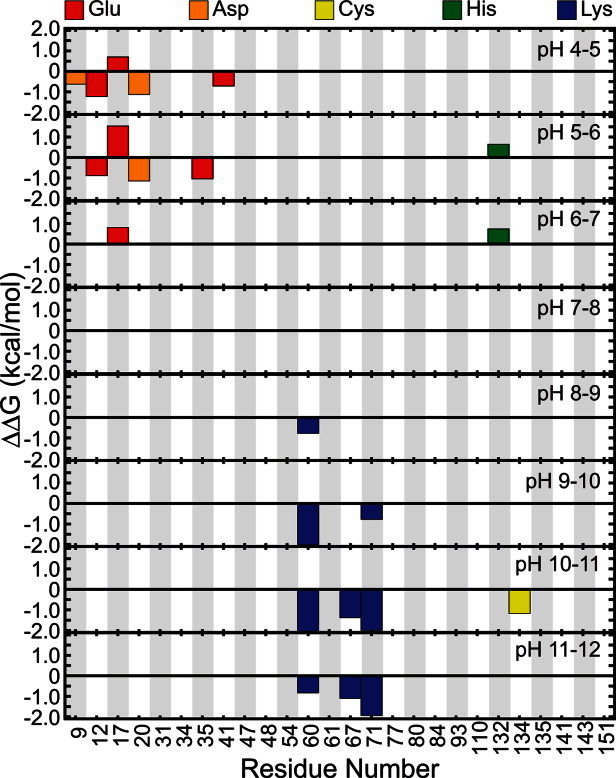
Individual contributions to binding stability at different pH ranges. Negative and positive contributions to binding stability will have and 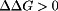, respectively, for a given titratable residue. Only residues with 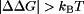are shown where 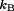is the Boltzmann constant and T is the temperature (298 K).

At 4 < pH < 6, deprotonation of Glu35 not only facilitates the formation of a salt bridge with Arg85 [Figs 3 and 4(F)] but it also leads to an increase in base stacking interactions between the nearby Trp39 and terminal RNA base pair [Fig. 4(G)]. Surprisingly, the Trp42–RNA base stacking interactions were not affected [Fig. 4(H)]. Glu12 and Asp20 are located near the p19–siRNA binding surface and likely destabilize the complex once they are deprotonated by conferring strong electrostatic repulsion with the siRNA (Fig. 3). Based on this observation, we hypothesize that replacing Glu12 and/or Asp20 to neutral glutamine and asparagine, respectively, would increase the overall binding stability.

At neutral pH, there was a small increase in 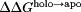that was caused by the deprotonation of Glu17 and His132 [Figs. 2(B) and 3]. In the crystal structure, His132 is positioned beside a buried Arg117 which is expected to be structurally less stable when both residues are protonated.⁹ We speculate that the neutralization of His132 reduces the local concentration of positive charges and ultimately stabilizes the p19 structure. In contrast, ionized Glu17 appears to facilitate the positioning of key lysine residues (Lys60, Lys67, and Lys71) along the protein–RNA interface by forming salt bridge interactions with Arg72 [Supporting Information Fig. S2 and Fig. 4(E)]. However, detailed correlation analyses revealed that the Glu17–Arg72 salt bridge formation and the Lys–RNA interactions are basically uncorrelated (with correlation coefficients, R, between −0.04 and 0.22). Alternatively, it has also been proposed that the Glu17–Arg72 salt bridge (and possibly Glu35–Arg85 and Glu41–Arg75 salt bridges) may play a role in positioning the end-capping tryptophan residues.^{9, 10} The importance of this specific salt bridge is further illustrated by previous studies that swapped Arg72 for glycine and found that the activity of p19 was severely compromised.^11,12,57,58

The computed dissociation constant profile [Fig. 2(C)] showed little change after the first 15 ns of production simulation time (Supporting Information Fig. S3) and was in good agreement with experiment.¹³ This suggests that the results from the CPHMD simulations were converged. Also, a much better correspondence with experiment was obtained when we shifted the dissociation constant profile horizontally by 1.5 pH units [see “CPHMD^shifted” in Fig. 2(C) and inset]. The shift in the log K_d profile can be attributed to an underestimation of the desolvation energy and has been shown to lead to a systematic underestimation of the pK_a values (from which the dissociation constant profiles are derived).⁵⁹ Henceforth, discussions of the computed dissociation constant profile will be in reference to the shifted profile (CPHMD^shifted).

The optimal range for siRNA binding appears to be between pH 7 and 10 where the binding stability fluctuates between −7.0 ≤ log K_d ≤ −6.5 [Fig. 2(C)]. From our simulations, we can attribute the highest experimentally observed pK_a of 10.6²⁷ to residues Lys60, Lys67, Lys71, and Cys134 (Fig. 3). These residues demonstrated the largest reduction in binding stability at high pH [Fig. 2(B)] and are excellent candidates for further mutational studies (see discussion above). Similarly, the lowest experimental pK_a value, 7.1, can be assigned to multiple residues (i.e., Asp9, Glu12, Asp20, Glu35, and/or Glu41) (Fig. 3). Ionization of all these residues appeared to have a synergistic destabilizing effect on the p19–siRNA complex. Finally, the last observed apparent pK_a of 8.0 corresponded to residues Glu17 and His132. These two residues were the only groups that were beneficial for significantly increasing the binding affinity upon deprotonation and we found them to be important for maintaining the structural integrity of p19.

Conclusions

In summary, we presented CPHMD simulations of a large protein–RNA complex in implicit solvent. Overall, the results agree well with experiment. We identified several titratable residues that are highly pH-dependent and that could be assigned to experimentally observed pK_a values. Lys60, Lys67, Lys71, and Cys134 appear to affect binding stability at pH > 9 while several glutamic and aspartic acids destabilize the complex at pH < 6. These residues were found to be important for maintaining the stability of the protein structure and/or for siRNA binding. The optimal pH range for siRNA binding is from about 7.0 to 10.0 and is largely stabilized by Glu17 and His132.

The CPHMD method has developed into an accurate and powerful tool for predicting protein pK_a values³⁰ and for generating pH-dependent binding stability curves that can be directly compared with experiment. Ultimately, identifying the key pH-sensitive residues using the CPHMD approach would allow us to design p19 proteins that have a higher affinity for siRNA which could be used to characterize RNA silencing complexes, to manage cellular levels of siRNA levels, and for discriminating between single-stranded RNA and dsRNA, and so forth.^13,23,26,60 Furthermore, understanding the pH-dependence of the viral protein could enable us to engineer plants that can survive outside of the virulent pH range and avoid infection altogether. This study clearly illustrates the value of complementing experiment with theoretical techniques and offers results that can be further validated.

Materials and Methods

Simulation setup

The CIRV p19 X-ray crystal structure bound to a 21-nt siRNA (PDBID: 1RPU)⁹ was used as our model. The unresolved short linker (residues 49–54) in each protein monomer was constructed using MODELLER^{61, 62} and the loop modeling facility in the MMTSB Tool Set.⁶³ Missing hydrogen atoms were added using the HBUILD algorithm in the CHARMM simulation package.⁶⁴ The holo (siRNA-bound) and apo (siRNA-free) systems contain 5889 and 4551 atoms, respectively. All simulations were performed in implicit solvent using the generalized born with a simple switching (GBSW) model^{65, 66} implemented in CHARMM along with the CHARMM27 protein–nucleic acid force field^{67, 68} and an energy correction map (CMAP).⁶⁹ A 50 ps⁻¹ friction coefficient was used for Langevin dynamics and the experimental salt concentration of 0.1 M²⁷ was simulated using the Debye–Hückel model for screening charge–charge interactions.⁷⁰ Consistent with previous GBSW simulations, the nonpolar surface tension coefficient was set to 0.005 kcal/mol/Å^253,65,71,72 and a switching cutoff that reduces the electrostatic solvation and van der Waals contributions to zero beginning from 20 Å to 24 Å was used. Optimized atomic radii for proteins^{65, 73} and nucleic acids⁷⁴ were used in place of the standard van der Waals radii for the GBSW calculations. The siRNA was harmonically restrained to its initial starting position using a 2 kcal/mol/Ų force constant to prevent large structural changes in the RNA. Both holo and apo systems were energy minimized and heated up slowly to a final temperature of 298 K followed by 500 ps of equilibration using a 1 fs simulation time step. All molecular images were created using PyMOL.⁷⁵

Constant pH MD simulations and pK_a calculations

A total of 28 independent simulations (14 for siRNA-bound and 14 for siRNA-free) ranging from pH 1 to 14 were conducted using the CPHMD methodology.^44–46 Each simulation was 25 ns long and resulted in a cumulative simulation time of 0.7 μs. The first 5 ns of each simulation were discarded in the analysis so that all 28 production simulations were each 20 ns long. Atomic charges for protonated and unprotonated states of aspartic acid, glutamic acid, histidine, lysine, and cysteine have been described previously.^44,68,76,77 Arginines, whose model pK_a value is typically ∼12,⁷⁸ were kept permanently in its protonated form because CIRV p19 was found experimentally to be unstable at pH > 12²⁷ All titratable residues were simulated following the CPHMD method originally developed in the Brooks research group where a continuous titration coordinate, 0 > λ_i ≤ 1, controls the protonation state for the ith titratable residue.^44–46 In that model, λ_i = 1 and λ_i = 0 correspond to the fully unprotonated and fully protonated states, respectively, and N(λ_i) is the number of simulation snapshots with protonation state λ. However, to increase the number of times that a titratable residue is considered to be fully protonated (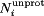 ) or fully unprotonated ( 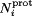), we have defined a more generous cutoff for λ:

(1)

Thus, the fraction of unprotonated states, , is given by:

(2)

and the pK_a of the ith titratable residue can be calculated by fitting a set of S^unprot (at different pH values) to the standard Hendersen–Hasselbalch equation:

(3)

where n represents the Hill coefficient. It has been discussed previously that small deviations in the Hill coefficient away from 1 have a negligible effect on the free energy^{53, 54} and, indeed, we find only small differences in n during the curve fitting process. Thus, we have set n = 1 for all our calculations. Finally, due to the fact that the experimentally determined pK_a values were extracted from a homodimer, we have combined the data from both monomers to effectively double the sampling for calculating and its corresponding pK_a.

pH-dependent binding stability and pH-dissociation constant profiles

The pH-dependent binding stability profile was calculated using the Wyman–Tanford linkage equation^{79, 80}:

(4)

where 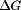is the dissociation free energy, R is the gas constant, and T is the temperature in Kelvins. is the difference in the net charge between the holo and apo states at a particular pH and is calculated from:

(5)

The average charge of the system, 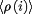, is obtained from:

(6)

where , defined previously,⁸¹ is equal to 1 or −1 for a basic and acidic group, respectively. Integrating Eq. (4) after substituting in Eqs. (5) and (6) gives the dissociation free energy at a given pH relative to a reference pH (pH_ref):

(7)

where 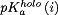and 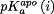are the pK_as for the holo and apo states, respectively. The final summation in Eq. (7) allows the binding stability to be decomposed into contributions from each titratable residue. The final dissociation constant profile was then computed by applying the basic relation:

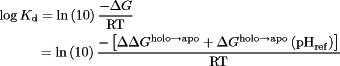(8)

where is the dissociation constant. However, as Eq. (7) gives us 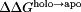, then the resulting 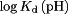in Eq. (8) at any given pH depends on 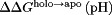and 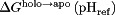, the latter of which is a constant. Thus, 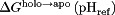was chosen to allow the best match of 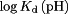to experiment.

Side chain conformational dynamics

Motivated by previous discussions,^8,9,27 the conformational dynamics of several different intraprotein and protein–RNA interactions were analyzed (from the holo simulations) by comparing the normalized probability of an interaction when a particular titratable side chain is either fully protonated ( ) or fully deprotonated ( ). Glu–Arg salt bridge distances were measured from the Glu-C_δ atom to the Arg-C_ζ atom. Trp–RNA base stacking distances were measured from the center-of-mass of the Trp side chain (not titrated) to the center-of-mass of the closest RNA base. Lys–RNA salt bridges were measured from the Lys-N_ζ atom to the closest RNA backbone phosphorus atom. The SASA was measured for the Cys-S_γ atom.

Glossary

Abbreviations

CIRV

carnation Italian ringspot virus

CPHMD

constant pH molecular dynamics

dsRNA

double-stranded RNA

MC

Monte Carlo

MD

molecular dynamics

miRNA

microRNA

RISC

RNA-induced silencing complex

RMSD

root mean squared deviation

RNAi

RNA interference

S_unprot

fraction of unprotonated states

siRNA

short-interfering RNA

TBSV

tomato bushy stunt virus

Supplementary material

Additional Supporting Information may be found in the online version of this article.