Different minimally important clinical difference (MCID) scores lead to different clinical prediction rules for the Oswestry disability index for the same sample of patients

Abstract

Background:

Minimal clinically important difference (MCID) scores for outcome measures are frequently used evidence-based guides to gage meaningful changes. There are numerous outcome instruments used for analyzing pain, disability, and dysfunction of the low back; perhaps the most common of these is the Oswestry disability index (ODI). A single agreed-upon MCID score for the ODI has yet to be established. What is also unknown is whether selected baseline variables will be universal predictors regardless of the MCID used for a particular outcome measure.

Objective:

To explore the relationship between predictive models and the MCID cutpoint on the ODI.

Setting:

Data were collected from 16 outpatient physical therapy clinics in 10 states.

Design:

Secondary database analysis using backward stepwise deletion logistic regression of data from a randomized controlled trial (RCT) to create prognostic clinical prediction rules (CPR).

Participants and Interventions:

One hundred and forty-nine patients with low back pain (LBP) were enrolled in the RCT. All were treated with manual therapy, with a majority also receiving spine-strengthening exercises.

Results:

The resultant predictive models were dependent upon the MCID used and baseline sample characteristics. All CPR were statistically significant (P < 001). All six MCID cutpoints used resulted in completely different significant predictor variables with no predictor significant across all models.

Limitations:

The primary limitations include sub-optimal sample size and study design.

Conclusions:

There is extreme variability among predictive models created using different MCIDs on the ODI within the same patient population. Our findings highlight the instability of predictive modeling, as these models are significantly affected by population baseline characteristics along with the MCID used. Clinicians must be aware of the fragility of CPR prior to applying each in clinical practice.

Introduction

In today’s healthcare environment an increased focus on providing cost-efficient care without compromising patient outcome has emphasized the importance of sound clinical decision making. A key element in clinical decision making is the ability to gage when meaningful changes occur in the patient’s condition. Minimal clinically important difference (MCID) scores for outcome measures are frequently used evidence-based guides to gage meaningful changes.¹ A MCID score is defined as the minimal change in score on an outcome instrument that coincides with the patient’s perception of beneficial change or recovery.² The MCID score is a single ‘cut point’, that is, a point estimate that either represents a change in the score (initial score minus the final score or a percentage-based change score from baseline) or a particular value for the final score.

As stated, MCID scores are calculated for a number of different outcome instruments. There are numerous outcome instruments used for analyzing pain, disability, and dysfunction of the low back; perhaps the most common of these is the Oswestry disability index (ODI). The ODI is a self-administered questionnaire containing 10 sections including pain intensity, personal care, lifting, walking, sitting, standing, sleeping, sex life, social life, and traveling. Each section contains six statements that are scored from 0 to 5, with 0 representing no difficulty in the activity and 5 representing maximal difficulty. The scores from each section are totaled and divided by the total possible score to obtain a final percentage of disability, with a higher per cent indicating greater disability.³ The ODI is a valid, reliable, and responsive clinical tool for analyzing disability status in individuals with low back pain (LBP).^2,4,5

A single agreed-upon MCID score has yet to be established for the ODI.¹ There have been a number of suggestions for MCIDs, which have mostly been represented by required change scores that have been anchored to a patient’s perception of clinical importance. Minimal clinically important difference change score cutpoints for the ODI that have been advocated include: 50% change,⁶ 30% change,^7,8 17-point change,⁹ 10-point change,^10,11 and 5- (and sometimes 6-) point change.^12–14 The creators³ of the ODI suggested that a final ODI score of ≤20% represented no disability. To our knowledge, the assumption that an ODI score of ≤20% represents no disability has not been supported beyond the original publication.³

For obvious reasons, this lack of clarity for the proper MCID may cause confusion among clinicians. In an attempt to explain the variations, authors have suggested a multitude of reasons for MCID variances, including: (i) the lack of a standardized methodological calculation approach;¹ (ii) the patient recall bias when using an anchor-based calculation approach;^1,15 (iii) the dependence on the sample size and lack of patient perspective when using distribution-based calculations;^1,16,17 and (iv) the influence of patient demographics and baseline characteristics.^1,18,19 Worth noting is that depending on interpretation by a clinician one may find very different results when scrutinizing the effectiveness of a particular intervention. For example, adoption of a MCID may result in fewer ‘successes’ with a 50% change from baseline than adoption of a 30% change score.

Baseline patient characteristics used during predictive modeling have been found to determine good or poor prognosis in patients with LBP regardless of the treatment provided.²⁰ Prognostic clinical prediction rules (CPR) are created by identifying baseline predictive characteristics of patients who are inclined to improve irrespective of the treatment provided. Recently, it was found that meeting the CPR for spinal manipulation,^21,22 which includes the presence of four out of five predictive variables at baseline (no pain below knee, symptoms less than 16 days, fear avoidance beliefs questionnaire work subscale [FABQ-w]<19, 1+ hips with an internal rotation range of motion of >35°, 1+hypomobile lumbar segment) is a universal predictor for good prognosis in patients with LBP regardless of the outcome tool used.²³ What is unknown is whether the selected baseline variables will be universal predictors regardless of the MCID used for a particular outcome measure. Therefore, the purpose of this study was to identify predictive variables for recovery in patients with LBP based on variable MCID cutpoints for the ODI. We hypothesized that the predictive model will be the same regardless of the MCID cutpoint used, since each cutpoint (50% change, 30% change, 17-point change, 10-point change, five-point change, and a final ODI score of ≤20%) has been found previously within the literature (with the exception of the original authors’ recommendation of ≤20%) to indicate meaningful recovery.

Method

Design

The study was a secondary database analysis using predictive modeling of a randomized controlled trial (RCT) comparing thrust and non-thrust manipulation in the treatment of LBP.²⁴ The RCT was registered with ClinicalTrials.gov: Identifier NCT01438203. Specific details of the trial are published elsewhere.²⁴ The study was approved by the Walsh University Human Ethics Review Board.

Participants

The RCT enrolled 149 patients with mechanically reproducible LBP who were aged 18 years or older. Participant exclusion criteria included the presence of a tumor, metabolic diseases, rheumatoid arthritis, osteoporosis, prolonged history of steroid use, past surgical history of the lumbar spine, current pregnancy, or signs consistent with nerve root compression (any of the following: reproduction of low back or leg pain with straight leg raise of <45°, muscle weakness involving a major muscle group of the lower extremity, diminished lower extremity muscle stretch reflex, or diminished or absent sensation to pinprick in any lower extremity dermatome).

Intervention

The intervention was a comprehensive rehabilitation intervention that included either thrust or non-thrust manipulation for the first two visits only, followed by physical therapist-directed treatment approach until discharge. In the RCT, there were no differences in any of the outcomes, including the ODI, between the thrust and non-thrust manipulation interventions.²⁴ All patients in the RCT were treated by one of the 17 highly trained physical therapists who had extensive manual therapy training including certification in orthopedic manual therapy or were Fellows within the American Academy of Orthopedic Manual Physical Therapists.

Minimal clinically important difference scores used for the ODI during creation of the predictive models

The modified version of the ODI was used for this study.¹⁴ Within the modified version,¹⁴ the sex-related question was replaced with a question associated with social life. Six MCID cutpoints were used in constructing the predictive models. These included:

1. a 50% change in disability from the initial to final ODI calculated as [(ODI raw score_initial−-ODI raw score_final)/ODI raw score_initial×100%]≧50%;⁶

2. a 30% change calculated as 30% change [(ODI raw score_initial−ODI raw score_final)/ODI raw score_initial×100%]≧30%;^7,8

3. a 17-point decrease calculated as 17-point change [ODI total score_initial−ODI total score_final]≧17;⁹

4. a 10-point decrease calculated as 10-point change [ODI total score_initial−ODI total score_final]≧10;^10,11

5. a 5–6-point decrease calculated as 5–6-point change [ODI total score_initial−ODI total score_final]≧5;^12,13,14

6. a final ODI score of 20% or less.

Prognostic variables used in the predictive models

Ten prognostic variables were selected based on prior representation within the published literature, or based on expectations derived from clinical experience. Irrespective of whether the subject met the CPR for spinal manipulation,³⁰ duration of symptoms (weeks), and age,²⁷ the variables, body mass index (BMI),^25,26 NPRS at baseline,²⁷ ODI at baseline,²⁸ fear avoidance beliefs questionnaire work subscale (FABQ-w) at baseline,²⁹ are well-represented within the literature, have been acknowledged as prognostic variables, and are the same variables used in a paper by Cook and colleagues.²³ The FABQ-w³¹ is a subset of the full FABQ and includes a seven-item questionnaire examining the subjects’ beliefs on the relationship between their work and pain. The CPR for manipulation^21,22 has been proposed to be both prescriptive and prognostic³² and was coded as present or not-present during the initial baseline visit with an operational definition of meeting the rule set for the presence of at least four out of five variables.

The variables irritability^32,33 and medical diagnosis (using the International Classification of Diseases, Ninth Edition (ICD-9 code)) were also used by Cook and colleagues²³ and were found to be prognostic. Irritability was a concept promoted by Maitland³⁴ and includes three related constructs: (i) the vigor of the activity required to provoke a patient’s symptoms; (ii) the severity of those symptoms; and (iii) the time it takes for the symptoms to subside once aggravated (i.e. pain persistence). The variable was dichotomously coded, as recommended by Maitland,³⁴ as present or not-present; with present qualified as any one or more excessive findings recognized on the three identifiers. We created a dichotomous variable titled ‘diagnosis’ by combining all strains and sprains (ICD-9 codes 8472 and 8460) into one group and combining the remaining codes (7221; 7242; 7246, and others) into another category.

Data analysis

All analyses were performed using Statistical Package for the Social Sciences (SPSS) version 18.0 (233 South Wacker Drive, Chicago, Illinois, 60606, USA). Baseline characteristics including means, standard deviations, and frequencies were reported.

Logistic regression analysis

A backward elimination binary logistic regression analysis was completed for each of the six dependent variables (definitions of MCID used for the ODI) using stepwise deletion (p  =  005 enter and 010 exit). Backward elimination involves starting with all predictive variables, testing the deletion of each variable using a chosen model comparison criterion, deleting the variable (if any) that improves the model the most by being deleted, and repeating this process until no further improvement is possible. All six dependent variables were dichotomized into successful and unsuccessful. Success for 50% improvement on the ODI was calculated as [(ODI raw score_initial − ODI raw score_final)/ODI raw score_initial × 100%] ≧50%. Success for 30% improvement on the ODI was calculated as [(ODI raw score_initial − ODI raw score_final)/ODI raw score_initial × 100%] ≧30%. Success for the 17, 10, and five-point improvement models on the ODI was calculated as [ODI total score_initial − ODI total score_final] ≧17, 10, or five, respectively. Success for a final ODI score of 20% or less was an ODI total score_final of ≤20%. If a baseline score was already below the cutpoint for success, the N was adjusted to exclude those patients. A second logistic regression was completed to account for the differences in sample size between models using the same process, but only including patients with an initial ODI above 20%. For all regression calculations a P value of ≤005 was considered significant.

Goodness of fit and collinearity

A Nagelkerke R² was used to assess goodness of fit, as it theoretically represents the proportion of variance in the criterion that is explained by the predictors. The Nagelkerke R² is a version of the Cox and Snell R², which overcomes the problem that this statistic has of not being able to reach its maximum value. Although controversial, the Nagelkerke R² is often used to determine how well the predictors explain the model variance (or, proposed explanation of the proportion of variance).³⁵ The R² was run for each of the six models.

Collinearity is a measure of the correlation between (and thereby, redundancy of) the predictive variables in the model. Collinearity is usually measured in terms of variance inflation factors (VIFs) for their predictors.³⁶ Variance inflation factors were calculated for each covariate in all six models. Ideally, VIF values should be low with a mean VIF close to 1, indicative of minimal collinearity, cut-offs of 5, 10, and sometimes 30 have been suggested as indicating problematic levels of multicollinearity.³⁶

Results

Table 1 summarizes the descriptive statistics of the sample population including frequencies, means, standard deviations, ranges, and percentages. The age range of the sample was diverse including individuals 18–88 years of age with a balanced mix of females and males (53% and 47%, respectively). The majority was Caucasian (913%), most did not display irritability at baseline (732%), and half (503%) demonstrated acute LBP. Body mass index (BMI) ranged from 187 to 467 with a mean of 264. The duration of symptoms ranged from 1 to 1000 weeks with an average of 339 weeks, the total visits ranged from 3 to 28, and the total days in care ranged from 3 to 150. The descriptive statistics were also reported for the subgroup of patients with a baseline ODI score above 20% to compare to the original sample. The subgroup of 107 patients had the same age range with the average age slightly increased to 497 years. The subgroup had a greater ratio of females (57%) to males (43%) and a higher percentage of irritable patients (318%). The characteristics of race, BMI, baseline LBP classification (acute  =  <6 weeks of symptoms, sub-acute  =  6 weeks to 6 months of symptoms, and chronic  =  >6 months of symptoms), diagnosis, baseline numeric pain scale rating, and treatment group allocation were all very similar to the original sample of 149 patients. The mean symptom duration of the subgroup decreased to 264 weeks with a range of 1–312 and baseline ODI increased to an average of 377%.

Table 1. Descriptive statistics of the sample. The first two columns represent the full sample (N  =  149) whereas the second two columns (N  =  107) represent subjects with a baseline Oswestry disability index (ODI) of <20.

Variable	(N  =  149)		(N  =  107)		P value
	Full sample		Partial sample of ODI <20
	Mean (SD)/frequency	Ranges/percentages	Mean (SD)/frequency	Ranges/percentages
Age (years)	482 (149)	18–88 years	497 (151)	18–88 years	043
Gender	70 = male	47%  =  male	46  =  male	43%  =  male	061
	79 = female	53%  =  female	61  =  female	57%  =  female
Irritability	39 = irritable	262%  =  irritable	34  =  irritable	318%  =  irritable	042
	109 = not irritable	732%  =  not irritable	73  =  not irritable	682%  =  not irritable
	1 = missing	07%  =  missing	0  =  missing	0%  =  missing
Race/culture	136 = white	913%  =  white	96  =  white	897%  =  white	099
	3  =  black	2%  =  black	2  =  black	19%  =  black
	3  =  hispanic	2%  =  hispanic	3  =  hispanic	28%  =  hispanic
	3  =  asian	2%  =  asian	3  =  asian	28%  =  asian
	2  =  other	13%  =  other	2  =  other	19%  =  other
	2  =  missing	13%  =  missing	1  =  missing	09%  =  missing
BMI	264 (48)	187–467	266 (50)	187–467	075
Baseline LBP classification	75  =  acute	503%  =  acute	54  =  acute	505%  =  acute	098
	43  =  sub-acute	289%  =  sub-acute	30  =  sub-acute	280%  =  sub-acute
	31  =  chronic	208%  =  chronic	23  =  chronic	215%  =  chronic
	0  =  missing	0%  =  missing	0  =  missing	0%  =  missing
Symptom duration (weeks)	339 (989)	1–1000 weeks	264 (502)	1–312 weeks	047
Diagnosis	70  =  sprains and strains	469%  =  sprains and strains	52  =  sprains and strains	486%  =  sprains and strains	089
	72  =  lumbago and degenerative conditions	484%  =  lumbago and degenerative conditions	50  =  lumbago and degenerative conditions	467%  =  lumbago and degenerative conditions
	7  =  missing	47%  =  missing	5  =  missing	47%  =  missing
Total visits	69 (46)	3–28 visits	76 (45)	2–28 visits	023
Total days in care	357 (299)	3–150 days	366 (305)	1–160 days	081
NPRS at baseline	52/10 (21)	1/10–10/10	55/10 (19)	1/10–10/10	024
ODI at baseline	306 (157)	2–78	377 (125)	22–78	<001
FABQ-w at baseline	119 (107)	0–43	1306 (110)	0–43	039
Met CPR	71  =  met rule	49%  =  met rule	46  =  met rule	43%  =  met rule	054
	78  =  did not meet rule	51%  =  did not meet rule	61  =  did not meet rule	57%  =  did not meet rule
Treatment group	73  =  non-thrust manipulation	49%  =  non-thrust manipulation	52  =  non-thrust manipulation	486%  =  non-thrust manipulation	095
	76  =  thrust manipulation	51%  =  thrust manipulation	55  =  thrust manipulation	514%  =  thrust manipulation

Table 2 displays the results for the logistic regression models, with all models deemed significant (P <001). After the backward stepwise deletion, three variables (meeting the CPR, younger age, and diagnosis of lumbago and degenerative disease) were significantly associated with the 50% change in the ODI, four variables (lower baseline FABQ, shorter symptom duration, younger age, and diagnosis of lumbago and degenerative disease) were significantly associated with the 30% change in the ODI, two variables (higher baseline ODI and meeting the CPR) were significantly associated with the 17-point reduction in the ODI, two variables (higher baseline ODI and younger age) were significantly associated with both the 10-point and five-point change in the ODI, and three variables (lower baseline ODI, younger age, and meeting the CPR) were significantly associated with a final ODI less than or equal to 20%. There was no single variable that was significant across all six models. Younger age was significant in five out of six models, followed by a higher baseline ODI score (three of six), meeting the CPR (three of six), diagnosis of lumbago and degenerative disease (two of six), and lower baseline FABQ, shorter symptom duration, and lower baseline ODI (each one of six). The Nagelkerke R² for each model is also reported in Table 2, indicating the proposed explanation of the proportion of variance. The model with the highest Nagelkerke R² involved the dependent variable of a final ODI score of 20% or less, with a lower baseline ODI, younger age, shorter symptom duration, diagnosis, and meeting the CPR accounting for 491% of predictive factors. The explanation of proportion of variance of all other models was not even half of that of a final ODI score of 20% or less, ranging from 245% down to 139%.

Table 2. Logistic regression modeling including final predictor variables, individual P values for each model variable, as well as odds ratios and 95% confidence intervals.

Model	Variables	Individual P value	Odds ratio (95% confidence interval)	Nagelkerke R2	Model P value	% Correct
ODI 50% change (N = 149)	Met CPR	0005	2916 (1380–6163)	0231	0000	570%
	Younger age	0003	1041 (1014–1069)
	Diagnosis	0014	0385(0180–0824)
ODI 30% change (N = 149)	Lower baseline FABQ	0044	1039 (1001–1079)	0214	0000	705%
	Shorter symptom duration	0012	1008 (1002–1014)
	Younger age	0001	1054 (1023–1087)
	Diagnosis	0012	0337 (0144–0788)
ODI 17-point change (N = 116)a	Higher baseline ODI	0010	0954 (0921–0989)	0245	0000	483%
	Shorter symptom duration	0064	1009 (0999–1020)
	Diagnosis	0063	0441 (0186–1046)
	Met CPR	0007	3387 (1402–8182)
ODI 10-point change (N = 138)b	Higher baseline ODI	0002	0951 (0921–0981)	0172	0001	667%
	Younger age	0020	1035 (1005–1065)
	Diagnosis	0091	0490 (0215–1120)
ODI five-point change (N = 144)c	Higher baseline ODI	0008	0956 (0924–0989)	0139	0006	792%
	Younger age	0043	1034 (1001–1068)
	Diagnosis	0082	0442 (0176–1110)
ODI final ≤20% (N = 107)d	Lower baseline ODI	0000	1113 (1055–1175)	0491	0000	561%
	Younger age	0002	1064 (1023–1105)
	Shorter symptom duration	0083	1009 (0999–1018)
	Diagnosis	0061	0366 (0128–1047)
	Met CPR	0029	3288 (1130–9566)

ODI  =  Oswestry disability index; CPR  =  Clinical prediction rule; FABQ-w  =  Fear avoidance beliefs questionnaire work subscale.

^a N adjusted for 33 patients with baseline ODI of less than 17%; ^b N adjusted for 11 patients with baseline ODI of less than 10%; ^c N adjusted for five patients with baseline ODI less than 5%; ^d N adjusted for 42 patients with baseline ODI of less than 20%.

After adjusting the sample to include only patients with a baseline ODI score greater than 20%, a second logistic regression produced six different, yet significant, models with the results presented in Table 3. Once again, there was no one predictive variable that was individually significant across all six models. Diagnosis of lumbago and degenerative disease was significant in four out of six models. Younger age, shorter symptom duration, and higher baseline ODI were each significant in three out of six models, however, not commonly significant in any model. Meeting the CPR followed in two of six and a new predictive variable of lower BMI was individually significant in the five-point change model only. A lower baseline ODI was found to be significant only in the final ODI of 20% or less model. A final ODI of 20% or less produced the model with the highest Nagelkerke R² of 491%, followed by the 50% change model at 271%, the 17-point change model at 260%, the 10-point change model at 217%, the five-point change model at 210%, and the 30% change model provided the lowest Nagelkerke R² at 191%. The VIFs for all models ranged from 1001 to 1121 indicating minimal to no covariance between the predictive variables within each model.

Table 3. Logistic regression modeling (only cases with initial Oswestry disability index (ODI) greater than 20%), including final predictor variables, individual P values for each model variable, as well as odds ratios and 95% confidence intervals.

Model	Variables	Individual P value	Odds ratio (95% confidence interval)	Nagelkerke R2	Model P value	% correct
ODI 50% change (N = 107)	Younger age	0020	1039 (1006–1072)	0271	0000	542%
	Shorter symptom duration	0062	1009 (1000–1018)
	Diagnosis	0004	0254 (0100–0645)
	Met CPR	0070	2347 (0933–5906)
ODI 30% change (N = 107)	Younger age	0029	1036 (1004–1069)	0191	0002	673%
	Shorter symptom duration	0011	1012 (1003–1022)
	Diagnosis	0043	0381 (0149–0972)
ODI 17-point change (N = 107)	Higher baseline ODI	0037	0961 (0926–0998)	0260	0000	514%
	Younger age	0093	1027 (0996–1060)
	Shorter symptom duration	0049	1010 (1000–1020)
	Diagnosis	0029	0354 (0140–0897)
	Met CPR	0034	2722 (1077–6882)
ODI 10-point change (N = 107)	Higher baseline ODI	0010	0939 (0894–0985)	0217	0002	720%
	Younger age	0058	1034 (0999–1070)
	Shorter symptom duration	0031	1010 (1001–1018)
	Diagnosis	0039	0346 (0126–0949)
ODI five-point change (N = 107)	Higher baseline ODI	0014	0924 (0807–0984)	0210	0008	822%
	Lower BMI	0016	1160 (1028–1308)
	Shorter symptom duration	0083	1009 (0999–1019)
	Diagnosis	0077	0348 (0108–1121)
ODI final <20% (N = 107)	Lower baseline ODI	0000	1113 (1055–1175)	0491	0000	561%
	Younger age	0002	1064 (1023–1105)
	Shorter symptom duration	0083	1009 (0999–1018)
	Diagnosis	0061	0366 (0128–1047)
	Met CPR	0029	3288 (1130–9566)

ODI  =  Oswestry disability index; CPR  =  Clinical prediction rules; FABQ-w  =  Fear avoidance beliefs questionnaire work subscale.

Figure 1 displays the success rate of the full sample based on the MCID cutpoint used. The five-point change produced the highest success rate with 792% of patients defined as ‘recovered’. A MCID cutpoint of 17 points manufactured the lowest success rate at 483% of patients ‘recovered’. Figure 2 shows the success rates of the subgroup of 107 patients with a baseline ODI greater than 20%. The five-point change continues to show the highest success rate at 822%, followed by a 10-point change (72% recovered), a 30% change (673% recovered), a final ODI of 20% or less (561% recovered), a 50% change (542% recovered), and a 17-point change (514% recovered).

Figure 1.

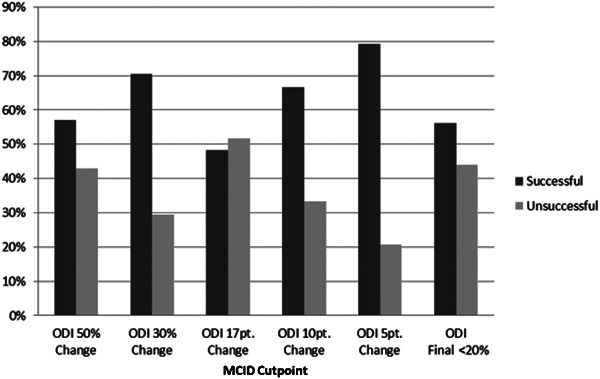
Patient success rate of full sample (N  =  149).

Figure 2.

Patient success rate of sub-group (N  =  106).

Discussion

Our study sought to determine the relationship between MCID and predictive variables within a single patient population and the outcome measures derived from that population. The results of this study show that different MCIDs used on the same outcome measure across the same patient population lead to notably different predictive models. In addition, after modifying our analyses for baseline ODI scores, we found different predictive models, using different MCID interpretations. We feel that there are a number of reasons why the results are different among predictive models including variations in baseline characteristics, differences in success ratios depending on MCID interpretation, challenges to using a single point estimate to report change, and inherent fragility of predictive modeling.

Previous research has suggested that patient baseline characteristics, especially severity measures, can significantly influence the MCID.¹ Wright et al.¹ report, ‘the use of the MCID score alone when determining treatment effects may be limited due to the inherent limitations of the methodology and baseline dependency of the sample’. In a study by Terwee et al.,¹⁸ a large variation was found in MCID scores on the ODI using the same methodology across several studies, suggesting that the differences could be explained by baseline population characteristics. In our second logistic regression analyses, we removed the subjects who failed to present with an initial ODI score of 20%, and our models were notably different. It is likely that enrolling only subjects with higher disability would result in different findings as well.

In clinical practice, MCIDs are utilized on outcome measures to determine whether or not a patient is successfully responding to treatment. Thus, difference in one’s interpretation of ‘success’ will lead to proportional differences between success and failure, when in reality the successive nature of recovery is likely present along a continuum. A MCID is a single point estimate and weaknesses of single point estimates involve the focus on measures of central tendencies, measures which may or may not truly represent change in a patient condition. The different MCID values for the ODI used in our study were captured from measures of central tendencies in different studies under different conditions. This is of considerable importance as the medical profession shifts from fee for service to fee for performance; recognizing the instability of the MCID and the need for a stable quality measure becomes more important to assure correct reimbursement.

The findings of our study also inherently suggest the fragility of predictive models. Without a universally stable definition of meaningful change, it is likely that different MCID scores will result in very different predictive variables in different patient populations. Clinical predictive rules are forms of predictive models and are assumed to be robust clinical tools that are usable in any given clinical situation. Our findings hint that this may not be the case. In our study, there were no variables that were universal predictors across all models, regardless of the baseline ODI measure. It is highly likely that models that do not involve universal predictors are not transferable across different patient spectrums (samples), as well as models that use different MCIDs.

Is there evidence to support which MCID is the best for determining clinically important differences? We would argue that there is not enough information available to support any of the choices provided in this manuscript. In an attempt to identify the most robust predictive models, we used the Nagelkerke R² to assess goodness of fit. The Nagelkerke R² theoretically represents the proportion of variance in the criterion that is explained by the predictors. Although it is not as discerning a measure as the R² used for a linear regression analysis, it does help define which predictive model is best able to explain the proportion of variance within the dedicated models. Our study findings suggest that the most robust predictive model for determining proportion of variance in the criterion is the original authors’³ definition (an ODI score of 20% or less), a value that has yet to be analyzed in any study, outside of ours. Further, this does not suggest that a ≤20% of the final ODI is best at discriminating clinically important recovery from disability, only that the variables within the model fit best when that definition was used as the dependent variable. All other models which used change scores or end point score were much less robust. We feel that the minimally clinical important change score is a unique concept that is likely different for each patient and that one value does not appropriately capture change for everyone. We endorse none of the measures presented herein.

Limitations

There are limitations to our study including patient population and study design. Our study utilized the data from a RCT, which is not the optimal study design for prognostic studies. A larger sample size would have allowed for better generalizations, indicating a cohort study as a more appropriate form of design. Furthermore, a larger sample size would improve the precision of regression-based estimates.

Conclusion

The main finding that our secondary database analysis demonstrates is the extreme variability between predictive models created by using different MCIDs on the ODI within the same patient population. Our findings highlight the instability of predictive modeling, as these models are significantly affected by population baseline characteristics along with the MCID used. The fragility of predictive modeling creates difficulty applying CPR to clinical practice and suggests that CPR may not be reliable across all patient populations.