Efficient Implementation of MrBayes on Multi-GPU

Abstract

MrBayes, using Metropolis-coupled Markov chain Monte Carlo (MCMCMC or (MC)³), is a popular program for Bayesian inference. As a leading method of using DNA data to infer phylogeny, the (MC)³ Bayesian algorithm and its improved and parallel versions are now not fast enough for biologists to analyze massive real-world DNA data. Recently, graphics processor unit (GPU) has shown its power as a coprocessor (or rather, an accelerator) in many fields. This article describes an efficient implementation a(MC)³ (aMCMCMC) for MrBayes (MC)³ on compute unified device architecture. By dynamically adjusting the task granularity to adapt to input data size and hardware configuration, it makes full use of GPU cores with different data sets. An adaptive method is also developed to split and combine DNA sequences to make full use of a large number of GPU cards. Furthermore, a new “node-by-node” task scheduling strategy is developed to improve concurrency, and several optimizing methods are used to reduce extra overhead. Experimental results show that a(MC)³ achieves up to 63× speedup over serial MrBayes on a single machine with one GPU card, and up to 170× speedup with four GPU cards, and up to 478× speedup with a 32-node GPU cluster. a(MC)³ is dramatically faster than all the previous (MC)³ algorithms and scales well to large GPU clusters.

Introduction

Phylogeny means the sequence of events involved in the evolutionary development of a species or taxonomic group of organisms. And it is typically formulated as phylogenetic trees. A great number of numerical methods have been presented for using DNA data to infer phylogenetic trees, including parsimony method (Swofford 1999), numerous distance matrix methods (Saitou and Nei 1987), maximum likelihood method (Olsen et al. 1994; Lewis 1998; Schmidt et al. 2002), and Bayesian method (Rannala and Yang 1996; Mau and Newton 1997; Yang and Rannala 1997; Mau et al. 1999; Li et al. 2000). The Bayesian method outstrips other methods in terms of phylogenetic inference, including easy interpretation of results, the capability to incorporate prior information (if any), and several computational advantages (Larget and Simon 1999).

Bayesian phylogenetic inference is an optimization-based method similar to maximum likelihood method (Huelsenbeck et al. 2001). The phylogenetic tree with the highest posterior probability might be chosen as the best estimate of phylogeny. (MC)³ algorithm is one of the numerical methods available to approximate the posterior probability. The detailed algorithm can be found in Altekar et al. (2004). (MC)³ runs H (usually H > 1) Markov chains, (H − 1) of which are heated. Compared with a cold (or unheated) chain, a heated chain is more likely to accept new trees (a new tree is proposed by stochastically perturbing an old tree). The procedure of (MC)³ is as follows:

1. Let φ_i denotes the current tree of Markov chain i. If this is the first iteration, randomly choose an initial value for φ_i. This is done for all H chains.

2. For all chains, i ∈ {1,2, … , H},

   1. Propose a new tree φ_i′ by stochastically perturbing φ_i.
   2. Calculate the acceptance probability R_i′ for φ_i′.

      (1)

      where for the cold chain, β_i = 1.
   3. Draw a random variable U_i from a uniform distribution on the interval (0, 1). If U_i < R_i′, then accept φ_i′, namely, let φ_i = φ_i′.
3. After all chains have advanced a given number of iterations, randomly choose two chains (j and k) to swap states. The acceptance probability R for swapping states is:

   (2)

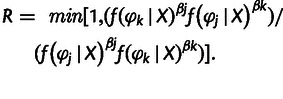
4. Draw a random variable U from a uniform distribution on the interval (0, 1). If U < R, then accept the swap of states, namely, chains j and k swap states.

5. Go back to step 2.

To calculate the acceptance probability of the proposed new tree φ_i′, chain i should first compute the global likelihood L, which is the most time-consuming part and is more often optimized by most parallel versions. To calculate L, Felsenstein presented a recursive algorithm (Felsenstein 1981). We denote the length of a given alignment of DNA sequences (i.e., the number of characters per taxa) M, the number of taxa N, and the number of chains H. Transition probability matrices Q = q_XY are calculated for all the nodes, except the root node of the new tree φ_i′. Q contains the instantaneous transition probabilities (q_XY) for a certain DNA nucleotide X to mutate into another nucleotide Y (X,Y ∈ A-Adenine, C-Cytosine, G-Guanine, T-thymine), according to the substitution model that chain i adopts. Then chain i traverses φ_i′ in post order and computes the conditional likelihoods of each internal node from the Qs and conditional likelihoods of its two (left and right) child nodes. After the conditional likelihoods of the root node have been figured out, chain i uses them to calculate all the local likelihoods of φ_i′ and, in turn, L.

Next-generation DNA sequencing technology has proved to decrease the cost and increase the throughput of DNA sequencing significantly, while maintaining the high quality of data, which gave rise to the “Big Bang” of DNA data. To speedup original (MC)³ algorithm, some improved and parallel algorithms have been presented. p(MC)³ (pMCMCMC) is a chain level coarse-grained parallel algorithm, which distributes all Markov chains involved among processes and then runs these processes in parallel (Altekar et al. 2004). Moreover, the p(MC)³ algorithm adopts a point-to-point synchronization strategy and a swapping-heats mechanism to minimize the interprocess communication overhead. However, the concurrency of p(MC)³ is limited by the number of chains used in the analysis, which is typically small for most of real-world applications. Both parallel implementation of Bayesian phylogenetic inference (Feng et al. 2003, 2006) and a hybrid parallel algorithm h(MC)³ (hMCMCMC) (Zhou et al. 2010) parallelize (MC)³ at two levels: the chain level and the DNA subsequence level. The difference between these two algorithms is how to implement the DNA subsequence level parallelism. Both algorithms improve the concurrency of (MC)³.

Recently, graphics processor unit (GPU) has become a programmable many-core coprocessor with strong computational power and high memory bandwidth. A GPU has a large number of cores grouped into “stream multiprocessors” (SMs), which can run thousands of threads concurrently. Many applications have been accelerated using GPU, from general signal processing or physics simulation to computational finance or computational biology (NVIDIA 2009). The compute unified device architecture (CUDA) introduced by NVIDIA is the most important reason of the prosperity of general purpose computing on graphics processing units. It is a general purpose parallel computing architecture and a parallel programming model. It allows developers to program NVIDIA GPU using a minimally extended version of C language in a fashion very similar to central processing unit (CPU) programming. The function of the GPU part of a CUDA program is called “kernel,” which is executed by thousands of threads organized into “blocks.” The threads in a block are divided into “warps.” The warp is the basic scheduling unit of GPU, and the threads in a warp must run synchronously on an SM. Another important consideration of CUDA programming is memory hierarchy. Global memory is the largest memory space but the slowest. So, loading data into much faster but much smaller shared memory and then accessing data in shared memory repeatedly is a common strategy.

To use the powerful GPU to speed (MC)³ up, a DNA subsequence level fine-grained parallel algorithm g(MC)³ (gMCMCMC) (Pratas et al. 2009) exclusively focuses on the calculation of conditional likelihoods. Nonetheless, the g(MC)³ algorithm is only a proof-of-concept work, because it barely uses GPU to accelerate part of (MC)³ and pays no attention to CPU–GPU communication overhead. The latest parallel algorithm n(MC)³ (nMCMCMC) (Zhou et al. 2011) on GPU is a CPU–GPU cooperative algorithm. It inherits part of the idea of g(MC)³, putting calculation of conditional likelihoods into GPU to accelerate it. It is worth noticing that this algorithm has resolved some significant drawbacks (e.g., too much CPU–GPU communication) of g(MC)³.

New Approaches

This article proposes an adaptive algorithm a(MC)³ to improve (MC)³ on the CUDA platform. First, compared with its previous version, n(MC)³, a(MC)³ determines the task granularity dynamically, so as to make full use of computing power with different data sets and different hardware configurations. n(MC)³ uses very fine grain parallelism, which guarantees high saturation of GPU computational units, but causes heavy communication cost and a waste of free threads. So, a(MC)³ uses fine-grain or coarse-grain tasks for different environments to reduce memory accesses, synchronization, or communication overhead, or redundant calculation.

a(MC)³ also develops a new task scheduling strategy to improve concurrency. “Node-by-node” pipelining model takes the place of “chain-by-chain” pipeline used in n(MC)³. This scheduling strategy overlaps data transmission with kernel execution and helps GPU units featuring computing capability 2.x or higher to execute multiple kernels in different streams concurrently. This will be introduced in detail in Materials and Methods section.

Furthermore, several optimization methods are used to reduce extra overheads. a(MC)³ also uses an adaptive method to split and combine DNA sequences to make full use of a large number of GPU cards. Experimental results show that, a(MC)³ is faster than all the known (MC)³ algorithms, either on a single machine with single or multiple GPU cards, or on a GPU cluster.

Results and Discussion

We evaluate the performance of a(MC)³ on two kinds of multi-GPU platforms, personal computer and GPU cluster. We first test it on a personal computer with four graphics cards, compared with other typical parallel (MC)³ algorithms in speed and scalability. And then experiments on a GPU cluster show that a(MC)³ has good scalability. a(MC)³ is implemented by modifying the parallel version of MrBayes version 3.1.2 into a CUDA version. For the compilation of the codes running on the GPU side, the compiler NVCC provided by NVIDIA CUDA Toolkit Version 4.2 is used. The compiler GCC version 4.46 with the -O3 flag is used to compile all the CPU-side source codes. For the chain level parallelism on the CPU side, MPICH2 version 1.2.1 is used. To get the result, we run each experiment five times. Each execution uses the 4 × 4 nucleotide substitution model with eight Markov chains and lasts for 100,000 generations.

Speedup

This experiment is conducted on a computer equipped with four NVIDIA GeForce GTX 480 graphics cards (table 1). As the control group, the performance of the n(MC)³ and the CUDA version of MrBayes 3.2.1 are also tested. The serial version of MrBayes 3.1.2 is chosen as the “fastest known” serial algorithm. Then, the speedups of other algorithms including a(MC)³ are computed according to it. We use five real-world data sets (table 2) and 10 artificial DNA data sets. The first two real data sets come from GenBank (Xie et al. 2005, 2008) and others from Dr. Qiang Xie’s personal communication. Artificial data sets are generated by replicating or cutting real data sets, which remain the same number of taxa (60) but have various DNA lengths from 1,000 to 10,000.

Table 1.

Systems Setup.

Personal Computer
OS	CentOS 6.2
CPU	1 × Intel(R) Xeon(R) CPU E5645 processor
Memory	2 × 2 GB DDR3 1333
GPU	4 × NVIDIA GeForce GTX 480
Graphics driver	NVIDIA device driver Version 295.41

Intel(R) Xeon(R) CPU E5645
Core family	6
No. of cores	6
Core clock	2.4 GHz

NVIDIA GeForce GTX 480
Compute architecture	Fermi
No. of CUDA cores	480
Core clock	1.4 GHz
Global memory	1,536 MB GDDR5
No. of kernels run concurrency	16

Table 2.

DNA Data Sets Used in Experiments on PC.

Data Set	Taxa	DNA Length(M)
1	26	1,546
2	37	2,238
3	111	1,506
4	234	1,790
5	288	3,386

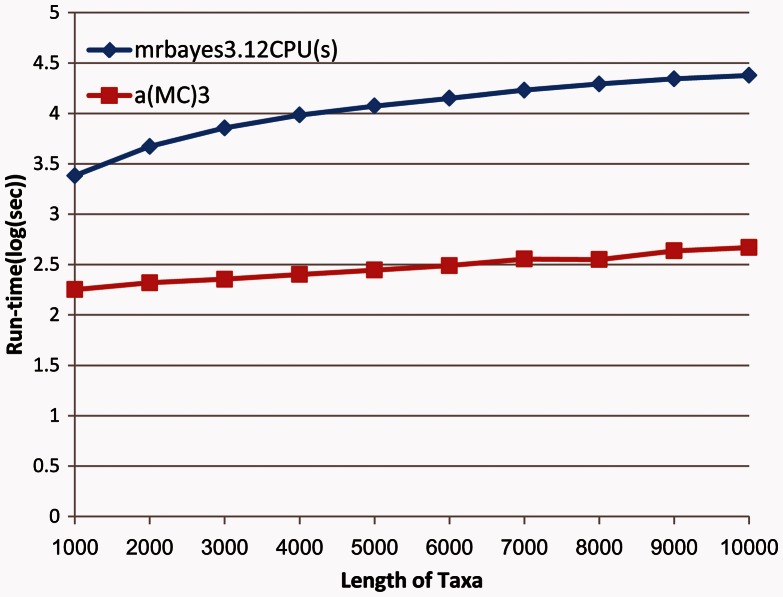
We compare the average execution time of the “fastest known” serial algorithm MrBayes 3.1.2 and a(MC)³ with one GPU card, using 10 artificial data sets (fig. 1). The new algorithm improves calculation speed greatly, and the gap widens as the scale of data set increases.

Fig. 1.

Execution time of the serial version of MrBayes 3.1.2 and a(MC)³. The horizontal axis represents the DNA length of 10 taxa, and the vertical axis is the logarithm of execution time.

We also test the run time of processing real-world data sets on the platforms and compute the speedup compared with the serial MrBayes 3.1.2 (table 3). All algorithms use one GTX 480 card. We can see that a(MC)³ spends the least time. What is more, with more taxa and a longer DNA sequence, a(MC)³ achieves higher speedup.

Table 3.

Performance of a(MC)³ on Real-World Data Compared with Other Algorithms.

Data Set	Generations	Run Time (s)				Speedup
		MrBayes 3.1.2	MrBayes 3.2.1 GPU	n(MC)3	a(MC)3	MrBayes 3.2.1 GPU	n(MC)3	a(MC)3
1	1,000,000	4,981	2,978	1,293	1,028	1.7	3.9	4.8
2	1,000,000	17,524	4,383	1,885	1,204	4.0	9.3	14.6
3	500,000	20,763	4,035	2,149	1,317	5.1	9.7	15.8
4	100,000	18,822	1,894	1,015	533	9.9	18.5	35.3
5	100,000	43,529	3,295	1,738	643	13.2	25.0	67.7

In addition, we can see speedups of several parallel algorithms with one GPU card on artificial data sets (fig. 2). We test both single- and double-precision versions of a(MC)³ and test only single precision versions of the control group. Double-precision a(MC)³ cannot analyze the last two data sets because of the insufficient global memory. We can see that a(MC)³ is much faster than the other two algorithms on all data sets. Its single-precision version is, respectively, up to 2.86× and 6.23× faster than n(MC)³ and MrBayes 3.2.1, even its double-precision version is up to 52% and 3.31× faster than the single-precision versions of the other two algorithms. Moreover, MrBayes 3.2.1 almost keeps a fixed speedup around 8 on data 5 to data 10. Similar problem happens to n(MC)³. a(MC)³, however, keeps smooth speedup improvement until the problem size (the length of taxa) approaches to 8,000, which implies that it can solve larger problems more efficiently on fixed hardware configuration, that is, it could well have good scalability.

Fig. 2.

Speedup of different parallel algorithms (a(MC)³ with single precision, a(MC)³ with double precision, and n(MC)³, MrBayes 3.2.1, on a single GPU card on artificial data sets. The horizontal axis represents the DNA length of 10 taxa, and the vertical axis is the speedup compared with the “fastest known” serial algorithm MrBayes 3.1.2.

Effectiveness of different strategies used by a(MC)³ is tested while n(MC)³ is used as the base line (fig. 3). n(MC)³ stream denotes the version only using “node-by-node” pipelining model, and similarly n(MC)³ kernel denotes the version only using dynamic task granularity.

Fig. 3.

Effectiveness of different strategies (only using “node-by-node” pipelining model, only using dynamic task granularity, and using both two strategies) used by a(MC)3. The horizontal axis represents the DNA length of 10 taxa, and the vertical axis is the speedup compared with n(MC)3.

We can see that n(MC)³-stream strategy achieves nearly 40% speedup and drops quickly when DNA length increases. It is because n(MC)³ uses very fine-grain parallelism, which guarantees enough threads saturation and utilization when there is a larger DNA length and more taxa. This reduces the benefit of overlapping data transmission of the pipelining model.

On the other hand, the finer tasks granularity, the heavier communication overhead. So, n(MC)³-kernel performs well on big data sets, which remedies the disadvantage of the pipelining model. As we can see, the two different strategies cooperate and achieve almost three times faster than n(MC)³. The next section explains the two strategies in detail.

Speedups of two fastest algorithms, a(MC)³ and n(MC)³, are tested on multiple GPUs (fig. 4). As MrBayes runs eight different Markov chains simultaneously, in this experiment, both algorithms distribute eight chains evenly among eight independent processes. And then these eight processes are assigned evenly to multiple GPU cards to implement the DNA subsequence level fine-grained parallelism. We can see that a(MC)³ is far superior to n(MC)³ in both wall time and scalability. It achieved up to 170× speedup over the serial algorithm on a quad-GPU configuration.

Fig. 4.

Speedup of the two fastest algorithms, n(MC)³ and a(MC)³ on 1/2/4 GPUs. The horizontal axis is the DNA length of 10 taxa, and the vertical axis is the speedup compared with the “fastest known” serial algorithm MrBayes 3.1.2.

Scalability

For any parallel algorithm (system), with a fixed problem size, its speedup will decrease as the number of processors increases because of the increasing ratio of communication overhead to effective computation. If a parallel algorithm achieves increasing speedup with increasing problem size on a fixed number of processors, it is possible to keep a constant efficiency (the ratio of speedup to the number of processors) by increasing both problem size and the number of processors, that is, the algorithm is scalable.

We can see that (fig. 4) the efficiency of a(MC)³ drops slightly faster than that of n(MC)³ as the number of GPU cards increases with the fixed length of taxa. However, with a fixed number of GPU cards, the efficiency of a(MC)³ increases much faster than that of n(MC)³ as the length of taxa increases. Taken together, a(MC)³ has better scalability than n(MC)³.

GPU Cluster

Experiments on GPU clusters use four large data sets that all come from real-world DNA data (Regier et al. 2010; Soltis et al. 2011; Thuiller et al. 2011; Wiegmann et al. 2011) and can be got freely from GenBank. To facilitate comparison with others, all data sets are cut to 80 taxa (table 4).

Table 4.

DNA Data Sets Used in Experiments on TH-1A.

Data Set	Taxa (N)	DNA Length (M)
1	80	15,106
2	80	19,976
3	80	25,260
4	80	41,976

To test a(MC)³ on GPU cluster, we choose Tianhe-1A (TH-1A) as our experimental platform. Tianhe-1A is one of the few Petascale supercomputers in the world, located at the National Supercomputing Center in Tianjin, China. It once became the world's fastest supercomputer with a peak performance of 2.507 petaflops in October 2010. Tianhe-1A is now equipped with 2,048 NUDT FT1000 heterogeneous processors, 14,336 Xeon X5670 processors, and 7,168 NVIDIA Tesla M2050 GPU cards.

We conduct our experiments on 32 nodes of TH-1A, each of which is equipped with one GPU card. Here, we use NVIDIA CUDA Toolkit Version 4.0 and GCC version 4.12.

We can see from experimental results on Tianhe-1A (fig. 5) that there is no result of the fourth data with one node because of the insufficient global memory. As expected, a(MC)³ shows good scalability. Even though the number of nodes increases to 32, the speedup still keeps a smooth growth.

Fig. 5.

Performance of a(MC)³ on GPU cluster, Tianhe-1A with four real-world data sets. The horizontal axis represents the number of GPU cards, and the vertical axis is the speedup compared with the “fastest known” serial algorithm MrBayes 3.1.2.

The efficiency remains a relatively stable value. a(MC)³ achieves 478× speedup over the serial algorithm with 32 nodes and the largest data set. This experiment tells us that a(MC)³ has ability to analyze large DNA data on large scale parallel systems efficiently.

Conclusion

An adaptive CUDA algorithm a(MC)³ has been proposed to accelerate (MC)³ algorithm for Bayesian inference of phylogeny. By determining task granularity dynamically according to the input data size and the hardware configuration, a(MC)³ can make full use of computing power of cores in a GPU card. An adaptive DNA sequence splitting and combining method is developed to improve scalability. A node-by-node task scheduling strategy is also proposed to improve concurrency. Experimental results show that a(MC)³ achieves up to 63× speedup over serial MrBayes on a single machine with one GPU card, and up to 170× speedup with four GPU cards. We also test a(MC)³ on a GPU cluster, Tianhe-1A. a(MC)³ shows good scalability and achieves up to 478× speedup with 32 nodes. To the best of the authors' knowledge, a(MC)³ is the first (MC)³ algorithm that analyzes massive real-world DNA data on large GPU cluster efficiently. The source codes and data sets used by a(MC)³ are available from: http://sourceforge.net/projects/mrbayes-gpu/, last accessed March 27, 2013.

In this article, a(MC)³ is implemented only for DNA data and 4 × 4 nucleotide substitution model. Bayesian phylogenetic inference using (MC)³ with other data types and evolutionary models can also be accelerated by means used in a(MC)³. Besides, insufficient global memory of GPU becomes an important limitation of performance and practicability. Rational use of global memory maybe our future work.

Materials and Methods

Algorithm

Dynamic Task Decomposition and Mapping

a(MC)³ has two design goals:

1. With a single GPU card, achieves stably good efficiency with different data sets.

2. Scales well from single GPU systems to multi-GPU systems or GPU clusters.

To realize these, we develop a new adaptive architecture of a(MC)³ (fig. 6). First, similar to n(MC)³, a(MC)³ also uses a CPU–GPU cooperative mechanism that parallelizes (MC)³ at both chain level and DNA subsequence level. CPU is in charge of the initial work preparation and the final global likelihood computation, whereas heavy computation of conditional likelihoods and local likelihoods is assigned to GPU. We develop dynamic task decomposition strategies at both chain level and DNA subsequence level.

Fig. 6.

The algorithm architecture of a(MC)³. Q represents the instantaneous rate matrix, and φ_i′ is the new phylogenetic tree. P_i is transition probability matrices; X_u denotes the DNA sequence data at site u; and π_m denotes the base frequencies of nucleotide m ∈ {A, C, G, T}. L_u is site likelihoods and cl is conditional likelihoods. Global likelihood is ƒ(X|φ_i′).

Because each CUDA kernel is responsible for calculating conditional likelihoods or local likelihoods of all sites of a unique node in the new tree, the total computation load of each kernel is determined by the length M of a given alignment of DNA sequences (i.e., the number of sites per taxa). In a fixed-grained algorithm, such as n(MC)³, M might impact parallel efficiency seriously. The number of CUDA threads invoked is linear with M, so when M is small, increasing M will lead more CUDA threads to be invoked on GPU, which will seriously improve parallel efficiency. However, as CUDA cores of a GPU card are limited, too many CUDA threads will cause heavy interaction, and it will finally drop the performance of the algorithm when M is too large.

To solve the problem, we rewrite the main CUDA kernel functions. These new CUDA kernel functions are coarse grained. Each thread is responsible for a long DNA subsequence, so that each thread is assigned enough computation work, while maintaining a reasonable number of threads. Moreover, this adaptive-grained task decomposition strategy incurs less redundant computation and less communication cost. It does improve the performance of the single kernel. How to decide the threshold T of M is challenging, which depends on the number of CUDA cores, global memory bandwidth, and the capacity of shared memory. Therefore, it is a simple and effective way to determine T by running a series of tests when deploying the software package. By using threshold T, we developed an adaptive task decomposition method at DNA subsequence level. After receiving an input instance, a(MC)³ compares its size M with a preset threshold T. If M ≤ T, fine-grained task decomposition is applied, that is, each CUDA thread is responsible for a relatively short DNA subsequence (i.e., relatively few sites). Otherwise, coarse-grained tasks are generated.

Using this dynamic strategy, a(MC)³ always maintains an appropriate concurrency (the number of CUDA threads), which is high enough to hide memory latency effectively without being too high to avoid heavy interaction overhead. Moreover, for a large M, coarse-grained task decomposition also helps to increase the ratio of effective computation to bookkeeping operations, which benefits parallel efficiency.

The task decomposition strategy n(MC)³ applies at chain level has a significant limitation, too. The smallest task granularity n(MC)³ assigned to each GPU card is one Markov chain, which limits its concurrency. For example, a typical real-world (MC)³ execution runs four to eight Markov chains. Consequently, even if we have a cluster with hundreds of GPU cards, n(MC)³ can only use up to eight of them to calculate likelihoods. On the other hand, because n(MC)³ always invokes a single kernel for a single Markov chain, when M is very small (although rarely in real-world phylogenetic inference), low concurrency may happen in each GPU card even if adaptive-grained task decomposition is applied.

To resolve these two difficulties, we develop an adaptive method to split and combine DNA sequences from different Markov chains according to M and the number of GPU cards G. If G > H, for each Markov chain, a(MC)³ splits DNA sequences into segments of the same length, so as to create as many tasks as the number of GPU cards. If M is extremely small, a(MC)³ will combine DNA sequences from different chains to create big enough tasks to make full use of computing power of each GPU card. It is worth noticing that these two cases may conflict. Consider a scenario in which we try to run few Markov chains that contain very short DNA sequences on a large GPU cluster, should we split or combine DNA sequences? However, it is a false dilemma. This input instance is too small to be worth using massive parallel processing. Nonetheless, if you decide to use the whole cluster to run it, a(MC)³ will split DNA sequences, which brings you shorter total running time but worse parallel efficiency. This adaptive method remarkably improves scalability. Now a(MC)³ can achieve good efficiency over quite different hardware configurations, from desktop PCs with single or multiple GPU cards to large GPU clusters.

By using adaptive-grained task decomposition and adaptive DNA sequence splitting and combining, we successfully achieve the two design goals of a(MC)³.

Likelihood Evaluation Procedure

The standard (MC)³ computational procedure is reorganized as shown in Algorithm 1, where N denotes the number of taxa. The whole flow consists of four main loops. The first loop and last loop are executed in CPU side, whereas the others run in GPU. In Loop1, all transition probability matrices for the proposed new tree are transferred from CPU to GPU after they have been figured out. Loop2 carries the majority of computation, where kernels will be called to calculate the conditional likelihoods for all internal nodes. This loop consists of a dual loop: the outer processes “node-by-node” and the inner “chain-by chain.” We can see that, similar to n(MC)³, a(MC)³ also submits the first node of the first chain to GPU in the first iteration. However, in the second iteration, a(MC)³ submits the first node of the second chain rather than the second node of the first chain, and then the first node of the third chain, and so on. The second node of the first chain cannot be submitted until the first node of the Hth chain is submitted. That is, a(MC)³ changes the “chain-by-chain” scheduling strategy used by n(MC)³ to a “node-by-node” scheduling strategy. We will show how this strategy improves the concurrency of CPU–GPU pipeline in detail later. Because “node-by-node” scheduling order is used, computation of conditional likelihoods and local likelihoods must be broken into two loops. Loop3 uses the conditional likelihoods of the root node just figured out by Loop2 to compute the local likelihoods for the proposed new tree and, afterward, transfers the results back to the CPU side. Because in Loop2 and Loop3, kernels responsible for computation of conditional likelihoods and local likelihoods of each Markov chain are invoked sequentially within a single CUDA stream, true data dependency between computations is guaranteed. Finally, in Loop4, the global likelihood L of a Markov chain is calculated by the accumulative product of local likelihoods L_u. Moreover, synchronization between CPU and GPU has been added to ensure the correctness of the final results. Notice that if DNA sequences have been split, partial results will be collected from multiple computational nodes to calculate L.

Algorithm 1: Likelihood evaluation in the proposed algorithm.

Require: instantaneous rate matrix, tree φ_i

Ensure: a more optimal tree φ_i′

for all chains, i ∈ {1,2, … , H}, Loop1

 propose a new tree φ_i′ by randomly perturbing φ_i

 for (k = 1; k ≤ 2N − 2; k ++)

  Calculate transition probability matrix Q_k

 end for

 Transfer Qs from CPU to GPU

end for

for (k = N + 1; k ≤ 2N − 1; k ++) Loop2

 for i ∈ {1,2, … , H} do

  if M < T then

   Call fine-grained kernel to calculate conditional likelihood of node k of chain i in parallel

  else

   Call coarse-grained kernel to calculate conditional likelihood of node k of chain i in parallel

  end if

 end for

end for

for all chains, i ∈ {1,2, … , H} Loop3

 if M < T then

  Call fine-grained kernel to calculate local likelihoods for φ_i′ in parallel

 else

  Call coarse-grained kernel to calculate local likelihoods for φ_i′ in parallel

 end if

 Transfer local likelihoods from GPU to CPU

end for

for all chains, i ∈ {1,2, … , H} Loop4

  Synchronize with corresponding GPU stream

  Set L = 1

  for (u = 1; u ≤ M; u++) do

   L = L × L_u

  end for

  Calculate acceptance probability (R) for (φ_i′) using L

  Accept/Reject φ_i′

end for

A Pipelining Model with Node-by-Node Scheduling

Given that high CPU–GPU communication overhead has resulted in the poor overall performance of previous algorithms, a(MC)³ uses a pipelining model with “node-by-node” scheduling, which further increases the concurrency of (MC)³, and overlaps the communication overhead between CPU and GPU.

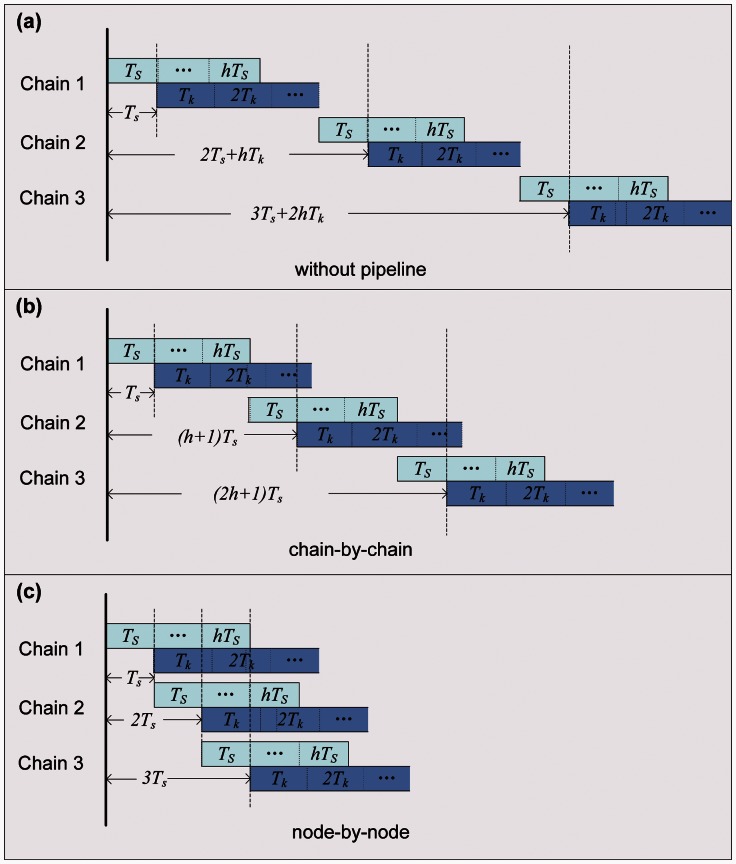
On the GPU side, the pipelining model views each Markov chain as a CUDA stream composed of sequential subtasks, uploading transition probability matrices onto GPU, calling kernels to calculate conditional likelihoods and local likelihoods on GPU, and downloading local likelihoods to CPU. Without any pipelining model (fig. 7a), all chains are run serially. For instance, chain i + 1 will not start the uploading step until its immediate predecessor chain i has transferred all the result data back to the CPU side.

Fig. 7.

Different pipelining models: without pipelining, “chain-by-chain,” and “node-by-node.” T_s denotes the kernel startup time of the s-th internal node, T_k denotes the kernel execution time of the k-th internal node, and h is the number of nodes in a chain.

A kind of pipelining model is used in n(MC)³ (fig. 7b), where data transfers and kernel executions of different chains can be done at the same time. We can see that chain i + 1 can transfer its data while chain i is executing its kernels. Especially, Fermi architecture allows at most 16 kernels from 16 different streams to be executed at the same time and Kepler even allows more. So we can also see overlap among computations belonging to different chains. However, not only kernel execution time but also kernel startup time should be considered. Each kernel will enter the work queue after being invoked and then wait to be executed. Consequently, the predecessor chain will probably have finished before the successor is really executed, as if kernel startup time is long enough and/or the input data size is too small. As figure 7b shows, chain i has finished while the first node of chain i + 2 is just at the beginning. There are only two chains running simultaneously on the GPU side, which does not make full use of GPU's computing power.

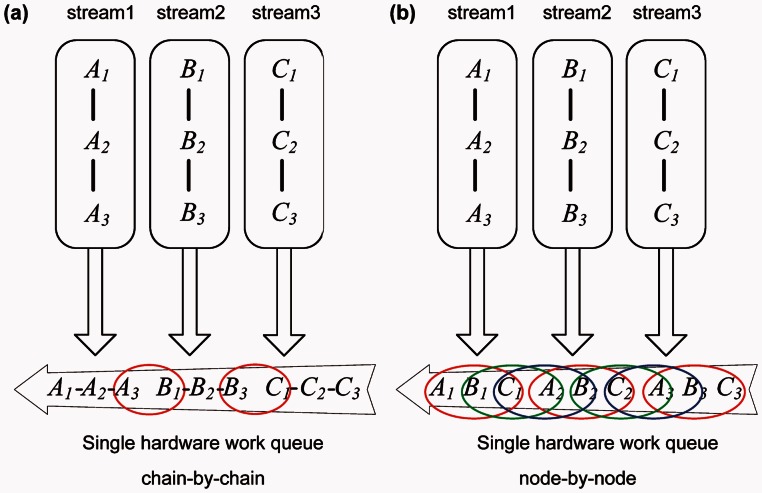
To increase concurrency further, we develop a new pipelining model (fig. 7c). It invokes transmissions and kernels in a “node-by-node” order rather than the “chain-by-chain” order used by n(MC)³. In this new scheduling strategy, because subtasks of different chains are invoked alternately, which significantly reduces the time intervals between them, kernels belonging to different chains have greater chance of running simultaneously in the GPU side. In figure 7c, we can see that the first nodes of chain i, chain i + 1, and chain i + 2 are invoked firstly, and then all the second nodes, and so on. By using “node-by-node” scheduling strategy, a(MC)³ runs as many as possible CUDA kernels concurrently. On the other hand, although it is declared that the Fermi architecture supports 16 different kernels from different streams, and ultimately, all the kernels are scheduled into the same work queue. Thus, dependent kernels within a stream are likely to prevent kernels in other streams from executing, which is called intrastream dependencies (NVIDIA 2012). For example, there are three streams, and each stream has three tasks (fig. 8). In “chain-by-chain” order, task A₁, A₂, A₃ in stream 1 are scheduled first, then task B₁, B₂, B₃ in stream 2, and finally, task C₁, C₂, C₃ in stream 3. Only (A₃, B₁) and (B₃, C₁) can run concurrently, owing to intrastream dependencies. As mentioned earlier, when the length of a DNA sequence M is large, coarse-grained tasks are applied, so that less CUDA threads are invoked and less SMs are used. For kernels in a stream, less SMs occupation means kernels in other streams can use more resources. However, intrastream dependencies waste free SM. Fortunately, by scheduling in “node-by-node” order, all kernels from different streams have the chance to run concurrently. As figure 8b shows (A₁, B₁, C₁), the three consecutively invoked kernels from different streams can run concurrently, so do (B₁, C₁, A₂) and (C₁, A₂, B₂). As shown in the previous section, “node-by-node” scheduling strategy improves inference speed dramatically. Kepler, NVIDIA's next-generation CUDA compute architecture, has resolved the intrastream dependencies problem on hardware, but the “node-by-node” scheduling is worth talking seriously.

Fig. 8.

Two kinds of single hardware work queue: “chain-by-chain” and “node-by-node.” The same letter denotes tasks from the same stream and the subscripts are the sequence numbers. Tasks in an ellipse can run concurrently.

Optimization

Memory Access Optimization

In CUDA architecture, global memory accessing is very likely to be the performance bottleneck because its latency is 400–600 clock cycles. Coalescing is the most important factor affecting global memory accessing performance. There is no bandwidth waste if data addressed by the threads of a warp can be coalesced as few as one global memory transaction. In a GPU card featuring Fermi architecture, 32 consecutive 4-byte words aligned to 128 bytes are fetched in a single global memory transaction. In a(MC)³, threads in a block access consecutive 4-byte words repeatedly, so we set the block size to 96, which guarantees peak memory bandwidth. Other block size might lead to poor effective bandwidth. For instance, if each block consists of 80 threads, the last 16 threads use only half of 32 consecutive 4-byte words fetched in a transaction and cause misalignment in successive accesses. Consequently, we use only 62.5% of peak bandwidth.

At shared memory level, bank conflict should be considered. In a Fermi GPU card, shared memory is divided into 32 banks, and successive 4-byte words are assigned to successive banks. When different threads of a warp access addresses belonging to the same memory bank, then a bank conflict occurs, and the accesses have to be serialized, which decreases performance seriously (Resios and Holdermans 2011). In n(MC)³, each thread accesses 16 consecutive elements from shared memory. So in each step, 16 threads in a warp conflict on bank i and the other 16 threads in the same warp conflict on bank i + 16. To avoid this serious 16-way bank conflict, we pad 1 dummy element to per 16 consecutive effective elements, which redirects all conflicted accesses to free banks.

Reduce Communication Overhead

Almost all GPU algorithms have to suffer from high CPU–GPU communication overhead. As mentioned earlier, an internal node of the phylogenetic tree requires the transition probability matrices and conditional likelihoods of its two children to calculate its own conditional likelihoods. Therefore, g(MC)³ naively launches two data transfers between CPU and GPU per node, which leads to poor overall performance. Transmissions in n(MC)³ are reduced to twice per chain: one transferring the transition probability matrices of all the nodes from CPU to GPU and another transferring the local likelihoods of the proposed new tree from GPU to CPU. Because CPU–GPU communication time is largely dominated by the number of transmissions, communication overhead is reduced effectively. By carefully assigning tasks between CPU and GPU, a(MC)³ reduces the number of transmission to only twice for all chains, which further reduces communication overhead. Besides optimization methods earlier, we also perform some other conventional CUDA optimizations. For example, a(MC)³ uses intrinsic math functions to improve instruction throughput while keeping enough precision.