A Unified Approach to Semiparametric Transformation Models under General Biased Sampling Schemes

Abstract

We propose a unified estimation method for semiparametric linear transformation models under general biased sampling schemes. The new estimator is obtained from a set of counting process-based unbiased estimating equations, developed through introducing a general weighting scheme that offsets the sampling bias. The usual asymptotic properties, including consistency and asymptotic normality, are established under suitable regularity conditions. A closed-form formula is derived for the limiting variance and the plug-in estimator is shown to be consistent. We demonstrate the unified approach through the special cases of left truncation, length-bias, the case-cohort design and variants thereof. Simulation studies and applications to real data sets are presented.

1 Introduction

Linear transformation models are a rich class of semiparametric regression models that are especially useful for the analysis of failure time data. They include the well-known proportional hazards model and proportional odds model as special cases (Clayton and Cuzick, 1985; Cuzick, 1988; Bickel, Klaassen, Ritov and Wellner, 1993; Cheng, Wei and Ying, 1995). Various inferential procedures have been proposed for the estimation of the regression parameters and the transformation function, including rank-based estimating equations, martingale estimating equations, and nonparametric maximum likelihood (Cheng et al., 1995; Chen, Jin and Ying, 2002; Zeng and Lin, 2007). These methods deal with data that are obtained via simple random sampling, in which case the sampling probability does not depend on the data. In many cases, either naturally or by design, data are not randomly sampled from the target population. The purpose of this article is to propose a unified approach for dealing with many commonly encountered biased sampling schemes where the sampling probabilities are data dependent. The usefulness of the proposed approach is seen from the fact that it covers such commonly encountered biased sampling schemes as length-biased sampling, left-truncation, the case-cohort design, as well as variants of the case-cohort design.

There is an extensive literature addressing various biased sampling schemes. Left truncation occurs naturally in astronomy on red shift (Segal, 1976) and in studies of HIV infection (Lagakos et al., 1988). It pertains to the existence of a second random variable, in addition to the variable of interest, such that the observation is truncated if the latter falls below the former. In other words, left truncation arises when individuals come under observation only at some known time after the time origin of the phenomenon under study. These data arise naturally from large-scale panel studies, when entry into the study depends on some event occurring before the event of interest. For left-truncated data, nonparametric estimators of the survivor function in the one-sample problem can be found in Turnbull (1976), Vardi (1982), Woodroofe (1985), Wang (1987), Tsai, Jewell and Wang (1987). Furthermore, Wang, Jewell and Tsai (1986), Keiding and Gill (1990) and Lai and Ying (1991a) derived large sample properties. For semiparametric regression models, readers are referred to Bhattacharrya, Chernoff and Yang (1983), Tsui, Jewell and Wu (1988), Lai and Ying (1991b), Wang, Brookmeyer and Jewell (1993) and Gross (1996).

Inference on length-biased data has been discussed in studies of ecology (McFadden, 1962), electron tube life (Blumenthal, 1967), fiber length (Cox, 1969), as well as in shrub data (Muttlak and MacDonald, 1990) and economic duration data (Kiefer, 1988; Helsen and Schmittlein, 1993; de Uña Álvarez, 2004). Under the length biased sample, the density of the observed sample is proportional to the original density multiplied by the length. The one-sample problem of estimating the survivor function has been explored in Vardi (1982, 1985), Bhattacharyya, Franklin and Richardson (1988), Jones (1991), Asgharian (2004), Assgharian, M’Lan and Wolfson (2002) and Asgharian and Wolfson (2005). In the context of regression analysis, Wang (1996) proposed inference for length-biased data using the Cox model with time-varying covariates but without censoring. More recently, Luo and Tsai (2009) proposed a pseudo-partial likelihood estimator for the Cox model and derived two nonparametric estimators; see also Huang and Qin (2011). Qin and Shen (2010) proposed estimating equations for the Cox model and Chen (2010) proposed inference for size-biased data using an accelerated failure time model. Shen, Ning and Qin (2009) extended a rank-based approach used by Cheng et al. (1995) to construct an unbiased estimating function for the parameters in an accelerated failure time model and linear transformation model.

The case cohort design was proposed by Prentice (1986) to save time and cost for large scale epidemiological studies. Its basic large sample properties were established in Self and Prentice (1988). Further developments can be found in Lin and Ying (1993), Chen and Lo (1999) and Chen (2001) among others. For the semiparametric linear transformation models, Kong, Cai and Sen (2004) extended the rank-based estimator of Cheng et al. (1995) to the case-cohort design, while Lu and Tsiatis (2006) extended the martingale estimating equations of Chen et al. (2002). Extensions of the classical case-cohort design to more complex sampling schemes can be found in Borgan et al. (2000), Kulich and Lin (2004), Breslow and Wellner (2007) and Samuelsen, Ånestad and Skrondal (2007).

In this paper, we develop a unified approach to linear transformation models under a general formulation of biased sampling schemes. We show that our approach leads to estimators that are consistent and asymptotically normal and we provide simple consistent variance estimators. The generality and usefulness of our approach are demonstrated through four special cases of biased sampling schemes, namely left truncation, length-biased sampling, case-cohort design and generalized case cohort designs.

The rest of the article is structured as follows. Section 2 introduces notation and specifies the models. Sections 3 presents details on the weight function for each specific biased sampling scheme, the estimation procedure as well as the large sample properties of the estimators. The algorithm and implementation are also explained. Simulation results together with applications on shrub data and nickel refinery data are included in Sections 4 and 5, respectively, followed by a discussion in Section 6. All the technical proofs are presented in the Appendix.

2 Model Specifications

Throughout this paper, we use T to denote the failure time of interest, C the censoring time and Z the p-vector of covariates. Let T̃ = min{T, C} and Δ = I(T ≤ C). We assume that T satisfies the transformation model which is specified through

$$H(T)=-{\mathit{Z}}^{\prime }\mathit{\beta }+\epsilon ,$$ (1)

where H(·) is an unknown monotone increasing function, β a p-vector of regression coefficients and ε an error term with a known distribution. In particular, when ε is specified to follow the extreme value distribution, (1) becomes the Cox (1972) proportional hazards regression model; when ε follows the logistic distribution, it becomes the proportional odds model (Bennett, 1983). When the error distribution is also not specified, only the direction of β is identifiable and we refer to Han (1987), Sherman (1993) and Chen (2002) for details about parameter estimation.

To introduce our biased sampling scheme, we first consider the situation of the usual random sampling from a population. Let q_Z(t, δ) (t ≥ 0, δ ∈ {0, 1}) denote the joint conditional density of (T̃, Δ) given covariates Z. Furthermore, let f_Z(F̄_Z) and g_Z(Ḡ_Z) denote the conditional density (survival) functions of T and C, respectively. Since T and C are assumed to be conditionally independent given Z, it follows that

$$q_Z(t,\delta )={\{f_Z(t){\overline{G}}_Z(t)\}}^{\delta }{\{g_Z(t){\overline{F}}_Z(t)\}}^{1-\delta },t\ge 0,\delta \in \{0,1\}.$$

Now suppose we have a biased sample from the population with biasing function w(t, δ), t ≥ 0, δ ∈ {0, 1}. Following Bickel et al. (1993, p. 86), the conditional joint density of (T̃, Δ) given Z then becomes

$${\stackrel{\sim }{q}}_Z(t,\delta )=\frac{w(t,\delta )q_Z(t,\delta )}{\int w(s,0)q_Z(s,0)ds+\int w(s,1)q_Z(s,1)ds}.$$ (2)

Note that such a sampling scheme depends on the outcome variables (T̃, Δ). Common examples include length-biased sampling with w(t, δ) = t (Vardi, 1982; Gill, Vardi and Wellner, 1988) and case-cohort sampling with w(t, δ) = δ + (1 − δ)p (Prentice, 1986), where p ∈ (0, 1) is a constant. In addition, we would like to point out that our general approach also handles the situation in which the biasing function is allowed to depend on Z and other observed covariates.

3 Main Results

In this section, we first derive the estimating equations for β and H(·) and establish the usual asymptotic properties for the resulting estimators. Subsection 3.2 presents an algorithm and discusses the implementation of the estimation procedure. Special examples that can aid understanding the generality and the scope of applicability of the new approach are provided in Subsection 3.3.

3.1 Estimating Equations and Asymptotic Results

Following the counting process notation commonly used in survival analysis, we let Y(t) = I(T̃ ≥ t) be the at-risk indicator and N(t) = I(T̃ ≤ t, Δ = 1) be the counting process that jumps to 1 when a failure occurs. Hazard and cumulative hazard functions of ε, which are completely specified under model (1), are denoted by λ(·) and Λ(·), respectively. Throughout the rest of the paper, we will suppress the subscript Z in q and q̃ when no ambiguity arises.

Under model (1), in the absence of sampling bias,

$$N(t)-{\int }_0^{t}Y(s)d\mathrm{\Lambda }\{{\mathit{Z}}^{\prime }{\mathit{\beta }}_0+H_0(s)\}$$

is a martingale process, where β₀ and H₀ denote the true values of β and H. In particular, this process has zero mean, a key property that gives unbiased estimating equations of Chen et al. (2002). Under the biased-sampling scheme, however, it is no longer a zero mean process and proper adjustment needs to be made. As we will see in Lemma 3.1, one such adjustment is to insert into the integrand of the compensator the following weight function

$$\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })=\frac{q(T,\mathrm{\Delta })}{\stackrel{\sim }{q}(T,\mathrm{\Delta })}\times \frac{\stackrel{\sim }{q}(t,1)}{q(t,1)},$$ (3)

which is a product of two terms, q(T, Δ)/q̃(T, Δ) and q̃(t, 1)/q(t, 1). These two terms can be viewed as the Radon-Nikodym derivatives between the true and the biased densities for the risk set and the counting process, respectively. Since both the counting process and the risk set are observed under biased sampling scheme, whereas the hazard function corresponds to the true density, we have to convert both dN(t) and the risk set Y(t) by the corresponding Radon-Nikodym derivatives so that all the components in estimating equation (4) that we are going to introduce are evaluated under the same measure. Our method resembles the idea of risk-set re-sampling first investigated in Wang (1996) that corrects the bias resulting from biased sampling. Note that the weight function ω may depend on Z.

With the above argument, we arrive at the following lemma which helps us obtain unbiased estimating equations.

Lemma 3.1

Under the biased sampling scheme, i.e. (T̃, Δ) follows q̃_Z given by (2) and ω(t, T̃, Δ) is defined by (3), we have

$$E_Z[dN(t)]=E_Z[\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })Y(t)\lambda (t)dt],$$ (4)

where E_Z denotes the conditional expectation given Z.

A formal proof of (4) is given in the Appendix. For truncation and case-cohort sampling, one may, as one of the referees suggested, view this problem from missing data perspective in the following sense: Let D = 1 or 0 be the indicator of observing an individual or not. Then, with a slight abuse of notation for T̃ = t, we can write

$$P(\stackrel{\sim }{T}=t,\delta \mid D=1,\mathit{Z})=\frac{{\{\pi (t,1)f_z(t){\overline{G}}_z(t)\}}^{\delta }{\{\pi (t,0){\overline{F}}_z(t)g_z(t)\}}^{1-\delta }}{P(D=1\mid \mathit{Z})},$$

where π(T̃, Δ) = P(D = 1|T̃, Δ) and $P(D=1\mid \mathit{Z})={\int }_0^{\tau }[\pi (t,1)f_z(t){\overline{G}}_z(t)+\pi (t,0){\overline{F}}_z(t)g_z(t)]dt$. It follows that

$$E[\mathrm{\Delta }I(\stackrel{\sim }{T}=t)\mid \mathit{Z}]=\lambda ({\beta }^{\prime }\mathit{Z}+H_0(t))E\left[\frac{I(\stackrel{\sim }{T}\ge t)\pi (t,1)}{\pi (\stackrel{\sim }{T},\mathrm{\Delta })}|\mathit{Z}\right]$$

and hence

$$E\left[\mathrm{\Delta }dN(t)-\frac{\pi (t,1)}{\pi (\stackrel{\sim }{T},\mathrm{\Delta })}Y(t)d\mathrm{\Lambda }({\beta }^{\prime }\mathit{Z}+H_0(t))|\mathit{Z}\right]=0.$$

Equation (4) leads to the following:

$$\sum _{i=1}^n\left[{dN}_i(t)-\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+H(t)\}\right]=0(0\le t\le \tau ),$$ (5)

$$\sum _{i=1}^n{\int }_0^{\tau }{\mathit{Z}}_i\left[{dN}_i(t)-\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+H(t)\}\right]=0,$$ (6)

where H is a nondecreasing function satisfying H(0) = −∞ and τ is a prespecified constant such that Pr{T̃ ≥ τ} > 0. They are analogous to the martingale estimating equations derived in Chen et al. (2002). Note that the condition on τ is common and is imposed to avoid possible tail instability with censored data.

For a fixed β, equation (5) entails that H is a uniquely defined and monotone increasing step function with jumps only at observed failure times t₁, …, t_K and H(t) = −∞ for all t < t₁. Let Ĥ(β; ·) be the unique solution to (5). Thus, the resulting estimator of β₀ satisfies U(β) = 0, where

$$U(\mathit{\beta })=\sum _{i=1}^n{\int }_0^{\tau }{\mathit{Z}}_i\left[{dN}_i(t)-\omega (t,{\stackrel{\sim }{T}}_i,{\delta }_i)Y_i(t)d\mathrm{\Lambda }\left\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+\widehat{H}(t,\mathit{\beta })\right\}\right].$$ (7)

We let β̂ denote the solution to (7) that estimates β₀. Thus Ĥ(t, β̂) estimates H₀(t). Numerical solutions to equations (5) and (6) may be obtained using iterative methods. More details on the implementation of the computational algorithm will be presented in Subsection 3.2.

Note that the expectations of (5) and (6) are zero. This unbiasedness is crucial for obtaining asymptotically unbiased estimators for β₀ and H₀. However, due to the bias-adjustment weight ω(t, T̃, Δ) that appears in (5) and (6), the process

$$M(t)=N(t)-{\int }_0^t\omega (s,\stackrel{\sim }{T},\mathrm{\Delta })Y(s)d\mathrm{\Lambda }\{{\mathit{Z}}^{\prime }{\mathit{\beta }}_0+H_0(s)\},$$ (8)

is no longer a martingale but a mean zero process instead. For this reason, the martingale argument given by Chen et al. (2002) to derive large sample properties needs to be modified accordingly. To identify the limiting distributions of the estimators, we define the following terms:

$$\begin{array}{l}{B}_1(t)=E[\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })Y(t)\stackrel{.}{\lambda }\{{\mathit{Z}}^{\prime }{\mathit{\beta }}_0+H_0(t)\}],\\ B_2(t)=E[\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })Y(t)\lambda \{{\mathit{Z}}^{\prime }{\mathit{\beta }}_0+H_0(t)\}],\\ B(t,s)=exp\left\{{\int }_s^t{B}_2^{-1}(u)B_1(u){dH}_0(u)\right\},\\ B_1^Z(t)=E[\mathit{Z}\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })Y(t)\stackrel{.}{\lambda }\{{\mathit{Z}}^{\prime }{\mathit{\beta }}_0+H_0(t)\}],\\ B_2^Z(t)=E[\mathit{Z}\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })Y(t)\lambda \{{\mathit{Z}}^{\prime }{\mathit{\beta }}_0+H_0(t)\}],\end{array}$$

where λ̇ denotes the first derivative of λ. These terms are similar to those defined in Chen et al. (2002) that are used to simplify the expression of the limiting distribution of β̂. In addition, we define

$$\mathit{z}(t)=\frac{1}{B_2(t)}\left[B_2^Z(t)+{\int }_{\ell }^{\tau }\{B_1^Z(s)-\frac{B_2^Z(s)B_1(s)}{B_2(s)}\}B(s,t){dH}_0(s)\right]$$ (9)

and

$$\begin{array}{l}{\mathit{\sum }}_{\ast }=E\left[{\int }_0^{\tau }\{\mathit{Z}-\mathit{z}(t)\}{\mathit{Z}}^{\prime }Y(t)\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })\stackrel{.}{\lambda }\{{\mathit{Z}}^{\prime }{\mathit{\beta }}_0+H_0(t)\}{dH}_0(t)\right],\\ {\mathit{\sum }}^{\ast }=E{\left[{\int }_0^{\tau }\{\mathit{Z}-\mathit{z}(t)\}dM(t)\right]}^{\otimes 2}.\end{array}$$

We need to impose the following regularity conditions:

• A1For any finite K, λ(x) is strictly positive and λ̇(x) is bounded and continuously differentiable on (−∞, K);
• A2The covariate vector Z is bounded in the sense that Pr{||Z|| < m} = 1 for some constant m;
• A3The true transformation function H₀ is continuously differentiable with a strictly positive derivative on [0, τ];
• A4 $E{[{\int }_0^{\tau }\mathit{Z}\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })Y(t)d\mathrm{\Lambda }\{{\mathit{Z}}^{\prime }\mathit{\beta }+H(t)\}]}^2<\infty$.
• A5Both Σ^* and Σ_* are nonsingular.

Remark

Condition A1 is a mild condition and is satisfied for distributions of ε in commonly encountered transformation models. Condition A2 is imposed so that modern empirical process theory can be applied without modification. Condition A4 is a mild assumption on the weight function ω(t, T̃, Δ). For case-cohort sampling as well as left-truncation, this condition can be easily verified. We can also show that the condition holds also for the length-biased sampling setup. Condition A5 is necessary since otherwise the problem becomes singular. Nonsingularity assumption on Σ^* is very mild. In fact, it basically means that the covariate vector Z does not reside in a lower dimensional hyperplane. For Σ_*, however, it is in general not trivial to verify the nonsingularity with a single simple-to-verify condition. However, we find that for specific families that are commonly used for the transformation models, namely, the proportional hazards model, the proportional odds model and the normal transformation model, we can show that Σ_* is nonsingular at β₀ = 0 due to the strictly increasing property of the corresponding hazard rate functions.

Theorem 3.1

Under Conditions A1 – A4, there exists a neighborhood of β₀ within which β̂ exists and is unique for all large n. Furthermore, $\sqrt{n}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0){\to }_d\mathcal{N}(\mathbf{0},{\mathit{\sum }}_{\ast }^{-1}{\mathit{\sum }}^{\ast }{({\mathit{\sum }}_{\ast }^{-1})}^{\prime })$ and $\sqrt{n}(\widehat{H}(t,\widehat{\mathit{\beta }})-H_0(t))$ converges weakly to a Gaussian process. Consistent estimators of Σ_* and Σ^* can be obtained by substituting β₀ and H₀ by their estimators, i.e.

$$\begin{array}{l}{\widehat{\mathit{\sum }}}_{\ast }=-\frac{1}{n}\sum _{i=1}^n{\int }_0^{\tau }\{{\mathit{Z}}_i-\widehat{\mathit{z}}(t)\}{\mathit{Z}}_i^{\prime }{Y}_i(t)\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)\stackrel{.}{\lambda }\left\{{\mathit{Z}}_i^{\prime }\widehat{\mathit{\beta }}+{\widehat{H}}_0(t)\right\}d{\widehat{H}}_0(t)\\ {\widehat{\mathit{\sum }}}^{\ast }=\frac{1}{n}\sum _{i=1}^n{\left[{\int }_0^{\tau }\{{\mathit{Z}}_i-\widehat{\mathit{z}}(t)\}d{\widehat{M}}_i(t)\right]}^{\otimes 2},\end{array}$$

where M̂_i(t) and ẑ(t) are similarly defined as in (8) and (9) with β₀ and H₀ replaced by their respective estimators.

The proof of Theorem 3.1 will be given in the Appendix. The limiting covariance function of $\sqrt{n}({\widehat{H}}_0-H_0)$ can be obtained through the usual asymptotic expansions and can be estimated by the same plug-in method.

3.2 Algorithm and Implementation

The computational algorithm closely follows that of Chen et al. (2002). First we choose an initial value β̂⁽⁰⁾, which can be obtained, for example, by using the maximum partial likelihood estimator and assuming the Cox proportional hazards model. With β̂⁽⁰⁾ being fixed, we then obtain an estimate of H(t₁), where t₁ is the first observed failure time, by solving:

$$\sum _{i=1}^n\omega (t_1,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t_1)\mathrm{\Lambda }\left\{{\mathit{Z}}_i^{\prime }{\widehat{\mathit{\beta }}}^{(0)}+H(t_1)\right\}=1.$$

This step is straightforward (e.g. via the Newton-Raphson algorithm) since Λ is a strictly monotone increasing function. We then estimate H(t_k) by solving successively, for k = 2, …, K,

$$\sum _{i=1}^n\omega (t_k,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t_k)\left[\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }{\widehat{\mathit{\beta }}}^{(0)}+H(t_k)\}-\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }{\widehat{\mathit{\beta }}}^{(0)}+H(t_{k-1})\}\right]=1.$$ (10)

The monotonicity of Ĥ(t) can be seen from (10) that in order for the right-hand side to be one H(t_k) > H(t_k−1) must hold since Λ(·) is a monotone increasing function while both ω(t, T̃_i, Δ_i) and Y_i(t) are non-negative. Note also that

$$\sum _{i=1}^n\omega (t_k,{\stackrel{\sim }{T}}_i{\mathrm{\Delta }}_i)Y_i(t_k)d\mathrm{\Lambda }({\mathit{\beta }}^{\prime }{\mathit{Z}}_i+H(t_k))\approx \sum _{i=1}^n\omega (t_k,{\stackrel{\sim }{T}}_i{\mathrm{\Delta }}_i)Y_i(t_k)\lambda ({\mathit{\beta }}^{\prime }{\mathit{Z}}_i+H(t_k-))\mathrm{\Delta }H(t_k).$$

Denote by Ĥ the resulting estimate, which clearly is monotone increasing, we estimate β₀ again by solving

$$\sum _{i=1}^n\sum _{k=1}^K{\mathit{Z}}_i\left([N_i(t_k)-N_i(t_{k-1})]-\omega (t_k,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t_k)\left[\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+\widehat{H}(t_k)\}-\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+\widehat{H}(t_{k-1})\}\right]\right)=0.$$

Recall that t₀ < t₁ and, therefore, N_i(t₀) = 0 for i = 1, …, n. Suppose β̂⁽¹⁾ is the new resulting estimate, we then substitute β̂⁽⁰⁾ by β̂⁽¹⁾ and repeat the procedure described above until convergence. Our experience indicates that convergence is usually achieved in a small number of iterations.

4 Special Cases

Biased sampling appears in many applications, either naturally or by design. Here we present six special cases involving biased-sampling that can be dealt with by our proposed method to obtain explicit expressions for the weight functions.

4.1 Length-biased Sampling

Under the length-biased sampling, the density of (T̃, Δ) can be expressed as

$$\stackrel{\sim }{q}(t,\delta )\propto tq(t,\delta ).$$

In this case, ω(t, T̃, Δ), the bias-adjustment weight function is, therefore, given by

$$\begin{array}{l}\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })=\frac{q(\stackrel{\sim }{T},\mathrm{\Delta })\stackrel{\sim }{q}(t,1)}{\stackrel{\sim }{q}(\stackrel{\sim }{T},\mathrm{\Delta })q(t,1)}\\ =\frac{t}{\stackrel{\sim }{T}}.\end{array}$$

Note that T̃ is the length of follow-up time. Therefore, equations (5) and (6) become

$$\sum _{i=1}^n\left[{dN}_i(t)-\frac{t}{{\stackrel{\sim }{T}}_i}{Y}_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+H(t)\}\right]=0(0\le t\le \tau ),$$ (11)

$$\sum _{i=1}^n{\int }_0^{\tau }{\mathit{Z}}_i\left[{dN}_i(t)-\frac{t}{{\stackrel{\sim }{T}}_i}{Y}_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+H(t)\}\right]=0.$$ (12)

It is noteworthy to mention that the current set up is designed for handling censoring first and followed by length biased sampling. This setting occurs naturally when cross-sectional sampling (censoring) is done in which the probability for a sample to be selected is proportional to the follow-up period T̃ instead of the event time T. In practice, there may be a second censoring following the length biased sampling. This additional censoring can be handled by inverse probability weighting similar to Shen et al. (2009). Note that which specific inverse probability weighting scheme to use depends on what assumptions are made on the censoring mechanism.

4.2 Left Truncation

Left truncation arises in situations in which individuals come under observation only when their survival times are beyond some prespecified time points; see, for example, Kalbfleisch and Prentice (2002, p. 14). The risk set just prior to an event time does not include individuals whose left truncation times exceed the given event time. In this case, denoting by U the truncation variable, the biased joint conditional density of (T̃, Δ) given U can be obtained by

$$\stackrel{\sim }{q}(t,\delta )\propto I(U<t)q(t,\delta ).$$

Writing q̃(t, δ) = κI(U < t)q(t, δ), where κ is the normalization constant, it follows that

$$\frac{q(\stackrel{\sim }{T},\mathrm{\Delta })}{\stackrel{\sim }{q}(\stackrel{\sim }{T},\mathrm{\Delta })}=\frac{1}{\kappa }I(U<\stackrel{\sim }{T})=\frac{1}{\kappa }$$

Note that I(U < T̃) = 1 since, for every observation, T̃ > U always holds. Furthermore,

$$\frac{q(t,\delta )}{\stackrel{\sim }{q}(t,\delta )}=\frac{1}{\kappa }I(U<t).$$

Combining the two ratios yields

$$\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })=I(U<t).$$ (13)

Under left truncation, with the weight function specified as in (13), equations (5) and (6) become

$$\sum _{i=1}^n[{dN}_i(t)-I(U_i<t)Y_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+H(t)\}]=0(0\le t\le \tau ),$$ (14)

$$\sum _{i=1}^n{\int }_0^{\tau }{\mathit{Z}}_i[{dN}_i(t)-I(U_i<t)Y_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+H(t)\}]=0.$$ (15)

This can be viewed as a natural extension of Chen et al. (2002) to accommodate the left truncation. If we assume specifically that the underlying model is the Cox proportional hazard model, (14) and (15) become the usual estimating equations derived from the partial likelihood of β; see Lawless (2003).

4.3 Case-cohort Design

Under the case-cohort design, complete covariate information is collected only on all cases (Δ = 1) and a random subset of censored subjects (Δ = 0). Suppose that the probability of selecting a censored individual into the sub-cohort is p, the weight function can be obtained, again, via considering the ratio between the biased and the unbiased conditional joint densities.

Since

$$\stackrel{\sim }{q}(t,\delta )\propto q(t,\delta )\delta +pq(t,\delta )(1-\delta )=q(t,\delta )[\delta +p(1-\delta )],$$

we have q(t, 1)/q̃(t, 1) = κ and

$$\begin{array}{l}\frac{q(\stackrel{\sim }{T},\mathrm{\Delta })}{\stackrel{\sim }{q}(T,\mathrm{\Delta })}=\frac{\kappa q(\stackrel{\sim }{T},\mathrm{\Delta })}{q(\stackrel{\sim }{T},\mathrm{\Delta })[\mathrm{\Delta }+p(1-\mathrm{\Delta })]}\\ =\frac{\kappa }{\mathrm{\Delta }+p(1-\mathrm{\Delta })},\end{array}$$

where κ is a normalization constant. This leads to the following weight function

$$\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })=\frac{1}{\mathrm{\Delta }+p(1-\mathrm{\Delta })}.$$

The resulting estimating equations are

$$\sum _{i=1}^n\left[{dN}_i(t)-\frac{1}{{\mathrm{\Delta }}_i+p(1-{\mathrm{\Delta }}_i)}{Y}_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+H(t)\}\right]=0,(0\le t\le \tau )$$ (16)

$$\sum _{i=1}^n{\int }_0^{\tau }{\mathit{Z}}_i\left[{dN}_i(t)-\frac{1}{{\mathrm{\Delta }}_i+p(1-{\mathrm{\Delta }}_i)}{Y}_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+H(t)\}\right]=0.$$ (17)

Note that (16) and (17) have the same form as equations (5) and (6) in Lu and Tsiatis (2006). However, in our model, (T̃_i, Δ_i) refer to the samples selected in the subcohort, which is slightly different from the set up specified in Lu and Tsiatis (2006).

4.4 Case-cohort Sampling on a Length-biased Sample

Suppose that a case-cohort design is applied to length-biased data arising from a cross sectional study. As a result, the biasing function is proportional to t[δ + p(1 − δ)] and

$$\stackrel{\sim }{q}(t,\delta )\propto t[\delta +p(1-\delta )]q(t,\delta ).$$

The corresponding weight function is, therefore, given by

$$\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })=\frac{t}{\stackrel{\sim }{T}[\mathrm{\Delta }+p(1-\mathrm{\Delta })]}.$$

In this case, the estimating equations are given by

$$\sum _{i=1}^n\left[{dN}_i(t)-\frac{t}{{\stackrel{\sim }{T}}_i\{{\mathrm{\Delta }}_i+p(1-{\mathrm{\Delta }}_i)\}}{Y}_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+H(t)\}\right]=0(0\le t\le \tau ),$$ (18)

$$\sum _{i=1}^n{\int }_0^{\tau }{\mathit{Z}}_i\left[{dN}_i(t)-\frac{t}{{\stackrel{\sim }{T}}_i\{{\mathrm{\Delta }}_i+p(1-{\mathrm{\Delta }}_i)\}}{Y}_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+H(t)\}\right]=0.$$ (19)

4.5 Stratified Case-cohort Design

Borgan et al. (2000) and Kulich and Lin (2004) proposed a stratified case-cohort design, in which the probability of selecting a censored observation into the subcohort is dependent on X, a vector of covariates that may or may not overlap with Z. Let p(X) denote this selection probability. Then, proceeding as in previous examples, we get

$$\stackrel{\sim }{q}(t,\delta )\propto q(t,\delta )\delta +p(\mathit{X})q(t,\delta )(1-\delta ).$$

Hence ω(t, T̃, Δ) = [Δ + p(X)(1 − Δ)]⁻¹ and the estimating equations take the same form as in Subsection 4.3, but with p being replaced by p(X).

4.6 Generalized Case-cohort Design

We now propose a generalized case-cohort design that covers the sampling schemes discussed in Subsections 4.3 and 4.5 as special cases. Under this design, cases are sampled with the sampling probability p₁(T̃, X) whereas controls are sampled into the subcohort with the selection probability p₂(T̃, X). It should be noted that the sampling probabilities now depend on Δ, T̃ and X.

The joint density of (T̃, Δ) can be shown to be

$$\stackrel{\sim }{q}(t,\delta )\propto q(t,\delta )[p_1(t,\mathit{X})\delta +(1-\delta )p_2(t,\mathit{X})]$$

and the weight function thus becomes

$$\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })={\left[p_1(\stackrel{\sim }{T},\mathit{X})\mathrm{\Delta }+(1-\mathrm{\Delta })p_2(\stackrel{\sim }{T},\mathit{X})\right]}^{-1}.$$

Therefore, we have the following estimating equations

$$\sum _{i=1}^n\left[{dN}_i(t)-\frac{1}{p_1({\stackrel{\sim }{T}}_i,{\mathit{X}}_i){\mathrm{\Delta }}_i+(1-{\mathrm{\Delta }}_i)p_2({\stackrel{\sim }{T}}_i,{\mathit{X}}_i)}{Y}_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+H(t)\}\right]=0,$$ (20)

$$\sum _{i=1}^n{\int }_0^{\tau }{\mathit{Z}}_i\left[{dN}_i(t)-\frac{1}{p_1({\stackrel{\sim }{T}}_i,{\mathit{X}}_i){\mathrm{\Delta }}_i+(1-{\mathrm{\Delta }}_i)p_2({\stackrel{\sim }{T}}_i,{\mathit{X}}_i)}{Y}_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }\mathit{\beta }+H(t)\}\right]=0.$$ (21)

5 Simulations

We first specify q(T̃, Δ) from which initial data are generated. In each subsection we describe how we resampled data with a weight proportional to the weight function ω described in Section 3. The simulation results are tabulated in Tables 1–6.

Table 1.

Estimates and standard errors for β in transformation models with a sample size of 50

Estimator	CP	r	β1				β2
			Bias	Var	$\widehat{\text{Var}}$	ECP	Bias	Var	$\widehat{\text{Var}}$	ECP
Proposed	0.10	0.0	−0.040	0.491	0.677	0.987	0.020	0.480	0.454	0.938
Chen			−0.388	0.462	0.645	0.777	0.367	0.487	0.630	0.815
Proposed	0.20		−0.040	0.512	0.842	0.994	0.049	0.544	0.535	0.946
Chen			−0.327	0.502	0.642	0.834	0.341	0.512	0.682	0.812
Proposed	0.10	0.5	0.010	0.841	1.013	0.975	−0.011	0.827	0.796	0.926
Chen			0.042	0.594	0.824	0.828	−0.036	0.635	0.811	0.867
Proposed	0.20		0.015	0.846	1.211	0.985	−0.064	0.834	0.919	0.956
Chen			0.058	0.624	0.814	0.864	−0.100	0.654	0.809	0.880
Proposed	0.10	1.0	0.097	1.397	1.348	0.945	−0.062	1.302	1.727	0.948
Chen			0.341	0.750	0.973	0.830	−0.294	0.797	0.993	0.855
Proposed	0.20		0.063	1.264	1.563	0.968	−0.025	1.279	1.832	0.970
Chen			0.278	0.757	0.982	0.854	−0.248	0.798	0.980	0.868

Note: Bias, Var, $\widehat{\text{Var}}$ and ECP are defined as the difference between the estimated and the true parameter values, the asymptotic variance estimated, the variance of the simulated estimated parameter values as well as the empirical coverage probability respectively.

Table 6.

Estimates and Standard Errors for β in Shrub Data Set

r	β1			β2
	Est	SE	P-value	Est	SE	P-value
0.0	0.7655	0.3387	0.0238	−0.0752	0.3273	0.8183
0.5	2.8583	1.0537	0.0067	0.7516	0.7531	0.3183
1.0	4.2925	2.1608	0.0470	1.0118	1.2033	0.4004

Following Chen et al. (2002), we generated data from H(T) = −β₁Z₁ − β₂Z₂ + ε, with the hazard function of ε, λ(x) = exp(x)/{1 + r exp(x)}, where r = 0, 0.5 and 1. For the transformation function H, we used H(t) = log(t) for r = 0 and log(r⁻¹e^t−r⁻¹) for other r values. Note that r = 0 corresponds to the proportional hazards regression while r = 1 corresponds to the proportional odds regression.

Covariates Z₁ and Z₂ were generated from uniform (0, 1) that are independent of each other. The parameters β₁ and β₂ were chosen to be −1.0 and 1.0. Two censoring proportions (CP) were used, namely 0.1 and 0.2 for the length-biased sampling as well as 0.8 and 0.9 for various case-cohort designs. The censoring time was generated by e^a+0.5U where U was a uniform random variable and values of a were set to attain desired censoring proportions.

5.1 Length-biased Sampling

Given the data we generated by q(T̃, Δ), units were resampled if U_i ≤ T̃_i/γ, where U_i’s are from the uniform (0, 1) distribution, and γ a constant larger than T̃_i for all i = 1, …, n. Computation was conducted on the resampled individuals of sizes 50 and 300; simulations were based on 1000 replications.

Tables 1 to 2 summarize the simulation results. The simulation results indicate that the proposed method performs well in large samples. The parameter estimates have negligible bias, compared to standard deviations and to the biased estimates of the unadjusted method of Chen et al. (2002). The means of estimated variance are close to the empirical variance of the parameter estimates, and the 95% confidence intervals (CI’s) are close to nominal coverage probability. Such CI’s obtained have a better coverage probability than that of the CI’s constructed using Chen et al. (2002) procedure that does not adjust for the length bias.

Table 2.

Estimates and standard errors for β in transformation models with a sample size of 300

Estimator	CP	r	β1				β2
			Bias	Var	$\widehat{\text{Var}}$	ECP	Bias	Var	$\widehat{\text{Var}}$	ECP
Proposed	0.10	0.0	−0.006	0.160	0.188	0.978	0.007	0.161	0.163	0.955
Chen			−0.163	0.206	0.212	0.857	0.163	0.207	0.213	0.866
Proposed	0.20		−0.003	0.183	0.239	0.978	−0.004	0.188	0.192	0.955
Chen			−0.129	0.218	0.230	0.894	0.121	0.219	0.236	0.901
Proposed	0.10	0.5	0.016	0.325	0.353	0.963	−0.011	0.324	0.330	0.959
Chen			0.066	0.282	0.292	0.937	−0.061	0.284	0.296	0.936
Proposed	0.20		−0.007	0.347	0.404	0.965	0.000	0.345	0.372	0.963
Chen			0.047	0.285	0.309	0.926	−0.053	0.287	0.308	0.931
Proposed	0.10	1.0	0.002	0.537	0.541	0.944	0.005	0.588	0.637	0.969
Chen			0.178	0.362	0.373	0.913	−0.165	0.364	0.375	0.915
Proposed	0.20		0.001	0.539	0.589	0.957	0.000	0.552	0.708	0.967
Chen			0.166	0.355	0.369	0.923	−0.159	0.358	0.380	0.912

Note: Bias, Var, $\widehat{\text{Var}}$ and ECP are defined as the difference between the estimated and the true parameter values, the asymptotic variance estimated, the variance of the simulated estimated parameter values as well as the empirical coverage probability respectively.

5.2 Case-cohort Design

A full cohort of sample size 3000 was generated and then case-cohort samples were selected from each full cohort by selecting from cases with a probability of p such that about two thirds of the selected samples in the subcohort are controls. The average sample size for a subcohort is 1000. The parameters β₁ and β₂ were set to be −1.0 and 1.0 respectively with the censoring proportions 0.8 and 0.9. Simulations were based on 1000 replications.

The performance of the proposed estimators under the case-cohort design is summarized in Table 3. The empirical biases were negligible and coverage probabilities were close to 0.95.

Table 3.

Estimates and standard errors for β in transformation models under case-cohort sampling scheme

CP	r	β1				β2
		Bias	Var	$\widehat{\text{Var}}$	ECP	Bias	Var	$\widehat{\text{Var}}$	ECP
0.90	0.0	0.001	0.224	0.235	0.963	−0.004	0.231	0.235	0.958
0.80		0.001	0.155	0.162	0.962	0.000	0.156	0.162	0.958
0.90	0.5	0.001	0.231	0.241	0.959	−0.004	0.240	0.246	0.956
0.80		0.001	0.165	0.170	0.962	0.000	0.166	0.175	0.963
0.90	1.0	0.000	0.248	0.254	0.961	−0.001	0.256	0.263	0.959
0.80		0.001	0.174	0.178	0.958	0.000	0.176	0.187	0.964

Note: Bias, Var, $\widehat{\text{Var}}$ and ECP are defined as the difference between the estimated and the true parameter values, the asymptotic variance estimated, the variance of the simulated estimated parameter values as well as the empirical coverage probability respectively.

5.3 Stratified Case-cohort Design

A full cohort of sample size 3000 was generated and then case-cohort samples were selected from each full cohort by selecting from cases with a probability of p_i = 1 − {1 + exp(1 + Z_1i)}⁻¹, and selecting among controls with a probability of p_i = 1 − {1+exp(−3+2Z_1i)}⁻¹. The average sample size for a subcohort is 1000, with one third of the samples are cases. The parameters β₁ and β₂ were set to be −1.0 and 1.0 respectively with the censoring proportions 0.8 and 0.9. Simulations were based on 1000 replications.

We assessed the performance of the proposed estimators under the case-cohort design. Table 4 summarizes the performance of the estimators using the average bias, 95% coverage probability, and estimated variances. For the models, the empirical biases were negligible and coverage probabilities were close to 0.95. The estimated variances were close to the variance from the simulations.

Table 4.

Estimates and standard errors for β in transformation models under stratified case-cohort sampling scheme

CP	r	β1				β2
		Bias	Var	$\widehat{\text{Var}}$	ECP	Bias	Var	$\widehat{\text{Var}}$	ECP
0.90	0.0	−0.014	0.263	0.267	0.956	0.002	0.261	0.265	0.956
0.80		0.013	0.212	0.213	0.947	0.005	0.204	0.210	0.961
0.90	0.5	−0.011	0.264	0.265	0.954	0.005	0.262	0.267	0.961
0.80		−0.005	0.243	0.222	0.936	−0.005	0.233	0.224	0.956
0.90	1.0	0.015	0.275	0.274	0.956	0.005	0.272	0.281	0.958
0.80		−0.012	0.240	0.234	0.946	0.003	0.226	0.241	0.968

Note: Bias, Var, $\widehat{\text{Var}}$ and ECP are defined as the difference between the estimated and the true parameter values, the asymptotic variance estimated, the variance of the simulated estimated parameter values as well as the empirical coverage probability respectively.

5.4 Generalized Case-cohort Design

Table 5 reports the results of simulations for the generalized case-cohort design where the probability of selection in the weight function depends on the follow-up time. Similar to the stratified case-cohort design simulation, we first generated 3000 samples and then randomly chose, on average, 1000 subjects into the subcohort, using the selection probability p(T̃) = 1 − {1 + exp(1 + T̃γ)}⁻¹, where γ = 1.2, 2 for p₁(T̃) and p₂(T̃) respectively. We found that the estimates for β were essentially unbiased and the means of the estimated standard error are close to the empirical standard errors. The coverage probabilities were close to 0.95. Simulations were based on 1000 replications.

Table 5.

Estimates and standard errors for β in transformation models under generalized case-cohort sampling scheme

CP	r	β1				β2
		Bias	Var	$\widehat{\text{Var}}$	ECP	Bias	Var	$\widehat{\text{Var}}$	ECP
0.90	0.0	0.007	0.260	0.262	0.947	0.005	0.259	0.263	0.952
0.80		0.008	0.206	0.209	0.954	−0.003	0.200	0.209	0.962
0.90	0.5	0.010	0.228	0.230	0.945	−0.004	0.230	0.235	0.956
0.80		0.028	0.212	0.213	0.953	−0.022	0.206	0.217	0.958
0.90	1.0	0.012	0.252	0.254	0.944	−0.006	0.257	0.264	0.960
0.80		0.044	0.187	0.189	0.947	−0.044	0.184	0.198	0.957

Note: Bias, Var, $\widehat{\text{Var}}$ and ECP are defined as the difference between the estimated and the true parameter values, the asymptotic variance estimated, the variance of the simulated estimated parameter values as well as the empirical coverage probability respectively.

6 Real Data Examples

6.1 Application to Shrub Data

We applied our estimation procedure to the data on 46 shrubs used by Wang (1996), originally described in Muttlak and McDonald (1990, Table 3). Data were collected using a line-intercept sampling method for vegetation. Under the biological sampling technique, the probability a shrub was included in the sample was proportional to the width, where the width was defined to be the distance between tangents of the shrub that are parallel to the transect (Muttlak and McDonald, 1990). Two indicator covariates were used to denote the three groups of transects to which the shrubs belonged. In Wang (1996), the first covariate Z₁ was an indicator of whether the shrub belonged to transect I, and Z₂ corresponded to transect II.

For the analysis reported in Table 6, we defined Z₁ and Z₂ to be indicators that the shrub belonged to transect I and transect III, respectively, so that the second transect was the reference group. The recoding of the covariate was to ensure that numerically more stable estimates can be obtained compared with the counterparts estimated by using the third transect as a reference group. This is due to the fact that only six observations belonged to this category. Table 6 reports the fitted transformation models with λ(x) = exp(x)/{1 + r exp(x)} for values of r = 0 (proportional hazards), 0.5 and 1 (proportional odds). The significant effect of β₁ does not change for different values of r. Qualitatively, the estimates for β₁ are significant and β₂ are not significant for all of the models that were fitted.

It is natural to compare which of the following models is more appropriate to fit the observed data: the proportional hazards (PH) model or the proportional odds (PO) model? We here suggest an ad hoc χ²-type goodness-of-fit selection criterion when Z is categorial as is the case here.

Under the length-biased sampling scheme, the conditional probability density function of T given Z is given by

$${\stackrel{\sim }{f}}_T(t\mid Z)=\frac{{tf}_{\epsilon }(H(t)+{\mathit{Z}}^{\prime }\mathit{\beta })H^{\prime }(t)}{\int {sf}_{\epsilon }(H(s)+{\mathit{Z}}^{\prime }\mathit{\beta })dH(s)},$$ (22)

where f_ε(·) denotes the density of ε. Based on (22), we can compute the expected number of observations within an interval, say [t_a, t_b], which is equal to ${\int }_{t_a}^{t_b}{\stackrel{\sim }{f}}_T(t)dt$. Recall that our estimation procedure provides users with both β̂ and Ĥ(t_k; β̂) where t_k is the kth ordered observation. Thus, the probability of T falls between t_k−1 and t_k is approximated by

$$\frac{(t_{k-1}+t_k)f_{\epsilon }(\widehat{H}(t_k)+{\mathit{Z}}^{\prime }\widehat{\mathit{\beta }})(\widehat{H}(t_k)-\widehat{H}(t_{k-1}))}{{\sum }_j(t_{j-1}+t_j)f_{\epsilon }(\widehat{H}(t_j)+{\mathit{Z}}^{\prime }\widehat{\mathit{\beta }})(\widehat{H}(t_j)-\widehat{H}(t_{j-1}))}.$$

For the shrub data, we divided t into three subintervals and constructed χ²-type statistics for transect I and transect II for the two families (extremely-value and logistic) of distributions. Transect III is not considered due to its small sample size. The resulting values for transect I are 11.9183 and 35.6116 for PH and PO models, respectively. For transect II, they are 2.2147 and 3.4971, respectively. For either transect, use of the PH model results in a lower χ² value. This provides some evidence that, between the two models, PH may be preferred.

6.2 Application to Case-cohort Design - Welsh Nickel Refiners Study

Data from Appendix VIII of Breslow and Day (1987) contain complete records for 679 workers employed in a nickel refinery in South Wales before 1925. The follow-up through 1981 uncovered 56 deaths from cancer of the nasal sinus. Lin and Ying (1993) reanalyzed the mortality data on the nasal sinus cancer using the Cox model with (modified) case-cohort design. Previous studies found three significant risk factors which include AFE (age at first employment), YFE (year at first employment) and EXP (exposure level).

In Table 7, the first column presents the estimated parameter values obtained from the full cohort dataset via estimating equations (5) and (6). In this case, p = 1 for all observations. The estimates are comparable to Lin and Ying (1993). The second column displays the results from fitting the same model to data obtained from a randomly drawn, hypothetical subcohort. Such a subcohort contains all the observed failures and some censored subjects that make up two third of the size of the subcohort. We also performed an analysis on another hypothetical subcohort which was drawn from the generalized case-cohort sampling scheme discussed in Section 4.6. We used selection probability p(T̃) = 1−{1+exp(1+T̃γ)}⁻¹, where γ = 0.012 and 0.020 for p₁(t) and p₂(t), respectively. The estimated values of β and their standard deviations, which are summarized in the third column of Table 7, are consistent with the conclusion of Lin and Ying (1993). All of these studies indicate that the covariates log(AFE − 10) and log(EXP + 1) are statistically significant. Compared with the full-cohort study, the estimated standard deviation of β̂ presented in the second and the third column of the table are slightly inflated. This is due to the fact that only a subset of the data is used for the estimation. The estimates obtained from this generalized case-cohort sampling scheme are closed to the corresponding values obtained by using a full cohort and Lin and Ying (1993). Under the generalized case-cohort setting, however, only 70% of the cases were included in the subcohort.

Table 7.

Cox regression analysis of time from the first employment to the nasal sinus cancer death for the Welsh nickel refiner study

Parameter	Full-cohort	Case-cohort	Generalized Case-cohort
log(AFE − 10)
Est.	2.2091	1.8426	2.1804
S.E	0.4097	0.4405	0.4323
P-value	3.48e – 08	3.44e – 05	4.57e – 07
(YFE − 1915)/10
Est.	0.0768	0.4801	0.0963
S.E	0.2925	0.3824	0.3418
P-value	0.6036	0.209	0.7781
(YFE − 1915)2/100
Est.	−1.2951	−1.2025	−1.4334
S.E	0.5104	0.6846	0.5913
P-value	0.006	0.079	0.0153
log(EXP + 1)
Est.	0.7883	1.1610	0.7654
S.E	0.1629	0.1934	0.1838
P-value	6.519e – 07	1.94e – 09	3.123e – 05

7 Discussion

We proposed a general inferential procedure for the regression parameter and transformation function in linear transformation models under biased sampling schemes. It provides a unified approach to all semiparametric linear transformation models as well as commonly encountered biased sampling schemes.

A key ingredient in the proposed approach is the weight function which is used to make appropriate adjustment to obtain unbiased estimating equations. It is important to note that, for the method to work in practice, the weight function needs to have a manageable form. Fortunately, as demonstrated in the examples, for many important cases the weight functions are simple.

Zeng and Lin (2007) proposed using the nonparametric maximum likelihood estimation (NPMLE) for the family of the semiparametric transformation models. They showed that the NPMLE gives consistent and asymptotically efficient estimators. It is certainly desirable to see if the NPMLE can be used in the setting with biased sampling, so that efficient estimation can be achieved. Unfortunately, the approach does not seem to be directly applicable. A major difficulty appears to be in that the censoring distribution cannot be factored out. On the other hand, one may include a general weight function in the integrand of the estimating function to improve the efficiency. Such an improvement, however, is obtained at the cost of increasing computational complexity. The asymptotic variance of the corresponding efficient estimator does not generally have a closed form representation. A simple inference procedure is not readily available as a result.

8 Appendix: Proofs

This appendix provides proofs of Lemma 3.1 and Theorem 3.1. Note that when there is no ambiguity, E and P denote, respectively, the conditional expectation and probability given Z.

A1. Proof of Lemma 3.1

By definition, N(t) = I(T̃ ≤ t, Δ = 1). Since q̃(t, 1) is the sub-density of T̃ on Δ = 1, it follows that E[dN(t)] = q̃(t, 1)dt. Therefore, it suffices to show that E[ω(t, T̃, Δ)Y(t)λ(t)dt] = q̃(t, 1)dt.

Recall that ω(t, T̃, Δ) = [q(T̃, Δ)q̃(t, 1)]/[q̃(T̃, Δ)q(t, 1)]. We have

$$\begin{array}{l}\frac{q(t,1)}{\stackrel{\sim }{q}(t,1)}E[\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })Y(t)]=E\left[\frac{q(\stackrel{\sim }{T},\mathrm{\Delta })}{\stackrel{\sim }{q}(\stackrel{\sim }{T},\mathrm{\Delta })}I(\stackrel{\sim }{T}\ge t)\right]\\ =\int \frac{q(s,1)}{\stackrel{\sim }{q}(s,1)}I(s\ge t)\stackrel{\sim }{q}(s,1)ds+\int \frac{q(s,0)}{\stackrel{\sim }{q}(s,0)}I(s\ge t)\stackrel{\sim }{q}(s,0)ds\\ =\int [q(s,1)+q(s,0)]I(s\ge t)ds\\ =[1-F(t)][1-G(t)].\end{array}$$

Hence, it follows that

$$\begin{array}{l}E[\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })Y(t)]\lambda (t)dt=[1-F(t)][1-G(t)]\frac{\stackrel{\sim }{q}(t,1)}{q(t,1)}\frac{f(t)}{[1-F(t)]}dt\\ =\stackrel{\sim }{q}(t,1)dt,\end{array}$$

where the last equality follows from the fact that q(t, 1) = f(t) [1 − G(t)].

A2. Proof of Theorem 3.1

Following Chen et al. (2002), we divide the proof into three steps:

Step 1

Let Ĥ₀(t) = Ĥ(t; β₀), where β₀ is the true parameter value. We first show that Ĥ₀ converges to H₀. Here, the proof follows closely the proof of Proposition in Lu and Ying (2004). Suppose H̃ is a limit of Ĥ₀. By Helly’s Lemma (van der Vaart, 2000), to show convergence of Ĥ₀ to H₀, it suffices to show that H̃ must be H₀. By (5) and the law of large numbers, we have

$$E[N(t)]={\int }_0^{t}E\left[Y(s)\omega (s,\stackrel{\sim }{T},\mathrm{\Delta })\right]\lambda \left\{{\mathit{Z}}^{\prime }{\mathit{\beta }}_0+\stackrel{\sim }{H}(s)\right\}d\stackrel{\sim }{H}(s).$$

This implies that H̃(·) is differentiable and must satisfy

$$\frac{d\stackrel{\sim }{H}(t)}{dt}=\frac{dE[N(t)]}{dt}{\left(E\left[Y(t)\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })\right]\lambda \left\{{\mathit{Z}}^{\prime }{\mathit{\beta }}_0+\stackrel{\sim }{H}(t)\right\}\right)}^{-1},$$ (A1)

which is a smooth function of t and H̃(t). Since (A1) is a Cauchy problem, its solution exists and is unique under local smoothness assumptions (Reinhard, 1987, Theorem 3.4.1). Note that by Lemma 3.1, H₀ satisfies (A1). Therefore, H̃ = H₀ and hence Ĥ converges to H₀.

For t in a compact subset of the interior of the support of T̃, we can show that the derivative of Ĥ(t, β) with respect to β is bounded in the neighborhood of β₀. Therefore, Ĥ(t, β_n) − Ĥ₀(t, β₀) → 0 provided that β_n converges to β₀. Since Ĥ₀(t) → H₀(t), it follows that Ĥ(t, β̂) → H₀(t) provided that β̂ is a consistent estimator.

We next show the consistency of β̂. Let U̇(β) denote the derivative of U(β) with respect to β. Applying the uniform law of large numbers (Pollard, 1990), we can show, for β in a neighborhood of β₀, that n⁻¹U(β) converges uniformly to a nonrandom limiting function u(β) and that n⁻¹U̇(β) converges uniformly to u̇(β). Thus, n⁻¹U̇(β) is nonsingular in a neighborhood of β₀, provided that u̇(β₀) = −Σ_*, which is to be shown in the next step. Since u(β₀) = 0, it follows that there exists a neighborhood of β₀ such that β̂ exists and is unique and that β̂ → β₀.

Step 2

We next show that n⁻¹U̇(β₀) converges to −Σ_*. Let a > 0 and b be constants and define

$$\begin{array}{l}{\lambda }^{\ast }\{H_0(t)\}=B(t,a)\\ {\mathrm{\Lambda }}^{\ast }(x)={\int }_b^x{\lambda }^{\ast }(s)ds,\end{array}$$

for t > 0 and x ∈ (−∞, ∞). Here, a and b are chosen such that the integrals are finite. By the definition of B(t, s), we easily see that

$${\lambda }^{\ast }\{H_0(s)\}/{\lambda }^{\ast }\{H_0(t)\}=B(s,t).$$ (A2)

Similarly, by the definition of B₁(t), we can get

$$d{\lambda }^{\ast }\{H_0(t)\}={\lambda }^{\ast }\{H_0(t)\}{dB}_1(t).$$

From these and mimicking Steps A2 and A3 of Chen et al. (2002, p. 666), we get

$${\frac{\partial }{\partial \mathit{\beta }}d\widehat{H}(t,\mathit{\beta })|}_{\mathit{\beta }={\mathit{\beta }}_0}=-B_2^{-1}(t)\left[{B_1^Z(t)+B_1(t)\frac{\partial }{\partial \mathit{\beta }}\widehat{H}(t,\mathit{\beta })|}_{\mathit{\beta }={\mathit{\beta }}_0}+o_p(1)\right]{dH}_0(t),$$ (A3)

$${\frac{\partial }{\partial \mathit{\beta }}\widehat{H}(t,\mathit{\beta })|}_{\mathit{\beta }={\mathit{\beta }}_0}=-{\int }_0^t\frac{B(s,t)}{B_2(s)}{B}_1^Z(s){dH}_0(s)+o_p(1).$$ (A4)

Finally,

$$\begin{array}{l}-\stackrel{.}{U}({\beta }_0)=\sum _{i=1}^n\frac{\partial }{\partial \mathit{\beta }}{{\int }_0^{\tau }{\mathit{Z}}_i\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t)\lambda \{{\mathit{Z}}_i^{\prime }\mathit{\beta }+\widehat{H}(t,\mathit{\beta })\}d\widehat{H}(t,\mathit{\beta })|}_{\mathit{\beta }={\mathit{\beta }}_0}\\ =\sum _{i=1}^n{\int }_0^{\tau }\left[{\mathit{Z}}_i-\frac{B_2^Z(t)}{B_2(t)}\right]\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t)\stackrel{.}{\lambda }\{{\mathit{Z}}_i^{\prime }{\mathit{\beta }}_0+H_0(t)\}{\mathit{Z}}_i^{\prime }{dH}_0(t)+n{\int }_0^{\tau }{\left[B_1^Z-\frac{B_1(t)B_2^Z(t)}{B_2(t)}\right]\frac{\partial }{\partial \mathit{\beta }}\widehat{H}(t,\mathit{\beta })|}_{\mathit{\beta }={\mathit{\beta }}_0}{dH}_0(t)+o_p(1),\end{array}$$

where the last equality follows from (A3) and definitions of B₁, B₂, $B_1^Z$ and $B_2^Z$. Combining this with (A4) and rearranging terms, we get

$$n^{-1}\stackrel{.}{U}({\beta }_0)=-n^{-1}\sum _{i=1}^n{\int }_0^{\tau }({\mathit{Z}}_i-\mathit{z}(t)){\mathit{Z}}_i^{\prime }\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t)\stackrel{.}{\lambda }\{{\mathit{Z}}_i^{\prime }{\mathit{\beta }}_0+H_0(t)\}{dH}_0(t)+o_p(1),$$

which converges to −Σ_*.

Step 3

Finally, we show the asymptotic normality of U(β₀). Write

$$U({\mathit{\beta }}_0)=\sum _{i=1}^n{\int }_0^{\tau }{\mathit{Z}}_i{dM}_i(t)-\sum _{i=1}^n{\int }_0^{\tau }{\mathit{Z}}_i\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t)d[\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }{\mathit{\beta }}_0+{\widehat{H}}_0(t)\}-\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }{\mathit{\beta }}_0+H_0(t)\}].$$ (A5)

Again by following the derivation of Chen et al. (2002, p. 667), we can show that the last term in (A5) is equal to

$$\sum _{i=1}^n{\int }_0^{\tau }\left[\frac{B_2^Z(t)}{B_2(t)}+\frac{{\lambda }^{\ast }\{H_0(t)\}}{B_2(t)}{\int }_0^{\tau }\left(\frac{B_1^Z(s)}{{\lambda }^{\ast }\{H_0(s)\}}-\frac{B_1(s)B_2^Z(s)}{B_2(s){\lambda }^{\ast }\{H_0(s)\}}\right){dH}_0(s)\right]{dM}_i(t)+o_p(n^{1/2}).$$

Combining this with (A.2), (A.5) and the definition of z(t), we get

$$U({\mathit{\beta }}_0)=\sum _{i=1}^n{\int }_0^{\tau }\{{\mathit{Z}}_i-\mathit{z}(t)\}{dM}_i(t)+o_p(n^{1/2}),$$

which is a sum of independent zero-mean random vectors. Thus the classical central limit theorem implies that n^−1/2U(β₀) converges to 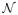(0, Σ^*). From this and the result of Step 2, we have $\sqrt{n}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)\to \mathcal{N}(\mathbf{0},{\mathit{\sum }}_{\ast }^{-1}{\mathit{\sum }}^{\ast }{({\mathit{\sum }}_{\ast }^{-1})}^{\prime })$. To show the weak convergence of $\sqrt{n}\{\widehat{H}(t,\widehat{\mathit{\beta }})-H_0(t)\},$, observe that

$$\begin{array}{l}\sqrt{n}\{\widehat{H}(t,\widehat{\mathit{\beta }})-H_0(t)\}=\sqrt{n}\{\widehat{H}(t,\widehat{\mathit{\beta }})-\widehat{H}(t,{\mathit{\beta }}_0)\}-\sqrt{n}\{\widehat{H}(t,{\mathit{\beta }}_0)-H_0(t)\}\\ ={\sqrt{n}\frac{\partial }{\partial \mathit{\beta }}\widehat{H}(t,\mathit{\beta })|}_{\mathit{\beta }={\mathit{\beta }}_0}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)-\sqrt{n}\{\widehat{H}(t,{\mathit{\beta }}_0)-H_0(t)\}+o_p(1).\end{array}$$ (A6)

By (A4), the first term on the right hand side of (A6) equals

$$\frac{1}{\sqrt{n}}A(t){\mathit{\sum }}_{\ast }^{-1}\sum _{i=1}^n{\int }_0^{\tau }\{{\mathit{Z}}_i-\mathit{z}(s)\}{dM}_i(s)+o_p(1),$$ (A7)

where $A(t)=-{\int }_0^t\frac{B(s,t)}{B_2(s)}{B}_1^Z(s){dH}_0(s)$. To tackle the second term, observe that

$$\begin{array}{l}\sum _{i=1}^n{dM}_i(t)=\sum _{i=1}^n{dN}_i(t)-\sum _{i=1}^n\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }{\mathit{\beta }}_0+H_0(t)\}\\ =\sum _{i=1}^n\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }{\mathit{\beta }}_0+\widehat{H}(t,{\mathit{\beta }}_0)\}-\sum _{i=1}^n\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t)d\mathrm{\Lambda }\{{\mathit{Z}}_i^{\prime }{\mathit{\beta }}_0+H_0(t)\}\\ =(1+o_p(1))\sum _{i=1}^n\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t)d\left(\lambda \{{\mathit{Z}}_i^{\prime }{\mathit{\beta }}_0+H_0(t)\}\left[\widehat{H}(t,{\mathit{\beta }}_0)-H_0(t)\right]\right).\end{array}$$ (A8)

Let $J_n(t)=\frac{{\sum }_{i=1}^n\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t)\stackrel{.}{\lambda }\{{\mathit{Z}}_i^{\prime }{\mathit{\beta }}_0+H_0(t)\}}{{\sum }_{i=1}^n\omega (t,{\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i)Y_i(t)\lambda \{{\mathit{Z}}_i^{\prime }{\mathit{\beta }}_0+H_0(t)\}}$ and $J(t)=\underset{n\to \infty }{lim}{J}_n(t)$. Then (A8) can be used to show that

$$\sum _{i=1}^n\frac{{dM}_i(t)}{{\sum }_{j=1}^n\omega (t,{\stackrel{\sim }{T}}_j,{\mathrm{\Delta }}_j)Y_j(t)\lambda \{{\mathit{Z}}_j^{\prime }{\mathit{\beta }}_0+H_0(t)\}}=(1+o_p(1))\left\{J_n(t)\left[\widehat{H}(t,{\mathit{\beta }}_0)-H_0(t)\right]{dH}_0(t)+d\left(\widehat{H}(t,{\mathit{\beta }}_0)-H_0(t)\right)\right\}.$$

Therefore,

$$e^{{\int }_0^{t}J(s)ds}\left(\widehat{H}(t,{\mathit{\beta }}_0)-H_0(t)\right)=\sum _{i=1}^n{\int }_0^t\frac{e^{{\int }_0^{s}J(u)du}{dM}_i(s)}{{\sum }_{j=1}^n\omega (s,{\stackrel{\sim }{T}}_j,{\mathrm{\Delta }}_j)Y_j(s)\lambda ({\mathit{Z}}_j^{\prime }{\mathit{\beta }}_0+H_0(s))}+o_p(n^{-1/2}).$$

It follows that

$$\widehat{H}(t,{\mathit{\beta }}_0)-H_0(t)=\frac{1}{n}\sum _{i=1}^n{\int }_0^t\frac{B(s,t)}{B_2(s)}{dM}_i(s)+o_p(n^{-1/2}).$$ (A9)

Combining (A8) and (A9), we have

$$\sqrt{n}\{\widehat{H}(t,\widehat{\mathit{\beta }})-H_0(t)\}=\frac{1}{\sqrt{n}}A(t){\mathit{\sum }}_{\ast }^{-1}\sum _{i=1}^n{\int }_0^{\tau }\{{\mathit{Z}}_i-\mathit{z}(s)\}{dM}_i(s)+\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^t\frac{B(s,t)}{B_2(s)}{dM}_i(s)+o_p(1).$$ (A10)

Both the first and the second terms on the right hand side of (A10) are sums of iid mean-zero variables. Observe that $\mid {\int }_0^t\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })Y(t)d\mathrm{\Lambda }\{{\mathit{Z}}^{\prime }\mathit{\beta }+H_0(t)\}\mid$ is bounded above by $\mid {\int }_0^{\tau }\omega (t,\stackrel{\sim }{T},\mathrm{\Delta })d\mathrm{\Lambda }\{{\mathit{Z}}^{\prime }\mathit{\beta }+H_0(t)\}\mid$ and by Condition A4, this envelope function has a finite second moment. Since B(s, t)/B₂(s) is bounded for all s and t, the second term on the right hand side of (A10) has also a finite second moment. By the multivariate central limit theorem, $\sqrt{n}\{\widehat{H}(t,\widehat{\mathit{\beta }})-H_0(t)\}$ converges in finite dimensional distribution to a mean-zero Gaussian process. Similar to Bilias et al. (1997), z(t) is of bounded variations, all the major terms on the right hand side of (A10) can be written as differences between two monotone functions in t. Since M_i(t) is also a difference of two monotone functions in t, it follows that, due to the fact that monotone functions have pseudodimension one, $\sqrt{n}\{\widehat{H}(t,\widehat{\mathit{\beta }})-H_0(t)\}$ is manageable in the sense of Pollard (1990). As a result, we can claim that the process $\sqrt{n}\{\widehat{H}(t,\widehat{\mathit{\beta }})-H_0(t)\}$ is tight and hence converges weakly to a Gaussian process (Pollard, 1990).