Abstract
Patients with repaired tetralogy of Fallot account for the majority of cases with late onset right ventricle (RV) failure. A new surgical procedure placing an elastic band in the right ventricle is proposed to improve RV function measured by ejection fraction. A multiphysics modeling approach is developed to combine cardiac magnetic resonance imaging, modeling, tissue engineering and mechanical testing to demonstrate feasibility of the new surgical procedure. Our modeling results indicated that the new surgical procedure has the potential to improve right ventricle ejection fraction by 2–7% which compared favorably with recently published drug trials to treat LV heart failure.
Keywords: Right ventricle, congenital heart disease, heart model, multiscale, pulmonary valve replacement, fluid-structural interaction
1 Introduction
Patients with repaired Tetralogy of Fallot (ToF), a congenital heart defect which includes a ventricular septal defect and severe right ventricular outflow obstruction, account for the majority of cases with late onset RV failure. The current surgical approach, which includes pulmonary valve replacement/insertion (PVR), has yielded mixed results with many patients not recovering RV function after pulmonary valve insertion with or without concomitant RV remodeling surgery [1–4]. Thus, there is a need for novel approaches to recover RV function in this rapidly growing patient group. A novel surgical procedure was developed where a more radical removal of RV patch and scar was performed with a smaller outflow patch (Fig. 1) [5]. A randomized clinical trial (NIH 5P50HL074734, Geva and del Nido) was developed to compare conventional pulmonary valve insertion with moderate patch removal vs. PVI with the more radical RV patch and scar removal (Fig 1a vs. Fig 1b). 64 patients who underwent ToF procedures in early childhood and fulfilled the defined clinical criteria for PVI were randomly assigned to undergo either PVI alone (n=34) or PVI with surgical RV remodeling (n=30). However, no significant difference was observed in the primary outcome (RV ejection fraction change 2–7% in the PVI alone group vs. 1–7% in the PVI with RV remodeling group; P=0.38) [6]. This study motivated the proposed new surgical procedures with band insertion to improve RV contraction and ejection fraction. In this paper, a novel surgical procedure with RV contracting band insertion is proposed to improve RV ejection fraction after PVI and RV remodeling. RV ejection fraction is a major index of RV function and an important determinant of clinical outcomes in patients with repaired ToF given by:
| (1) |
where RVEDV is RV end diastolic volume and RVEDV is RV end systolic volume.
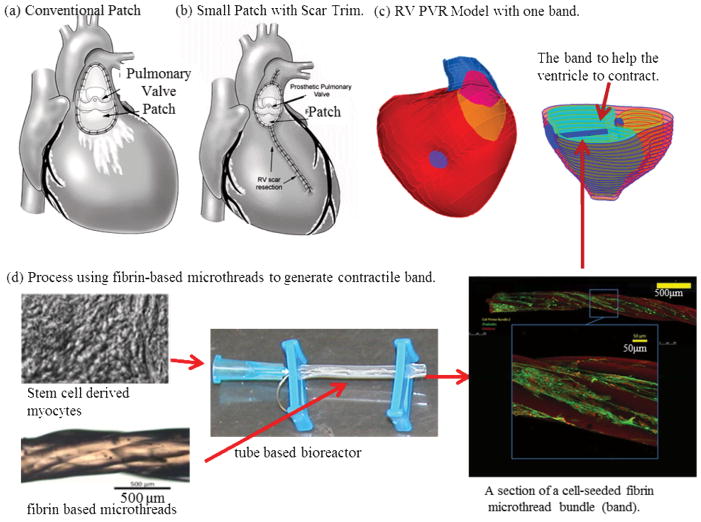
Figure 1.
A interdisciplinary multiscale approach for an innovative pulmonary valve insertion/replacement (PVI/PVR) surgery with RV remodeling and band insertion to improved surgical outcome after surgery. (a) RV pulmonary valve insertion (PVR) (current practice); (b) RV after PVR with reduction of RV outflow patch and removal of RV scar (RV remodeling); (c) RV PVR with one band insertion (patient-specific geometry); (d) A process using fibrin-based cell-seeded microthreads to generate contractile band.
Figure 1 shows the conventional patch, a smaller patch with RV remodeling, a patch model with band insertion, and a tissue engineering process using fibrin-based microthreads to generate contractile bands. The idea is that the contracting band will help RV to contract, which may lead to significant improvement of RV function. An interdisciplinary approach integrating multiscale modeling, surgery, CMR, tissue engineering and mechanical engineering is proposed to tackle this challenging and important surgical problem with high impact to public health. The contracting band was added to our previous patient-specific MRI-based RV/LV/Patch models to investigate its impact and potential improvement on RV cardiac function and mechanical performance. The band models include: (a) an elastic band connecting the RV anterior free wall and the septum; (b) fluid-structure interactions to obtain both structure and flow shear stress conditions to identify optimal mechanical conditions for potential cell-seeded band tissue regeneration. (c) two-layer ventricle myocardial wall construction with realistic epicardial and endocardial fiber orientations; (d) anisotropic material properties for both RV and LV tissues; (e) a patch/scar area with different materials. The 3D CMR-based RV/LV/Patch/Band models were solved to obtain 3D ventricular deformation and stress/strain distributions for accurate assessment of RV cardiac function and mechanical conditions. The computational models were validated by CMR data first and then used to assess the effect of different band approaches with the ultimate goal of improving recovery of RV function after surgery. Initial evidence showing improvement of RV ejection fraction using RV/LV/Patch models with band insertion and detailed band stress/strain and flow shear stress conditions are presented.
Recent advances in computational modeling, methods and computer technology have made it possible for computer-simulated procedures to be used in clinical decision-making process to replace empirical and often risky clinical experimentation to examine the efficiency and suitability of various reconstructive procedures in diseased hearts [7–20]. Peskin pioneered heart modeling effort with his celebrated immersed boundary method [7–8]. More recently, Hunter, McCulloch, Guccione, Kerckhoffs, Costa, Axel, Saber and many other authors have made great contributions to passive and active ventricle modeling, including the Physiome Project and the Continuity package [9–16]. In our previous papers, patient-specific cardiac magnetic resonance (CMR) image-based computational right and left ventricle (RV/LV) models with fluid-structure interactions were introduced to assess outcomes of various RV reconstruction techniques with different scar tissue trimming and patch sizes [17–20]. A recent review can be found in [17].
2. Data Acquisition, Models and Methods
2.1 Data acquisition, 3D geometry re-construction and band location
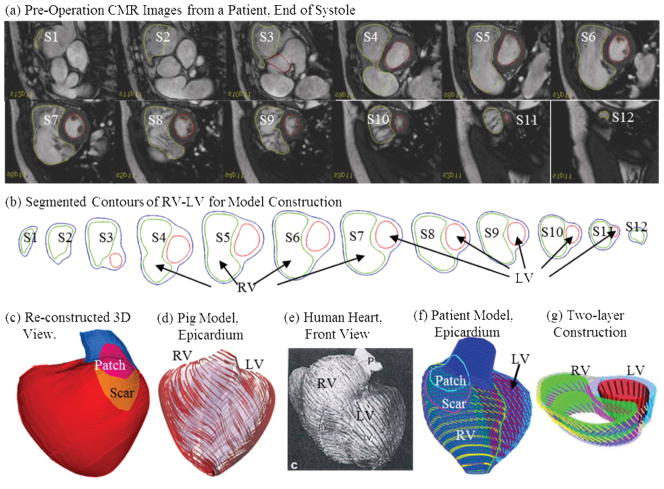
CMR studies were performed by Dr. Tal Geva to acquire patient-specific ventricular geometry for a patients needing RV remodeling and pulmonary valve replacement operations (Fig. 2). The RV and LV were imaged using ECG-gated, breath-hold steady state free precession cine MR in the ventricular short axis (12–14 equidistant slices covering the ventricles from base to apex; slice thickness 6–8 mm; interslice gap 0–2 mm; 30 frames per cardiac cycle). The valve and patch positions were determined with cine MR imaging, flow data, and delayed enhancement CMR to delineate location and extent of scar/patch. The CMR findings were subsequently confirmed by the intra-operative observations (del Nido). Band location was determined by Dr. del Nido based on his surgical experience and ventricle anatomic limitations (Fig. 1). As patient-specific fiber orientation data was not available in practice, we chose to construct a two-layer RV/LV model and set fiber orientation angles using fiber angles given in Hunter et al. [13] (see Fig. 4). Fiber orientation can be adjusted when patient-specific data becomes available [21]. Three-dimensional RV/LV geometry and computational mesh were constructed following the procedures described in [17–19]. Figure 2 shows pre-operative CMR images from the patient with repaired TOF and severe RV dilatation, the segmented contour pots, the stacked contours showing the location and orientation of the hypothetic elastic band, the 3D re-construction RV/LV geometry, ventricular fiber orientations from human and a pig hearts and a section of the model showing how the two-layer RV/LV model was constructed [13,17,21].
Figure 2.
CMR-based model construction process. (a) CMR images of a patient; (b) segmented contours; (c) reconstructed 3D geometry; (d)–(f) fiber orientation from a pig model [13] and a human heart [21]; (g) two-layer construction.
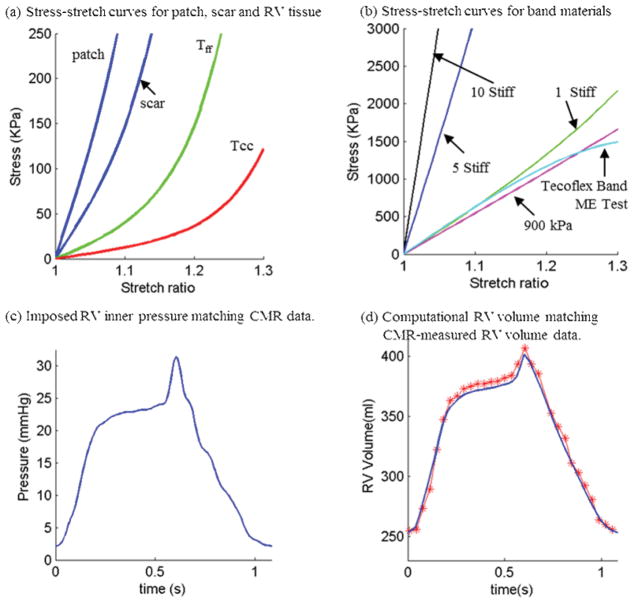
Figure 4.
Material Stress-Stretch curves, pressure conditions used in the paper and computational RV volume curve matching CMR-measured data. (a) Stress-Stretch curves from Mooney-Rivlin isotropic patch, scar and anisotropic RV tissue models used in this paper. Model parameter values (c2=0 for all models): Anisotropic RV model (out-layer given in plot): c1=5.746 kPa, c2=0, D1=1.479 kPa, D2=3.0, K1=23.413 kPa, K2=3.2; Scar: c1=19.227 kPa, c2=0, D1=19.227 kPa, D2=9.0; Patch: c1=38.454 KPa, c2=0, D1=38.454 kPa, D2=9.0; Tff: Stress in the fiber direction; Tcc: Stress in fiber circumferential direction. (b) Stress-Stretch curves from Mooney-Rivlin isotropic models for passive band materials. “1 Stiff”: c1=600 kPa, D1=300 kPa, D2=1.4; “5 Stiff”: c1=3,000 kPa, D1=1,500 kPa, D2=1.4; “10 Stiff”: c1=6,000 kPa, D1=3,000 kPa, D2=1.4; Curve fitting ME testing data: c1=1,510 kPa, D1= -221.9 kPa, D2=2.0; 900 kPa band: c1=900 kPa, D1= 0 kPa, D2= 0. (c) Imposed inner RV pressure; (d) Model validation: computational RV volume from the baseline no-band FSI model matching CMR-measured RV volume Data.
2.2 Direct biaxial testing of human myocardium tissue material properties
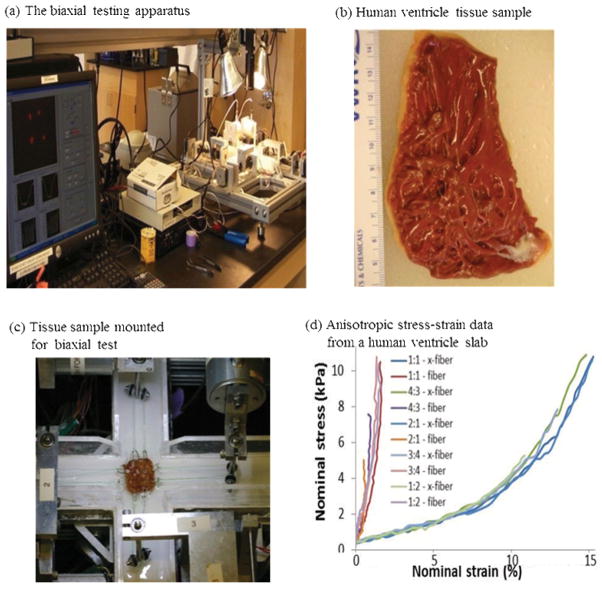
Based on methods of Sacks and Choung [22] for canine hearts and informed by our previous biaxial testing [23] and the methods of Humphrey and colleagues [24–26], we generated the first complete multiaxial mechanical data set for passive human ventricle tissues using a cadaveric heart sample (Fig 3). A detailed description of the custom planar biaxial testing device and method has been previously described [22]. Approximately 20 mm x 20 mm x 2mm slices of the right free ventricular wall and left ventricular wall specimens were dissected from two human hearts obtained within 24 hours of harvest from donors (without a history of heart disease) from National Disease Research Interchange (NDRI, Philadelphia, PA), perfused and shipped in chilled cardioplegic solution to eliminate contraction of the muscle [27–28]. For the right ventricular free wall, one epicardial sample was obtained due to the thinness of the wall. For the left ventricular wall, sequential thin planar specimens (~2 mm) epicardial-to-endocardial samples were obtained using a commercial stainless steel high speed rotating slicer [26]. The preferred fiber direction was determined visually, and the sample was mounted on the biaxial test device with the horizontal direction aligned with the fiber direction. Following 10 equibiaxial preconditioning cycles, five biaxial loading protocols were applied to samples immersed in room-temperature oxygenated cardioplegic solution. The applied maximum preferred-axis:cross-preferred-axis stress ratios were 1:1, 1:1.33, 1:2, 2:1, and 1.33:1 (see example engineering stress:strain plot for all protocols in Fig. 3d). The forces along the axes were measured via two torque transducers with 7.6 cm Plexiglass arms extending out of the bath (effective resolution ~2 mN), and the deformation gradient, F, was measured by a CCD camera, detecting the positions of four graphite particles attached to the sample (effective resolution ~0.07 %).
Figure 3.
Biaxial mechanical testing and initial results. (a) The biaxial testing apparatus in Dr. Billiar’s lab; (b) a human right ventricle tissue sample; (c) tissue sample mounted for biaxial test; (d) anisotropic data from a human right ventricle sample.
For the elastic band model, uniaxial mechanical testing was performed using three sample bands made of Tecoflex EG-80A (Lubzizol Advanced Materials, Inc., Cleveland, Ohio, USA) to obtain material parameter values for our band material. The stress-stretch curves from Mooney-Rivlin model fitting ME test data of the Tecoflex band and other materials are shown by Fig. 4 in next section.
2.3. The FSI RV/LV/Patch/Band model with isotropic and anisotropic material models
Blood flow in the right ventricle was assumed to be laminar, Newtonian, viscous and incompressible. The Navier-Stokes equations with arbitrary Lagrangian-Eulerian (ALE) formulation were used as the governing equations. The RV and LV materials were assumed to be hyperelastic, anisotropic, nearly-incompressible and homogeneous. Patch and band materials were assumed to be hyperelastic, isotropic, nearly-incompressible and homogeneous. With the same assumptions and boundary conditions given in [18], the FSI RV/LV/Patch/Band model is given below:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
where u and p are fluid velocity and pressure, ug is mesh velocity, ρ stands for RV inner wall, fi,j stands for derivative of f with respect to the jth variable (or time t), σr and σs are fluid and structure stress tensors, and nr and ns are their outward normal directions, respectively, σs is the strain tensor, vs is displacement, and σs is material density. The normal stress was assumed to be zero on the outer RV/LV surface and equal to the normal stress imposed by fluid pressure on the inner RV/LV surfaces. Structure-only LV models were used to save model construction effort and computing time.
The nonlinear Mooney-Rivlin model was used to describe the nonlinear anisotropic and isotropic material properties. The strain energy function for the isotropic modified Mooney-Rivlin model is given by [17,29]:
| (11) |
where I1 and I2 are the first and second strain invariants given by,
| (12) |
C =[Cij] = XTX is the right Cauchy-Green deformation tensor, X=[Xij] = [∂xi/∂aj], (xi) is the current position, (ai) is the original position, ci and Di are material parameters chosen to match experimental measurements [17,22,30]. The strain energy function for the anisotropic modified Mooney-Rivlin model anisotropic model was obtained by adding an additional anisotropic term in Eq. (3) [29,31]:
| (13) |
where I = Cij (nf)i (nf)j, Cij is the Cauchy-Green deformation tensor, nf is the fiber direction, K1 and K2 are material constants [29]. A two-step least-squares method was used to determine the parameter values in (5) to fit the experimental data given in [11]. Choosing c1=0.351 kPa, c2=0, D1=0.0633 kPa, D2 =5.3, K1=1.913 kPa, K2 =6.00, it was shown [17–18] that stress-strain curves derived from Eq. (13) agreed very well with the stress-strain curves from the dog model given in [11]. Parameter values were then adjusted to fit CMR-measured RV volume data. The stress-stretch curves and parameter values of the RV/LV tissues, patch, scar and band are given in Fig. 4. Imposed RV pressure conditions and computational RV volume data from our baseline no-band model were given in Fig. 4 (c)–(d). Good agreement between computational and CMR-measured volume data was found (error < 2%).
Three active band contraction models (with 10%, 15% and 20% band zero-stress length reduction) were evaluated to measure improvements in RV EF. “Actively contracting band” should be made of material which is able to contract the same way as normal myocardium does. This paper is mainly to demonstrate the potential benefit of actively contracting bands if such materials could be made available. A tissue engineering process generating materials for the contacting band is proposed and some brief information will be given in the Discussion session. Active band contraction was achieved by using an iterative procedure and coupling a separate simple band-only model to the whole RV/LV/Patch/Band model to adjust band zero-stress length (contraction at the start of systole and relaxation at the start of diastole), re-calculate band displacement, stress and strain using the band-only model, and assign the displacement, stress and strain values to the band in the right ventricle as the start for the whole model with a new zero-stress band length.
2.4 Mesh generation: a pre-shrink process and geometry-fitting technique for patient-specific CMR-based models
Under the in vivo condition, the ventricles were pressurized and the zero-stress ventricular geometries were not known. In our model construction process, a pre-shrink process was applied to the in vivo end-systolic ventricular geometries to generate the starting shape (zero ventricle pressure) for the computational simulation. The initial shrinkage for the inner ventricular surface was 2–3% and end-systolic pressure was applied so that the ventricles would regain its in vivo morphology. The outer surface of the ventricular shrinkage was determined by conservation of mass so that the total ventricular wall mass was conserved. Without this shrinking process, the actual computing domain would be greater than the actual ventricle due to the initial expansion when pressure was applied.
Because ventricles have complex irregular geometries with patch and scar tissue component inclusions which are challenging for mesh generation, a geometry-fitting mesh generation technique was developed to generate mesh for our models. Figure 2-(g) gives an illustration of RV/LV geometry between two slices. Each slice was first divided into geometry-fitting areas (called “surfaces” in ADINA). The neighboring slices were stacked to form volumes. Using this technique, the 3D RV/LV domain was divided into many small “volumes” to curve-fit the irregular plaque geometry with patch as an inclusion. For the baseline RV/LV/Patch FSI model constructed in this paper, the structure model had 1752 small volumes, 29443 nodes, and 25694 elements. The fluid model had 485 small volumes, 12526 nodes, and 65540 elements. Fine fluid mesh had 22786 nodes and 125175 elements. Mesh analysis was performed by decreasing mesh size by 10% (in each dimension) until solution differences were less than 2%. The mesh was then chosen for our simulations.
2.5 The model list, solution methods, and simulation procedures
A total of 11 models were constructed: the no-band solid-only and FSI models; 3 passive band models (PBM) with 3 different material stiffness (1 Stiff, 5 Stiff, and 10 Stiff, parameter values given in Fig. 3), 3 different active band models (10%, 15% and 20% zero-stress band length reductions), and three active band models with viable patch materials. These full RV/LV/Patch/Band models were solved by ADINA (ADINA R&D, Watertown, MA, USA) using unstructured finite elements and the Newton-Raphson iteration method [29]. RV ejection fraction was calculated to seek the optimal surgical design for potential RV EF improvement. Stress/strain distributions and flow shear stress conditions on the band were calculated which will provide important information for band design and tissue regeneration.
3. Results
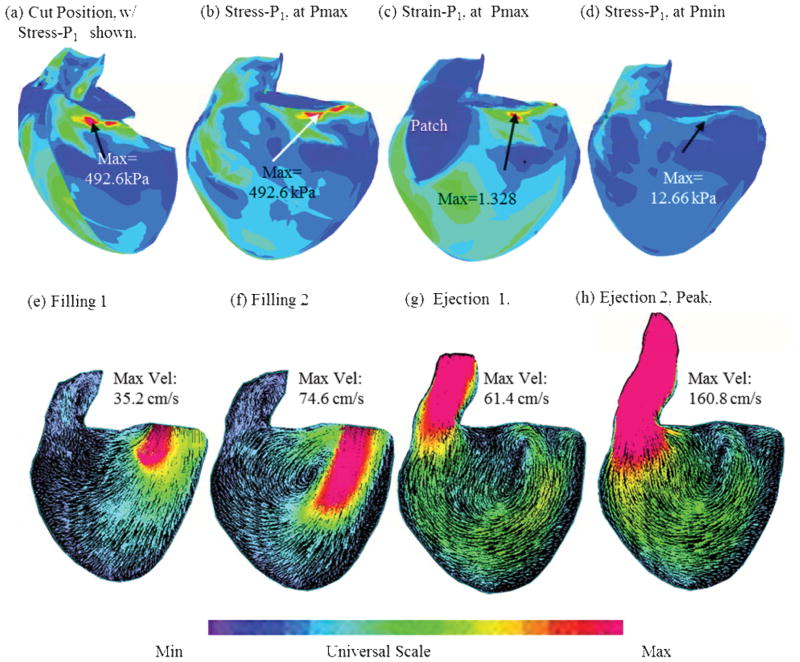
To give a general overview of the solution features, Figure 5 presents plots of maximum principal stress (Stress-P1), strain (Strain-P1) and flow velocity from the RV/LV/Patch/Scar FSI baseline model (no band) corresponding to maximum and minimum pressure condition and different filling and ejection phases. Impact of passive and active bands on ejection fraction and detailed stress/strain and flow shear stress on the band are given below.
Figure 5.
Stress-P1, Strain-P1 and flow velocity plots from the RV/LV/Patch/Scar FSI model (no-band) corresponding to maximum and minimum pressure condition and different filling and ejection phases.
3.1 Impact of band material stiffness and length on RV ejection fraction
Table 1 presents a summary of RV ejection fraction from the baseline no-band FSI model and 3 FSI passive band models (PBM1, PBM2, PBM3), with 3 stiffness. We started from “Stiff 1” which is close to the stiffness of the Tecoflex material we tested and the stress-stretch curve was given in Fig. 4. The band was then made stiffer with the hope that stiffer material would have more contracting force and would lead to better EF. Our results indicated that the passive band did not improve EF as we originally hoped. The addition of a passive elastic band led to about 3–5% EF reduction for the 3 models considered. Stiffer bands further reduced ejection fraction (EF was 1.4% lower).
Table 1.
Summary of RV ejection fractions (RVEF) from 5 models: No-band solid-only and FSI models and 3 passive band models with band stiffness variations. Stiffer band provided slightly lower ejection fraction. RVEF rates from all passive band models were about 4–5% lower than the no-band model. Mooney Rivlin model parameters for the 3 band stiffness variations were given in Fig. 4.
| Models | Band Stiffness | Band Length | RVESV (ml) | RVEDV (ml) | RVEF |
|---|---|---|---|---|---|
| CMR Data | 254.5 | 406.9 | 37.45% | ||
| Solid Model | N/A | No Band | 252.5 | 403.8 | 37.48% |
| FSI Model (Base) | N/A | No Band | 252.8 | 402.3 | 37.16% |
| FSI PBM 1 | 1 Stiff | 100% | 246.9 | 372.6 | 33.74% |
| FSI PBM 2 | 5 Stiff | 100% | 246.3 | 365.1 | 32.53% |
| FSI PBM 3 | 10 Stiff | 100% | 246.1 | 363.9 | 32.37% |
3.2 Impact of active band contraction on RV ejection fraction (EF)
Since passive band materials led to lower EF rates, three active contractions (band zero-stress length reduced by 10%, 15% and 20%) were added to the band seeking possible RV EF improvements. Table 2 shows the EF values from the three active band models (ABM1-ABM3) for RV with patch and scar improved from 33.74% (PBM1, the corresponding passive band model) to 37.12%, 39.17%, and 39.58%, respectively. The EF improvement from PBM1 to ABM3 was 5.48%. When the patch and scar were replaced by “normal RV tissue”, i.e. the scar area was replaced by myocardial tissue with normal contractile properties, the EF values from the three active band models (ABM4-ABM6) were further improved to 39.30%, 40.73%, and 41.47%, respectively. The EF improvement from PBM1 to ABM6 was 7.73%.
Table 2.
Summary of RV ejection fractions from 6 active band models (ABM) compared with the corresponding passive band model. Zero-stress end of systole band length for the passive band model was 4.18 cm. The zero-stress end of systole band length for the active band models with 10%, 15% and 20% active contraction were 3.76, 3.55, and 3.34 cm, respectively. Parameter for band material: c1=900 kPa, D1=0 kPa, D2=0.
| Models | Active Band Contraction (ABC) | RVESV (ml) | RVEDV (ml) | RVEF |
|---|---|---|---|---|
| Models with Patch and Scar | ||||
| FSI, No Band | N/A | 252.8 | 402.3 | 37.16% |
| FSI PBM 1 | Passive | 246.9 | 372.6 | 33.74% |
| FSI ABM1 | ABC=10% | 246.8 | 392.5 | 37.12% |
| FSI ABM2 | ABC =15% | 238.5 | 392.1 | 39.17% |
| FSI ABM3 | ABC =20% | 234.6 | 388.3 | 39.58% |
| Models with Patch and Scar Replaced by Normal Tissue | ||||
| FSI ABM4 | ABC=10% | 247.5 | 407.8 | 39.30% |
| FSI ABM5 | ABC =15% | 239.2 | 403.6 | 40.73% |
| FSI ABM6 | ABC =20% | 235.0 | 401.5 | 41.47% |
3.3 Stress/strain distributions and blood flow have complex patterns in the ventricle
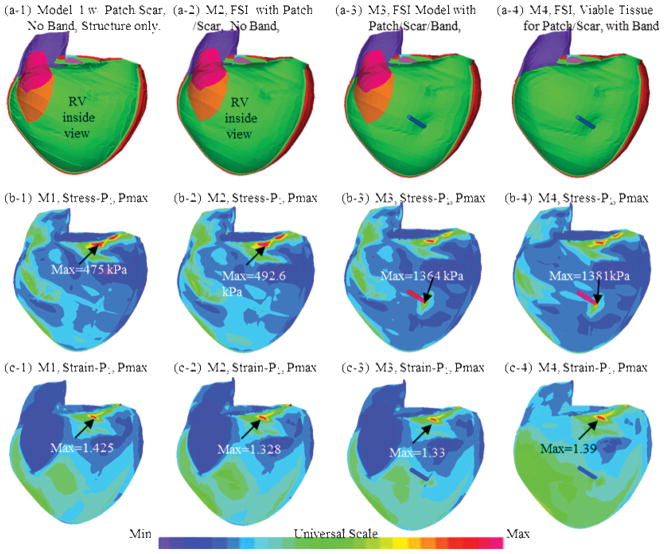
Figure 6 shows the inner RV surface viewed from one cut plane, the corresponding maximum principal stress (Stress-P1) and strain (Strain-P1) plots from four selected models: (a) M1, solid-only model with patch and scar, no band; (b) M2, baseline FSI model with patch and scar, no band; (c) FSI passive band model with patch and scar; (d) FSI passive band model with patch and scar replaced by normal tissue. Clearly the RV geometry, curvature, material properties, patch, scar and band all have considerable contributions to RV stress/strain distributions. Large curvature caused noticeable stress/strain concentrations in all four models. High stress/strain concentrations were also found where the band was connected to RV. Replacing patch and scar by normal tissue led to smoother stress/strain distributions. This could become possible if and when viable myocardium tissues could be generated using tissue engineering techniques under development [32–34].
Figure 6.
Stress and strain plots from four models corresponding to maximum pressure condition showing complex stress/strain behaviors.
3.4 Mechanical stress and flow shear stress on the band
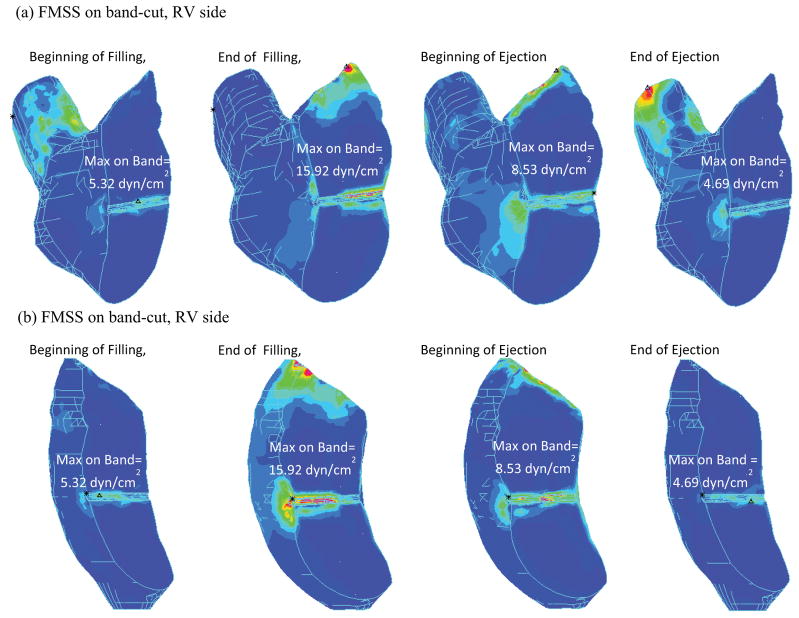
Figure 7 shows Stress-P1 and flow maximum principal shear stress (FMSS) on the band from our baseline FSI RV/LV/Patch/Band model. “Band stress” and “band FMSS” will be used from here on when no confusion arises. Band stress varies considerably (from 56 kPa to 950 kPa) during a cardiac cycle, which poses requited strength for band materials. Band FMSS was in general under 20 dyn/cm2 and was more influenced by flow near the tricuspid valve, and less influenced by the ejection flow. To provide more information about the flow environment surrounding the band, Fig. 8 plots FMSS with a cut plane passing through the band. Both RV side and LV side were presented. It should be noted that global maximum FMSS occurred near the tricuspid and pulmonary valve area, as expected.
Figure 7.
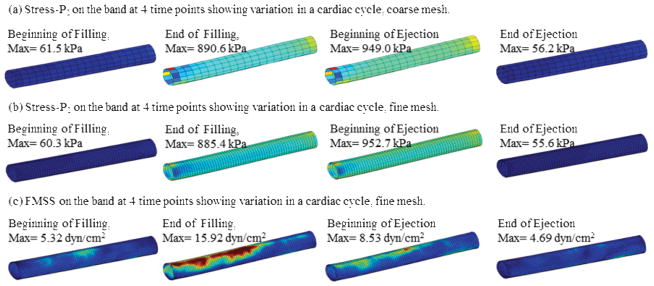
Plots of band Stress-P1 and flow maximum shear stress (FMSS) showing band stress and FMSS variations in a cardiac cycle.
Figure 8.
Flow maximum principal stress viewed with a cut-plan passing through the band showing overall FMSS distributions and FMSS on the band.
4. Discussion
4.1. Motivation to develop the band model and its clinical potential
With the rapidly increasing number of late survivors of Tetralogy of Fallot repair, surgical management of patients with right ventricular dysfunction has become a major clinical challenge. Dr. del Nido and Dr. Geva et al. have proposed aggressive scar tissue removal and RV volume remodeling as a way to improve RV function after pulmonary valve replacement surgery [5]. However, in a randomized prospective clinical trial, this aggressive approach did not result in measurable improvement in RV ejection fraction or RV end-diastolic volume compared to pulmonary valve insertion and RVOT patch reduction alone [6]. Innovative surgical ideas are needed to meet the major clinical challenge. That motivated the current proposed band insertion approach. The band will not only assist the ventricle to contract and improve its EF, it will also help the tricuspid valve to close properly and address the associated regurgitation issue which is not included in our current models. Originally, we thought that the elastic band would help the ventricle to contract and improve RV ejection fraction. Our results given by Table 1 proved that passive band would actually reduce ejection fraction. That is because while the band could help the RV to contract, it would also resist ventricle expansion (relaxation). That prompted us to try active contracting band. If an active contracting material or actuator could be used for the band material, the band may be able to augment the contraction of the RV.
Combined with the tissue regeneration techniques that restore RV myocardium, the combined scar tissue replacement plus active band approach has the potential to improve ejection fraction by 7.7% (41.47% from ABM6 over 33.73% from PBM1) and 4% (41.47% from ABM6 over 37.45% from CMR EF data). The impact on functional status will depend on a number of factors such as LV function. However, a 7% increase in RVEF (or even the 4% over CMR EF data) compares favorably with recently published drug trials to treat heart failure where an improvement in LVEF of 3–4% resulted in a significant improvement in functional capacity [35].
It should be noted that the proposed surgical procedure requires long-term efforts from multi-disciplines to get close to and be implemented in clinical practice. The computational simulations (virtual surgery) provided “proof of concept” for further investigations using in vitro experiments, animal models and final patient studies. Computational models are non-invasive and may be used to supplement/replace empirical and often risky clinical experimentation, or even guide the design of new clinical trials to examine the efficiency and suitability of various reconstructive procedures in diseased hearts. Tissue engineering and regeneration techniques also need to be developed to generate the contracting bands and viable myocardium.
Similar passive ventricular restriction approaches to the one proposed here have been evaluated and implanted in patients with left ventricular dilation and functional mitral regurgitation. An example of this approach is the Coapsys device (Myocor, Maple Grove, MN, USA). As the Coapsys device demonstrated effectiveness in reducing not only functional mitral regurgitation but also short-axis LV dimensions [36], the proposed RV band approach may also be expected to improve RV dimensions and may even be effective in treating functional tricuspid regurgitation, which is seen in these patients. Considering that annular and ventricular dilatation contributes to tricuspid regurgitation, the passive band may be effective in reducing regurgitation, even though the passive band had little effect on EF in the present study.
4.2. A tissue engineering process to generate active contracting bands
Proulx et al. described a band made from fibrin that could be seeded with mesenchymal stem cells and stitched through a collagen gel [34]. Seeding these fibrin bands with contractile cells, possibly derived from stem cells, may provide an actively contracting band. Also, recent work suggests that contractile cells can be generated to replace scarred myocardium, providing a contracting scaffold [32–33]. Our group is currently developing tissue engineering techniques to generate contracting bands by seeding induced pluripotent stem cell derived myocytes (iPS-myocytes) on fibrin microthreads (Fig. 1). Rat and porcine models will be employed first to test the feasibility of the band insertion procedures.
4.3. Multiscale modeling and its relevance to band design, cell retention and detachment
It is well known that mechanical forces play an important role in biological processes. The in vivo MRI-based human RV/LV/Patch/Band model is adding the band into consideration as a potential surgical option for ventricle repair. However, actual material for the contracting band must be available so that clinical implementation could be possible. The modeling approach will not only demonstrate the feasibility of the innovative RV PVR surgical procedure, it also provides detailed localized mechanical stress and flow conditions which will be used as guidance in our band design (Figures 7 & 8). In our band designing process, mechanical testing will be performed to make sure that the band will be strong enough to meet the stress conditions predicted by our models. Another important issue for cell-seeded band placement is cell retention. It is critical that the cells remain attached to the microthreads upon implantation so that they may continue to generate a functionally contractile band [37–40]. Based on fibroblast adhesion data, we expect over half of our cells will remain attached for over an hour at 350 dynes/cm2 [38]. This compares favorably to the band FMSS predicted by our FSI models. To more closely recapitulate the environment in the heart, we plan to utilize a parallel-plate flow chamber, the most common device for quantifying effects of shear stress on adherent cells, modified to accommodate our cell-seeded bands. Micro-level CFD simulations will be used to accurately determine the shear stresses on the undulating surface of the microthread bundle. The flow rates utilized in the experiment will be informed by the macro-level FSI simulations.
4.4 Model limitations and future directions
Several improvements can be added to our models in the future for better accuracy and applicability: a) multi-band design for better tricuspid valve closure to address the regurgitation issue; b) inclusion of both tricuspid and pulmonary valve mechanics in the model to simulate regurgitation; c) direct measurements of tissue mechanical properties for improved accuracy of our models; d) proper ways to model active contraction by adding active stress and techniques adjusting zero-stress sarcomere fiber length; e) multi-scale models including organ, cell, and gene investigations. This will allow mechanical conditions obtained from organ level to pass to micro level and cell activities obtained from micro level to organ level to discover mechanisms governing tissue regeneration process.
5. Conclusion
The CMR-based RV/LV/Patch/Band models with fluid-structure interactions introduced in this paper provides a “proof of concept” for using contracting bands to improve RV cardiac function. The impact of band material stiffness variations and active contraction were investigated. Our preliminary results indicate that the band insertion, combined with active band contraction and tissue regeneration techniques that restore RV myocardium, has the potential to improve right ventricle ejection fraction by 7.7% over passive band model and 4.0% over CMR-measured RVEF. Model-predicted band stress and band flow shear stress will provide useful guidance for our proposed tissue engineering techniques to generate contracting bands. The computational simulations suggested that further investigations using in vitro experiments, animal models and final patient studies are warranted.
Acknowledgments
This research was supported in part by NIH-1R01-HL 089269 (del Nido, Tang, Geva), NIH–HL63095 (PI: del Nido) and NIH-NHLBI 5P50HL074734 (PI: Geva; Co-Investigator: del Nido). Chun Yang’s research is supported in part by National Sciences Foundation of China 11171030 and the Fundamental Research Funds for the Central Universities.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Therrien J, Marx GR, Gatzoulis MA. Late problems in tetralogy of Fallot--recognition, management, and prevention. Cardiol Clin. 2002;20:395–404. doi: 10.1016/s0733-8651(02)00010-3. [DOI] [PubMed] [Google Scholar]
- 2.Therrien J, Siu SC, McLaughlin PR. Pulmonary valve replacement in adults late after repair of tetralogy of Fallot: are we operating too late? J Am Coll Cardiol. 2000;36:1670–5. doi: 10.1016/s0735-1097(00)00930-x. [DOI] [PubMed] [Google Scholar]
- 3.Vliegen HW, Van Straten A, De Roos A, Roest AA, Schoof PH, Zwinderman AH, Ottenkamp J, Van Der Wall EE, Hazekamp MG. Magnetic resonance imaging to assess the hemodynamic effects of pulmonary valve replacement in adults late after repair of tetralogy of Fallot. Circulation. 2002;106:1703–1707. doi: 10.1161/01.cir.0000030995.59403.f8. [DOI] [PubMed] [Google Scholar]
- 4.Waien SA, Liu PP, Ross BL, Williams WG, Webb GD, McLaughlin PR. Serial follow-up of adults with repaired tetralogy of Fallot. J Am Coll Cardiol. 1992;20:295–300. doi: 10.1016/0735-1097(92)90093-3. [DOI] [PubMed] [Google Scholar]
- 5.del Nido PJ. Surgical management of right ventricular dysfunction late after repair of Tetralogy of Fallot: right ventricular remodeling surgery. Semin Thorac Cardiovasc Surg Pediatr Card Surg Annu. 2006:29–34. doi: 10.1053/j.pcsu.2006.02.007. [DOI] [PubMed] [Google Scholar]
- 6.Geva T, Gauvreau K, Powell AJ, Cecchin F, Rhodes J, Geva J, del Nido P. Randomized Trial of Pulmonary Valve Replacement With and Without Right Ventricular Remodeling Surgery. Circulation. 2010 Sep 14;122(11 Suppl):S201–8. doi: 10.1161/CIRCULATIONAHA.110.951178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Peskin CS. Numerical analysis of blood flow in the heart. J Com Phys. 1977;25:220–252. [Google Scholar]
- 8.Peskin CS. A three-dimensional computational method for blood flow in the heart. J Comp Physics. 1989;81:372–405. [Google Scholar]
- 9.Axel L. Biomechanical dynamics of the heart with MRI. Annu Rev Biomed Eng. 2002;4:321–347. doi: 10.1146/annurev.bioeng.4.020702.153434. [DOI] [PubMed] [Google Scholar]
- 10.Costa KD, Takayama Y, McCulloch AD, Covell JW. Laminar fiber architecture and three-dimensional systolic mechanics in canine ventricular myocardium, Am J Physiol. 1999;276(2 Pt 2):H595–607. doi: 10.1152/ajpheart.1999.276.2.H595. [DOI] [PubMed] [Google Scholar]
- 11.McCulloch AD, Waldman L, Rogers J, Guccione JM. Large-scale finite element analysis of the beating heart. Critical Rev in Biomedical Engineering. 1992;20(5,6):427–449. [PubMed] [Google Scholar]
- 12.Kerckhoffs RC, Neal ML, Gu Q, Bassingthwaighte JB, Omens JH, McCulloch AD. Coupling of a 3D finite element model of cardiac ventricular mechanics to lumped systems models of the systemic and pulmonic circulation. Ann Biomed Eng. 2007 Jan;35(1):1–18. doi: 10.1007/s10439-006-9212-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hunter PJ, Pullan AJ, Smaill BH. Modeling total heart function, Annu Rev Biomed Eng. 2003;5:147–77. doi: 10.1146/annurev.bioeng.5.040202.121537. [DOI] [PubMed] [Google Scholar]
- 14.Nash MP, Hunter PJ. Computational Mechanics of the Heart, From tissue structure to ventricular function. Journal of Elasticity. 2000;61:113–141. [Google Scholar]
- 15.Guccione JM, Waldman LK, McCulloch AD. Mechanics of active contraction in cardiac muscle: Part II--Cylindrical models of the systolic left ventricle. J Biomech Eng. 1993;115(1):82–90. doi: 10.1115/1.2895474. [DOI] [PubMed] [Google Scholar]
- 16.Saber NR, Gosman AD, Wood NB, Kilner PJ, Charrier CL, Firman DN. Computational flow modeling of the left ventricle based on in vivo MRI data: initial experience. Annals of Biomech Engng. 2001;29:275–283. doi: 10.1114/1.1359452. [DOI] [PubMed] [Google Scholar]
- 17.Tang D, Yang C, Geva T, del Nido PJ. Image-Based Patient-Specific Ventricle Models with Fluid-Structure Interaction for Cardiac Function Assessment and Surgical Design Optimization. Progress in Pediatric Cardiology. 2010;30:51–62. doi: 10.1016/j.ppedcard.2010.09.007. PMC3041970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tang D, Yang C, Geva T, Gaudette G, del Nido PJ. Multi-Physics MRI-Based Two-Layer Fluid-Structure Interaction Anisotropic Models of Human Right and Left Ventricles with Different Patch Materials: Cardiac Function Assessment and Mechanical Stress Analysis. Computers & Structures. 2011;89:1059–1068. doi: 10.1016/j.compstruc.2010.12.012. PMC3134331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tang D, Yang C, Geva T, del Nido PJ. Patient-specific MRI-based 3D FSI RV/LV/Patch models for pulmonary valve replacement surgery and patch optimization. J of Biomech Engineering. 2008;130(4):041010. doi: 10.1115/1.2913339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yang C, Tang D*, Geva T, Rathod R, Yamauchi H, Gooty V, Tang A, Gaudette G, Billiar KL, Kural MH, del Nido PJ. Using Contracting Band to Improve Right Ventricle Ejection Fraction for Patients with Repaired Tetralogy of Fallot, a Modeling Study Using Patient-Specific CMR-Based Two-Layer Anisotropic Models of Human Right and Left Ventricles. The Journal of Thoracic and Cardiovascular Surgery. 2012 Apr 7; doi: 10.1016/j.jtcvs.2012.03.009. [Epub ahead of print]. NIHMSID 364569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sanchez-Quintana D, Anderson R, Ho SY. Ventricular myoarchitecture in tetralogy of Fallot. Heart. 1996;76:280–286. doi: 10.1136/hrt.76.3.280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sacks MS, Chuong CJ. Biaxial mechanical properties of passive right ventricular free wall myocardium. J Biomech Eng. 1993;115:202–205. doi: 10.1115/1.2894122. [DOI] [PubMed] [Google Scholar]
- 23.Billiar KL, Sacks MS. Biaxial mechanical properties of the natural and glutaraldehyde treated aortic valve cusp--Part I: Experimental results. J Biomech Eng. 2000;122(1):23–30. doi: 10.1115/1.429624. [DOI] [PubMed] [Google Scholar]
- 24.Humphrey JD, Strumpf RK, Yin FC. Biaxial mechanical behavior of excised ventricular epicardium. Am J Physiol. 1990 Jul;259(1 Pt 2):H101–8. doi: 10.1152/ajpheart.1990.259.1.H101. [DOI] [PubMed] [Google Scholar]
- 25.Humphrey JD, Yin FC. Biaxial mechanical behavior of excised epicardium. J Biomech Eng. 1988 Nov;110(4):349–51. doi: 10.1115/1.3108452. [DOI] [PubMed] [Google Scholar]
- 26.Novak VP, Yin FC, Humphrey JD. Regional mechanical properties of passive myocardium. J Biomech. 1994 Apr;27(4):403–12. doi: 10.1016/0021-9290(94)90016-7. [DOI] [PubMed] [Google Scholar]
- 27.Allen TJ, Mikala G, Wu X, Dolphin AC. Effects of 2,3-butanedione monoxime (BDM) on calcium channels expressed in Xenopus oocytes. J Physiol. 1998 Apr 1;508(Pt 1):1–14. doi: 10.1111/j.1469-7793.1998.001br.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cutaia M, Rudio K. Effects of Na-K-ATPase inhibition on catecholamine reactivity in rat pulmonary artery. Am J Physiol. 1992 Sep;263(3 Pt 2):H910–8. doi: 10.1152/ajpheart.1992.263.3.H910. [DOI] [PubMed] [Google Scholar]
- 29.Bathe KJ. Finite Element Procedures. Prentice Hall, Inc; New Jersey: 1996. [Google Scholar]
- 30.Humphrey JD. Cardiovascular Solid Mechanics. Springer-Verlag; New York: 2002. [Google Scholar]
- 31.Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of matereial models. J of Elasticity. 2000;61:1–48. [Google Scholar]
- 32.Kochupura PV, Azeloglu EU, Kelly DJ, Doronin SV, Badylak SF, Krukenkamp IB, Cohen IS, Gaudette GR. Tissue-engineered myocardial patch derived from extracellular matrix provides regional mechanical function. Circulation. 2005;30,112(9 S):I144–9. doi: 10.1161/CIRCULATIONAHA.104.524355. [DOI] [PubMed] [Google Scholar]
- 33.Kelly DJ, Rosen AB, Schuldt AJ, Kochupura PV, Doronin SV, Potapova IA, Azeloglu EU, Badylak SF, Brink PR, Cohen IS, Gaudette GR. Increased myocyte content and mechanical function within a tissue-engineered myocardial patch following implantation. Tissue Eng Part A. 2009;15(8):2189–2201. doi: 10.1089/ten.tea.2008.0430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Proulx MK, Carey SP, Ditroia LM, Jones CM, Fakharzadeh M, Guyette JP, Clement AL, Orr RG, Rolle MW, Pins GD, Gaudette GR. Fibrin microthreads support mesenchymal stem cell growth while maintaining differentiation potential. J Biomed Mater Res A. 2011;96(2):301–12. doi: 10.1002/jbm.a.32978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Aleksova A, Masson S, Maggioni AP, Lucci D, Urso R, Staszewsky L, Ciaffoni S, Cacciatore G, Misuraca G, Gulizia M, Mos L, Proietti G, Minneci C, Latini R, Sinagra G on the behalf of the CandHeart Investigators. Effects of Candesartan on Left Ventricular Function, Aldosterone and BNP in Chronic Heart Failure. Cardiovasc Drugs Ther. 2012 Feb 3; doi: 10.1007/s10557-012-6370-8. [Epub ahead of print] [DOI] [PubMed] [Google Scholar]
- 36.Grossi EA, Woo YJ, Schwartz CF, Gangahar DM, Subramanian VA, Patel N, Wudel J, DiGiorgi PL, Singh A, Davis RD. Comparison of Coapsys annuloplasty and internal reduction mitral annuloplasty in the randomized treatment of functional ischemic mitral regurgitation: Impact on the left ventricle. J Thorac Cardiovasc Surg. 2006;131:1095–8. doi: 10.1016/j.jtcvs.2005.11.046. [DOI] [PubMed] [Google Scholar]
- 37.Lu H, Koo LY, Wang WM, Lauffenburger DA, Griffith LG, Jensen KF. Microfluidic Shear Devices for Quantitative Analysis of Cell Adhesion. Anal Chem. 2004;76:5257–5264. doi: 10.1021/ac049837t. [DOI] [PubMed] [Google Scholar]
- 38.van Kooten TG, Schakenraad JM, Van der Mei HC, Busscher HJ. Development and use of a parallel-plate flow chamber for studying cellular adhesion to solid surfaces. J Biomed Mater Res. 1992 Jun;26(6):725–38. doi: 10.1002/jbm.820260604. [DOI] [PubMed] [Google Scholar]
- 39.van Kooten TG, Schakenraad JM, van der Mei HC, Dekker A, Kirkpatrick CJ, Busscher HJ. Fluid shear induced endothelial cell detachment from glass--influence of adhesion time and shear stress. Med Eng Phys. 1994 Nov;16(6):506–12. doi: 10.1016/1350-4533(94)90077-9. [DOI] [PubMed] [Google Scholar]
- 40.Furukawa KS, Ushida T, Nagase T, Nakamigawa H, Noguchi T, Tamaki T, Tanaka J, Tateishi T. Quantitative analysis of cell detachment by shear stress. Materials Science and Engineering: C. 2001;17(1–2):55–58. [Google Scholar]