Abstract
This study investigated whether rhesus monkeys show evidence of metacognition in a reduced, visual oculomotor task that is particularly suitable for use in fMRI and electrophysiology. The 2-stage task involved punctate visual stimulation and saccadic eye movement responses. In each trial, monkeys made a decision and then made a bet. To earn maximum reward, they had to monitor their decision and use that information to bet advantageously. Two monkeys learned to base their bets on their decisions within a few weeks. We implemented an operational definition of metacognitive behavior that relied on trial-by-trial analyses and signal detection theory. Both monkeys exhibited metacognition according to these quantitative criteria. Neither external visual cues nor potential reaction time cues explained the betting behavior; the animals seemed to rely exclusively on internal traces of their decisions. We documented the learning process of one monkey. During a 10-session transition phase, betting switched from random to a decision-based strategy. The results reinforce previous findings of metacognitive ability in monkeys and may facilitate the neurophysiological investigation of metacognitive functions.
Keywords: cognitive neuroscience, metacognition, decision making, eye movements, monitoring
Humans possess the ability to monitor and control cognition, a function known as metacognition. We monitor our cognition, for example, when contemplating whether we understood a poem. Likewise, we control our cognition when planning to reread the poem to better grasp its meaning.
Behavioral studies have concluded that rhesus macaques can engage in metacognitive processes. Some studies, using opt-out paradigms, tested monkeys’ abilities to monitor their own uncertainty (e.g., Smith, Shields, Allendoerfer, & Washburn, 1998). Monkeys were offered a choice to take or opt out of a test of varied difficulty. They tended to opt out more often when offered a difficult test, suggesting they can monitor their own uncertainty. Other studies, using betting paradigms, provided more direct evidence (Kornell, Son, & Terrace, 2007; Shields, Smith, Guttmannova, & Washburn, 2005). Such studies test monkeys’ abilities to monitor their previous decisions, referred to as retrospective monitoring (Nelson & Narens, 1990). A betting paradigm involves two steps: The monkey takes a test of varying difficulty, then places a bet to indicate whether its test choice had been correct. Reward is based on how appropriate the bet is relative to test choice; that is, a correct test choice should be followed by a high bet and an incorrect test choice should be followed by a low bet to earn maximum reward. The general conclusion has been that monkeys can advantageously wager on their own recent decisions, indicating that they are able to monitor those decisions.
Betting paradigms have advantages over opt-out paradigms when assessing metacognition (for a discussion, see, e.g., Metcalfe, 2008). For example, in opt-out paradigms, the opt-out stimulus is presented concurrently with the test choice stimuli, so no memory of a decision is required to make an advantageous response, and the monkey may even interpret the opt-out stimulus as simply a third test choice option (for exceptions, see Foote & Crystal, 2007; Hampton, 2001).
Results from betting paradigms should also be interpreted carefully. Subjects may place bets that are influenced by factors extraneous to the internal trace of the decision. Humans, when asked to assess the accuracy of a memory, can rely on a host of factors beyond directly monitoring the memory (for a summary, see Benjamin & Bjork, 1996). A few such factors include degree of familiarity with the task subject matter, perceptual stimuli related to the task, latency with which a response is made, and the amount and type of information associated with the memory. Reliance on factors such as these has been shown to influence judgments that supposedly rely on memory (Benjamin, Bjork, & Schwartz, 1998; Brewer & Sampaio, 2006; Chandler, 1994). In the pioneering studies with monkeys, metacognitive tasks have involved complex visual inputs at the decision stage, for example, clouds of dots in a numerosity judgment task (Shields et al., 2005.) or elaborate reward procedures, such as attainment of a threshold number of virtual tokens that are gained or lost across trials (Kornell et al., 2007). Although the prior tasks involved both elements of retrospective monitoring—decision and bet—their additional features may have recruited cognitive processes irrelevant to metacognition (e.g., assessment of gradual accumulation of tokens). Moreover, in all of the prior tasks, decisions were reported with limb or wrist movements; hence, the animals could keep track of their decisions not only internally but also externally, by watching their effectors or sensing postural adjustments. Historically, researchers faced these types of potential confounds in early studies of working memory as well (Fuster & Alexander, 1971; Jacobsen, 1936; Kubota & Niki, 1971; reviewed by Wang, 2005). Goldman-Rakic and colleagues (Funahashi, Bruce, & Goldman-Rakic, 1989; reviewed by Goldman-Rakic, 1995) offered an improvement by designing a highly controlled and reduced paradigm, the oculomotor delayed-response task. Their simplified task has become central to the modern study of working memory at both the neurophysiological and psychological levels.
We have developed a simplified betting paradigm that eliminates as many as possible of the confounding issues discussed above. We apply it here to achieve what we consider the most demanding test yet of the hypothesis that monkeys are capable of metacognition. The task requires a decision and then a bet but little else. Extraneous cognitive demands and spurious cues that might aid performance are minimized. Additionally, the task is immediately suitable for studying metacognition in monkeys at the single neuron level, and this is a future goal of our work. Following the example set in the working memory field, our paradigm is set in a visual oculomotor context that offers many advantages (Goldman-Rakic, 1995). First, it permits little variability in how the task can be performed. The monkeys sit still in a primate chair and report choices using only eye movements, which are stereotyped from trial to trial. No task-related skeletal movements are involved. Second, the task minimizes variability in the perceptual and cognitive state of the animal. The visual environment is tightly controlled, and each trial represents a self-contained unit of decision, bet, and outcome (with no dependence on trial history as in Kornell et al., 2007). Third, we can interpret our findings in the context of decades of research on the primate oculomotor system. Fourth, with only trivial alterations, the task could be used in functional imaging experiments (on monkeys or humans) by any investigators who can display visual stimuli and track eye movements in their scanner. A host of regions have been implicated in metacognition with fMRI, such as prefrontal cortical regions and posterior parietal cortex (e.g., Chua et al., 2006; Kikyo, Ohki, & Miyashita, 2002; Maril, Simons, Mitchell, Schwartz, & Schacter, 2003).
We trained two monkeys on the oculomotor betting task and found that the hypothesis was supported: The animals exhibited metacognitive behaviors within a few weeks and maintained near optimal betting behavior thereafter. Our findings confirm that monkeys can monitor and use information about their decisions in a task that is a simple extension of standard oculomotor paradigms and of immediate use to neuroscientists.
Method
Monkeys
Two rhesus monkeys (Macaca mulatta) served as the subjects. Monkey N had substantial previous experience performing oculo-motor tasks. Monkey S was initially naïve to all laboratory tasks. Each monkey was implanted with scleral search coils to monitor eye position with high spatial (0.1-degree) and temporal (1-ms) precision (Judge, Richmond, & Chu, 1980). The temporal resolution was particularly important for us, because we wanted to study saccadic reaction times and, in future work with these animals, correlate the eye movements with 1-ms resolution neuronal data. The use of scleral search coils is not critical, however, and standard video eye-tracking methods could be used for implementing the task in purely psychophysical or imaging studies. A plug for connecting to the eye coil leads and a plastic post for keeping the head still during experiments were bound with acrylic and affixed to the skull with bone screws using aseptic techniques while animals were anesthetized (Sommer & Wurtz, 2000). Procedures were approved by and conducted under the Institutional Animal Care and Use Committee of the University of Pittsburgh.
Task
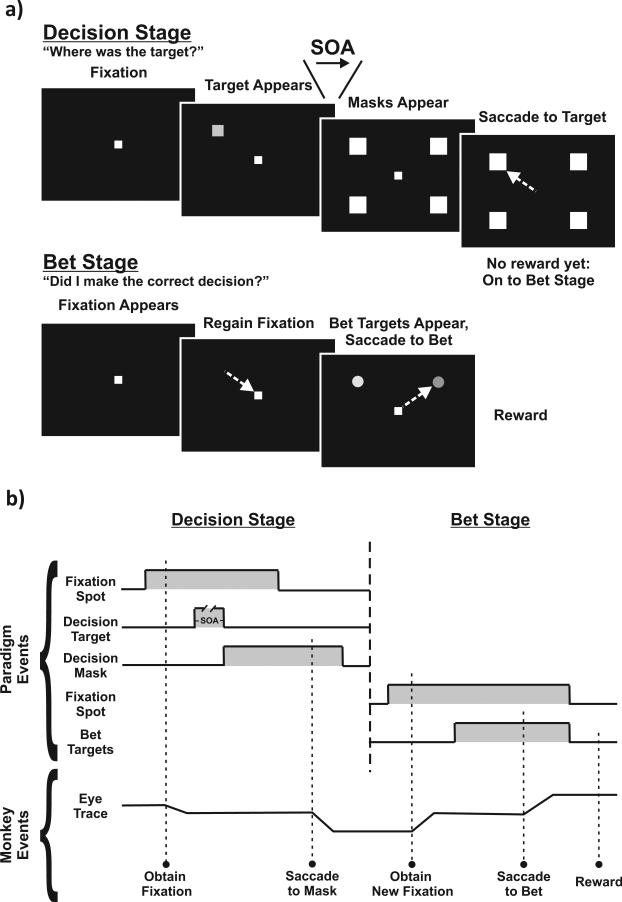
A monkey sat in a primate chair facing a tangent display screen in a dimly lit room. Visual stimuli from a 60-Hz LCD projector were back-projected onto the screen. The REX real-time system (Hays, Richmond, & Optican, 1982) was used to control behavioral paradigms and collect eye position data at 1 kHz. Every trial of the task included a decision stage followed by a bet stage (Figure 1a, spatial layout; Figure 1b, timing).
Figure 1.
Spatial aspects and timing of task. (a) Spatial layout: Each trial consisted of two stages—a decision stage (top) and a bet stage (bottom). In the decision stage, monkeys foveated a fixation spot. A target appeared at one of four locations in the periphery, and after a variable time (stimulus onset asynchrony [SOA]), masks appeared at the four locations. A correct decision was made (shown) if a saccade went to the location of the target. A saccade to any other location was an incorrect decision. In the bet stage, monkeys foveated a new fixation spot, then the two bet targets appeared in the periphery. A bet was made when a saccade went to one of the two targets, completing a single trial. (b) Timing: Top bracket shows when stimuli were visible (gray shading) and invisible (flat line) during each trial. Bottom bracket shows a hypothetical eye trace and actions performed by monkeys during the sequence of events.
Decision stage
The animal's goal in the decision stage (Figure 1a, top; Figure 1b, left) was to detect and report the location of a peripheral target (Thompson & Schall, 1999). The monkey fixated a center spot for 500–800 ms (randomized by trial). Then a dim target appeared in one of four possible locations (also randomized). The locations were constant throughout a session but often varied between sessions; they were always mirror symmetric about the vertical axis, with one location in each quadrant, but their eccentricities could range from 5 to 25 degrees, and their directions, relative to the horizontal meridian, could range from 0 to 60 degrees in angle. Varying the location is not a necessary feature of the task but was meant to accustom the animals to stimuli presented over a wide range of space, because in subsequent neurophysiological recordings, we expected that the centers of neuronal response fields would vary considerably. After the target appeared, mask stimuli appeared at all four locations. The interval between target appearance and appearance of the masks, the stimulus onset asynchrony (SOA) was randomized by trial: 16.7, 33, 50, or 66.7 ms. The monkey had to decide, “Where was the target?” Shorter SOAs made the target more difficult to detect, and longer SOAs made it easier. After the masks appeared, a randomized 500–1,000 ms delay ensued during which the monkey continued maintaining fixation while the masks remained visible. The fixation spot was then extinguished, cueing the monkey to report its decision by making a saccade to the perceived target location within 1,000 ms. The monkey received no performance feedback until after the bet stage of the task, but the computer tracked whether the decision was correct (saccade landed in an electronic window around the target location) or incorrect (saccade landed anywhere else). The size of the electronic window was adjusted to contain typical scatter of saccadic endpoints for particular target amplitudes. If at any time during the decision stage, the monkey broke fixation, made a saccade before cued to go, or failed to make a saccade, the trial was aborted, (and repeated again later) and the next trial began immediately. Such an early abort might occur for many reasons—for example, if the monkey failed to see the target at all or simply wanted to rest—so we neither penalized nor quantified such trials. In all trials, the saccade ended the decision stage and started the bet stage.
Bet stage
The goal in the bet stage of each trial (Figure 1a, bottom; Figure 1b, right) was to wager on the decision just made. A new fixation spot appeared, and the monkey foveated it. After a brief delay (500–800 ms), two bet targets appeared: a red high-bet target and a green low-bet target (for Monkey N; this color assignment was reversed for Monkey S). A monkey reported its bet by making a saccade to one of the targets, then received a reward or a time-out as described below, and the trial ended. A monkey would optimize its reward if it bet high after a correct decision and low after an incorrect decision.
In a given session, the bet targets always appeared in the same two locations. Within those two locations, the appearance of either bet target was randomized by trial. If, during the bet stage, the monkey broke fixation or made a saccade to a non–bet-target location, the trial was aborted, and a brief time-out ensued before a new trial began.
Reward
The amount of reward delivered after each trial was based on how appropriate the bets were relative to the decisions. If the monkey made a correct decision and bet high, it earned the maximum reward: five drops of juice. If the monkey made an incorrect decision and bet high, it received no reward and a 5-s time-out. Betting low earned a sure but minimal reward: three drops after a correct decision and two drops after an incorrect decision. The reward schedule was based on previous studies (Kornell et al., 2007; Persaud, McLeod, & Cowey, 2007) and fine-tuned to elicit the best performance in our monkeys.
Training
Retrospective monitoring tasks are challenging for monkeys to learn (see Son & Kornell, 2005), so we first familiarized the animals with each stage separately. We ran blocks of trials in which monkeys performed only the decision stage of the task, receiving immediate reward for correct trials. We also ran blocks of trials in which they performed only the bet stage. For those we assigned fictitious, random correct and incorrect variables to control reward that would be delivered after a bet target choice. The bet stage–only sessions exposed the animals to the two bet targets and the potential reward-related outcomes associated with each.
After the monkeys became familiar with the decision and bet stages, we started training them on the full task: the decision stage followed by the bet stage. The animals learned by trial and error. Training of the first animal (Monkey N) proceeded somewhat sporadically, because we tried various stimulus parameters and adjusted the computer programs. We did not document that animal's learning curve. Training of Monkey S was accomplished thereafter, involved no changes to the task, and provided detailed data on the learning progression (see Results).
Results
Average Performance
Decision stage
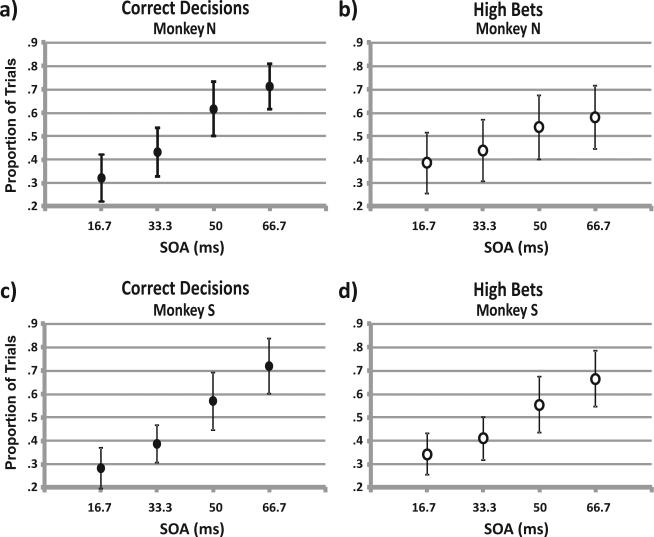
As expected, and in agreement with previous work (Thompson & Schall, 1999), both monkeys’ proportion of correct decisions increased with stimulus onset asynchrony (SOA). Figure 2a shows Monkey N's average proportion of correct decisions for each SOA (49 experimental sessions; 8,735 trials). Figure 2c shows the same data for Monkey S (55 sessions; 11,201 trials). All data are from steady-state performance after training. Chance performance is probability .25. At the shortest SOA (16.7 ms), both monkeys performed only slightly above chance (~.3; p < .01, one-sample t test). At the longest SOA (66.7 ms), performance greatly exceeded chance; the probability of making a correct decision was ~.7. One-way analysis of variance (ANOVA) confirmed a significant effect of SOA on correct decisions (p < .001 for each monkey). Hence, the range of SOAs resulted in a decision task that varied smoothly in difficulty from hard (but not impossible) at the shortest SOA to easy (but not trivial) at the longest SOA.
Figure 2.
Average decisions and bets. (a) Overall proportion of correct decisions made by Monkey N plotted as a function of each of the four stimulus onset asynchronies (SOAs). Total trials = 8,735 over 49 sessions. (b) Overall proportion of high bets made by Monkey N plotted as a function of each of the four SOAs during the same sessions as in Panel a. (c) Overall proportion of correct decisions made by Monkey S plotted as a function of each of the four SOAs. Total trials = 11,201 over 55 sessions. (d) Overall proportion of high bets made by Monkey N plotted as a function of each of the four SOAs during the same sessions as in Panel c. Error bars represent standard deviations.
Bet stage
We predicted that if the monkeys were using metacognition, that is, basing their bets on their decisions, then, on average, their proportion of high bets would increase with SOA in parallel with their decisions. Figures 2b and 2d show each monkey's average rate of high bets for each SOA for the same sessions as Figures 2a and 2c. An ANOVA showed that high bets occurred with probability ~.35 at the 16.7-ms SOA and rose steadily to probability ~.6 at the 66.7-ms SOA (p < .001 for each monkey). Hence, on average, the monkeys’ bets tracked their decisions.
Trial-by-Trial Performance
Our operational definition of metacognition is that a monkey displays metacognition if its bets track its decisions. As reported above, this was true on average, but, in principle, the same results could occur without metacognition. A monkey could use an external cue such as the sequence of visual stimulation during the decision stage, betting low after short SOAs and high after long SOAs, regardless of its decisions. To test this possibility, we performed a trial-by-trial analysis.
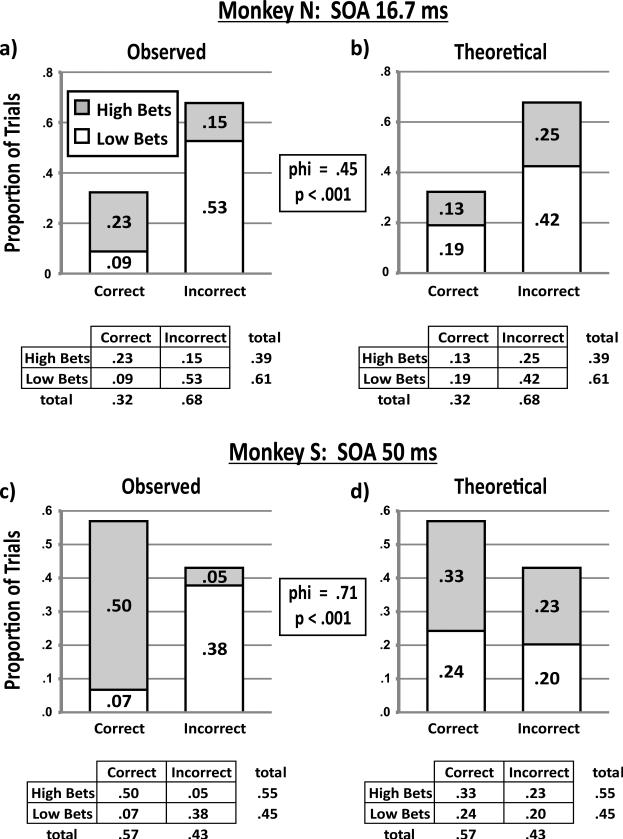
In the trial-by-trial analysis, we examined whether a monkey's bets were correlated with its decisions independent of the sensory stimulation that it experienced. If true, then for identical visual input (constant SOA), a monkey should make more low bets after incorrect decisions and more high bets after correct decisions. Figure 3 illustrates an example of the analysis for each monkey. Figure 3a shows the distribution of Monkey N's decisions and bets for all 16.7-ms SOA trials (n = 2,207) over 49 sessions. After correct decisions, the animal was much more likely to make a high bet (probability .23 over all four possible trial outcomes, gray shading) than a low bet (probability .09, white shading). Conversely, after incorrect decisions, the animal was less likely to make a high bet (probability .15) and more likely to make a low bet (probability .53). Figure 3b shows the theoretical response rates for the case in which the animal made bets irrespective of its decisions, that is, if it made a constant proportion of high to low bets whether its decision was correct or incorrect. Considering just the subset of correct decision trials, we note that high bets would occur with overall probability .13 and low bets would occur with probability .19. In the incorrect decision trials, high bets would occur with overall probability .25 and low bets, with probability .42 (these four probabilities add to .99, rather than 1, because of rounding error). The table below each graph summarizes the proportions of bets (rows) and decisions (columns), illustrating that the marginal distributions—the average probabilities of making the particular bets and decisions—were identical in the observed and simulated data (the latter having been calculated from the former). Consistent with previous analyses (Kornell et al., 2007), we compared these two distributions and found them to be significantly different, χ2(1, N = 2,207) = 439, p < .001. Results are also shown for Monkey S's 50-ms SOA trials (Figures 3c and Figure 3d; N = 2,786 from 55 sessions), and the conclusions were the same, χ2(1, N = 2,786) = 1,417, p < .001.
Figure 3.
Trial-by-trial analysis for example stimulus onset asynchronies (SOAs). (a) The distribution of trial outcomes for Monkey N's 16.7-ms SOA trials over 49 sessions, 2,207 trials. The bar graph shows the observed proportions of high bets (gray shading) and low bets (white shading) among correct and incorrect decisions. Below the bar graph, the table shows these same outcome proportions listed with the marginal totals. (b) Theoretical response rates if the monkey placed bets on the basis of an external variable (the SOA) rather than tracking its decisions. Note that the total proportion of high bets, low bets, correct decisions, and incorrect decisions are the same in Panels a and b. Chi-square between the distributions of Panels a and b indicate that they are significantly different (p < .001), with a phi correlation of .45. (c) The distribution of trial outcomes for Monkey S's 50-ms SOA trials over 55 sessions, 2,786 trials. As above, the bar graph shows the observed proportions of high bets (gray shading) and low bets (white shading) among correct and incorrect decisions. Below the bar graph, the table shows these same outcome proportions listed with the marginal totals. (d) Theoretical response rates if the monkey placed bets on the basis of an external variable (the SOA) rather than tracking its decisions. Note that the total proportion of high bets, low bets, correct decisions, and incorrect decisions are the same in Panels c and d. Chi-square between the distributions of Panels c and d indicate that they are significantly different (p < .001), with a phi correlation of .71. In the tables, some rows and columns do not add precisely to marginal distributions because of round-off error.
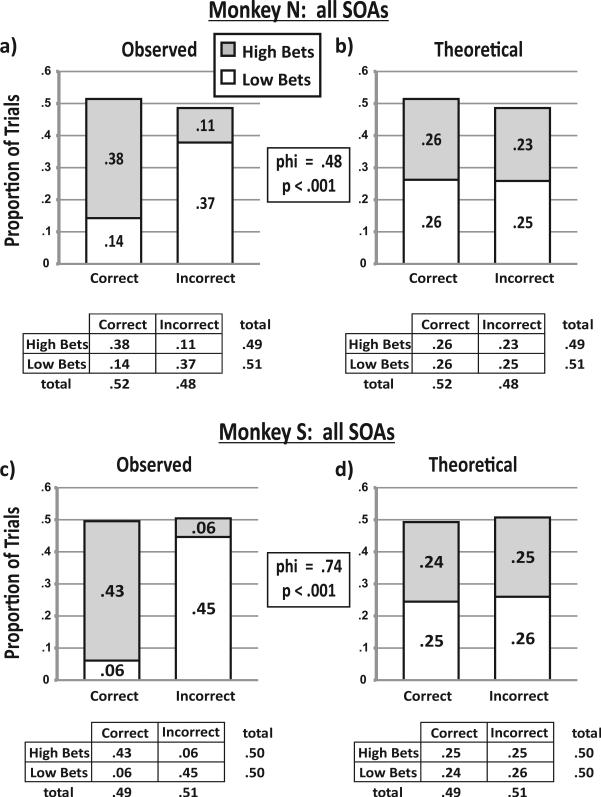
To quantify the magnitude of the difference between observed betting and random (theoretical response rate) betting, we calculated the phi correlation (the chi-square statistic normalized for the total number of trials). A phi correlation of 0 indicates that two distributions are identical, and a phi correlation of 1 indicates that they are unrelated. As shown in Figure 3, the phi correlation was .45 for Monkey N's 16.7-ms SOA trials and .71 for Monkey S's 50-ms SOA trials. We repeated the analysis for every SOA and pooled the data to provide an overall trial-by-trial result (Figure 4). The overall phi correlation was .48 for Monkey N and .74 for Monkey S. All the phi correlations were greater than zero (p < .001) and represented nonrandom betting behavior at a level of skill similar to that reported in previous studies (Kornell et al., 2007). Table 1 shows the phi correlations for each SOA; all were significant (p < .001) and varied little across SOA (the standard deviations were <5% of the means for both monkeys, and relationships with SOA were insignificant, p > .05 for both monkeys, Pearson's test). In sum, both animals’ bets tracked their decisions above chance on a trial-by-trial basis, satisfying our criterion for metacognitive behavior.
Figure 4.
Trial-by-trial analysis for all stimulus onset asynchronies (SOAs) combined. (a) The distribution of trial outcomes for Monkey N's trials combined. The bar graph shows the observed proportions of high bets (gray shading) and low bets (white shading) among correct and incorrect decisions. Below the bar graph, the table shows these same outcome proportions listed with the marginal totals. (b) Theoretical response rates if the monkey placed bets on the basis of an external variable (the SOA) rather than tracking its decisions. Note that the total proportion of high bets, low bets, correct decisions, and incorrect decisions are the same in Panels a and b. Chi-square between the distributions of Panels a and b indicate that they are significantly different (p < .001), with a phi correlation of .48. (c) The distribution of trial outcomes for all of Monkey S's SOA trials combined. As above, the bar graph shows the observed proportions of high bets (gray shading) and low bets (white shading) among correct and incorrect decisions. Below the bar graph, the table shows these same outcome proportions listed with the marginal totals. (d) Theoretical response rates if the monkey placed bets on the basis of an external variable (the SOA) rather than tracking its decisions. Note that the total proportion of high bets, low bets, correct decisions, and incorrect decisions are the same in Panels c and d. Chi-square between the distributions of Panels c and d indicate that they are significantly different (p < .001), with a phi correlation of .74. In the tables, some rows and columns do not add precisely to marginal distributions because of round-off error.
Table 1.
Phi Correlations
| Stimulus onset asynchrony |
|||||
|---|---|---|---|---|---|
| Monkey | 16.7 ms | 33.3 ms | 50.0 ms | 66.7 ms | M (SD) |
| N | .45 | .46 | .46 | .42 | .45 (.02) |
| S | .68 | .74 | .71 | .67 | .70 (.03) |
Note. Phi correlations for each monkey (rows) calculated for each stimulus onset asynchrony and averaged over all stimulus onset asynchronies (columns). All values were significantly greater than zero (p < .001).
Saccade Latencies
Our trial-by-trial analyses indicate that the monkeys were not using external cues to make bets. Another possibility is that the monkeys could detect their saccade latencies during the decision stage and use this information to help place their bets. In metacognition paradigms, humans tend to make shorter latency responses when confident than when not confident (Costermans, Lories, & Ansay, 1992). Likewise, Kornell et al. (2007) found a negative correlation between monkeys’ response latencies (of an arm movement to touch a screen) and high bets but found that the correlation could not account for all of the betting data.
We tested whether our monkeys might have based their bets on their decision stage latencies. First, we examined whether there was a significant difference in saccade latencies between correct and incorrect decisions (using all trials). As expected, both monkeys made correct decisions faster than incorrect decisions (for Monkey N, 218.8 ± 18.6 ms vs. 236.7 ± 22.6 ms; for Monkey S, 175.3 ± 15.9 vs. 186.1 ± 19.4 ms, both ps < .01 with Mann–Whitney rank sum test). Next, we compared latencies across the four outcomes. If the monkeys used saccade latencies as criteria for betting, we would predict differences between correct-high and correct-low outcomes and between incorrect-high and incorrect-low outcomes. All results were negative, however (p > .05 for all, Holm–Sidak multiple comparison tests). These data are summarized in Table 2. In short, we found no evidence that the monkeys were using latencies to make bets.
Table 2.
Saccade Latencies
| Outcome |
||||
|---|---|---|---|---|
| Correct decision |
Incorrect decision |
|||
| Monkey | High bet | Low bet | High bet | Low bet |
| N | 217.5 | 221.8 | 240.4 | 235.5 |
| S | 174.2 | 178.9 | 186.2 | 186.6 |
Note. Latencies (presented in milliseconds) to saccade onset during the decision stage for each monkey across each trial outcome.
Implicit Opt-Out Behavior
The task offered an implicit opt-out option: A monkey could complete the decision stage but then fail to look at a bet target. Such aborts incurred a longer penalty (10-s time-out) than the worst outcome of betting, so as one might expect, they were rare (Figure 5). Nonetheless, they were more frequent for the difficult, short SOA trials than for the easier, long SOA trials (p < .05, ANOVA). This pattern is reminiscent of data from classic opt-out experiments (Hampton, 2001; Smith et al., 1998) and provides further evidence of metacognition in our animals.
Figure 5.
Implicit opt-out behavior. Average proportion of trials aborted during the bet stage as a function of stimulus onset asynchrony (SOA) for (a) Monkey N and (b) Monkey S. In an analysis of variance, p < .05 for both panels. Error bars represent standard deviations.
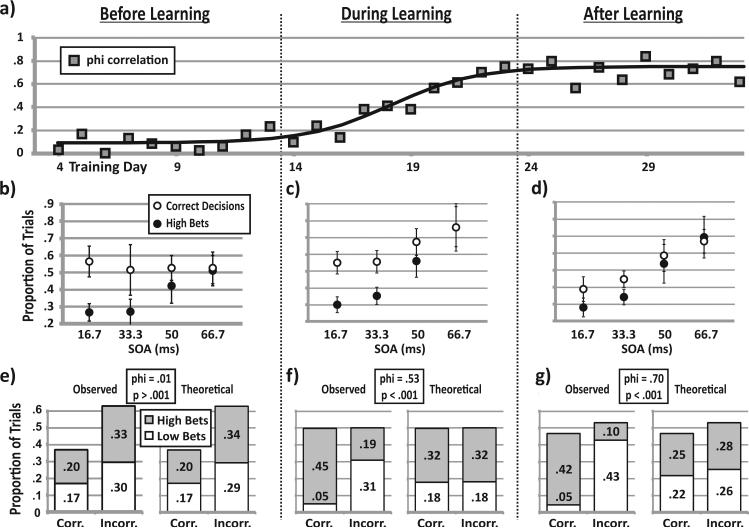
Learning
We documented the learning curve of Monkey S during its first 33 days of training on the full task (Figure 6a). Its phi correlations were near zero until approximately Day 13 and then rose steadily to asymptote at around Day 23. We fit the learning curve with a sigmoid function (Figure 6a, black line, R2 = .805) and found that the inflection point occurred between Days 18 and 19. For quantification, we defined a “during” learning period that spanned 10 sessions around the inflection point, Sessions 14–23. In an ANOVA, we compared these data with the 10-session periods that immediately preceded learning (“before” phase, Sessions 4–13) and followed learning (“after” phase, Sessions 24–33). We found that, as expected, in the “before” learning period, the animal was not skilled at betting appropriately (Figure 6b). On average, the animal made high bets with probability .55 regardless of its decisions or SOA (p = .98). In the during learning period (Figure 6c), bets started to parallel decisions. Although the animal maintained a high-bet probability of around .60 for the more difficult (shorter SOA) trials, it increased its proportion of high bets on the easier (longer SOA) trials (p < .001). In the after learning phase (Figure 6d), the monkey attained stable, accurate performance; high bets were rare on more difficult trials but frequent on easier trials (p < .001) so that bets closely paralleled decisions.
Figure 6.
Learning curves for Monkey S, divided into three stages. (a) Phi correlation (gray squares) measures how well the bets tracked the decisions on a trial-by-trial basis on Days 4–33 of training (x-axis). A sigmoid function fit the data (black line, R2 = .805, inflection point = 18.1 days). Panels b through d presents the average proportion of correct decisions (solid circles) and high bets (open circles) as a function of stimulus onset asynchrony (SOA) (b) before learning, (c) during learning, and (d) after learning to make bets based on decisions. Error bars represent standard deviations. Panels e through g present trial-by-trial analyses during each phase of learning: (e) The distribution of trial outcomes for Monkey S before learning for all trials combined. The bar graph shows the observed proportions of high bets (gray shading) and low bets (white shading) among correct (Corr.) and incorrect (Incorr.) decisions, as well as the theoretical response rates if the monkey placed bets on the basis of an external variable (the SOA) rather than tracking its decisions. Chi-square between the distributions of observed and theoretical proportions indicates that they are not significantly different (p > .001). The phi correlation is only .01. (f) The distribution of trial outcomes for Monkey S during learning for all trials combined. Chi-square between the distributions of observed and theoretical proportions indicates that they are significantly different (p < .001), with a phi correlation of .53. (g) The distribution of trial outcomes for Monkey S after learning for all trials combined. Chi-square between the distributions of observed and theoretical proportions indicates that they are significantly different (p < .001), with a phi correlation of .70.
Figures 6e–6g summarize the trial-by-trial analysis during each learning period. Before learning, betting was not significantly different from chance (Figure 6e, phi = .027, p > .05). During learning, the monkey's bets became nonrandom, with appropriate tracking of decisions, and thus began to meet our criterion for metacognition (Figure 6f, phi = .28, p < .05). The animal's bets showed that it clearly tracked its decisions in the 10 sessions after learning (Figure 6g, phi = .68, p < .05).
Signal Detection Theory
There has been recent interest in applying signal detection theory to metacognitive task data (see, e.g., Higham, 2007; Masson & Rotello, 2009). Signal detection theory (Green & Swets, 1966) assumes that an individual sets a criterion by which to detect a signal (which might be present or absent) in order to make a response (a report of presence or absence). In a retrospective monitoring task such as ours, the signal is the decision (correct or incorrect), and the response is the bet (high or low). In the nomenclature of signal detection theory, a high bet after a correct decision would be a hit, a low bet after a correct decision would be a miss, a high bet after an incorrect decision would be a false alarm, and a low bet after an incorrect decision would be a correct rejection. Applying these signal detection theory principles, we calculated d’ for the bet patterns of our monkeys (Clifford, Arabzadeh, & Harris, 2008).
If the monkeys based their bets on their decisions and not on visual inputs, then d’ should remain constant across SOA. Conversely, if visual information contributed to the bets, then d’ values should increase with SOA, because additional visual information (integrated over time as SOA increases) would serve as additional signal on which to bet. Table 3 shows that d’ was, in fact, steady across SOA (p > .05, Pearson's correlation).
Table 3.
d′ Values
| Stimulus onset asynchrony |
||||
|---|---|---|---|---|
| Monkey | 16.7 ms | 33.3 ms | 50 ms | 66.7 ms |
| N | 1.38 | 1.33 | 1.40 | 1.33 |
| S | 2.30 | 2.40 | 2.35 | 2.40 |
Note. d′ for each monkey (rows) was calculated for each stimulus onset asynchrony (columns).
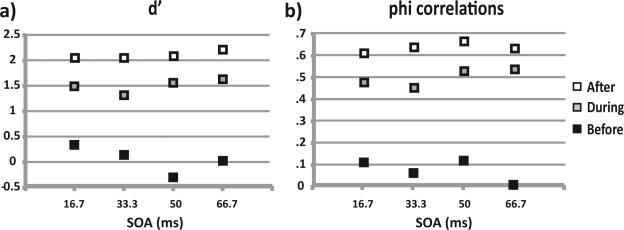
We found a difference in d’ between monkeys (~1.35 for Monkey N and ~2.35 for Monkey S), and this agrees with our previous analyses (Figures 3 and 4) that the task seemed more challenging for Monkey N. We examined how d’ changed throughout Monkey S's training (Figure 7a), plotting d’ as a function of SOA for the three learning phases described above. As would be expected, there was an overall increase in d’ with learning. For comparison, we also plotted phi correlations for each SOA during training (Figure 7b) and found the same pattern. We tested whether there was a correlation between d’ and SOA in each learning phase, which would suggest an influence of sensory input on bets. There was a significant effect of SOA on d’ before learning (p < .05, Pearson's), but this became insignificant during and after learning (p > .05).
Figure 7.
Signal detection theory analysis of the data: (a) d’ as a function of stimulus onset asynchrony (SOA) through the three learning phases for Monkey S and (b) phi correlations for the same data, for comparison.
Strategies for Performing the Task
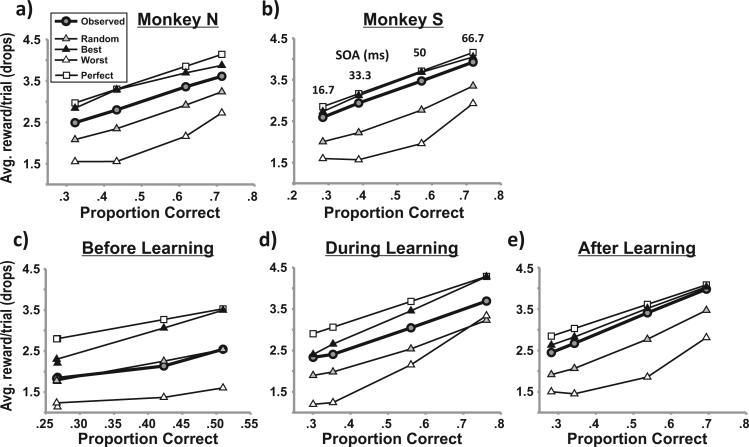
We analyzed how well the monkeys’ strategy for performing the task earned reward for them, in comparison with idealized strategies. For each SOA, we calculated the monkeys’ observed rate of reward collection in units of juice drops per trial as well as the reward rates that would have resulted from three modeled strategies (Figures 8a and 8b). We used the observed proportions of correct decisions and high bets to assign bets to decisions in three different theoretical ways. First, the gray triangles show reward rates that result from random assignment, that is, if the monkeys had placed bets regardless of their decisions. Black triangles show the rates that result from optimal assignment, that is, high bets after all correct decisions and low bets after all incorrect decisions (constrained by the observed, average proportions of bets and decisions). White triangles show the worst possible reward rates, that is, the opposite betting assignment. Finally, we performed a fourth analysis that used only part of the observed data, the decision data alone, to compute the result expected for absolutely perfect betting (white squares). This analysis assigned high bets to each correct decision and low bets to each incorrect decision. We found that both monkeys adopted strategies (black circles) that were near optimal and that for Monkey S, betting was nearly perfect.
Figure 8.
Strategies for performing the task for (a) Monkey N and (b) Monkey S and for the learning phases of Monkey S: (c) before learning, (d) during learning, and (e) after learning. In each panel, reward rate (drops of juice per trial) is plotted for each stimulus onset asynchrony (SOA) as a function of proportion of correct decisions. The observed reward rate (gray circles and bold lines) is compared with other hypothetical reward rates from various strategies, given the observed distribution of correct decisions and high bets. The alternative strategies were best possible betting (black triangles), random betting (gray triangles), and worst possible betting (white triangles). For comparison, white squares show reward rates that would have occurred for perfect betting (given the monkeys’ observed distribution of correct decisions but not the observed high bets).
We performed the same analysis for Monkey S's learning phases (Figures 8c–8e). Before learning the task, the monkey's bets were random (Figure 8c). During the learning phase, its strategy improved (Figure 8d) and reached near optimal levels as soon as the learning phase concluded (Figure 8e). There was little change in strategy from this immediate postlearning phase to the longer, steady-state period (cf. Figure 8b).
Discussion
We designed a visual oculomotor task that required monkeys to retrospectively monitor their own decisions. Two monkeys learned to perform the task advantageously and then maintained that level of performance. Behavior was best explained by metacognitive processes with little or no reliance on sensory (SOA) or motor (reaction time) cues. The results demonstrate that monkeys can monitor their own decisions in a highly reduced task that is suitable for imaging studies and electrophysiology.
Our experiment used a betting paradigm, but this is not the only possible approach. A recent single-neuron study (Kiani & Shadlen, 2009) utilized an opt-out paradigm. The betting approach has some advantages over the opt-out approach, primarily the constant pairing of an explicit decision followed by an explicit bet on the accuracy of that decision. This permits a direct comparison of behavioral (and eventually neuronal) data from both stages of the task: decisions and bets. In the terminology of Nelson and Narens (1990), we may compare an object-level cognitive process (the decision) with its associated meta-level cognitive process (the bet, which results from monitoring the decision). The animals complete the same sequence of events in every trial, from initial fixation through final bet selection, facilitating analysis of neuronal activity related to decisions and bets, for example, allowing for direct identification of firing rates related to metacognitive signals. The neuronal correlates of such signals should predict trial-by-trial bets after identical target–mask stimuli and identical decisions. And if one is interested in opt-out behavior, the betting task is still useful, because it contains an implicit opt-out component. This is not to say that betting tasks are always best for studying metacognition. Hampton (2001), for example, used an opt-out task elegantly to show that monkeys can monitor the integrity of their visual object memory. Betting and opt-out tasks are different tools, and either might be best for answering a particular experimental question.
Our task design ensured that monkeys earned maximal reward only by monitoring decisions to make bets. It was theoretically possible, however, for monkeys to earn rewards with other strategies. Before learning, we did see evidence of nonmetacognitive strategies (Figures 7a, 7b, and 8c), but they were superseded by decision-based betting after successful training, as indicated by multiple analytical methods. During steady-state, trained behavior it was unlikely that the monkeys based their bets on differences in the visual stimuli across trials, because the visual stimuli were the same for each trial; they differed only in location of the masked target and SOA. Keeping track of location would not help, because it contained no information (target location varied randomly by trial). Visual information provided by the SOA could help, as correct trials occurred more often with long SOAs. However, our trial-by-trial analysis indicated that monkeys did not exploit the information. A final alternative explanation might be that the monkeys failed to see the target on shorter SOA trials and used this to their advantage. If a monkey failed to see the target, it could abort the trial to start a new one immediately, or it could continue the trial and make a randomly directed saccade. In the latter scenario, the monkey might know that the saccade was random because it knew that it did not see the target. The best utility of this knowledge would be to switch to a new strategy of betting only low (which can be shown with simple calculations to yield optimal reward for random saccades). Such a scenario is unlikely for two reasons. First, it is not parsimonious. Presuming that the monkeys adopted a new betting strategy when they failed to see a target is more complicated than simply presuming that they aborted such trials. Second, the scenario has no empirical support. Using a special strategy to obtain more reward after failing to see a target (more likely at shorter SOAs) should lead to an anomalous drop in high bets and rise in reward rates at shorter SOAs. We found no hint of either deviation (Figures 2b, 2d, 8a, and 8b). Taken together, all this evidence supports our original hypothesis that the task encouraged covert monitoring of decisions and betting on the basis of those decisions on individual trials.
We proposed an operational definition of metacognition because monkeys cannot use language to relate their cognitive experience. Principled, accepted criteria are needed for inferring their cognition through their behavior. But the definition that we established is not entirely new. Son and Kornell (2005) calculated phi correlations for two monkeys performing a betting paradigm directly analogous to the task we used. The authors did not state that phi correlation values significantly above zero counted as metacognitive behavior, but they indicated as much by stating that the monkeys were “able to make accurate confidence judgments” (p. 311). Our main contribution was to explicitly define the criteria for metacognitive behavior.
What exactly was the cognitive operation that linked the animals’ decisions to their subsequent wagers? Heightened arousal or vigilance seems unlikely to play a role, because monkeys had to fully complete every trial. Placing a low bet required as much effort as placing a high bet. A more convincing explanation is to invoke levels of confidence, which may be considered a weak form of metacognition. High confidence would encode that the decision was correct without necessarily conveying details about the decision. A stronger metacognitive signal would encode decision-related details such as target location. Many studies have examined how metacognition and confidence are related (see, e.g., Brewer & Sampaio, 2006; Koriat, Lichtenstein, & Fischhoff, 1980), but few experiments have studied how confidence is distinct from metacognition. One report compared human participants’ standardized measures of self-confidence with their standardized measures of metacognitive awareness (Kleitman & Stankov, 2007). The authors of that study concluded that confidence and metacognition are separate processes but found a correlation between the two.
For the sake of simplicity, we have been anthropomorphizing monkey behavior. Doing so facilitates discussion but should not be taken literally. Although monkeys can be trained to monitor their decisions and perform subsequent behaviors based on them, it is unknown to what extent they do this in everyday behavior. Their metacognition may be entirely implicit, below any level of awareness, such as the blindsight process by which monkeys correctly identify stimuli in a blind hemifield (Cowey & Stoerig, 1995). It may well be that any animal capable of making decisions also maintains an internal record of those decisions for future use. Tests of metacognition in animals phylogenetically distinct from primates or dolphins (Smith et al., 1995) have yielded mixed results thus far. Pigeons seem unable to utilize an opt-out response in a manner reflecting metacognition (Roberts et al., 2009; Sutton & Shettleworth, 2008), but such data should be interpreted cautiously (as discussed by Shields et al. 2005, e.g.). Rodents have utilized an opt-out response effectively (Foote & Crystal, 2007), and they may monitor their confidence levels in a task where a choice is made but a reward is delayed (they tend to abort trials before the potential for reward after making incorrect decisions; Kepecs, Uchida, Zariwala, & Mainen, 2008). We suggest a point of comparison in the realm of motor behavior. As far as is known, every animal that moves also issues internal signals about its movements, called corollary discharge, for use in multiple functions such as analysis of sensory input (Crapse & Sommer, 2008). One could think of metacognition as involving a corollary discharge; when brain networks accomplish a decision, they may issue an internal record of that decision to the rest of the brain for multiple potential purposes.
In the specific context of monkeys performing our task, the frontal eye field seems to contribute to the target-selection decision stage (Thompson & Schall, 1999). It may send a corollary discharge of the decision-related signals to higher areas such as dorsolateral prefrontal cortex, which use the information to wager optimally in the bet stage of the task. Such a hypothesis is testable using the present task and neurophysiological methods of recording, stimulation, and inactivation, or using imaging methods combined with analyses to search for correlated activations in separate, defined areas (e.g. Friston, Harrison, & Penny, 2003; Goebel, Roebroeck, Kim, & Formisano, 2003). We hope future studies will cast light on the neurobiological bases of metacognitive functions in a similar way that studies beginning 40 years ago (Fuster & Alexander, 1971; Kubota & Niki, 1971), and refined 20 years ago with streamlined tasks (Funahashi et al., 1989), began to elucidate the neuronal bases of working memory.
Acknowledgments
This research was supported by the National Institute of Mental Health (Ruth L. Kirschstein National Research Service Award F31 MH087094 to Paul G. Middlebrooks) and the National Eye Institute (Research Grant EY017592 to Marc A. Sommer).
Contributor Information
Paul G. Middlebrooks, Department of Neuroscience, Center for Neuroscience at the University of Pittsburgh, and Center for the Neural Basis of Cognition, University of Pittsburgh
Marc A. Sommer, Department of Biomedical Engineering, Center for Cognitive Neuroscience, Duke University, and Department of Neuroscience, Center for Neuroscience, and Center for the Neural Basis of Cognition, University of Pittsburgh.
References
- Benjamin AS, Bjork RA. Retrieval fluency as a metacognitive index. In: Reder LM, editor. Implicit memory and metacognition. Erlbaum; Mahwah, NJ: 1996. pp. 309–338. [Google Scholar]
- Benjamin AS, Bjork RA, Schwartz BL. The mismeasure of memory: When retrieval fluency is misleading as a metamnemonic index. Journal of Experimental Psychology: General. 1998;127:55–68. doi: 10.1037//0096-3445.127.1.55. doi: 10.1037/0096-3445.127.1.55. [DOI] [PubMed] [Google Scholar]
- Brewer WF, Sampaio C. Processes leading to confidence and accuracy in sentence recognition: A metamemory approach. Memory. 2006;14:540–552. doi: 10.1080/09658210600590302. doi:10.1080/09658210600590302. [DOI] [PubMed] [Google Scholar]
- Chandler CC. Studying related pictures can reduce accuracy, but increase confidence, in a modified recognition test. Memory and Cognition. 1994;22:273–280. doi: 10.3758/bf03200854. [DOI] [PubMed] [Google Scholar]
- Chua EF, Schacter DL, Rand-Giovannetti E, Sperling RA. Understanding metamemory: Neural correlates of the cognitive process and subjective level of confidence in recognition memory. NeuroImage. 2006;29:1150–1160. doi: 10.1016/j.neuroimage.2005.09.058. doi:10.1016/j.neuroimage.2005.09.058. [DOI] [PubMed] [Google Scholar]
- Clifford CW, Arabzadeh E, Harris JA. Getting technical about awareness. Trends in Cognitive Sciences. 2008;12:54–58. doi: 10.1016/j.tics.2007.11.009. doi:10.1016/j.tics.2007.11.009. [DOI] [PubMed] [Google Scholar]
- Costermans J, Lories G, Ansay C. Confidence level and feeling of knowing in question answering: The weight of inferential processes. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1992;18:142–150. doi:10.1037/0278-7393.18.1.142. [Google Scholar]
- Cowey A, Stoerig P. Blindsight in monkeys [Letter]. Nature. 1995;373:247–249. doi: 10.1038/373247a0. [DOI] [PubMed] [Google Scholar]
- Crapse TB, Sommer MA. Corollary discharge across the animal kingdom. Nature Reviews Neuroscience. 2008;9:587–600. doi: 10.1038/nrn2457. doi: 10.1038/nrn2457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foote AL, Crystal JD. Metacognition in the rat. Current Biology. 2007;17:551–555. doi: 10.1016/j.cub.2007.01.061. doi:10.1016/j.cub.2007.01.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Harrison L, Penny W. Dynamic causal modelling. NeuroImage. 2003;19:1273–1302. doi: 10.1016/s1053-8119(03)00202-7. doi:10.1016/S1053-8119(03)00202-7. [DOI] [PubMed] [Google Scholar]
- Funahashi S, Bruce CJ, Goldman-Rakic PS. Mnemonic coding of visual space in the monkey's dorsolateral prefrontal cortex. Journal of Neurophysiology. 1989;61:331–349. doi: 10.1152/jn.1989.61.2.331. [DOI] [PubMed] [Google Scholar]
- Fuster JM, Alexander GE. Neuron activity related to short-term memory. Science. 1971 Aug 13;173:652–654. doi: 10.1126/science.173.3997.652. doi:10.1126/science.173.3997.652. [DOI] [PubMed] [Google Scholar]
- Goebel R, Roebroeck A, Kim DS, Formisano E. Investigating directed cortical interactions in time-resolved fMRI data using vector autoregressive modeling and Granger causality mapping. Magnetic Resonance Imaging. 2003;21:1251–1261. doi: 10.1016/j.mri.2003.08.026. doi:10.1016/j.mri.2003.08.026. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS. Cellular basis of working memory. Neuron. 1995;14:477–485. doi: 10.1016/0896-6273(95)90304-6. doi:10.1016/0896-6273(95)90304-6. [DOI] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal detection theory and psychophysics. Wiley; New York: 1966. [Google Scholar]
- Hampton RR. Rhesus monkeys know when they remember. Proceedings of the National Academy of Sciences of the United States of America. 2001;98:5359–5362. doi: 10.1073/pnas.071600998. doi:10.1073/pnas.071600998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hays AV, Richmond BJ, Optican L. Unix-based multiple-process system for real-time data acquisition and control. WESCON Conference Proceedings. 1982;2:1–10. [Google Scholar]
- Higham PA. No Special K! A signal detection framework for the strategic regulation of memory accuracy. Journal of Experimental Psychology: General. 2007;136:1–22. doi: 10.1037/0096-3445.136.1.1. doi:10.1037/0096-3445.136.1.1. [DOI] [PubMed] [Google Scholar]
- Jacobsen CF. Studies on cerebral function in primates. Comparative Psychological Monographs. 1936;13:1–60. [Google Scholar]
- Judge SJ, Richmond BJ, Chu FC. Implantation of magnetic search coils for measurement of eye position: An improved method. Vision Research. 1980;20:535–538. doi: 10.1016/0042-6989(80)90128-5. doi:10.1016/0042-6989(80)90128-5. [DOI] [PubMed] [Google Scholar]
- Kepecs A, Uchida N, Zariwala HA, Mainen ZF. Neural correlates, computation and behavioural impact of decision confidence. Nature. 2008;455:227–231. doi: 10.1038/nature07200. doi:10.1038/nature07200. [DOI] [PubMed] [Google Scholar]
- Kiani R, Shadlen MN. Representation of confidence associated with a decision by neurons in the parietal cortex. Science. 2009;324:759–764. doi: 10.1126/science.1169405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kikyo H, Ohki K, Miyashita Y. Neural correlates for feeling-of-knowing: An fMRI parametric analysis. Neuron. 2002;36:177–186. doi: 10.1016/s0896-6273(02)00939-x. doi: 10.1016/S0896-6273(02)00939-X. [DOI] [PubMed] [Google Scholar]
- Kleitman S, Stankov L. Self-confidence and metacognitive processes. Learning and Individual Differences. 2007;17:161–173. doi: 10.1016/j.lindif.2007.03.004. [Google Scholar]
- Koriat A, Lichtenstein S, Fischhoff B. Reasons for confidence. Journal of Experimental Psychology: Human Learning and Memory. 1980;6:107–118. doi:10.1037/0278-7393.6.2.107. [Google Scholar]
- Kornell N, Son LK, Terrace HS. Transfer of metacognitive skills and hint seeking in monkeys. Psychological Science. 2007;18:64–71. doi: 10.1111/j.1467-9280.2007.01850.x. [DOI] [PubMed] [Google Scholar]
- Kubota K, Niki H. Prefrontal cortical unit activity and delayed alternation performance in monkeys. Journal of Neurophysiology. 1971;34:337–347. doi: 10.1152/jn.1971.34.3.337. [DOI] [PubMed] [Google Scholar]
- Maril A, Simons JS, Mitchell JP, Schwartz BL, Schacter DL. Feeling-of-knowing in episodic memory: An event-related fMRI study. NeuroImage. 2003;18:827–836. doi: 10.1016/s1053-8119(03)00014-4. doi:10.1016/S1053-8119(03)00014-4. [DOI] [PubMed] [Google Scholar]
- Masson MEJ, Rotello CM. Sources of bias in the Goodman–Kruskal gamma coefficient measure of association: Implications for studies of metacognitive processes. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2009;35:509–527. doi: 10.1037/a0014876. doi:10.1037/a0014876. [DOI] [PubMed] [Google Scholar]
- Metcalfe J. Evolution of metacognition. In: Dunlosky J, Bjork RA, editors. Handbook of metamemory and memory. Psychology Press; New York, NY: 2008. pp. 29–46. [Google Scholar]
- Nelson TO, Narens L. Bower GH, editor. Metamemory: A theoretical framework and new findings. The psychology of learning and motivation. 1990;26:125–171. doi:10.1016/S0079-7421(08)60053-5. [Google Scholar]
- Persaud N, McLeod P, Cowey A. Post-decision wagering objectively measures awareness. Nature Neuroscience. 2007;10:257–261. doi: 10.1038/nn1840. doi:10.1038/nn1840. [DOI] [PubMed] [Google Scholar]
- Roberts WA, Feeney MC, McMillan N, Macpherson K, Musolino E, Petter M. Do pigeons (Columba livia) study for a test? Journal of Experimental Psychology: Animal Behavior Processes. 2009;35:129–142. doi: 10.1037/a0013722. doi:10.1037/a0013722. [DOI] [PubMed] [Google Scholar]
- Shields WE, Smith JD, Guttmannova K, Washburn DA. Confidence judgments by humans and rhesus monkeys. The Journal of General Psychology. 2005;132:165–186. [PMC free article] [PubMed] [Google Scholar]
- Smith JD, Schull J, Strote J, McGee K, Egnor R, Erb L. The uncertain response in the bottlenosed dolphin (Tursiops truncatus). Journal of Experimental Psychology: General. 1995;124:391–408. doi: 10.1037//0096-3445.124.4.391. doi: 10.1037/0096-3445.124.4.391. [DOI] [PubMed] [Google Scholar]
- Smith JD, Shields WE, Allendoerfer KR, Washburn DA. Memory monitoring by animals and humans. Journal of Experimental Psychology: General. 1998;127:227–250. doi: 10.1037//0096-3445.127.3.227. doi:10.1037/0096-3445.127.3.227. [DOI] [PubMed] [Google Scholar]
- Sommer MA, Wurtz RH. Composition and topographic organization of signals sent from the frontal eye field to the superior colliculus. Journal of Neurophysiology. 2000;83:1979–2001. doi: 10.1152/jn.2000.83.4.1979. [DOI] [PubMed] [Google Scholar]
- Son LK, Kornell N. Meta-confidence judgments in rhesus macaques: Explicit versus implicit mechanisms. In: Terrace HS, Metcalfe J, editors. The missing link in cognition: Origins of self-reflective consciousness. Oxford University Press; New York, NY: 2005. pp. 296–320. [Google Scholar]
- Sutton JE, Shettleworth SJ. Memory without awareness: Pigeons do not show metamemory in delayed matching to sample. Journal of Experimental Psychology Animal Behavior Processes. 2008;34:266–282. doi: 10.1037/0097-7403.34.2.266. doi:10.1037/0097-7403.34.2.266. [DOI] [PubMed] [Google Scholar]
- Thompson KG, Schall JD. The detection of visual signals by macaque frontal eye field during masking. Nature Neuroscience. 1999;2:283–288. doi: 10.1038/6398. doi:10.1038/6398. [DOI] [PubMed] [Google Scholar]
- Wang XJ. Discovering spatial working memory fields in prefrontal cortex. Journal of Neurophysiology. 2005;93:3027–3028. doi: 10.1152/classicessays.00028.2005. doi: 10.1152/classicessays.00028.2005. [DOI] [PubMed] [Google Scholar]