Abstract
Ordinal data appear in a wide variety of scientific fields. These data are often analyzed using ordinal logistic regression models that assume proportional odds. When this assumption is not met, it may be possible to capture the lack of proportionality using a constrained structural relationship between the odds and the cut-points of the ordinal values (Peterson and Harrell, 1990). We consider a trend odds version of this constrained model, where the odds parameter increases or decreases in a monotonic manner across the cut-points. We demonstrate algebraically and graphically how this model is related to latent logistic, normal, and exponential distributions. In particular, we find that scale changes in these potential latent distributions are consistent with the trend odds assumption, with the logistic and exponential distributions having odds that increase in a linear or nearly linear fashion. We show how to fit this model using SAS Proc Nlmixed, and perform simulations under proportional odds and trend odds processes. We find that the added complexity of the trend odds model gives improved power over the proportional odds model when there are moderate to severe departures from proportionality. A hypothetical dataset is used to illustrate the interpretation of the trend odds model, and we apply this model to a Swine Influenza example where the proportional odds assumption appears to be violated.
Keywords: Non-proportional odds, Constrained cumulative odds, Influenza, Latent distributions, Logistic distribution
1. Introduction
Ordinal data are often analyzed using the Proportional Odds Model (POM). Conceptually introduced by Aitchison and Silvey in 1957, developed by Snell in 1964, and further developed by McCullagh in 1980, the Proportional Odds model is a popular extension of logistic regression to ordinal data [1, 2]. Odds are considered proportional when all possible dichotomizations of high versus low outcomes result in the same odds metric. This proportional odds assumption has been justified by a theoretical underlying logistic distribution with shift in location but constant scale [2]. McCullagh also introduced a linear “multiplicative model” that relaxes the assumption of a constant scale of the underlying logistic distribution by introducing scale parameters to be estimated [2]. Peterson and Harrel suggested that the lack of proportionality might be relaxed for some of the covariates by introducing intermediate constrained structural relationship between the odds and the cut-points [3].
In this paper, we illustrate and investigate a monotone class of Peterson and Harrel’s constrained non-proportional model, which we will term a Trend Odds model (TOM). We first review the notation of the cumulative odds model, emphasizing proportional and trend classes, and give a hypothetical data example where the linear TOM holds. We then show how latent distributions relate to the TOM, with particular attention given to the logistic distribution. We show how to fit the TOM using SAS Proc Nlmixed, and present some simulation results when the data follow the Proportional Odds model and when they follow the TOM. Finally, we apply the TOM to a swine influenza dataset that appears to come from a non-proportional-odds process.
2. Cumulative Odds Models: Proportional Odds and Trend Odds models
The Trend Odds model (TOM) belongs to the cumulative ordinal class of models. To better understand its structure, we revisit the generalized structures of cumulative odds models. For simplicity we will consider the single predictor case. The models are organized conceptually and not necessary chronologically.
Suppose there is an observed ordinal outcome Y with I+1 categories (Y=0, 1,…, I), and a single covariate X. We define Ψix as the log cumulative odds, or the odds of Y having a level at least as high as each cut-point I, given X. That is, Ψix= log(P(Y≥i|X=x)/(1-P(Y≥i|X=x))). The general form of the cumulative odds model is known as Unconstrained Cumulative Odds model, represented as:
Note that this model allows a different odds ratio relating X to Y for each cut-point, since the β terms are indexed by i. For example, suppose that X represents an exposure status that is being investigated, with X=1 for exposed and X=0 for unexposed. Several different and unrelated odds ratio for exposed versus unexposed can be calculated depending on the cut-point (i.e., θ1=eβ1, θ2=eβ2,…, θI=eβI).
In contrast, a commonly-used cumulative ordinal model known as the Proportional Odds model constrains the above model by assuming that all βi are equal to a common β [2]. For the single predictor case, we will notate the Proportional Odds model [4] as:
| (1) |
With this model, the odds of being at or above any cut-point are assumed to be the same for all cut-points; this is known as the “proportional odds” assumption. In other words, instead of having several different odds ratio for exposed versus unexposed, a single odds ratio is calculated (θ=eβ). When the parameter β is greater than zero and X increases, the response Y is consistently more likely to be in a higher end. While the Proportional Odds model makes a strong assumption, it is easy to fit and interpret [5].
When the proportional odds assumption is not met, it may be possible to capture the lack of proportionality using intermediate constrained structural relationship between the odds and the cut-points [1, 3, 6–8]. In general this can be accomplished by adding a parameter, say γ, and a multiplicative scalar that varies with the cut-point, say ti. For the single predictor case, we will define the Constrained Cumulative Odds model as
| (2) |
In general the Constrained Cumulative Odds models could potentially have any set of scalars, as long as the odds ratios from the resulting model adequately fit the data. Consider again the investigation of exposure status. If this generalized model is used with a set of scalars that includes consecutive zero values, then there would be proportionality of odds ratios across some of the cut-points within the same covariate. For example, the scalar values of t1=1, t2=−1, t3=0, and t4=0 would yield the odd ratios of θ1=eβeγ, θ2=eβe−γ, and θ3= θ4=eβ. In other words, under the family of constrained non-proportional odd models, the scalar set can be unstructured.
The TOM is a structured Constrained Cumulative Odds model. Although many types of trends may be possible, we define the TOM to have a monotonic structure, such that t1≤t2≤…≤tI. Hence, for the single predictor case, the TOM is
| (3) |
The parameter space of αi and β is similar to the Proportional Odds model, being comprise of any real number from minus infinity to infinity. In contrast, based on the underlying theory that is going to be presented in the following section, the parameter space of γ∙x depends on the scale of the theoretical underlying distribution of X. A trend in log-odds ratios will result when the γ is non-zero. If exposure status is being used to predict the ordinal outcome, and if the proportional odds assumption does not appear reasonable, then the researcher can test for a trend in the cumulative odds ratio as the ordinal outcome (or the cut-points thereof) increases. Depending on the values of t1, β, and γ, the odds ratios may all be below 1, all be above 1, or span the value of 1, but their trend must be monotonic.
3. Latent Logistic Motivation for the TOM Model
Suppose that a response variable, Y*, follows a logistic distribution with location and scale parameters (m and s) being functions of a predictor variable, X, such that
| (4) |
Hence, E(Y*|X=x)=mx and Var(Y*|X=x)=π2sx2/3. For I specific values of interest, say ci, for i=1, 2, …, I, we would have the cdf of Y*
| (5) |
By taking the logit function and rearranging terms we have
| (6) |
Suppose that the ordinal variable, Y, takes on values 0, 1, 2, …, I, based on the latent variable, Y*, according to the ci values. Specifically, let
| (7) |
and
| (8) |
where c0=−∞ and cI+1=∞.
So, in terms of the ordinal variable from a latent logistic distribution, Equation (6) becomes
| (9) |
The Logistic distribution can be related to the TOM through known cut-points. In the TOM introduced in the previous section (Equation (2)), we have, for i=1, 2, …I,
| (10) |
where the ti are monotonic values specified when fitting the model, and α, β, and γ are parameters estimated by the fitting procedure. If the cut-points, c1, c2, …cI, are known, we can choose ti=ci, and then we use the superscript * to indicate the parameters fit in this situation, such that Ψix = αi*+ (β* + γ* ci)x.
Hence, combining (9) and (10) when ti=ci, we get
| (11) |
To get interpretations of the parameters (αi*, β*, and γ*), we consider what happens under various values of X. When X=0, we have (m0 − ci)/s0 = αi* + (β* + γ* ci)0, implying
| (12) |
For X=x we have
| (13) |
Combining (12) and (13) and subtracting (m0 − ci)/s0 from both sides, we get
| (14) |
Gathering the terms that the index i together, we get
| (15) |
Hence, for x≠0, the parameters are defined as
| (16) |
and
| (17) |
There is no restriction on the parameter space of αi* and β* as there is no restriction on the space of the Logistic distribution mean. In contrast, the parameter space of γ* is restricted as the Logistic distribution scale can only assume positive values (i.e. −1/sx < γ*x < 1/s0).
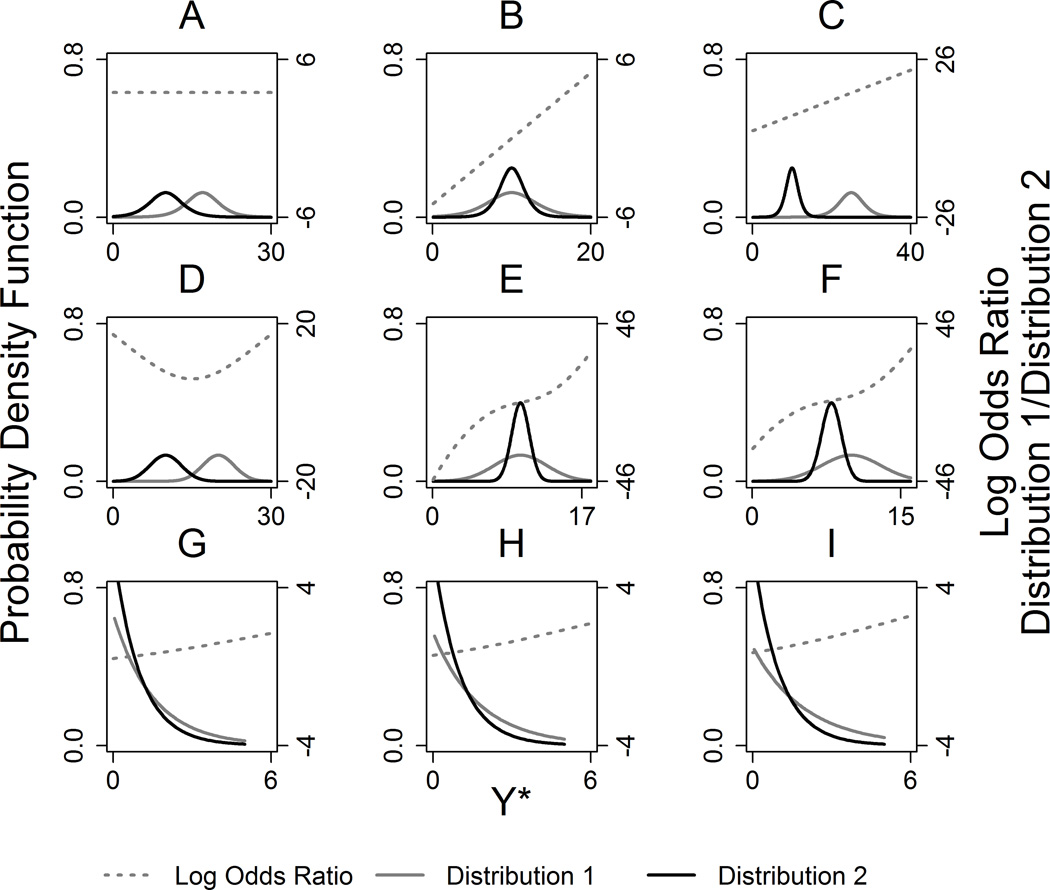
Figures 1A–1C illustrate the trend in log odds ratio with underlying latent logistic distributions with location shift only (Figure 1A), scale shift only (Figure 1B), and scale and location shift (Figure 1C) for a simple binary covariate X.
Figure 1.
Panel of underlying logistic, normal, and respective log ratios. (A) Logistic(17,2) versus (10,2),(B) logistic(10,2) versus (10,1), (C) logistic(25,2) versus (10,1), (D) N(20,3) versus (10,3), (E) N(10,3) versus (10,1), (F) N(10,3) versus (8,1), (G) exponential(1.5) versus (1), (H) exponential(1.75) versus (1), and (I) exponential(2) versus (1).
Conversely, we can also find expressions for the sx and mx functions in terms of the TOM parameters. This is particularly relevant to better understand the association with continuous covariates. Solving for sx in (17), we get
| (18) |
Note that TOM holds for x values satisfying γ*x < 1/s0. The parameter γ* dictates the non-linearity in the location shifts, and simultaneously dictates the heteroskedasticity, associated with changing x values. In contrast, when γ* is 0 or close to 0 the latent logistic has a mean that shifts linearly with changes in x, with constant variance (sx ≈ s0).
Solving for mx in (16) and sx defined in (18) we get
| (19) |
Note that (8) and (9) have respectively the form of
| (20) |
and
| (21) |
where a=−β*s0/m0 and b=−γ*s0.
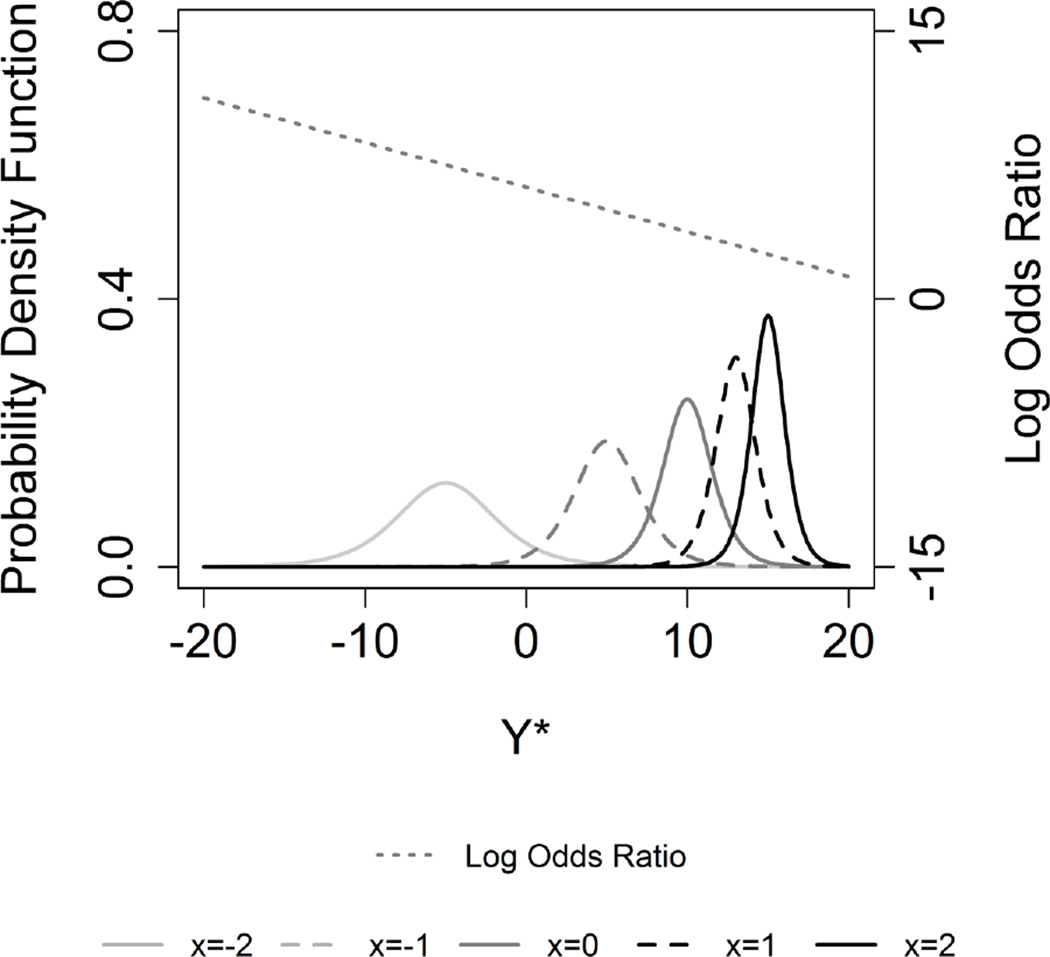
Hence, equations (20) and (21) show how the parameters of a latent logistic distribution must depend on the covariate X in order for the TOM to hold, when the cut-points (ci) used for categorizing the data are known. For example, a negative trend in log odds ratio is obtained with underlying latent logistic distributions with scale and location shift as a function of a continuous covariate X, when m0=10, s0=1, a=0.625 and b=0.25 (Figure 2, Supporting Information).
Figure 2.
Underlying Logistic and respective log odds ratio for continuous X. Logistic(mx, sx) where mx and sx are defined by equation 19 and 20, and m0=10, s0=1, a=0.625 and b=0.25.
4. Other underlying distributions
The logistic distribution provides a theoretical basis for the Proportional Odds model and for the TOM. It is feasible, however, that the trend odds assumption could hold when the underlying latent variable Y* follows other distributions (Figures 1D to 1I). To investigate this, we calculated log odds ratios from two-group situations with Y* following normal and exponential distributions. Figures 1D to 1F illustrate the log odds ratio with underlying latent normal distributions with location shift only (Figure 1D), scale shift only (Figure 1E), and scale and location shift (Figure 1F) for a simple binary predictor X. Note that when a scale shift occurs, the trend is monotonic non-linear, with the log odds ratio spanning the value of 0. For the location shift only (Figure 1D), the trend is non-monotonic, but the log odds ratio is always positive. Figures 1G to 1I illustrate the log odds ratio with underlying latent exponential distribution with increasing shift in location-scale for a simple binary predictor X. Note that these log odds ratio trends are all monotonic, and nearly linear.
Table 1 shows the log odds ratio as a function of ci that follows logistic, normal or exponential distributions. The existence of a closed form solution makes it possible to show theoretically when the proportional odds or the trend odds assumption holds. For the logistic distribution, using Equation (9), the log odds ratio would be
| (22) |
Table 1.
Some examples of distributions for the hypothetical underlying latent variable Y* and holding relation with log odds ratios
| Latent Distribution | Parameter shift from X=0 to X=x | Log Odds Ratio Ψix -Ψi0) |
Holds |
|---|---|---|---|
| Logistic | Location (m) | (mx− m0)/s | Proportional Odds |
| Logistic | Scale (sx) | (m − ci)(1/sx− 1/s0) | Trend Odds – linear monotonic |
| Logistic | Location (mx) and scale (sx) |
(mx−ci)/sx−(m0−ci)/s0 | Trend Odds – linear monotonic |
| Normal | Mean (µx) and variance (σx) |
log((1−Φ(ci/σx −µx/σx))/Φ(ci/σx −µx/σx))− log((1-Φ(ci/σ0 −µ0/σ0))/Φ(ci/σ0−µ0/σ0)) |
Trend Odds – non-linear monotonic |
| Normal | Variance (σx) | log((1−Φ(ci/σx −µ/σx))/Φ(ci/σx −µ/σx))− log((1−Φ(ci/σ0 −µ/σ0))/Φ(ci/σ0 −µ/σ0)) |
Trend Odds – non-linear monotonic |
| Normal | Mean (µx) | log((1−Φ(ci/σ −µx/σx))/Φ(ci/σ −µx/σ))− log((1−Φ(ci/σ −µ0/σ0))/Φ(ci/σ −µ0/σ)) |
Quadratic |
| Exponential | Location-scale (λ0) | log(eciλ0−1)−log(eciλx−1) | Trend Odds – non-linear monotonic |
When the scale is the same (s=sx=s0) but there is a location shift, the log odds can be represented by (mx-m0)/s, which is independent of ci (proportional odds assumption holds). That is, for a Proportional Odds model, the common log odds ratio is proportional to the distance in mean underlying response given two values of a predictor X [9, 10]. In contrast, if there is a shift in scale with or without a shift in location the log odds ratio, then the trend in odds has a slope proportional to the inverse difference in scale (trend odds assumption holds). The first derivative
| (23) |
is a constant, that can be shown to correspond to cix or −(b/s0)x by using respectively equations (17) or (20).
For the exponential distribution, with parameter λx (i.e., with a mean of 1/λx) the log odds ratio can be represented by
| (24) |
Shifts in location-scale result in log odds ratio (provided in Table 1) that are a monotonic non-linear function of ci (trend odds assumption holds). The first derivative
| (25) |
has a limit of
| (26) |
That is, although the finite trend is non-linear, it approaches linearity with increasing y*.
5. Simulation Study
The properties of the TOM were compared to the Binary Logistic Model at different cut-points, and the Proportional Odds model. Simulation was performed in SAS considering the simulation steps suggested by Burton et al. [11]. Simulated scenarios included different sample sizes (50 to 1000 per group), different reference multinomial distribution, and combinations of β and γ to represent holding proportional odds assumption or trend odds assumption. A total of 1000 datasets were randomly generated from a multinomial distribution using different seeds. The data were modeled with the binary logistic model, the Proportional Odds model, and the TOM. This was accomplished using Proc Logistic and Proc Nlmixed in SAS. Bias, coverage, accuracy performance, test size and power were evaluated in the statistical methods for different scenarios.
Table 2 shows the simulation results of modeling using TOM and the Proportional Odds model. The Proportional Odds model was performed in SAS Proc Logistic and Proc Nlmixed, with practically identical results. In the scenarios where the proportional odds holds (γ=0; flat trend), mean and median common estimated odds ratios are very close to the true odds ratio (3.0). The observed coverage for the 95% confidence intervals was between 93% and 96%. In the scenarios where the trend odds holds, mean and median common estimated odds a ratio are close to the odds ratio of the first cut-point due to higher frequency of lower titers. Not surprisingly, coverage was poor for this situation, as the confidence interval for the estimate common odds does not cover 3 levels of true odds ratios.
Table 2.
Result of simulations for the Trend Odds model with SAS proc nlmixed and Proportional Odds Model with SAS proc logistic or proc nlmixed. Simulated scenarios considering 4 levels of antibody titers and 1000 repeats. Non-exposed group outcome follows a multinomial (n, (0.50,0.40,0.092,0.008))
| Trend Odds holds. |
Proportional Odds holds. |
|||||||
|---|---|---|---|---|---|---|---|---|
| Parameters | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| Sample size per group | 50 | 100 | 400 | 1000 | 50 | 100 | 400 | 1000 |
| True Odds Ratio | ||||||||
| cut-point 1 | 1.5 | 1.5 | 1.5 | 1.5 | 3.0 | 3.0 | 3.0 | 3.0 |
| cut-point 2 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 |
| cut-point 3 | 6.0 | 6.0 | 6.0 | 6.0 | 3.0 | 3.0 | 3.0 | 3.0 |
| True parameters | ||||||||
| β | 0.4 | 0.4 | 0.4 | 0.4 | 1.1 | 1.1 | 1.1 | 1.1 |
| γ | 0.7 | 0.7 | 0.7 | 0.7 | 0.0 | 0.0 | 0.0 | 0.0 |
| Estimated Mean Odds Ratio | ||||||||
| POM | 2.52 | 2.44 | 2.35 | 2.34 | 3.30 | 3.14 | 3.04 | 3.01 |
| TOM, cut-point 1 | 1.63 | 1.58 | 1.52 | 1.51 | 3.93 | 3.35 | 3.10 | 3.04 |
| TOM, cut-point 2 | 3.37 | 3.17 | 3.03 | 3.01 | 3.42 | 3.18 | 3.05 | 3.02 |
| TOM, cut-point 3 | 7.99 | 6.81 | 6.14 | 6.07 | 3.38 | 3.17 | 3.03 | 3.01 |
| Estimated Median Odds Ratio | ||||||||
| POM | 2.34 | 2.32 | 2.34 | 2.34 | 3.07 | 2.99 | 3.01 | 3.01 |
| TOM, cut-point 1 | 1.48 | 1.50 | 1.50 | 1.51 | 3.11 | 2.96 | 3.04 | 3.02 |
| TOM, cut-point 2 | 3.08 | 3.01 | 3.00 | 3.00 | 3.10 | 2.99 | 3.02 | 3.00 |
| TOM, cut-point 3 | 6.17 | 6.06 | 5.97 | 5.99 | 3.06 | 3.02 | 2.99 | 2.99 |
| Coverage (percent) | ||||||||
| POM, cut-point 1 | 79% | 60% | 9% | 0% | 95% | 93% | 95% | 96% |
| POM, cut-point 2 | 88% | 83% | 53% | 13% | 95% | 93% | 95% | 96% |
| POM, cut-point 3 | 30% | 7% | 0% | 0% | 95% | 93% | 95% | 96% |
| TOM, cut-point 1 | 96% | 95% | 94% | 96% | 95% | 95% | 95% | 96% |
| TOM, cut-point 2 | 95% | 94% | 95% | 96% | 95% | 93% | 95% | 96% |
| TOM, cut-point 3 | 96% | 94% | 95% | 95% | 96% | 94% | 94% | 95% |
| LRT (percent significant) | ||||||||
| POM | 65% | 83% | 100% | 100% | 85% | 99% | 100% | 100% |
| TOM | 83% | 98% | 100% | 100% | 78% | 97% | 100% | 100% |
In the scenarios where the proportional odds holds (flat trend), mean and median common estimated odds ratios are very close to the true odds ratio (3.0), with acceptable coverage for the parameters 94% to 96% (γ=0 and β=1.1). In the scenarios where the trend odds holds, the mean estimated odds ratio per cut-point is higher than expected for smaller samples but approaches the true odds ratio as the sample increases. The median estimated odds ratio is close to the true odds ratio regardless of the sample size. Coverage for the parameters is acceptable, from 95% to 96% (γ=0.7 and β=0.4).
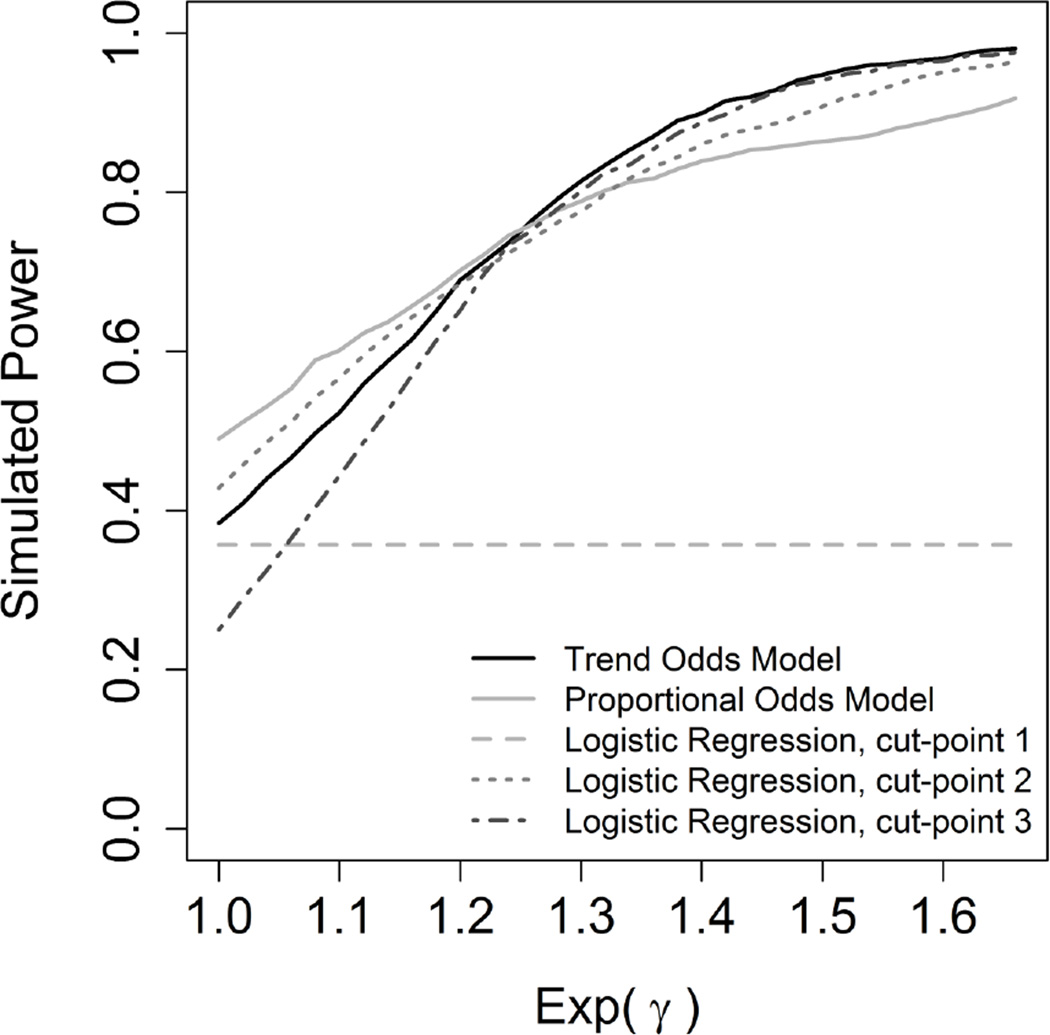
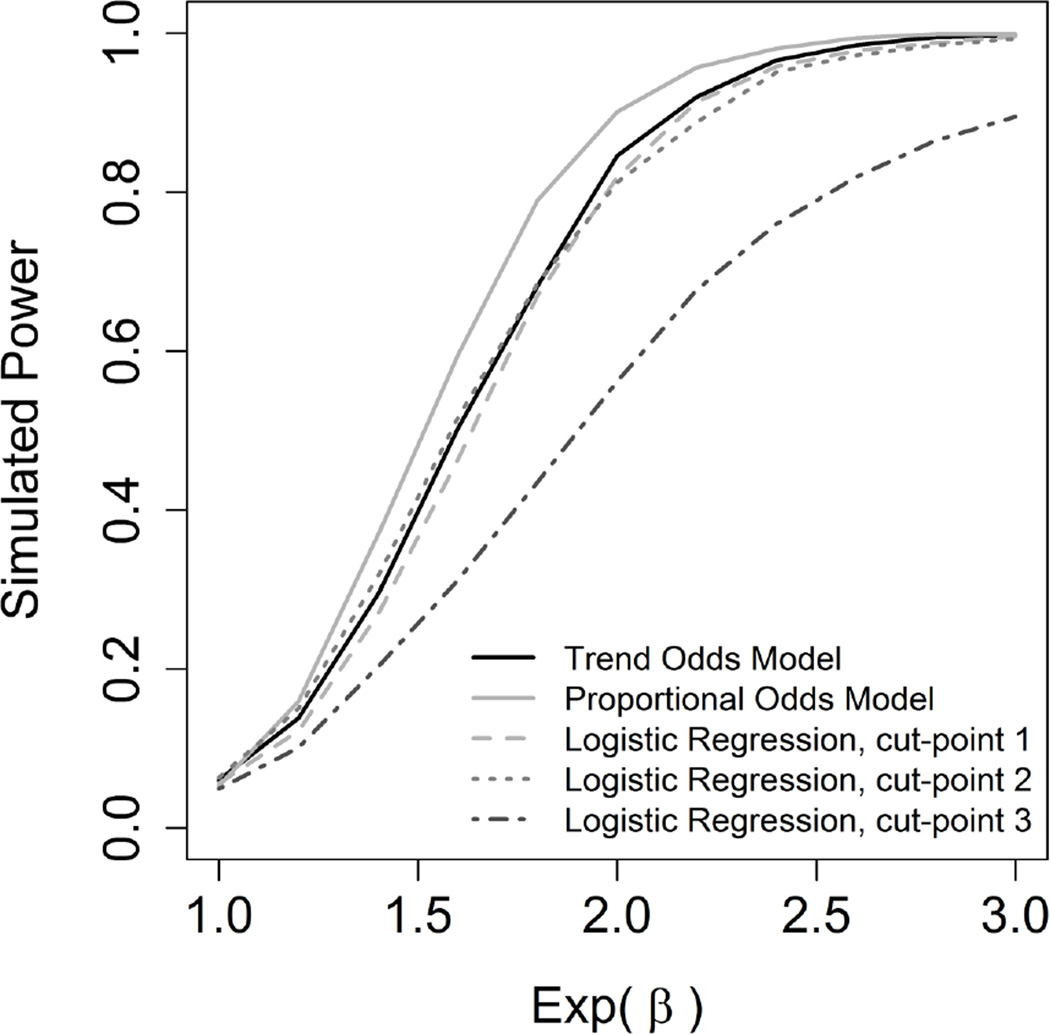
Test size and power were investigated in the simulations by varying sample size, β and γ. Overall, when using the likelihood ratio test with the intercept only model as a reference, the models performed well. The percentage of simulated models that was significant using this test is reported in Table 2. Initial simulation of power were obtained with a fixed sample size of 150 per group, a fixed β of log (1.5), and varying values of eγ, which can be thought of a multiplicative factor. As eγ gets larger, the TOM becomes more powerful than Proportional Odds model, with the crossover point being when eγ is around 1.25 (Figure 3, Supporting Information). In this example that would represent a series of odds ratios of 1.5, 1.875 (or 1.5 times 1.25) and 2.34 (or 1.875 times 1.25). Additional simulation of power were obtained with a fixed sample size of 150 per group, a fixed eγ=1.0 (proportional odds is true; flat trend), and varying β. The Type I error rate of the models stayed in an expected level around 0.05. The level of the Type I error for TOM was reasonable. The Proportional Odds model presented a superior simulated power in this setting where there is a real proportionality of odds with no trend (Figure 4, Supporting Information).
Figure 3.
Simulation of power with the non-exposed group outcome following a multinomial(n=150,(0.30, 0.26,0.24,0.20)), β of log(1.5), sample size of 150 per group and 1000 replications.
Figure 4.
Simulated power with the non-exposed group outcome following a multinomial(n,(0.30,0.26,0.24,0.20)), γ of 0 (no trend in odds ratios), sample size of 150 per group and 1000 replications.
6. Application to swine influenza data
Zoonotic influenza A viruses, such as avian and swine influenza, have caused many human pandemics. Introduction of avian influenza to humans was thought to be the cause of pandemics in 1918–1919, 1957–1958, and 1968–1969. These human pandemics left more than 20 million people dead. A swine influenza H1N1 outbreak in 1976 resulted in thousands of infected humans [12, 13]. Influenza virus transmission is complex. Viral shedding depends on several factors. For example children, and individuals who are immunocompromised and symptomatic may shed higher titers than other individuals, whereas, people with subclinical or asymptomatic infection are may shed lower titers than others. In addition to the viral shedding variation, there are several possibilities for contact with the virus. Transmission may occur by contacting aerosolized respiratory droplets, or by touching respiratory secretions contaminated objects [14]. Influenza can also be transmitted interspecies. Swine are thought to have a major role in interspecies transmission because they have receptors for both human and avian influenza viruses. For this reason swine are considered a “mixing vessel host for creation of novel reassortant progeny virus” [15, 16].
In some epidemiological studies of zoonotic influenza, researchers try to understand the etiology of the disease by retrospectively studying populations considered at risk. These researchers try to link infections to certain exposures or risk factors. Human response to influenza virus infection involves antibody response that can be used as evidence of previous infection. Using antibody titers is often an important diagnostic tool in epidemiological assessment of infections, especially in studies where infection may be sub-clinical. The use of some laboratory methods based on titers often produces data that are categorized into ordinal levels. Examples of these methods are microneutralization and hemagglutination inhibition [17] where dilutions are reported. The ordinal titer categories are recorded based on the sequence of dilution used (e.g. “< 1:10”; “1:10”; “1:20”, “1:40” etc.). The inverse of the dilutions is usually equal spaced in the log scale. The first recorded level represents antibody concentration that cannot be detected at the first dilution (e.g. “<1:10”). The second recorded level represents antibody concentration that is detected at the first dilution but cannot be detected at the second dilution (e.g. “1:10”), and so on. In general, the data would fall into K+1 categories based on K cut-points.
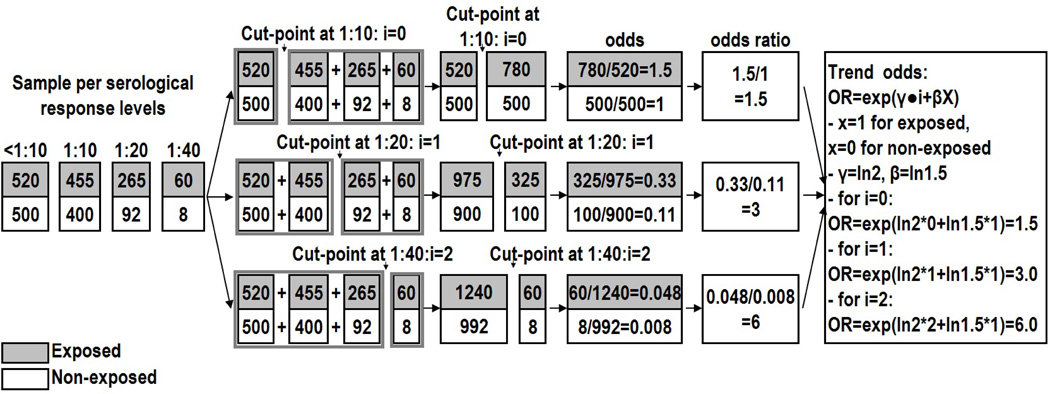
For didactical reasons, we start by illustrating the trend odds concept with simple hypothetical frequencies across titer levels (Figure 5). Suppose a cross-sectional study obtained exposure status (exposure versus non-exposure) and levels of antibody titers (<1:10, 1:10, 1:20 and 1:40). In the general TOM, any monotonic scalar set, ti, could potentially be adopted. It is, however, of practical use to consider structures that eases the model interpretation, provided that they adequately fit the data. Scalar sets starting at zero are convenient so that β is interpreted as the baseline odds ratio (the odds ratio at the first cut-point, θ=eβ). That is,
| (27) |
Figure 5.
An illustration of the trend odds concept.
In addition, one may consider a set such that ti=i−1 (where ti=0,1, 2, …I), for a model interpretation based on increments in the ordinal observed variable Y. When data are collected in equal spacing, it may be reasonable to say that i∙k=ci−c0, where k is an unknown constant. Related odds ratio can then be calculated from the baseline odds ratio using δ=eγ, so that, for i=1, 2, …I,
| (28) |
In this simple example, there are 3 cut-points and 3 possible odds ratios. In our hypothetical example the odds ratios present an increasing trend with a positive γ giving a δ>1 (in this case, δ=2). The baseline θ is 1.5, meaning that exposed participants have at least fifty percent higher odds of having higher antibody titers. The odds ratio doubled with increasing ordinal titer levels. The next odds ratios can be calculated as 1.5 • 2=3.0, and 3.0 • 2=6.0.
To illustrate the TOM and its interpretation in practice, we now use actual real data from a cross-sectional occupational epidemiology study among farmers, meat processing workers, veterinarians, and healthy controls. The data were collected from 2002 to 2004 in the Center for Emergency Infectious Diseases at the University of Iowa [15]. Age was collected at enrolment using a questionnaire, and sera were collected and tested according to the Centers for Disease Control and Prevention (CDC) HI serologic protocol. In this example we use age (in decades) to predict the hemagglutination inhibition (HI) titers against swine H1N2 (A/Swine/WI/R33F/01) virus. Modeling was performed in SAS with Proc Nlmixed. A reference code is provided (Appendix A, Supporting Information). The TOM indicates a significant negative trend in odds ratios (γ=0.515, SE(γ)=0.052, p-value=0.01). Odds of having increased antibody titers against swine H1N2 are significantly higher for older participants but the effect decreases with increasing antibody titers. As seen in Table 3, estimated odds ratios are 1.67 at baseline (first cut-point, 1:10, β=0.133, SE(β)=0.085, p-value <0.01) and decreases as titers go up (eγ=δ = 0.88). That is the increase in one level in antibody titer decreases the odds ratio in 12%. In practice such information can raise several hypotheses about the transmission of the virus, as mentioned in the discussion section.
Table 3.
Data on antibody titers against swine H1N2 influenza, modeled as a function of age (in decades). Example of univariate comparison using the Trend Odds Model fit in SAS (model has proportional odds assumption violated and there is a trend in OR).
| Total (n=349) |
Antibody titer level | |||||
|---|---|---|---|---|---|---|
| <1:10 (n=214) |
1:10 (n=56) |
1:20 (n=38) |
1:40 (n=28) |
≥1:80 (n=13) |
||
| Odds Ratio (per decade age) | ||||||
| Estimated from individual logistic regression models |
--- | --- | 1.68 | 1.39 | 1.33 | 1.25 |
| Estimated from Trend Odds model (TOM) |
--- | --- | 1.67 | 1.47 | 1.28 | 1.12 |
7. Discussion
When fitting data with statistical models, there is often a tradeoff between model simplicity and adequate fit. Although the Proportional Odds model has a somewhat simple interpretation, it may give inadequate fit when its proportionality assumption is violated. In this case, the TOM is a type of Constrained Cumulative Odds model that may be a good compromise when dealing with this tradeoff. Specifically, it may give improved model fit at the added complexity of only one additional parameter.
This paper examines the relationship between the trend odds model and underlying latent distributions, especially the logistic distribution. The Trend Odds model can do an adequate job in describing non-proportional odds even when the latent variable distribution is unknown. Although we did not explore this issue in this paper, it is likely that the choice of the ti could make a difference in the adequacy of model fit, depending on how different the ti are from the ci and what the underlying distribution is. If the ti happen to be chosen to be proportional to, or a linear transformation of, the ci, then the incorrect specification could be accommodated by the model through the β and γ parameters, in order to provide meaningful odds ratios. Similarly, if the ti are highly correlated with the ci, the model may still give reasonable estimates. In future work we hope to examine the robustness of the choice of the ti.
As a matter of convenience in practice, it may work well to assign t1=0 so that the estimate of β will correspond to the log odds ratio at the lowest cut-point. This is why we set ti=i−1 in our two data examples. It is possible, however, to use other parameterizations. For example, in some applications with clear neutral central level, it may make sense to set a middle ti value to zero, so that β would be a central cumulative odds ratio.
Note that the Trend Odds model, with β>0, does not guarantee that the probability of high values of Y increases with X at all cut-points. For the distribution shown in Figure 1B, for example, the odds ratio would be 0.08 at Y*=5, 1.0 at Y*=10, and 12.18 at Y*=15 (or respectively log odds of −2.5, 0 and 2.5). Hence, if the variances are different but the means are the same at two different values of X, then one is likely to see odds ratios that cross the value of 1 as cut-points go from smallest to largest.
Analyses based on the entire spectrum of the ordinal outcome are particularly important in studies that seek the etiological understanding of the disease spread and identification of high-risk groups. These analyses serve as justification and motivation for the development of the TOM. While the Proportional Odds model allows researchers to identify populations at a uniform higher risk of worse outcomes, the TOM allows the identification of populations whose wider variability results in a non-uniform but increasingly higher risk of worse outcomes. The interpretation of both the Proportional Odds model and the TOM is based on odds ratios, a statistic that is familiar to most health professionals. The identification of a trend has public-health implications. It is important not only to find populations with constantly higher odds of worse outcomes, but also to identify populations whose wider variability yields higher odds of worse outcomes for certain individuals. Trends in odds can also indicate an underlying higher variability that may be caused by lurking variables, generating further hypothesis to be tested. For example, in our influenza real data example we saw a decreasing risk of higher titers with increasing age. That may be associated to the fact that antibody titers tend to vary with time from infection. That may also indicate that younger populations have other risk factors that increase the variability by yielding higher odds of worse outcomes for certain individuals. Short term, this information is important in the implementation of preventive measures such as the use of protective equipment [18]. Long term, it can increase knowledge about the disease by hypothesis generation for future research.
For certain applications the use of dichotomization has scientific justification. In this case, optimal cut-point methods such as the ROC curve technique [19] may be an alternative. When there is no strong reason to dichotomize the data, fitting multiple binary Logistic models for different cut-points may be useful as an exploratory step [20], before fitting the TOM.
Although not the scope of this work, it is important to note that there are some alternative analyses to the model proposed. One can, for example, explore different link families to obtain parallelism or proportionality, or seek to estimate the underlying latent distribution parameters (i.e. predicting location and scale) [2, 21].
In this paper, we have focused on models with a single predictor variable. With multiple covariates, Peterson and Harrell [3] presented models to accommodate a mixture of covariates that do and do not adhere to the proportional odds assumption. Extending this idea, it is feasible to allow the effect of some of the covariates to adhere to the proportional odds assumption, some to adhere to the TOM assumptions, some to require non-trend constraints, and some to be completely unconstrained. Furthermore, it is unclear whether all covariates that are fit with the TOM assumption should have the same set of scalars or whether they should vary, and, if the latter, whether this can be data dependent. Further study on these issues is needed.
Supplementary Material
Acknowledgments
This work was supported by the NIOSH Occupational Epidemiology Training Program within the Heartland Center for Occupational Health and Safety (T42 OH008491; R. William Field, PI) and US Armed Forces Health Surveillance Center - Global Emerging Infections Surveillance Operations and National Institute of Allergy and Infectious Diseases (R01 AI068803; Gregory C Gray, PI)). The authors thank Dr. Joseph Lang and Dr. Peter McCullagh for their comments and insights. We also thank Dr. Gregory Gray and Dr. Kendall Myers for the use of the swine influenza data.
Footnotes
Supporting information may be found in the online version of this article.
References
- 1.Aitchison J, Silvey SD. The generalization of probit analysis to the case of multiple responses. Biometrika. 1957;44(1/2):131–140. [Google Scholar]
- 2.McCullagh P. Regression models for ordinal data. Journal of the Royal Statistical Society. Series B (Methodological) 1980;42(2):109–142. [Google Scholar]
- 3.Peterson B, Harrell FE., Jr Partial proportional odds models for ordinal response variables. Journal of the Royal Statistical Society. Series C (Applied Statistics) 1990;39(2):205–217. [Google Scholar]
- 4.O'Connell AA. Quantitative Applications in the Social Sciences. Thousand Oaks, California: SAGE Publications; 2006. Logistic Regression Models for Ordinal Response Variables. [Google Scholar]
- 5.Capuano AW, Dawson JD, Gray GC. Maximizing power in seroepidemiological studies through the use of the proportional odds model. Influenza and Other Respiratory Viruses. 2007;1(3):87–93. doi: 10.1111/j.1750-2659.2007.00014.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ananth CV, Kleinbaum DG. Regression models for ordinal responses: A review of methods and applications. International Journal of Epidemiology. 1997;26(6):1323–1333. doi: 10.1093/ije/26.6.1323. [DOI] [PubMed] [Google Scholar]
- 7.Greenland S. Alternative models for ordinal logistic regression. Statistics in Medicine. 1994;13(16):1665–1677. doi: 10.1002/sim.4780131607. [DOI] [PubMed] [Google Scholar]
- 8.Lall R, Campbell MJ, Walters SJ, Morgan K. A review of ordinal regression models applied on health-related quality of life assessments. Statistical Methods Medical Research. 2002;11(1):49–67. doi: 10.1191/0962280202sm271ra. [DOI] [PubMed] [Google Scholar]
- 9.Agresti A. Analysis of Ordinal Categorical Data. 2nd ed. Hoboken, New Jersey: Wiley; 2010. [Google Scholar]
- 10.Agresti A. Categorical Data Analysis. 2nd ed. New York: Wiley-Interscience; 2002. [Google Scholar]
- 11.Burton A, Altman DG, Royston P, Holder RL. The design of simulation studies in medical statistics. Statistics in Medicine. 2006;25(24):4279–4292. doi: 10.1002/sim.2673. [DOI] [PubMed] [Google Scholar]
- 12.Kawaoka Y, Krauss S, Webster RG. Avian-to-human transmission of the PB1 gene of influenza A viruses in the 1957 and 1968 pandemics. Journal of Virology. 1989;63(11):4603–4608. doi: 10.1128/jvi.63.11.4603-4608.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Reid AH, Fanning TG, Janczewski TA, Taubenberger JK. Characterization of the 1918 "spanish" influenza virus neuraminidase gene. Proceedings of the National Academy of Sciences of the United States of America. 2000;97(12):6785–6790. doi: 10.1073/pnas.100140097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Van-Tam J, Sellwood C. Introduction to Pandemic Influenza. Cambridge, MA: CABI: Wallingford, Oxfordshire; 2010. [Google Scholar]
- 15.Myers KP, Olsen CW, Setterquist SF, Capuano AW, Donham KJ, Thacker EL, Merchant JA, Gray GC. Are swine workers in the United States at increased risk of infection with zoonotic influenza virus? Clinical Infectious Diseases. 2006;42(1):14–20. doi: 10.1086/498977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Webster RG, Sharp GB, Claas EC. Interspecies transmission of influenza viruses. American Journal of Respiratory and Critical Care Medicine. 1995;152(4 Pt 2):S25–S30. doi: 10.1164/ajrccm/152.4_Pt_2.S25. [DOI] [PubMed] [Google Scholar]
- 17.Meijer A, Bosman A, van de Kamp EE, Wilbrink B, Du Ry van Beest Holle M, Koopmans M. Measurement of antibodies to avian influenza virus A(H7N7) in humans by hemagglutination inhibition test. Journal of Virological Methods. 2006;132(1–2):113–120. doi: 10.1016/j.jviromet.2005.10.001. [DOI] [PubMed] [Google Scholar]
- 18.Ramirez A, Capuano AW, Wellman DA, Lesher KA, Setterquist SF, Gray GC. Preventing zoonotic influenza virus infection. Emerging Infectious Diseases. 2006;12(6):996–1000. doi: 10.3201/eid1206.051576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pepe MS, Janes H, Longton G, Leisenring W, Newcomb P. Limitations of the odds ratio in gauging the performance of a diagnostic, prognostic, or screening marker. American Journal of Epidemiology. 2004;159(9):882–890. doi: 10.1093/aje/kwh101. [DOI] [PubMed] [Google Scholar]
- 20.Bender R, Grouven U. Using binary logistic regression models for ordinal data with nonproportional odds. Journal of Clinical Epidemiology. 1998;51(10):809–816. doi: 10.1016/s0895-4356(98)00066-3. [DOI] [PubMed] [Google Scholar]
- 21.Poon WY. A latent normal distribution model for analysing ordinal responses with applications in meta-analysis. Statistics in Medicine. 2004;23(14):2155–2172. doi: 10.1002/sim.1814. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.