dNTP-dependent Conformational Transitions in the Fingers Subdomain of Klentaq1 DNA Polymerase

Background: Conformational selection plays a key role in the polymerase cycle.

Results: Klentaq1 exists in conformational equilibrium between three states (open, closed, and “nucleotide-binding”) whose level of occupancy is determined by the bound substrate.

Conclusion: The “nucleotide-binding” state plays a pivotal role in the reaction pathway.

Significance: Direct evidence is provided for the role of a conformationally distinct “nucleotide-binding” state during dNTP incorporation.

Abstract

DNA polymerases are responsible for the accurate replication of DNA. Kinetic, single-molecule, and x-ray studies show that multiple conformational states are important for DNA polymerase fidelity. Using high precision FRET measurements, we show that Klentaq1 (the Klenow fragment of Thermus aquaticus DNA polymerase 1) is in equilibrium between three structurally distinct states. In the absence of nucleotide, the enzyme is mostly open, whereas in the presence of DNA and a correctly base-pairing dNTP, it re-equilibrates to a closed state. In the presence of a dNTP alone, with DNA and an incorrect dNTP, or in elevated MgCl₂ concentrations, an intermediate state termed the “nucleotide-binding” state predominates. Photon distribution and hidden Markov modeling revealed fast dynamic and slow conformational processes occurring between all three states in a complex energy landscape suggesting a mechanism in which dNTP delivery is mediated by the nucleotide-binding state. After nucleotide binding, correct dNTPs are transported to the closed state, whereas incorrect dNTPs are delivered to the open state.

Introduction

Accurate replication of DNA is essential for the viability of all organisms. This process is performed by DNA polymerases, which select a 2′-deoxyribonucleoside-5′ triphosphate (dNTP) based on its complementarity to a templating base and incorporate it onto the 3′ end of a primer DNA strand. There is ample experimental evidence that the selection of correct over incorrect dNTPs cannot be accounted for by Watson-Crick base pairing alone and must involve additional mechanisms (1–3).

Kinetic studies have provided the basic mechanism by which polymerases perform their function (Fig. 1A) (4–8). The initial event in the nucleotide incorporation cycle is the formation of the polymerase:primer/template (E:p/t)⁸ complex (step 1). This is followed by association of the dNTP substrate to form a loose E:p/t:dNTP complex (step 2). The E:p/t:dNTP complex then undergoes a rate-limiting transition to form an activated E′:p/t:dNTP complex (step 3). This conformational change is rate-limiting and is also the main discrimination step against misincorporation for most polymerases. Step 3 is followed by formation of a phosphodiester bond and release of pyrophosphate (steps 4 and 5).

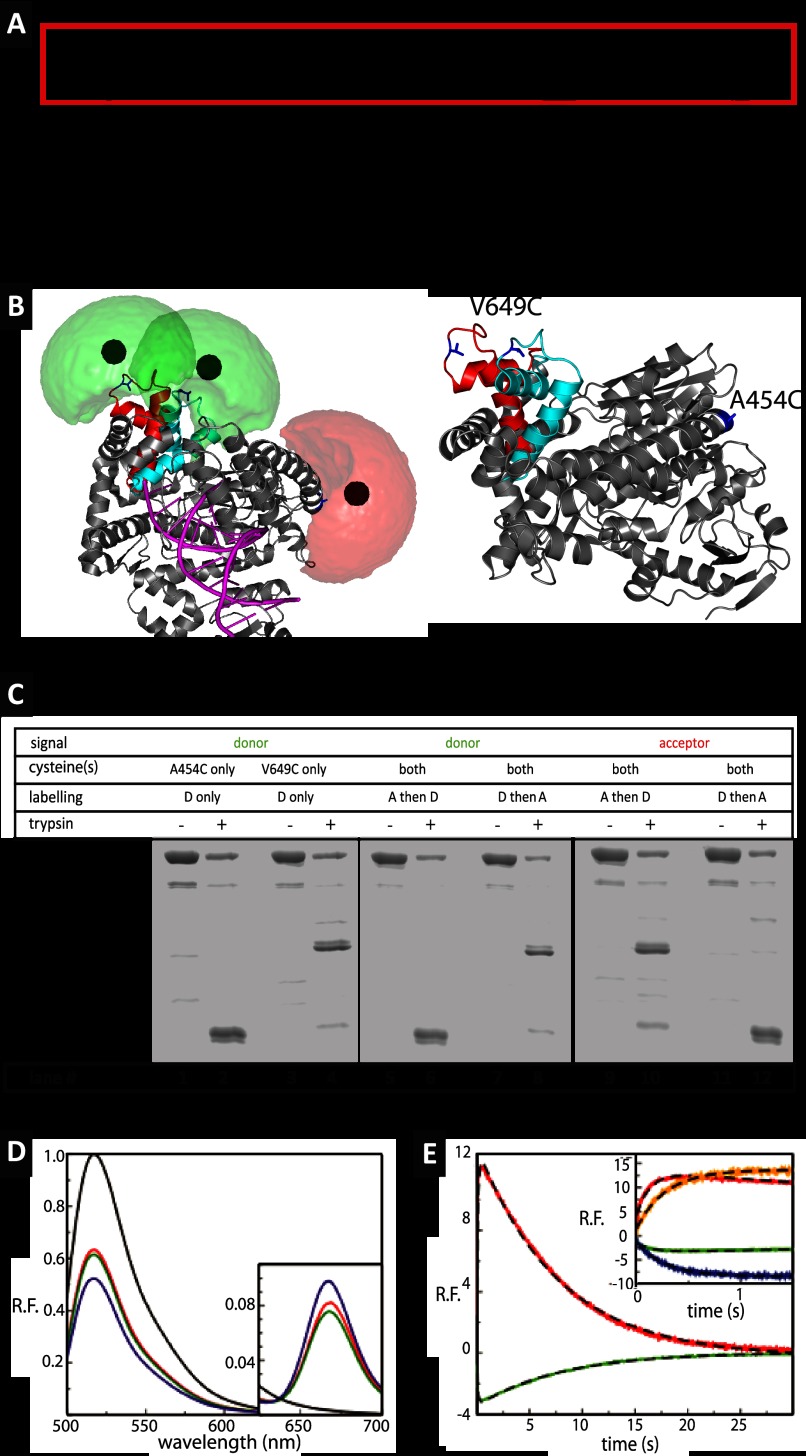
FIGURE 1.

Polymerase cycle and ensemble level results. A, general basic model for the DNA polymerase reaction cycle, see text for description, as described in a classical Michaelis-Menten framework. The red box indicates the parts in which conformational selection dictates the expansion of the scheme to include additional conformational states (“catalytic network” paradigm). B, structure of KT^DA. Crystal structure of Klentaq1 in complex with DNA shown in gray schematics fitted inside the surface (gray) with DNA shown in magenta. The change in position of the O-helix is shown in red for the E:p/t complex and in cyan for the closed complex (E:p/t:dNTP_(correct)). Fluorophore clouds are shown in green for Alexa 488 and red for Alexa 647 with the mean positions shown as solid spheres. For calculated distance changes, see main text and Table 1. An alternative view of the structure is also displayed for highlighting the positions of the amino acids in blue used for labeling. C, fluorescence scans of an SDS-PAGE before or after limited proteolysis of labeled KT with 2 μg/ml trypsin. Digestion of the labeled single mutants KT^A454C[A488] (lanes 1 and 2) and KT^V649C[A488] (lanes 3 and 4) reveals product bands diagnostic of the labeling position (V649C band and A454C band). When KT^V649C/A454C is labeled with acceptor first and then the donor, the vast majority of the donor appears in the A454C band (lanes 5 and 6), and the vast majority of the acceptor appears in the V649C band (lanes 9 and 10). Conversely, when KT^V649C/A454C is labeled with the donor first and then the acceptor, the donor predominantly localizes to the V649C band (lanes 7 and 8), whereas most of the acceptor is in the A454C band (lanes 11 and 12). It can thus be concluded that the V649C position is more accessible to fluorophores and is preferentially labeled by whichever fluorophore is added first. D, steady state fluorescence emission spectra of doubly labeled Klentaq1, KT^{V649C[A488]/A454C[A647]}, with various substrates, after excitation of the donor at 493 nm. The spectra for E, E:p′/t′:ddGTP, and E:p′/t′:ddGTP with the addition of the next correct dNTP (dCTP) are shown in red, green, and blue, respectively. The spectrum of donor only, KT^V649C[A488], is shown in black for direct comparison. Inset shows close-ups of the wavelength range in which acceptor emission is recorded. E, results of stopped flow data of dCTP incorporation by the pre-formed binary complexes of KT:primary/template at 20 °C. Relative fluorescence emission of the donor (green) and acceptor (red) after excitation of the donor after mixing pre-formed binary complexes KT:p′/t′ with dCTP leading to incorporation events. The corresponding fits are given with dashed black line. The incorporation data are described by two exponentials (dashed line), with the rates of fingers closure at 7.52 and 7.78 s⁻¹, and the rates of opening at 0.125 and 0.131 s⁻¹ for donor and acceptor, respectively (see inset for comparison). Inset, difference between incorporation and binding. The results presented in the main graph are shown again (green and red curves) for a direct comparison with the results obtained for dTTP binding to the terminated p/t DNA. In this case, a single exponential describes the kinetics with the donor (blue line) and acceptor rates (orange line) of 3.55 and 3.51 s⁻¹, respectively.

X-ray crystallography studies of DNA polymerases, as exemplified by Klentaq1 (an active truncated form of Thermus aquaticus DNA polymerase 1 (9), referred to hereafter as KT, have solved many intermediates in the reaction pathway (10–13). The basic architecture of a DNA polymerase has been likened to a right hand consisting of a fingers, palm, and thumb subdomain (14). Binding of the p/t DNA leads to a conformational change in the thumb subdomain, and binding of the correct dNTP to the E:p/t complex leads to a large structural change in the fingers subdomain, from an open form to a catalytically active closed form. For many years, it was believed that the structural change in the fingers subdomain may correspond to the kinetically defined rate-limiting conformational change at step 3 (E:p/t:dNTP to E′:p/t dNTP in Fig. 1A). However, several studies have now established that this is not the case; the large conformational transition affecting the fingers subdomain is fast and not rate-limiting (15–20), and the kinetically derived conformational change occurs in the closed state of the enzyme. Another conformational transition in the E:p/t complex, likely to involve the templating base, was also characterized, based on the nucleotide concentration dependence of the open to closed transition (9). Thus, the minimal reaction scheme in Fig. 1A has to be extended to reflect the existence of additional reaction intermediates with still unknown structural and functional properties.

Although rapid progress has been made to characterize the nature of the open-to-closed conformational transition affecting the fingers subdomain, including single-molecule (sm) studies on the Klenow fragment, which show that the enzyme exists in a structural equilibrium between the open and closed conformation (21, 22), many questions remain unanswered as follows: (i) Are additional states needed to facilitate the transition from open to closed? (ii) How do incorrect (non-base pairing) dNTPs affect the conformational equilibrium of the enzyme? (iii) How does the pathway from open to closed change in response to different substrates/cofactors (dNTPs, p/t, MgCl₂)? These issues cannot be addressed using an ensemble of unsynchronized polymerase molecules, and thus experiments at the sm level with high precision Förster resonance energy transfer (smFRET) measurements are required.

Here, we describe high precision FRET measurements on a newly designed, site-specifically labeled KT system monitoring fingers subdomain motions in KT, and we show that it can directly resolve various conformational species co-existing in the apo, E:p/t, and E:p/t:dNTP (correct and incorrect) states. The results show that the enzyme alone adopts three relevant conformations in solution (open (O), nucleotide-binding (NB), and closed (C)) and that binding of the p/t DNA and/or nucleotides affects the relative populations within the observed conformational equilibria. Using geometric modeling of the fluorophore positions, we could resolve the O and C conformations to within 2 Å of the calculated distance between the two fluorophores. The NB state corresponds to a conformation between O and C and was identified to be analogous to the state characterized as “ajar” by recent crystallographic data for the large fragment of DNA polymerase I from Bacillus stearothermophilus (Bacillus fragment (BF)) (23). Analysis of the fluorescence using time window analysis suggests the existence of fast (∼1 ms time range) processes in the apo-form, although direct observation of KT undergoing state transitions indicates the additional existence of slower transitions (10–100-ms time range). In the presence of an incorrect dNTP, we observe a slow process occurring between the NB and the O state, although in the presence of a correct dNTP, transitions between the NB and the C states are identified, suggesting a pivotal role of the NB state in dNTP delivery.

EXPERIMENTAL PROCEDURES

Molecules

The primer and template oligonucleotides used were ordered from IBA (Göttingen, Germany), and are named p for the primer terminated with ddC (used to study nucleotide binding), p′ for the nonterminated primer (used for incorporation measurements), and t and t′ for the corresponding templates. The unpaired 5′-overhangs of the templates when hybridized with primer are marked in boldface as follows: p, 5′CAGCGCCACTGGGTCAGTCCGAGCCGTCGCAGCCTACCGTddC3′; p′, 5′CAGCGCCACTGGGTCAGTCCGAGCCGTCGCAGCCTACCGT3′; t, 5′TGGTTAATCTCTCTAGACGGTAGGCTGCGACGGCTCGGACTGACCCAGTGGCGCT G3′, and t′, TGGTTAATCTCTTAGCACGGTAGGCTGCGACGGCTCGGACTGACCCAGTGGCGCTG3′. The primer/template complexes were formed using a 10% molecular excess of template over primer in a buffer consisting of 50 mm Tris-HCl (pH 7.0) and 20 mm NaCl. The mixtures were heated to 95 °C for 5 min and allowed to cool slowly to room temperature over several hours.

Proteins were mutated, expressed, and purified as described previously (13). Cysteines were introduced at positions 649 and 454 (Fig. 1B) and labeling of KT^V649C, KT^A454C and KT^V649C/A454C was performed as described previously (17, 24). For further details see under “Design of a High Precision FRET System for Single-Molecule Studies” under the “Results.” Protein concentrations were determined spectrophotometrically using an extinction coefficient at 280 nm of 69,622 m⁻¹ cm⁻¹. Double labeling of the KT^V649C/A454C with Alexa 488 C₅-maleimide (donor; D) and Alexa 647 C₂-maleimide (acceptor; A) and single labeling of KT^V649C and KT^A454C with Alexa 488 C₅-maleimide were performed as described previously (24). The degree of labeling was determined as per the manufacturer's instructions and was typically between 90 and 105% for each fluorophore. Protein concentration after labeling was typically in the range of 20–60 μm.

Basic FRET Equations

For a given dye pair, the efficiency, E_FRET, of FRET depends on the interdye distance R_DA and the Förster radius, R₀ (25, 26) as shown in Equation 1,

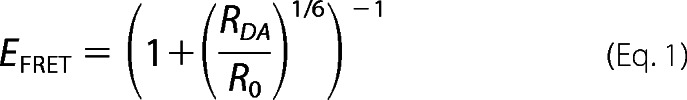For the Alexa 488-Alexa 647 pair used in this study, R₀ was determined to be 51.4 Å. The fluorescence quantum yields of D in the absence of transfer (Φ_FD(0)) and of A (Φ_FA) were determined by independent measurements to be 0.81 and 0.32, respectively.

The efficiency of energy transfer can be calculated from a number of different parameters, including the fluorescence intensities of the donor or acceptor (F_D or F_A), donor lifetime (τ_D(A)) in the presence of acceptor, and from the anisotropy (r) of either the donor or the acceptor fluorophore (25–27). We determined the efficiency of the energy transfer using the fluorescence intensity ratio between the donor and acceptor, F_D/F_A (27, 28). For analysis of these data, the signal intensities (S_G and S_R) were corrected for background counts (typically 0.9 kHz for the green (donor) channels, B_G, and 0.4 kHz for the red (acceptor) channels, B_R), spectral cross-talk, α (0.017), and the ratio of the detection efficiencies, g, between the green and red channels determined experimentally on a daily basis (g_G/g_R = 0.29–0.56) (see Equation 2).

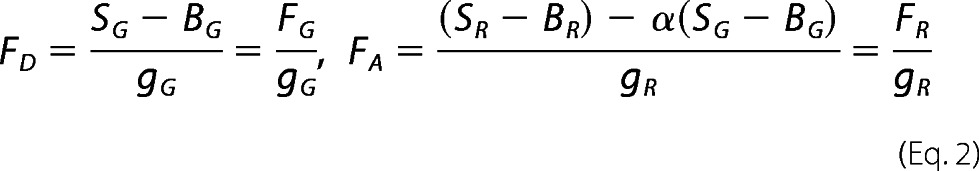The FRET efficiency is related to the experimental data as shown in Equation 3,

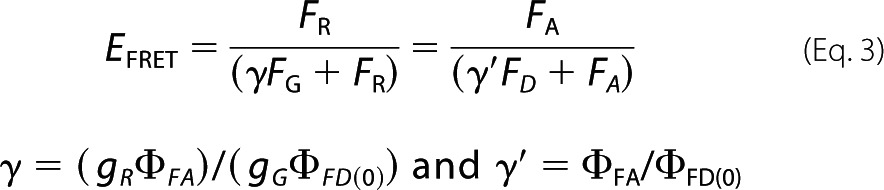The fluorescence lifetime is determined for each burst in two steps as follows: (i) by generating a histogram of photon arrival times, and (ii) by fitting the histograms to a single exponential using a maximum likelihood estimator and iterative convolutions to account for the scatter contribution (29). The lifetime of the donor molecule (τ_D(0)) coupled to either the V649C position or the A454C position was determined to be 3.9 ns. The efficiency of energy transfer is related to fluorescence lifetimes through (Equation 4),

where τ_D(A) and τ_D(0) are the lifetimes of the donor in the presence and in absence of the acceptor, respectively. Combining the previous equations (Equations 3 and 4) leads to the expression for the “static FRET line” illustrated in Fig. 2 and as shown in Equation 5,

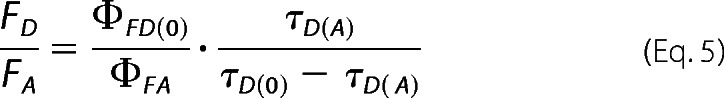The rotational mobility of a fluorophore can be described by the rotational correlation time, ρ, which can be determined indirectly from the anisotropy of the dye that is related to the fluorescence lifetime via the Perrin equation. For the case of D, the anisotropy is denoted as r_D, and its rotational correlation time as ρ_D, and the Perrin equation can be written as shown in Equation 6,

where r₀ is the fundamental anisotropy of emission of D.

FIGURE 2.

Frequency histograms of single-molecule bursts for KT^DA under various conditions. Frequency is shown as an increasing gray scale from white to black normalized to the same number of events. In the upper panel, donor lifetime, τ_D(A), is plotted versus F_D/F_A (see “Experimental Procedures”). Direct excitation of the acceptor is negligible. The black line shown is the static FRET line described under “Experimental Procedures.” In the lower panel, donor lifetime, τ_D(A), is plotted versus donor anisotropy, r_D, together with three overlaid curves computed from the Perrin equation, using a value for fundamental anisotropy of r₀ = 0.37 and a mean rotational correlation time, ρ_D, of either 0.7, 1.5, or 4 ns. The mean F_D/F_A value of the different species are indicated with a blue line (open, O), a green line (nucleotide binding, NB), and a red line (closed, C).

TCSPC Measurements

Ensemble time-correlated single photon counting (TCSPC) measurements were performed using an IBH-5000U (IBH, Scotland, UK) system for the determination of the lifetime of the acceptor (Alexa 647) attached to KT. The excitation source was a 635-nm diode laser (LDH-8-1 126, Picoquant, Berlin, Germany) operating at 10 MHz for direct acceptor excitation. The emission wavelength was set to 665 nm. The corresponding monochromator slits were set to 2 nm (excitation path) and 16 nm (emission path) resolution. An additional cutoff filter was used to reduce the contribution of the scattered light (>640 nm for acceptor emission). All measurements were performed at room temperature. Fluorescence intensity decay curves were fitted using the iterative re-convolution approach (30). The maximum number of counts was typically 25,000. The fits approximately range from the maximum of the instrument response functions to the first time channel with less than 100 detected photons. The fluorescence decays F(t) were modeled by single or double exponential decays. The recorded decay was determined to be bi-exponential (τ₁ = 1.17 ns and τ₂ = 1.76 ns with corresponding fractions 62 and 38%).

Single-Molecule Spectroscopy

Standard single-molecule multiparameter fluorescence detection experiments (smMFD) were performed in 20 mm Tris-HCl (pH 7.5), 50 mm NaCl, 2 mm MgCl₂ using KT^DA at concentrations below 50 pm, and terminated p/t DNA and dNTP concentrations of 1 and 500 μm, respectively, unless otherwise stated. Experiments were essentially performed as described previously (24, 28). Briefly, the experiments were carried out with a confocal epi-illuminated setup. The fluorescent donor molecules (Alexa 488) are excited by a linearly polarized, active mode-locked argon-ion laser (496.5 nm, 73.5 MHz, 150 ps). The laser is focused into the dilute solution (<50 pm) of labeled KT molecules by a water immersion objective (Olympus UPLSAPO 60×W, NA 1.2).

Each molecule generates a brief burst of fluorescence photons as it traverses the detection volume. This photon train is divided initially into its parallel and perpendicular components via a polarizing beam splitter and then into wavelength ranges below and above 595 nm (Q595LPXR, AHF). Additionally, red (HQ 720/150, AHF) and green (HQ 533/46, AHF) filters in front of the detectors ensure that only fluorescence photons coming from the acceptor and donor molecules are registered. An estimate of the focal geometry is acquired by determining the diffusion correlation time of 200 ± 13 μs for rhodamine 110 and knowing its diffusion coefficient of 0.34 ± 0.03 μm²/ms. Moreover, correction factors l₁ = 0.0308 and l₂ = 0.0368 are used to account for the mixing of polarization by the microscope objective, and a factor G = 0.964 is applied to compensate for the slightly different detection efficiency of the two polarization components. Detection is performed using four avalanche photodiodes (SPCM-AQR-14, Laser Components, Germany, for acceptor emission and PDM Series, MPD, Italy, for the donor emission). The signals from all detectors are passed through a passive delay unit and two routers to two synchronized time-correlated single photon counting boards (SPC-132, Becker and Hickl GmbH, Germany) in a PC. Fluorescence bursts are distinguished from the background of 1–2 kHz by applying certain threshold intensity criteria (29). For single-molecule measurements, the protein was diluted in three steps using the measurement buffer (20 mm Tris-HCl (pH 7.5), 50 mm NaCl, 2 mm MgCl₂) to 625 nm then 6.25 nm, followed by dilution into the 50-μl sample droplet to between 25 and 50 pm. To suppress protein adsorption, cover slides were coated with 100 μg/ml κ-casein as described previously (28). For measurements in the presence of DNA or dNTPs, the protein was incubated for 5 min under single-molecule conditions before the addition of substrate to a concentration of 1 or 500 μm, respectively. For the formation of the ternary complex, the E:p/t complex was incubated for 5 min before the addition of dNTP to a concentration of 500 μm. Measurements were typically performed for 1 h at 25 °C.

Photon Distribution Analysis (PDA)

Histograms of the FRET indicator F_D/F_A were calculated from experimental data sets. Fits to experimental histograms were generated by applying Equations 2 and 3 to theoretical distributions P(S_G, S_R), which were calculated using the reported PDA theory (31, 32). In terms of accuracy of the analysis, the choice of other FRET indicators for one-dimensional histograms (e.g. S_G/S_R ratio, FRET efficiency, or apparent donor-acceptor distance) has only a negligible effect (32). The experimental histograms were fitted using software developed in-house. The minimal model for fitting PDA histograms of all measurements is based on statistical arguments: residuals, reduced χ-squared, χ_r², F-test, which demonstrates the statistical significance in the improvement of the fit for a given number of species (see Fig. 4, supplemental Tables 1 and 2, and supplemental Fig. 1). Four FRET species and a signal pattern characteristic for the donor-only sample were needed to describe the data satisfactorily. The addition of a fifth FRET species was not justified statistically for any of the measurements. The pattern accounting for the donor-only population and contaminants (D-o + C) was usually populated to no more than 2%. Only for the cases of buffers containing high Mg²⁺ did the percentage increase slightly (always less than 10%) due to the presence of contaminants in Mg²⁺ salt preparation.

FIGURE 4.

Justification of the number of states. Justification of the number of states used for PDA fitting of experimentally obtained FRET efficiency distributions for the case of free KT^DA is given. The same data set is fitted including shot-noise limited FRET ratios (accounting for donor-only and contaminants) and progressively one, two, three, four relevant FRET states. The same color coding as in Fig. 3 is applied. A–D, overall fit is shown in black over the data (gray bar histogram) obtained for KT^DA under indicated experimental conditions along with the corresponding residuals shown above. FRET species of interest are represented in dark yellow, red, green, and blue for MC, C, NB, and O, respectively. The residuals and reduced χ² values, χ_r², are shown in each case for direct visual inspection. F-test was performed for justifying the addition of another FRET state as shown for all cases in supplemental Table 1 and supplemental Fig. 1. The addition of a fifth state was not justified in any of the measurements. E–H, obtained mean distances and the corresponding relevant percentile fraction of each state are indicated by bar diagrams. Same color coding as before was applied. The percentages of donor only and contaminant (D-o+C) are shown in black. For all measurements, the mean interdye distances corresponding to each FRET state agree very well (see Table 1 and supplemental Tables 2–4).

The remaining species account for the FRET states of interest and were broadened beyond the shot-noise limit to account for the photophysical properties of the acceptor as described by Kalinin et al. (33). In an ideal system, the width of the fluorescence distributions obtained should be determined solely by shot-noise considerations and real distance distributions. However, previous studies (33) have shown that the lifetime properties of the acceptor result in an additional broadening of the observed FRET distributions, so that a single mean donor-acceptor distance 〈R_DA〉 can be well approximated by an apparent Gaussian distance distribution with mean distance 〈R̃〉. The half-width of this acceptor-induced broadening can be calculated from the acceptor properties (see below) and is linearly proportional to 〈R̃〉. Thus, the half-width can be described by a single fixed proportionality factor, P_A, given as a constant percentage of the mean distance. TCSPC experiments (see “Experimental Procedures”) on Alexa 647 coupled to KT^A454C show that Alexa 647 has two fluorescence lifetimes of 1.17 and 1.76 ns with amplitudes of 62 and 38%, respectively. These values are similar to those described previously (33). Based on the acceptor properties under different conditions, a proportionality factor P_A between 0.048 and 0.070 is to be expected. This prediction agrees nicely with our experiments where the minimum P_A of 0.05 was required to reproduce the experimentally determined widths of FRET distributions. This factor was used to describe each FRET species by an acceptor-induced apparent Gaussian distance distribution with a mean distance and an half-width (P_A × 〈R̃〉). For the fast dynamic analysis by PDA, the minimum photon number threshold (S_min) was selected such that the mean FRET efficiency calculated from the best PDA fit was independent of the time window length. This allowed us to separate the apparent shift in species fractions due to dynamics on the millisecond time scale (which does not change the mean E), from undesired brightness effects.

Multimolecular Events and Slow Dynamics Burst Enrichment

We developed here a procedure for preferentially selecting bursts in which one or two dynamic transitions between states occur, although the molecule is diffusing through the observation volume (see “Results”). This procedure, termed slow dynamics (SD) burst enrichment, was employed because only a small proportion of the bursts were expected to contain dynamic events. However, one should make sure that multimolecular events are not misinterpreted as dynamic bursts. To estimate the probability of such “fused” bursts, we adapted Equation 4 from Ref. 34, which in our case reads as indicated in Equation 7,

where r_MM is the frequency of multimolecular events (s⁻¹); r₁ is the frequency of bursts due to state 1 (s⁻¹); r₂ is the frequency of bursts due to state 2 (s⁻¹), and 〈t_bd〉 is the mean burst duration (seconds). The overall burst rate is then r_T = r₁ + r₂. Experimentally, r_T and 〈t_bd〉 were determined to be 1 s⁻¹ and 8 ms for free enzyme. For r₁ = r₂ = 0.5 s⁻¹, the worst case scenario in terms of multimolecular events, the frequency of multimolecular event can be calculated as r_MM = 0.5 s⁻¹ × 0.5 s⁻¹ × 0.008 s = 0.002 s⁻¹. The probability of multimolecular events is therefore as shown in Equation 8,

To conclude, the likelihood of multimolecular events is significantly lower than the fraction of bursts with slow dynamics (see under “Results”). The employment of the slow dynamics burst enrichment procedure was dictated by the fact that the expected fraction of dynamic bursts is low. To estimate the probability of observing no transitions between states i = 1…n within a burst duration t_bd, we use Equation 9,

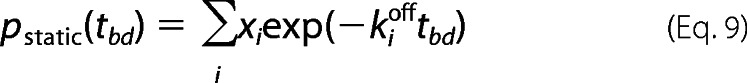where x_i is the equilibrium fraction of state i and k_i^off is the sum of rate constants of all transitions starting from state i. Considering the experimental distribution of burst durations p(t_bd), the overall fraction of dynamic bursts is given by Equation 10,

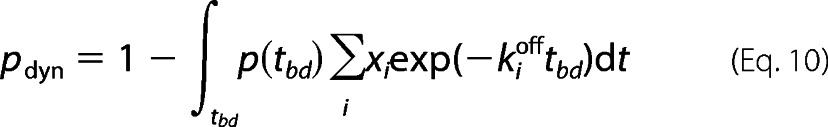As an example, a calculation of p_dyn was performed for a two-state dynamic system with rates similar to those expected for KT, assuming k₁₂ = 10 s⁻¹ and k₂₁ = 30 s⁻¹, yielding p_dyn = 0.15. Thus, in this typical case, transitions between states would be observed in only 15% of all detected bursts.

Dynamics and Slow Dynamics (SD) Burst Enrichment, Simulations

SD burst enrichment was first extensively tested on simulated data generated by an in-house developed software for Brownian dynamics simulations (35) using parameters identical to the experiment (see also corresponding section under “Results” for the developed procedure). Taking a minimum value θ for the mean photon time difference (i.e. |T_G − T_R| >θ) Fig. 6B, clearly shows that SD burst enrichment reduces the fraction of static bursts considered for further analysis. The SD burst enrichment could be assessed by examining the fraction of percentage of bursts, f_θ, with a time difference |T_G − T_R| >θ. Because of random fluctuations of the signal, bursts during which no dynamics occurs could also be selected to a small extent by SD burst enrichment. It is therefore useful to define a more quantitative measure for the presence of dynamics by introducing the normalized fraction of selected bursts, f_{N, θ}, as given by Equation 11,

A value of f_{N, θ} close to 1 for a given measurement would mean that in that particular measurement either no transition occurs or that all transitions taking place are fast compared with the residence time of diffusing molecules in the observation volume (see below under “Results” (Fig. 6)).

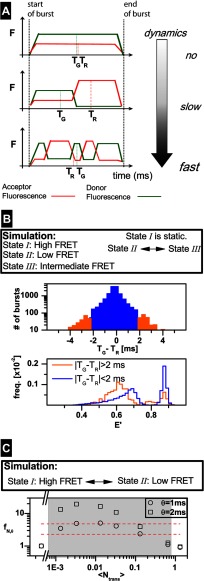
FIGURE 6.

Slow dynamics burst enrichment procedure for KT^DA. A, time scale of dynamics is defined with respect to the mean burst duration, 〈t_bd〉. The top panel shows a burst in which no transition is occurring. For this case |T_G − T_R| is close to 0 ms. The middle panel shows a burst in which only one transition occurs. During detection time, the donor fluorescence (green) decreases and the acceptor fluorescence (red) increases. The average detection time for the photons constituting the green, T_G, and red, T_R, trace within the burst are shifted toward opposite directions. The lower panel shows a burst, in which many transitions are occurring. Also for this case |T_G − T_R| is close to 0 ms. B, simulated data of freely diffusing molecules (state 1, high FRET; state 2,: low FRET; state 3, intermediate FRET). State 1 is static, whereas transitions occur between state 2 and state 3. Upper panel, selection of bursts based on |T_G − T_R| criterion. Lower panel, normalized histograms of FRET efficiencies as calculated for each burst. For the case of bursts with |T_G −T_R| >2 ms (orange), the static part (High FRET state) is suppressed in comparison with the histogram of all bursts with |T_G − T_R| <2 ms. C, series of simulated data of freely diffusing molecules exhibiting dynamics between 2 states (state I, high FRET; state II, low FRET). For each case, the corresponding f_{N, θ} is given (for definition see Equation 11), for θ = 1, 2 ms, as a function of the mean number of transitions per burst over the overall detected bursts 〈N_trans〉. The total rate, k_total of the transitions was varied, from 0 to 40 s⁻¹, whereas the equilibrium constant remained unchanged. The mean burst duration, 〈t_bd〉, was 32.8 ms. The shaded region illustrates the range for which SD burst enrichment is useful (see “Experimental Procedures” for details). The red dashed lines indicate the region in which f_{N, θ}, obtained from measurements on KT, was found.

For transitions between given FRET states, the useful time range of dynamics for SD burst enrichment is determined by an appropriate ratio between the relaxation rate constant of dynamics k_r (for two-state system, k_r = k₁₂ + k₂₁) and the mean time of burst duration 〈t_bd〉, from which the mean number of transitions per burst (for all detected bursts) 〈N_trans〉 = k_r 〈t_bd〉 can be calculated. Simulations of transitions from states with FRET efficiencies similar to those obtained for O, NB, and C showed that SD burst enrichment is useful (f_N,θ >1 for 〈N_trans〉 smaller than 0.66). Considering free KT as an example (with expected k_r = 40 s⁻¹, 〈t_bd〉 = 8 ms), we obtain 〈N_trans〉 = 0.32, indicating that SD burst enrichment will be helpful. This expectation was confirmed by the experimentally obtained f_N,θ values, which are found in the range 2.3–4.8 (see dashed red lines in Fig. 6C).

An additional simulation was performed to show directly that the static bursts are removed by SD burst enrichment. In this additional simulation, we considered a scenario similar to the experimental conditions for KT with three FRET states as follows: state I, high FRET; state II, low FRET, and state III, intermediate FRET. State I is static, whereas transitions occur only between state II and state III at a very slow rate (〈N_trans〉 = 0.005).

Excluding Artifacts by Photobleaching

In fluorescence experiments with a confocal setup, high laser power densities are usually applied, and acceptor photobleaching can become relevant. As shown before in Ref. 36, the difference between burst-averaged macroscopic photon arrival times (T_G-T_R) also allows for the identification of acceptor photobleaching events. Upon acceptor photobleaching, the acceptor signal disappears and T_G increases. For such experiments, the overall (T_G-T_R) distribution becomes asymmetric, and bursts with photobleaching events accumulate only at positive values of (T_G-T_R). Under our measurement conditions the (T_G-T_R) distributions were always symmetric for all FRET levels (typical MFD plots are shown in supplemental Fig. 3). Moreover, our analysis of the burst traces showed jumps between distinct FRET levels and not jumps to donor-only intensity levels (see below). Thus, photobleaching can safely be excluded from these measurements.

Time Trace Analysis

Fluorescence bursts obtained from smMFD experiments were analyzed using a 1-ms time window. Time traces were exported using software developed in-house. The green and red signal intensities were used to create an “apparent” efficiency trace, corrected for detection efficiency, cross-talk, and quantum yields of the donor and acceptor. Only bursts, with FRET efficiency values between 0.05 and 0.80 over the whole length of the trace, were analyzed. Data were fitted to a four-state model using HaMMy software (37, 38).

RESULTS

Design of a High Precision FRET System for Single-Molecule Studies

We designed a new KT system to measure intramolecular FRET during the fingers subdomain closure. KT containing cysteines introduced at positions 649 and 454 (Fig. 1B) was labeled by first under-labeling the protein with the donor (D) fluorophore, Alexa 488, so that a mixture of unlabeled, singly, and doubly labeled protein was produced. The singly labeled protein was then purified from the two other species using anion exchange chromatography and was labeled with a second fluorophore, the acceptor (A), Alexa 647. This process results in a high degree of doubly labeled DA protein while excluding DD- and AA-labeled proteins. Labeling heterogeneities can be a major problem in single-molecule FRET experiments due to slightly different properties of the DA- or AD-labeled protein. To determine the relative populations of proteins labeled KT^{V649C[A488]/A454C[A647]} or KT^{V649C[A647]/A454C[A488]}, a trypsin digest was performed on the labeled protein (Fig. 1C). This results in a low molecular weight fragment containing the V649C position and a higher molecular weight fragment containing the A454C position. SDS-PAGE analysis reveals that labeling of the protein is asymmetric, with over 95% of whichever label is used first localizing to the V649C position (Fig. 1C). KT^{V649C[A488]/A454C[A647]} (in which the protein is first labeled with Alexa 488), referred to as KT^DA, was used for all subsequent experiments.

KT^DA maintains equivalent activity to the two FRET systems described previously, as assessed by single nucleotide incorporation experiments (17, 24), and it undergoes fluorescence changes similar to them in response to finger closure (Fig. 1, D and E).

The use of KT^DA has the unique advantage for single-molecule fluorescence spectroscopy in that we are not limited by the amount of p/t, due to the fact that the DNA is now unlabeled. The structural states of the enzyme can therefore be measured at the sm level by using low concentrations of the doubly labeled protein (<50 pm) in combination with elevated p/t DNA concentrations (>1 μm) to ensure complex formation.

To derive high precision distances between fluorophores from available crystal structures, we carried out “accessible volume” (AV) simulations on the structures of the E, E:p/t (corresponding to the open conformation), and E:p/t:dNTP (corresponding to the closed conformation) states (see Fig. 1B). The AV modeling approach has been described previously in detail (39–41). In contrast to simple C-β to C-β distances, the simulated FRET-averaged interdye distances 〈R_DA〉_E can be directly compared with the experimental distances obtained from fluorescence intensity measurements. Considering the dyes coupled to V649C and A454C, simulation-derived 〈R_DA〉_E are 62.4, 64.0, and 49.9 Å for the E, E:p/t, and the E:p/t:dNTP structures, respectively. The dye pair used for this study has a Förster radius of R₀ = 51.4 Å as calculated experimentally and is therefore ideal for measuring such distances, enabling the monitoring of the open to closed conformational transition in KT ^DA with high sensitivity (42).

Ensemble Studies of KT

The functionality of the labeled KT was verified in ensemble measurements as described previously (17, 24). Fig. 1D shows steady state fluorescence spectra of the doubly labeled protein under various conditions. The fluorescence spectrum of donor only labeled KT, KT^D, is shown as a black line in Fig. 1D (the spectrum is identical for KT^A454C[A488] or KT ^{V649C [A488]}). The doubly labeled protein, KT^DA (Fig. 1D, red line), shows a donor quenching of ∼30% due to FRET and a corresponding peak for the Alexa 647 fluorophore. To study the FRET change generated by the fingers subdomain closure, 900 nm of p′/t′ primer/template DNA was added to 1 μm KT^DA and terminated by incorporation of ddGTP (Fig. 1D, green line). ddGTP lacks the 3′OH group required for incorporation of the next nucleotide, allowing subsequent dNTP binding without catalysis. Addition of the next correct dNTP (Fig. 1D, blue line) leads to an increase in FRET, although addition of an incorrect dNTP results in no change in the steady state FRET signal. This shows that the system is able to monitor fingers subdomain closure specifically induced by binding of the “correct” dNTP.

The doubly labeled protein was also investigated by pre-steady state measurements (Fig. 1E) using stopped flow. Complexes of KT^DA:p/t or KT^DA:p′/t were mixed with dTTP or dCTP, respectively, to study dNTP binding or incorporation, respectively (see “Experimental Procedures”). The p/t DNA is terminated at the 3′ terminus, whereas the p′/t DNA is nonterminated. For dNTP incorporation (using the p′ primer), anti-correlated changes in the donor (green) and acceptor (red) signals are observed; a fast increase in FRET due to the fingers subdomain closure, followed by a slow decrease in FRET due to the fingers subdomain reopening after incorporation, has occurred. For dNTP binding using the p primer (see the inset in Fig. 1E, blue and orange for donor and acceptor, respectively), an increase in FRET is seen due to the fingers subdomain closure. However, because incorporation cannot occur, there is no subsequent decrease in FRET from fingers subdomain reopening.

smMFD of Freely Diffusing Molecules of KT

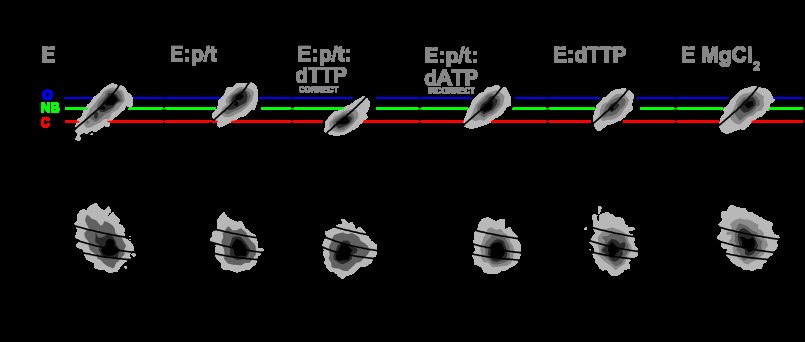
We investigated the conformation of the fingers subdomain of KT using single-molecule multiparameter fluorescence detection, smMFD. Very dilute solutions of the enzyme (<50 pm) were measured in the absence of any substrate (E) or in the presence of either 1 μm p/t DNA (E:p/t; note that in all the single-molecule experiments the primer is terminated as described under “Experimental Procedures”), 500 μm dNTP (E:dNTP state), 1 μm p/t DNA, and 500 μm dTTP (the correct nucleotide; E:p/t:dTTP_(correct)), 1 μm terminated p/t DNA and 500 μm dATP (an incorrect nucleotide; E:p/t:dATP_(incorrect)), or 50 mm MgCl₂ (E:MgCl₂). Labeled molecules diffusing through a confocal detection volume generate brief bursts of fluorescence over the diffusion time (ranging from 3 to 15-ms bursts duration), which can then be used to determine fluorescence intensities (F), lifetimes (τ), and anisotropies (r) of both D and A probes. For high precision FRET studies the following fluorescence parameters are most informative: F_D and F_A, which denote the corrected donor and acceptor fluorescence signals, the lifetime of D in the presence of A, τ_D(A), and r_D that is the anisotropy of the donor emission. Additional fluorescence parameters were analyzed as well for control purposes (data not shown).

Fig. 2 shows two-dimensional histograms of F_D/F_A and r_D plotted against the donor lifetime in the presence of the acceptor, τ_D(A), obtained from single-molecule experiments on the apo-form and various liganded states of KT^DA. Data obtained from smMFD burst-wise analysis is instrumental in visually determining the average properties and their distributions within a system. Such data are illustrated by two-dimensional histograms of key parameters (MFD plots: see Fig. 2). In these two-dimensional MFD plots, each apparent FRET population is seen as a separate “island” or as a “peninsula” (i.e. tail). The shape and location of the FRET “island(s)” act as indicators of distance, heterogeneity, and potential fluorescence artifacts (27, 33).

Before discussing the significance of the results it is worth commenting on the values for the individual fluorescence parameters to be expected in an MFD analysis. In general, in the absence of the acceptor, the lifetime of Alexa 488 (τ_D(0)) ranges between 3.9 and 4.1 ns (in our case 3.9 ns), depending on the environment to which the fluorophore is subjected. The ratio F_D/F_A is high as there is almost no acceptor fluorescence. A correlated decrease in both τ_D(A) and F_D/F_A indicates an increase in FRET efficiency and hence a decrease of the distance between the donor and acceptor fluorophores. To assess whether both τ_D(A) and F_D/F_A decrease in a correlated manner, the theoretical relationship between τ_D(A) and F_D/F_A (black sigmoidal line called “static FRET line” and described under “Experimental Procedures”) is also plotted. Major deviations from this line could be indicative of changes in τ_D(A) and/or F_D/F_A, caused by donor/acceptor quenching of other origins than changes in FRET efficiency (27). For all measurements, the FRET populations recovered are centered on or close to the static FRET line, indicating no major artifacts caused by donor or acceptor quenching.

To assess any potential uncertainties on calculated distances caused by changes in fluorophore mobility and orientation, the r_D of the fluorophore (Fig. 2, lower panel) is also shown. Restricted mobility and dye stacking in specific orientations could generate an uncertainty factor in the Förster radius via the orientation factor κ² (43). In all cases, the anisotropy of the donor fluorophore is low indicating a high mobility with mean rotational correlation times ranging from 0.7 to 1.5 ns (derived from the three lines obtained from calculations carried out using the Perrin equation and three different constant rotational correlation times (0.7, 1.5, or 4 ns)). The mobility of the dyes remained nearly constant for all various measurements and is in all cases high enough to be of little or no consequence to the distance values calculated from the distinct FRET levels.

When comparing all measurements shown in Fig. 2, it can be seen that the major peak for KT^DA (Fig. 2A) and KT^DA:p/t (Fig. 2B) is located at an F_D/F_A value of 7 (see blue line) and a τ_D(A) of 2.9 ns. This corresponds to a FRET-averaged interdye distance 〈R_DA〉_E of ∼61 Å, close to the distance of 63 Å that was determined by AV simulations of the fluorophore positions using the crystallographic structures of KT's apo- and DNA-bound forms (see above and Table 1). This species is therefore assigned as the open complex (O) determined by x-ray crystallography. The major difference in MFD plots between KT^DA and KT^DA:p/t measurements is that the FRET populations of KT^DA are tailing toward shorter distances (lower F_D/F_A) indicative of a larger degree of heterogeneity.

TABLE 1.

Experimental and theoretical interdye distances

Experimentally derived distances for Alexa 488 coupled to V649C and Alexa 647 coupled to A454C are presented for direct comparison with the distances obtained from analysis performed as described previously (41), based on the structure of the dyes, the linker length, and the structure of Klentaq1 (see “Experimental Procedures”). R_Cβ is the distance between the Cβ atoms of the amino acid used for linking the dye to Klentaq1. 〈R_DA〉_E is the FRET averaged mean distance given as: 〈R_DA〉_E = R₀ (〈E〉⁻¹ − 1)^1/6. The following structures from the Protein Data Bank were used (closed, 1QTM; open, 1KTQ).

FRET states	Closed	Nucleotide binding	Open
Experimental distances
〈RDA〉E	49.5 ± 0.8 Å	55.5 ± 0.8 Å	60.7 ± 0.6 Å
Calculated distances
〈RDA〉E	49.9 Å	NA	62.4 Å
RCβ	40.2 Å	NA	52.0 Å

To determine whether we could monitor the open to closed transition using single-molecule spectroscopy, experiments were performed on the ternary complex KT^DA:p/t:dTTP_(correct) (Fig. 2C). In the presence of a correctly base pairing dNTP, we see a strong decrease in τ_D(A) to 2 ns and F_D/F_A to 2 (Fig. 2C, red line). The derived distance 〈R_DA〉_E of 50 Å corresponds closely to that of 49.9 Å determined from AV simulations using the closed ternary complex crystallographic structure of KT (see Table 1). Hence this state is assigned as closed (C).

The major populations in both the ternary complex with the incorrect dNTP, KT^DA:p/t:dATP_(incorrect) (Fig. 2D), and the binary complex with dTTP, KT^DA:dTTP (Fig. 2E), have a slightly but significantly reduced fluorescence lifetime (2.5 ns) and reduced F_D/F_A (F_D/F_A ≈ 5; green line), compared with the open KT^DA (Fig. 2A) and KT^DA:p/t (Fig. 2B) complexes. This is due to a reduction in distance between the two fluorophores. The derived distance (〈R_DA〉_E) of 55.4 Å (green line) corresponds to a previously uncharacterized state. Because of the prevalence of this state in the presence of dNTP alone and in the presence of incorrect dNTPs, this conformational state was termed the “nucleotide-binding (NB)” state. Interestingly, in the presence of elevated concentrations of MgCl₂ (50 mm), the NB state becomes more pronounced even for the case of the apo-enzyme (Fig. 2F).

Quantitative Analysis of Freely Diffusing KT Molecules

To further resolve and quantify heterogeneities within the measured FRET distributions, PDA was employed (Fig. 3). For this analysis each burst is divided into time windows and then for each t.w. the fluorescence parameters are calculated. PDA is a powerful technique that allows for the determination of the minimum width of a FRET distribution arising from a single interdye distance (31, 32). This minimum width is determined by the photon shot-noise that arises from the fact that the number of photons detected per single-molecule burst is relatively small (typically a few hundreds photons). PDA has been already utilized for discriminating multiple species in the same solution and highlighting dynamic behavior of single molecules (32, 44, 45).

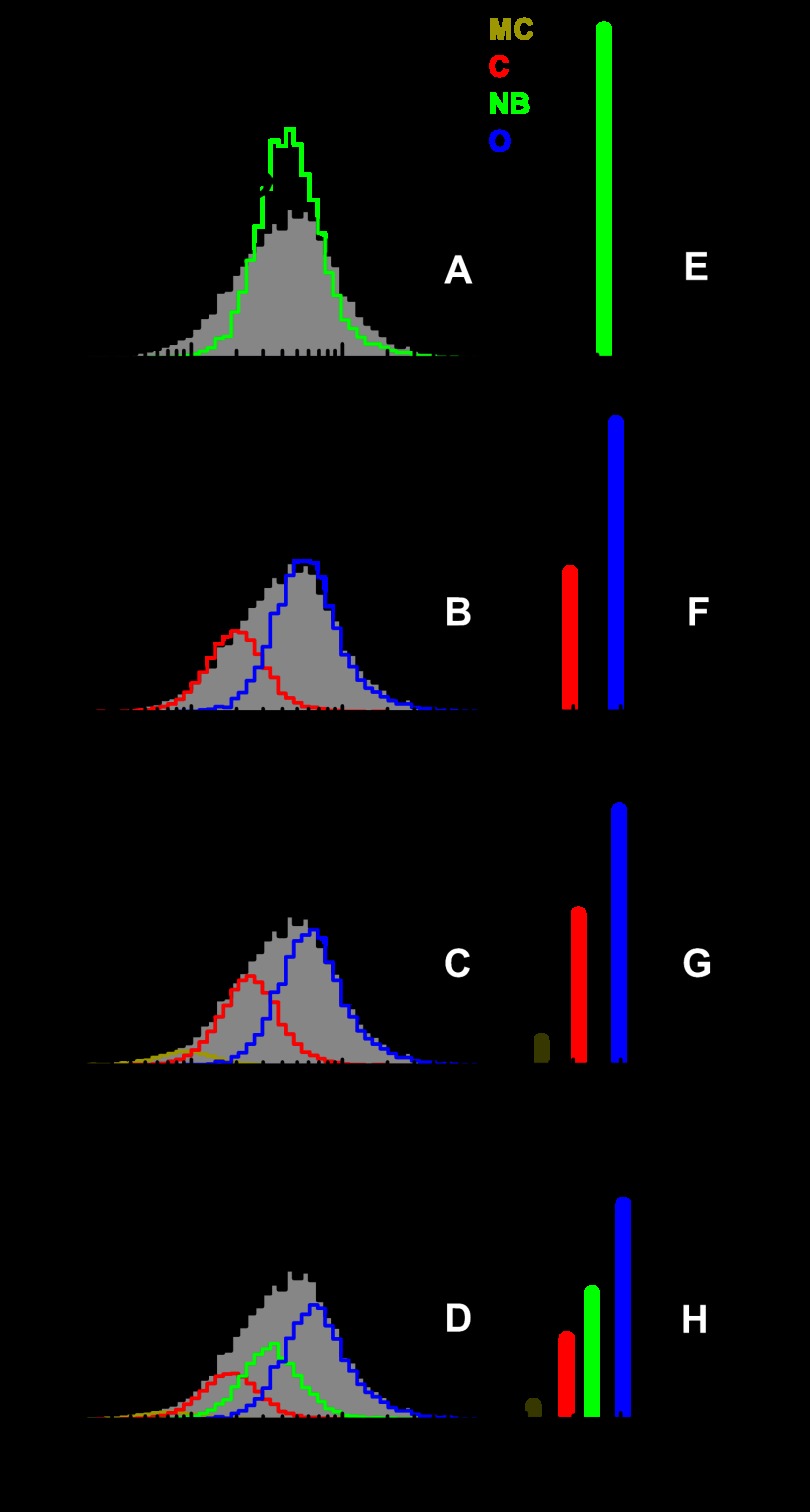
FIGURE 3.

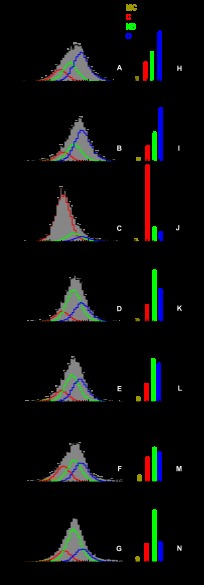
Photon distribution analysis for time windows. A–G, overall fit is shown in black over the data (gray bar histogram) obtained for KT^DA under indicated experimental conditions along with the corresponding residuals shown above. FRET species of interest are represented in dark yellow, red, green, and blue for MC, C, NB, and O, respectively. For clarity, only the FRET species of interest are shown in (A–G). H–N, recovered mean distances and the corresponding relevant percentile fraction of each state are indicated by bar diagrams. Same color coding as before was applied. The percentages of donor only and contaminant (D-o+C) are shown in black.

Using a t.w. of 2 ms, the fit results obtained for measurements on various KT^DA complexes are shown in Fig. 3. To determine whether all identified states were present under each measurement condition, and to quantify the amount of each state, the data were analyzed by PDA. Each data set was fitted progressively by using models with a donor only pattern and one, two, three, four, or five FRET species, respectively (see “Experimental Procedures”). As shown in Fig. 4 for the case of free KT^DA (see details for all measurements in supplemental Table 1 and supplemental Fig. 1), the minimal model for fitting PDA histograms of all measurements, based on statistical arguments (residuals, reduced χ², F-test), consisted of four FRET states. The addition of a fifth FRET state was not justified statistically for any of the measurements.

Initial estimates of the major states of 50, 55.4, and 61 Å, were determined by visual inspection of the data for KT^DA:p/t:dNTP_(correct), KT^DA:p/t:dATP_(incorrect), and KT^DA:p/t, respectively. An additional minor state was also seen at a shorter distance of ∼42.0 Å, which we term “more closed” (MC). This additional state is always populated to fractions lower than 5%, so it will not be discussed further; and no conclusion will be drawn from its presence (which is statistically justified by the fitting procedure). A pattern present to donor-only labeled species and contaminants was also included in the fit (denoted (D-o+C) in Fig. 3).

To determine the reproducibility of the data, measurements were performed several times on KT^DA, KT^DA:p/t, and KT^DA:p/t:dTTP_(correct) (Table 1 and supplemental Tables 3 and 4). The FRET-derived mean distances and the standard deviations for the C, NB, O, and MC states are 49.5 ± 0.8, 55.5 ± 0.8, 60.7 ± 0.6, and 42.0 ± 1.0 Å, respectively. Applying rigorous experimental calibration procedures, the average distances and errors obtained from different high precision-FRET measurements have only minimal variations and hence a high degree of statistical confidence in the discrimination between the states (differences in amplitude arise solely from the presence of substrates).

The bar diagrams alongside the individual fits for each measurement condition (Fig. 3 and supplemental Table 2) show large variations in the relative populations of the various conformational states of the enzyme. The apo-enzyme E (Fig. 3, A and H) favors the O conformation (48%) with smaller fractions of the NB conformation (28%) and C conformation (18%). Upon binding of the DNA p/t (Fig. 3, B and I), this equilibrium is shifted more toward the O conformation (53%) mainly due to a reduction of the C state, which now constitutes 15% of the population. On addition of a correct nucleotide to the KT^DA:p/t complex (KT^DA:p/t:dTTP_(correct)), we observe an inversion of the populations of states; the C state is now by far the most favored constituting 75% of the total population with the NB and O states now representing 13 and 9%, respectively (Fig. 3, C and J). Addition of dTTP to KT^DA to produce the binary E:dTTP complex (Fig. 3, E and L) or addition of dATP to KT^DA:p/t complex to form an KT^DA:p/t:dATP_(incorrect) complex (Fig. 3, D and K) results in the NB conformation being favored, constituting 42 and 50% of the total population, respectively. Both the KT^DA:p/t:dATP_(incorrect) and E:dTTP have reduced levels of the O conformation and similar levels of the C state, as compared with the E and E:p/t measurements. No structural data exist for the NB state of KT, but this state may be analogous to the ajar state retrieved crystallographically for the large fragment of the related DNA polymerase I from B. stearothermophilus (23) in which the fingers subdomain occupies an intermediate state between the open and closed conformation.

The predominance of the NB state in the presence of a dNTP alone and in the presence of an “incorrect” dNTP for the E:p/t complex suggests it plays a key role in dNTP binding. We also found that addition of higher concentrations of MgCl₂ alone also favors the NB state. In the presence of 50 mm MgCl₂, we observe a reduction in the O state and an increase in the NB state as compared with apo-KT^DA. In the presence of 500 mm MgCl₂, the occupancy of the NB state is further increased, with a concomitant decrease in the amount of O state as compared with apo-KT^DA. This re-equilibration appears to be mainly controlled by transitions between the NB and O states as only small changes are seen in the amount of closed C form. The remarkable finding of these experiments is that under all measurement conditions KT exists in a conformational equilibrium between three structurally distinct states (O, C, and NB), which were identified with high precision and whose level of occupancy is defined by the nature of the bound substrate.

Fast Conformational Dynamics of KT

To gain insight into the dynamics of the observed conformations, PDA analyses were performed using different t.w. If kinetics occurs between two FRET states within a given time range, this can be detected as a mixing of states, which results in the emergence of a peak with average inter-dye distance value in the PDA histograms. The relative fraction of this emerging peak should be higher for a longer time window. For example, if there are transitions occurring between the O and the C states within a given t.w., a peak similar in position to the NB state would be expected.

We tested whether the NB state is indeed a real conformational state or a peak resulting from possible kinetics between the O and C states, by fitting PDA histograms obtained from KT^DA for a short and a long t.w. of 2 and 10 ms. In Fig. 5, A and B, each t.w. background signal was included (see Equation 2) in such a way that the average efficiency of the FRET species was independent of the t.w. length. This correction leads to a slight change (<5%) in the species populations as compared with the static background correction used for normal PDA analysis (Fig. 3). It is evident that the obtained distributions are significantly different for the two t.w. and that different model functions are needed to fit the data in each case. Fig. 5, A and B, shows that the best fit model for the 10-ms t.w. data fails to fit the 2-ms t.w., and vice versa. This behavior means that the distribution of states is different for a 2-ms t.w. and a 10-ms t.w., indicating that KT is transiting between conformations within the chosen time windows.

FIGURE 5.

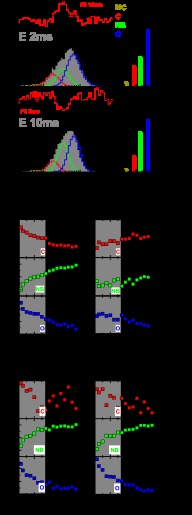
Time window analysis. A and B, data (gray bar histogram) obtained for KT^DA for a 2-ms time window and a 10-ms time window with states of interest colored as in Fig. 3. Residuals are shown above each fit for the correct model (black) or when using a 10-ms fit for a 2-ms t.w. or a 2-ms fit for a 10-ms t.w. (red). C and D, mean distances and % of each are indicated by bar diagrams of the same color as well as the % of donor only and contaminant (D-o+C) shown in black. E–P, relative amplitudes for C, NB, and O are plotted against varying widths of time windows and are shown in red, green, and blue, respectively, for the various measurements. A shaded area acts as a guide for the direct separation of the two time scales of the recovered decays (fast, 1–5 ms; slow, 10–100 ms; see text for details). E–G, free enzyme; H–J, E:p/t:dTTP_Correct; K–M, free enzyme + high Mg²⁺; N–P, E:p/t−dATP_Incorrect.

To characterize this time-dependent change in the observed FRET distributions, the distances for the MC, C, NB, and O states were fixed in PDA (at distances obtained for a 0.5-ms t.w.), and the change in amplitude occurring between t.w. of 0.2–14 ms was fitted. The percentages determined using this fit approach are shown in the projections for a 2-ms and 10-ms t.w. (Fig. 5, C and D), and the percentages for each state over various t.w. are shown in Fig. 5, E–G, for KT^DA. The data show a fast reduction in both the O and C states and an increase in the NB state as the t.w. increases. In this case, the NB state could potentially arise from exchange between the O and C states, i.e. if these two states were interchanging on a fast time scale, the mixing peak would be close to the NB state. Nevertheless, even at a low t.w. (0.2 ms), this state is still present to a significant extent (20%), suggesting that in all measurements a significant part of the observed fraction of this state is due to a distinct conformation rather than mixing of O and C states. A similar fitting procedure was performed on the E:p/t:dTTP_(correct) complex (see Fig. 5, H–J), revealing a minor decrease in the O state and a minor increase in the C state. However, the NB state stays constant within the error limits of the analysis. Because of the changes in O and C states, populations are so small within the used t.w. that all FRET states for the ternary complex E:p/t:dTTP_(correct) appear to be pseudo-static over the fitted time range. This is not surprising as the C state formed in the presence of a correct base pairing dNTP is thought to be extremely stable. In contrast, for the incorrect ternary complex, E:p/t:dTTP_(incorrect) (Fig. 5, N–P), the dynamic behavior of the populations of O and NB state is clearly observed. Furthermore, it is striking that the dynamic behavior of the populations of states for E:p/t:dTTP_(incorrect) is qualitatively similar to the dynamic behavior observed for the measurement in apo-KT in the presence of 50 mm Mg²⁺ (Fig. 5, K–M).

When considering the measurements for the E state, the population of the O conformation undergoes an initial fast (on the order of milliseconds) decay (gray-shaded in Fig. 5, I–L) followed by a slow decay (10–100 ms range) suggesting that the O state population is depleted by two different mechanisms. Although these results suggest that dynamic processes are occurring on the measurement time scale with various substrates (plots for E:p/t, E:p/t:dATP_(incorect), E:dTTP, and E:MgCl₂ are given in supplemental Fig. 2 and apparent rate constants in supplemental Table 5), it is important to note that it is hard to gain quantitative information about individual rates due to overlapping dependences, e.g. possible dynamics between the O and C states could result in a distribution overlapping the C and NB states.

Obtaining Transition “Snapshots” by Slow Dynamics Burst Enrichment, Principles

The above time window analysis indicates that KT molecules are undergoing conformational transitions as they diffuse through the observation volume. We here present a new method to assess whether KT transitions directly between two states (state I to state II) or whether it must pass through an intermediate state (state III). This approach uses the same measurements of the diffusing single molecule described above and has the advantage that no immobilization of the molecule of interest is required (immobilization has been shown in many cases to affect activity if not performed carefully (46–48)).

The problem is that freely diffusing molecules reside within the observation time only for a few milliseconds, whereas some of the conformational changes of KT are expected to occur at rates of ∼1 s⁻¹ (17). Thus, out of several thousand bursts registered in a single-molecule experiment, transitions will occur only in a small fraction of the detected bursts (for the kinetic rate constants expected for free KT^DA, this fraction is calculated to be 15%; for detailed calculations see “Experimental Procedures”). It is therefore essential for a meaningful data analysis to develop a criterion for the preferential selection of these bursts.

Such a selection criterion, referred to as “slow dynamics” burst enrichment, is developed based on the signal time traces (green and red fluorescence) created for each selected burst. We define the burst-averaged mean photon times of green and red fluorescence, T_G and T_R, respectively, as the mean value of the detection times (time that has elapsed between the start of each burst and the detection of a photon) for a green or red photon belonging to that burst (Fig. 6A) (36). For a burst with no dynamics (static case), it is valid that the time difference between mean photon times |T_G − T_R| ≈ 0 ms (Fig. 6A, top). If a FRET change results from a single state transition occurring during a burst, the intensity will increase for one channel and decrease for the other (slow dynamics case). This results in a shift of T_G and T_R in opposite directions. Thus, |T_G − T_R| will deviate from 0 (Fig. 6A, middle). However, if many transitions occur between FRET states (fast dynamics case), |T_G − T_R| will become again close to zero, because one transition will cancel the effect of the other in terms of the shifts of T_G and T_R (Fig. 6A, bottom). For fluorescence experiments with a confocal setup, high laser power densities are usually applied, and acceptor photobleaching can become relevant. However, as shown in Ref. 36, the characteristic symmetric shape of the T_G − T_R distributions allows us to exclude significant photobleaching artifacts in our KT measurements (see “Experimental Procedures” and supplemental Fig. 3).

SD burst enrichment was first extensively tested on simulated data generated by an in-house developed software for Brownian dynamics simulations (35) using parameters identical to the experiment (see “Experimental Procedures”). Considering a minimum value θ for the mean photon time difference (i.e. |T_G − T_R| >θ) Fig. 6B clearly shows that SD burst enrichment considerably suppresses the fraction of static bursts. Normalized histograms of uncorrected FRET efficiencies, E′, as calculated for each burst, are shown. For the case of bursts with |T_G − T_R| >2 ms (Fig. 6B, orange) the static part (high FRET state) is suppressed, and the intermediate E′ is enriched in comparison with the histogram of all bursts with |T_G − T_R| <2 ms. Because of random fluctuations of the signal in confocal experiments, bursts during which no dynamics occurs could also be selected to a small extent. It is therefore useful to use a more quantitative measure for the presence of dynamics by introducing the normalized fraction of selected bursts, f_N,θ, where the experiment is normalized by the simulated static case with all relevant FRET states present (see Equation 11). Fig. 6C illustrates (for the exemplary case of a two-state dynamic systems) that the useful time range of dynamics for SD burst enrichment is determined by an appropriate ratio between two factors as follows: 1) relaxation rate constant of dynamics k_r (for the two-state system, k_r = k₁₂ + k₂₁), and 2) the mean time of burst duration 〈t_bd〉, from which the mean number of transitions per burst (for all detected bursts) 〈N_trans〉 = k_r 〈t_bd〉 can be calculated. Generally, the 〈N_trans〉 values are low, because for most bursts no transition occurs. The gray region in Fig. 6C illustrates the range for which SD burst enrichment is useful. SD burst enrichment can be safely applied to KT measurements which exhibit significantly increased f_N,θ values within the region depicted by red dashed lines in Fig. 6C (for further simulation results see “Experimental Procedures”).

Obtaining Transition Snapshots by SD Burst Enrichment, Application to KT

We apply SD burst enrichment to preferentially select the bursts with transitions of specific rates (burst exhibiting slow dynamics) by analyzing only bursts with |T_G − T_R| >1 ms. Typical time traces for green and red signals as well as uncorrected FRET efficiencies E′ of representative bursts separated by gray lines are shown in Fig. 7, A and B, respectively. We used the Hidden Markov Model algorithm as implemented in the HaMMy software package (37, 38) to detect FRET transitions and the corresponding FRET efficiency levels (E′_Start, E′_End) in the signal traces of the selected bursts. To determine whether we could discriminate real FRET transitions (between states relatively close to each other) from stochastic fluctuations in the fluorescent signal arising from freely diffusing KT^DA, we ran simulations using the experimental values obtained for KT^DA including three states (O, NB, and C) with uncorrected FRET levels E′ close to experiment (E′(O) = 0.25, E′(NB) = 0.39, and E′(C) = 0.54). We considered four different cases as follows: (i) O ↔ C equilibrium (rate constants k_O,C = 10 s⁻¹ and k_C,O = 25 s⁻¹) and NB static; (ii) O ↔ NB equilibrium (k_O,NB = 15 s⁻¹ and k_NB,O = 25 s⁻¹) with C static; (iii) NB ↔ C equilibrium (k_NB,C = 20 s⁻¹ and k_C,NB = 30 s⁻¹) and O static; and (iv) a fully static system with O, NB, and C. The validity of the overall analysis procedure for simulated and experimental data is judged by two criteria as follows: 1) How large is the normalized fraction of bursts, f_{N, θ = 1} (θ = 1 ms)? 2) Are the recovered FRET levels meaningful with respect to the previous results?

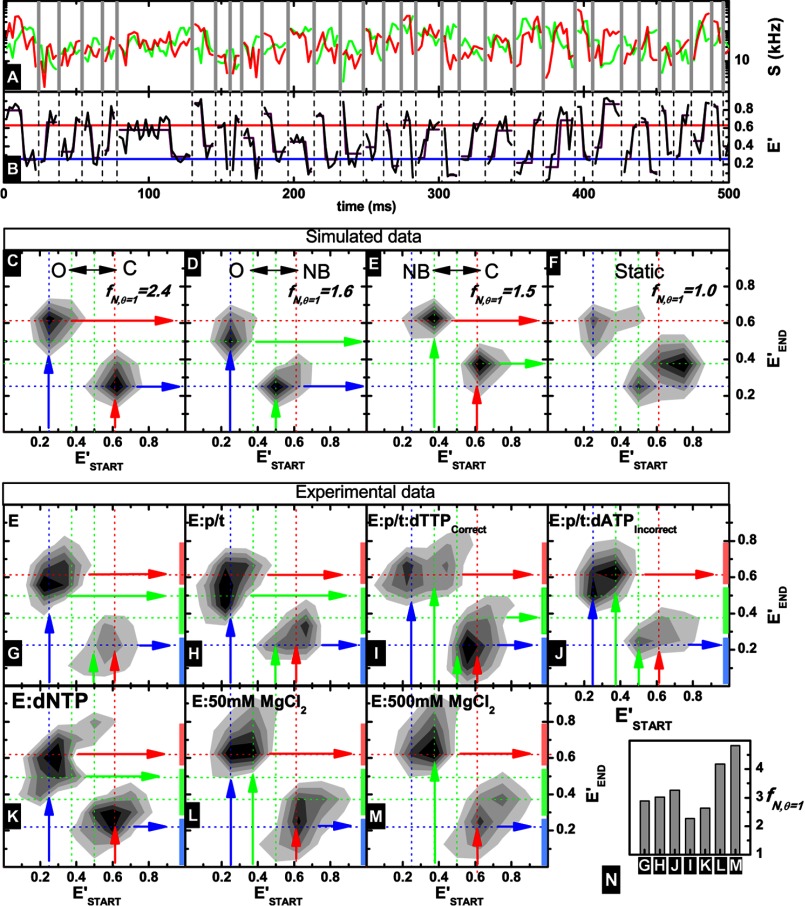
FIGURE 7.

Slow transition data obtained for KT^DA under various conditions. A, green and red fluorescence intensity traces recovered from fluorescent bursts (using time windows of 1 ms) are shown in corresponding colors, with different bursts separated by gray vertical lines. B, uncorrected efficiency traces of burst fragments (black) with HaMMy fit shown in purple. The mean fitted efficiency for O and C is also indicated in red and black, respectively. C–F, transition matrices (with E′_START and E′_END as defined in the main text) obtained from fitting of simulated data using HaMMy for an O-C transition (C), O-NB transition (D), C-NB transition (E), and no transitions (F). For a complete description see text. Also indicated are the originating states shown in blue, green, and red vertical arrows for O, NB, and C, respectively, although the state after a transition is shown as a horizontal arrow in the same colors. Guide lines for O, NB, and C are shown in blue, green, red dotted lines, respectively. For each case the corresponding f_{N, θ = 1} is given (for definition see Equation 11) as a measure of the effectiveness of the SD burst enrichment (see text for details). G–M, transitions matrices obtained for indicated experimental data. A transition, from or to, a single state is indicated by an arrow (blue for O, green for NB, and red for closed). The length of the vertical bars along the y axis of each plot are representative of the uncertainty in the determination of the FRET level of each state (closed, light red; nucleotide binding, light green; and open, light blue). N, f_{N, θ = 1} values for all measurements. It is clear that in all cases more transitions are registered than in the case of the simulated static system.

We found that it is possible to discriminate between “pseudo-transitions” due to background fluctuations and real conformational transitions. First, all simulated dynamic cases and all experimental measurements had higher fractions of bursts with |T_G − T_R| >1 ms compared with the simulated static case. For the experimental data, f_{N, θ = 1} has a median value of 3.0 (minimum, 2.1; maximum, 4.8; see Fig. 6N). Thus, for all experimental cases we can be sure that we are not analyzing random fluctuations in the fluorescent traces. Moreover, under our measurement conditions (concentrations <50 pm), the probability that a “jump” in the fluorescent trace is caused by a multimolecular event is negligible (p = 0.3% calculated as described previously (34, 49)). This probability is lower than the absolute fractions f_θ obtained for the different experiments (varying between f_{θ = 1} = 9.7–22.1% for the experimental data with median value of f_{θ = 1} = 14.0%). The absolute fractions of selected bursts, f_{θ = 1}, obtained from the various experiments are in good agreement with the expected fractions of bursts for which at least one transition occurs (15%) as it was calculated for KT by assuming reasonable rates from stopped-flow data (17) (see “Experimental Procedures”).

Fitted transitions (typically ∼100 transitions per measurement condition) are conveniently illustrated in two-dimensional plots (normalized transition density plots) by plotting the starting level of a transition in terms of starting uncorrected FRET efficiency (E′_START) against the ending level (E′_END). The fit model in the HaMMy analysis included three states with the characteristic FRET levels of the states O, NB, and C. At first, we analyzed simulated data. For the case of O ↔ C (Fig. 7C), we observe a transition starting at an apparent efficiency of 0.25 (blue vertical arrow) and ending at an efficiency of 0.6 (red horizontal arrow) and a second transition starting at 0.6 (red vertical arrow) and ending at 0.25 (blue horizontal arrow), very close to the simulated uncorrected efficiency levels. For the equilibria, O ↔ NB (C static; Fig. 7D) and NB ↔ C (O static; Fig. 7E), we obtain different uncorrected efficiency levels (0.5 and 0.4) for the NB state (green arrows). For the static system in Fig. 7F, we recover a few “pseudo” transitions exhibiting a main peak, which does not correspond to any of the simulated FRET states (see Fig. 7D).

Next, we analyzed data of various experiments. The transition matrices are plotted in Fig. 6, G–M, with guide lines (dotted) to indicate the expected efficiency levels obtained from the simulated data (Fig. 7, C–E). For the E and E:p/t measurements shown in Fig. 6, G and H, we see a transition occurring between an efficiency of 0.25 (O) to a broad peak between 0.5 and 0.65 (a mixture of transition from C and NB). For the reverse transition, we see a similar behavior in which the peak transitions from a mixture of efficiencies (between NB and C) to the O conformation. This suggests that both the C and NB states transition to O and vice versa.

In the cases of the ternary complexes, E:p/t:dTTP_(correct) and E:p/t:dATP_(incorrect) (Fig. 7, I and J), we see direct transitions occurring between the NB and C states that were not observed in the E and E:p/t measurements suggesting that the NB state may be important in binding and delivery of correct dNTP to the polymerase active site. This transition is not apparent in the presence of a dNTP alone (E:dNTP; Fig. 7K) suggesting that that the p/t is an absolute requirement for the efficient transition to a closed ternary complex via the NB state. Thus, the important finding here is that the ternary complex can adopt the C conformation using two pathways as follows: (a) directly by a (fast) transition from O to C, and (b) via the NB state.

Interestingly in the presence of 50 mm MgCl₂ transitions between the O and NB states are not visible, and instead transitions from O and NB to C and vice versa are recovered. At even higher concentrations of MgCl₂ (500 mm), we recover transitions from NB to C and in the reverse direction from C to O.

DISCUSSION

Because it was established that the fingers subdomain of DNA polymerases undergoes a conformational change upon addition of a correct nucleotide to the DNA-bound form, the role of this conformational change has been the subject of much debate. The fingers subdomain plays crucial roles in DNA polymerase function because it provides the primary binding site for the incoming nucleotide, and it acts as a delivery device for the incoming nucleotide (8). Whether it plays a role in nucleotide selection and thus in fidelity is unknown.

Some polymerases, such as KT, discriminate poorly against incorrect nucleotides at the nucleotide-binding step (step 2 in Fig. 1A) and rely on the selectivity provided by step 3 in Fig. 1A. Evidence from studies on members of the polymerase family have indicated that the transition between the O and C states of the enzyme involves additional states. The recent crystal structure of the large fragment of DNA polymerase I from B. stearothermophilus bound to DNA, and a mismatched nucleoside triphosphate indicated the existence of an additional conformation (termed ajar) of the fingers subdomain (23). In smFRET studies of the Klenow fragment of DNA polymerase I from E. coli, an apparent shift in the FRET state corresponding to the O conformation was observed, suggesting the presence of an additional state in between the O and C conformations (21, 22). However, this additional state was not further characterized. As this study was being finalized, a study on immobilized molecules of the Klenow fragment of DNA polymerase I was published identifying an intermediate conformation (ajar) in the presence of most of the substrates (50). Nevertheless, the conformations were not quantitatively characterized in terms of their corresponding mean distances, and transitions from the open to ajar state could not be resolved for all substrates. Finally, recent NMR studies on KT in the presence of the incorrect dNTP indicated that the ternary complex with a mismatched nucleotide adopts a conformation different from those of the O and the C states (51).

In this study, we provide a complete characterization of the conformational states of KT in response to its substrates. These states were determined with high precision, being quantitatively defined using PDA. Moreover, further insight into the role of the NB state was obtained by determining the changes in its occupancy upon addition of Mg²⁺. Finally, we could provide qualitative information on substrate-induced transitions between each state. The dynamics observed involve transitions with characteristic times spanning the approximate millisecond to approximate second range (Figs. 5 and 7) indicative of a complex energy landscape.

We observed three distinct conformations, O, NB, and C, the distribution of which is defined by the nature of the substrate. For the apo- and DNA-bound forms of KT, the O state predominates, and in the presence of dNTP alone, DNA and incorrect dNTP, or elevated concentrations of MgCl₂, the NB state is the major conformation. Only in the case of a correct dNTP is a stable C complex formed. The high levels of the NB state in the presence of a dNTP alone suggest that this state is stabilized by an incoming dNTP, even in the absence of DNA. Whether this is due to an initial binding of the dNTP in the open form followed by a conformational change or to direct binding to and stabilization of the NB state is unclear. Interestingly, in the presence of elevated MgCl₂ concentrations, we find a conformational equilibrium similar to that seen for DNA and incorrect dNTPs. High MgCl₂ concentrations are known to have detrimental effects on replication fidelity (52). Whether increased levels of NB to C transitions in the presence of MgCl₂ are correlated to replication infidelity remains to be explored.

The nature of the bound substrate appears to play a crucial role in how the enzyme is able to transition between the observed states. Interestingly, both direct transitions between C and O and indirect transitions via NB were observed, consistent with the fact that the kinetic rates involved span from approximate milliseconds to approximate seconds (see Figs. 5 and 7). For the apo- and DNA-bound forms of KT, it appears that the enzyme can undergo all transitions seen in Fig. 7A. The binding of DNA and correct dNTP not only induces a dramatic equilibrium shift in favor of the closed form of the enzyme, but also the rates of the transitions occurring between the O, NB, and C states are slowed as illustrated by the study of dynamics in the approximate millisecond time range using PDA (Fig. 5). Slow transitions are detected between the NB and C conformations, and no transitions are seen between O and NB. In contrast, the incorrect nucleotide triggers a significant redistribution of the O/NB/C conformational equilibrium in favor of the NB form. Presumably, this shift toward the nucleotide-binding state of the E:p/t:dNTP_(incorrect) complex allows for quick release of incorrect nucleotide by forcing the enzyme to “oscillate” mainly between the NB and O states. Our findings strongly support the idea that the NB/ajar conformation is indeed a key intermediate on the reaction pathway of nucleotide incorporation (see Fig. 8A). It should be noted, however, that our analysis could not exclude the presence of a short lived transient state, which acts as a hub between the O, NB, and C states (Fig. 8B).

FIGURE 8.

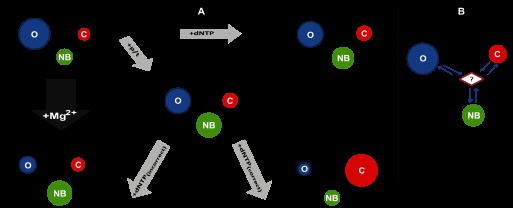
Toward a mechanism based on conformational selection. A, minimal plausible kinetic scheme includes three states. For the apo-form, E, and each of the complexes: E:p/t, E:dNTP, E:p/t:dNTP_(correct), and E:p/t:dNTP_(incorrect), the interchange of KT^DA between its various conformational states is illustrated. Each conformational state is depicted by a colored circle: blue, red and green for O, C, and NB, respectively. The relative area of each circle qualitatively represents the relative populations of each state at equilibrium. The arrow lengths qualitatively represent to the relative forward and reverse rates and are proportional to its reaction rate. B, presence of an additional transient intermediate which acts as a hub between states cannot be excluded by our analysis.

We show that for KT the conformational transition affecting the fingers subdomain, first thought to be triggered by a correct incoming nucleotide, does not require a trigger but is in fact an intrinsic oscillating motion, encoded in the enzyme's fold and occurring both in the unbound and substrate-bound enzyme. The energetic barriers for the conformational transition for the case of KT at room temperature are high enough to allow detection of all three states, whereas for the Klenow fragment of E. coli DNA polymerase 1, only the transitions between the O and C states could be characterized in detail. Our results definitely suggest that the mechanism of the incorporation of the correct nucleotide and of the rejection of the incorrect one could not be a pure “induced fit mechanism” (53, 54). The discovery of a conformational equilibrium in the unbound and bound states of the polymerase illustrates that a fundamental way in which proteins operate, namely conformational selection, plays an important role (55–58). Intrinsic intramolecular motions between thermodynamically stable states are exploited for function (59). For example, enzymes can use rapid domain movements to overcome the opposing requirements of an easily accessible substrate-binding site and a tight, highly specific active site. Similar intrinsic intramolecular motions have been unraveled in other enzymes such as Syk kinase (60) and adenylate kinase (61). However, in the case of polymerases, one of the states (the closed state) is by design less energetically favored, providing a thermodynamic brake on incorrect nucleotide insertion. Only the insertion of a correct nucleotide results in a change of the free energy for closing, so the closed state is substantially populated. We believe that such a mechanism will prove to be general.