On the Use of Fractional Polynomial Models to Assess Preventive Aspect of Variables: An Example in Prevention of Mortality Following HIV Infection

Abstract

Background:

Identification of disease risk factors can help in the prevention of diseases. In assessing the predictive value of continuous variables, a routine procedure is to categorize the factors. This yield to inability to detect non-linear relationship, if exist. Multivariate fractional polynomial (MFP) modeling is a flexible method to reveal non-linear associations. We aim to demonstrate the impact of choice of risk function on the significance of variables.

Methods:

We selected 6508 HIV-infected persons registered in the Australia National HIV Registry between 1980 and 2003 to assess the predictors associated with the risk of death after HIV infection prior to AIDS. First, CD4 count as a categorical factor with three other categorical variables (age, sex, and HIV exposure category) was entered into the Cox regression model. Second, CD4 counts as a continuous variable along with other categorical variables were entered into the fractional polynomial (FP) model.

Results:

Both the Cox and FP models showed age ≥ 40 years and hemophiliac patients were significantly associated with increased risk of death. In the categorized model, the CD4 variable did not reach the significance level. However, this variable was highly significant in the MFP model. The FP model showed slightly better performance in terms of discrimination ability and goodness of fit.

Conclusions:

The FP model is a flexible method in detecting the predictive effect of continuous variables. This method enhances the ability to assess the predictive ability of variables and improves model performance.

INTRODUCTION

Prognostic models are tools that help in decision making, which combine items of patient data to predict clinical outcomes (such as death due to HIV/AIDS). This in turn helps the management of future patients to prevent adverse events. Therefore, identification of risk factors to be used as predictors is necessary.

To detect the predictive ability of variables, the Cox regression model is frequently used to analyze follow-up data. One of the most important assumptions for this model is the linearity of effects.[1]

Although regression models (such as Cox or logistic regression) rely on linearity assumption, a recent review of 99 articles published in two major epidemiology journals (Journal of Clinical Epidemiology and American Journal of Epidemiology) showed that fewer than 20% of papers using multifactorial regression described conformity for linearity gradient.[1,2]

In the case of skewed data, the linearity assumption might be doubtful. In such cases, it is common in prognostic modeling to apply a pre-specified transformation such as logarithmic, prior to analysis, to make a linearity assumption plausible (even if not optimal). An alternative method frequently used is to categorize the continuous variables so as to simplify the analysis.[1–4]

However, the answer to the question “Is there an effect?” depends to a great extent on the choice of optimum risk function.[5] These practical challenges make it difficult to identify the optimum form of association. Fractional polynomial (FP) modeling is a flexible tool that reveals non-linear associations and is simple to communicate with the clinical audience. All commonly used transformations such as the logarithmic, square, cubic, or reciprocal are embedded in the FP method. Modeling explores the data to identify optimum power transformation for a variable. It should be emphasized that if one offers transformed variables to the model, interpretation of results is not straightforward. For example, in the case of linear regression, if one applies a logarithmic transformation to an independent variable, the estimated coefficient indicates change in the dependent variable per one unit change in the logarithm of the independent variable.

As an example of application of the FP method in the literature, this method was used to detect the best functional form for age and progesterone receptor in a series of 686 node-positive breast cancer patients.[6] It was revealed that patients aged less than 40 years had a markedly increased risk of recurrence, followed by a fairly constant plateau for those aged 40-55 years, with a slight increase again after 55 years. In addition, a logarithmic transformation was proposed for progesterone receptor.

The prognostic role of CD4 lymphocyte count in HIV-infected individual to either AIDS or to death has been established by a number of studies.[7–15] This role has been explained by CD4 count independently at baseline[7,9,10,12,14,15] and also in connection with some other factors such as HIV-1 RNA level,[8] treatment,[11] and socio-demographic factors.[15,12]

Classic regression models assume a linear relationship between independent and dependent variables. However, this assumption might be questioned when distribution is far from being normal. In the case of skewed variables, such as CD4 counts, there is a considerable chance that the perfect linearity assumption might not be justified.[16] Therefore, it is of importance to establish the correct functional form of association.[16] In a previous study to assess the risk factors of survival following HIV prior to AIDS, the CD4 counts were entered to the Cox model as a categorical variable. This variable did not show significant association with the outcome.[9] The aim of this paper is to address the impact of choice of risk function (FP vs. categorization) on the significance of prognostic variables. Methods were applied on an HIV data set as an example.

METHODS

Data sources and outcome of study

We identified 6508 HIV-infected persons with CD4 counts data available registered in the National HIV Registry (NHR) between 1980 and 2003 in Australia. Those HIV diagnoses were selected after a correlation between the matched HIV/AIDS databases and the Australia National Death Index to obtain complete data on fatality after HIV prior to AIDS and after AIDS, which is explained thoroughly elsewhere.[17]

The primary outcome was survival following HIV prior to AIDS, whereas survival time was calculated as the time from date of HIV diagnosis to the date of death, or December 31, 2003. Moreover, survival time for HIV diagnoses followed by a subsequent AIDS diagnosis was censored at the date of AIDS diagnosis.

The candidate variables to be entered in the models included age (<40 vs. ≥40 years), sex, HIV exposure category, and CD4 counts. Since in Australia, the majority of HIV is transmitted through male homosexual contact, HIV exposure category was combined with sex into a single covariate categorized as male homosexual contact and heterosexual contact, injecting drug use, recipient of blood products, and “other exposures” – for males and females separately.

Statistical analysis

Categorization model

In the categorized model, CD4 counts were categorized into four levels including <200, 200-300, 300-500, and ≥500. CD4 less than 200 has been accepted as the standard definition of AIDS. Other cut-offs were selected so as to have enough number of patients in each group. Then a multifactorial Cox regression model in conjunction with ENTER variable selection method was fitted to all categorical variables.

Fractional polynomial modeling

FP modeling is a powerful tool to detect non-linear associations.[18] There are two classes of FP: First degree (FP1) and second degree (FP2) FPs.[19] The first degree FP technique (FP1), performing eight tests, detects whether fit is improved by a power transformation of the variable X, X^p, where P is chosen from S = {–2, –1, –0.5, 0, 0.5, 1, 2, 3}. FP with value of P = 1 is synonymous with a linear regression and P = 0 indicates that a logarithmic transformation is required for optimum linear modeling of a risk factor. A polynomial model of degree 2 (FP2) is an extension to β₁X^p1 + β₂X^p2 which compares 36 different power combinations. It is observed that (p₁ = 1, p₂ = 2) is equivalent to quadratic regression. The case p₁ = p₂ is known as repeated power model and has been defined as β₁X^p+ β₂X^pLn X.[18]

A multivariate fractional polynomial (MFP) approach was used for predictive model fitting using the ENTER method, which after fitting of categorical variables ascertains whether model fit would be improved by using a polynomial form for CD4 counts. MFP modeling involves three main steps: Test of inclusion, test of non-linearity of effect, and test of simplicity of power transformation required. For the CD4 variable, the following steps were carried out in the multifactorial setting: Fit the best FP2 model and test it against the null model (test of inclusion). If it is not significant, drop the variable and stop. If it is significant, test the best FP2 versus a linear fit (test of non-linearity). If it is not significant, declare the final model to be a straight line and stop. If it is significant, test the best FP2 versus the best FP1 (test of simplicity, in terms of goodness of fit). If the test is significant, declare the final model to be FP2. Otherwise, the best model would be the best FP1.

We should emphasize that there are alternative modeling strategies to deal with non-linear effects such as quadratic regression and spline-based models. However, it has been shown that FP is the best method to capture the effect of variables. Therefore, we focused only on the FP technique.

Comparison of performance of models

Discrimination of models was compared using Harrell's Concordance Index (C-Index). This statistic varies between 0.5 and 1 where values close to 1 indicate high discrimination power. Then, the bootstrap procedure with 200 replications was applied to estimate the bias-corrected C-indices.

Software

A series of packages that work under the R software (version 2.5.1) were used.[20] The FP model was developed using the MFP package. Performance of models was assessed using Design and Hmisc libraries.

RESULTS

The study population consisted of 6508 HIV-infected individuals registered in the NHR between 1980 and 2003 in Australia. The median follow-up time was 3.4 years. The median age at HIV diagnosis was 34 years. The majority of HIV transmission was reported to be through male homosexual sex (71%). The median CD4 lymphocyte count at diagnosis was 410 cells/μl [Table 1].

Table 1.

Demographic characteristics of HIV diagnoses

The histogram of the CD4 counts suggests a positively skewed distribution. First, second, and third quartiles were 190, 410, and 620, respectively. Minimum and maximum values were 1 and 4180, respectively. Table 2 compares the Cox model (where CD4 was categorized into four levels) and the MFP model in the case of linearity and polynomial association between predictors and mortality following HIV infection prior to AIDS. In the categorical model, age 40 years or more (compared to ages under 40 years as the reference category) (P = 0.001) and hemophiliac patients (compared to homosexual men) (P = 0.01) were associated with the increased risk of death. Estimated Hazard Ratios (HR) were 2.3 (95% confidence interval [CI] 1.89, 279) and 2.19 (95% CI 1.23, 3.93), respectively. Similar results were observed in the FP model.

Table 2.

Comparison between categorical and fractional polynomial risk functions on the prediction of mortality following HIV infection prior to AIDS

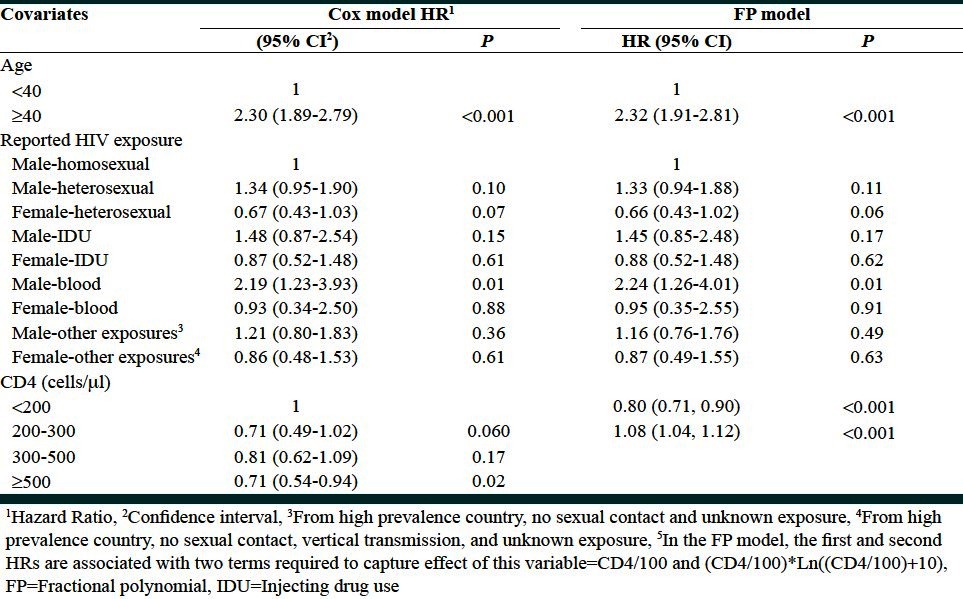
However, in the categorized model, the CD4 variable did not reach the significance level. HIV-diagnosed cases with CD4 counts less than 200 were chosen as the reference group. The HR of death for those with CD4 counts in the range 200-300 and 300-500 was not significantly different with the baseline group. Only CD4 counts higher than 500 were associated with 29% reduction in the risk of death (P = 0.02).

On the other hand, in the MFP analysis, the test of inclusion of the CD4 counts to the model was highly significant with P = 0.001. P value corresponding to the linear Cox model was 0.23. Therefore, applying the FP1 and FP2 models, we checked the test of non-linearity. A P value of 0.001 suggested that the nature of the association was not linear. The best FP1 model suggested a logarithmic transformation (optimum power was 0). We offered the logarithm of CD4 counts to the univariate and multifactorial models (after adjustment for age and HIV/sex variables). In the univariate model, a P value of 0.01 indicated a significant association between logarithm of CD4 counts and survival following HIV prior to AIDS. However, this effect was not observed in multifactorial modeling (P = 0.24).

We finally performed FP2 and compared goodness of fit of the FP2 and FP1 models. It has been shown that FP2 provides the best fit with P value of 0.002. The optimum powers selected were 1 and 1.

We then compared the performance of models in terms of goodness of fit and discrimination ability. Keeping the CD4 count in the continuous form and expressing its effect with the MFP model led to an improvement of two percentage points in the discrimination ability (62% vs. 60%).

DISCUSSION

In medical applications, researchers often categorize continuous covariates prior to modeling analyses. From the statistical point of view, this eliminates the need for linearity assumption and allows for simple interpretation of results.[4] On the other hand, dichotomization can result in the loss of information and power, if a linear rather than threshold association pertains.[21,22]

A comparison of the ability of different statistical techniques to detect the correct form of risk function for continuous variable shows that FP is the best technique to deal with “linear and polynomial” effects, with noticeable potential to detect threshold effects.[5] Furthermore, and importantly, FP does not inflate type one error.[23]

CD4 count is one of the most important key factors used to predict mortality after HIV diagnosis and also to initiate antiretroviral therapy in HIV infection.[7,14] In a previous population-based study in Australia, the Cox regression model and then the Weibull model were fitted to both national HIV and AIDS databases to predict risk factors associated with survival and also mortality following both HIV and AIDS, respectively.[9] Although CD4 count was entered into the Cox model as a categorical variable, no significant association was found between CD4 count level and survival following HIV infection prior to AIDS. Therefore, CD4 count was not entered in the Weibull model to predict future mortality following HIV infection before AIDS consequently. In this study, we selected those HIV diagnoses with CD4 counts data available out of all HIV diagnoses, which were entered in those analyses. In this study, comparison between the Cox regression and MFP models produced no significant association between categorized CD4 counts and survival after HIV infection by fitting the Cox model once again. On the other hand, we found a significant association by using the MFP model.

It is emphasized, however, that the flexibility of the FP models can result in serious over-fitting with results, which contradict current medical knowledge. To avoid such conflicting results, achieving consistency should be the primary purpose.[6] Here, our finding is in agreement with other studies regarding the role of CD4 count in predicting mortality among HIV-infected persons.

CONCLUSION

In summary, we have compared the effect of two risk functions on the assessment of predictive value of variables by using an example of survival data. Although the categorization method has the advantage of easy interpretation, this method cannot deal with polynomial effects. Royston and Sauerbrie[24] explained that a realistic FP function can discover polynomial, monotone, and linear relationship. Our analyses have fortified the FP model in showing a monotically association between a continuous variable, CD4, and risk of death. Furthermore, having obtained the same results as the categorical method in dealing with categorized variables in a cross-sectional survival data setting, our analysis has indicated one of the advantages of the FP model such as generalizability to a different setting, which has also been emphasized by other studies.[24] In contrast to a previous study[9] in which the CD4 counts failed to enter the predictive model, our model reveals the effect of this key factor in predicting mortality following HIV infection.