Intraclass Correlation Associated with Therapists: Estimates and Applications in Planning Psychotherapy Research

Abstract

It is essential that outcome research permit clear conclusions to be drawn about the efficacy of interventions. The common practice of nesting therapists within conditions can pose important methodological challenges that affect interpretation, particularly if the study is not powered to account for the nested design. An obstacle to the optimal design of these studies is lack of data about the intraclass correlation coefficient (ICC), which measures the statistical dependencies introduced by nesting. To begin the development of a public database of ICC estimates, the authors report ICCs for a variety outcomes reported in 20 psychotherapy outcome studies. The magnitude of the N = 495 ICC estimates varied widely across measures and studies. The authors provide recommendations regarding how to select and aggregate ICC estimates for power calculations and show how researchers can use ICC estimates to choose the number of patients and therapists that will optimize power. Attention to these recommendations will strengthen the validity of inferences drawn from psychotherapy studies that nest therapists within conditions.

Many psychotherapy outcome studies use more than one therapist to administer the intervention; in these studies, it is common to have patients nested within therapists and therapists nested within conditions. This nesting creates an opportunity to study therapist effects (Wampold, 2001), but it creates statistical dependencies that can lead to erroneous conclusions about both treatment outcomes and therapist effects (Crits-Christoph & Mintz, 1991; Wampold & Serlin, 2000).

Optimal design of these studies requires a good estimate of the dependence expected among observations taken on patients who have the same therapist, indexed by the intraclass correlation coefficient (ICC). Unfortunately, because most psychotherapy outcome studies have not considered this issue, few have reported ICCs for therapists. To address this problem, our research group has begun building a database of therapist ICCs for outcomes commonly used in psychotherapy research. ICC databases in public health and education have helped researchers design studies in those disciplines (c.f. Donner & Klar, 2000; Gulliford, Ukoumunne, & Chin, 1999; Hedges & Hedberg, 2007; Murray & Blitstein, 2003; Murray et al., 1994; Murray, Varnell, & Blitstein, 2004; Verma & Le, 1996). The purposes of this paper are to review the statistical effects of nesting and explain essential concepts; to report therapist ICCs from recent psychotherapy outcome studies; to provide guidelines for selecting and aggregating ICC estimates; and to show how to use ICC estimates to design new studies.

Nested Designs in Psychotherapy Research

Nested designs in psychotherapy research can take many forms. Patients may be seen in groups or as individuals. Randomization may occur at the level of the patient, the therapist, at both levels, or there may be no randomization. Nesting may occur in all conditions or in some conditions but not others (e.g., a wait-list condition). This paper focuses on the statistical issues that exist in all studies in which patients are nested within therapists and therapists are nested within at least one condition. Previous reports discuss the design and analysis of nested designs generally (e.g., Cornfield, 1978; Zucker, 1990; Murray et al., 2004; Pals et al., 2008; Roberts, 1999; Roberts & Roberts, 2005; Schnurr, Friedman, Lavori, & Hsieh, 2001) and in psychotherapy research (e.g., Baldwin, Murray, & Shadish, 2005; Crits-Christoph & Mintz, 1991; Martindale, 1978; Wampold & Serlin, 2000). We add to this work by providing therapist ICC estimates and illustrating their use in power calculations for psychotherapy research.

A key concept in these nested psychotherapy designs is statistical dependence associated with therapist. Observations are dependent if they are correlated, and in any nested design, we expect some level of correlation (Kish, 1965; Cornfield, 1978; Zucker, 1990). Where patients select their therapist or are assigned to therapists based on a non-random assignment rule, their observations may be correlated even before therapy begins, due to shared selection factors or prior exposures. Once patients are assigned to therapists, their observations may become correlated over time through mutual interaction and common exposures, including exposure to the same therapist. Whatever the origin, the degree of within-therapist correlation is indexed with an ICC (Kenny, Mannetti, Peirro, Livi, & Kashy, 2002).

Like other correlations, ICCs can be positive or negative. Positive ICCs may reflect differential effectiveness among therapists due to their skill level in developing a working alliance with patients (cf. Baldwin, Wampold, & Imel, 2007), their general competence, their adherence to treatment protocols, or any variable that differs among therapists. A meta-analysis of ICCs from 15 psychotherapy clinical trials found that ICCs varied widely (range 0 to 0.729) with an average around 0.08 (Crits-Christoph et al., 1991). Similar results have been found in clinical trial data (Elkin, Falconnier, Martinovich, & Mahoney, 2006; Kim, Wampold, & Bolt, 2006) and clinical practice data (Baldwin, Wampold, & Imel, 2007; Lutz, Leon, Martinovich, Lyons, & Stiles, 2007; Okiishi, Lambert, Nielsen, & Ogles, 2003; Wampold & Brown, 2005). Ignoring positive ICCs increases the rate of Type I errors—that is, concluding that a treatment is effective when it is not (Cornfield, 1978; Zucker, 1990; Crits-Christoph & Mintz, 1991; Wampold & Serlin, 2000; Pals et al., 2008).

Negative ICCs could occur if patients responded to the same therapist differently; whereas most patients enter treatment functioning relatively poorly, some leave treatment functioning well, some do not change, and some deteriorate (Bergin, 1966). If this increased variability occurs more within therapists that between therapists, a negative ICC could result. Negative ICCs could occur if there is a competition among patients within a therapist, such as competition for attention from a therapist in a group therapy setting. Negative ICCs could occur if there is an unequal distribution of resources, such as a therapist getting burned out toward the end of a study. Ignoring negative ICCs reduces the Type I error rate and so reduces power—that is, mistakenly concluding that a treatment is ineffective (Kenny et al, 2002; Murray, Hannan, & Baker, 1996; Swallow & Monahan, 1984).

Regardless of whether the population ICC is positive or negative, large or small, ICCs can be estimated as positive or negative, large or small, due to sampling error. If the population value of the ICC is close to zero, ICCs will be estimated as negative about half the time. If the sample size is small, there will be less precision in the estimates, so that some estimates may be quite large or small relative to the population value, whether positive or negative. The best way to get an accurate estimate of the population value is to estimate the ICC from studies involving many therapists and patients or by pooling estimates from several smaller studies.

Expected within-therapist dependence must be addressed when the study is planned in order to ensure adequate power and to do so, investigators need good estimates of ICCs appropriate to their study. In the next sections of this paper, we report 495 ICC estimates drawn from 20 recent psychotherapy studies. In addition, we provide power formulae and illustrate how to use the ICCs from our database to plan future studies.

Intraclass Correlation Database

Studies

We identified potential studies in two ways. First, we performed manual searches for the years 2003–2004 of journals that regularly publish psychotherapy research (Journal of Consulting and Clinical Psychology, Journal of Counseling Psychology, Behavior Therapy, Behaviour Research and Therapy, Archives of General Psychiatry, American Journal of Psychiatry, Psychotherapy Research, and Cognitive Therapy Research). Recent issues were used to increase the likelihood that authors would be familiar with and interested in using their data in this study. We sampled broadly with respect to treatment type and design so that the database would be as useful as possible. Potential studies had to include at least one condition that involved an intervention aimed at reducing an emotional or behavioral problem. Therapy had to be delivered to individuals and not to groups. In addition, participants in the intervention conditions had to interact with a therapist. Given the increasing use of internet-based treatments, we included them if the treatment involved interaction with a therapist (e.g., supplemental phone calls). Finally, studies had to include at least two therapists per condition and each therapist had to see at least two patients so that we could distinguish between therapist and patient variability.

The manual search produced 38 potential studies. We wrote to the corresponding authors and asked them to perform several analyses that would allow us to compute ICCs (see below) and provide us with the output. We also invited the authors to join us as co-authors on the resulting manuscript. Sixteen authors agreed to participate in the study. Of the 22 authors who did not participate, the majority indicated time constraints as the reason. One study in our database was published after 2004 (Carlbring et al., 2006). The study we contacted the corresponding author about did not meet our inclusion criteria; however, the author suggested that we use data from a newer study instead. Because we wanted to calculate as many ICC estimates as possible we included Carlbring et al. (2006) in our database.

Our second method for identifying studies was to locate published ICC estimates from psychotherapy outcome studies. We performed an electronic literature search using the search terms intraclass correlation, therapist variability, or therapist effect. Additionally, we reviewed the reference section of articles on therapist effects. We located four new studies that published ICC estimates (Baldwin et al., 2007; Dinger, Strack, Leichsenring, Wilmers, & Schauenburg, 2008; Kim et al., 2006; Wampold & Brown, 2005).

Calculation of ICCs

We calculated ICCs from an ANOVA source table; therapist was included in the model as a fixed effect. The information from the source table was inserted into the following formula:

$$\widehat{\rho }=\frac{{MS}_{\mathit{\text{therapist}}}-{MS}_{\mathit{\text{error}}}}{{MS}_{\mathit{\text{therapist}}}+(\overline{m}-1){MS}_{\mathit{\text{error}}}}$$ (1)

where MS_therapist is the mean square for therapist, MS_error is the mean square for patient, and m̄ is the average number of patients per therapist; because the number of patients per therapist varied within studies, we used the harmonic mean. This formula is appropriate both for continuous outcomes (Snedecor & Cochran, 1989) and for dichotomous outcomes (Fleiss, Levin, & Paik, 2003). The ICC will be positive when MS_therapist > MS_error, negative when MS_therapist < MS_error, and zero only if MS_therapist = MS_error. Donner (1986) noted that this ANOVA estimator is consistent but slightly biased, though the degree of bias is usually ignorable.

We asked each study author to calculate a one-way ANOVA with therapist as the independent variable for each outcome variable separately at pretest and at posttest. We also requested an ANCOVA with therapist as the independent variable and the pretest value of the dependent variable as the covariate. To control for differences among treatment types, all analyses were done separately for each treatment condition. Each author provided us with the MS_therapist and MS_error from each ANOVA and ANCOVA, and the information needed to determine m̄. Thus, for each outcome variable and treatment type we calculated a pretest ICC (ρ̂_pre), a posttest-only ICC (ρ̂_post), and a posttest adjusted for pretest ICC (${\widehat{\rho }}_{\mathit{\text{post}}}^{\prime }$).

It is also possible to calculate ICCs from the output of a mixed-model ANOVA or ANCOVA. Such programs generally do not provide mean squares and instead provide estimates of components of variance. We did not use this approach because the default for most such programs is to constrain all estimates to be non-negative. As we discuss later, this approach prevents calculation of negative ICCs, with a number of unintended consequences.

Study Characteristics

Table 1 and Table 2 provide descriptive information about the 20 studies. Most treatments were behavioral or cognitive behavioral. Sixteen studies used a treatment manual. The number of sessions was fixed in some studies and allowed to vary in others. The number of sessions ranged from 1 to 22.9 (Mdn = 10.6). The number of therapists (k) ranged from 2 to 581 (Mdn = 5). The average number of patients per therapist (m) ranged from 2.2 to 51.1 (Mdn = 4.9). Table 2 provides the study-level averages for k and m. Eight studies used full-time clinicians, one used Ph.D. level clinical researchers, four used clinicians in training, two used both full-time clinicians and Ph.D. level clinical researchers, three used clinical researchers and clinicians in training, and two used full-time clinicians and clinicians in training.

Table 1.

Descriptive Information for Each Study Regarding Sample Size and the Intervention Delivered.

Study	N	Treated Problem	Treatment Type (# of Sessions)	Manual
Efficacy Studies
Abramowitz, Foa, & Franklin (2003)	40	Obsessive Compulsive Disorder	1. ERP – Intensive (15),	Yes
			2. ERP – Twice Weekly (15)
2. Carlbring et al. (2006)	30	Panic Disorder	1. Internet Based CBT with Supplemental Phone Calls (10)	Yes
3. Carroll et al. (2004)	104	Cocaine Dependence	1. CBT + Medication (12), 2. CBT + Placebo (12), 3. IPT + Medication (12), 4. IPT + Placebo (12)	Yes
4. Christensen et al. (2004)	134	Marital Distress	1. IBCT (22.9), 2. TBCT (22.9)	Yes
5. Ehlers et al. (2003)	28	Posttraumatic Stress Disorder	1. CT (11.4)	Yes
6. Kim et al. (2006)	86	Depression	1. CBT (16.2), 2. IPT(16.2)	Yes
7. Koch, Spates, & Himle (2004)	40	Small Animal Phobia	1. Behavioral Exposure (1), 2. Cognitive Behavioral Exposure (1)	Yes
8. Lange et al. (2003)	69	Posttraumatic Stress	1. Interapy (10)	Yes
9. Szapocznik et al. (2004)	129	HIV-Positive African Americans: Distress, Hassles, Support	1. SET (12.15), 2. PCA (6.78)	Yes
10. Taylor et al. (2003)	60	Posttraumatic Stress Disorder	1. EMDR (8), 2. Exposure (8), 3. Relaxation (8)	Yes
11. The Marijuana Treatment Project Research Group (2004)	276	Cannabis Dependence	1.2-Session MET (2), 2. 9-Session MET, CBT, & Case Management (9)	Yes
12. van Minnen, Hoogduin, Keijsers, Hellenbrand, & Hendriks (2003)	15	Trichotillomania	1. BT (6)	Yes
13. Watson, Gordon, Stermac, Kalogerakos, & Steckley (2003)	66	Depression	1. CBT (16), 2. PET (16)	Yes
Effectiveness Studies
14. Baldwin et al. (2007)	331	Mixed	1. TAU (7.32)	No
15. Dinger, Strack, Leichsenring, Wilmers, & Schauenburg (2008)	2554	Mixed (inpatients)	1. Inpatient TAUa	No
16. Kuyken (2004)	105	Depression	1. CT (14.11)	Yes
17. Lincoln et al. (2003)	147	Social Phobia	1. CBT (40)	Nob
18. Merrill, Tolbert, & Wade (2003)	186	Depression	1. CT (7.8)	Yes
19. Trepka, Rees, Shapiro, Hardy, & Barkham (2004)	30	Depression	1. CT (15.52)	Yes
20. Wampold & Brown (2005)	6146	Mixed	1. TAU (10.63)	No

Note: a = The specific number of sessions during the hospital stay was not available; b = Although there was no treatment manual for this study, the treatment was structured—in vivo exposure and cognitive restructuring; N = total sample size; CBT = Cognitive Behavior Therapy; CT = Cognitive Therapy; EMDR = Eye Movement Desensitization and Reprocessing; ERP = Exposure and Response Prevention; IPT = Interpersonal Therapy; IBCT = Integrative Behavioral Couples Therapy; MET = Motivational Enhancement Therapy; PCA = Person Centered Approach; PET = Process Experiential Therapy; SET = Structural Ecosystems Therapy; TBCT=Traditional Behavioral Couples Therapy; TAU=Treatment as Usual

Table 2.

Descriptive Information for Each Study Regarding Therapists.

Study	k	m	Type of Therapists	Therapist Training	Therapist Supervised
Efficacy Studies
1. Abramowitz et al. (2003)	5	2.87	FTC and CR	Yes	Yes
2. Carlbring et al. (2006)	3	7.43	CR and NC/CT	Yes	Yes
3. Carroll et al. (2004)	5.25	3.86	FTC and CR	Yes	Yes
4. Christensen et al. (2004)	7	8.39	FTC	Yes	Yes
5. Ehlers et al. (2003)	3	8.31	FTC	Yes	Yes
6. Kim et al. (2006)	17	5	FTC	Yes	Yes
7. Koch et al. (2004)	4	3.62	NC/CT	Yes	Yes
8. Lange et al. (2003)	18	2.92	NC/CT	Yes	Yes
9. Szapocznik et al. (2004)	3	18.40	CR and NC/CT	Yes	Yes
10. Taylor et al. (2003)	2	7.75	CR	Yes	Yes
11. The Marijuana Treatment Project Research Group (2004)	12	7.04	FTC	Yes	Yes
12. van Minnen et al. (2003)	5	2.51	NC/CT	Yes	Yes
13. Watson et al. (2003)	7.5	4.25	CR and NC/CT	Yes	Yes
Effectiveness Studies
14. Baldwin et al. (2007)	80	4.1	FTC and NC/CT	No	Noa
15. Diner et al. (2008)	50	51.1	FTC and NC/CT	No	Noa
16. Kuyken (2004)	20	3.32	FTC	Yes	Yes
17. Lincoln et al. (2003)	9.5	2.92	NC/CT	Yes	Yes
18. Merrill et al. (2003)	8	17.19	FTC	Yes	Yes
19. Trepka et al. (2004)	6	4.18	FTC	Yes	Yes
20. Wampold & Brown (2005)	581	9.68	FTC	No	No

Note. k = Study-level mean number of therapists contributing to any given intraclass correlation; m = Study-level mean number of patients per therapist contributing to any given intraclass correlation; CR = Clinical Researchers; FTC = Full Time Clinicians; NC/CT = Non-Clinicians/Clinicians in Training; a = Although there was supervision for the therapists in training, the supervision was not explicitly a part of the study.

Intraclass Correlation Estimates

We were able to compute N = 152 estimates of ρ̂_pre, N = 170 estimates of ρ̂_post, and N = 164 estimates of ${\widehat{\rho }}_{\mathit{\text{post}}}^{\prime }$. There were fewer estimates of ρ̂_pre and ${\widehat{\rho }}_{\mathit{\text{post}}}^{\prime }$ than ρ̂_post because several outcome variables involved behavior during treatment or were posttest only variables, making baseline values or adjusting for baseline values impossible. Additionally, we located N = 1 published estimates of ρ̂_post and N = 8 published estimates of ${\widehat{\rho }}_{\mathit{\text{post}}}^{\prime }$. The number of estimates per study ranged from 1 to 36 (Mdn = 6) for ρ̂_pre, 1 to 42 (Mdn = 6) for ρ̂_post and 1 to 36 for ${\widehat{\rho }}_{\mathit{\text{post}}}^{\prime }$ (Mdn = 5.5). A table listing all ICCs is available from the first author or can be downloaded at http://psychology.byu.edu/Faculty/SBaldwin/Home.dhtml.

The distributions for ρ̂_pre, ρ̂_post, ${\widehat{\rho }}_{\mathit{\text{post}}}^{\prime }$ were symmetric and quite similar. The estimates for ρ̂_pre ranged from −.475 to 0.579 (Q1 = −.099, Q2 = −.014, Q3 = 0.063) and 54.6% were negative. The estimates for ρ̂_post ranged from −.345 to .532 (Q1 = −.113, Q2 = −.026, Q3 = .046) and 63.7% were negative. The estimates for ${\widehat{\rho }}_{\mathit{\text{post}}}^{\prime }$ ranged from −.343 to .45 (Q1 = −.104, Q2 = −.018, Q3 =.079) and 57% were negative.

Applications

Selecting and Combining Estimates

Researchers can use these ICC estimates to plan future psychotherapy studies involving therapists nested within conditions. When multiple ICC estimates are available, the precision of the power calculations can be increased by meta-analytically combining them (Blitstein et al., 2005). Methodologists typically recommend that researchers only aggregate estimates from studies that are closely matched to their planned study (Blitstein et al., 2005; Murray, 1998). For example, Blitstein et al. recommend that researchers only combine estimates from studies that had outcomes, research designs, and statistical analyses similar to those planned for the new study. That recommendation is based on the authors' experience that ICCs vary appreciably as a function of those variables.

We followed Blitstein et al.’s recommendation and combined estimates that came from the same measure, research design, and statistical model. Specifically, we combined ICC estimates for the Beck Depression Inventory (BDI; Beck, Ward, Mendelson, Mock, & Erbaugh, 1961), the most common measure in our database (N = 12, one study used the BDI-II; Beck, Steer, & Brown, 1996) and we combined estimates separately for efficacy (N = 8) and effectiveness studies (N = 4), as some have speculated that ICCs from efficacy studies may be smaller than ICCs from effectiveness studies because of the higher levels of control and standardization in efficacy studies (Elkin et al., 2006). We used a Q-test to determine whether there was significant heterogeneity among the ICCs and I² to determine the proportion of the total variation in the ICCs that is due to heterogeneity rather than chance (Higgins & Thompson, 2002). We report only the results from the adjusted posttest analyses because adjusted analyses are more common than unadjusted analyses, though in general, results from the unadjusted analyses were similar.

For the BDI data, the random effects mean ICC for the effectiveness studies was ρ̄′ = 0.049 and not statistically significant (p = 0.335). There was no heterogeneity among the estimates (I² = 0, Q(3) = 0.981, p = 0.821), suggesting that the mean ICC is a good estimate for power calculations. For the efficacy studies the mean ICC was ρ̄′ = −0.073 and not statistically significant (p = 0.21). Heterogeneity was large and statistically significant (I² = 75.49, Q(7) = 24.478, p < .001). Thus, the mean ICC from the efficacy studies would not be a good estimate for power calculations. This may be a consequence of the fact that three of the four effectiveness studies involved cognitive therapy for the treatment of depression, whereas the efficacy studies were more heterogeneous and involved a variety of treatments aimed at a variety of problems. In situations like this, the investigator should choose the individual study that most closely matches the planned study and use the ICC estimate from that study to plan the new study.

There is one important caveat to remember regarding the selection of ICC estimates for power calculations. When the population ICC is close to zero, the probability that the ICC will be estimated as negative is high; further, the probability increases as the number of patients per therapist decreases. When the negative value is likely the result of sampling error, it would be imprudent to assume that the ICC in the new study will also be negative. If the investigator makes that assumption, but the ICC in the new study proves to be positive, the new study may be substantially underpowered. On the other hand, if the investigator takes a conservative approach, and uses a positive ICC in the power calculations, the investigator will have some insurance against an underpowered study and will have extra power if the ICC in the new study turns out to be smaller than the value used in the power calculations. For this reason, we recommend that when the best ICC estimate is negative and based on a large number of therapists, researchers use a small, but positive ICC (e.g., 0.01) in their sample size calculations. This a conservative approach, but will ensure that sample size will be sufficient even if the ICC proves to be small but positive. When the estimate is negative and based on a small number of therapists, we recommend that researchers use a larger positive ICC (e.g., .025 or .05) or a range of values (e.g., 0, .025, .05) to see how sample size requirements change as the ICC varies. The goal is to avoid underestimating the ICC, which would underpower the new study, but also to avoid overestimating the ICC, which would lead to a new study that was larger than it needed to be. This situation is particularly challenging for psychotherapy research, where most of the existing studies are small.

Example Power Analyses

We now present detectable difference formulae that can be used to plan new psychotherapy trials where therapists will be nested within conditions. We illustrate the use of the formulae for two common designs: a trial comparing two treatments involving therapists and a trial comparing a treatment involving therapists to a condition that does not.

Detectable Difference – Treatment versus Treatment

The formula for this detectable difference is adapted from Murray (1998):

$$\mathrm{\Delta }=\sqrt{{\sigma }_y^2(\frac{(1+(m_1-1){\rho }_1)}{N_1}+\frac{(1+(m_2-1){\rho }_2)}{N_2}){(t_{\mathit{\text{critical}}:\alpha /2}+t_{\mathit{\text{critical}}:\beta })}^2}$$ (2)

where Δ is the detectable difference between condition means (i.e., the treatment effect); ${\sigma }_y^2$ is variance of the dependent variable; m₁ and m₂ are the number of patients per therapists for treatment condition one and two; ρ₁ and ρ₂ are the ICCs for treatment condition one and two; N₁ and N₂ are the number of participants in condition one and two; t_{critical:α/2} is the critical value for t needed to ensure the Type I error rate is α given a two-tailed test and available degrees of freedom; and t_critical:β is the critical value for t needed to ensure the Type II error rate is β.

In the approach we present, the degrees of freedom for t_{critical:α/2} and t_critical:β are k₁ + k₂ − 2, where k₁ and k₂ are the number of therapists in condition one and two. However, there may be situations (e.g., highly unbalanced designs, small ICCs) where the Satterthwaite (1946) approximation may be needed (Roberts & Roberts, 2005). When using our approach, we recommend that k₁ and k₂ be equal, as this protects against inflated Type I error rates when there is heteroscedasticity in the therapist variance component (Gail, Mark, Carroll, Green, & Pee, 1996). Roberts and Roberts (2005) argue that if ρ₁ ≠ ρ₂ and/or m₁ ≠ m₂, power will be maximized for a given sample size by allocating more patients to the condition with the greatest variance inflation. However, their optimal allocation ratio assumes a fixed total sample size and static values for m₁ and m₂, requiring imbalance in k₁ and k₂. In light of Gail et al.’s (1996) findings, we recommend that researchers compare various combinations of m₁ and m₂ —ensuring that k₁ = k₂—to find the most powerful combination of values given the study’s hypotheses and budgetary constraints.

Detectable Difference – Treatment versus Comparison Condition

Equation (2) requires a slight modification for designs comparing a treatment involving therapists (condition one) to one that does not (condition two). Because the patients in the comparison condition do not interact with each other or with a common therapist, observations in the comparison condition are independent, ρ₂ = 0 and Equation (2) reduces to:

$$\mathrm{\Delta }=\sqrt{{\sigma }_y^2(\frac{(1+(m_1-1){\rho }_1)}{N_1}+\frac{1}{N_2}){(t_{\mathit{\text{critical}}:\alpha /2}+t_{\mathit{\text{critical}}:\beta })}^2}$$ (3)

A reasonable estimate for the degrees of freedom for this design is k₁ + N₂ − 2, though there may be situations where the Satterthwaite approximation may be needed.

Because therapists are involved in only one condition, imbalance in the number of therapists per condition is unavoidable. When the ICC due to therapist is greater than zero, power will be maximized by allocating more patients to the condition involving therapists. The optimal allocation ratio (R) is (Roberts & Roberts, 2005):

$$R=\sqrt{(1+(m_1-1){\rho }_1)}$$ (4)

where ρ₁ is the ICC and m₁ is the number of patients per therapist in the condition involving therapists. If ρ₁ =.15 and m₁ = 10, R equals 1.53. Power will be maximized for a given total sample size (N_T) if N₁ is 1.53 times the size of N₂. N₁ and N₂ can be calculated from N_T and R:

$$N_1=\frac{N_{T}R}{R+1}$$ (5)

$$N_2=\frac{N_T}{R+1}$$ (6)

Example Power Analysis – Treatment versus Treatment

Suppose we want to design an effectiveness study to compare cognitive therapy for depression versus treatment-as-usual (TAU). We plan to randomly assign patients to receive 16 sessions of either cognitive therapy or TAU. A primary outcome measure will be the BDI, which the patients will complete prior to treatment and immediately following the 16th session. We would like to determine the detectable difference for the BDI, assuming 80% power, a two-tailed test, a Type I error rate of 5%, and anticipated sample size.

We will estimate treatment effects with an analysis of posttest BDI data adjusted for the baseline value of the BDI. We would like to recruit 200 total participants and would like to recruit 10 therapists for each condition (k₁ = k₂ = 10). Thus, each therapist will see 10 patients (m₁ = m₂ = 10), making the sample size for each condition 100 (N₁ = N₂ = 100). Given the analysis plan, we use the aggregate ICC estimate for the BDI from effectiveness studies calculated above (ρ̄′ = 0.05). We assume ρ̄′ will be equivalent in the CT and TAU conditions (ρ₁ = ρ₂). Because we are using a standardized metric, in this case Cohen’s d, ${\sigma }_y^2$ is one. The values for the t-variates are taken from the t-distribution with 10 + 10 − 2 = 18 df.

To determine the detectable difference we insert the relevant values into Equation (2):

$$.505=\sqrt{1(\frac{(1+(10-1).05)}{100}+\frac{(1+(10-1).05)}{100}){(2.101+0.862)}^2}$$

Thus, with 10 therapists per condition, each seeing 10 patients, and assuming ρ₁= ρ₂ = 0.05 we would have 80% power to detect a treatment effect of d =.505. Given that the hypothetical study compares two active treatments, we would likely want to detect a smaller effect size. We can easily vary the values in Equation (2) to reflect the assumptions we make about the data. For example, suppose we can increase our total sample size to 260 patients by including more therapists per condition, more patients per therapist, or some combination. The first five columns of Table 3 illustrate the effects of manipulating either the number of therapists per condition or patients per therapist to bring the total sample size to 260. As can be seen in Table 3, increasing the number of therapists per condition has a greater effect on the detectable difference than increasing the number of patients per therapist. Likewise, power is increased if the number of patients per therapist is balanced across conditions. Both points are quite general and well established in the literature on group-randomized trials (Donner & Klar, 2000; Murray, 1998).

Table 3.

Detectable difference varying the number of therapists per condition, patients per therapist, and intraclass correlation.

				ρ1 =.05	ρ1 =.10	ρ1 =.15	ρ1 =.20
k1	k2	m1	m2	ρ2 =.05	ρ2 =.01	ρ2 =.01	ρ2 =.01
13	13	10	10	.436	.443	.475	.505
10	10	16	10	.473	.483	.523	.561
10	10	14	12	.466	.475	.516	.554
10	10	13	13	.465	.474	.515	.552
10	10	12	14	.466	.474	.515	.552
10	10	10	16	.473	.479	.519	.556

Note. k₁, k₂ = the number of therapists in condition one and two; m₁, m₂ = the number of patients per therapists in condition one and two; ρ₁ρ₂ = the intraclass correlation for condition one and two The power analyses assume 80% power, 5% Type I error rate, and two-tailed tests. The detectable difference is in the standardized mean difference metric (d).

Up to this point, we assumed that ρ₁ and ρ₂ were equivalent. However, it is possible for ρ₁ and ρ₂ to differ systematically. Columns six through eight of Table 3 provide detectable difference values where ρ₁ and ρ₂ differ for the increased sample size of 260. For a given value of ρ₂, the detectable difference will increase as ρ₁ increases. As before, power is maximized by increasing the number of therapists per condition and balancing the patients per therapist.

Example Power Analysis – Treatment versus Comparison Condition

Consider another effectiveness study where we evaluate the effects of cognitive therapy (condition 1) for depression versus bibliotherapy (condition 2) and use a design similar to the study described above: random assignment to conditions, two time points, 16-weeks of treatment, and the BDI as a primary outcome variable. As before, we will estimate treatment effects with an analysis of posttest BDI data adjusted for the baseline value of the BDI and we will use the aggregate ICC estimate for the BDI effectiveness studies (ρ̄′ = 0.05). We would like to recruit approximately 150 patients (N_T = 150) and would like the therapists in the cognitive therapy condition to treat 10 patients each (m₁ = 10). The optimal allocation ratio (R) is:

$$1.20=\sqrt{(1+(10-1)0.05)}$$

so that the cognitive therapy condition should have 1.20 times as many patients as the bibliotherapy condition.

Using R and N_T we calculate N₁ and N₂ as follows:

$$N_1=81.82=\frac{150*1.20}{1.20+1}{N}_2=68.18=\frac{150}{1.20+1}$$

N₁ will need to be rounded to 90 as that will provide an integer value for the number of therapists in the cognitive therapy condition. As there are no therapists in the bibliotherapy condition, we round N₂ to 75 to maintain allocation ratio of 1.20. The values for the t-variates are taken from the t-distribution with 9 + 75 − 2 = 82 df.

We insert the relevant values into Equation (3) to determine the detectable difference:

$$.487=\sqrt{1(\frac{(1+(10-1)0.05)}{90}+\frac{1}{75}){(1.99+.85)}^2}$$

Thus, with a total sample size of 165 patients, with nine therapists each seeing 10 patients in the cognitive therapy condition and 75 patients in the bibliotherapy condition, we would have 80% power to detect a treatment effect of d =.487. As before, we can vary the parameters in Equation (3) as needed.

Discussion

Estimated Intraclass Correlations

The distributions for ρ̂_pre, ρ̂_post, and ${\widehat{\rho }}_{\mathit{\text{post}}}^{\prime }$ as calculated in this study were symmetric and quite similar. The 25^th, 50^th, and 75^th percentiles were −0.099, −0.014, and 0.063 for ρ̂_pre, −0.113, −0.026, and 0.046 for ρ̂_post, and −0.104, −0.018, and 0.079 for ${\widehat{\rho }}_{\mathit{\text{post}}}^{\prime }$. Importantly, 54.6%, 63.7%, and 57% of the estimates for ρ̂_pre, ρ̂_post, and ${\widehat{\rho }}_{\mathit{\text{post}}}^{\prime }$ were negative. Noting that all previously published estimates were positive with an average value of about 0.08, we conducted a series of post hoc investigations help us understand the apparent discrepancy.

Inspection of the published ICCs in psychotherapy research revealed that those investigators likely did not allow negative values (e.g., Crits-Cristoph et al., 1991). This practice is so common that it has a name (the non-negativity constraint, Swallow & Monahan, 1984) and is the default in many software packages used to estimate components of variance (e.g., SAS PROC MIXED, HLM). This practice reflects the common interpretation of an ICC as the proportion of variance, which cannot be negative; as a result, many researchers fix negative ICC estimates to zero (c.f., Maxwell & Delaney, 2004). At the same time, this practice ignores the more general meaning of an ICC as a correlation, which can be negative (Kenny et al., 2002, p. 127; Pinheiro and Bates, 2000, p. 228; Snedecor & Cochran, 1989, p. 243; Kish, 1965, p. 163). We hypothesized that the apparent discrepancy between the published ICCs and our own findings was do to the non-negativity constraint in the calculation of the ICCs in the published studies.

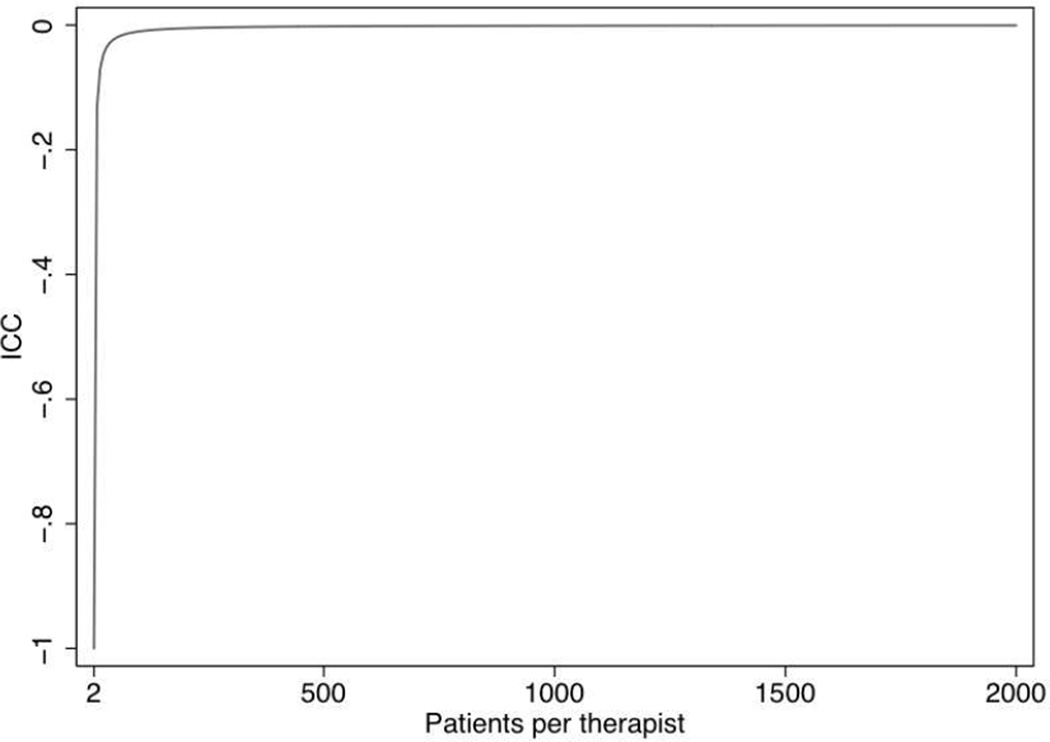
The theoretical range of ICCs is −1/(m - 1) to 1 (Kenny et al., 2002; Pinheiro & Bates, 2000; Snedecor & Cochran, 1989; Kish, 1965, p. 163). Thus, if each therapist sees two patients, ICCs can range from −1 to 1. If each therapist sees three patients, ICCs can range from −0.5 to 1. If each therapist sees 10 patients, ICCs can range from −0.11 to 1. As m approaches infinity the lower bound of the ICC approaches zero (see Figure 1). Given that m in the studies examined for this paper ranged from 2.2 to 51.1, ICCs could range from −0.83 to 1 in the smallest study and from −0.02 to 1 in the largest study; the observed range was −0.475 to 0.579.

Figure 1.

The relationship between the number of patients per therapist and the lower bound of an intraclass correlation (ICC).

We used Monte Carlo simulation to investigate the impact of m on the frequency of negative ICC estimates. We also varied k (the number of therapists) and the population ICC. We allowed m to equal 2, 4, 8, 32, 64, 128, or 256, k to equal 5, 10, 20 or 40, and the ICC to equal −0.001, 0.001, 0.05, and 0.1. We generated 1500 data sets for each cell in the simulation. For each replication we estimated a one-way ANOVA and used Equation (1) to calculate the ICC. All data were generated and analyzed in Stata (version 11; StataCorp, 2009).

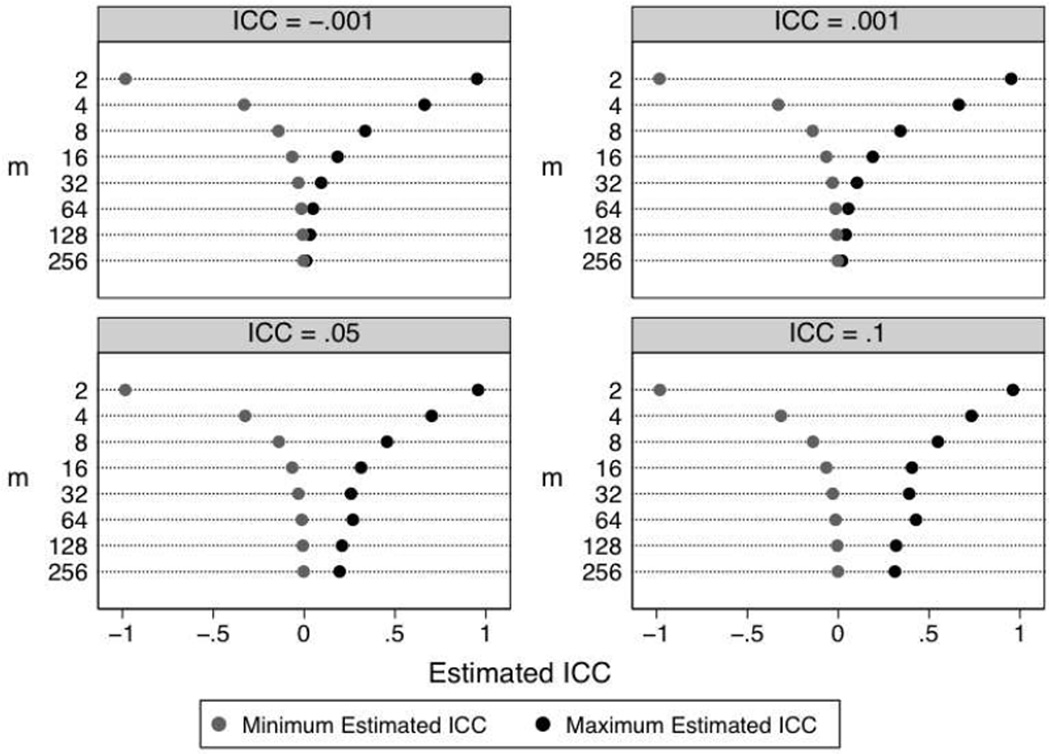
Table 4 presents the percentage of negative estimates by m, k, and population ICC. Three patterns emerge from the results. First, when m and k were relatively small, many of the estimates were negative. When k = 5 and m = 4, similar to the median values in our sample of studies, the percentage of negative ICCs ranged from 40% to 57%. Second, as cluster size increased, the number of negative ICCs declined except when the population ICC was −.001. In that case, increasing k and m increased the percentage of negative estimates. Third, k had less influence on the proportion of negative estimates than m, especially when m was small. Together, these results suggest that our observed ICCs are very plausible given the sample sizes in our sample of studies and common in psychotherapy research (see also Figure 2).

Table 4.

Percentage of negative intraclass correlation estimates in simulated data.

ICC
	−.001				.001				.05				.10
m	k = 5	k = 10	k = 20	k = 40	k = 5	k = 10	k = 20	k = 40	k = 5	k = 10	k = 20	k = 40	k = 5	k = 10	k = 20	k = 40
2	51	50	52	49	51	50	52	48	46	45	44	36	43	39	36	26
4	57	56	55	53	57	55	54	52	48	43	33	25	40	32	20	09
8	61	58	55	54	60	57	53	51	44	29	19	09	31	15	06	01
16	61	57	56	55	59	54	52	50	29	17	06	01	16	05	01	00
32	62	60	57	59	58	55	50	48	18	06	01	00	07	01	00	00
64	63	62	62	63	56	51	48	41	08	01	00	00	03	00	00	00
128	66	67	69	74	52	47	40	31	03	00	00	00	01	00	00	00
256	76	80	84	92	48	38	29	18	01	00	00	00	00	00	00	00

Note. m = patients per therapist; k = therapists; ICC = intraclass correlation

Figure 2.

Simulated minimum and maximum values of the intraclass correlation (ICC) stratified by patients per therapist (m) and population ICC. Each cell of the simulation was replicated 1500 times. The number of therapists (k) was five. The pattern of results with other values of k was similar. Full results are available from the first author.

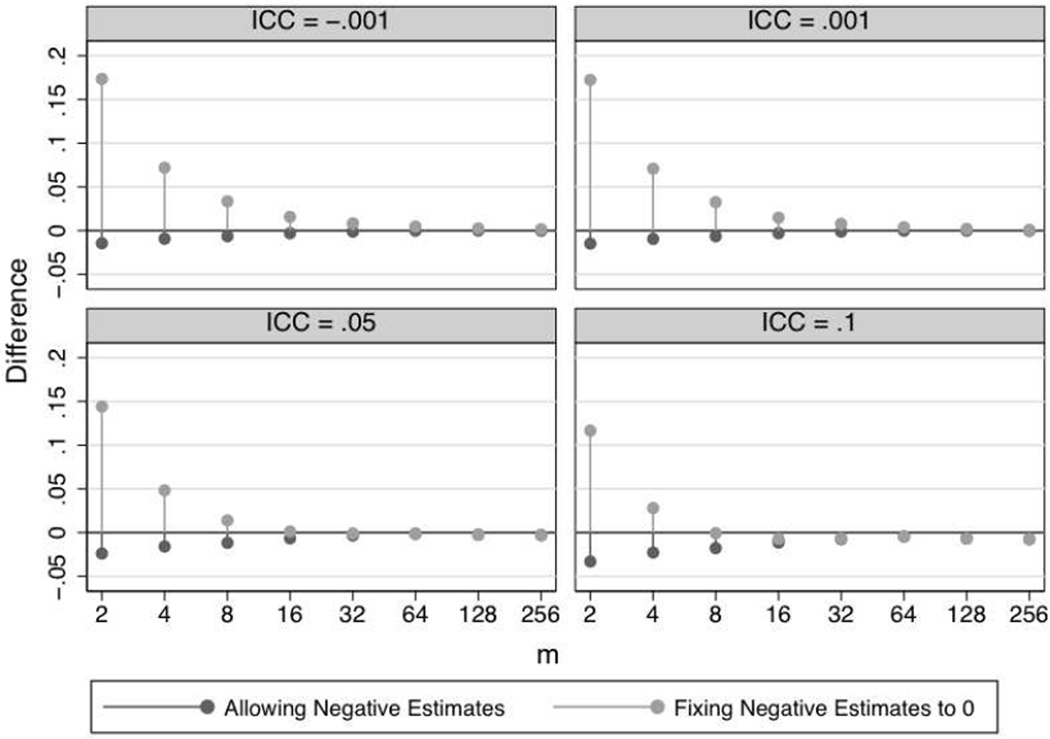
Fixing negative values to zero creates an upward bias in the ICC estimate. To test our post hoc hypothesis about the non-negativity constraint, we calculated the bias that would occur by fixing negative values to zero in our simulated data. We calculated ICCs twice, first allowing negative estimates, and second fixing the negative estimates to zero. We calculated the bias in each case by subtracting the population ICC from the mean estimated ICC across the 1500 replications for each cell. A positive result indicates that the mean ICC overestimated the population ICC whereas a negative result indicates that the mean ICC underestimated the population ICC. Figure 3 displays the magnitude of bias across levels of m and the population ICC. Figure 3 only presents results for k = 5, although the pattern of results was the same across all levels of k. When we allowed for negative estimates, there was a very slight negative bias when m was very small, especially for smaller ICCs, and no bias when m was larger. When we fixed negative estimates to zero, there was a much larger positive bias when m was small, especially for smaller ICCs, and no bias when m was larger.

Figure 3.

Difference between the average estimated intraclass correlation (ICC) and the population ICC stratified by patients per therapist (m) and population ICC. Each cell of the simulation was replicated 1500 times. The number of therapists (k) was five. The pattern of results with other values of k was similar. Full results are available from the first author.

Recall that a meta-analysis of ICCs averaged about 0.08 based on a median m of about 7. If the population ICC in those studies was really −0.001, Figure 3 suggests that fixing negative estimates to zero would result in a bias of about 0.04, for an estimated average ICC of 0.039. If the population ICC in those studies was really 0.05, Figure 3 suggests that fixing negative estimates to zero would result in a bias of about 0.025, for an estimated average ICC of 0.075. Thus it is quite likely that if the published estimates employed the non-negativity constraint, the true average ICC is between 0.001 and 0.05. This would largely explain the apparent discrepancy between our findings and the previously published results. Taken together, the results of our simulations provide considerable support for the validity of the estimates we report in this paper.

Implications for Future Research

Statistical dependencies within therapists are an important methodological issue that affects interpretation of intervention trials. This is true whether the dependencies are pre-existing, are due to the therapist, or have some other origin. To address this issue, researchers must account for dependencies when planning their studies and when analyzing their data. To plan studies adequately, researchers need ICC estimates; researchers also need to know how to select and use those estimates. Our primary aims were (a) to report an initial database of ICC estimates associated with therapist for a variety of measures and treatment conditions from a sample of recently published studies in leading psychotherapy journals and (b) to provide guidelines for the selection and use of ICC estimates for power calculations.

This study has made clear that the size of typical psychotherapy studies leads to imprecise ICC estimates, especially compared to other disciplines. For example, the ICC estimates for academic achievement reported in Hedges and Hedberg (2007) were based on hundreds and sometimes thousands of schools and thousands of students. In the current database, the median number of therapists contributing to an ICC was five and the median number of patients per therapist was five. Although these values can be reasonably increased in future studies, most psychotherapy studies typically have relatively small numbers of therapists (less than 20) each treating a modest amount of patients (10–20). Thus, ICC estimates in psychotherapy research will rarely match the precision of ICC estimates in other disciplines. As a result, we recommend that researchers use a range of estimates. This will become less of an issue as the ICC database gets larger because researchers will be able to meta-analytically combine estimates from many studies. Therefore, it is critical for researchers to contribute to the ICC database by routinely reporting ICC estimates.

The results of the illustrative power analyses underscore three points. First, when the ICC is greater than zero, power to detect a treatment effect is reduced as compared to when the ICC is zero (or negative). Consequently, planning for statistical dependence when designing studies is essential. If researchers do not attend to these issues until the analysis stage of their study, a proper analysis will be underpowered to detect a treatment effect despite having an otherwise well designed study. Second, when comparing a treatment involving therapists to a comparison condition that does not, power will be maximized by allocating more patients to the treatment condition. As Roberts and Roberts (2005) point out, if the treatment is more effective than control, this unequal allocation has the practical benefit of providing the treatment to more people. Third, reducing the ICC via standardization (Crits-Christoph, Tu, & Gallop, 2003) or covariates (Murray & Blitstein, 2003), may produce the biggest increase in power at the lowest cost, followed by increasing the number of therapists, and then increasing the number of patients per therapist.

The aggregate ICC estimates were not statistically significant. Consequently, investigators might be tempted to conclude that the ICCs can be ignored or that we should conduct an initial significance test for the ICC and only model therapists as a random effect if it is significant (cf. Crits-Christoph et al., 2003). We disagree strongly for three reasons. First, the power to detect a significant ICC is typically too low to allow such tests to be trustworthy, even with liberal p-values or in a meta-analysis (Kenny, Kashy, & Bolger, 1998; Murray, 1998; Roberts & Roberts, 2005). For example, if a study included 5 therapists per condition with 10 patients per therapist, the study would have only 23% power to detect an ICC of .05. A study with 10 therapists per condition with 10 patients per therapist would have only 37% power to detect an ICC of .05 (Winer, Brown, & Michels, 1991). Thus, even if a study is adequately powered to detect a desired treatment effect when the population ICC is .05, it may include too few therapists to be adequately powered to detect an ICC of that size. Trustworthy significance tests in meta-analysis will not likely be available until researchers consistently report ICCs. Second, even if ICCs are estimated as zero or close to zero, the degrees of freedom still need to be based on the number of therapists, not the number of patients (Baldwin et al., 2005; Murray et al., 1996; Pals et al., 2008). Third, the problems created by statistical dependence do not depend upon the statistical significance of the ICC estimate (Kenny et al., 2002; Murray, 1998; Roberts & Roberts, 2005), and instead are a function of both the magnitude of the ICC and the number of patients treated by each therapist. Consequently, we join methodologists in public health and psychology and recommend that researchers model the dependencies in their data regardless of the statistical significance of the ICC to safeguard the Type I error rate in their studies (Donner & Klar, 2000; Kenny et al., 2002; Murray, 1998).

Conclusions

Accounting for statistical dependencies associated with therapist has proven to be a significant challenge in psychotherapy research. A major hurdle has been that accounting for statistical dependencies increases the cost and complexity of the already expensive and difficult process of psychotherapy research. Indeed, accounting for statistical dependencies associated with therapist involves not only recruiting more patients, but recruiting, training, and supervising more therapists. Nevertheless, accounting for statistical dependencies is a priority because ignoring them threatens the validity of the inferences drawn about treatment efficacy. Several disciplines face similar methodological challenges, such as education and public health. Researchers in these disciplines have begun to adapt their research design and analytic methods to address these issues (Varnell, Murray, Janega & Blitstein, 2004; Murray, Pals, Blitstein, Alfano, & Lehman, 2008). We hope that the material presented in this report will help psychotherapy researchers move in the same direction.