Photosystem II Does Not Possess a Simple Excitation Energy Funnel: Time-Resolved Fluorescence Spectroscopy Meets Theory

Abstract

The experimentally obtained time-resolved fluorescence spectra of photosystem II (PS II) core complexes, purified from a thermophilic cyanobacterium Thermosynechococcus vulcanus, at 5–180 K are compared with simulations. Dynamic localization effects of excitons are treated implicitly by introducing exciton domains of strongly coupled pigments. Exciton relaxations within a domain and exciton transfers between domains are treated on the basis of Redfield theory and generalized Förster theory, respectively. The excitonic couplings between the pigments are calculated by a quantum chemical/electrostatic method (Poisson-TrEsp). Starting with previously published values, a refined set of site energies of the pigments is obtained through optimization cycles of the fits of stationary optical spectra of PS II. Satisfactorily agreement between the experimental and simulated spectra is obtained for the absorption spectrum including its temperature dependence and the linear dichroism spectrum of PS II core complexes (PS II-CC). Furthermore, the refined site energies well reproduce the temperature dependence of the time-resolved fluorescence spectrum of PS II-CC, which is characterized by the emergence of a 695 nm fluorescence peak upon cooling down to 77 K and the decrease of its relative intensity upon further cooling below 77 K. The blue shift of the fluorescence band upon cooling below 77 K is explained by the existence of two red-shifted chlorophyll pools emitting at around 685 and 695 nm. The former pool is assigned to Chl45 or Chl43 in CP43 (Chl numbering according to the nomenclature of Loll et al. Nature2005, 438, 1040) while the latter is assigned to Chl29 in CP47. The 695 nm emitting chlorophyll is suggested to attract excitations from the peripheral light-harvesting complexes and might also be involved in photoprotection.

Introduction

Photosystem II (PS II) plays a crucial role in the photoinduced water oxidation in oxygenic photosynthesis of plants, cyanobacteria, and algae.¹ The water oxidation catalyzed by the Mn–Ca cluster in PS II results in emission of oxygen molecules as residual, which most of aerobia on the earth rely on. The proteins constituting PS II bind a large number and several kinds of pigment molecules, such as, chlorophyll-a (Chl-a), pheophytin-a (Pheo-a), β-carotene, and plastoquinone. Most of the pigments are bound in light-harvesting antennae, and only a minor number of a different type, including Chl-a, Pheo-a, and plastoquinones, are used as electron carriers along the electron-transfer chain in the reaction center.

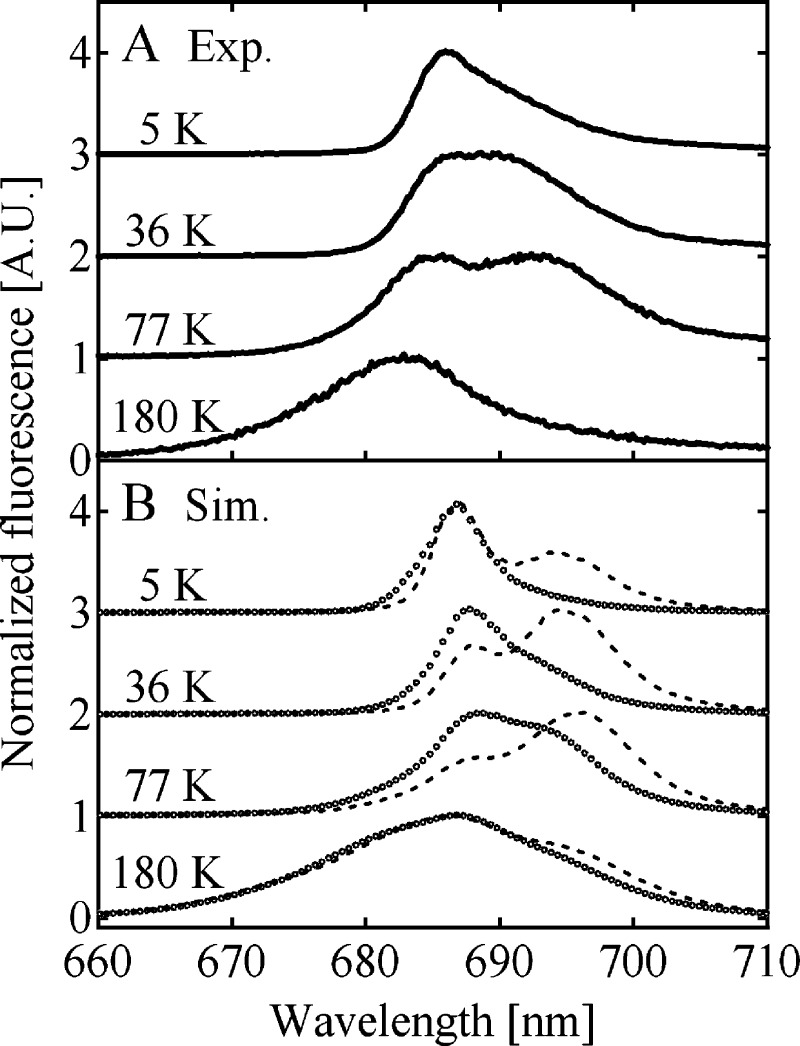
During the past decade, the spatial resolution of the crystallographically determined structures of PS II has been continuously improving.²⁻⁴ In 2011, Umena et al. have reported the crystal structure of PS II with 1.9 Å spatial resolution,⁴ which presently provides the most detailed structure, in particular of the Mn–Ca cluster. This study undoubtedly represents a great step toward elucidating the water-oxidation mechanism in PS II. The improved structural information also offers greater opportunities for a structure-based simulation of the light-harvesting dynamics of the antenna system of PS II. PS II has been known to show a peculiar temperature dependence of the fluorescence spectrum.⁵⁻⁷ Figure 1A shows the temperature dependence of the fluorescence spectrum of the PS II core complex (PS II-CC) preparation from a thermophilic cyanobacterium, Thermosynechococcus vulcanus. The data displayed in Figure 1A were obtained by time integrals of our time–wavelength 2-D images obtained by a streak scope setup. Lowering temperature down to 77 K results in an emergence of a sub-band at around 695 nm, which hereafter we call F695 according to its peak wavelength. This apparent red shift of the fluorescence peak upon cooling suggests the existence of Chl pool(s) with lower excited-state energy(ies) than the primary donor (PD) on which the first photoinduced charge separation takes place. Figure 1A shows that the relative intensity of F695 again decreases upon further cooling. At 5 K, the main fluorescence band is located at around 685 nm; hereafter we call this band F685. The blue shift of the fluorescence peak below 77 K is against the expectation because lowering temperature in general suppresses thermal activations of uphill energy transfers, and so one might expect a further enhancement of the fluorescence originating from F695. It is quite timely and pertinent to examine whether this peculiar temperature dependence of the PS II fluorescence spectrum can be explained on the basis of the fine structural information now available.

Figure 1.

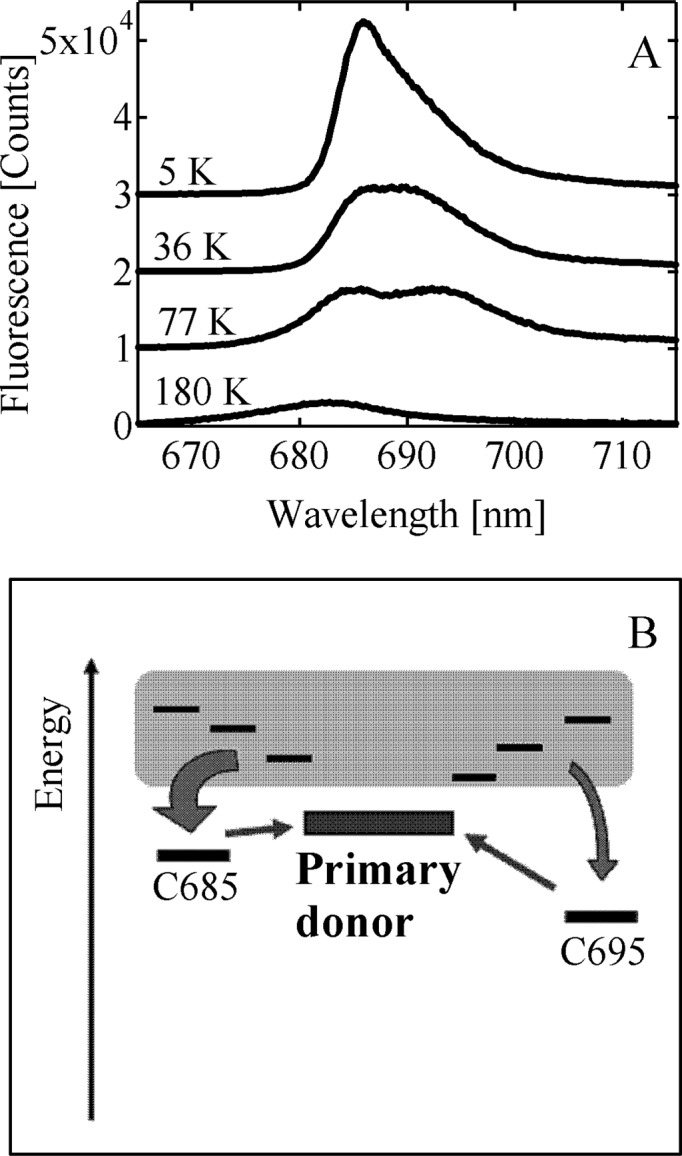
(A) Temperature dependence of the fluorescence spectrum of PS II-CC dimer from T. vulcanus. The excitation wavelength was 430 nm. (B) Schematic description that accounts for the spectral change of the PS II fluorescence spectrum upon lowering temperature. Thin horizontal lines within the gray box indicate the exciton levels with higher excited-state energies than that of the primary electron donor. Those of the red-shifted Chls, C685, and C695 are indicated by the thick horizontal lines below the gray box. The excited state of the primary donor is shown with the closed box. Arrow shows the excitation-energy flow, and its thickness indicates a rough measure of the energy flux.

A qualitative explanation for the experimental observation shown in Figure 1A can be given by assuming two different pigment pools, both having lower excited-state energies than that of PD. This model is schematically depicted in Figure 1B. We designate hereafter the two pigment pools as “C685” and “C695” according to their fluorescence peak wavelengths. At 77 K, the energy gap between C695 and PD becomes inaccessible by the thermal energy, while the uphill energy transfer from C685 to PD is still active, and then an excited state is trapped on C695 resulting in the enhancement of F695. Further lowering temperature suppresses the uphill energy transfer from C685 to PD as well, and therefore the relative intensity of F685 increases.

As described above, the overall tendency of the observation could be explained on the basis of the qualitative model in Figure 1B. It has been established that C695 resides in the tightly bound proximal antenna protein, CP47, according to the similarity of the low-temperature fluorescence peak positions between the isolated CP47 and PS II-CC.⁵⁻¹¹ C685, on the other hand, has been considered to be bound to the other proximal antenna, CP43,^7,8 although the involvement of the pigments in CP47 cannot be excluded. Many research groups have assigned C695 to Chl29 (Chl numbering throughout this paper is according to the nomenclature of Loll et al.)² in CP47 on the basis of the site-directed mutation study,⁹ the negative linear dichroism component in the red tail of the absorption spectrum of CP47.¹⁰ The theoretical study by Raszewski and Renger¹² also supported this assignment. Their study also suggested that C685, tentatively assigned to the lowest excited state in CP43, is contributed mainly from Chl37 in CP43.

Recent studies by the Jankowiak group,^11,13 on the other hand, raised a question on the above assignment of C695 to Chl29. They indicated that the fluorescence peak position of CP47 is highly preparation dependent.¹³ It was shown that storing of a diluted CP47 solution at 77 K considerably degrades the protein and results in the blue shift of its fluorescence peak at 5 K. They suggested that the above assignment of C695 to Chl29 was based on the optical spectra of partly degraded CP47 samples. They also showed that the high efficiency of nonphotochemical hole burning (NPHB) at lower temperatures is partly a cause of the blue shift of the fluorescence spectrum of CP47 upon lowering temperature. According to the fitting of the absorption, fluorescence, and HB spectra of the “intact” CP47 preparation, they concluded Chl26 to be a more probable candidate for C695¹¹ rather than Chl29. Their conclusion with respect to the lowest excited state in CP43 was also somewhat different¹⁴ from that drawn from the latest theoretical study by Müh et al.¹⁵

As described above, controversial opinions exist about the identity of Chl molecules responsible for F695 and F685. More reliable assignments of these red-shifted Chl pools will offer better opportunities to elucidate their functional roles. The major difficulty is in the determination of the transition energy of each pigment molecule experiencing various perturbations at its binding site, an energy which is therefore called “site energy”. Another difficulty is the appropriate description of the interplay between exciton-vibrational coupling and excitonic coupling. Whereas the latter tries to delocalize the excited states, the former may lead to a dynamic localization. One way to treat this problem is to implicitly take into account dynamic localization by grouping the pigment molecules into several coherent domains.^12,15−17 The local modulation of transition energies by the protein dynamics is described on the basis of the spectral density that can be extracted from fitting of fluorescence line narrowing data.¹⁸ As discussed above, a critical part of the simulation of exciton transfer and optical spectra is the determination of parameters, in particular the site energies of the pigments. One way, used by Raszewski and Renger,¹² is to determine them from a fit of optical spectra of the CP43, CP47, and RC- subunits. Of course, a direct structure-based simulation of site energies would be preferable but is highly nontrivial,^{15,17,19−22} because of the complexity of the problem.

Here, we stress that the qualitative explanation based on the schematic model in Figure 1B requires the following conditions to be fulfilled: (1) The energy transfer between C695 and C685 is very slow or practically inhibited below 77 K, and (2) the majority of the excitation energy is funneled into C685, while only a minor part flows into C695. If one of the above two conditions is not fulfilled, then the fluorescence peak below 77 K should be fixed at around 695 nm. This means that the light-harvesting dynamics in PS II at cryogenic temperatures is highly sensitive to the actual locations of C685 and C695 within PS II-CC. The simulation of cryogenic light-harvesting dynamics of PS II-CC using several possible assignments of C695 will thus enable us to evaluate these assignments.

This work is organized in the following way: We start with a characterization of the materials and experimental and theoretical methods used. Next, the optical spectra of the CP43, CP47, and RC subunits are investigated and used for the determination of site energies. These site energies are applied next, together with the excitonic couplings obtained for the latest structure of PS II-CC determined by Umena et al.,⁴ to model stationary and time-resolved optical spectra of the core complex and compare with experimental data obtained in this study. In addition, we investigate the predictive power of different sets of site energies from the literature. Finally, we discuss the results and relate them to the physiological function of photosystem II.

Materials and Methods

PS II-CC dimer was purified from cells of a thermophilic cyanobacterium, T. vulcanus, grown at 52–54 °C as described previously.^23,24 Briefly, thylakoid membranes were isolated from cells and solubilized with n-dodecyl-n,n-dimethylamine-n-oxide (LDAO) to obtain crude PS II particles. The crude PS II particles were then solubilized with 1% (w/v) sodium n-dodecyl-β-d-maltoside (DDM), and the solubilized samples were passed through an anion-exchange chromatography column to isolate the PS II dimer complex. The obtained PS II dimer complex was suspended in 20 mM MES-NaOH (pH 6.0), 20 mM NaCl, 3 mM CaCl₂, and 25% (w/v) glycerol and stored in liquid N₂ until use. A typical optical density of the stock solution was about 110 cm^–1 at the peak of the Q_y band. Storing the solution with this high protein concentration is important to maintain the intactness of the sample which was judged from the strong F695 emission at 77 K shown in Figure 1 A.

For measurements at cryogenic temperatures, a stock solution of the sample was diluted with a 33 mM MES-NaOH buffer (pH 6.0) containing 5 mM CaCl₂, 33 mM NaCl, and 0.05% DM. The diluted solution was mixed with twice the volume of glycerol to maintain its transparency at cryogenic temperatures. The final optical density of the sample was ∼0.1 mm^–1 at the peak of the Q_y band. The solution was contained in a 1-mm light-path cuvette and dark adapted for at least 10 min for complete relaxation of the sample to the S₁–Q_A configuration. The solution was then inserted into the sample room of a liquid-helium flow-type cryostat (CF1204, Oxford Instruments, Inc., Abingdon, Oxfordshire, U.K.) precooled down to ∼80 K.

The streak camera set-ups for the time-resolved fluorescence measurements are basically the same as those described in the previous studies.^25,26 The sample was excited by the frequency-doubled light at 430 nm from a Ti:sapphire laser (MaiTai; Spectra-Physics, Mountain View) with a pulse duration of 110 fs and a repetition rate of 80 MHz. A relatively high excitation power of ∼100 μW (1.3 pJ/pulse) was needed to obtain a high enough S/N ratio in the present study. The excitation laser was focused on the sample by using a 150-mm focal length lens. The fluorescence emitted to the direction perpendicular to the incidence of the excitation light was collected by two lenses and focused into the entrance slit of the polychromator. The beam diameter at the focal plane was roughly estimated to be 130 μm by using the numerical aperture of 0.5/150. Then, the excitation power per unit area was ∼0.5 W/cm² (we took into account the 45° angle between the sample window normal and the incidence of the excitation light). Typically, it took 1 h for the data accumulation. A global multiexponential fitting analysis was performed as described in previous papers^7,25 to obtain the fluorescence decay-associated spectra (DAS).

As indicated by Neupane et al.,¹³ this irradiation dose should result in the saturated NPHB at 5 K. The measurement was done in the order of the lowest to highest temperatures. Thus, the measurement at 5 K was done first, then those at higher temperatures followed. Since the relative F695 intensity at 77 K did not change in spite of the high irradiation dose in the precedent measurements at 5 and 36 K, we consider that the lowest excitonic state in CP47 was maintained intact after the several data accumulations. Hughes et al.²⁷ suggested that the rather intense irradiation of PS II-CC at cryogenic temperature results in the formation of a stable Q_A^– (closed RC) state. Therefore, the excitation intensity used here results in a complete conversion of the sample to the stable Q_A^– state. By using the molar extinction coefficient of Chl-a at 430 nm of 1.15 M^–1 cm^–1 and the above estimated excitation power, we can estimate the averaged frequency of excitation for an individual molecule to be 1.7 × 10⁴ s^–1. It was reported that, on the other hand, in the closed PS II-CC the primary charge-separated state is converted with a high quantum efficiency to the charge-recombined triplet state.^28,29 This triplet state has been traditionally called the P680 triplet or ³P680, while it is now known to reside on the accessory Chl of the D1 branch.³⁰⁻³² The half-life of the P680 triplet was reported to be a mixture of 1.5 μs (50%) and 15 μs (50%).²⁹ These half-life times are considerably shorter than the averaged excitation cycle of the present study. Thus, in the present excitation configuration, the molecules are considered to be populated dominantly in the Q_A^– state, while only a limited part of the molecules are trapped in ³P680 state.

The absorption spectra of the sample at various temperatures were measured by using a conventional spectrometer (UV-3100, Shimazu, Kyoto) equipped with the helium flow-type cryostat. The CD spectrum at a liquid nitrogen temperature was measured by using a conventional CD spectrometer (J700, JASCO, Tokyo) equipped with a liquid nitrogen bath-type cryostat (DN2, Oxford Instruments, Inc., Abingdon, Oxfordshire, U.K.). The solution was contained in a 10-mm light-path acrylic cuvette in both cases. Baseline of the CD spectrum was corrected by subtracting the signal obtained at the same temperature with the same cuvette containing the solvent only.

Theory

The spectral profiles and the exciton-transfer dynamics were simulated on the basis of the dynamical theory of optical spectra, which was detailed in previous papers.^12,18,32 The calculations were based on the latest PS II crystal structure by Umena et al.⁴ Since the dimeric form of PS II is considered to be the intact state under physiological conditions,^33,34 we evaluated the importance of energy transfer between the two monomers within a dimer. In order to examine this effect, all the 74 pigments (70 Chl-a’s and 4 Pheo-a’s) contained in the PS II-CC dimer were included in the simulations.

The pigment molecules in the PS II-CC dimer were divided into several exciton domains. A pigment having an excitonic coupling higher than a certain threshold with any pigment of an exciton domain is assumed to belong to the same domain, and the delocalization of the excited states was restricted to the pigments in the same domain.¹² The dynamic localization of the exciton was thus accounted for in an implicit way. The threshold was set to 30 cm^–1, which is a typical value for the reorganization energy of the local pigment–protein coupling. Since the excitonic couplings between pigments in different PS II-CC monomers are weaker than this threshold, the pigments of the two monomers are in different domains, and the stationary optical spectra of PS II-CC monomers are identical to those of PS II-CC dimers. Exciton dynamics was calculated by the combined application of Redfield theory and generalized Förster theory^12,35,36 for the transfer between exciton states in the same and in different domains, respectively, using non-Markovian time-local theory for the optical transitions in the exciton domains.

Input parameters of the simulation are the excitonic couplings between the pigments, the site energies, the electron-vibrational coupling strength (Huang–Rhys factor S), the primary charge-separation rate, and the spectral density J(ω) characterizing the frequency dependence of the exciton-vibrational coupling. The excitonic couplings were calculated with the Poisson-TrEsp method established earlier^15,17,21 by using the pigment coordinates from the crystal structure.⁴ The electrostatic calculations of Poisson TrEsp were performed before using the program MEAD³⁷ with the transition charges determined from the fit of the electrostatic potential of the quantum chemically determined transition density of the S₀ → S₁ transition energies of Chl-a and Pheo-a. According to the previous study,¹² the excitonic coupling between the special pair Chls P_D1 and P_D2 was assumed to be 158 cm^–1 instead of the value calculated from the Poisson-TrEsp method in order to take into account the electron exchange interactions between the two Chls. The electron–phonon coupling S was determined to be 0.6 from a simulation of the experimentally observed spectral broadening upon temperature rise. In order to include static disorder, the spectra were averaged with respect to a Gaussian distribution function for the site energies of the pigments by using a Monte Carlo method.

The primary charge-separation was assumed to start at the accessory Chl in the D1 branch (Chl_D1).³² The primary charge-separation rate constant k_M→RP from an exciton state |M> to the primary radical pair state |RP> is described by |c_ChlD1^(M)|²k_intr, where |c_ChlD1|² is the probability of finding Chl_D1 excited in the Mth exciton state and k_intr is the intrinsic rate constant for electron transfer. According to the previous study,¹²k_intr was taken as (100 fs)⁻¹ and (6 ps)⁻¹ for open and closed RCs, respectively. Since the experimental data considered were obtained at cryogenic temperatures, the charge-recombination reactions were not included in the present study.

We used an approximate form of the spectral density J(ω), which was extracted¹⁸ from fluorescence line-narrowing (FLN) spectra of the B777 complex,³⁸ as in the previous paper:¹²

1

with s₁ = 0.8, s₂ = 0.5, ℏω₁ = 0.069 meV, and ℏω₂ = 0.24 meV. It has been successfully applied to a number of different pigment–protein complexes and found to be very similar in shape to the J(ω) extracted from FLN spectra of a different complex.³⁹ In general it is found that the shape of J(ω) is very similar, but the amplitude varies somewhat between different complexes. Independent evidence for the validity of this finding is due to the fact that in the case of pigment-containing glass forming materials, the functional profile of the spectral density shows no significant dependence on the material hosting the pigment, while the value S is host dependent.⁴⁰ We assumed that the present experimental condition using the excitation at 430 nm results in a nonselective excitation of Chls. Accordingly, we assumed a uniform initial excited population among all the pigments in the simulation of the fluorescence dynamics.

Results

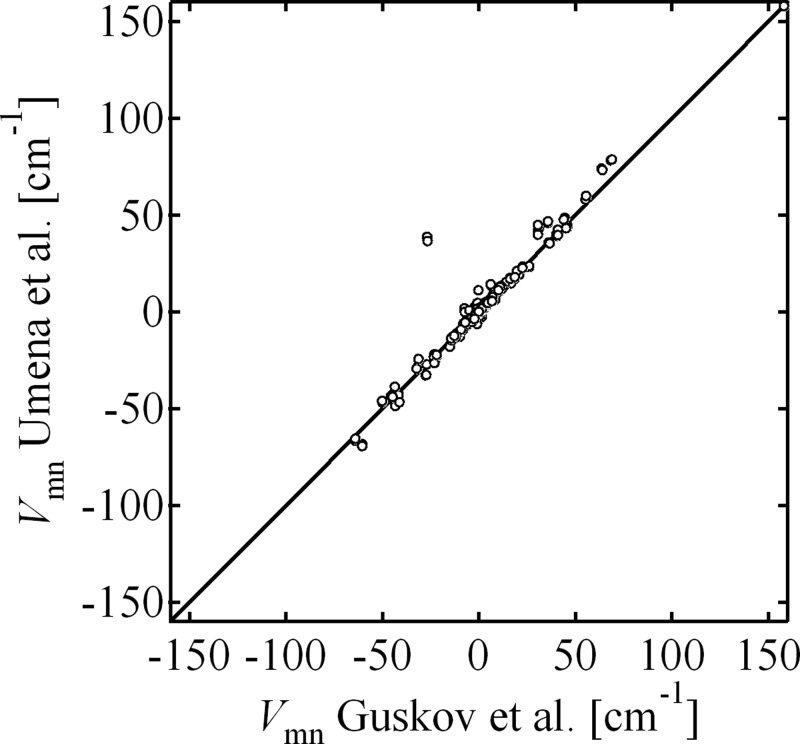
The excitonic couplings V_mn calculated using the latest PS II structure by Umena et al.⁴ are plotted against those calculated using the structure by Guskov et al.³ in Figure 2. The numerical values of these couplings are compiled in a file “coupling_SI.xls” in the Supporting Information (SI). Alterations in the excitonic couplings were only minor except for the pair Chl11–Chl12 in CP47. A large change in the excitonic coupling for this pair was due to the modified configuration of Chl11. In the latest structure, its molecular plane was flipped along the axis connecting the 5- and 15-carbon to give a 90° rotation of its Q_y transition dipole moment from that in the previous structure. This alteration resulted in only limited modifications of the simulated spectra.

Figure 2.

Correlation between the excitonic couplings between pigments in the PS II-CC dimer calculated based on the latest structure by Umena et al.⁴ and on that by Guskov et al.³

We simulated the static spectra of the isolated subunits using the excitonic couplings obtained here, treating the site energies as fit parameters with initial values taken from the literature. For this purpose, we used the site energies reported by Raszewski and Renger¹² for the spectral simulations of the CP47 and RC subunits, while we applied those reported by Müh et al.¹⁵ for the CP43 subunit. The site energies for CP43 were obtained from a combination of structure-based quantum chemical/electrostatic calculations with a subsequent refinement fit and comparison with the experimental data. The inhomogeneous width of the distribution function for the site energies was set at similar values as those employed in the previous studies,^12,15,32 with Δ_inh = 180 cm^–1 for the RC pigments and Δ_inh = 150 cm^–1 in CP43 and CP47 with the following exceptions: 120 cm^–1 for the accessory Chl in the D1-branch of the RC^12,32 and Δ_inh = 90 cm^–1 for Chl43 and Chl45 in CP43. These exceptive values for the two Chls in CP43 were necessary to fit the prominent peaks observed in the absorption spectra. The simulated spectra were compared with experimental data from the literature. The study by Neupane et al.¹³ revealed that the spectra of the isolated CP47 in the early reports were somewhat different from those obtained for more intact preparations. However, so far no LD and CD spectra were reported for the latter.

The calculations using the previously determined site energies well reproduced the experimental spectra. However, the fittings were not as good as in the previous studies because of the utilization of the slightly different structure. In order to improve the fitting quality, we refined the site energies through an optimization procedure, in which the site energies were adjusted to give the local minimum of the χ² value defined as

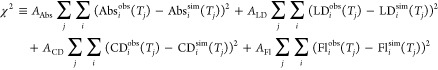2

Here, Abs(T)/LD(T)/CD(T)/Fl(T) are the absorption/linear dichroism/circular dichroism/fluorescence spectra at temperature T. The superscript “obs/sim” indicates the experimental/simulated spectrum. Since the fitting quality for the CD, LD, and fluorescence spectra was not as good as that for the absorption spectra in general, the A factors were introduced to balance the contribution from each spectrum to the χ² value. Here, we set A_Abs = 1, A_LD = A_Fl = 0.2, and A_CD = 0.04.

Comparisons of the experimental and simulated subunit spectra are given in Figures S1 (RC), S2 (CP47), and S3 (CP43). For example, Figure S3 shows various static spectra of the isolated CP43 at 4 and 77 K reported in the literature in comparison to the simulations. Quantitative agreements are obtained between the experimental and simulated curves except for the CD spectrum. The experimental CD spectrum of CP43 has a nonconservative profile, which cannot be explained by the present exciton theory, which gives a conservative CD signal. Despite a large deviation of the CD spectrum, its overall features, e.g., the negative and positive peak positions, could still be reproduced in the simulation. Using the CP43 site energies by Müh et al.¹⁵ resulted in a better fitting of the CD spectrum to the experimental one than the results by Raszewski and Renger.¹² The obtained site energies for RC, CP47, and CP43 are listed in Tables 1, 2, and 3, respectively. The coherent domains that each pigment belongs to are listed in the third rows of these tables.

Table 1. Site Energies of Pigments in RC, Optimized by a Fit of the Linear Optical Spectra^a.

PD1	PD2	ChlD1	ChlD2	PheD1	PheD2	ChlZD1	ChlZD2
664	668.5	678 (682)	667	666 (667.5)	675	666	669.5
1	1	1	1	1	1	isolated	isolated

^aThe 4 nm red-shifted value in parentheses for Chl_D1 is the value in the PS II-CC. The value in parentheses for PheD1 is that for Q_A reduced. The values in third row indicate the coherent domain of the pigment.

Table 2. Site Energies of Chls in CP47, Optimized by a Fit of the Linear Optical Spectra^a.

Chl11	Chl12	Chl13	Chl14	Chl15	Chl16	Chl17	Chl21
681	664.5	675.5	667	677.5	669.5	659	671
2	2	2	3	2	2	3	4

Chl22	Chl23	Chl24	Chl25	Chl26	Chl27	Chl28	Chl29
670.5	656	683.5	663.5	669.5	675	670.5	689.5
4	4	4	4	4	4	isolated	isolated

^aThe values in third rows indicate the coherent domain of the pigment.

Table 3. Site Energies of Chls in CP43, Optimized by a Fit of the Linear Optical Spectra^a.

Chl33	Chl34	Chl35	Chl37	Chl41	Chl42	Chl43	Chl44
669	666.5	669	677	669	669	676.5	671.5
isolated	5	isolated	5	6	isolated	6	6

Chl45	Chl46	Chl47	Chl48	Chl49
679.5	658	666	670.5	662
6	6	6	isolated	isolated

^aThe values in third rows indicate the coherent domain of the pigment.

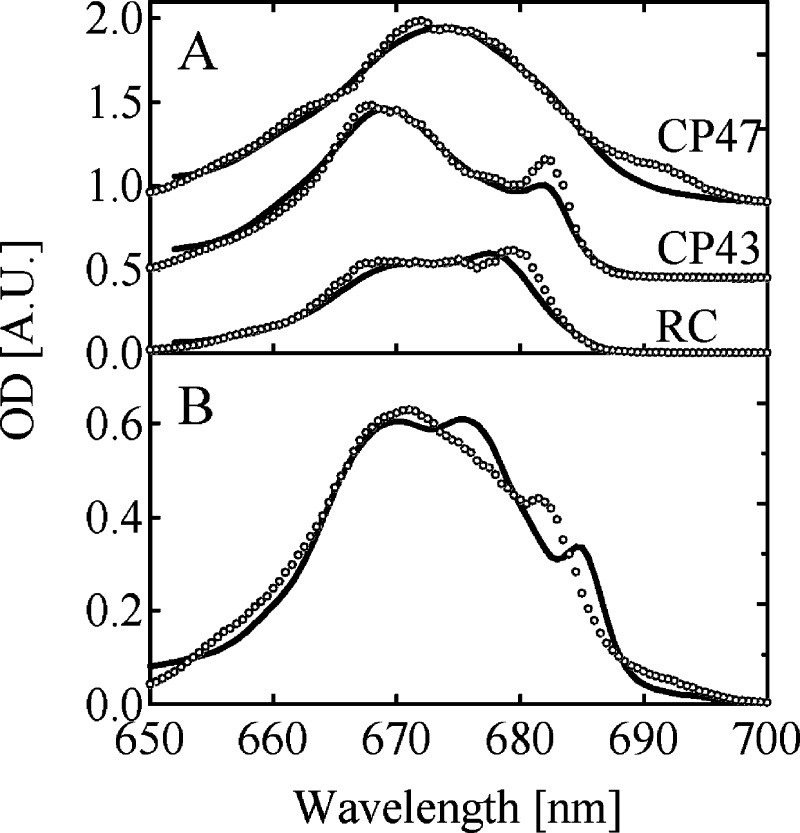
Figure 3 shows the comparison of the experimental absorption spectrum (solid line) of the isolated subunits at 4 K (panel A) and of the PS II-CC dimer at 5 K (panel B) with the simulated curves (open circles). The simulated spectrum of PS II-CC was calculated using the site energies determined through the refinement process described above and corresponds to the sum of the three simulated subunit spectra. The experimental subunit spectra in panel A are normalized so that the ratio of the spectral area, RC:CP43:CP47, gives the value 8:13:16 that follows from the pigment stoichiometry. Although quantitative fittings were obtained for the subunit spectra, the simulated spectrum of PS II-CC looks qualitatively different from the experimental one. The most conspicuous discrepancy is the position of the shoulder peak, occurring at around 684 nm in the experimental spectrum and at around 682 nm in the calculations.

Figure 3.

Comparison of the experimental absorption spectra (solid lines) of the (A) isolated CP47, CP43, and RC at 4 K and (B) PS II-CC dimer from T. vulcanus at 5 K with the calculated curves (circles) using the site energies in Tables 1, 2, and 3.

One problem could arise from the fact that the subunit spectra had to be taken from higher plants, whereas the PS II-CC spectra are those of T. vulcanus.. Recently, Boehm et al.⁴¹ have reported the low-temperature absorption and fluorescence spectra of the isolated cyanobacterial CP43 and CP47 complexes, which are only slightly different from the isolated CP43 and CP47 complexes from higher plants. The sum of the subunit absorption spectra of the cyanobacterial CP43, CP47, and RC complexes still significantly deviates from the experimental PS II-CC spectrum in Figure 3B (data not shown). Most likely, alterations in the protein conformations during the isolation procedure cause modifications of the site energies and result in the poor fitting in Figure 3B. Further adjustments of the site energies were needed to describe these spectra.

Nevertheless, we found that the simulations using the site energies from the fits of subunit spectra gave qualitatively similar time-resolved spectra of the PS II-CC as the experiment (data not shown), indicating that these site energies are already close to the optimal values. We carried out a further refinement of the site energies in PS II-CC to improve the fitting. Here, we paid attention to the peak in the experimental absorption spectrum of PS II-CC at around 684 nm, which was located at around 682 nm in the simulation. This band is obviously assigned to the peak in the CP43 subunit spectrum at around 682 nm. Actually, Boehm et al.⁴¹ have reported a red shift of this band in the cyanobacterial CP43 complex from that in the higher plant CP43. Thus, the shifted peak position of this peak indicates that at least the site energies in CP43 have to be refined for a better description of the experimental spectra.

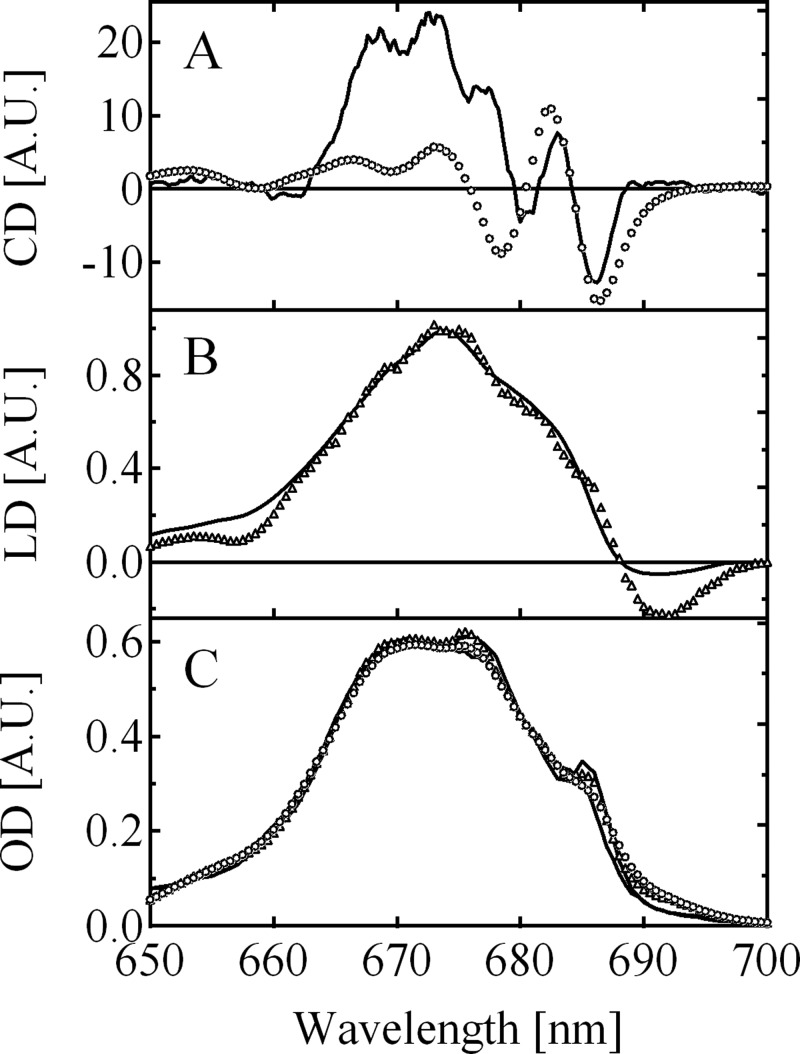
We note that we included already the 4 nm red shift of the accessory Chl of the D1-branch occurring between RC and PS II-CC preparations as inferred before from light-induced difference spectra of the cyanobacterial PS II-CC.^32,42 Here, we investigated whether the PS II-CC spectra can be simulated if, in addition, only the site energies of CP43 are allowed to vary. Figure 4 shows the comparison of the simulated and experimental CD (present study), absorption, and LD spectra from the literature⁴³ of PS II-CC. The fitting was drastically improved by the optimization procedure, in which we searched for the local minimum of the χ² value defined as

3

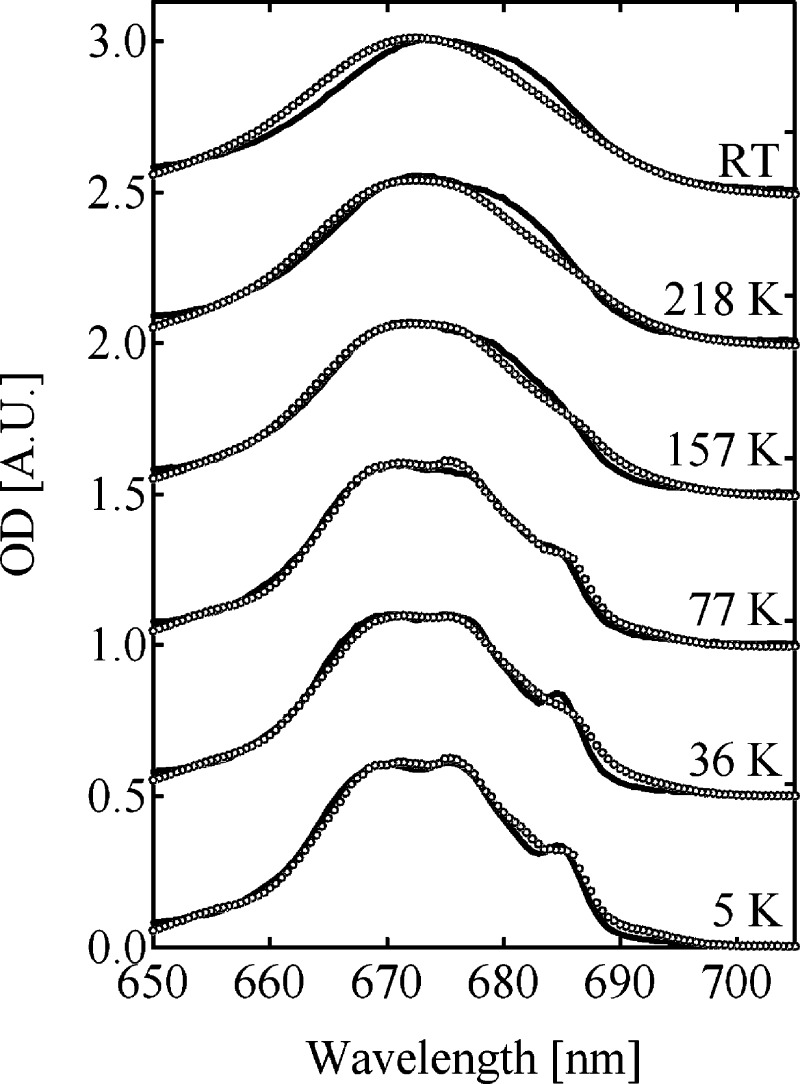
Adjustments of the site energies were restricted to CP43. The CD spectrum is not included in the χ² calculation, because the experimental CD spectrum of PS II-CC is highly nonconservative. Nevertheless, the simulation could roughly reproduce the overall peak positions of the CD spectrum as shown in Figure 4A. The obtained optimized site energies, which are listed in Table 4, were used to calculate the temperature dependence of the absorption spectrum of PS II-CC as shown in Figure 5. A qualitatively correct description of the temperature dependence of the experimental data is obtained. The deviations are slightly larger at temperatures above 157 K.

Figure 4.

Comparison of the experimental (A) circular dichroism (present study),(B) linear dichroism,⁴³ and (C) absorption (present study) spectra of the cyanobacterial PS II-CC dimer from Thermosynechococcus sp. with the calculated spectra using the site energies in Tables 1 and 2 (RC and CP47, respectively) and modified ones in CP43 listed in Table 4. The solid lines show the experimental data at 5 and 77 K. The triangles and circles show the calculated spectra at 5 and 77 K, respectively.

Table 4. Site Energies of Chls in CP43, Optimized by a Fit of the Absorption and LD Spectra of the PS II-CC as Shown in Figure 4^a.

Chl33	Chl34	Chl35	Chl37	Chl41	Chl42	Chl43	Chl44
673	665.5	666	678	676	668.5	673.5	668
isolated	5	isolated	5	6	isolated	6	6

Chl45	Chl46	Chl47	Chl48	Chl49
682	652	677.5	673	663
6	6	6	isolated	isolated

^aThe values in third rows indicate the coherent domain of the pigment.

Figure 5.

The temperature dependence of the experimental absorption spectrum (solid lines) of the PS II-CC dimer from T. vulcanus, compared with the calculated ones (open circles) using the site energies listed in Tables 1, 2, and 4.

We confirmed that the obtained set of site energies actually gave the local minimum of the χ² value defined in eqs 2 and 3 by plotting its dependences on slight perturbations of the site energies. In Figures S4 and S5, it is shown that the χ² value takes its local minimum at the optimized site energies. The curvature of the χ² vs site-energy perturbation plot can be a rough measure of the relative reliability of the determined site energy. Chls with relatively low site energies tended to show high curvatures of the plot. Thus, we can say that the site energies of Chls with low site energies were determined with higher reliabilities as compared with those with high site energies.

Using the refined site energies, we carried out the simulation of the time-resolved fluorescence spectrum of PS II-CC at 5, 36, 77, and 180 K. Under the present experimental condition, RC is expected to be in the closed form, where the intrinsic rate constant of the primary charge separation, k_intr, was inferred to be (6 ps)⁻¹.¹² In addition, we took into account the electrochromic shift induced by the reduction of Q_A as described previously.¹² The shift of the site energy of Pheo_D1 amounts to 1.5 nm to the red. The shifts of the other pigments were calculated to be <1 nm and then omitted in the present study.

Figure 6 shows the comparison of the experimental time–wavelength 2D fluorescence images (left column) with the simulated ones (right column). The simulated 2D images were convoluted with the instrumental response function of the experiment with fwhm of 89 ps. The overall tendency of the fluorescence dynamics is well reproduced. The simulations reveal the emergence of the 695-nm peak with a slow decay rate upon lowering temperature down to 77 K and its relative suppression upon further cooling. The simulated and experimental temperature dependencies of the time-integrated spectra are shown in Figure 7. Although the peak wavelengths in the simulated spectra are not exactly the same as those in the experimental ones, the spectral features and their temperature dependences are qualitatively well reproduced. It should be noted that in Figure 6 a slow fluorescence decay component at around 683 nm in the experimental dynamics at 77 and 180 K is missing in the simulated dynamics. The slight discrepancy in the peak position of the time-integrated spectrum at 180 K in Figure 7 might be due to the lack of the slow decay component in the simulated dynamics. We further tried to refine the site energies by adjusting those in CP47, in addition to those in CP43. However, fitting of CP47 site energies did not improve the overall fit of experimental data (data not shown). If the site energies of CP47 proposed recently by Reppert et al.¹¹ are used, a less satisfactorily description is obtained (dashed lines in Figure 7).

Figure 6.

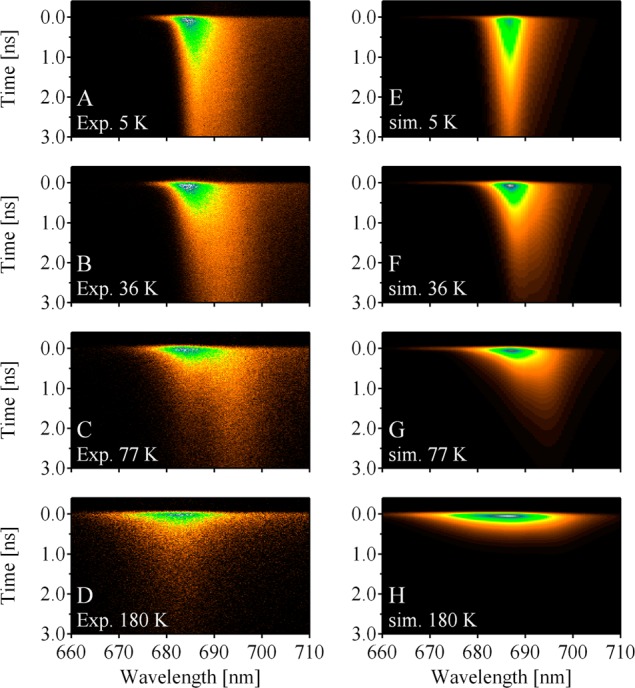
The temperature dependence of the experimental (left, A–D) time-resolved fluorescence spectrum of the PS II-CC dimer from T. vulcanus, compared with the calculated (right, E–H) ones using the site energies in Tables 1, 2, and 4. The calculated time-resolved fluorescence spectra were convoluted with the instrumental response functions, which were approximated by a Gaussian function with fwhm of 89 ps.

Figure 7.

(A) Temperature dependence of the experimental static fluorescence spectra of the PS II-CC dimer from T. vulcanus. (B) The calculated static fluorescence spectra of PS II-CC dimer (circles) from T. vulcanus, using the site energies in Tables 1, 2, and 4. The dashed lines show the spectra calculated by replacing the site energies in Table 2 (CP47) by the values reported by Reppert et al.¹¹

Discussion

In the present study, a refined set of the site energies for the pigments in isolated CP43, CP47, and RC preparations was obtained from a fit of optical spectra of these subunits. It was found that further adjustment of site energies in particular of the CP43 pigments, is necessary in order to explain the optical spectra of PS II-CC. This change most likely reflects conformational changes that occur during the isolation procedure of the subunits. With these site energies an explanation is obtained for the inverse temperature dependence of the fluorescence spectrum of PS II-CC between 77 and 5 K. This explanation is closely related to the identity and nature of low-energy excited states in the antenna. The temperature dependence can be explained by two different red-shifted Chl pools, C695 responsible for F695 and C685 responsible for F685. The blue shift of the fluorescence occurring below 77 K reflects the fact that the majority of the excitation energy is funneled into C685, while only a minor part is transferred to C695.

Assignment of C695

In the present study, we assigned C695 to Chl29 in CP47 in agreement with previous work.¹² Chl29 is an isolated Chl which does not constitute a coherent domain with other Chls, mainly because of an unfavorable orientation of its Q _y transition dipole moment with respect to those of the other nearby Chls. This orientation of the Q_y transition dipole moment is consistent with the LD spectrum of the isolated CP47 complex showing a slight negative sign in its long-wavelength tail region. Because of its position at the periphery and relatively weak excitonic coupling to the nearby Chls, only a minor part of the excitation energy flows into Chl29. These features of Chl29 are important for the temperature dependence of the fluorescence spectrum, as will be discussed in more detail below. We note that Reppert et al.¹¹ have proposed an alternative assignment of C695 to Chl26 based on their fitting of the absorption and the NPHB spectra. We carried out the calculations by using the site energies reported by Reppert et al.¹¹ As shown in Figures S2 and S6, the calculated CD and LD spectra of the isolated CP47 as well as the time-resolved fluorescence spectra of PS II-CC are qualitatively different from the experimental ones. The latter simulations overestimate the relative intensity of F695 at 5 K. The simulated time-resolved fluorescence shows a separate peak at around 695 nm even at 5 and 36 K, in contrast to the experimental data.

We note that there are still some systematic deviations between the experimental LD spectrum and the one calculated for the present site energies concerning the contribution of C695 occurring at the low-energy side of the spectrum that need to be explained in future work.

Assignment of C685

According to the previous work by Müh et al.¹⁵ and by Raszewski and Renger¹² the low-energy pigments in CP43 are Chl37, Chl43, and Chl45. The present refinement fits of optical spectra of the CP43 subunit (Table 3) roughly agree with this assignment. A slight alteration in the present study is that Chl37 belongs to another coherent domain and does not contribute to the low-energy exciton state in CP43. Importantly Chl43 and Chl45 are part of a large exciton domain, and the present fit of optical spectra of PS II-CC (Table 4) suggests that in PS II-CC, in addition, two other Chls (41 and 47) of the same exciton domain get low site energies. Therefore, there is a lot more oscillator strength in C685 of CP43 as compared to C695 in CP47. This difference explains why at very low T (5 K) the fluorescence maximum is around 685 nm rather than 695 nm. At this low temperature, energy transfer and nonradiative trapping by the RC are frozen out, and the higher oscillator strength of F685 determines the position of the maximum. If temperature is increased, fast thermal activation of low-energy excitons in CP43 sets in, and the subsequent trapping by the RC diminishes the fluorescence yield of F685. Since energy transfer from C695 in CP47 to the RC is still blocked, F695 now has the largest fluorescence yield and determines the maximum of the fluorescence. This effect explains the inverse temperature shift of the fluorescence maximum observed between 5 and 77 K in PS II-CC.

We note that Neupane et al.¹³ reported that saturated NPHB induces a blue shift of the 695 nm fluorescence of CP47 to 692 nm. To exclude interference of this effect with our interpretation, we measured the 5 K fluorescence before the 77 K fluorescence and still found the 77 K fluorescence peak at 695 nm. Hence NPHB induced bleaching of the low-energy state of CP47 can be excluded in the present experiments.

It is interesting to note that the common picture of a light-harvesting antenna as providing an excitation energy funnel for guiding the excitons to the RC is not met by CP47, which exhibits a low-energy trap state far away from the reaction center. Of course, at physiological temperature thermal energy is sufficient to allow for an easy escape of excitons from this trap. However, the existence of such states shows that the RC in PS II is a very shallow trap. In fact, because of the more or less isoenergetic site energy landscape throughout PS II-CC, the entropic factor (larger number of antenna than reaction center pigments) gives rise to an about three times larger rate for exciton transfer from the RC to the core antennae than vise versa.¹² Nevertheless, the ultrafast electron transfer in open RCs still catches nearly every exciton that reaches the RC. If, however, the RC is closed, then the slower electron transfer allows the excitons to escape back in the antennae. The low site energy of Chl29 in CP47 will give the population of this pigment a large weight in (quasi) thermal equilibrium, and hence the question arises about the functional role of Chl29 being responsible for C695.

Energy-Transfer Pathways in PS II-CC

By assuming fast intradomain exciton relaxations, we can calculate an effective energy-transfer rate from an equilibrated domain a to a domain b as

4

Here, the Boltzmann factor f(M_a) of an exciton state M_a in domain a is given by

5

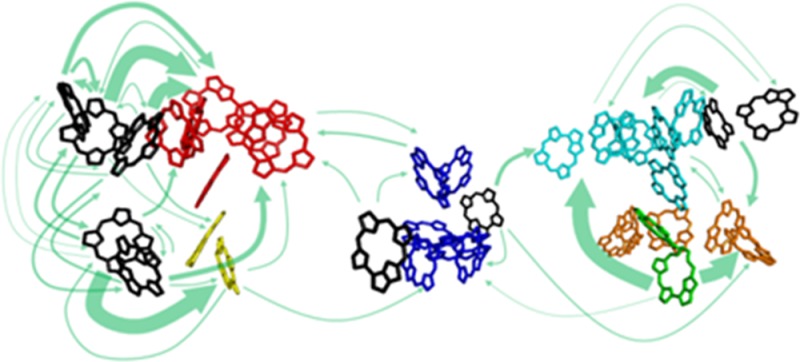
where k_B is the Boltzmann constant and ε_Ma is the energy of the exciton state M_a. The individual rate constants k_Ma→_Mb for exciton transfer from exciton state M_a in domain a to exciton state M_b in domain b are obtained from generalized Förster theory, as described previously.¹² The green arrows in Figure 8 show important energy-transfer paths between domains with rate constants calculated according to eqs 4 and 5. Here, we show only the transfer paths whose rate constants at 77 K were estimated to exceed 10 ns^–1. The thickness of an arrow in Figure 8 is proportional to the square root of the interdomain rate constant at 77 K, which was calculated by disorder averaging the rate constant given by eq 4. The disorder averaged rate constants in unit of ns^–1 are compiled in a file “InterdomainRate_SI.xls” available in the SI.

Figure 8.

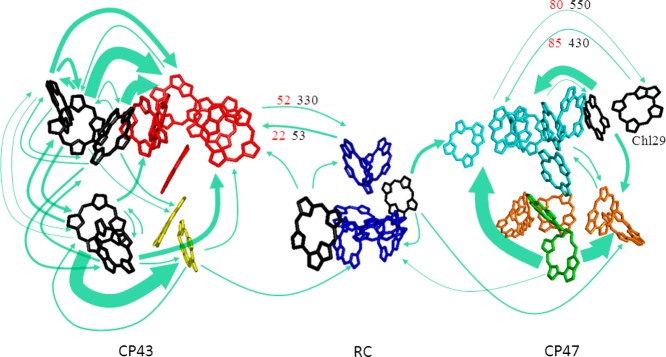
Arrows show important interdomain energy-transfer paths, whose rate constants at 77 K exceed 10 ns^–1. The thickness of an arrow is proportional to the square root of the transfer rate constant at 77 K between domains connected by the arrow. Two examples of highly temperature-dependent transfer paths are indicated with their disorder averaged inverse rate constants in unit of picoseconds at 77 K (red) and 5 K (black). Chls (and Pheos) in blue, orange, green, cyan, yellow, and red belong to the domains 1–6, respectively. Isolated Chls are shown in black.

Some of the transfer paths shown in Figure 8 are highly sensitive to lowering temperature below 77 K. Two important examples of such temperature-sensitive transfer paths are indicated by the numbers in red (77 K) and black (5 K) beside arrows, which are the inverse rate constants in unit of picoseconds between the domains connected by the arrows. The inverse rate constant in CP47 from domain 4 to Chl29, the C695 primary candidate, is 80 ps at 77 K, while it slows down to 550 ps at 5 K. The reverse transfer also shows a similar temperature dependence. Hence, at 77 K the equilibration between the large domain 4 and Chl29 is still fast compared to the radiative lifetime. Since the transfer from domain 4 to the RC at this temperature is already very slow (the inverse rate constant is ∼150 ps), domain 4 effectively functions as an antenna for Chl29. Upon lowering the temperature further to 5 K, this antenna practically becomes decoupled from Chl29, and therefore, the intensity of emission from this state goes down. Another important temperature-dependent path is that from domain 6 in CP43 to domain 1 including the PD, showing an inverse rate constant of 52 ps at 77 K and 330 ps at 5 K. The reverse transfer rate constant through this path does not change so much upon lowering temperature. Thus, the equilibrium between CP43 and the RC drastically shifts toward the former at 5 K. Since domain 6 is responsible for F685, the much slower transfer through this path at 5 K is relevant to the longer lifetime and the increased intensity of F685 below 77 K.

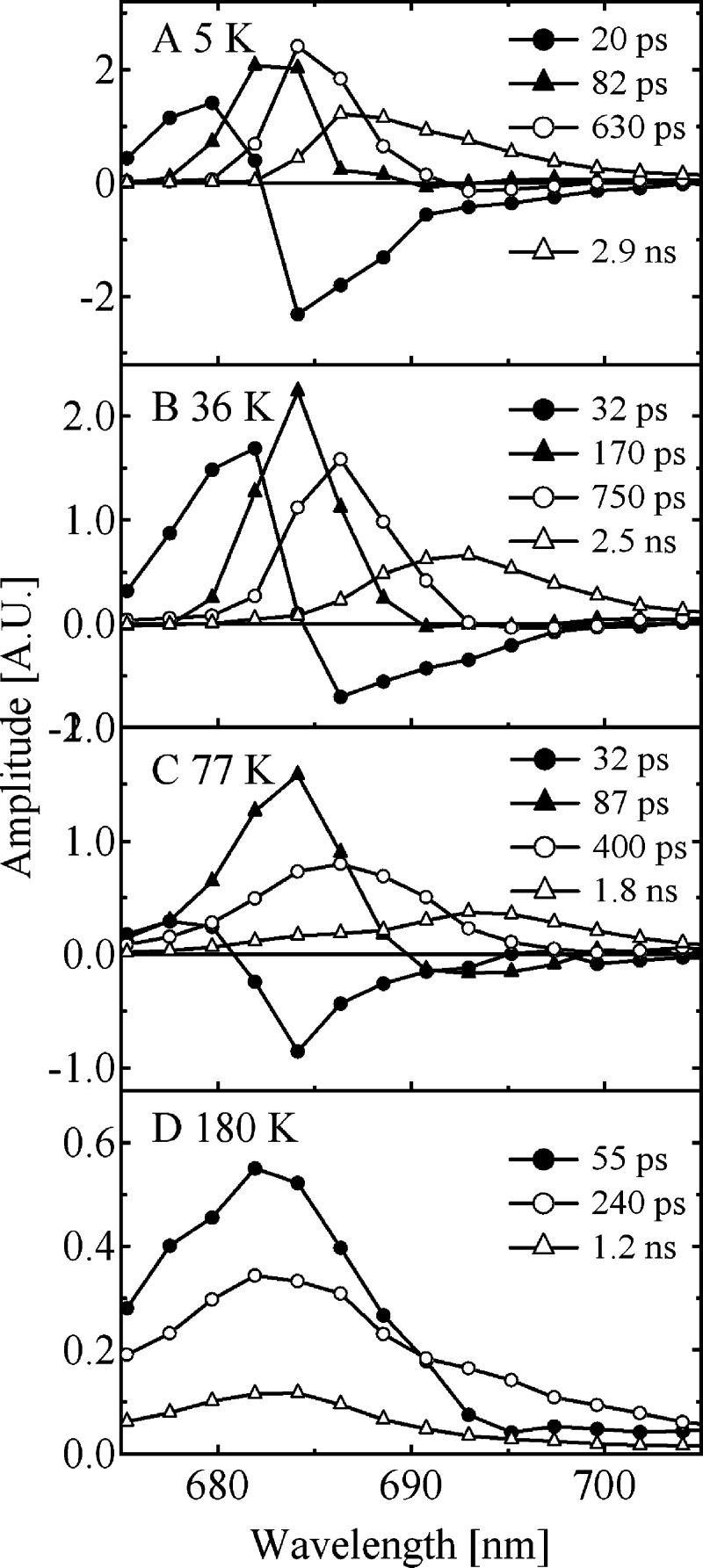
Figure 9 shows DAS obtained by a global-fitting analysis of the present experimental time-resolved fluorescence data. At 77 K, a DAS component with a time constant of 87 ps shows a negative peak at around 695 nm, indicating an energy-transfer process to F695. At 5 K, the only component with a negative amplitude at 695 nm in the DAS has a lifetime of 630 ps. This behavior is well reflected by the transfer times between domain 4 and Chl29 in CP47 (Figure 8), which slows down from 80 ps at 77 K to 550 ps at 5 K. The maximum of the DAS component with the largest time constant (ranging from 1.2 ns at 180 K to 2.9 ns at 5 K) between 180 and 77 K shifts to longer wavelengths and, when temperature is further decreased, gradually shifts back to shorter wavelengths. Whereas the red shift between 180 and 77 K reflects the effective decoupling of CP47 from the RC, the subsequent blue shift results from the decoupling of CP43 from the RC and the decoupling of Chl29 from the remaining pigments in CP47.

Figure 9.

DAS calculated by a global multiexponential analysis of the fluorescence decay curves of PS II-CC at (A) 5 K, (B) 36 K, (C) 77 K, and (D) 180 K. The estimated time constant of each DAS is specified in the figure.

The Functional Role of C695

As shown in Figure 8, C695 is located at the peripheral region of PS II-CC. This might suggest a function of C695 as an energy sink at the interfacial region between the peripheral and core antennae. At first glance it seems not to be the optimal solution to place an energy sink at the periphery of a light-harvesting complex far away from the RC. However, when considering the whole photosystem II including also the peripheral light-harvesting complexes CP26, CP29, and LHC-II,⁴⁴ it becomes obvious that Chl29 might act as an entrance for excitation energy from CP29. Hence, excitation energy from the peripheral antennae might be efficiently focused on C695 due to its low-lying energy. The focusing function of C695 is effective especially for higher-plant PS II supercomplexes, in which the core and peripheral antennae are rather isoenergetic. Caffari et al.,⁴⁴ based on their single-particle electron microscopy study, concluded that Chl11 in domain 2 of CP47 might act as a linker between CP29 and CP47. The close proximity between this pigment and Chl29 would indeed allow for efficient energy transfer between the two complexes.

Another reason for the location of the energy sink of CP47 at Chl29 might be a possible photoprotective function of this pigment. In 1998, Schweitzer et al.⁴⁵ have reported a fluorescence quenching effect in PS II induced by an addition of potassium hexachloroiridate. The primary candidate for the quencher was assigned to the oxidized form of Chl_Z. It is well-known that Chl cations exhibit a red-shifted absorbance compared to the singlet ground state of Chl.⁴⁶ Most likely, a β-carotene (Car_D2) in the D2-branch of the RC mediates electron transfer between Chl_ZD2 and the oxidized special pair in the RC.^47,48 It is interesting to note that, based on an analysis of optical difference spectra involving reduced quinone Q_A^– and oxidized β-carotene in the RC, it can be excluded that the β-carotene of the D1-branch is involved in secondary electron transfer.^47,48 The exclusive use of Car_D2, therefore, generates cationic states predominantly in the CP47 subunit, which is connected to the D2-branch of the RC. It seems not unlikely that the low-energy excitons that accumulate at Chl29 in CP47 are quenched by those cationic states:

So far, photoprotective quenching within the core complex of PS II has been considered not to be a major contributor of the nonphotochemical quenching (NPQ). This conclusion is based on early experiments using Chl-b less mutant, which revealed that substantial suppression of LHC II resulted in suppression of NPQ.⁴⁹ On the other hand, Miyake et al.⁵⁰ recently suggested a possibility that in a lichen-symbiotic green alga under drought stress, an exciton quencher emerges and functions within the PS II core antenna in addition to those within peripheral antennae to avoid unexpected charge separations at PD. The present study implies a potential ability of Chl29 to play a role as a core-antenna exciton quencher in emergency, although we admit that a direct proof of this hypothesis is still missing and will be an important future goal.

Slow Fluorescence Component in the Experimental Data

As shown in Figure 6, the experimental fluorescence dynamics at 77 and 180 K contains a slowly decaying component at around 685 nm, which is absent in the simulated dynamics. There have been several papers that reported slow fluorescence decay components in PS II^51,52 similar to those observed in the present study. These earlier studies concluded that the slow decay components reflect the emission from the excited states induced by the charge recombination at PD. Such a charge-recombination-induced fluorescence seems unlikely because the large energy gap of the charge recombination is unsurpassable at low temperatures. This apparent inconsistency was solved by inferring a suppression of the relaxation of the charge-separated state, which results in much reduced free energy gap at low temperature.^52,53 In the present simulations we have not considered these effects, which would, however, not change our explanation of the inverse temperature dependence of fluorescence.

Validity of the Present Theoretical Framework

The introduction of exciton domains in the present study is based on qualitative arguments concerning the relative strength of excitonic and exciton-vibrational coupling. An explicit treatment of dynamic localization effects of excitons by the exciton-vibrational coupling would be desirable for a more accurate description of exciton transfer. Nonperturbative theories have been developed in recent years (as discussed, eg., in Renger and Müh)⁵⁴ that, in principle, could be used for this purpose. However, so far these approaches are numerically too expensive for a system as large as PS II-CC. An important future goal will be to develop more efficient nonperturbative calculation schemes. We believe that the present treatment will still be valid to describe the overall behavior of the fluorescence dynamics. Another open point concerns the temperature dependence of site energies, which was neglected, or in a very few cases inferred from the fit of optical spectra.⁴² Close inspection of the absorbance spectrum of PS II-CC in Figure 5 suggests that the deviation between theory and experiment is somewhat larger above 150 K. One reason could be a temperature-dependent shift of site energies, e.g., due to temperature-dependent protonation patterns in the protein interior. The enhanced conformational fluctuation above the glass transition point might also contribute to such a shift.⁵⁵⁻⁵⁷ Further development concerning the structure-based calculation of site energies are required to clarify this point.

Conclusions

In the present work, time- and temperature-dependent fluorescence spectroscopy has been combined with theory to investigate the nature and connectivity of low-energy excited states in PS II-CC. The inverse temperature shift of the fluorescence band observed between 5 and 77 K reflects the different nature of low-energy excited states in the CP43 and CP47 core antennae. Whereas in CP43 these states are part of a large exciton domain that is well connected to the RC, in CP47 a single pigment far away from the RC is responsible for the fluorescence at low temperature. Whereas only small thermal activation is required to connect the low-energy excited states of CP43 with the RC giving rise to fluorescence quenching by primary electron transfer, the low-energy excited state, localized on Chl29 in CP47, stays disconnected up to 77 K, thus determining the fluorescence maximum of PS II-CC at this temperature. The existence of such low-energy excited states which are not well connected with the RC seems to be in obvious contradiction to an efficient excitation energy funnel that is commonly expected in photosynthesis. Obviously getting enough excitons into the RC is not the only demand of nature in PS II. For closed RCs, because of the much diminished primary electron-transfer rate, excitons have a high probability to leave the RC back to the antennae. Unwanted secondary electron transfer is known to proceed along the D2-branch, most likely involving Car_D2, ChlZ_D2, and cytb559, on the CP47 side of the RC. We suggest that singlet excited states on Chl29 in CP47 may be quenched by these cationic states, thus protecting the RC from being overloaded with excitation energy. Hence, the requirement for photoprotection might be one reason that has led to the present unconventional excitation energy landscape in PS II-CC. In addition, Chl29 most likely acts as a focusing point for excitation energy arriving from the peripheral antenna.

Supporting Information Available

Numerical values of couplings. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^∥ Department of Chemistry, Graduate School of Science, Tohoku University, Aramaki aza Aoba, Aoba-ku, Sendai 980-8578, Japan.

Author Present Address

^⊥ The OCU Advanced Research Institute for Natural Science & Technology (OVARINA), Osaka City University, 3-3-138 Sugimoto, Sumiyoshi, Osaka 558-8585, Japan.

The authors declare no competing financial interest.