Comparison of cardiac displacement and strain imaging using ultrasound radiofrequency and envelope signals

Abstract

Echocardiographic strain imaging is a promising new method for quantifying and displaying the health of cardiac muscle. Accurate regional myocardial function analysis requires high spatial and temporal resolution in addition to fidelity to the underlying deformation. However, all current clinical approaches use speckle-tracking algorithms applied to B-mode images derived from envelope signals. Such approaches are inherently of lower spatial resolution, since they require larger data blocks for deformation tracking due to the absence of phase information. In this paper, we compare the strain estimation performance using B-mode, envelope and radiofrequency signals, utilizing data acquired from a uniformly elastic tissue mimicking phantom, cardiac simulation, and clinical in vivo data. Signal-to-noise ratio improvements using radiofrequency signals for linear and phased array geometries were 5.80 dB and 9.48 dB over that obtained with envelope signals (at peak strain) in phantom studies, respectively. Cardiac simulation studies demonstrate that when averaged over the two cardiac cycles, the mean standard deviation of estimated strain using envelope signals from two of the six segments for a short-axes view (anterior and anterolateral) were 48% and 44% higher than that obtained using radiofrequency signals. These segments were chosen since one was along while the other was situated lateral to the beam propagation direction. In a similar manner, in vivo analysis on a volunteer also indicate that the standard deviation of the estimated strain using B-mode and envelope signals were 16% and 42% higher than that obtained using radiofrequency signals in the anteroseptal segment, and 45% and 27% in the anterior segment. These results demonstrate the significant reduction in the variability of strain estimated along with improvements in the spatial resolution and signal-to-noise ratios obtained using radiofrequency signals.

Introduction

Ultrasound elastography, is a novel and emerging imaging modality used for depicting tissue elastic properties estimated using ultrasound radiofrequency (RF), envelope or B-mode echo signals to track tissue deformations [1–5]. Local displacement and strain information as surrogates of tissue stiffness are calculated by tracking local tissue deformation using normalized cross-correlation analysis of the pre- and post-deformation ultrasound data. Steady state quasi-static elastography can be classified based on the tissue deformation applied, into three distinct categories [6]. Steady-state quasi static deformation is generally used for evaluation of variations in tissue stiffness in superficial organs. Applications include detection of breast mass pathologies including differentiation of benign from malignant masses [7–9] and assessments of lymph node stiffness [10]. Low frequency (1–10Hz) deformations comprise the second category. These are generated to perturb tissue along with approaches to track the resulting deformation [8]. The third category utilizes quasi static deformations generated by physiological excitation, such as respiratory motion, cardiac muscle deformations and cardiac generated vascular deformations. Strain imaging performed for detection of carotid artery plaques [11–12] and cardiac strain imaging are examples for this category.

Most of the peer-reviewed literature for strain imaging describe the use of linear array transducers, where displacement and strain estimations are generally performed using one-dimensional (1D) [1–2], two dimensional (2D)[3, 13–15], and even three-dimensional (3D) [16–17] deformation tracking. 1D approaches track and estimate deformations along the beam propagation direction, using a gated data segment or window on the pre and post-deformation echo signals. These methods are computationally efficient; however, lateral deformation information is not estimated [1–2]. 2D deformation tracking algorithms, utilize small 2D data blocks also called kernels to track tissue deformations and were initially developed for linear array transducers. Many of the shortcomings with the technique, such as coarse lateral deformation information, computation time and poor performance in cases where the displacement fields were not continuous have been addressed. Konofagou et al. [3] performed computationally intensive weighted interpolation between neighboring RF A-lines, to obtain higher precision lateral displacement estimates that was not limited by the pitch of the transducer used. Zhu and Hall [14] used a modified block-matching algorithm to reduce the search range in 2D block-matching, to improve computational speeds for real-time implementation. In their method, displacement estimates obtained from the previous row were used to predict displacements in lower rows, thereby reducing the search range and increasing computational efficiency. Shi and Varghese [13] successfully estimated discontinuous displacement fields utilizing a 2D multi-level algorithm. In their algorithm, a pyramidal search scheme was utilized where sub-sampled envelope signals were used in the upper levels of the pyramid while RF signals were used in the lowest level of the pyramid for deformation tracking. Chen et al. [15] developed a quality guided algorithm for ultrasound displacement tracking over geometrically irregular and disjointed regions, that was guided by the value of the normalized cross-correlation coefficient.

In general, for deformation tracking and strain estimation using ultrasound echo signals, signal decorrelation due to tissue deformation within the processing window or kernel due to changes in both signal amplitude and phase between the pre and post-deformation signal has to be considered [18–21]. As the window length or kernel increases in dimension, signal decorrelation due to the deformation increases concomitantly within the processing window or kernel[5]. RF echo signals mapping larger applied deformation or strain decorrelate faster when compared to smaller applied strain or deformation. The decorrelation rate is lower with envelope signals since only amplitude information is present in these signals [22–23]. Therefore, the deformation information contained within similar sized data segments is lower with envelope when compared to RF signals. This enables the use of smaller windows or data segments when RF echo signals are utilized. As the window become smaller, the information contained with only envelope signals become ambiguous for accurate tracking of the underlying deformations. On the other hand, since RF signals contain both amplitude and phase information accurate deformation tracking is possible with reduced decorrelation for smaller window lengths, thereby improving the spatial resolution for strain or deformation imaging [24].

Cardiac strain imaging [25–29], for the analysis of regional and global cardiac function, has been rapidly developing into a clinical diagnostic modality. Current clinical estimations of cardiac regional strain are performed using speckle-tracking algorithms applied to B-mode signals [25]. B-mode signals that are generated from envelope signals are inherently limited in spatial resolution when compared to RF signals, which also include phase information. Varghese et al. [23] has previously discussed tradeoffs associated between RF and envelope signals using the 'strain filter' concept [30]. The 'strain filter' provides a theoretical framework for predicting the performance of strain estimation algorithms, by plotting variations in the elastographic signal-to-noise ratios (SNR_e) with applied strain. In their theoretical and simulation results, they show that while SNR_e obtained using RF signals is significantly higher than envelope signal for low applied strains, the tracking ability deteriorates for larger applied strain when compared to envelope signals due to signal decorrelation. Low strain regions in the 'strain filter' refer to cases where signal decorrelation can still be modeled using the Cramer Rao lower bound for partially correlated signals [31] and amplitude and phase information are present in the signals thereby providing high SNRe. High strain regions on the other hand refer to signals where only amplitude information is present and phase information is ambiguous due to wrap around errors in the phase; in these cases displacement estimation is governed by the Barankin bound [32]. The 'strain filter' varies with ultrasound system parameters such as center frequency, bandwidth, beamwidth, and processing parameters for strain imaging such as the window length or kernel dimensions, overlap, ID or 2D deformation tracking among other parameters [30].

Because of the reduced storage requirement and strain estimation performance with reduced signal decorrelation at higher applied deformations, envelope or B-mode signals were used in commercial applications of the strain and strain-rate in cardiac speckle-tracking based imaging [33–35]. Use of B-mode or envelope signals, however, require longer data segments or windows for 1D processing and larger 2D blocks or kernels to obtain reasonable SNR_e in the resulting strain images. While the temporal resolution is determined by the frame rate, improved spatial resolutions, require the use of small cross-correlation data segments or kernels. Several studies have shown that RF signals have significant performance advantages over envelope signal, as also described above [18, 36–37]. Lopata et al. [36] performed quantitative analysis on local displacements estimated using 2D tracking between RF and envelope signals in a linear array geometry, using a simulated uniformly elastic homogeneous phantom. Their results show that for the same applied deformation or strain, the root mean square error (RMSE) for estimated displacements is lower with RF signals. Idzenga et al. [37] estimated strain using cross-correlation kernels on the order of 0.32×1.22 mm with data from linear array transducers obtaining SNR_e values of 5.6 dB with RF signals when compared to 1.3 dB obtained using envelope signals.

Despite all the reports presented above by various researchers, to our knowledge, no published work has specifically addressed the performance of RF, envelope and B-mode strain estimations for cardiac or echocardiographic strain imaging. Phased array transducers with its small footprint are the de facto standard for echocardiography, due to the limited acoustic windows available for imaging the heart. Deformation tracking and strain imaging with phased array transducers are challenging due to the ultrasound beam being steered over a ±45° or larger imaging or scanning planes. Unlike linear array transducers, displacement and strain images generated using a phased array transducer have limited lateral resolution at deeper depths, since the beams diverge. Most of the deformation tracking and strain imaging approaches for cardiac strain imaging therefore utilize 1D cross-correlation analysis using data segments on the order of 3 mm [26] or 4.6 mm [38] as reported in the literature. Our laboratory has developed a hybrid 2D method for deformation tracking and strain estimation [39], which was recently expanded to provide a Lagrangian description [40] of the strain using kernel lengths on the order of a wavelength in the beam direction and 3 A-lines in the lateral direction [39–40]. Linear interpolation is utilized for deeper locations to improve the spatial localization of the lateral displacements. Spatial resolution on the order of a wavelength based on kernel dimensions represent the best spatial resolution reported for cardiac strain imaging thus far in the literature [39–40].

In this paper, we compare the performance of deformation tracking and strain estimation using RF and envelope signals for cardiac strain imaging using RF data acquired from both linear and phased array transducers. Comparisons were performed using a uniformly elastic tissue-mimicking (TM) phantom, cardiac simulation data and in vivo clinical data. Cyclic deformations were applied to a uniformly elastic TM phantom during the acquisition of RF data. A cardiac simulation model was used to demonstrate the differences in strain estimation using RF and envelope signals over several cardiac cycles. Finally a comparison using RF, envelope and system generated B-mode data from a healthy volunteer was performed. A Lagrangian deformation tracking [40] scheme previously developed in our laboratory was adapted to estimate regional Lagrangian strains for performance comparisons obtained with RF, envelope and system generated B-mode echo signals.

Materials and Methods

TM Phantom Study

A cyclic deformation system previously designed in our laboratory was used to evaluate the strain estimation performance with a uniformly elastic TM phantom manufactured in our laboratory by Madsen et al. [41]. The device generates cyclic deformations that deform and release the TM phantom placed in the middle of a compression platform [42]. The uniformly elastic TM phantom used was a cube with dimensions 10 × 10 × 10 cm. The Young’s modulus of the TM material was 43.08±1.97 kPa, measured using an EnduraTEC ELF 3220 mechanical testing system. (EnduraTEC Systems Group, Minnetonka, MN, USA). During the experiment the phantom was placed on the lower platform; a 3% pre-compression was applied using the upper compression plate to ensure proper contact. A cyclic deformation frequency of 0.7 Hz, which is close to the human heart rate, was applied to the deformation of the lower platform using a DC motor. The ultrasound system used for RF data acquisition was a Siemens Acuson S2000 real-time clinical scanner (Siemens Ultrasound, Mountain View, CA, USA) equipped with a VFX 9L4 linear-array transducer with a center frequency of 6 MHz and a 4V1 phased array transducer operating at 4 MHz. The imaging depth was 8 cm with a single transmit focus set at 5 cm for both transducers, and dynamic focusing was used on receive. The RF data acquisition frame rate was 18 Hz for the linear array transducer and 36 Hz for the phased array transducer under our imaging acquisition settings. The phased array transducer had a higher frame rate due to the fewer number of beam-lines within the imaged region. Frame skipping was applied to the phased array data to match the frame rate of 18 Hz obtained using the linear array before further processing. This frame rate has been proven to be sufficient to track displacement and strain variations in our experimental setup [42]. The RF signal was digitized at a sampling frequency of 40 MHz using the ultrasound research interface on the Siemens system.

Finite Element Analysis (FEA) based Cardiac Simulation

A 3D canine heart model [43–44] that was previously incorporated into an ultrasound simulation program in our laboratory [45] was used to generate RF data with cardiac deformation. RF data over two cardiac cycles of tissue deformation information was obtained using this canine heart model with a temporal sampling rate of 250 frames/second. Over 1 million scatterers were randomly distributed in the canine heart model to ensure Rayleigh statistics for the generation of the simulated ultrasound RF data. In this study, a 2D mid-cavity slice of the left ventricle along the short axis view was selected and RF data simulated for this view.

Ultrasound in vivo Data Acquisition and strain estimation

Under a protocol approved by the UW-Madison Health Sciences Institutional review board, in vivo data on a volunteer used in this study was acquired at University of Wisconsin-Madison Adult Cardiology Clinics. Informed consent was obtained prior to ultrasound scanning. The volunteer was scanned using a GE Vivid 7 system (GE Ultrasound, Waukesha, WI, USA) with a 2.5 MHz phased array transducer. RF signals along a parasternal short axis view at mid-cavity at a frame rate of 34.1 fps was acquired at a 20MHz sampling rate.

2D Processing for Displacement Tracking and Strain Estimation

Envelope signals were generated from the RF data using Hilbert transformation [46–47]. The resulting RF and envelope signals were then processed using a multi-level speckle tracking method [39] to generate the local displacement field along the beam propagation direction. For the in-vivo data on the volunteer the B-mode cine loop directly generated from the ultrasound system was utilized. Our displacement tracking and strain imaging algorithm clearly indentifies the location of the pre- and post- deformation signals over the data loop. Four levels of tracking were performed with 75% window overlaps at each level. 2D cross-correlation processing kernels on the order of a single wavelength along the beam direction and three A-lines in the lateral direction were used for the final processing kernel dimensions unless specified otherwise. A 9-point least squares linear fit of the displacements was then used to compute the local strain field.

Regional accumulated displacements and strains for the cardiac simulation and in vivo data set were then calculated using our Lagrangian tracking method [40], which enables tracking of tissue deformation around a point/region in myocardial tissue as it moves/traverses through space and time. We have previously demonstrated that Lagrangian tracking outperforms traditional Eulerian tracking where deformations around a fixed spatial coordinate are tracked through time [40].

Although scanning was performed with different transducer center frequencies for the TM phantom, and in-vivo data respectively due to the different imaging depths, all the comparisons between RF, envelope and B-mode signals were performed on the same exact data set. In addition, for data processing the final kernel dimension is always specified in terms of the ultrasound wavelength and not based on the center frequency. The performance comparison between RF, envelope and B-mode signals was the focus of this paper.

Results

Uniformly elastic TM Phantom Results

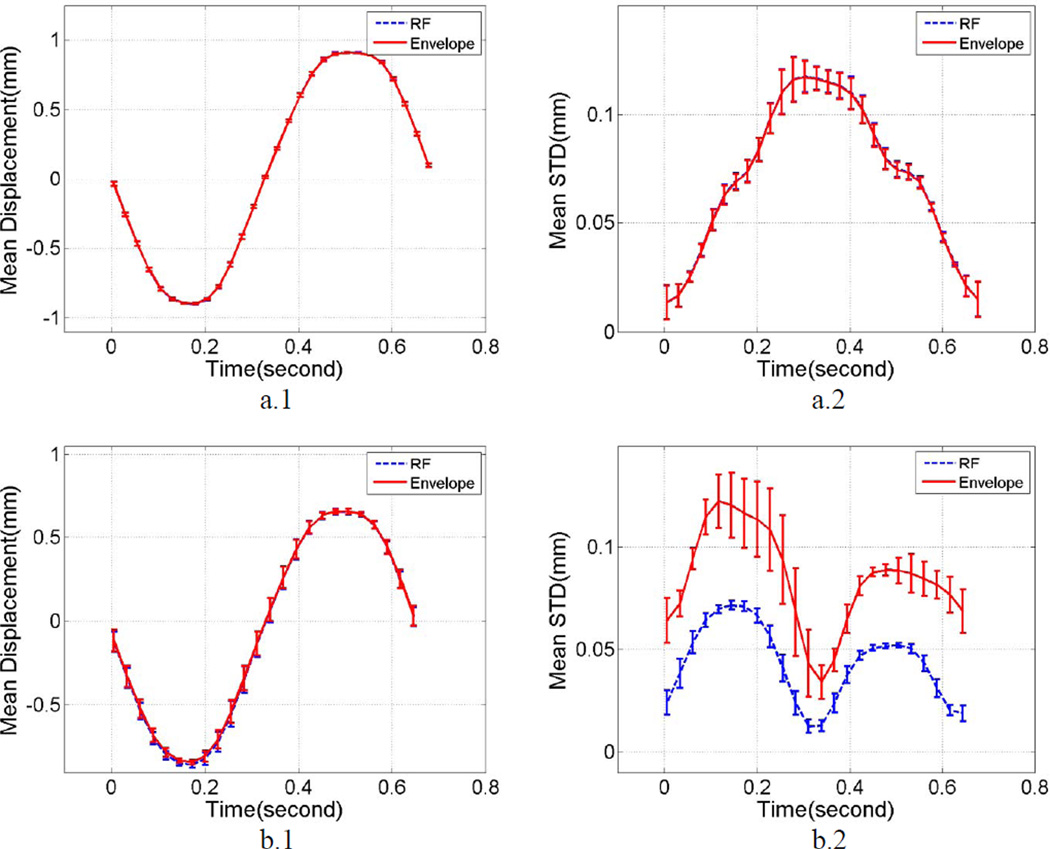
Plots of the mean displacement estimates along the beam direction and within a small region of interest (ROI) at the center of the uniformly elastic TM phantom are shown in Figure 1. A 1 cm² ROI was selected at the center of the phantom at a 5 cm depth, where the focus of the transducer was placed. The mean and standard deviation of the local displacements estimated were computed over this ROI for 10 independent cyclic deformations of the phantom in the compression apparatus described in the previous section. Figure 1 (a.1) presents the variations in the mean displacement estimated over 10 independent data sets acquired using a linear array transducer for both RF and envelope signals. Errorbars on the plots denote the variation in the mean displacement over the independent realizations. Both the curves are similar and no significant differences are observed between the mean displacements estimated using the linear array transducer. Figure 1 (a.2) shows the variation in the standard deviation of the displacements estimated, with the errorbars denoting its variation over the independent realizations respectively.

Figure 1.

Mean displacement and standard deviation estimates obtained using a cyclic deformation of a uniformly elastic TM phantom study using a) linear array transducer, b) phased array transducer. Plots a.1 and b.1 depict mean displacement variation within the ROI, while plots a.2 and b.2 show the mean standard deviation of displacement estimates. Errorbars denote the standard deviation of the mean displacement/strain/standard deviation over 10 independent realizations.

Figure 1 (b.1) and (b.2) depict similar analysis of the mean and standard deviation of the local displacements estimated using a phased array transducer. Again, a 1 cm² ROI was selected at the center of the phantom at a 5 cm depth. Figure 1 (b.1) presents the variations in the mean displacement estimated over 10 independent data sets acquired using a phased array transducer for both RF and envelope signals. Errorbars on the plots denote the variation in the mean displacement over the independent realizations. Figure 1 (b.2) shows the variation in the standard deviation of the displacements estimated, with errorbars denoting its variation over the independent realizations respectively. Observe that, while the mean displacement variations remain indistinguishable between RF and envelope signals, the peak standard deviation obtained using envelope signals is 96% higher than that obtained using RF signals, indicating a more noisy estimation of the displacements from envelope signal in the phased array setup.

Strain variations along the beam direction for the TM phantom study are shown in Figure 2. Figure 2 (a.1) presents the mean strain over 10 independent realizations within the ROI with data acquired from linear array transducer. Figure 2 (a.2) shows the standard deviation of strain distribution over the independent realizations. Errorbars denote the variations of mean strain and standard deviation over the 10 independent realizations in these figures. Figure 2 (a.3) presents plots of the mean SNR_e over 10 independent realizations, where SNR_e is defined as previously described in [30] :

$${\text{SNR}}_{\mathrm{e}}=\frac{{\mathrm{S}}_1}{{\mathrm{\sigma }}_1}$$ (1)

where S₁ denotes the mean strains over the ROI and σ₁ is the corresponding standard deviation. Errorbars denotes the variations of mean SNR_e over the 10 independent realizations. Note that we are able to plot the SNR_e since we utilize a uniformly elastic phantom, where the strain distribution would be uniform for a specified applied deformation. Figure 2 (a.1) shows that estimated mean strains are very similar for both RF and envelope processing. However, the mean values of the standard deviation are significantly larger for strains estimated using envelope signals when compared to that obtained using RF signals over the entire cyclic deformation. Results obtained using a phased array transducer are shown in Figures 2 (b.1)–(b.3). In Figure 2 (b.1), for the peak strain values, envelope processing fails to depict the sinusoidal shape of the deformation generated by the compression system. The variation in the mean standard deviation observed between envelope and RF signal are higher than that seen for the linear array transducer, which leads to the significant SNR_e difference between RF and envelope results for the phased array data.

Figure 2.

Variations in the mean strain and standard deviation obtained using a cyclic deformation of a uniformly elastic TM phantom using linear array (a.1–a.3) and phased array transducers (b.1–b.3). Plots a.1 and b.1 depict mean strain variation within the ROI while a.2 and b.2 plot the variation in the mean standard deviation of the strain. Plots a.3 and b.3 show the mean SNR_e for the two transducer geometries. Errorbars denote the standard deviation of the mean displacement/strain/standard deviation over 10 independent realizations.

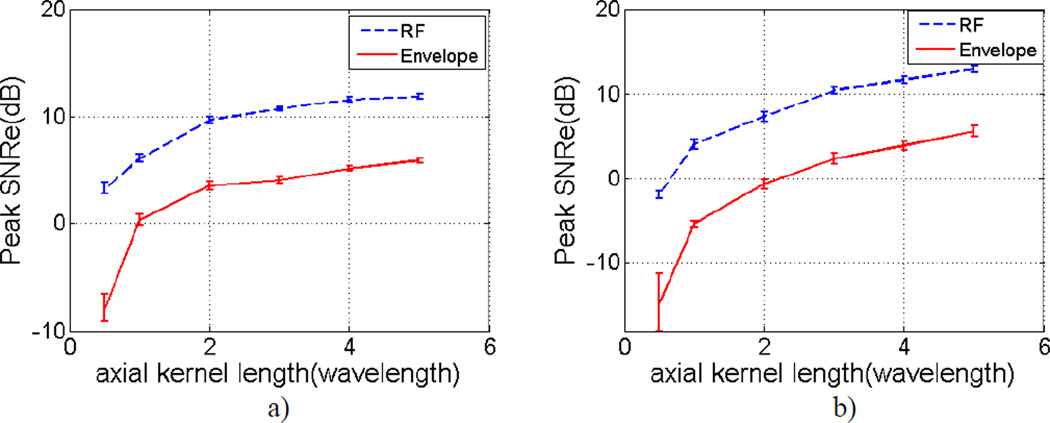
Figure 3 provides an overview of variations in the mean SNR_e values for different lengths of the final processing kernel along the beam direction used in the multi-level speckle tracking method. Comparisons were made between RF and envelope signals. Mean SNR_e values were obtained at the peak strain value and computed over 10 independent realizations. Errorbars denotes the variations in the mean SNR_e over the 10 independent realizations. Figure 3.a and Figure 3.b represent results from linear array and phased array transducers respectively. SNR_e values for RF signals are significantly higher than envelope signals in both plots. For the final processing kernel’s dimension of 1 wavelength along the beam direction, the SNR_e improvement using RF signals for linear and phased arrays was 5.80 dB and 9.48 dB respectively, when compared with envelope signals.

Figure 3.

Variations of the mean SNR_e at the peak strain value with respect to the final processing kernel's axial dimension over 10 independent realizations for a) linear array and b) phased array transducers. Comparisons are made between RF and envelope signals.

Simulation Results

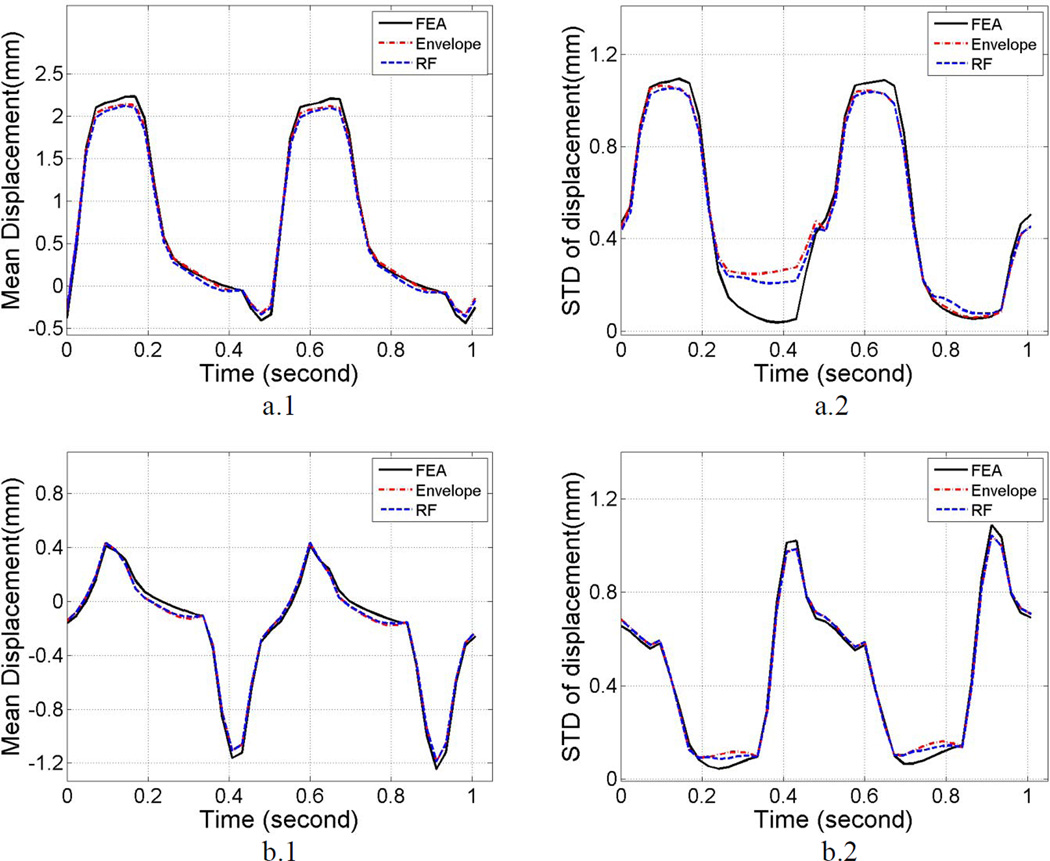
Segmental mean accumulated displacement variations over time estimated from the cardiac FEA model and subsequent ultrasound simulations obtained using Lagrangian tracking are shown in Figure 4 (a.1) and Figure 4 (b.1) for two of the segments. The left ventricular wall was segmented based on the standard proposed by the American Society of Echocardiography [48]. Comparisons between RF and envelope results are shown over two cardiac cycles for the anterior and anterolateral segment, plotted separately in Figure 4 (a.1) and Figure 4 (b.1). These segments were selected since in the simulation setup, the anterior part of left ventricular wall mainly moves parallel to the insonification direction whereas the anterolateral segment incurs more perpendicular or lateral deformation with respect to the insonification direction. This is observed when comparing Figure 4 (a.1) with Figure 4 (b.1), where the peak amplitude of mean displacement in the anterior segment (2.25mm) is higher than that of anterolateral segment (0.42mm). Similar to the result obtained using the phantom study using the linear array transducer, Figure 4 (a.1) and 4 (a.2) show that mean displacement curves generated by RF and envelope signals are comparable, and both curves closely follow the mean displacement provided by the FEA model solution. Percent differences between RF, envelope and FEA results are calculated for the mean displacement curves over two cardiac cycles, as shown in Table 1. Absolute values of the displacement were utilized to determine the error between RF and envelope processing when compared to the FEA result. Observe that in the anterior segment; the difference between envelope and RF results was 2.8%, while they deviate from the FEA results by −3.8% for the envelope and 2.8% with RF processing respectively. For the anterolateral segment, these differences were 0.8%, −1.9% and −2.7% respectively. The standard deviation of the accumulated displacement estimates over time with each segment are plotted in Figure 4 (a.2) and Figure 4 (b.2) for the anterior and anterolateral segments respectively. The variation in the standard deviation plots for both RF and envelope processing closely follow FEA results. The percent difference between envelope and RF results for the anterior segment was 2.1%, while they deviate from FEA results by −4.6% using envelope and 2.4% using RF signals respectively. For the anterolateral segment, these differences were 0.8%, 2.2% and 1.5% respectively.

Figure 4.

Comparison of the mean segmental accumulated displacement variation (left) and its standard deviation (right) with time for RF, envelope and FEA results. Plots a) and b) correspond to results from anterior and anterolateral segment respectively.

Table 1.

Percent differences between RF, envelope and FEA results for the cardiac simulation study over two cardiac cycles. Absolute values were used for displacement and strain estimates for computation of the percent difference.

	Percent difference
	Mean displacement	Displacement standard deviation	Mean strain	Strain standard deviation
Anterior segment
RF vs. FEA	−6.4%	2.4%	29%	110%
Envelope vs. FEA	−3.8%	4.6%	11%	212%
Envelope vs. RF	2.8%	2.1%	−14%	48%
Anterolateral segment
RF vs. FEA	−2.7%	1.5%	−2.3%	5.3%
Envelope vs. FEA	−1.9%	2.2%	2.4%	51%
Envelope vs. RF	0.8%	0.8%	4.8%	44%

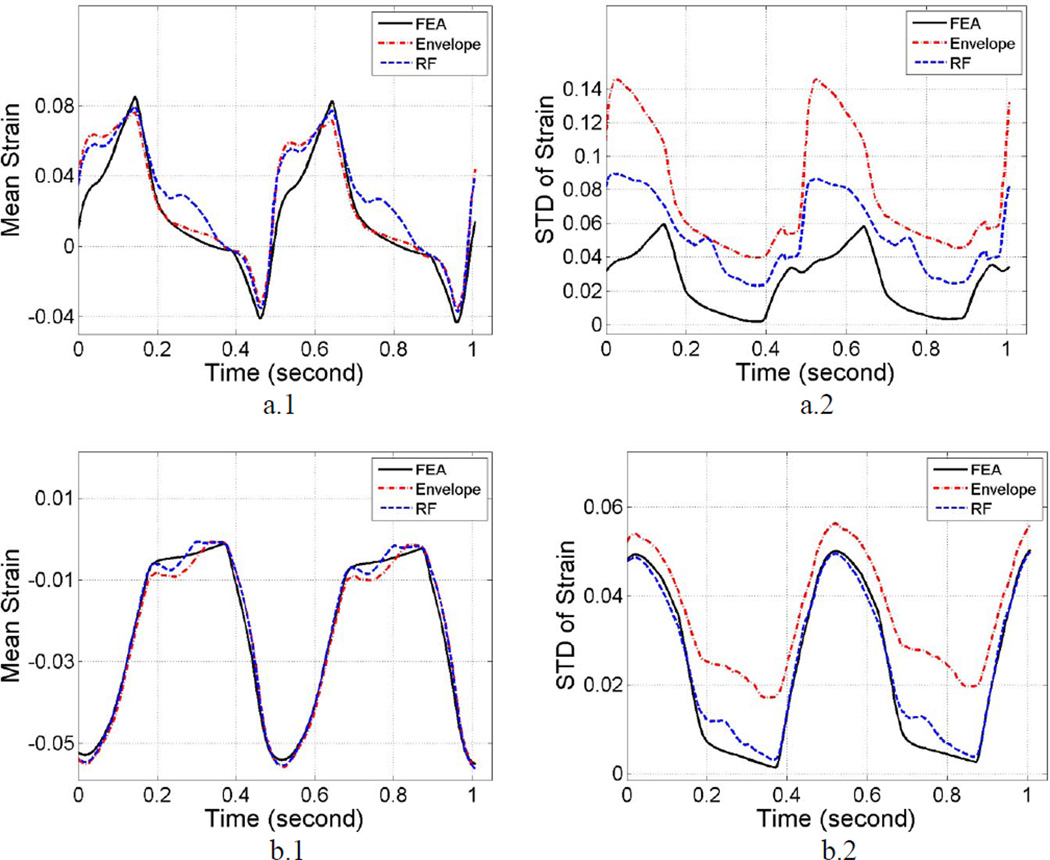
Differences in the segmental mean accumulated strains are shown in Figure 5 (a.1) and Figure 5 (b.1). Similar to the results shown with the phantom study, mean strains generated from RF and envelope data are similar and follow the ideal FEA generated strains. As shown in Table 1, the percent difference between envelope and RF based strain estimation results in the anterior segment was −14%. The envelope results deviate from FEA results by 11% and 29% with the RF estimations respectively. In the anterolateral segment, these differences were 4.8%, 2.4% and −2.3% respectively. Absolute strain estimates were utilized for the difference calculations. The standard deviation of the estimated RF strains follow the standard deviation of the 3D canine FEA model, the envelope estimates on the other hand deviate significantly from the ideal FEA curve, as shown in Figure 5 (a.2) and Figure 5 (b.2). Observe that after averaging over the two cardiac cycles, the percent difference between envelope and RF results in the anterior segment was 48%. Note that the mean deviation from FEA results was 212% using envelope signals and 110% for the RF data respectively. For the anterolateral segment, these percent differences were 44%, 51% and 5.3% respectively. Note that SNR_e plots are not presented for the cardiac simulations since cardiac tissue is anisotropic and the deformations generated are complex with translation, rotation and torsional deformations all present during a cardiac cycle.

Figure 5.

Comparison of the mean segmental accumulated strain variation (left) and its standard deviation (right) with time for RF, envelope and FEA results. Plots a) and b) correspond to results from anterior and anterolateral segment respectively.

In vivo results

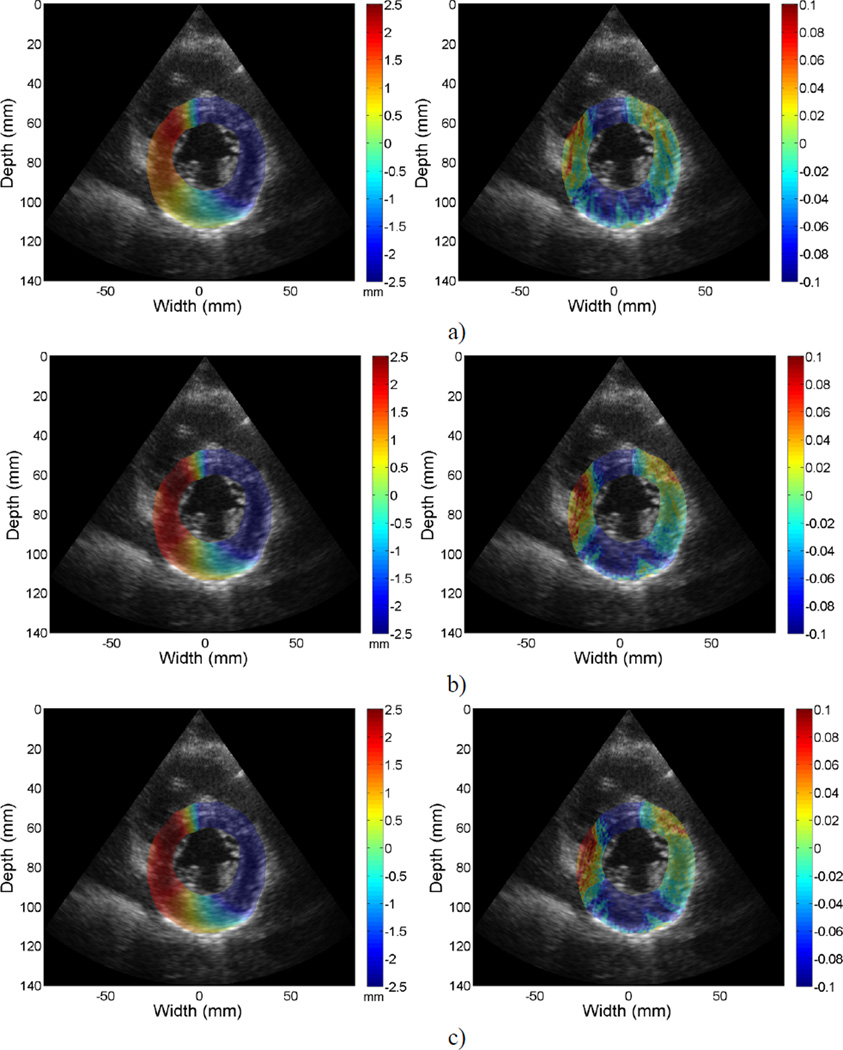
Figure 6 provides a representative example of the accumulated displacement and strain mapping at the end-systolic phase of the cardiac cycle. Only the regions within the left ventricular wall contours are shown overlaid on their corresponding B-mode images. Due to the noisy nature of lateral displacements and strains generated with a phased array setup, displacements and strains displayed were estimated along each A-line. Figures 6 (a–c) represent results from RF, envelope and system generated B-mode signals respectively. Images along the left column are displacement maps, and images on the right column are strain maps. Both positive (red) and negative (blue) strain information (with respect to the ultrasound beam propagation direction) is shown indicating both contractile, where tissue sections move closer together depicted as red regions, and stretching of the cardiac muscle as blue regions. For displacement mapping, the inferior side of myocardium provide positive displacement values while the anterior side present with negative displacement values, indicating that the myocardium is undergoing a counter clock-wise twist at end-systole. Negative strain values along the anteroseptal, inferolateral and inferior segments for strain mapping indicate contraction in those regions at end-systole.

Figure 6.

Accumulated displacement (left) and strain (right) images acquired in-vivo for a volunteer at the mid-systolic phase of a cardiac cycle superimposed on the B-mode image. From a) to c), images represent results using a) RF, b) envelope and c) system generated B-mode results. Displacement in the insonification direction towards the transducer is negative (blue) while displacement away from the transducer is positive (red) with respect to the beam propagation direction.

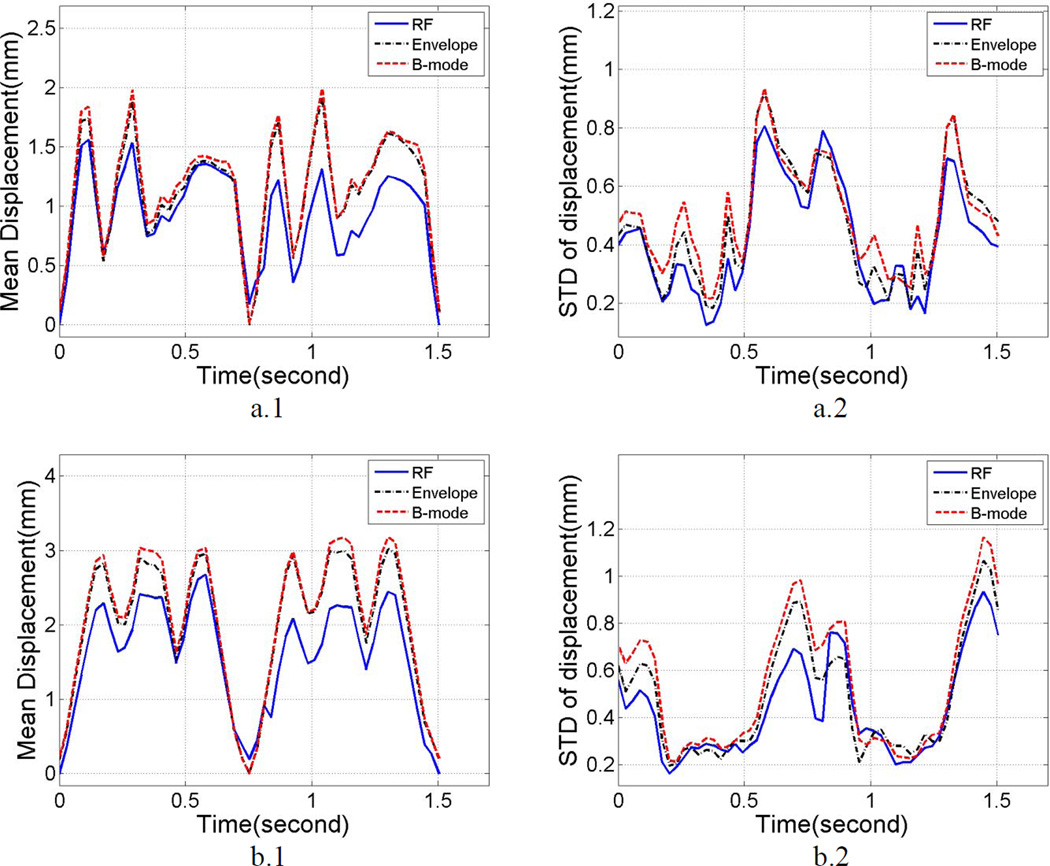
In-vivo comparisons of the mean segmental accumulated displacement variations over time between RF, envelope and system generated B-mode signals for a volunteer are shown in Figure 7 (a.1) and Figure 7 (b.1), for the anteroseptal and anterior segments. Using the fact that, in a healthy heart, myocardial walls will return to its original status after each cardiac cycle, the lowest values in the curves were set to 0 to ensure better visual comparison. The standard deviation of the segmental accumulated displacements are presented in Figure 7 (a.2) and Figure 7 (b.2). Percent difference calculations between B-mode, envelope and RF results are shown in Table 2. Note that, when averaged over two cardiac cycles, the standard deviation of the estimated displacement from anteroseptal and anterior segment for B-mode signals were 18% and 54% higher than that obtained for corresponding RF signal estimations. For both these segments the differences were 11% between envelope and RF signals.

Figure 7.

Comparison of the mean segmental accumulated displacement variation and its standard deviation with time for RF, envelope and system generated B-mode results. Plots a) and b) represent results from the anteroseptal and anterior segments respectively.

Table 2.

Percent differences between RF, envelope and B-mode results using mean standard deviation values estimated over 2 cardiac cycles. Mean displacements and strains were not compared since an actual estimate is not available for in vivo data.

	Percent difference
	Displacement standard deviation	Strain standard deviation
Anteroseptal segment
B-mode vs. RF	18%	16%
Envelope vs. RF	11%	42%
Anterior segment
B-mode vs. RF	54%	45%
Envelope vs. RF	11%	27%

In a similar manner, mean segmental accumulated strain variations over time between RF, envelope and system generated B-mode signals for a volunteer are shown in Figure 8 (a.1) and Figure 8 (b.1), for the anteroseptal and anterior segments. Standard deviation of the segmental accumulated strains are shown in Figure 8 (a.2) and Figure 8 (b.2), while quantitative comparison results are shown in Table 2. Over two cardiac cycles, the standard deviation of strain estimated from B-mode signals from the anteroseptal and anterior segment are 16% and 45% higher than that obtained with RF signal estimations. Comparison between envelope signals for these segments indicated a 42% and 27% difference when compared to strain estimated using RF signals.

Figure 8.

Comparison of the mean segmental accumulated strain variation and its standard deviation with time for RF, envelope and system generated B-mode results. Plots a) and b) represent results from the anteroseptal and anterior segments respectively.

Discussion

In this paper we compare the performance of displacement tracking and strain estimation using RF and envelope signals for cardiac or echocardiographic strain imaging. The comparisons were done using a uniformly elastic TM phantom, cardiac simulation data and in-vivo clinical data. We utilized a final cross-correlation kernel length of one wavelength along the beam direction for processing using RF, envelope and system generated B-mode signals. The purpose of such a small processing kernel is to ensure high spatial resolution in the estimated displacement and strain images. The pre- and post-deformation data segments were positioned using our multi-level hybrid 2D algorithm [39], and the performance comparison directly reflects the fact that displacement and strain estimation was obtained with correctly aligned signals. This alignment is crucial and may not be achieved with other algorithms that do not make this additional processing a priority.

Figure 1 indicates comparable displacement estimation performance using linear arrays between RF and envelope signals. For the phased array transducer, the variation in the standard deviation of the displacements estimated is higher (96%) for envelope when compared to RF signals. Figure 2 suggests that strains estimated using RF signals provide improved SNR_e performance when compared to envelope signals for linear (5.8 dB) as well as phased array transducers (9.5 dB). Our results indicate a higher variability in envelope strain estimation when a small cross-correlation kernel is used.

For a comparison of SNR_e improvement at different spatial resolutions, only the final processing kernel’s dimension was varied in Figure 3. The dimensions of the kernel in the first three levels of tracking kernels, the final processing kernel’s lateral dimension, window overlap percentage and least squares fit length method remained unchanged. When the processing kernel’s dimension along the beam propagation direction is reduced to a half wavelength, the SNR_e obtained with envelope signals are lower than 0 dB for both linear and phased array transducers, suggesting that the estimated strain signal and noise signals are indistinguishable.

Results from the cardiac simulation study demonstrate similar results as described in the uniformly elastic TM phantom study, as shown in Figures 4 and 5. The regional mean accumulated strain are similar, however, the mean standard deviation is significantly higher (48% and 44% from anteroseptal and anterior segment) for strain estimated using envelope signals when compared to RF signals, indicating increased spatial variability in the estimates. This result suggests that strain estimated using envelope signals may yield more unstable results than that estimated using RF echo signals.

The clinical study included three different data formats instead of the two evaluated using TM phantom and simulation studies. We also utilized the system generated B-mode images to evaluate similarities and differences between RF and RF generated envelope signals. As illustrated in Table 2, displacement and strain estimated from the system generated B-mode and envelope signals indicate larger percent differences in the mean standard deviation plots when compared to that obtained using RF echo signals.

Conclusion

In this paper, we illustrate the performance advantage obtained with utilizing RF echo signals over envelope or B-mode signals for cardiac or echocardiographic strain imaging. This is particularly true when small speckle tracking kernels are utilized to improve spatial resolution in the strain images. Temporal resolution is determined by the frame rate of the system. Two performance metrics, namely the regional mean displacement/strain and the standard deviation of the regional mean displacement/strain were evaluated in this paper. In phantom studies, the SNR_e improvement obtained using RF signals for linear and phased array geometries was 5.80 dB and 9.48 dB respectively, when compared to that obtained with envelope signals at the peak strain value. Results obtained from the cardiac simulation study also indicate that when averaged over two cardiac cycles, the standard deviation of estimated strain using envelope signals from the anterior and anterolateral segment are 48% and 44% higher than that obtained using RF signals. In vivo analysis on a volunteer shows that the standard deviation of the estimated strain using B-mode and envelope signals were 16% and 42% higher than that obtained using RF signals in the anteroseptal segment, and 45% and 27% in the anterior segment.

• Comparison of strain estimation between radiofrequency (RF) and envelope signals for cardiac strain imaging.

• Accurate regional myocardial function analysis with high spatial and temporal resolution.

• Signal-to-noise ratio improvement using RF over envelope signals for linear arrays was 5.80 dB.

• Signal-to-noise ratio improvement using RF over envelope signals for phased arrays was 9.48 dB.