Abstract
Purpose: Digital breast tomosynthesis (DBT) is a promising breast cancer screening tool that has already begun making inroads into clinical practice. However, there is ongoing debate over how to quantitatively evaluate and optimize these systems, because different definitions of image quality can lead to different optimal design strategies. Powerful and accurate tools are desired to extend our understanding of DBT system optimization and validate published design principles.
Methods: The authors developed a virtual trial framework for task-specific DBT assessment that uses digital phantoms, open-source x-ray transport codes, and a projection-space, spatial-domain observer model for quantitative system evaluation. The authors considered evaluation of reconstruction algorithms as a separate problem and focused on the information content in the raw, unfiltered projection images. Specifically, the authors investigated the effects of scan angle and number of angular projections on detectability of a small (3 mm diameter) signal embedded in randomly-varying anatomical backgrounds. Detectability was measured by the area under the receiver-operating characteristic curve (AUC). Experiments were repeated for three test cases where the detectability-limiting factor was anatomical variability, quantum noise, or electronic noise. The authors also juxtaposed the virtual trial framework with other published studies to illustrate its advantages and disadvantages.
Results: The large number of variables in a virtual DBT study make it difficult to directly compare different authors’ results, so each result must be interpreted within the context of the specific virtual trial framework. The following results apply to 25% density phantoms with 5.15 cm compressed thickness and 500 μm3 voxels (larger 500 μm2 detector pixels were used to avoid voxel-edge artifacts): 1. For raw, unfiltered projection images in the anatomical-variability-limited regime, AUC appeared to remain constant or increase slightly with scan angle. 2. In the same regime, when the authors fixed the scan angle, AUC increased asymptotically with the number of projections. The threshold number of projections for asymptotic AUC performance depended on the scan angle. In the quantum- and electronic-noise dominant regimes, AUC behaviors as a function of scan angle and number of projections sometimes differed from the anatomy-limited regime. For example, with a fixed scan angle, AUC generally decreased with the number of projections in the electronic-noise dominant regime. These results are intended to demonstrate the capabilities of the virtual trial framework, not to be used as optimization rules for DBT.
Conclusions: The authors have demonstrated a novel simulation framework and tools for evaluating DBT systems in an objective, task-specific manner. This framework facilitates further investigation of image quality tradeoffs in DBT.
Keywords: virtual trials, breast tomosynthesis, task-specific, image quality, projections, model observers
INTRODUCTION
Digital breast tomosynthesis (DBT) is an attractive limited-angle tomographic alternative to conventional 2D screening mammography because it has potential to improve both sensitivity and specificity (call-back rates).1, 2 However, this potential improvement is difficult to quantify because it depends not only on the imaging system, but also on the specific patient population and clinical task of interest. Even if we assume that DBT improves screening, the challenge remains to quantitatively assess the merits of different DBT imaging systems.
Studies have shown that the optimal x-ray spectrum for full-field digital mammography (FFDM) imaging depends on patient characteristics.3, 4 Some commercial FFDM systems are designed with selectable parameters in order to optimize the x-ray spectrum for a given patient at the time of the examination. The automatic-exposure-control subsystems of these devices automatically optimize over the space of mammography system parameters (e.g., tube voltage, tube current-exposure time product) based on pre-exposure measurements of patient characteristics (compressed breast thickness, breast attenuation measured by a low-level test exposure).5 However, these FFDM optimization parameters are only a subset of the factors affecting image quality in DBT (Table 1). We expect that ongoing investigations into DBT will reveal improved algorithms for optimizing image quality on a patient-specific basis. Thus, DBT researchers continue to develop prototypes and explore the parameter space of this modality to find optimal imaging conditions.
Table 1.
Key image quality factors in mammography and DBT.
| Mammography | Digital breast tomosynthesis |
|---|---|
| Target/filter materials | Target/filter materials |
| Tube voltage | Tube voltage |
| Tube current-exposure product | Tube current-exposure product |
| Breast thickness | Breast thickness |
| Breast density | Breast density |
| Detector properties | Detector properties |
| Display device | Display device |
| X-ray source scan angle | |
| X-ray source angular sampling | |
| Dose delivery scheme | |
| Reconstruction algorithm |
Because physical prototype development is expensive and time-consuming, some groups are researching strategies for DBT system optimization based on simulation studies. Specifically, optimization of the x-ray source scan angle and angular sampling scheme is an area of interest in recent literature.6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 These studies could reduce the number of physical prototype iterations and eventually lead to task- and patient-specific optimization of tomosynthesis. But to achieve these goals, we first need accurate, task-based strategies for evaluating key DBT system parameters in simulation. In practice, various assumptions are necessary to reduce the optimization space and design tractable simulations; this work is no exception. We sacrifice some realism in order to introduce a virtual framework for quantifying the tradeoffs between factors that influence DBT image quality. In this paper, we begin by developing a model for generating tomosynthesis data (Sec. 2). Then, we apply a flexible, task-based assessment strategy using model observers (Sec. 3). Finally, we show specific examples of how our approach can be used to assess image quality tradeoffs for different scan and sampling angle combinations in DBT (Sec. 4). Section 5 provides a direct comparison of our framework to other relevant publications, and details on the limitations of our framework are found in Sec. 6.
DBT SYSTEM MODEL
For DBT system evaluation, we need a computationally tractable x-ray imaging model that supports anthropomorphic digital breast phantoms, accurate radiation transport in multiprojection geometries, a detector response/noise model, and a relationship to mammographic x-ray dose quantities. To meet these model requirements, we first generated a large ensemble of 3D voxelized breast phantoms (Sec. 2A). Then, we used open-source codes based on the PENELOPE Monte Carlo framework18 to simulate multiprojection x-ray scans (Sec. 2B). Next, we modeled the statistics of an idealized indirect-type x-ray detector (Sec. 2C). Finally, we related the simulated x-ray projection data to standard measures of dose in mammography (Sec. 2D).
The digital phantom ensemble
There are a number of software phantoms in the literature which seek to approximate the structural nature of breast tissue in digital or analytical form.19, 20, 21, 22, 23, 24, 25 We needed three specific features in a software phantom: (1) the ability to generate random breast parenchymal patterns, (2) projection image statistics that match mammogram statistics, and (3) the ability to generate a large batch of phantoms relatively quickly. Bakic's voxelized breast phantom model was chosen to meet these requirements.19, 26, 27 Various studies have demonstrated that Bakic's phantom can be used to simulate realistic breast parenchymal patterns.28, 29, 30 We created an ensemble of 1000 compressed breast phantoms having the same volume (450 mL) and approximately the same percent density (25% fibroglandular, 75% adipose). Based on recent results by Yaffe et al.,31 we chose a 25% density model as a more appropriate representation of the “standard” clinical breast than a 50–50 model.
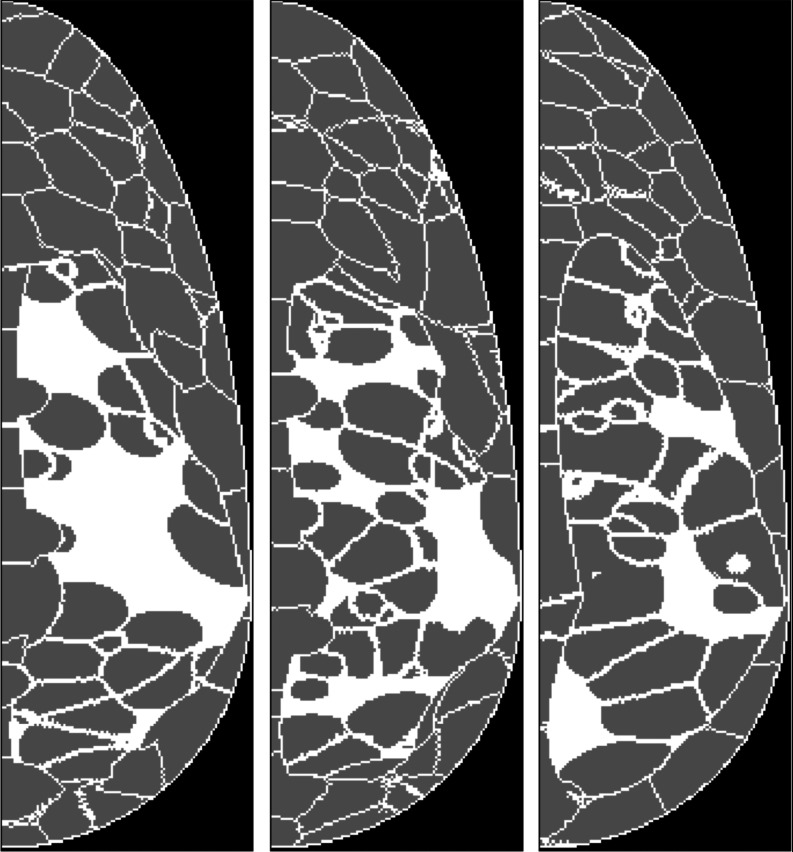
Each phantom contained random numbers of fibroglandular and adipose compartments (drawn from Poisson distributions) randomly localized within the phantom volume. Figure 1 shows example sagittal cross-sections from three uncompressed breast phantoms with randomly-generated compartments, illustrating variations in the adipose (dark gray) and fibroglandular breast structures (white). Before simulating the forward problem, the phantoms were compressed via finite element methods.32, 33 Material types were mapped to tissue density coefficients based on previously reported values,34 but to simulate a more challenging detection task, we set the signal density to 1.0 g/cm3 instead of using the reported value for carcinoma density (1.044 g/cm3). Table 2 lists shared parameters of the breast phantom ensemble.
Figure 1.
Breast phantoms (before compression) in sagittal cross-section with randomly-generated compartments of adipose (gray) and fibroglandular tissues (white), showing example tissue structures for the simulated class of patients.
Table 2.
Shared parameters of the virtual breast ensemble.
| Sagittal dimensions | 20.45 × 6.5 cm |
| Breast thickness (compressed) | 5.15 cm |
| Voxel size | 500 μm |
| Adipose tissue density | 0.928 g/cm3 |
| Fibroglandular tissue density | 1.035 g/cm3 |
| Signal mass density | 1.0 g/cm3 |
Multiprojection x-ray imaging
Full 3D x-ray simulation with scatter is challenging due to heavy computational requirements. To assess image quality, we have the additional need to produce hundreds or thousands of multiprojection scans in a reasonable amount of time. To simulate multiprojection scans, we began by generating scatter-free images using a voxelized version of the PENELOPE photon-electron transport code called penEasy.35, 36 We used the penEasy package (v. 2010-09-02) in ray-tracing mode and ran simulations in parallel on a 190-node cluster of AMD Opteron and Intel Xeon servers in order to generate large image sets quickly. In penEasy ray tracing, a noise-free mean image is generated by casting a small number of deterministic rays from the focal spot to different positions inside each pixel to estimate the probability of x rays arriving at the pixel without interacting along the track. The ray-tracing image is scaled by the probability of emitting the x rays within the solid angle covering each pixel, assuming that the source is collimated to exactly cover the detector surface. The output is a normalized image with units eV/cm2 per source photon.
We modeled an x-ray point source which radiates monoenergetic photons (20 keV), traces an arc of radius R = 59 cm through a maximum scan angle (θscan) of 96° at variable angular sampling intervals (Δθ), and projects onto a 26 × 7 cm2 detector region-of-interest (ROI) with 500 μm pixels (Fig. 2). θscan = 96° corresponds to a wide-angle DBT system with acquisition parameters outside the range of published values for scanning-source DBT prototype systems (see Table 2 of Reiser and Nishikawa15). Wider angles were considered to allow for static-source systems where gantry speed is not an issue. We inserted a 1.5 cm air gap between the phantom and the detector, introducing a slight magnification. By translating the detector ROI with x-ray source angle, we modeled partially-isocentric motion with the center-of-rotation inside the breast phantom volume.
Figure 2.
We modeled a partially-isocentric breast tomosynthesis acquisition geometry (schematic not to scale).
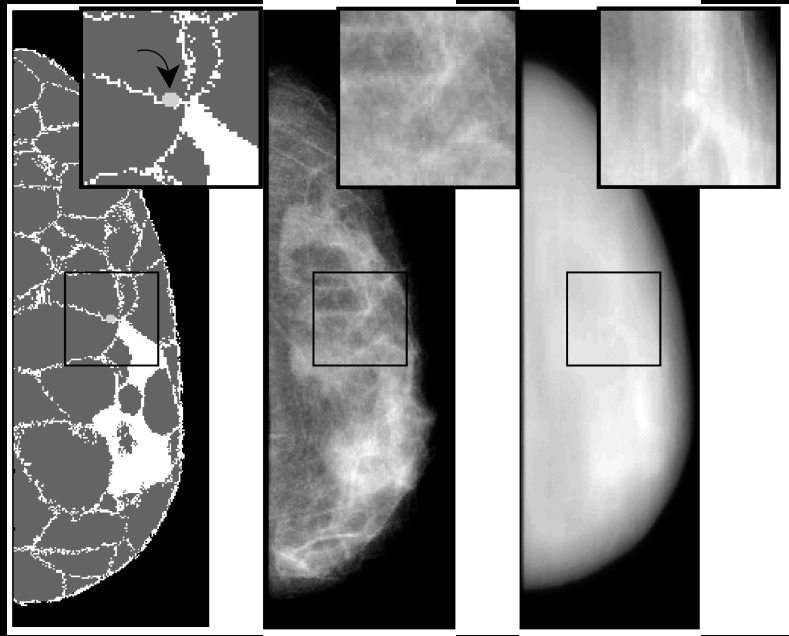
We generated a total of 97 000 projection images in penEasy corresponding to 1000 different phantom realizations with 97 projections per scan (Δθ = 1°). For the observer studies in Sec. 3, we created a signal-known-exactly (SKE) task by inserting a small spherical signal mass (3 mm diameter) in half of the breast phantoms at the center-of-rotation of the x-ray source arc. The mass was inserted by changing the density coefficients of the voxels at the signal location to the signal mass density given in Table 2. A 3 mm mass corresponds to an early-stage cancer with a favorable five-year prognosis,37 and its small size makes it susceptible to anatomical masking—a good scenario for testing the benefits of DBT. Figures 23 together illustrate the forward problem for one of the breast phantoms. The projected signal was invisible to the human eye in a noise-free projection at θ = 0° [Fig. 3 (center)]. For illustrative purposes only, we show that the signal is visible in a simple back projection reconstruction with θscan = 96° and 25 projection angles [Fig. 3 (right)]. This corresponds to the kind of detection task where DBT may provide an advantage over conventional mammography. In Sec. 4, however, all results are for raw images without reconstruction.
Figure 3.
From left-to-right: Sagittal slice through a compressed phantom (z = 6 cm) with 3 mm diameter signal (light gray), ray-tracing projection at θ = 0°, and simple back projection reconstruction from 25 equally-spaced ray-tracing projections with θscan = 96° (refer to Fig. 2 for geometry).
For modeling scatter, we generated a uniform phantom with the same shape as the structured phantoms and a nominal density 0.955 g/cm3 (for 75%–25% adipose-fibroglandular) based on results of Hammerstein et al.38 We used the open-source MC-GPU code39 with slight modifications to support partially-isocentric DBT geometries, to simulate one high-exposure (1012 source photons) acquisition at each projection angle. In MC-GPU, the source was defined as a fan beam with fixed polar (24°) and azimuthal (7°) aperture angles, producing a 27.6 × 8.0 cm2 rectangular field (at θ = 0°). Each Monte Carlo run with 1012 source photons took about 20 min to simulate using 8 NVIDIA GTX 580 GPUs in parallel.
MC-GPU stores separate images for the primary and scattered photons. The scatter-only image is normalized with units eV/cm2 per source photon, which matches the output from penEasy ray tracing. At a given angle, we formed “noise-free” hybrid images by adding the high-exposure, scatter-only image of the uniform phantom to the penEasy ray-tracing images for each structured phantom. Thus, our scatter model depended on the projection angle, but not on the distribution of tissues in a given structured phantom. We used this “noise-free” hybrid model, instead of the total MC images, to allow for analyzing various noise levels in postprocessing.
Detector model
After storing the “noise-free” hybrid images from penEasy/MC-GPU in units of eV/cm2 per source photon, we needed a practical detector noise model. We modeled an indirect-type detector with a CsI:Tl phosphor layer deposited onto a photodiode array. Relevant detector parameters are shown in Table 3. There were three primary assumptions in the model: (1) noise-free gain in the phosphor material, (2) no depth-of-interaction effects, and (3) no energy-dependent effects. Also, the quantum efficiency of x-ray absorption was assumed to be independent of incident angle. In this idealized model, we can write the mean output voltage in pixel m as
| (1) |
where η is the quantum efficiency of the phosphor, A is the pixel area, N0 is the total number of source photons summed over all projections, is the mean optical gain (number of optical secondaries per x-ray primary), Γ is the electronic gain (photodiode output voltage per optical secondary), P is the number of projections in the DBT scan, is the mean x-ray energy, and pm is the noise-free penEasy/MC-GPU pixel value for pixel m. Note that we assumed Γ is independent of m, which may not be true for real photodiode arrays. Also note that this model assumes the source photons are divided equally among the P projections. The variable gm is used here for consistency with the M × 1 image vector g described later in Sec. 3A. CsI:Tl has a gain of 55 optical photons per keV of incident x-ray energy.40 For 20 keV photons, we assumed η(20 keV) ≈ 70% so optical secondaries per x-ray primary. The electronic gain parameter Γ was calculated from Eq. (12.301) in Ref. 41, reproduced here:
| (2) |
where e is the electron charge, ηpd is the quantum efficiency of the photodiode, and Cpd is the photodiode's capacitance. For a 500 × 500 μm, 1-μm-thick a-Si:H photodiode, we used ηpd = 0.8 and Cpd = 25 pF (pp. 260–261 of Ref. 40) and found an effective gain Γ = 5.13 × 10−9 volts per optical secondary.
Table 3.
DBT model source, detector, and dose parameters.
| Source Parameters: | |
|---|---|
| Monoenergetic source () | 20 keV |
| Maximum scan angle () | 96° |
| Source-image distance (at θ = 0°) | 65 cm |
| Detector Parameters: | |
| Detector type | Indirect (CsI:Tl) |
| Pixels per projection (M) | 520 × 140 |
| Pixel Area (A) | 0.25 mm2 |
| Phosphor efficiency (η) | 0.7 |
| Optical gain () | 1050 |
| Electronic gain (Γ) | 5.13 × 10−9 |
| Dose Parameters: | |
| mGy per source photon (at 0°) | 4.2 × 10−12 |
To model the quantum noise in a pixel, we invoked the noise-free gain assumption so that the quantum noise variance of gm may be written as the mean number of absorbed x rays times the total gain squared (pp. 1110–1111 of Ref. 41). This model can be considered as a “special case” of the Burgess variance theorem.41 In the notation of Eq. 1, we have:
| (3) |
where again we emphasize the assumption that no additional variance is introduced during the x-ray-to-voltage conversion process in the detector. For a CsI:Tl detector, the Swank factor is close to unity (p. 250 of Ref. 40), so we could reasonably assume a noise-free gain mechanism in the phosphor. This model makes the noise more computationally tractable, because we can model the quantum noise in a pixel by sampling from a Gaussian distribution with the appropriate variance. We modeled multiprojection scans by dividing the total number of photons N0 equally among the projections, so scans with more projections suffered from more quantum noise (Fig. 4).
Figure 4.

From left-to-right: Zero-angle projection ROIs (128 × 128 pixels) from scans with P = 1, 5, and 15 total projections. Applying Eq. 3 with fixed total exposure (N0 = 1010 source photons) and increasing P leads to increased quantum noise per projection.
In addition to modeling quantum noise, we added Gaussian noise with variance to approximate the effects of electronic noise in the detector. Reported empirical values for electronic noise in indirect x-ray detectors are variable and highly dependent on the measurement conditions, but one author estimated the overall electronic noise to be about 1000 electrons.42 Another group estimated the standard deviation at 2200 electrons.6 For a theoretical reference point with units matching Eq. 3, we assumed a simple model of electronic noise given by where kB is Boltzmann's constant, and T is the temperature. This corresponds to the reset noise for a gated integrator (p. 722 of Ref. 41). At room temperature, this noise model produces a voltage variance (volts)2, corresponding to a standard deviation of ≈2500 electrons (σelec/Γ). Note that we used larger pixels than the references above. Also, may underestimate the variance in real detectors because we neglected other noise sources such as dark current and 1/f noise. Still, we report a value to give context to the results in Sec. 4A.
Dose considerations
Working in simulation, it is important to relate our study conditions to standard measures of breast dosimetry. Using the dose tally feature in MC-GPU version 1.2, we computed the mean glandular dose (MGD) as a function of projection angle for all 500 phantoms in the signal-absent phantom set (Fig. 5). We assumed that the MGD was symmetric about θ = 0°. In MC-GPU, we simulated N0 = 1010 source photons at each projection angle. At each angle, we recorded the average dose tally for each phantom material type in units of electron volts per gram per source photon and converted the average glandular dose to milliGray per source photon. At θ = 0°, the mean glandular dose was ≈4 × 10−12 mGy per source photon. The 1997 MQSA/NEXT survey average in NCRP Report 149 for mean glandular dose in mammography was 1.6 mGy, corresponding to N0 ≈ 4 × 1011 source photons in our model.
Figure 5.
The mean glandular dose (in milliGray per source photon) declined slightly with projection angle θ (in degrees). This trend qualitatively agrees with results from Sechopoulos et al. (Ref. 11) for a phantom with similar chest-to-nipple distance (e.g., Figs. 8(c) and 9(c) of Ref. 44). Error bars are ±2σ based on a set of 500 phantoms.
TASK-BASED IMAGE QUALITY ASSESSMENT
In Secs. 3A, 3B, 3C, 3D, we provide background on task-based assessment and key relations for evaluating DBT systems. Section 3A frames the signal detection task. Section 3B describes channels and considerations for designing a robust observer model. Section 3C gives details about the figure of merit we used to evaluate systems. Finally, Sec. 3D introduces covariance decomposition in the context of DBT as a tool for accelerating system evaluation and visualizing tradeoffs between various parameters.
Detection of small masses
In mammography, one important task is to detect small, low-contrast masses in the breast. To understand DBT's potential advantages for performing the same task, we started with the task of detecting small signals in the raw multiprojection data. It is important to first quantify signal detectability in the raw data because different postprocessing and reconstruction algorithms may lead to differences in task performance.43
We represented the discrete-to-discrete x-ray imaging process with the imaging equation:
| (4) |
where f is the voxelized phantom object (N × 1 voxels), H is a nonlinear operator (M × N) which approximates the physical interactions that occur between x-ray source and detector plane, n is the measurement noise, and g is the resulting discrete projection image (M × 1 pixels). In a mutiprojection image acquisition with P projections, H changes with each projection angle. If we stack these H operators to form a multiprojection H operator (M′ × N) and concatenate the projections from a DBT scan into a single vector, Eq. 4 still holds with M′ = PM. In Sec. 2, we describe a simulation framework for Eq. 4, modeling n with a combination of quantum and electronic noise. In practice, the multiprojection H operator was too large to save (∼40 terabytes for P = 25), so only f and g were stored.
Consider a detection task with n0 signal-absent and n1 signal-present DBT scans given by
| (5) |
| (6) |
where we have used different subscripts to indicate that the fi and fj phantoms come from independent phantom sets. The vector sj is the signal in the jth phantom. As described in Sec. 2B, sj corresponds to changes in the voxel density coefficients inside the 3 mm signal volume. Therefore sj depends on the pre-existing density coefficients in fj at the signal location.
Dimensionality reduction using channels
Linear discriminant analysis (LDA) is a common tool for measuring the separability of two data classes, as in our detection task. In the medical imaging community, the ideal linear discriminant is known as the Hotelling observer (HO).44 It involves computing a score t for each data set g using a linear template as follows:
| (7) |
where is the mean difference in the data under the signal-present and signal-absent classes (PM × 1, superscript t for transpose) and Kg−1 is an inverse intraclass covariance matrix (PM × PM). Standard LDA depends on estimating the data covariance matrix from samples, which is usually not possible when the data dimension PM exceeds the number of data samples n = n0 + n1. To circumvent this problem, we performed dimensionality reduction (aka feature transformation) using channels which extract salient features from the data for the given task. For example, with P = 25 projections and M = 72 800 pixels per projection, standard LDA would require estimation and inversion of an exceedingly large matrix (P2M2 > 1012 elements). We would need at least as many phantoms as matrix elements to estimate Kg by standard methods. Instead, we first channelized each projection image by applying Laguerre-Gauss (LG) channels (Fig. 6). We chose LG channels for two reasons: (1) our signal is approximately rotationally-symmetric, and (2) Witten et al. showed that for both circular and elliptical signals in non-Gaussian, randomly-varying backgrounds, channelized-ideal observer performance approached the ideal observer's performance with relatively few LG channels (Fig. 6 of Ref. 45). Barrett et al. originally proposed using LG channels in similar types of detection tasks since they form a basis on the space of rotationally-symmetric functions.46 The channelization step is given by
| (8) |
where U is a channel matrix with dimensions PM × PC and C is the number of channels. Projecting onto the LG basis reduces the size of each multiprojection data vector from PM × 1 to PC × 1. Reformulated in terms of channel outputs, Eq. 7 becomes
| (9) |
where the covariance Kv now has dimensions PC × PC. This is the channelized-Hotelling observer (CHO) score – the score computed in the LG feature space.
Figure 6.
Zoomed ROIs (only the central 24 × 24 pixels shown) from the first six (of C) LG channels used to reduce the dimensionality of g. The LG width parameter a = 6, and the full ROIs were 128 × 128 to match the image dimensions in Fig. 4.
The inverse operation in Eq. 9 can still present difficulties, particularly when the covariance matrix is ill-conditioned. In this work, we used MATLAB's truncated SVD pseudoinverse algorithm (pinv function) to perform the inverse. Singular values below a default tolerance are set to zero.
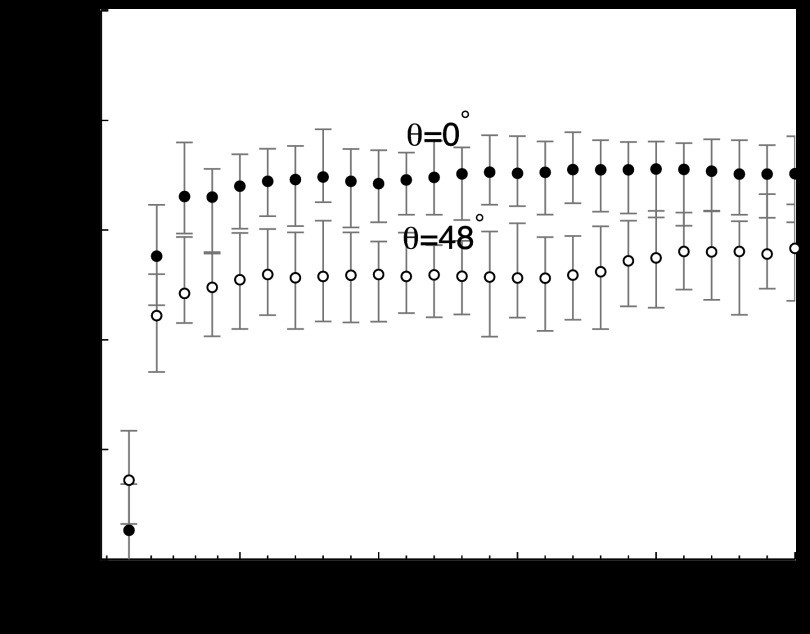
An important question for robust system evaluation is how to choose the LG width parameter a and the number of channels C. For a rotationally-symmetric signal, Gallas and Barrett argued that the CHO's performance should asymptote to the performance of the ideal observer as the number of channels increases.47 Then, the optimal strategy is to choose a and C to achieve the asymptotic limit of the ideal observer with as few channels as possible. Gallas' simulated signals and backgrounds differ from ours, but we followed a similar line of reasoning. Our problem is complicated by the fact that the signal loses rotational symmetry at larger projection angles. The signal diameter varies from 3.3 mm in the 0° projection to 3.45 mm in the 48° projection (≈6–7 pixels). To address this variation, we started with a = 6 pixels (the signal diameter before magnification/angular effects). Then, we computed the area under the receiver operating characteristic curve (AUC) as a function of C for the smallest (θ = 0°) and largest (θ = 48°) projection angles in our study (Fig. 7). There was no electronic noise, and the simulation parameters were set as in Table 3. Since the signal shape changes with angle, the optimal C could also change with θ. Based on Fig. 7, we chose C = 6 as a reasonable compromise between achieving asymptotic AUC at all θ and maintaining a small, consistent number of channels for practical figure-of-merit calculations.
Figure 7.
AUC versus the number of channels for θ = 0° and θ = 48° projection angles. We chose C = 6 for approximately asymptotic performance. N0 = 5 × 1011 and .
Figures of merit
To calculate figures of merit for signal detectability, we first rearranged the channel data into training and testing subsets of equal size (ntrain = ntest = 500 scans). In each subset, half of the phantoms were signal-absent and half contained embedded signals. From Eq. 9, the score for each testing scan takes the form
| (10) |
where is the mean difference in the channelized multiprojection training data under the signal-present and signal-absent classes (PC × 1) and is the inverse intraclass covariance matrix (PC × PC). The hats indicate quantities estimated from samples. The first term () is just a sample mean, and we will discuss covariance estimation in Sec. 3D. After computing scores for all 500 testing scans, we used the perfcurve function in MATLAB's Statistical Toolbox v7.6 to estimate the area under the ROC curve (AUC) along with bootstrap confidence intervals.
Covariance decomposition
One way to estimate AUC is to generate noisy sample projections, channelize the data, compute their scores by Eq. 10, and then compute an ROC curve. Generating thousands of noisy sample projections is time-consuming, however, so we sought faster alternatives to estimate AUC more efficiently across a range of system parameters.
Under broad assumptions, we can write the total covariance in Eq. 7 as a sum of components:44
| (11) |
The “poiss” term is the Poisson photon-counting noise, the “gain” term describes the noise in the gain processes, the “elec” term lumps together all of the electronic/excess noise effects, and the “obj” term is the covariance in the data due to anatomical variations in the breast phantoms. The full decomposition includes other terms, but we ignored them in this work. Also, this model assumes that the signals from the mass lesions are weak, so the covariance components are effectively unperturbed by the presence of masses (i.e., Kg|0 ≈ Kg|1). Note that although Eq. 11 is written as a sum, the terms contributing to the total covariance are not all statistically-independent. For example, changing the characteristics of the breast phantom ensemble could change both the “poiss” and “obj” terms in the decomposition. Expanding the first three terms of Eq. 11 according to the detector model in Sec. 2C, we can write (in the channelized data space):
| (12) |
where is a PM × PM diagonal matrix with the mean noise-free multiprojection vector along the diagonal; is a PM × PM electronic noise matrix; and is a PC × PC matrix. As before, hats indicate the quantities that we estimate from sample data. We assumed independent, identically-distributed electronic noise, so we can replace with since U is unitary for LG channels. Note that due to the noise-free gain assumption in Sec. 2C, the first two terms in Eq. 11 reduced to a single, diagonal “quantum noise” matrix. We found sparse matrix tools helpful for computing this term.
Next, we modified the object covariance to express it in terms of noise-free channelized projection data vp, where vp = Utp. This introduces a quadratic dependence on the total number of source photons N0, and the total covariance becomes:
| (13) |
This equation shows how the DBT data covariance matrix in our model depends on key system and object parameters. It contains two diagonal parts and a structured object covariance part. Using Eq. 13, we can estimate the total covariance for systems having different mean x-ray energies (), quantum efficiencies (η), gain parameters (), total numbers of source photons (N0), numbers of projections (P), or electronic noise variances (). Only two terms – and – are estimated from the training set of ntrain noise-free DBT scans. Due to the weak-signal assumption, we estimated from the signal-absent scans only and computed as the average of the signal-absent and signal-present sample covariances. The same ntrain scans were used to estimate the sample mean (). Then, by Eq. 10, it is straightforward to compute scores and AUC. This saves time compared to the alternative of simulating noisy projections for every possible combination of the above system parameters. Note, however, that in this study we limited the phantom ensemble to one breast volume class from a specific phantom-generating algorithm, so , , and AUC should be re-computed for different phantom sizes and phantom-generating models.
RESULTS
Covariance decomposition
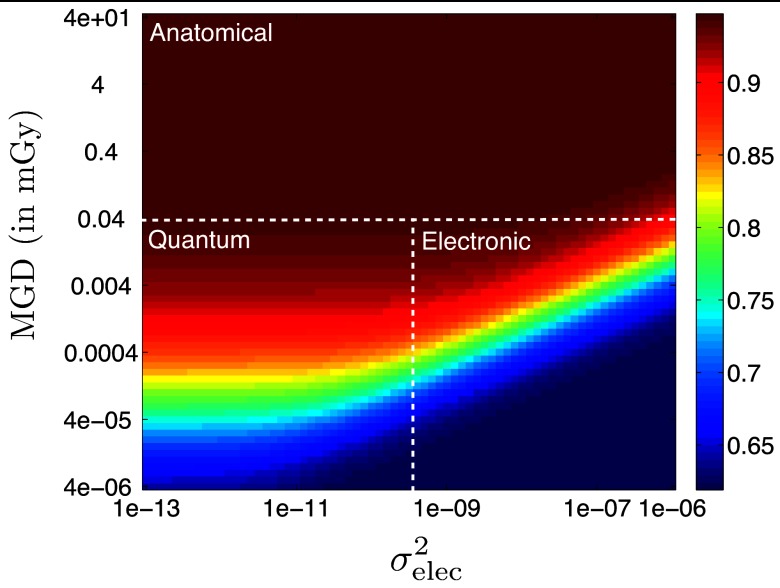
For a given task, we want to know which noise source is the limiting factor in observer performance. The covariance decomposition described in Sec. 3D makes it straightforward to visualize noise tradeoffs in our model (Fig. 8). Each data point in the figure was calculated by changing the values of N0 and in the covariance decomposition and recomputing AUC. We then computed the corresponding MGD using the normalized dose coefficients from Fig. 5.
Figure 8.
AUC map as a function of total MGD for the whole scan and electronic noise variance () illustrates the tradeoffs in our covariance decomposition noise model. In this case P = 5 and θscan = 64°, and the dotted lines are approximate boundaries between different performance-limiting factors.
By visual inspection of Fig. 8, we can divide the AUC map into approximate zones corresponding to ranges of MGD and where the performance-limiting factor is anatomical, quantum, or electronic in nature. In the specific case shown (P = 5 and θscan = 64°), the dominant “noise” is anatomical variability for doses higher than about 40 μGy. Above 40 μGy, the AUC appears to saturate at a value close to 0.95. In this regime, more dose does not lead to better image quality – the image quality is limited by the anatomical backgrounds present in our phantoms. Below 40 μGy, we can distinguish the quantum and electronic regimes by drawing a vertical dividing line approximately where the slope of the rainbow band changes from zero to positive. This is the point where is large enough that electronic noise begins to dominate.
For a typical single-view mammography dose of about 1.6 mGy, we are clearly operating in the Anatomical regime in Fig. 8. However, the behavior of Fig. 8 may depend on the scan angle and number of projections. Section 4B focuses on AUC tradeoffs at a clinically-relevant dose point in the Anatomical regime, but we also investigate two other test cases in the MGD- space (Table 4). The total MGD for the whole scan varies with P, so the cases are described in terms of a fixed N0 and an approximate MGD value.
Table 4.
| Abbr. | N0 | Approx. MGD | Limiting factor | |
|---|---|---|---|---|
| A | 5 × 1011 | 2 mGy | 0 | Anatomical variability |
| Q | 108 | 0.4 μGy | 0 | Quantum noise |
| E | 108 | 0.4 μGy | 10−9 | Electronic noise |
Image quality tradeoffs: scan angle and number of projection angles
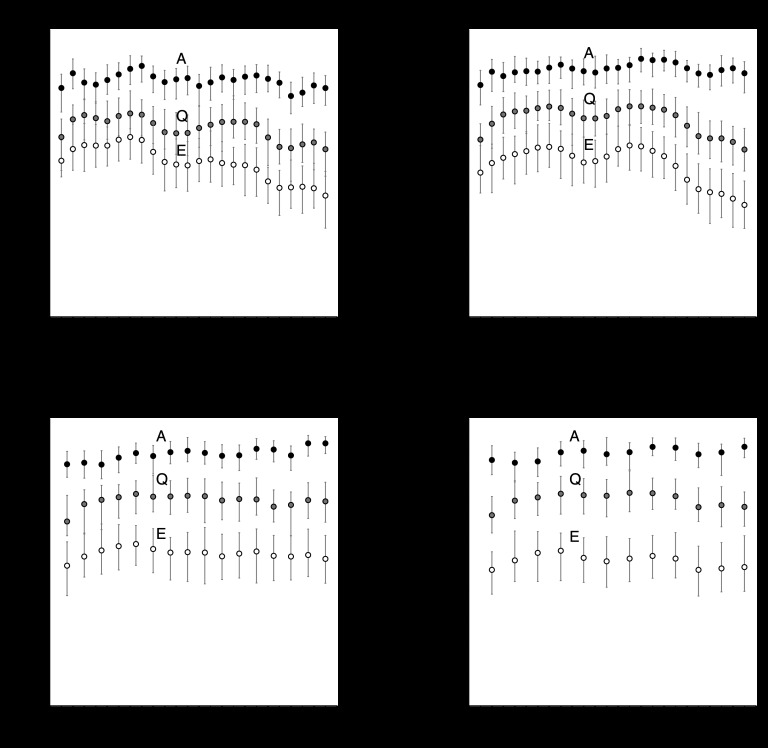
The DBT scan angle and number of projections are key image quality parameters that separate DBT from conventional mammography. In this section, we isolate these two parameters and evaluate AUC as a function of each. First, we analyzed AUC versus scan angle for four different numbers of projections (Fig. 9). For each test case in Table 4, AUC was computed using covariance decomposition and MATLAB LDA tools as described in Secs. 3C, 3D. The projection angles were evenly-spaced, so the number of points in each plot varies depending on whether projection data were available at the required sampling angles for a given scan angle. The error bars are 95% confidence intervals computed from 100 bootstrap samples.
Figure 9.
In the anatomical-variability-limited (A) regime, AUC appears to be independent of scan angle. In the Q and E regimes, the trends appear similar to the A regime trends except at large θscan. Error bars are 95% confidence intervals computed from 100 bootstrap samples.
Figure 9 shows that in the Anatomical (A) regime, AUC does not appear to depend on scan angle. The trends suggest a slight increase in AUC at larger scan angles for P > 5, but the error bars are overlapping so it is difficult to conclude that increasing the scan angle improves detectability. In the Q and E regimes, the trends look similar except at the largest scan angles where AUC appears to decrease slightly relative to the A regime curves.
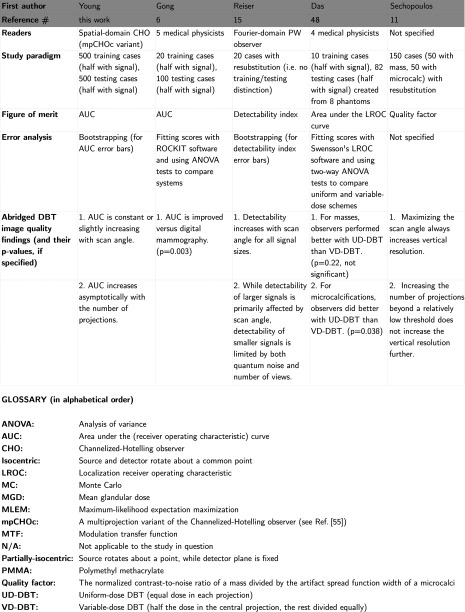
To evaluate the impact of the number of projections, we fixed the scan angle and evaluated different subsets of equally-spaced projection angles. For example, with θscan = 96°, P = 3 gives the subset θ = 0, ±48° and P = 5 gives the subset θ = 0, ±24, ±48°. P = 1 corresponds to single-view mammography, so the AUC value is the same for all scan angles. We computed AUC versus P at three different scan angles for the three regimes in Table 4 (Fig. 10). For θscan = 24° and 60°, AUC clearly increases from P = 1 to P = 3 in the A regime, but there appears to be minimal improvement when P > 3. For θscan = 96°, however, the AUC in the A regime seems to increase more gradually and reach a threshold around P = 7 projections. For all three scan angles, the A and Q regime curves trend upward, while the E regime curves generally decrease with P. Taken as a whole, Figs. 910 suggest that to maximize the AUC for our task, we can operate at any of the three scan angles; but the optimal number of projections depends on the chosen scan angle.
Figure 10.
Multiprojection imaging (P > 1) improved AUC for all three scan angles (in the A regime), though the optimal number of projections appears to depend on scan angle. For θscan = 96°, there is a threshold number of projections around P = 7 for maximum AUC. Error bars are 95% bootstrap confidence intervals.
The θscan = 60° and 96° curves do not appear to represent smooth functions. At P = 5 in particular, something causes the AUC to deviate from neighboring data points. We suspect that this is caused by certain angles having relatively stronger/weaker signal content than others due to the characteristics of the phantom model. For example, θscan = 60° and P = 5 corresponds to θ = 0°, ±15°, ±30°. For the same scan angle, P = 7 corresponds to θ = 0°, ±10°, ±20°, ±30°. The AUC “deviation” at P = 5 should then be related to the differences between the projections at θ = ±10°, ±15°, ±20°. This appears to be a consequence of using a nonuniform phantom model. While many studies rely on uniform phantoms, our results suggest that it may be clinically important to investigate nonuniform phantom effects to understand the effects of patient variability on DBT design choices.
LITERATURE ANALYSIS
Several groups have published simulation studies for evaluating DBT systems in a virtual environment. In this section, we summarize a number of studies in this vein. Figure 11 is not exhaustive, as it does not include studies involving physical prototype DBT systems. We have limited the comparison to DBT studies where the patient population and image acquisition are entirely virtual, as in our study. Two of the studies in Fig. 11 used human readers,6, 48 but we still consider those studies to be consistent with a virtual trial paradigm. Also, in the Das and Sechopoulos studies, some details of their noise models are cross-referenced, so we have included relevant reference numbers49, 50, 51, 52, 53, 54 in the appropriate boxes in Fig. 11.
Figure 11.
Comparison of five virtual DBT trial frameworks (continued on the next page).
DISCUSSION
Image quality metrics for assessing DBT systems abound in the literature. Some metrics are related to each other by simple transformations (e.g., AUC and SNRCHO), while others come from entirely different interpretations of image quality. In this work, we used a spatial-domain observer model (in projection space) with the AUC figure of merit because this approach offers distinct advantages over other spatial and Fourier domain approaches. Most importantly, AUC is a task-specific metric. It depends on all the parameters of the detection task, such as signal size, detector noise correlations, breast phantom variability, pixel size, and observer strategy. By contrast, a task-generic metric like CNR assumes pixel-independent noise in the data (no correlations).
Working in projection space is both a limitation and an advantage. It is a limitation because human observers only look at reconstructions. However, it is advantageous to separate the analysis of DBT systems into analysis of the raw projection images (with model observers) and analysis of the reconstruction algorithms we use to visualize the data (with human or model observers). Take, for example, the result in Fig. 10 which says that for θscan = 24°, P = 3, and P = 9 give about the same AUC. While a reconstruction from 3 projections would generally be considered unacceptable due to artifacts, this indicates a failure in the reconstruction algorithm, not necessarily a lack of information in the raw data. Our results suggest that some information gets lost in the reconstruction process for P = 3. The only way to measure this detectability loss is with a projection-space reference point.
A logical next step is to apply this framework to detecting microcalcifications. In this study, we were limited by the phantom voxel size – 500 μm was state-of-the-art at the time of this work. This leads to voxel-edge artifacts in the images when the pixel size is less than the voxel size. By using larger 500 μm pixels, we avoided voxel-edge artifacts at the cost of somewhat distorting the task; larger pixels may explain why the AUC remained high even at an exposure level of N0 = 109 source photons, which corresponds to less than 1% of typical mammography dose. In the task of detecting a 3 mm mass, anatomical noise appears to be the dominant noise source, since we only saw AUC degradation for ultra-low dose levels. However, for the task of detecting microcalcifications, quantum noise could start to dominate at a higher dose threshold (i.e. the “Quantum” zone in Fig. 8 could shift upwards). Based on a recently updated method for the generation of Bakic software phantoms,55 it may be possible to efficiently simulate breast anatomy with smaller voxel sizes and investigate microcalcification detection within our framework.
We used a homogeneous phantom to model scattering in this study. There is some precedent for using the scatter from a homogeneous phantom (e.g., Refs. 6 and 11), though we have not seen a DBT study quantifying the impact of randomly-varying scatter from an ensemble of heterogeneous phantoms on lesion detectability. While breast compression was used in the phantom model, there was no breast support plate in this work. Since the breast support plate affects scattering in an angle-dependent fashion, we expect that it could impact the magnitude of our AUC values and the AUC trends versus scan angle. However, these effects are likely small compared to the effects of breast compression. In this work, we used a binarized version of the UPenn phantom model for simplicity (i.e., fewer tissue material definitions). However, the penEasy and MC-GPU codes are general and they can accept any voxelized phantom model. Non-binary phantom models are worth exploring to increase the clinical relevance of our simulated detection tasks with little change in total computation time.
A strength of the framework is the use of large sets of anthropomorphic phantoms. There is no standard patient/phantom ensemble size in the DBT assessment literature for demonstrating that image quality gains are statistically significant. Anatomical noise may be the limiting factor in many imaging situations, so it is important to model anatomical variability as realistically as possible. We treated this often overlooked issue by using a large phantom ensemble and computing bootstrap confidence intervals on our AUC metrics, but we discovered that we may need even larger phantom ensembles to reduce the variance to acceptable levels. Fukunaga and Hayes56 showed that the number of data samples required for a reliable estimate of the covariance of a classifier grows quickly with the size of the data vector. For example, their criteria suggest that a 128-element data vector requires n = 9396 samples, or a factor of 73 times the vector size. In this work, we were limited to n = 500 scans for training the model observer. This corresponds to a factor of about 28 times the smallest vector size PC = 18 and a factor of only 3.5 times the largest channel vector size PC = 150. Therefore, an area of future work is to improve the reliability of our covariance estimates by increasing the size of our phantom sets or using more efficient channels.
Choosing appropriate channels to reduce images to their salient features is an important and active area of research.45, 57 Efficient channels reduce the data dimensions as much as possible while yielding approximately the same AUC as the original (non-reduced) data. In other words, AUCCHO/AUCHO ≈ 1 for an efficient CHO. We used 2D Laguerre-Gauss channels because LG channels seem to be robust for capturing statistical information and approximating the HO for circular and elliptical signals in non-Gaussian, randomly-varying backgrounds.45 Diagnostic findings correspond to three-dimensional lesions, however, so 2D LG channels may not be efficient for real clinical tasks. In addition, the effects of using rotationally-symmetric LG channels on asymmetric signals have not been thoroughly investigated, to our knowledge. New 3D observer model and channel designs, like those proposed by Platiša et al.,57 could improve our understanding of the theoretical limits of detectability.
The aim of this work was to provide a framework for determining the upper bounds of signal detectability in projection space for different DBT system configurations. Abbey and Boone have shown – using Markov-chain Monte Carlo (MCMC) – that the ideal observer outperforms the HO in a binary model of breast parenchymal tissue.58 However, their work required a parametric, correlated Gaussian phantom model and smaller data dimensions. For the large phantom and data dimensions in our framework, it is infeasible to estimate the true covariance required by the MCMC approach. Thus we were limited in using the channelized-HO as an approximation to the ideal observer.
In Sec. 3D, we introduced covariance decomposition in the context of DBT as a tool for isolating the effects of different noise sources and accelerating DBT evaluation over a range of system parameters. With assumptions about the form of the data covariance matrix as in Eq. 13, we can quickly evaluate systems at different dose levels as we did in Fig. 8, for example. We can characterize the impact of additional noise sources simply by adding terms to the decomposition in Eq. 11. We hope to extend the covariance decomposition approach to more realistic noise models in future work.
For the purposes of framework development, we neglected some additional detector characteristics such as spatial blur, excess noise in the gain mechanism, and the effect of reabsorbed Compton-scattered and characteristic x rays. In future work, we can improve the detector model by incorporating energy-, depth-, and angle-dependent information.59, 60, 61, 62 As the simulations grow faster and more efficient, it should also become practical to investigate polyenergetic source models and scatter models that incorporate the effects of nonuniform phantoms. More realistic physics models combined with computationally efficient model observers can lead to faster and more accurate assessment of image quality in DBT.
CONCLUSIONS
We developed a simulation framework for quantifying DBT signal detectability from projection images. The framework incorporates anthropomorphic voxelized phantoms, open-source tools for modeling the forward problem and estimating dose, and a channelized-Hotelling observer model with covariance decomposition for computing figures of merit. We studied detectability tradeoffs as a function of the DBT scan angle and number of projections, and compared our findings with relevant conclusions from other authors. We believe our framework is a viable tool for further investigation of image quality tradeoffs in DBT through task-based objective assessment.
ACKNOWLEDGMENTS
The author would like to acknowledge Dr. Matthew Kupinski for helpful discussions and reading early drafts, Drs. Jonathan Boswell and Andreu Badal for their computing expertise and help in the use of the FDA in-house compute cluster and Monte Carlo codes, Dr. Harrison Barrett for his thoughts on noise, and Mr. Kyle Anderson for his early work on PenVT. The authors would also like to acknowledge funding support from the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Oak Ridge Institute for Science Education (ORISE) Research Participation Program at the Center for Devices and Radiological Health (CDRH) of the FDA, and the FDA Office of Women's Health.
References
- J. T.DobbinsIII, “Tomosynthesis imaging: At a translational crossroads,” Med. Phys. 36, 1956–1967 (2009). 10.1118/1.3120285 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker J. A. and Lo J. Y., “Breast tomosynthesis: State-of-the-art and review of the literature,” Acad. Radiol. 18, 1298–1310 (2011). 10.1016/j.acra.2011.06.011 [DOI] [PubMed] [Google Scholar]
- Jennings R. J., Eastgate R. J., Siedband M. P., and Ergun D. L., “Optimal x-ray spectra for screen-film mammography,” Med. Phys. 8, 629–639 (1981). 10.1118/1.595021 [DOI] [PubMed] [Google Scholar]
- Fahrig R., Maidment A. D. A., and Yaffe M. J., “Optimization of peak kilovoltage and spectral shape for digital mammography,” Proc. SPIE 1651, 74–83 (1992). 10.1117/12.59405 [DOI] [Google Scholar]
- Klausz R. and Shramchenko N., “Dose to population as a metric in the design of optimised exposure control in digital mammography,” Radiat. Prot. Dosim. 114, 369–374 (2005). 10.1093/rpd/nch579 [DOI] [PubMed] [Google Scholar]
- Gong X., Glick S. J., Liu B., Vedula A. A., and Thacker S., “A computer simulation study comparing lesion detection accuracy with digital mammography, breast tomosynthesis, and cone-beam CT,” Med. Phys. 33(4), 1041–1052 (2006). 10.1118/1.2174127 [DOI] [PubMed] [Google Scholar]
- Chawla A. S., Samei E., Saunders R., Abbey C., and Delong D., “Effect of dose reduction on the detection of mammographic lesions: A mathematical observer model analysis,” Med. Phys. 34(8), 3385–3398 (2007). 10.1118/1.2756607 [DOI] [PubMed] [Google Scholar]
- Gifford H. C., Didier C. S., Das M., and Glick S. J., “Optimizing breast-tomosynthesis acquisition parameters with scanning model observers,” Proc. SPIE 6917, 69170S-1–69170S-9 (2008). 10.1117/12.771018 [DOI] [Google Scholar]
- Zhao B., Zhou J., Hu Y.-H., Mertelmeier T., Ludwig J., and Zhao W., “Experimental validation of a three-dimensional linear system model for breast tomosynthesis,” Med. Phys. 36, 240–251 (2009). 10.1118/1.3040178 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mertelmeier T., Ludwig J., Zhao B., and Zhao W., “Optimization of tomosynthesis acquisition parameters: Angular range and number of projections,” in Digital Mammography, Lecture Notes in Computer Science Vol. 5116, edited by Krupinski E. (Springer, Berlin, 2008), pp. 220–227. [Google Scholar]
- Sechopoulos I. and Ghetti C., “Optimization of the acquisition geometry in digital tomosynthesis of the breast,” Med. Phys. 36, 1199–1207 (2009). 10.1118/1.3090889 [DOI] [PubMed] [Google Scholar]
- Young S., Park S., Anderson S. K., Badano A., Myers K. J., and Bakic P., “Estimating breast tomosynthesis performance in detection tasks with variable-background phantoms,” Proc. SPIE 7258, 72580O-1–72580O-9 (2009). 10.1117/12.813900 [DOI] [Google Scholar]
- Chawla A. S., Lo J. Y., Baker J. A., and Samei E., “Optimized image acquisition for breast tomosynthesis in projection and reconstruction space,” Med. Phys. 36(11), 4859–4869 (2009). 10.1118/1.3231814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gang G. J., Tward D. J., Lee J., and Siewerdsen J. H., “Anatomical background and generalized detectability in tomosynthesis and cone-beam CT,” Med. Phys. 37(5), 1948–1965 (2010). 10.1118/1.3352586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiser I. S. and Nishikawa R. M., “Task-based assessment of breast tomosynthesis: Effect of acquisition parameters and quantum noise,” Med. Phys. 37(4), 1591–1600 (2010). 10.1118/1.3357288 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren B., Ruth C., Wu T., Zhang Y., Smith A., Niklason L., Williams C., Ingal E., Polischuk B., and Jing Z., “A new generation FFDM/tomosynthesis fusion system with selenium detector,” Proc. SPIE 76220, 76220B (2010). 10.1117/12.844555 [DOI] [Google Scholar]
- Young S., Bakic P., Myers K. J., and Park S., “Performance tradeoffs in a model breast tomosynthesis system,” in Digital Image Processing and Analysis (Optical Society of America, Washington, DC, 2010), p. DTuA3. [Google Scholar]
- Salvat F., Fernandez-Varea J. M., and Sempau J., “PENELOPE, A Code System for Monte Carlo Simulation of Electron and Photon Transport,” Workshop Proceedings Issy-les-Moulineaux, France 7–10 July 2003 (OECD Nuclear Energy Agency, Paris, France, 2003).
- Bakic P. R., Albert M., Brzakovic D., and Maidment A. D. A., “Mammogram synthesis using a 3D simulation. I. Breast tissue model and image acquisition simulation,” Med. Phys. 29(9), 2131–2139 (2002). 10.1118/1.1501143 [DOI] [PubMed] [Google Scholar]
- Bliznakova K., Bliznakov Z., Bravou V., Kolitsi Z., and Pallikarakis N., “A three-dimensional breast software phantom for mammography simulation,” Phys. Med. Biol. 48, 3699–3719 (2003). 10.1088/0031-9155/48/22/006 [DOI] [PubMed] [Google Scholar]
- Hoeschen C. et al. , “A high-resolution voxel phantom of the breast for dose calculations in mammography,” Radiat. Prot. Dosim. 114, 406–409 (2005). 10.1093/rpd/nch558 [DOI] [PubMed] [Google Scholar]
- Reiser I., Sidky E., Nishikawa R., and Pan X., “Development of an analytic breast phantom for quantitative comparison of reconstruction algorithms for digital breast tomosynthesis,” in Digital Mammography, Lecture Notes in Computer Science Vol. 4046, edited by Astley S., Brady M., Rose C., and Zwiggelaar R. (Springer, Berlin, 2006), pp. 190–196. [Google Scholar]
- Michael O'Connor J., Das M., Didier C., Mah'D M., and Glick S. J., “Using mastectomy specimens to develop breast models for breast tomosynthesis and CT breast imaging,” Proc. SPIE 6913, 691315 (2008). 10.1117/12.772666 [DOI] [Google Scholar]
- Hussein K., Vaughan C. L., and Douglas T. S., “Modeling, validation and application of a mathematical tissue-equivalent breast phantom for linear slot-scanning digital mammography,” Phys. Med. Biol. 54, 1533–1553 (2009). 10.1088/0031-9155/54/6/009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C. M., Segars W. P., Tourassi G. D., Boone J. M., and J. T.DobbinsIII, “Methodology for generating a 3D computerized breast phantom from empirical data,” Med. Phys. 36, 3122–3131 (2009). 10.1118/1.3140588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C., Bakic P. R., and Maidment A. D. A., “Development of an anthropomorphic breast software phantom based on region growing algorithm,” Proc. SPIE 6918, 69180V-1–69180V-10 (2008). 10.1117/12.773011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakic P. R., Zhang C., and Maidment A. D. A., “Development and characterization of an anthropomorphic breast software phantom based upon region-growing algorithm,” Med. Phys. 38, 3165–3176 (2011). 10.1118/1.3590357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakic P. R., Albert M., Brzakovic D., and Maidment A. D. A., “Mammogram synthesis using a 3D simulation. II. Evaluation of synthetic mammogram texture,” Med. Phys. 29(9), 2140–2151 (2002). 10.1118/1.1501144 [DOI] [PubMed] [Google Scholar]
- Tischenko O., Hoeschen C., Dance D. R., Hunt R. A., Maidment A. D. A., and Bakic P. R., “Evaluation of a novel method of noise reduction using computer-simulated mammograms,” Radiat. Prot. Dosim. 114, 81–84 (2005). 10.1093/rpd/nch517 [DOI] [PubMed] [Google Scholar]
- Kontos D., Zhang C., Ruiter N., Bakic P., and Maidment A., “Evaluating the effect of tomosynthesis acquisition parameters on image texture: A study based on an anthropomorphic breast tissue software model,” in Digital Mammography, Lecture Notes in Computer Science Vol. 5116, edited by Krupinski E. (Springer, Berlin, 2008), pp. 491–498. [Google Scholar]
- Yaffe M. J., Boone J. M., Packard N., Alonzo-Proulx O., Huang S.-Y., Peressotti C. L., Al-Mayah A., and Brock K., “The myth of the 50–50 breast,” Med. Phys. 36, 5437–5443 (2009). 10.1118/1.3250863 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruiter N. V., Stotzka R., Muller T.-O., Gemmeke H., Reichenbach J. R., and Kaiser W. A., “Model-based registration of x-ray mammograms and mr images of the female breast,” IEEE Trans. Nucl. Sci. 53, 204–211 (2006). 10.1109/TNS.2005.862983 [DOI] [Google Scholar]
- Ruiter N. V., Zhang C., Bakic P. R., Carton A.-K., Kuo J., and Maidment A. D. A., “Simulation of tomosynthesis images based on an anthropomorphic software breast tissue phantom,” Proc. SPIE 6918, 69182I (2008). 10.1117/12.770372 [DOI] [Google Scholar]
- Johns P. C. and Yaffe M. J., “X-ray characterisation of normal and neoplastic breast tissues,” Phys. Med. Biol. 32, 675–695 (1987). 10.1088/0031-9155/32/6/002 [DOI] [PubMed] [Google Scholar]
- Sempau J., Badal A., and Brualla L., “A PENELOPE-based system for the automated Monte Carlo simulation of clinacs and voxelized geometries–Application to far-from-axis fields,” Med. Phys. 38, 5887–5895 (2011). 10.1118/1.3643029 [DOI] [PubMed] [Google Scholar]
- Badal A., “Development of advanced geometric models and acceleration techniques for Monte Carlo simulation in medical physics,” Ph.D. dissertation, Univ. Politecnica de Catalunya, Catalunya, Spain (2008). [Google Scholar]
- Carter C. L., Allen C., and Henson D. E., “Relation of tumor size, lymph node status, and survival in 24740 breast cancer cases,” Cancer 63, 181–187 (1989). [DOI] [PubMed] [Google Scholar]
- Hammerstein G. R., Miller D. W., White D. R., Masterson M. E., Woodard H. Q., and Laughlin J. S., “Absorbed radiation dose in mammography,” Radiology 130, 485–491 (1979). [DOI] [PubMed] [Google Scholar]
- Badal A., Kyprianou I., Banh D. P., Badano A., and Sempau J., “penMesh-Monte Carlo radiation transport simulation in a triangle mesh geometry,” IEEE Trans. Med. Imaging 28, 1894–1901 (2009). 10.1109/TMI.2009.2021615 [DOI] [PubMed] [Google Scholar]
- Rowlands J. A. and Yorkston J., “Flat panel detectors for digital radiography,” Handbook of Medical Imaging: Volume 1. Physics and Psychophysics (Society of Photo-Optical Instrumentation Engineers, Bellingham, WA, 2000), Chap. 4, pp. 223–328. [Google Scholar]
- Burgess R. E., “Homophase and heterophase fluctuations in semiconducting crystals,” Discuss. Faraday Soc. 28, 151–158 (1959). 10.1039/df9592800151 [DOI] [Google Scholar]
- Wieczorek H., “Physical aspects of detector design,” Radiat. Meas. 33, 541–545 (2001). 10.1016/S1350-4487(01)00055-5 [DOI] [Google Scholar]
- Van de Sompel D., Brady Sir M., and Boone J., “Task-based performance analysis of FBP, SART, and ML for digital breast tomosynthesis using signal CNR and channelised Hotelling observers,” Med. Image Anal. 15, 53–70 (2011). 10.1016/j.media.2010.07.004 [DOI] [PubMed] [Google Scholar]
- Barrett H. H. and Myers K. J., Foundations of Image Science (Wiley, New York, 2004). [Google Scholar]
- Witten J. M., Park S., and Myers K. J., “Partial least squares: A method to estimate efficient channels for the ideal observers,” IEEE Trans. Med. Imaging 29, 1050–1058 (2010). 10.1109/TMI.2010.2041514 [DOI] [PubMed] [Google Scholar]
- Barrett H. H., Abbey C. K., Gallas B. D., and Eckstein M. P., “Stabilized estimates of Hotelling-observer detection performance in patient-structured noise,” Proc. SPIE 3340, 27–43 (1998). 10.1117/12.306181 [DOI] [Google Scholar]
- Gallas B. D. and Barrett H. H., “Validating the use of channels to estimate the ideal linear observer,” J. Opt. Soc. Am. A 20, 1725–1738 (2003). 10.1364/JOSAA.20.001725 [DOI] [PubMed] [Google Scholar]
- Das M., Gifford H. C., O'Connor J. M., and Glick S. J., “Evaluation of a variable dose acquisition technique for microcalcification and mass detection in digital breast tomosynthesis,” Med. Phys. 36, 1976–1984 (2009). 10.1118/1.3116902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vedula A. A., Glick S. J., and Gong X., “Computer simulation of CT mammography using a flat-panel imager,” Proc. SPIE 5030, 349–360 (2003). 10.1117/12.480015 [DOI] [Google Scholar]
- Gong X., Vedula A. A., and Glick S. J., “Microcalcification detection using cone-beam CT mammography with a flat-panel imager,” Phys. Med. Biol. 49, 2183–2195 (2004). 10.1088/0031-9155/49/11/005 [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H., Antonuk L. E., El-Mohri Y., Yorkston J., Huang W., Boudry J. M., and Cunningham I. A., “Empirical and theoretical investigation of the noise performance of indirect detection, active matrix flat-panel imagers (AMFPIs) for diagnostic radiology,” Med. Phys. 24, 71–89 (1997). 10.1118/1.597919 [DOI] [PubMed] [Google Scholar]
- Ghetti C., Borrini A., Ortenzia O., Rossi R., and Ordóñez P. L., “Physical characteristics of ge senographe essential and ds digital mammography detectors,” Med. Phys. 35, 456–463 (2008). 10.1118/1.2828185 [DOI] [PubMed] [Google Scholar]
- Saunders R. S. and Samei E., “A method for modifying the image quality parameters of digital radiographic images,” Med. Phys. 30, 3006–3017 (2003). 10.1118/1.1621870 [DOI] [PubMed] [Google Scholar]
- Mainprize J. G., Bloomquist A. K., Kempston M. P., and Yaffe M. J., “Resolution at oblique incidence angles of a flat panel imager for breast tomosynthesis,” Med. Phys. 33, 3159–3164 (2006). 10.1118/1.2241994 [DOI] [PubMed] [Google Scholar]
- Pokrajac D. D., Maidment A. D. A., and Bakic P. R., “Optimized generation of high resolution breast anthropomorphic software phantoms,” Med. Phys. 39, 2290–2302 (2012). 10.1118/1.3697523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukunaga K. and Hayes R. R., “Effects of sample size in classifier design,” IEEE Trans. Pattern Anal. Mach. Intell. 11, 873–885 (1989). 10.1109/34.31448 [DOI] [Google Scholar]
- Platiša L., Goossens B., Vansteenkiste E., Park S., Gallas B. D., Badano A., and Philips W., “Channelized Hotelling observers for the assessment of volumetric imaging data sets,” J. Opt. Soc. Am. A 28, 1145–1163 (2011). 10.1364/JOSAA.28.001145 [DOI] [PubMed] [Google Scholar]
- Abbey C. K. and Boone J. M., “An ideal observer for a model of x-ray imaging in breast parenchymal tissue,” in Proceedings of the 9th international workshop on Digital Mammography, IWDM'08 (Springer-Verlag Berlin, Heidelberg Germany, 2008), pp. 393–400.
- Gallas B., Boswell J. S., Badano A., Gagne R. M., and Myers K. J., “An energy- and depth-dependent model for x-ray imaging,” Med. Phys. 31(11), 3132–3149 (2004). 10.1118/1.1806293 [DOI] [PubMed] [Google Scholar]
- Badano A., Kyprianou I. S., Jennings R. J., and Sempau J., “Anisotropic imaging performance in breast tomosynthesis,” Med. Phys. 34(11), 4076–4091 (2007). 10.1118/1.2779943 [DOI] [PubMed] [Google Scholar]
- Reiser I. S., Nishikawa R. M., and Lau B. A., “Effect of non-isotropic detector blur on microcalcification detectability in tomosynthesis,” Proc. SPIE 7258, 72585Z (2009). 10.1117/12.813808 [DOI] [Google Scholar]
- Freed M., Park S., and Badano A., “A fast, angle-dependent, analytical model of CsI detector response for optimization of 3D x-ray breast imaging systems,” Med. Phys. 37, 2593–2605 (2010). 10.1118/1.3397462 [DOI] [PMC free article] [PubMed] [Google Scholar]