A new segmentation framework based on sparse shape composition in liver surgery planning system

Abstract

Purpose: To improve the accuracy and the robustness of the segmentation in living donor liver transplantation (LDLT) surgery planning system, the authors present a new segmentation framework that addresses challenges induced by the complex shape variations of patients’ livers with cancer. It is designed to achieve the accurate and robust segmentation of hepatic parenchyma, portal veins, hepatic veins, and tumors in the LDLT surgery planning system.

Methods: The segmentation framework proposed in this paper includes two important modules: (1) The robust shape prior modeling for liver, in which the sparse shape composition (SSC) model is employed to deal with the complex variations of liver shapes and obtain patient-specific liver shape priors. (2) The integration of the liver shape prior with a minimally supervised segmentation algorithm to achieve the accurate segmentation of hepatic parenchyma, portal veins, hepatic veins, and tumors simultaneously. The authors apply this segmentation framework to our previously developed LDLT surgery planning system to enhance its accuracy and robustness when dealing with complex cases of patients with liver cancer.

Results: Compared with the principal component analysis, the SSC model shows a great advantage in handling the complex variations of liver shapes. It also effectively excludes gross errors and outliers that appear in the input shape and preserves local details for specific patients. The proposed segmentation framework was evaluated on the clinical image data of liver cancer patients, and the average symmetric surface distance for hepatic parenchyma, portal veins, hepatic veins, and tumors was 1.07 ± 0.76, 1.09 ± 0.28, 0.92 ± 0.35 and 1.13 ± 0.37 mm, respectively. The Hausdorff distance for these four tissues was 7.68, 4.67, 4.09, and 5.36 mm, respectively.

Conclusions: The proposed segmentation framework improves the robustness of the LDLT surgery planning system remarkably when dealing with complex clinical liver shapes. The SSC model is able to handle non-Gaussian errors and preserve local detail information of the input liver shape. As a result, the proposed framework effectively addresses the problems caused by the complex shape variations of livers with cancer. Our framework not only obtains accurate segmentation results for healthy persons and common patients, but also shows high robustness when dealing with specific patients with large variations of liver shapes in complex clinical environments.

INTRODUCTION

Liver cancer has been one of the most life-threatening diseases with high mortality and poor prognosis all over the world. In 2008, it was estimated that about 750 000 people were diagnosed with liver cancer and nearly 696 000 people died from this disease worldwide.¹ Since it is hard to detect the early signs, most liver cancers are in end-stage when they are diagnosed. The best treatment method is liver transplantation, and an important alternative is liver resection, under the consideration of the scarcity of donor.² Living donor liver transplantation (LDLT) plays a crucial role to extend the scarce donor pool, which prevents waiting list mortality.³ A detailed knowledge of patient-specific liver anatomy is of great significance in the surgery strategy planning for LDLT. To achieve the best resection plan, surgeons need to identify the location of the liver portion that would be cut off, together with the distribution of intrahepatic vessels and tumors. As a result, the preoperative planning based on medical image is highly important.

The most essential module in the LDLT surgery planning system is the segmentation of liver, intrahepatic vessels, and tumors. However, there are several challenges in the liver segmentation. First, the gray levels of liver and its adjacent organs are very similar. Therefore, there may not be obvious boundaries between these organs and thus traditional methods, such as edge detection and region growing, may include adjacent organs easily. Second, in clinical environments, some special pathologies such as tumor and metastasis usually lead to inhomogeneous gray level appearance. In these cases, tumor and metastasis are quite different from healthy liver regions in terms of gray levels, which may result in under-segmentation of these tissues by traditional methods relying on gray level information. To address these two challenges, shape priors are greatly helpful, since they can assist to separate adjacent organs and preserve intrahepatic tissues despite of the inhomogeneous gray level caused by tumor and metastasis.

Though shape prior-based segmentation seems promising, the effectively modeling liver shape prior is extremely challenging. The reason is that liver shapes and anatomies from different individuals vary considerably, and tumor and metastasis usually make liver shapes even more complex and harder to model. The liver shape variations induced by liver cancer and other pathologies mainly include four types: (1) the expansion of hepatic lobes, (2) the shrinkage of hepatic lobes, (3) the bending of liver shapes, and (4) local gross shape changes due to tumors. In addition, combinations of these basic types result in more complex liver shape variations. Figure 1 shows some liver images from a healthy person and three patients with liver cancer. These images are from computed tomography (CT) scans and include the porta hepatis, a special anatomic structure of the liver. In Fig. 1b, the right liver lobe is much narrower than the normal one in Fig. 1a, while the left liver lobe extends to the left of the body in a larger degree than the normal one. In Fig. 1c, the left liver lobe shrinks greatly and the right lobe is also much smaller than the normal one. In Fig. 1d, the tumor in the left lobe expands the liver dramatically. It can be noticed that both the shape of the whole liver and the local details change in a very large scale among different persons. The variations of liver shapes are so complex that it is very challenging to model them effectively. In clinical environments, it is also very common that tumor and metastasis largely deform the liver, and the resulting high variations of liver shapes among different patients make the accurate modeling and segmentation extremely difficult.

Figure 1.

Examples of the complex variations of liver shapes. (a) shows a transverse slice through the porta hepatis of a healthy person. (b)–(d) show the counterparts of (a) from three patients with liver cancer. The right and left circles show the left and right lobe of the liver, respectively. Notice the large variations of liver shapes.

In this paper, we propose a novel shape prior based segmentation framework to address the aforementioned challenges in the segmentation module of the LDLT surgery planning system. The main contribution of this work is threefold: (1) To address the challenges caused by the complex variations of liver shapes, we employ the sparse shape composition (SSC) to model the shape prior of liver. The SSC model does not have any assumption of the parametric distributions of liver shapes, and it preserves local details of liver shapes well. As a result, the shape prior is patient-specific and accurate enough to model the complex variations of liver shapes. (2) The shape prior method is combined with a minimally supervised segmentation algorithm to segment hepatic parenchyma, intrahepatic vessels and tumors simultaneously. (3) The novel segmentation framework is successfully applied to the clinical application of the LDLT surgery planning system. It achieves robust segmentation when dealing with complex cases of liver cancer patients in clinical environments.

RELATED WORK

Many approaches have been proposed for the segmentation in liver surgery planning systems. In some early researches, the segmentation framework in such systems relied greatly on user interactions, and the liver was segmented slice by slice. For example, the German Cancer Research Center in Heidelberg proposed a framework for liver surgery operation planning system.⁴ The segmentation framework in this system is based on anatomical landmarks identified by user interactions in each slice. Though the user interaction helps achieving accurate segmentation results, it is time consuming. The Center for Medical Diagnostic Systems and Visualization in Germany also developed a software application for the preoperative planning of liver surgery.⁵ The liver segmentation in that system is performed with a semiautomatic edge-oriented algorithm. It requires users to specify a few seed points per slice to identify the liver contour. In the following years, 3D image segmentation approaches were employed and some efforts were made to reduce user interactions. Researchers in Graz University of Technology proposed a liver surgery planning system using virtual reality.⁶ The segmentation module in this system employs the active appearance model (AAM) (Ref. ⁷) to separate the heart and the liver in CT data, with an extended 3D multiobject fuzzy connectedness approach that lets users contribute their knowledge to improve the final segmentation.

Besides, the aforementioned segmentation methods that have been incorporated into liver surgery planning systems, a variety of other effective approaches have also been proposed in recent years. To achieve the automatic segmentation, Ruskó et al.⁸ developed a region growing method that involves several pre- and postprocessing steps to eliminate oversegmentation. Rikxoort et al.⁹ and Klein et al.¹⁰ employed methods based on atlas matching. Kainmüller et al.,¹¹ and Zhang et al.¹² incorporated statistical shape models into their liver segmentation methods. In addition, learning-based liver segmentation methods were also proposed. The algorithm proposed by Ling et al.¹³ employs a hierarchical shape representation and a learning-based boundary localization technique. Zhan et al.¹⁴ also proposed a learning-based hierarchical deformable model that can be used across different imaging modalities. However, automatic methods are not always robust in clinical environments. Thus, a lot of semiautomatic approaches were proposed to improve the robustness of the segmentation. Liu et al.¹⁵ used a gradient vector flow (GVF) snake for the delineation of liver contours slice by slice. Beichel et al.¹⁶ combined a graph cut method with a 3D virtual reality based refinement approach for liver segmentation. Zheng et al.¹⁷ also developed a graph cut-based segmentation algorithm to refine coarse manual segmentation results of liver tumors. Oliveira et al.¹⁸ proposed an effective deformable segmentation model based on level set for surgical planning. However, it is implemented at each slice sequentially. Fernandez-de-Manuel et al.¹⁹ employed 3D level set in a semiautomatic liver segmentation method based on active surface, but it is designed for the segmentation of healthy cases of the liver. The newest proposed methods can usually obtain satisfactory performance when dealing with healthy persons and common patients. However, most of them have the same problem: the robustness cannot be ensured in many special cases where the tumor and metastasis deform the liver regions to unusual and complex shapes. Therefore, a lot of user interactions are frequently needed to refine the segmentation results. In order to make these systems applicable in complex clinical environments, improving the robustness of the segmentation is still under research.

In recent years, the shape priors have shown great importance for liver image segmentation. Shape prior-based methods usually achieve better performance than methods solely relying on the appearance cues.²⁰ However, to our knowledge, there is a lack of LDLT surgery planning systems employing the shape prior-based segmentation method to robustly handle complex cases of patients with liver cancer.

A key problem of shape prior-based segmentation is how to model the complex shape variations appropriately. Many statistic shape modeling methods have been used in medical image segmentation, among which the active shape model (ASM) (Ref. ²¹) and its variations²² are the most prevalent. However, the modeling of liver shapes of patients with liver cancer is much more challenging than that of many other organs. The variations of liver shapes from different patients are too complex to accurately model with parametric probability distributions. Besides, since the shape prior should be patient-specific and adaptive in LDLT surgery planning systems, it is critical to handle gross errors and outliers and preserve local details for different patients. The sparse shape composition^{23, 24} proposes a new way to implicitly model the shape prior and it is effective in modeling complex shape variations.

A variety of methods have also been proposed to extract vessels form medical images.^{25, 26} Zheng et al.²⁷ proposed a learning-based scheme using a set of features for the detection of vessels from retinal fundus images. These features are used to describe the variation patterns of the image's local geometric structures across various scales. Goch et al.²⁸ proposed an approach based on the GVF for the segmentation of hepatic vascular system. This approach avoids multiscale analysis and related scale space problems. Bauer et al.²⁹ presented a method based on shape priors and graph cuts for the segmentation of tubular tree structures and applied it to the segmentation of portal and hepatic veins in liver surgery planning. However, despite the large amount of previous methods, the segmentation of 3D liver vessels is still a challenging task, due to the complex vascular anatomy and the high variability of size and curvature of vessels.^{25, 30}

METHODS

The novel shape prior-based segmentation framework in the LDLT surgery planning system proposed in this paper focuses on addressing the challenges in the modeling of liver shape priors for patients with liver cancer, as well as the challenges in the accurate segmentation of liver, intrahepatic vessels and tumors. The segmentation framework includes two important modules: (1) Shape prior modeling for liver. The SSC model is employed to deal with the complex variations of liver shapes with its ability to handle non-Gaussian errors and preserve local detail information. (2) Accurate segmentation of hepatic parenchyma, portal veins, hepatic veins, and tumors using clinical enhanced CT scans. It is based on a combination of the patient-specific shape prior and a minimally supervised segmentation algorithm. This algorithm can segment multiobjects simultaneously. We apply this segmentation framework to our previously developed LDLT surgery planning system to enhance its accuracy and robustness when dealing with complex cases of patients with liver cancer. Besides the proposed segmentation framework, our system also consists of another two basic components in a typical liver surgery planning system: one is the liver segment approximation that partitions the liver into several functionally independent segments based on intrahepatic vessels, and the other is the visualization of the segmentation results and different liver segments.

Sparse shape representation for liver

The SSC model represents the shape prior by a sparse linear combination of shapes in the shape repository. It does not rely on any assumption of parametric distribution models. It can also preserve the local detail information that presents in the training set. Therefore, it addresses the main challenges in the modeling of the complex shape variations and patient-specific shape priors.

In the segmentation framework proposed in this paper, a repository consisting of training shapes from a large range of healthy persons is constructed. Each training shape is obtained from the manually segmented result by experienced experts, and it can be regarded as the gold standard of the corresponding liver. All the manual segmentation results are converted to surface meshes. The number of vertices on the mesh is chosen as a tradeoff between the shape prior variability and the computation time: a small number of vertices might not be enough to model the complex shape variations, while a large number increases the computation time. As a compromise, we set the number of vertices to near 1000 according to our empirical experience. Since the spatial position and orientation of different meshes in the repository vary a lot, prealignment of the training shapes is performed based on the generalized Procrustes analysis,³¹ so that they are in a common coordinate system. The one-to-one correspondence of vertices on different meshes is obtained by taking an arbitrary shape in the repository as the reference and registering it to the others using adaptive focus deformable model (AFDM).^{32, 33} To remove the bias caused by the selection of the reference, the mean shape is computed and then is registered to all the shapes again. For a patient who needs a surgery plan, a rough initial liver segmentation based on simple region growing method is rapidly performed. The initial segmentation result is converted to a surface mesh. The point correspondence between the new mesh and the mean shape of the repository is also computed using AFDM. In our application, the appearance cues of some CT images, such as scans from patients with liver cancer, may be weak or misleading and can easily result in the oversegmentation or the under-segmentation in the segmented shapes, i.e., gross errors. These gross errors can be very large but these regions are relatively sparse compared with the whole shape. Traditional shape models such as ASM usually represent shape distributions by the mean shape and the major variations, based on the assumption that the errors follow some Gaussian distributions. However, this assumption does not hold for gross and sparse errors. As a result, we explicitly model the errors as a sparse vector e. The liver shape of the patient is approximated by an optimized sparse linear combination of a subset of the repository. The optimization problem is formulated as²⁴

$$\underset{x,e,\beta }{\arg \min }{‖T(y,\beta )-Dx-e‖}_2^2+{\lambda }_1{‖x‖}_1+{\lambda }_2{‖e‖}_1,$$ (1)

where D is a matrix that describes the training set. Each column of D is a vector representing the vertices’ coordinates of one mesh in the shape repository. x represents the coefficients for the training samples. y is a column vector representing the input shape which needs to be refined. T(y, β) is a global transformation operator with parameter β, which is estimated using the generalized Procrustes analysis.³¹ It aligns the input shape y to the mean shape of the repository. e denotes the gross errors or outliers in the input shape. In our application, it means the oversegmentation or the under-segmentation that appears in the initial segmentation result of liver. λ₁ and λ₂ control the sparseness of x and e, respectively. The optimized sparse shape representation Dx − e is transformed to the original coordinate system of y by the inverse transformation of T(y, β). The result of the transformation is treated as the shape prior for y.

Accurate segmentation based on SSC shape prior

After the patient-specific shape prior is achieved by the SSC model, it can be employed to guide the accurate segmentation of hepatic parenchyma, portal veins, hepatic veins, and tumors. A minimally supervised classification method that considers both statistical and spatial information is employed to segment these tissues in the liver region. This method was originally designed for 2D image segmentation,³⁴ and we extended it to 3D image segmentation and incorporated it with the SSC shape prior.

The segmentation method is an iterative classification approach using Bayesian level set method.³⁵ It can be described as a growing of high-confidence (HC) points of each tissue. HC points are points with the least chance to be misclassified. In the first iteration, HC points of each tissue are selected based on the statistical threshold of intensity and size threshold of the connected blobs of HC points. We consider the image histogram as a Gaussian mixture model (GMM) and use the expectation maximization (EM) (Ref. ³⁶) algorithm to estimate the mean value and the standard deviation of each tissue from seed points. Then a narrow intensity range is obtained to select HC points with the least chance of misclassification. In addition, when the image's signal-to-noise ratio (SNR) is low or intensity ranges of different tissues (such as portal veins and hepatic veins) have large overlap, a size threshold of HC points blobs is used to get rid of misclassified points. This is because the HC points blob in very small size is more likely to be noise due to the spatial continuity of tissues. Based on the statistical threshold and size threshold, the HC points of one given tissue are approximately evenly distributed throughout the region of that tissue. Examples of HC points are shown in Fig. 4.

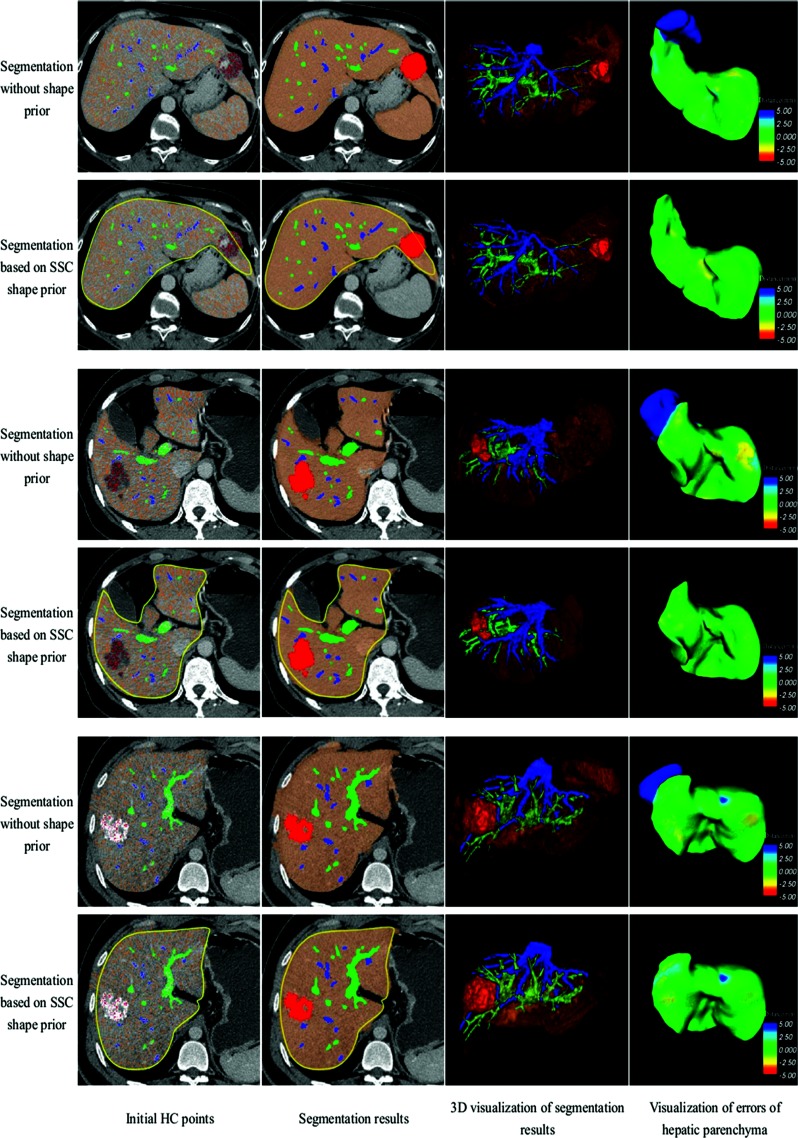
Figure 4.

Segmentation results of hepatic parenchyma, portal veins, hepatic veins, and tumors for three patients with liver cancer. Every two rows show one case. The first, third, and fifth rows are results of segmentation without shape prior, while the second, fourth, and sixth rows employ SSC shape prior.

After the selection of HC points in the first iteration, a fast marching level set method³⁷ is used to compute the marching process of the surface of HC points blobs, thus the arrival time at each unclassified point can be obtained. The marching speed at each unclassified point is based on its intensity and the spatial relationship between that point and the liver shape prior

$$V(x,c)=\omega V_{\mathrm{intensity}}(x,c)+(1-\omega )V_{\mathrm{shape}}\left(x\right),$$ (2)

where x denotes the unclassified point. c indicates one certain tissue. ω and 1 − ω are coefficients controlling the weights of the intensity term V_intensity and the shape term V_shape. ω is in a range of 0.0–1.0,

$$V_{\mathrm{intensity}}(x,c)=\frac{1+\underset{m}{min}\left(\right|I\left(x\right)-\overline{I\left(m\right)}\left|\right)}{1+|I\left(x\right)-\overline{I\left(c\right)}|},$$ (3)

where I(x) is the intensity of voxel point x. $\overline{I\left(c\right)}$ is the average intensity of HC points of tissue c. The maximum of V_intensity(x, c) is obtained when I(x) is the closest to $\overline{I\left(c\right)}$,

$$V_{\mathrm{shape}}\left(x\right)=\frac{\Phi \left(x\right)}{\max \left(\Phi \right(x\left)\right)},$$ (4)

where Φ(x) is a signed distance function based on the liver shape prior. The sign of Φ(x) is positive if x is inside the shape prior, while negative if x is outside the shape prior. For one certain tissue c and an unclassified point x, the larger the difference between $\overline{I\left(c\right)}$ and I(x), or the lower value of Φ(x), the slower the marching speed V(x, c).

After the marching process, the arrival time of HC points marching to each unclassified point is obtained. We classify each point into the tissue with the least arrival time at that point, based on which new HC points are selected for each tissue again, and then a new iteration step begins. The iteration will terminate when the percentage of increase in the volume of hepatic parenchyma is below a given threshold. Thus, the simultaneous segmentation of hepatic parenchyma, portal veins, hepatic veins, and tumors is achieved.

Liver segment approximation and visualization

The proposed segmentation framework is incorporated into our previously developed LDLT surgery planning system, which also includes the liver segment approximation and visualization modules. The liver segment approximation module partitions the liver into several functionally independent segments that can be used as ablation units according to the branching structure of portal veins. In our system, the nearest neighbor segment approximation (NNSA) (Ref. ³⁸) approach and the visualization toolkit (VTK) (Ref. ³⁹) are employed for liver segment approximation and 3D data visualization, respectively.

RESULTS

Clinical abdominal image data of enhanced CT from Shanghai Renji Hospital was used in the experiments. The data were acquired using a GE Discovery CT750 HD system with the following scanning protocol: slice thickness = 1.25 mm, image resolution = 512 × 512, pixel spacing = 0.683594 × 0.683594 mm. The scanning was automatically triggered when the system detects the contrast agent flowing into the hepatic artery, portal veins, and hepatic veins, respectively. The average time delay for the three scans was about 25, 40, and 70 s, respectively after the injection of the contrast agent. We collected the manual segmentation results of livers from 50 healthy persons, aged from 18 to 75, to construct the training data. The image datasets from 18 patients were analyzed by the liver surgery planning system. Most of the patients had tumors or metastasis close to major vessels, and some patients had one part of the liver resected previously. The gray levels of tumor and metastasis are significantly different from those of healthy liver regions. The liver shapes of these patients also vary in a large range.

In our previous study, we found that the performance of SSC is not sensitive to λ₁ and λ₂, and a fixed set of ω also gives stable results for different patients. Therefore, we fixed these parameters when dealing with different patients. The best parameter set was found offline using the training dataset. It was achieved by traversing each parameter within a large range to find its optimum. During each iteration step, one parameter was tuned, while other two parameters were fixed. Finally, we obtained the best parameter set and fixed it during the experiments. The parameter set for SSC was λ₁ = 50, λ₂ = 0.3. ω in Eq. 2 was set differently for four tissues. For hepatic parenchyma, we enhanced the weight of the shape term in the speed function, and we set ω to 0.6. For portal veins, hepatic veins and tumors, ω was set to 0.2, 0.2, and 0.8, respectively.

Sparse shape composition

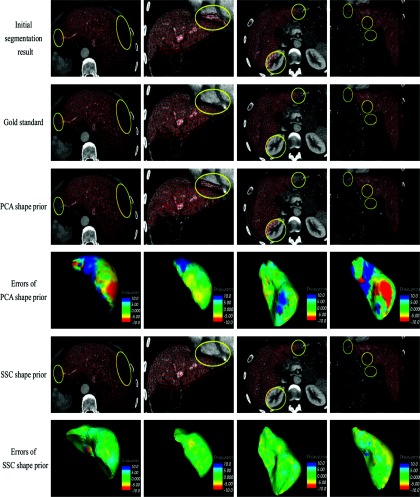
For each patient, the SSC shape prior of liver region was compared with the corresponding gold standard and the PCA shape prior. The same training set was used by PCA and SSC for fair comparisons. All the experiments were performed on a 2.4 GHz PC with 2G RAM, with PYTHON 2.5 and C++ implementations. The average running time of using PCA and SSC was 3.44 and 6.52 s, respectively. Figure 2 shows some visual comparisons between the shape priors based on PCA and SSC. Each column shows one case. The initial segmentation result, the manual segmentation result, the PCA shape prior and its visualized errors, the SSC shape prior and its visualized errors are shown from the top row to the bottom row, respectively. The shortest Euclidean surface distance is measured in millimeters (mm) in the visualization of errors.

Figure 2.

Visual comparisons between shape prior based on PCA and SSC in four cases. (First column) a liver with a large region of tumor in the posterior portion of the right lobe. (Second column) a liver that is adjacent to the heart. (Third column) a liver that is adjacent to the kidney. (Forth column) a liver with a tumor in the interior portion of the left lobe. Notice the SSC shape prior has much less errors compared with PCA shape prior.

In the first column of Fig. 2, a large region of tumor appears in the posterior portion of the right liver lobe. Since the gray level of the tumor region is much lower than that of the healthy liver region, the region growing method fails to extract the tumor region in the initial segmentation result. Both PCA and SSC models restore the posterior portion of the right liver lobe, since a liver lacking that portion does not appear in healthy liver shapes and it will not present in the shape repository. However, the PCA model only restores and preserves the principal components of the input liver shape, which leads to some local details, such as the corner of the left liver lobe, being discarded in the outputted shape prior. However, the SSC model effectively preserves the local details in the corner of the left lobe when it restores the posterior portion of the right liver lobe.

In the application of LDLT surgery planning system, the undersegmentation is mainly caused by tumor and metastasis due to the difference in the intensity between these regions and healthy liver regions. The oversegmentation also occurs frequently, since the heart and abdominal organs, such as the kidney and the spleen, are very close to the liver and they have similar gray levels. In the second column of Fig. 2, the oversegmented region in the heart leads to gross errors in the initial segmentation result. The oversegmented region does not appear in the training set, but it is still well reconstructed by the PCA model. Statistically, the oversegmented region in the heart is approximately in the first mode of liver shapes (i.e., along the direction of the PCA's first principal component). The eigenvalue of the first principal component is large so that the first mode of liver shapes has a large variance, which can easily cover the oversegmented region in the heart. As a result, this region is usually well reconstructed and preserved by PCA during the shape refinement procedure (even including the gross errors). In contrast, such gross errors near by the heart region can be captured by the SSC model successfully. This is benefited from the explicitly modeling the gross and sparse errors. Thus, the SSC model excludes the oversegmented region in the heart effectively. PCA and SSC representations of the oversegmentation occurring in the kidney region are similar to the situation in the heart region, as shown in the third column of Fig. 2. Another case is shown in the fourth column of Fig. 2, where both the undersegmentation and the oversegmentation appear in the initial segmentation result of a liver with cancer. All these results illustrate that the SSC model handles gross errors in the initial segmentation results robustly, but almost does not affect correctly segmented regions that are consistent with training samples in the shape repository.

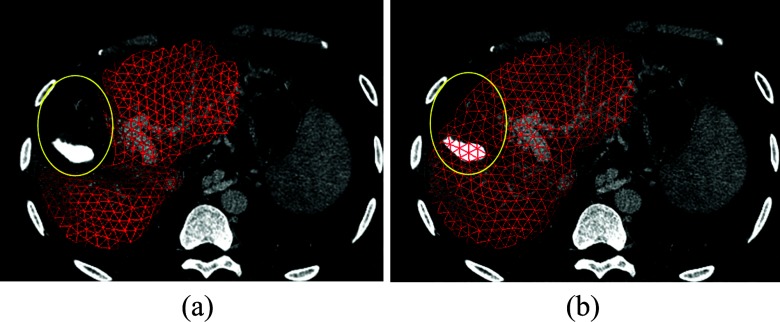
For the patient a part of whose liver has been resected previously, the integrated liver could not be found in the CT scans so that a common liver surgery planning system could just segment and visualize the remaining part of that liver. However, it is still necessary for surgeons to estimate the whole volume of such liver in order to analyze the liver function change. Figure 3 shows an example of a patient who accepted a resection treatment followed by a radiofrequency ablation in the past. The SSC representation of the liver segmentation result restores the resected portion, which helps surgeons analyze the function of the remaining liver for a comparison with the whole one. Benefited from its robustness against outliers, the SSC model has the capability to reconstruct the integrated liver region, which assists surgeons in achieving a better understanding of the whole liver when making surgery strategy as well as evaluating the surgery result.

Figure 3.

The segmentation result of a liver with one portion resected and its SSC representation. (a) Segmentation result of a liver with one portion resected; (b) The SSC representation of the segmentation result.

Accurate segmentation

The hepatic parenchyma, portal veins, hepatic veins, and tumors are accurately segmented with the liver shape prior. For each patient with liver cancer, the final segmentation results of two methods are compared: Method I is the original minimally supervised classification method without shape prior.³⁴ Method II is our method that employs SSC shape prior.

Figure 4 shows the segmentation results of three typical patients with liver cancer. The first, third, and fifth rows illustrate the segmentation results of Method I, while the second, fourth, and sixth rows show the segmentation results of Method II. The first column shows the initial HC points of hepatic parenchyma, portal veins, hepatic veins, and tumors in the first iteration. The four types of HC points are labeled in four different colors respectively. The second column shows the segmentation results of these tissues, and the third column shows the 3D visualization of them. The segmentation errors of hepatic parenchyma are visualized in the fourth column. We also use the shortest Euclidean surface distance measured in millimeters in the visualization of errors. Yellow curves are the corresponding liver shape priors based on SSC.

The minimally supervised classification method works well on 2D CT data,³⁴ but 3D abdominal images are more challenging due to the similar gray levels of adjoining organs. The first row of Fig. 4 shows that the initial HC points of hepatic parenchyma cover not only the region of liver but also the region of spleen. The reason is that the two tissues adjoin in 3D space and the gray levels of them are almost in the same range. The second row shows the corresponding result of segmentation based on our proposed method using SSC shape prior. The HC points outside the shape prior are excluded in the first iteration and the spleen does not appear in the final segmentation result. Since the SSC shape prior describes the liver shape adaptively, the segmentation results based on the shape prior are quite accurate, with overcoming undersegmentation and oversegmentation effectively.

Experiments on other two patients in Fig. 4 also show that the SSC shape prior plays a great role in improving the accuracy and robustness of the segmentation. In addition, high order branches of intrahepatic vessels are extracted successfully by our proposed method: for hepatic veins, the fourth order branches are captured; and for portal veins, the fifth and higher order branches are segmented, as shown in Figs. 46. Compared with previous methods^{30, 40} capturing the third and fourth order branches, our algorithm has a better performance in extracting high order vessel branches. This is useful for surgeons to analyze the location relationship between portals veins, hepatic veins, and tumors, based on which an accurate and optimal surgery plan can be achieved.

Figure 6.

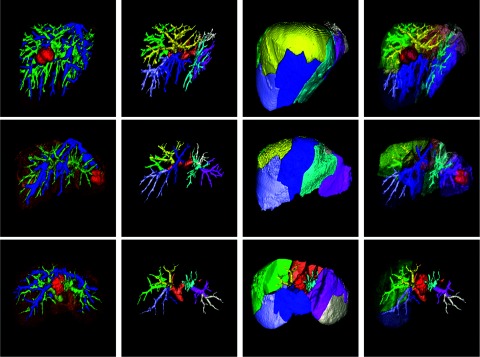
Liver segment approximation and visualization. (First column) accurate segmentation result. (Second column) different portions of the portal veins. (Third column) different liver segments. (Fourth column) a semitransparent visualization of the liver segments, portal veins, and tumors. Some liver segments are hided in the third row for a better visualization of the intrahepatic tumor.

The performance of the SSC shape prior modeling and the accurate segmentation was measured using radius of curvature (ROC) curves with respect to each parameter, as shown in Fig. 5. We plotted the fraction of true positive rate versus false positive rate for a wide range of each parameter. The true positive rate is the sensitivity and the false positive rate is defined as one-specificity. Since the modeling of the shape prior and the segmentation are two independent modules in the framework, we analyzed the ROC curves of the two modules, respectively. Figure 5a shows the ROC curve of the SSC shape prior for a wide range of λ₁, with λ₂ fixed to 0.25. Figure 5b shows the ROC curve of the SSC shape prior for a wide range of λ₂, with λ₁ fixed to 50. Figure 5c shows the ROC curves of the segmentation of hepatic parenchyma, hepatic veins, portal veins, and tumors. These four curves are produced by varying the set of ω, with λ₁ and λ₂ fixed to 50 and 0.25, respectively.

Figure 5.

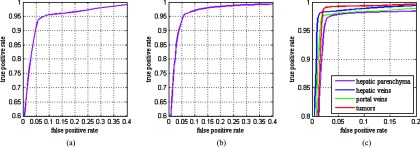
ROC curves of the SSC shape prior and the segmentation. (a) ROC curve of the SSC shape prior with respect to λ₁; (b) ROC curve of the SSC shape prior with respect to λ₂; (c) ROC curve of the segmentation with respect to ω.

We employ the average symmetric surface distance (ASD) (Ref. ²⁰) and Hausdorff distance⁴¹ to evaluate the accuracy of the segmentation method quantitatively. Both the segmentation results of Methods I and II are compared with the gold standard manually segmented by experienced experts

$$\begin{array}{ccc}\hfill \mathrm{ASD}(A,B)& =& \frac{1}{\left|S\left(A\right)\right|+\left|S\left(B\right)\right|}\left(\sum _{S_A\in S\left(A\right)}d(S_A,S\left(B\right))\right.\hfill \\ & & \left.+\sum _{S_B\in S\left(B\right)}d(S_B,S\left(A\right))\right),\hfill \end{array}$$ (5)

where S(A) and S(B) denote the set of surface voxels of two segmentation results A and B, respectively. S_A is an arbitrary point on surface S(A), and d(S_A, S(B)) is the shortest Euclidean distance of S_A to the surface S(B).

The Hausdorff distance is defined as the maximum of all the Euclidean distances from a point on the surface of the segmentation result to the closest point on the surface of the gold standard. The average ASD mean value and standard deviation from the 18 patients are shown in Table 1. The average Hausdorff distances from these patients are shown in Table 2. Method II, the SSC shape prior-based method, achieves better performance than Method I, the original minimally supervised classification method without shape prior. The SSC shape prior not only significantly improves the accuracy and robustness of the segmentation of hepatic parenchyma but also contributes to the accurate segmentation of intrahepatic vessels and tumors. In addition, we measured the runtime of the whole segmentation process. The initial segmentation of the liver and the modeling of the shape prior, which were required for Method II but not for Method I, consumed an average time of 4.25 min. The runtime of the classification algorithm in the segmentation stage was 18.22 min with eight iterations in average for Method I, while 10.53 min with four iterations in average for Method II, as shown in Table 2. The result shows that less iteration is required for Method II, which reduces the runtime remarkably. In each iteration, the most time consuming portion is the computation of the arrival time of HC points marching to each unclassified point. It is achieved by sequential computation for hepatic parenchyma, portal veins, hepatic veins, and tumors. However, it is possible to significantly accelerate this process by using parallel computation based on GPUs implementation of the algorithm.

Table 1.

Comparison of ASD between Methods I and II. Method I: the original minimally supervised classification method without shape prior. Method II: our method that employs the SSC shape prior.

Method	Hepatic parenchyma (mm)	Portal veins (mm)	Hepatic veins (mm)	Tumors (mm)
Method I	4.69 ± 2.84	1.42 ± 0.35	1.30 ± 0.41	1.58 ± 0.45
Method II	1.07 ± 0.76	1.09 ± 0.28	0.92 ± 0.35	1.13 ± 0.37

Table 2.

Comparison of Hausdorff distance and runtime between Methods I and II.

Method	Hepatic parenchyma (mm)	Portal veins (mm)	Hepatic veins (mm)	Tumors (mm)	Runtime (min)
Method I	21.49	7.06	6.84	8.45	18.22
Method II	7.68	4.67	4.09	5.36	10.53

Figure 6 shows some results of liver segment approximation and visualization. The first column shows the accurate segmentation results and the second column illustrates the portal veins in each liver segment labeled in different colors. Different liver segments are shown in the third column. The last column shows a semitransparent visualization of these liver segments, portal veins, and tumors.

CONCLUSIONS

In this paper, we proposed a new shape prior-based segmentation framework for the LDLT surgery planning system. The strengths of this proposed method include: (1) modeling complex liver shape variations effectively, (2) achieving patient-specific liver shape prior, and (3) accurate and robust segmentation of liver, intrahepatic vessels, and tumors. We applied this framework to our previously developed LDLT surgery planning system. The framework was validated on a large range of clinical data from patients with liver cancer, and it achieved good performance in shape prior modeling and segmentation. The SSC model is employed in this framework to deal with complex variations of liver shapes and it preserves local detail information of the input shape well, so that the shape prior is adaptive to different patients. The SSC shape prior is combined with a minimally supervised segmentation algorithm. The framework achieves an accurate segmentation of hepatic parenchyma, portal veins, hepatic veins, and tumors simultaneously. Compared with the segmentation methods in state-of-the-art liver surgery planning systems, our framework not only obtains accurate segmentation results for healthy persons and common patients but also shows high robustness when dealing with specific patients with large variations of liver shapes in complex clinical environments. As a result, the framework improves the reliability and applicability of the LDLT surgery planning system remarkably.

Compared with our previous work only modeling the shape prior of healthy livers, the contribution of this paper mainly includes the application of the SSC model in the segmentation of liver with cancers in complex clinical environments, which is significantly more challenging. In addition, we combined it with the minimally supervised segmentation method to obtain accurate and robust results. Our future work will focus on improving the efficiency of the proposed framework by implementing the algorithms on GPUs. We will construct the training dataset with more shape samples, and the extraction of the most representative shapes in the repository will be a research interest in the future.