Maximizing the biological effect of proton dose delivered with scanned beams via inhomogeneous daily dose distributions

Abstract

Purpose: Biological effect of radiation can be enhanced with hypofractionation, localized dose escalation, and, in particle therapy, with optimized distribution of linear energy transfer (LET). The authors describe a method to construct inhomogeneous fractional dose (IFD) distributions, and evaluate the potential gain in the therapeutic effect from their delivery in proton therapy delivered by pencil beam scanning.

Methods: For 13 cases of prostate cancer, the authors considered hypofractionated courses of 60 Gy delivered in 20 fractions. (All doses denoted in Gy include the proton's mean relative biological effectiveness (RBE) of 1.1.) Two types of plans were optimized using two opposed lateral beams to deliver a uniform dose of 3 Gy per fraction to the target by scanning: (1) in conventional full-target plans (FTP), each beam irradiated the entire gland, (2) in split-target plans (STP), beams irradiated only the respective proximal hemispheres (prostate split sagittally). Inverse planning yielded intensity maps, in which discrete position control points of the scanned beam (spots) were assigned optimized intensity values. FTP plans preferentially required a higher intensity of spots in the distal part of the target, while STP, by design, employed proximal spots. To evaluate the utility of IFD delivery, IFD plans were generated by rearranging the spot intensities from FTP or STP intensity maps, separately as well as combined using a variety of mixing weights. IFD courses were designed so that, in alternating fractions, one of the hemispheres of the prostate would receive a dose boost and the other receive a lower dose, while the total physical dose from the IFD course was roughly uniform across the prostate. IFD plans were normalized so that the equivalent uniform dose (EUD) of rectum and bladder did not increase, compared to the baseline FTP plan, which irradiated the prostate uniformly in every fraction. An EUD-based model was then applied to estimate tumor control probability (TCP) and normal tissue complication probability (NTCP). To assess potential local RBE variations, LET distributions were calculated with Monte Carlo, and compared for different plans. The results were assessed in terms of their sensitivity to uncertainties in model parameters and delivery.

Results: IFD courses included equal number of fractions boosting either hemisphere, thus, the combined physical dose was close to uniform throughout the prostate. However, for the entire course, the prostate EUD in IFD was higher than in conventional FTP by up to 14%, corresponding to the estimated increase in TCP to 96% from 88%. The extent of gain depended on the mixing factor, i.e., relative weights used to combine FTP and STP spot weights. Increased weighting of STP typically yielded a higher target EUD, but also led to increased sensitivity of dose to variations in the proton's range. Rectal and bladder EUD were same or lower (per normalization), and the NTCP for both remained below 1%. The LET distributions in IFD also depended strongly on the mixing weights: plans using higher weight of STP spots yielded higher LET, indicating a potentially higher local RBE.

Conclusions: In proton therapy delivered by pencil beam scanning, improved therapeutic outcome can potentially be expected with delivery of IFD distributions, while administering the prescribed quasi-uniform dose to the target over the entire course. The biological effectiveness of IFD may be further enhanced by optimizing the LET distributions. IFD distributions are characterized by a dose gradient located in proximity of the prostate's midplane, thus, the fidelity of delivery would depend crucially on the precision with which the proton range could be controlled.

INTRODUCTION

One important aspect of modern proton radiotherapy, which has not been sufficiently explored and evaluated for its clinical effectiveness, is the biological advantage of using temporally and spatially heterogeneous dose distributions. From radiobiological considerations, uniform temporal dose distributions are often suboptimal in achieving the goal of maximizing tumor control probability (TCP) while minimizing normal tissue complication probability (NTCP). As early as two decades ago, it was demonstrated that allowing target dose distribution to be inhomogeneous (for nonmodulated photon beams) actually increases TCP while decreasing the NTCP.¹ Additionally, it has been shown that when incomplete repair is taken into account, nonuniform temporal distribution of dose reduces the corresponding NTCP.² The extent of expected improvement is dependent on the model parameters, and fractional dose distribution may be designed to maximize the TCP gain specifically for a certain assumed range of parameters, without increasing the estimated NTCP.³ The challenge is that accurate model parameters to calculate tumor control, complication probabilities, and cellular effects are not known for all relevant endpoints.

In proton therapy, inhomogeneous absorbed dose distributions can be achieved by temporally modulating the current while creating the spread-out Bragg peaks in scattered-beam treatments, or in delivery using pencil beam scanning (PBS). Inverse optimization and deployment of intensity-modulation technique with PBS produce inhomogeneous fields with desired distribution of the physical dose and relative biological effectiveness (RBE), due to variations in proton's linear energy transfer (LET).⁴ Thus, PBS allows for delivery of steeper dose gradients not just to better spare normal structures, but also to generate biologically advantageous heterogeneous dose distributions within the target volume. Importantly, dose distributions of intensity-modulated proton therapy (IMPT), including built-in inhomogeneities (e.g., integrated partial volume boost), can be designed in a robust manner, so that the delivered dose would minimally deviate from the plan, despite the uncertainties and variations in the patient setup and delivery procedures.⁵

The potential of hypofractionated radiation therapy to improve tumor control, as well as to reduce the duration and cost of treatment, has been widely recognized. In particular, for prostate cancer, a number of clinical trials indicated that the α/β ratio, the measure of fractionation response in the linear-quadratic model, of the prostate is equal or lower than that of surrounding organs.⁶ Estimated α/β-values as low as 1.5 Gy have been reported.^{7, 8} Ongoing trials investigate the relative safety of hypofractionation in prostate proton treatments.⁹

In this study, we evaluate the potential gain in therapeutic effect from combining the delivery of daily inhomogeneous fractional dose (IFD) distributions in proton therapy, using pencil beam scanning, with hypofractionation. We also discuss the dependence of therapeutic gain on several model parameters and the sensitivity to range uncertainties.

METHODS AND MATERIALS

Patient selection

We randomly selected 13 patients with low-grade prostate cancer, who were treated at Massachusetts General Hospital. Three of these patients were treated with endorectal balloon (ERB) in place for immobilization of the prostate. The study was conducted within the IRB-approved protocol which covered the use of anonymized clinical data to investigate potential improvements in treatment approaches.

Computer tomography (CT) scanning was performed in the supine position with the resolution of 0.977 mm in the axial planes and slice thickness of 2.5 or 1.25 mm. The attending physicians outlined the entire prostate, 1 cm of proximal seminal vesicles, rectal wall, urinary bladder, and femoral heads. For the patients treated with endorectal balloon, the balloon was present during the CT scans.

For each patient, the gross tumor volume (GTV) was considered the prostate gland, and the clinical target volume (CTV) was defined as the whole prostate and seminal vesicles. Planning target volume 1 (PTV1) and planning target volume 2 (PTV2) were defined as 5 mm uniform expansions around CTV and GTV, respectively. The patients received a course of 3D-conformal proton therapy in 39 fractions of 2 Gy, the prescription dose to PTV1 and PTV2 was 50 and 78 Gy, respectively. Here and below, all doses denoted in Gy include proton's mean RBE of 1.1.

Treatment planning for pencil beam scanning

Plans were optimized with treatment planning system (TPS) Astroid, which is used for clinical PBS.¹⁰ The dose was calculated on an isotropic grid of 2.5 × 2.5 × 2.5 mm³. Pencil beam Bragg peaks (spots) were distributed throughout the scanned volume, which was formed by expanding the target volumes: a lateral expansion of 15 mm and a distal expansion of 10 mm were used to allow placement of spots outside of the PTV to improve homogeneity and conformity of the dose distribution.¹¹ The expansion of the scanned volume is a standard practice for PBS-based delivery. It is aimed to improve the dose coverage of the target in the planning approaches which place beam spots on a rectilinear grid.¹² Note that the scanned volume expansion is different from the PTV margins. The size of the necessary expansion of the scanned volume is defined by the spacing of the beam spots on the grid, which, in its turn, is dictated by the characteristics of the beam: for proton energies relevant to prostate treatment, we currently use the lateral spacing of 10–15 mm (one σ of the pencil beam) and the depth spacing of 7–10 mm [full width at 80% maximum (w₈₀)]. Consequently, the lateral and distal expansions of the scanned volume were 15 and 10 mm, respectively.

Using inverse planning algorithms, the intensity values of discrete position control points of the scanned beam spots, were iteratively optimized to deliver the dose that conformed to the prescription, and tissue tolerance constraints. The implementation of multicriteria optimization in Astroid allows multiple goals: maximizing the minimum dose to PTV1 and PTV2; minimizing the maximum dose to rectum and bladder; and minimizing the mean dose to PTV1.

Research plans were optimized for delivery with PBS, for a hypofractionated course of 20 fractions of 3 Gy. Assuming α/β = 1.5 Gy, the equivalent dose to PTV2 in 2 Gy fractions (ED2Gy) is 20 fx × 3 Gy/fx × (α/β + 3 Gy)/(α/β + 2 Gy) = 77.1 Gy. The constraints for the treatment plan optimization are listed in Table 1.

Table 1.

Dose constraints for the treatment plan optimization.

GTV	Minimum	60 Gy
PTV2	Minimum	57 Gy
PTV1	Minimum	40 Gy
	Maximum	66 Gy
Rectum	Maximum	64.6 Gy
	<15% of volume	57.7 Gy
	<25% of volume	53.8 Gy
Bladder	Maximum	64.6 Gy
	<25% of volume	57.7 Gy
	<35% of volume	53.8 Gy
Femoral heads	Maximum	38.5 Gy

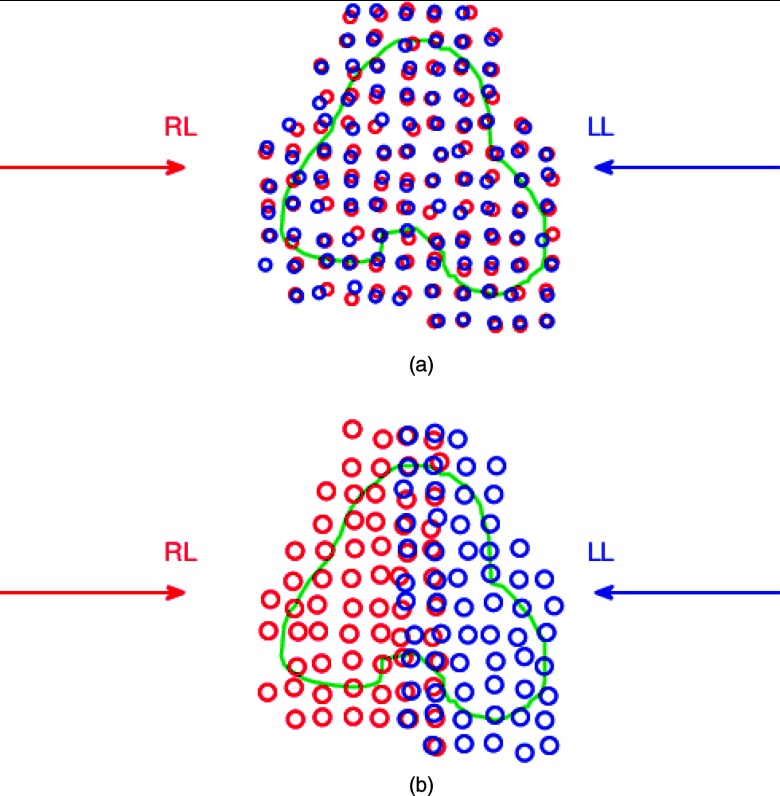
As the first step, for each patient, two auxiliary plans were optimized, both using two opposed lateral beams to deliver a uniform dose to the entire planning volume: (1) in conventional full-target plans [FTP, Fig. 1a] each beam irradiated the entire gland; (2) in split-target plans [STP, Fig. 1b], both beams irradiated only the respective proximal hemispheres. FTP and STP were both optimized with three-dimensional modulation.^{11, 13} FTP represents a conventional method of IMPT optimization, in which the same target volume is used by several beams, and the intensities of spots are optimized simultaneously. Optimization of STP uses a feature available in Astroid TPS which allows one to define separate target volume for each beam, and to optimize the dose simultaneously for all targets and beams. The planning target volume was split sagittally along the prostate midplane, and the two subvolumes were assigned as targets for two opposed lateral beams. Scanning volumes were created as target expansions separately for each beam, and thus overlapped along the split plane [Fig. 1b]. STP, notably, introduces high gradients at the junction of doses delivered by individual fields. While both types of plans delivered similar uniform dose to the prostate, they yielded distinctly different spot intensity maps: FTP plans preferentially required higher intensity of spots in the distal part of the target, while STP, by design, employed proximal spots.

Figure 1.

Schematic illustration of beam placement for (a) FTP and (b) STP. The transversal cross section of the planning target volume is outlined in green. Two opposed lateral beams were used: right lateral (RL), and left lateral (LL). Open circles represent the pencil beam spots: red for the RL beam and blue for the LL beam. In (a) FTP, both beams targeted the entire gland. In (b) STP, each beam only targeted the respective proximal hemisphere. As the result of expansion of the scanned volume, the spots from RL and LL beams overlap near the midplane.

Planning of IFD

In the next step, IFD plans were constructed by combining and rearranging the delivery sequence of beam intensity maps optimized for FTP and STP.

Assuming the linear-quadratic relationship between the biological response and dose, for a given number of fractions of delivery and the same total dose, the tissue response is always higher when the dose per fraction is varied rather then when it is constant.³ Thus, generally, in order to maximize the response in tumor tissue and to limit the risk of normal tissue toxicity, one would desire to maximize the fraction-to-fraction variation in the local dose delivered to the target tissue, and minimize such variation in healthy tissues. Accordingly, the IFD fractional distributions in this study were designed with built-in inhomogeneities: a dose gradient was introduced in the vicinity of the prostate's sagittal midplane so that one (boosted) hemisphere of the prostate would receive a relatively higher mean dose, compared to the other (nonboosted) hemisphere. Thus, IFD required two separate sub-plans, which boosted either left or right hemisphere, alternating the boost location from fraction to fraction. The workflow for the process of constructing plans for left- and right-side boosting fractions is illustrated in Fig. 2.

1. IFD initialization: Optimized spot intensity maps from either FTP or STP plan could be used as the source. The scanned volume was partitioned into four sections as shown in Fig. 3: (1) left and (2) right hemispheres of the scanned volume, split along the prostate midplane, excluding the organs at risk (OARs, i.e., rectum and bladder, which are partially overlapped by the scanned volume), (3) scanned volume overlapped with rectum, and (4) scanned volume overlapped with bladder. Note that both of the lateral beams employed in the source plan use spots located in all four sections of the scanned volume (see Figs. 13). The intensities of the beam spots were then redistributed between the two IFD fractions according to the spot location. For example, for the IFD fraction targeting the right hemisphere, the intensities of the spots located in the right side of the scanned volume were doubled, and the intensities of spots on the left side were set to zero. (Note that, because the total dose at a point is contributed from a large number of spots (i.e., entry dose, lateral, and distal penumbra of many pencil beams), setting the intensity of a spot to zero does not automatically render zero the total dose at that spot's position.) And vice versa for the fraction boosting the left hemisphere. The spots inside OARs were not modified, and were the same for both left- and right-boosting fraction. Thus, the first step preserved the total beam intensity from the source plan (i.e., FTP or STP), and the combined physical dose delivered in every two fractions, which was uniform on the target. The dose delivered in each fraction was nonuniform and introduced a dose gradient between the left and right hemispheres of the prostate.

2. Enhancement: Although the combined physical dose from two IFD fractions was uniform on the target, due to the quadratic dose-response, the biological equivalent dose was lower near the plane of splitting than at the periphery. To compensate for this shortfall in biological dose, the intensities of spots within 10 mm of the split plane (dark red region in Fig. 3), but outside of all OARs, were further enhanced by 25%. (Note that an enhancement of 25% on spot intensity does not increase the dose at the spot by 25%, since the dose at a point is contributed by a number of spots, including those which were not enhanced. Although the exact value of intensity enhancement required to equalize the dose response at the midplane and on prostate's periphery depends on the dose gradient, and is different, e.g., in FTP- and STP-sourced IFD plans, the same average value of 25% was applied to all cases for simplicity.)

3. Mixing: Steps (i) and (ii) were repeated for both FTP and STP plans to produce, respectively, FTP- and STP-sourced IFD plans. Due to the differences between FTP and STP spot intensity distributions, the FTP-sourced and STP-sourced IFD plans represented two distinctly different solutions that produced a dose gradient between the prostate hemispheres in individual fractions. To investigate intermediate cases, additional IFD plans were created as a linear combination of the FTP- and STP-sourced IFD. The mixing factor m was defined as the share of the contribution to the beam weight coming from the FTP-sourced plan. Thus m = 0 and m = 1 correspond, respectively, to the STP-sourced and FTP-sourced IFD; and 0 < m < 1 corresponds to a combination of the two IFD plans.

4. Normalization: The equivalent uniform dose (EUD) was calculated as described in Sec. 2D. IFD plans were normalized so that the EUD of OAR (rectal or bladder) would not exceed that of the hypofractionated 20-fraction uniform-dose course (FTP). Namely, if the EUD of rectum or bladder was found to increase in an IFD plan, the IFD spot intensities were uniformly rescaled by the minimum amount necessary to reduce the EUD of both structures to the same level as (or below) those in the baseline FTP plan.

Figure 2.

Workflow used to generate and evaluate IFD plans.

Figure 3.

Schematic illustration of construction of intensity maps for two consecutive fractions delivering IFD, which boosted (a) right and (b) left hemisphere of the prostate. Target contour is shown in white; contours of the bladder and rectum are shown in yellow. Intensities of spots within the rectum or bladder (blue) were not modified. Spots outside of organs at risk were doubled on the proximal side of the target, and suppressed on the distal side. The spots within 10 mm of the plane of splitting were further enhanced by 25%.

Dose evaluation

The ED2Gy for each voxel i was calculated as

$$d_i=\sum _{n=1}^{20}{d}_{i,n}\frac{\frac{\alpha }{\beta }+d_{i,n}}{\frac{\alpha }{\beta }+2\mathrm{Gy}},$$ (1)

where d_{i, n} is the dose delivered to voxel i in the nth fraction. The EUD was then calculated for ED2Gy distributions as

$$\mathrm{EUD}={\left(\frac{1}{N}\sum _{i=1}^N{d}_i^a\right)}^{\frac{1}{a}},$$ (2)

where d_i is the voxel ED2Gy, a is a tissue-specific parameter, and N is the total number of voxels.¹⁴ The α/β-values used were 1.5 ± 0.5 Gy for prostate, 8 ± 2 Gy for rectum, and 3 ± 1 Gy for bladder. The EUD parameters used were $a=-{10}_{-5}^{+3}$ for target volume, $5_{-2}^{+3}$ for rectum, and $7_{-3}^{+5}$ for bladder.¹⁵

The TCP and NTCP were calculated with an EUD-based model^{16, 17}

$$\mathrm{TCP}/\mathrm{NTCP}=\frac{1}{1+{\left(\frac{D_{50}}{\mathrm{EUD}}\right)}^{4{\gamma }_{50}}}.$$ (3)

D₅₀ is the dose corresponding to 50% of TCP/NTCP when the tumor or normal tissue is homogeneously irradiated. γ₅₀ is a unitless parameter that is specific to the tumor or normal tissue of interest. It describes the slope of the dose-response curve: the slope at D₅₀ is γ₅₀/D₅₀. The model parameters are summarized in Table 2. The values were provided by the author of the model, Niemierko.

Table 2.

Tumor control and NTCP model parameters.

	D50 (Gy)	γ50	Endpoint
Prostate	65	2.5
Rectum	80	2.7	Fistula
Bladder	80	3.6	Contraction

The analysis was repeated for IFD plans created with different values of mixing factors 0 ⩽ m ⩽ 1, and the value corresponding to maximum gain in target EUD was identified. The percentage EUD gain, ΔEUD%, was evaluated as

$$\Delta \mathrm{EUD}\%:=\frac{{\mathrm{EUD}}_{\mathrm{IFD}}-{\mathrm{EUD}}_{\mathrm{uniform}}}{{\mathrm{EUD}}_{\mathrm{uniform}}}\times 100$$ (4)

for prostate, rectum, and bladder, where the reference EUD_uniform is for the hypofractionated 20-fraction uniform-dose FTP course, as indicated in Fig. 2. The EUD gain was evaluated for a range of α/β and a values to investigate the sensitivity to model uncertainties.

Serial CT data from individual fractions were not available for the patients in this study. Previously, it was demonstrated that the interfractional variations in prostate patients' anatomy and setup result in the shift of the proton beam penetration depth with the standard deviation (SD) of up to 2.5 mm.¹⁸ A simplified model of the interfractional motion, assuming that the range shift is uniform for every position of the scanned beam, was used to evaluate the sensitivity of the IFD dose distributions within the target volume to random range uncertainties: For each beam in every fraction, the dose was randomly shifted along the beam direction. The amount of the shift in individual fractions was sampled from a unbiased Gaussian distribution with 2.5 mm SD. The total delivered dose was calculated as the sum of shifted fractional doses. This simulation was performed 1000 times, and the resulting SD of ΔEUD% was taken as the uncertainty due to random range shift in the therapeutic gain from IFD. Systematic range errors, which may result from CT-to-stopping-power conversion, or systematic anatomical changes, are not evaluated here. The same approach can be used to evaluate the effect of a specific value of the systematic range shift. Plans which are relatively stronger affected by random errors would also be stronger affected by systematic errors.

Dose-averaged LET distributions for FTP, STP, and IFD courses were calculated with Monte Carlo.⁴

RESULTS

Representative patient case

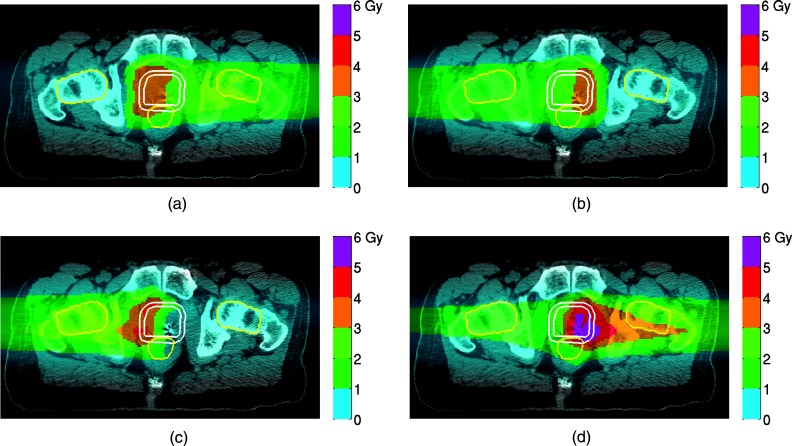
Dose distributions from two consecutive IFD fractions constructed from FTP (m = 1) and STP (m = 0) are illustrated in Fig. 4 for a representative case. Because FTP plans favored dose delivery with distal spots, this feature remained in the IFD distributions constructed from FTP (m = 1), i.e., the LL beam delivered the bulk of the dose to the right hemisphere in the right-boosting fraction [Fig. 4a], and vice versa [Fig. 4b]. Due to the contribution from the entry dose deposited in transit through the proximal side of the target, the extent of achievable dose differential between the left and right hemispheres of the prostate was limited in the FTP-sourced IFD fraction.

Figure 4.

IFD distributions of two consecutive fractions for a representative patient case. (a) and (b) m = 1 (FTP-sourced IFD); (c) and (d) m = 0 (STP-sourced IFD). In each fraction both fields are used. The summed dose of two fractions is approximately uniform on the whole target. The contour for PTV1 is shown in white. Contours for OARs are shown in yellow. The colorscales are identical in all three subfigures.

In contrast, in IFD distributions obtained from STP (m = 0), the dose in fractions boosting a given hemisphere was delivered preferentially by the proximal beam, i.e., the RL beam delivered the bulk of the dose in the right-boosting fraction of IFD, while the LL beam contributed only a small amount of dose delivered by spots in the proximity of the prostate's midplane [Fig. 4c]. Note that both the RL and LL beams are used to deliver the dose in both left-boosting and right-boosting fractions of the corresponding IFD.

To make a fair comparison with the conventional uniform-dose plan in terms of normal organ toxicity, the IFD physical dose was normalized to eliminate any increase of rectal or bladder EUD in IFD compared to the hypofractionated 20-fraction uniform-dose FTP course, as shown in Table 3. For a series of plans created with a range of values of the mixing factor 0 < m < 1, the optimal value was then identified which yielded the maximum gain in target EUD. The dependence of EUD gain on m is shown in Fig. 5, where ΔEUD% was defined in Eq. 4 for each volume. The largest observed gain in target EUD exceeded 8%, and occurred with 4:1 mixing ratio of STP and FTP spot intensities (m = 0.2). This increase of EUD resulted in an estimated increase of TCP from 88% to 94% (Table 2), while the NTCP for both rectum and bladder were below 1%. TCP estimates are typically subject to considerable model uncertainties. Notably, in this example, a roughly twofold reduction in the estimated control failure rate (1 − TCP) holds for the values of D₅₀ within the range of 60–70 Gy: the estimated TCP increases from FTP to IFD (m = 0.2) was, respectively, from 94% to 97% assuming D₅₀ = 60 Gy, and from 78% to 88% assuming D₅₀ = 70 Gy. Similarly, the TCP increases from 83% to 90% for γ₅₀ = 2, and from 92% to 97% for γ₅₀ = 3.

Table 3.

EUD gain in IFD plans for a representative patient case, with physical dose normalized subject to the rectal and bladder EUD constraints (ΔEUD ⩽ 0 for rectum and bladder).

Mixing factor m	DGTV, min (Gy)	ΔEUD (Gy)			ΔEUD%
		GTV	Rectum	Bladder	GTV	Rectum	Bladder
1	59.2	0.3	0	−0.5	0.3	0	−1.0
2/3	58.1	4.3	−0.3	0	5.4	−0.7	0
1/2	56.9	5.5	−0.7	0	7.0	−1.3	0
1/3	55.7	6.5	−0.9	0	8.1	−1.9	0
0	52.8	6.1	−1.4	0	7.8	−2.8	0

Figure 5.

Percentage EUD gain in IFD plans constructed with different mixing factors m (i.e., relative weight of FTP) for a representative patient case. The physical dose of the IFD plans was renormalized to eliminate any increase of rectal or bladder EUD. A range of α/β-values was considered. The solid lines correspond to α/β of 1.5 Gy for GTV, 8 Gy for rectum, and 3 Gy for bladder, and nominal beam range. The shadowed bands correspond to the likely interval of the ΔEUD% due to (a) the uncertainty of α/β (±0.5 Gy for GTV, ±2 Gy for rectum, ±1 Gy for bladder) and (b) range shift (2.5 mm SD).

For m ⩽ 0.8, the dose level is constrained by the bladder tolerance, i.e., were the IFD not normalized down, the bladder EUD would be higher than that in 20-fraction uniform course. Conversely, for m > 0.8, the dose escalation is constrained by the rectum.

With m = 0.2, the right side of the GTV receives mean doses of 3.3 and 2.9 Gy in the two types of fractions, respectively. The left side, however, receives mean doses of 1.7 and 4.4 Gy in the two types of fractions. On average, the boosted side receives 3.8 Gy, and the other side 2.3 Gy. This asymmetry in the dose is reduced with the value of m, i.e., larger for m = 0 (STP-sourced IFD) and smaller for m = 1 (FTP-sourced IFD). In this particular case, the interfractional dose inhomogeneity for the left side is considerably larger than that for the right side. The asymmetry in fractional dose reflects the asymmetry of the spot positions with respect to the split plane, as well as the asymmetric distribution of the optimized weights. This will be further discussed in Sec. 4.

Due to the poor contrast on CT scans, urethra is not routinely segmented and considered in planning, however, urethral toxicity is of concern in radiation therapy of prostate cancer. An estimate of the dose to urethra can be made by calculating the mean dose delivered to the midplane of the prostate, e.g., a 5 mm thick sagittal section of the GTV. The method used here to construct IFD plans produces a dose gradient between the higher-dosed boosted hemisphere and the lower-dosed hemisphere, thus the dose delivered at the midplane of the prostate is roughly the same (∼3 Gy) in every fraction. Consequently, the increase in the equivalent dose to the urethra is mitigated, compared to the increase in the prostate EUD. For the IFD plans in this study, the estimated mean dose to urethra increased by less than 2 Gy, and the maximum increase was observed for $m\sim \frac{2}{3}$.

The dose-volume histograms (DVHs) on target corresponding to 2:1 mixing of STP and FTP ($m=\frac{1}{3}$) are shown in Fig. 6, compared to the hypofractionated 20-fraction uniform-dose FTP course, and the conventional 39-fraction uniform course FTP. The conventional course of 39 fractions delivered 78 Gy in total. The hypofractionated FTP course and the IFD course both delivered approximately 60 Gy to the target. The uniform course of 39 fractions and 20 fractions delivered approximately the same equivalent dose to the target. In contrast, the ED2Gy of IFD course was enhanced by the alternating elevated and reduced local doses, from inhomogeneous distributions delivered in consecutive hemisphere-boosting fractions. Notably, The DVH indicates the presence of volumes of lower physical dose (i.e., cold spots) in the IFD plan. Although, the minimum physical dose was 55.7 Gy as shown in Table 3, these cold spots received distinctly different dose in consecutive fractions of IFD, thus the ED2Gy for the entire course approached, or even exceeded, 78 Gy due to the quadratic response.

Figure 6.

Dose-volume histograms (DVHs) of the prostate (GTV) for the standard uniform-dose FTP course of 78 Gy in 39 fractions (red), the hypofractionated FTP course of 60 Gy in 20 fractions (green), and the 20-fraction IFD course ($m=\frac{1}{3}$, blue), for a representative patient case. (a) Physical dose; (b) ED2Gy.

Considering the uncertainty of α/β-value, its effect on EUD was generally larger for IFD distributions generated with smaller m, dominated by the STP contribution. This trend also holds for uncertainties due to the variation of EUD parameter a, and the random proton range changes due to interfractional variations. For FTP-sourced IFD distributions (m = 1), the EUD turned out rather insensitive to the parameter a, since the dose inhomogeneity was limited by the relatively higher entry dose, deposited in transit to the boosted hemisphere [Figs. 4(a) and 4(b)]. The uncertainty of ΔEUD% due to the interfractional range variation (assuming 2.5 mm SD) is estimated as between ±1% [for m = 1, see the right-hand side of Fig. 5b] and ±4% [m = 0, left-hand side of Fig. 5b]. For IFD with $m=\frac{1}{3}$, the value of a corresponds to an uncertainty of ±2 for ΔEUD%. For $m=\frac{1}{3}$, the relative gain compared to the conventional uniform-dose plan for a range of a-values are shown in Table 4.

Table 4.

The gain in EUD and TCP for IFD plan of a representative patient case ($m=\frac{1}{3}$) compared to conventional uniform-dose FTP, for a range of a-values.

a	EUD(Gy)		ΔEUD%	TCP
	Uniform 20 fx	IFD 20 fx		Uniform 20 fx	IFD 20 fx
−7	79.7	86.5	8.5	88%	95%
−10	79.6	86.1	8.2	88%	94%
−15	79.6	85.3	7.2	88%	94%

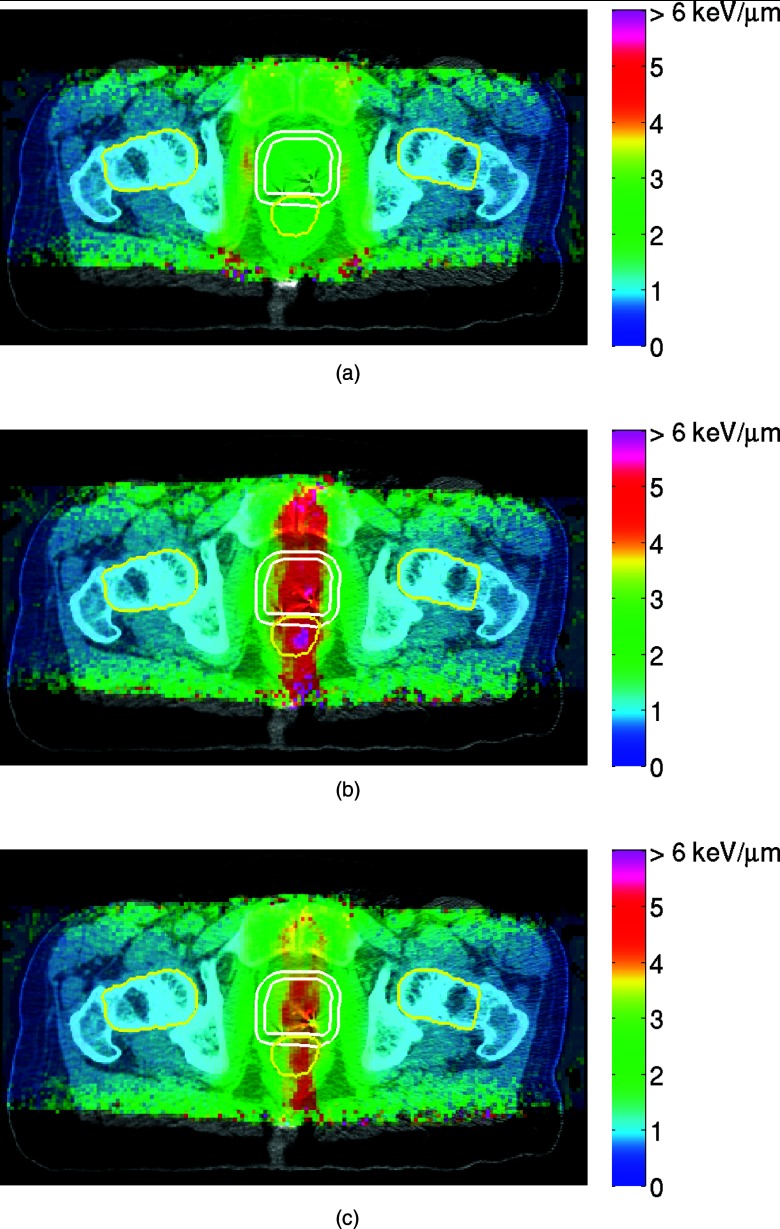
The dose-averaged LET distributions calculated with Monte Carlo are shown in Fig. 7. LET increases at the end of proton range, and reaches the maximum just after the Bragg peak of dose. The STP, in which the protons were stopped near the median sagittal section, yielded higher LET, and thus, potentially, higher local relative biological effect, within the target, but also in the rectum, bladder and urethra. In contrast, for FTP, which preferred higher weighting of the beam spots located in the distal part of the target, the LET distribution is more uniform, with some increase in the LET at the periphery. Because IFD was designed as a linear combination of the spot intensities from FTP and STP plans, the LET distribution, to the leading-order approximation, is a linear combination as well. Thus the LET distribution in IFD may be designed appropriately to maximize the desired biological effect.⁴

Figure 7.

LET distributions calculated with Monte Carlo for (a) FTP, (b) STP, and (c) IFD course ($m=\frac{1}{3}$), for a representative patient case. Contours for GTV and PTV1 are shown in white. Contours for OARs are shown in yellow. The colorscales are identical in all three subfigures.

Overview of 13 cases

A range of IFD plans were designed with the mixing factor m varied between 0 and 1 with step 0.1, and the analysis performed for 13 patients. The physical dose of the IFD plans was renormalized to eliminate any increase of rectal or bladder EUD. The optimal value of m, that yielded the maximum EUD gain on GTV, varied for different patients, as plotted in Fig. 8. The difference in the mean dose between boosted and nonboosted hemispheres was higher in cases for which a smaller value of m was found to maximize the target EUD. On average, boosted hemispheres of the target received 3.7 Gy, and the other hemisphere received 2.5 Gy per fraction. The uncertainty in the EUD gain stems from the uncertainty of the model parameter α/β [Fig. 5a]. For the patient case described in detail in Sec. 3A, the maximum gain in EUD was achieved with m = 0.2. IFD distributions created with m ⩾ 0.6, dominated by the contribution from FTP, generally yielded a moderate gain in the target EUD. The maximum increase in EUD (over 5%) was observed in IFD plans with m ⩽ 0.2, dominated by the STP contribution. For one case (a different patient from the one shown in Sec. 3A) with m = 0, a gain of over 13% was achieved, which corresponded to an increase in TCP from 88% to 96%, i.e., a threefold reduction in the estimated control failure rate from 12% to 4%.

Figure 8.

Maximum target EUD gain for 13 patients and the corresponding mixing factor m, (i.e., relative weight of FTP contribution). The physical dose of the IFD plans was renormalized to eliminate any increase of rectal or bladder EUD. The data points corresponding to the three patients treated with endorectal balloon for immobilization are circled.

The increase in the GTV EUD was limited by the bladder dose constraint in four cases out of 13, and by the rectal constraint in the other nine cases. Within the context of the limited number of cases, no apparent difference is observed in the distribution of the estimated EUD gain between plans for patients imaged with ERB and those without (only the anatomical differences, e.g., extended rectal volume, reduced separation from GTV, are considered here, but not the potential effect on the setup variations, which is expected to be smaller in patients treated with ERB in place).

DISCUSSION

Linear-quadratic dose response gives rise to a substantial gain in the biological effect in hypofractionated treatment of targets with low α/β ratio. Due to various limitations (e.g., concerns about acute side effects), however, there is a practical limit to how far the number of fractions can be reduced. This presents a motivation to explore the additional gain in the biological effect stemming from the physical properties of the dose distribution, without further reduction in the number of treatment fractions. In this study, we demonstrated that a considerable gain in the therapeutic effect could be achieved by spatially modifying the fractional dose distribution, with the IFD plans, constructed as a mixture of the beam spot intensities optimized for uniform-dose plans. IFD achieves the increased biological response in the target volume by alternating, in consecutive fractions, between local dose boost and limited dose reduction. We introduced fractional dose inhomogeneity in a straightforward manner, i.e., by splitting the target into subvolumes, and redistributing the delivery of pencil beams spots between two fractions, in order to maximize the dose differential on the prostate gland, while attempting to limit it in the adjacent organs. Two distinctly different types of PBS plans were used: one that favored the distal placement of beam spots (FTP), and the medial placement (STP). A number of mixing weights m were used to explore how the results depend on the weighting of beam spots. This was done by “manually” creating the mixed IFD plans, since direct “computer-based” optimization of such plans is not intuitive and relies on the choice of a large number of planning parameters (constraints, priority factors, etc.). Potentially, the biological effect could be incorporated into the treatment planning system, which would allow the optimizer to consider EUD, ED2Gy, LET, RBE, TCP, etc., directly in the objectives and constraints. This presents a logical next step toward “biological optimization.” Our systematic investigation of the trade-offs between the target and OAR doses within the context of model and delivery uncertainties provides the data, that would be of use in fine-tuning such automated optimization approaches.

We have observed a substantial gain in EUD from the delivery of IFD plans. Partial dose boosting of the target in IFD, alternating the location between fractions, allowed for taking advantage of the hypofractionation effect on the therapeutic ratio. We find that the gain in EUD was not uniform across the patient cohort. It was maximized for various values of the mixing factor m, and was limited by either rectal or bladder EUD constraints. The variation in the maximum gain between different patients was mainly due to the difference in the fractional volume of PTV that overlapped with rectum or bladder.

Our estimation of the range variation due to interfractional changes was simplified, because the serial imaging data were not available for our selection of patients. However, this simple model qualitatively demonstrated the sensitivity of the gain from IFD to the range uncertainty due to interfractional variations. The introduction of IFD, especially when dominated by the contribution from STP beam spots, leads to delivery of steep dose gradients within the target volume, which make treatment plans particularly sensitive to range errors.¹⁹ In our estimate, we only considered the effect of randomly distributed error due to interfractional variations.¹⁸ The presence of systematic error in proton range (e.g., due to patient's weight loss or gain, errors in CT-to-stopping power conversion) would increase the risk of misalignment of the modulated doses delivered by several beams in IMPT, and, consequently, a deviation of the delivered dose from the plan. In order to avoid severe degradation of dose distributions and fully exploit the potential of IMPT, range uncertainties can be considered in planning employing robust optimization methods.¹⁹ A reduction in the overall uncertainty of the proton range using in vivo verification methods (e.g., endorectal dose measurements,²⁰ imaging of positron-emitter activation²¹ and prompt gamma²²) would be expected to further increase the confidence in delivery of the IFD plans as well as their clinical relevance.

Systematic intrafractional motion (position drift) is insignificant within the time frame required to deliver dose with a scanned beam to the prostate (1–2 min), and can be minimized with the use of ERB. Due to the dynamic nature of PBS delivery, some limited interplay between the prostate motion and beam position is possible. However, a recent study identified no significant effect from intrafractional motion in PBS on D_min, $D_{98\%}$, and EUD in target.²³

The setup of patient's pelvic anatomy is far from being perfectly symmetric. Thus, the radiological depths to the prostate commonly differ by 5 mm or more between the left and right beams.¹⁸ The prostate was partitioned into hemispheres along the sagittal plane through the isocenter in all patient cases. However, the glands were not perfectly symmetric around this split plane. As a consequence, the optimized beam spot weights in the auxiliary FTP and STP plans, were not symmetric between left and right beams. Further, by design, the placement of the spots was not symmetric around the split plane. Consequently, in the generated IFD plans, the dose was not symmetric between the right-side- and left-side-boosting fractions.

In designing treatment plans for this study, we used the beam model which described the current state of our PBS system, with a relatively large lateral spread of the beams (σ_x ∼ σ_y > 10 mm). There are two consequences of this wide lateral spreading. First, the introduction of IFD to the target significantly affects the dose distributions in rectum and bladder, thus, as a result of the quadratic response, the ED2Gy for the OARs also increase with the IFD. Even though we constrained the intensities of beam spots within the OAR (Sec. 2C), the beam spots outside but in the proximity of the OARs still contributed to the dose. The lateral penumbra, and the lateral expansion of the scanned volume, will be reduced with the use of smaller spot width, which will be available when our PBS system upgrade is completed. Second, the expansion of the scanned volume, and the lateral penumbra of the beam lead to the corresponding wide spread of the LET distributions. As shown in Fig. 7, the high LET region expands into the rectum and bladder, thus potentially increases the RBE of proton radiation in the critical organs. This region of high LET region could also be reduced with smaller spot width.

Our results demonstrate that the local distribution of proton LET depends strongly on how IFD distributions are constructed (e.g., the mixing factor m). This indicates that were the LET considered directly in treatment planning, it would be possible to affect the beam placement and weighting to further suppress the high LET regions within the OARs.⁴ Although the RBE of protons is conventionally assumed to be constant at 1.1, it does depend on α/β as well as local LET.²⁴ Thus the gain in RBE is likely to be higher in the prostate (low α/β) as compared to rectum and bladder (higher α/β). Direct optimization of LET and RBE is the focus of ongoing studies, and is beyond the scope of this manuscript.

The approach to design IFD distributions, described in this paper, can be applied to any fractionation regimen. Consider a fraction size d. To half of the target, one can deliver doses of (1 − δ)d and (1 + δ)d in consecutive fractions, where the dimensionless number δ characterizes the inhomogeneity introduced. The value of δ is technically between 0 to 1, but is practically limited by the entry dose of the beams irradiating subvolumes of the target. (E.g., in our example with 3 Gy fractions, $\delta =\frac{1}{3}$ corresponds to alternating between 2 and 4 Gy.) Compared with uniform fractionation, the relative gain in biological effect can be shown as

$$\frac{{\mathrm{ED}2\mathrm{Gy}}_{\mathrm{IFD}}-{\mathrm{ED}2\mathrm{Gy}}_{\mathrm{uniform}}}{{\mathrm{ED}2\mathrm{Gy}}_{\mathrm{uniform}}}={\delta }^2\frac{1}{\frac{\alpha }{\beta d}+1}.$$ (5)

Remarkably, not only the gain increases with δ, but it also increases with d/(α/β). For tumors with large α/β (α/β ≫ d), the gain due to IFD would be limited. For tumors with small α/β (relative to the fraction size d), the gain could be as large as δ². As a result, even larger gain is expected for more aggressive hypofractionation regimens for tumors with small α/β, such as prostate carcinoma.

CONCLUSIONS

We evaluated the gain in prostate EUD from delivery of alternating IFD distributions in hypofractionated treatment of prostate cancer. A substantial enhancement was achieved with IFD in most cases, including one in which the estimated rate of failure was reduced from 12% to 4%, while the estimated rate of normal organ toxicity did not increase. The amount of EUD enhancement depended on the anatomical configuration of the volume of interest, as well as model parameters. The introduction of dose gradients within the target poses a serious challenge to precise delivery of IFD presently due to the uncertainties in proton's range in tissue, however, the anticipated reduction in the range uncertainty can be expected to enhance the confidence of IFD delivery and its clinical relevance in the future.