Effectiveness of robust optimization in intensity-modulated proton therapy planning for head and neck cancers

Abstract

Purpose: Intensity-modulated proton therapy (IMPT) is highly sensitive to uncertainties in beam range and patient setup. Conventionally, these uncertainties are dealt using geometrically expanded planning target volume (PTV). In this paper, the authors evaluated a robust optimization method that deals with the uncertainties directly during the spot weight optimization to ensure clinical target volume (CTV) coverage without using PTV. The authors compared the two methods for a population of head and neck (H&N) cancer patients.

Methods: Two sets of IMPT plans were generated for 14 H&N cases, one being PTV-based conventionally optimized and the other CTV-based robustly optimized. For the PTV-based conventionally optimized plans, the uncertainties are accounted for by expanding CTV to PTV via margins and delivering the prescribed dose to PTV. For the CTV-based robustly optimized plans, spot weight optimization was guided to reduce the discrepancy in doses under extreme setup and range uncertainties directly, while delivering the prescribed dose to CTV rather than PTV. For each of these plans, the authors calculated dose distributions under various uncertainty settings. The root-mean-square dose (RMSD) for each voxel was computed and the area under the RMSD-volume histogram curves (AUC) was used to relatively compare plan robustness. Data derived from the dose volume histogram in the worst-case and nominal doses were used to evaluate the plan optimality. Then the plan evaluation metrics were averaged over the 14 cases and were compared with two-sided paired t tests.

Results: CTV-based robust optimization led to more robust (i.e., smaller AUCs) plans for both targets and organs. Under the worst-case scenario and the nominal scenario, CTV-based robustly optimized plans showed better target coverage (i.e., greater D_95%), improved dose homogeneity (i.e., smaller D_5% − D_95%), and lower or equivalent dose to organs at risk.

Conclusions: CTV-based robust optimization provided significantly more robust dose distributions to targets and organs than PTV-based conventional optimization in H&N using IMPT. Eliminating the use of PTV and planning directly based on CTV provided better or equivalent normal tissue sparing.

INTRODUCTION

In principle, intensity-modulated proton therapy (IMPT) can provide highly conformal tumor target coverage while sparing adjacent healthy organs.^{1, 2} IMPT offers both the high-dose conformality of intensity-modulated radiation therapy and the lower integral dose of protons (low dose bath effect). IMPT is considered particularly promising for cancers of the head and neck (H&N) because of the number and proximity of critical structures encountered. However, the characteristics of protons (e.g, tissue density dependent finite range) make IMPT highly vulnerable to uncertainties.^{3, 4, 5, 6, 7, 8} These uncertainties arise from interfractional variations such as tumor shrinkage, patient weight, and patient set up. Furthermore, there are uncertainties in proton range due to uncertainties in computed tomography (CT) numbers and their conversion to stopping power ratios.

The major purpose of this work is to compare the effectiveness of the different methods to account for uncertainties in the IMPT treatment planning through a patient population study in the H&N site. Previously, researchers have shown that the conventional planning target volume (PTV) concept to provide robust target coverage is not adequate for proton therapy.⁹ For passive scattering proton therapy, patient setup uncertainties, range uncertainties, and misalignment of tissue heterogeneity are dealt by modifying beam-specific hardware such as apertures and compensators. However, scanning beam proton therapy does not require such beam-specific hardware, therefore lacks the method of appropriately accounting for the uncertainties in order to provide adequate target coverage. Recently, Park et al.¹⁰ have demonstrated that beam specific planning target volume (bsPTV) could take into account of both setup and range uncertainties for scanning beam plans generated with single field optimization.¹⁰ However, bsPTV is not applicable to the multifield optimized IMPT plans. In the absence of a suitable alternative, the current practice for managing patient setup uncertainties in IMPT is similar to that for photons:^{4, 11} a PTV is generated by geometrically expanding a clinical target volume (CTV) with fixed and predefined margins based on the past patient population setup uncertainty model. Individual spots are placed inside the PTV plus a penumbra margin and their weights are optimized to deliver uniform dose across the PTV volume under the nominal scenario. The resulting dose distributions are generally not robust in the face of uncertainties (i.e., the delivered dose distributions may differ from what was planned) because cold and hot spots can occur within the CTV as a result of changes in tissue density along the beam line due to setup and range uncertainties, which may have unforeseen clinical consequences. Furthermore, due to the fact that PTV is always larger than CTV, this leads to unnecessary irradiation of normal tissues surrounding the CTV and may result in increasing dose to critical structures.

Different approaches of robust optimization have been reported.^{7, 8, 12, 13, 14, 15, 16, 17, 18, 19} We have developed one such method that accounts for uncertainties during plan optimization via “worst-case” robust optimization.¹⁷ The concept of representing plan robustness in terms of “worst-case” dose distribution was introduced by Lomax et al.²⁰ and the first robust optimization scheme using the “worst-case” concept was reported by Pflugfelder et al.⁶ In our previous study, we showed that robust optimization can render IMPT plans less sensitive to uncertainties and by eliminating the needs to irradiate PTV, we were able to achieve better sparing of normal tissues than conventional plans optimized on the basis of margins.^{16, 17} The robust optimization method takes into account setup and range uncertainty directly during the spot-weight optimization, therefore it does not require extra volume to be irradiated. In other words, with robust-optimization technique, a robust plan is generated using CTV as a primary target to be irradiated and no longer requires geometrically expanded PTV. Although the robust optimization algorithm does not work directly to reduce doses to normal tissues under the nominal scenario, the fact that it does not require irradiating the large volume defined by the PTV actually improves plan quality under the nominal scenario when compared to the conventional, PTV-based, optimization method.

The significance and effectiveness of robust optimization may be treatment site-dependent. Since robust optimization is computationally expensive, it is worthwhile to investigate its value for individual sites and determine the subset of patient and tumor characteristics where it might be of benefit. We sought here to evaluate the effectiveness of the worst-case robust optimization method for H&N cancer comparing its results for 14 cases with optimization done via the conventional “PTV-based” approach.

METHODS AND MATERIALS

Patient data and beam configurations

We retrospectively evaluated plans from 14 H&N patients that are randomly selected from the first 46 H&N cancer patients treated using IMPT in our clinic (Table I in the supplementary material²⁷). The treated disease subsites were five in nasopharynx, six in oropharynx, two in paranasal sinus, and one with an unknown primary with metastatic disease to the right neck. All plans were designed using three beam angles that are the same as the clinical plans and were chosen by experienced dosimetrists/clinical physicists at our clinics. The basic principles for beam angle selection are: (1) avoiding two beams too close; (2) avoiding directing the beam to the abutting critical organs; (3) avoiding the beam angles with much inhomogeneities along the beam path. However, we do not have the plan robustness taken into account when the beam angles are chosen. For each patient, two methods of optimization (“worst-case” robust optimization and PTV-based optimization) were used to account for uncertainties in setup (±3 mm) and beam range (±3.5%), which are the current standard of practice for proton therapy at our institution. The dose grid resolution for all cases was 2.5 mm. CTVs were delineated by physicians, with CTV1 defined as gross disease plus a 1-cm margin, CTV2 encompassing the high-risk nodal volume adjacent to gross disease in the neck, and CTV3 encompassing an additional margin beyond CTV2 for patients with pharyngeal tumors and uninvolved nodes in the neck considered to be at risk of harboring subclinical disease. We created the PTV1, 2, and 3 by uniform expansion of CTV1, 2, and 3 by 3 mm. The simultaneous integrated boost (SIB) technique was used to treat these patients.

The beamlet spot arrangements were identical for both PTV-based and robust optimization. A margin for penumbra was added to allow lateral dose fall-off (Table II of the supplementary material²⁷). While the CTV to PTV margin is meant to account for setup uncertainties, an additional margin for penumbra is required to ensure that the PTV is covered with the prescribed dose (or to some acceptable level, e.g., 95% of the prescribed dose). The prescription doses for PTVs are the same as the ones for the corresponding CTVs as indicated in Table I of the supplementary material.²⁷ Institutional dose-volume constraints for H&N cancer radiation were used. They are as follows: the maximum dose to the brainstem is limited to ≤54 Gy(RBE); the spinal cord to ≤45 Gy(RBE); and the brain to ≤50 Gy(RBE). The mean dose to the parotids is limited to ≤26 Gy(RBE) and oral cavity to ≤35 Gy(RBE).

Optimization algorithms

We used a “worst-case” robust optimization method described in a previous publication,¹⁷ in which the objective function value for a given iteration is computed using the “worst-case” dose distribution.⁵ The interfractional patient setup uncertainties are considered to be random, and are incorporated by shifting the isocenter of the patient in the antero-posterior (A-P), superior-inferior (S-I), and lateral (R-L) directions by the same margin as is used for defining the PTV, yielding six dose distributions and the corresponding “influence matrices” (i.e., beamlet dose distributions per unit intensity). Range uncertainties for one single patient are systematic and propagate through the whole course of the treatment. But they are random for a patient population. They are incorporated by scaling the stopping power ratios by −3.5% and 3.5% to generate two additional dose distributions and influence matrices corresponding to maximum and minimum proton ranges, respectively. The worst-case dose distribution is then represented by the minimum of the nine doses in each voxel in the CTV and the maximum of the nine doses in each voxel outside the CTV.⁵

For robust optimization, we used a standard quadratic objective function

$$\begin{array}{ccc}\hfill F\left({\omega }_j\right)& =& \sum _{i\in \mathrm{CTV}}{p}_{\mathrm{CTV},\min }{(D_{i,\min }-D_{0,\mathrm{CTV}})}^2\hfill \\ & & +\underline{\sum _{i\in \mathrm{CTV}}{p}_{\mathrm{CTV},\max }{(D_{i,\max }-D_{0,\mathrm{CTV}})}^2}\hfill \\ & & +\sum _{i\in \mathrm{OARs}}{p}_{\mathrm{OARs}}H(D_{i,\max }-D_{0,\mathrm{OARs}})\hfill \\ & & \times {(D_{i,\max }-D_{0,\mathrm{OARs}})}^2,\hfill \end{array}$$ (1)

where p denotes the penalty weight of the corresponding term and D₀ denotes the prescribed dose for the corresponding organ. The underlined term is the modification that minimizes hot spots. The Heaviside function, H(⟨D_i⟩ − D₀), is defined conventionally (i.e., its value is unity if ⟨D_i⟩ > D₀ but zero if ⟨D_i⟩ ⩽ D₀). Dose-based, dose volume based,²¹ and equivalent uniform dose based objectives²² are implemented. The terms $D_{i,\min }=\underset{m}{\min }\left\{D_i^m\right\}$ and $D_{i,\max }=\underset{m}{\max }\left\{D_i^m\right\}$ in Eq. 1, respectively, indicate the minimum and maximum dose among the m possible doses $D_i^m$ in voxel i (m = 9 here), which are calculated using $D_i^m=\sum _j{\mathrm{IM}}_{i,j}^m{\omega }_j^2$ in each iteration. The mth IMs ${\mathrm{IM}}_{i,j}^m$, incorporating range and setup uncertainties, were precalculated using an inhouse dose calculation engine for proton pencil beams of a finite size²³ and stored in local memory for efficient optimization. Our robust optimization approach inherits the simplicity of worst-case robust optimization and does not require a detailed model for uncertainties.

The optimization was performed using the limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) method²⁴ included in the optimization software OPT++ (Ref. ²⁵) parallelized with beamlet domain decomposition. In order to reduce long computation time and demanding memory required for robust optimization, we implemented our method in parallelization via memory distribution on a multiprocessor system.

Quantifying plan robustness

It should be stressed that the nominal dose distributions (i.e., without the consideration of uncertainties) do not represent the dose distributions actually realized in the face of uncertainties. Therefore, when comparing plan qualities under the influence of uncertainties, it is necessary to incorporate the effect of uncertainties on the planned dose distribution. In theory, one can look at all possible uncertainty situations. However, it would require significant computation time and data processing effort to evaluate plans under all realizable perturbed doses from the uncertainties.

In order to simplify method of comparing the robustness of the PTV-based conventionally optimized plan and the CTV-based robustly optimized plan, we used a root-mean-square dose (RMSD) per voxel as a measure of robustness of dose in the voxel. This approach is different from the dose volume histograms (DVHs) derived from the worst-case dose distribution²⁰ and the DVH family bandwidth method¹⁸ and is independent of the method used for robust optimization. In order to account for the impact of the combined uncertainties, we calculated the RMSD of the 21 doses for each voxel, i.e., for each of nominal, minimum, and maximum proton range, the isocenter of the patient is at the nominal position and rigidly shifted in the A-P, S-I, and R-L directions, respectively, yielding 21 dose distributions (7 per proton range). We calculated RMSD-volume histograms [RVH, analogous to the error-bar volume histograms (EVHs) proposed by Albertini et al.¹¹]. Each pair of RVH plots of a given structure, one for PTV-based conventionally optimized and one for CTV-based robustly optimized plan, give relative assessment of a plan's robustness. The area under the RVH curve (AUC) gives a numerical index summarizing plan robustness similar to the way that equivalent uniform dose summarizes a DVH: the smaller AUC value indicates the better plan robustness.

We should emphasize that an important characteristic of the methods for robustness quantification used in this study do not need a detailed model for the considered uncertainties^{5, 6} and they serve the purpose of relative comparison between two treatment plans with different optimization techniques.

Evaluating target dose coverage, homogeneity, and normal tissue sparing

To evaluate or compare the optimality of IMPT plans created by PTV-based optimization or CTV-based robust optimization, we used the conventional method of DVH analysis. In this method, for each of nominal, minimum, and maximum proton range, the isocenter of the patient is at the nominal position and is rigidly shifted in the A-P, S-I, and R-L directions, respectively, yielding 21 dose distributions (7 per proton range). Two DVHs are generated for targets: one by choosing the minimum of the nine doses in each voxel in the targets and the other by choosing the maximum of those nine doses. The DVH corresponding to minimum voxel doses represents the worst-case scenario for target coverage. We used the lowest dose covering 95% of the volume in this DVH, i.e., D_95% to assess target coverage. Similarly, we used D_5% of the maximum dose DVH as a measure of the worst-case hot spot of the target. Thus, the worst-case target inhomogeneity is represented by D_5% − D_95%. The corresponding D_95% and D_5% minus D_95% doses in the nominal scenario (without any uncertainties considered) are also derived. Those values of each case are then normalized to the corresponding prescription doses (Table I of the supplementary material²⁷).

The DVHs for organs at risk (OARs) based on the worst-case dose distributions (by choosing the maximum of the 21 doses in each voxel outside the targets) and based on the nominal dose distribution were also generated. OAR sparing was evaluated in terms of: D_1cc (the highest dose that covered 1 cc of the structure volume) for spinal cord and brainstem, D_mean (the mean dose) to the oral cavity and parotids, and D_1% (the dose that covered 1% of the structure volume) for other organs. Those values of each case are then normalized to the corresponding prescription doses (Table I of the supplementary material²⁷).

Statistical analysis

The means of the AUCs, D_5% and D_95% of targets, and evaluation metrics of sparing of OARs of the 14 H&N cases from the robustly optimized plans and the PTV-based plans were calculated and compared statistically by the paired t-tests (or by the Wilcoxon test if outliers existed) using SPSS 19.0 software (International Business Machines, Armonk, New York). A derived value of p < 0.05 was considered statistically significant.

RESULTS

Comparison of plan robustness

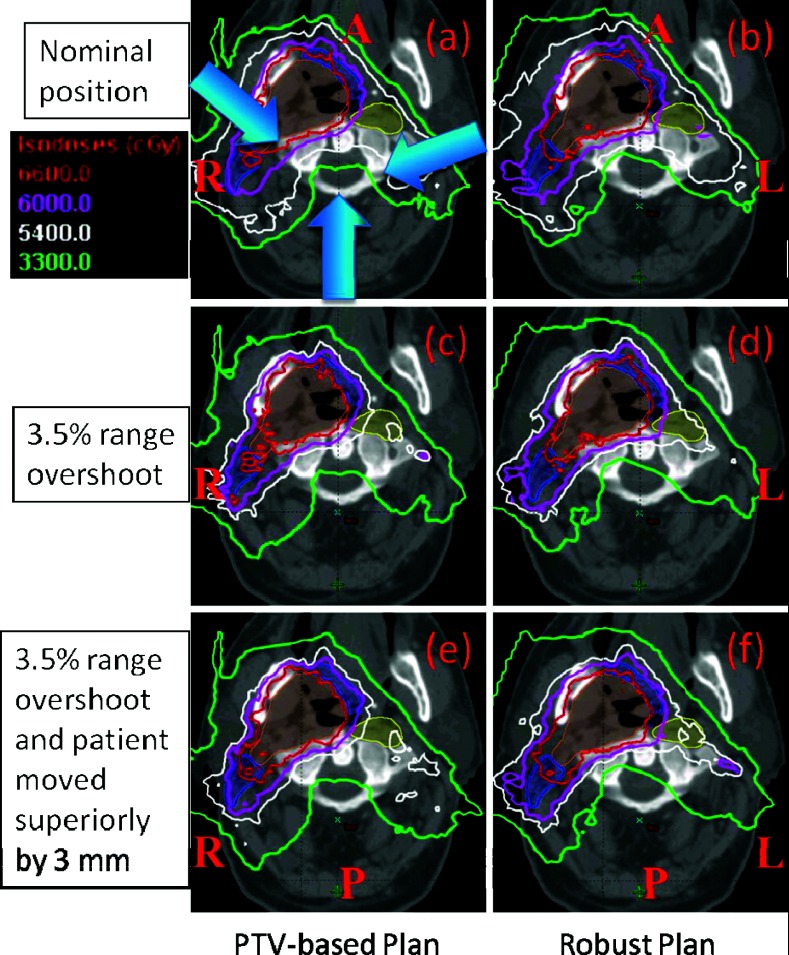
Plans for a representative H&N case generated with conventional PTV-based optimization and robust optimization (Fig. 1) illustrate the reduction in the impact of range and setup uncertainties on dose distribution in the robustly optimized plan.

Figure 1.

Dose distributions in the transverse plane for a representative patient illustrate the insensitivity of the robustly optimized plan (right panels) to range and set up uncertainties compared with the conventional PTV-based optimized plan (left panels). Top panels (a) and (b) show dose distributions in nominal position; whereas the middle panels (c) and (d) show corresponding data with 3.5% larger range and the bottom panels (e) and (f) are for 3.5% larger range and 3 mm superior shift. CTV1: left top big filled area; CTV2: two left small filled area abutting CTV1; CTV3: right small filled area disconnected from CTV1. Isodose lines in the PTV-based plan are perturbed to a significantly greater degree than in robustly optimized plan. For instance, CTV1 is not adequately covered with the prescribed dose of 66 Gy(RBE) in panel (c) and CTV3 is not covered with 54 Gy(RBE) in panels (c) and (e).

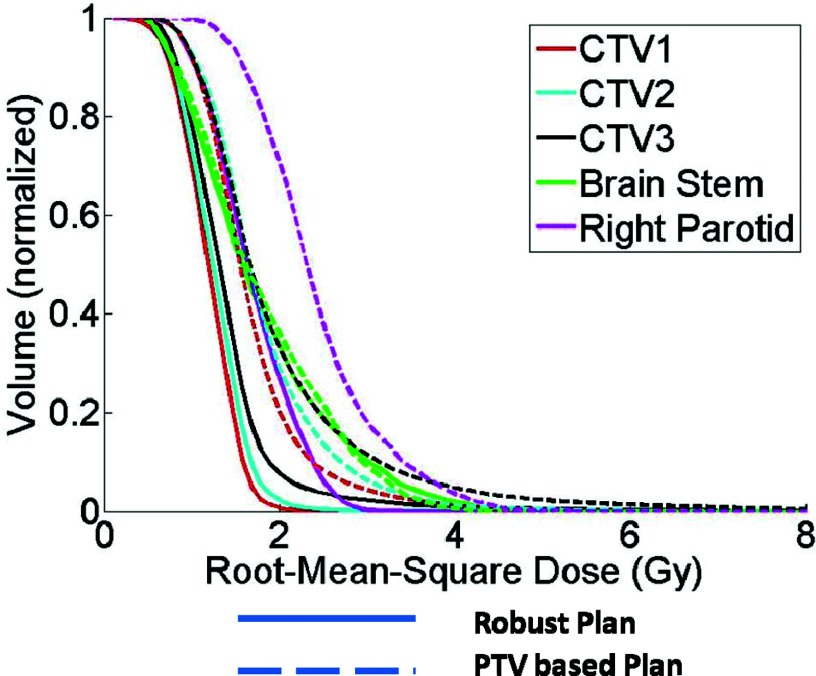
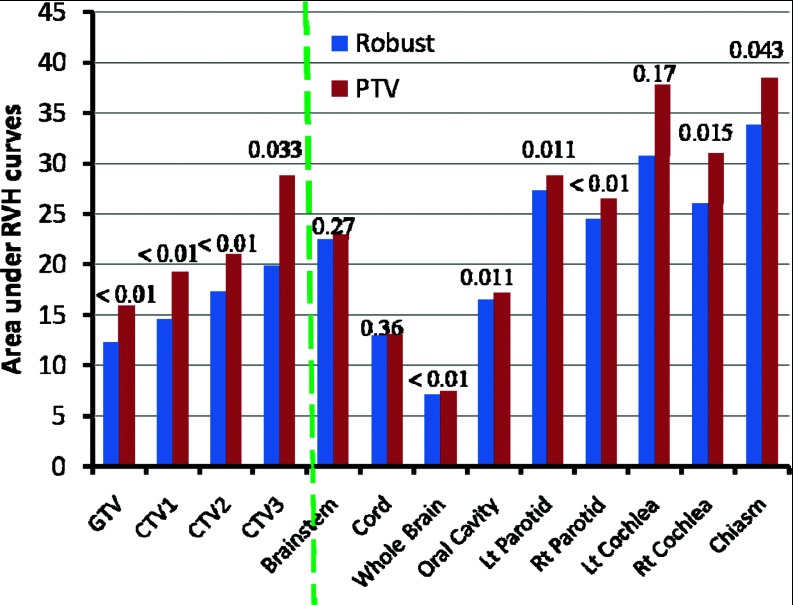
Comparison of plan robustness for the same H&N case using RVHs also illustrates improved robustness in the face of uncertainties for the robustly optimized plan (Fig. 2). In Fig. 2, the solid lines are for CTV1, CTV2, CTV3, Brain Stem, and Right Parotid, respectively from left to right. AUCs in the dose distribution for the targets and critical normal tissues in the robustly optimized plans (solid lines) are smaller than those in the PTV-based optimized plan [dashed lines; CTV1 (red) 10.8 vs 15.4; CTV2 (cyan) 11.4 vs 16.7; CTV3 (black) 12.8 vs 18.2; brainstem (green) 16.3 vs 16.5; right parotid (magenta) 15.5 vs 22.5]. The corresponding calculations of AUCs averaged over 14 cases (Fig. 3) is another indicator that robust optimization is less affected by uncertainties for both targets and organs than PTV-based optimization. (Numerical values are given in Table III in the supplementary material.²⁷) Differences for all endpoints except for the spinal cord are statistically significant.

Figure 2.

RVHs derived from a robustly optimized plan (solid lines) and from a PTV-based optimized plan (dashed lines) for patient 10. All curves are normalized to the total volume of the corresponding organs. Areas under the RVH curves of the robustly optimized plan are smaller than those of the PTV-based optimized plan. The solid lines are for CTV1, CTV2, CTV3, Brain Stem, and Right Parotid, respectively from left to right.

Figure 3.

Areas under the RVH curves for various structures (averaged over 14 H&N cancer cases) derived from the robustly optimized plans (left bar for each structure) and the PTV-based optimized plans (right bar for each structure) indicate the improved robustness of the robustly optimized plans. Data for targets (GTV; CTV) are to the left of the dashed line, and data for normal tissues are to the right. Numbers at the top of the columns are P values.

Comparison of plan target dose coverage, target dose homogeneity, and normal tissue sparing in both the worst-case scenario and the nominal scenario

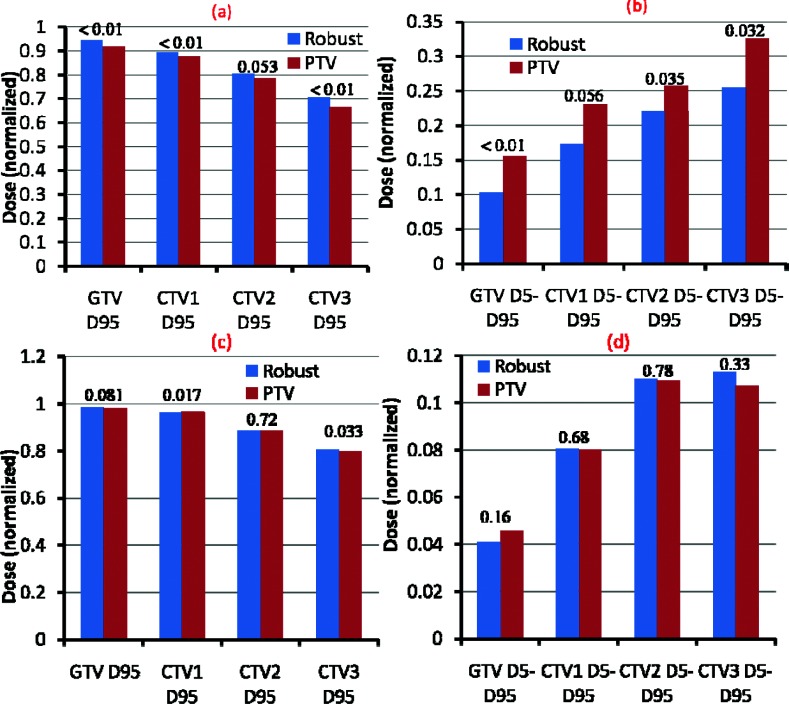
As seen in Figs. 4a, 4b, in the worst-case scenario robust optimization led to statistically significant improvement in dose coverage of the targets than did PTV-based plans (average over the 14 cases) [D₉₅ gross target volume, GTV 94.6% vs 91.9% (p < 0.01); CTV1 89.6% vs 87.6% (p < 0.01); CTV2 80.4% vs 78.7% (p = 0.053); CTV3 70.5% vs 66.5% (p < 0.01)] and more homogeneous dose distributions [D₅ − D₉₅ GTV 10.3% vs 15.5% (p < 0.01), CTV1 17.4% vs 23.0% (p = 0.056); CTV2 22.0% vs 25.8% (p = 0.035); CTV3 25.5% vs 32.5% (p = 0.032)]. In the nominal scenario (without any uncertainties considered), robust optimization led to similar target dose coverage and homogeneity as PTV-based optimization (average over the 14 cases) [D₉₅ GTV 98.5% vs 98.1% (p = 0.081); CTV1 96.1% vs 96.7% (p = 0.017); CTV2 88.5% vs 88.6% (p = 0.72); CTV3 80.5% vs 79.9% (p = 0.033); D₅ − D₉₅ GTV 4.1% vs 4.6% (p = 0.16); CTV1 8.1% vs 8.0% (p = 0.683); CTV2 11.0% vs 10.9% (p = 0.78); CTV3 11.3% vs 10.7% (p = 0.33)] [Figs. 4c, 4d].

Figure 4.

(a) and (b) D_95% doses and D_5% averaged over 14 H&N cases illustrate the improved target coverage and superior dose homogeneity of the robust optimization process (left bar for each structure) to the PTV-based optimization (right bar for each structure) in the worst-case scenario. (c) and (d) D_95% doses and D_5% averaged over 14 H&N cases illustrate the comparable target coverage and similar dose homogeneity of the robust optimization process (left bar for each structure) to the PTV-based optimization (right bar for each structure) in the nominal scenario. Numbers at the top of the columns are P values. The values of each case are normalized to the corresponding prescription doses before averaging [see Table I of the supplementary material (Ref. ²⁷)].

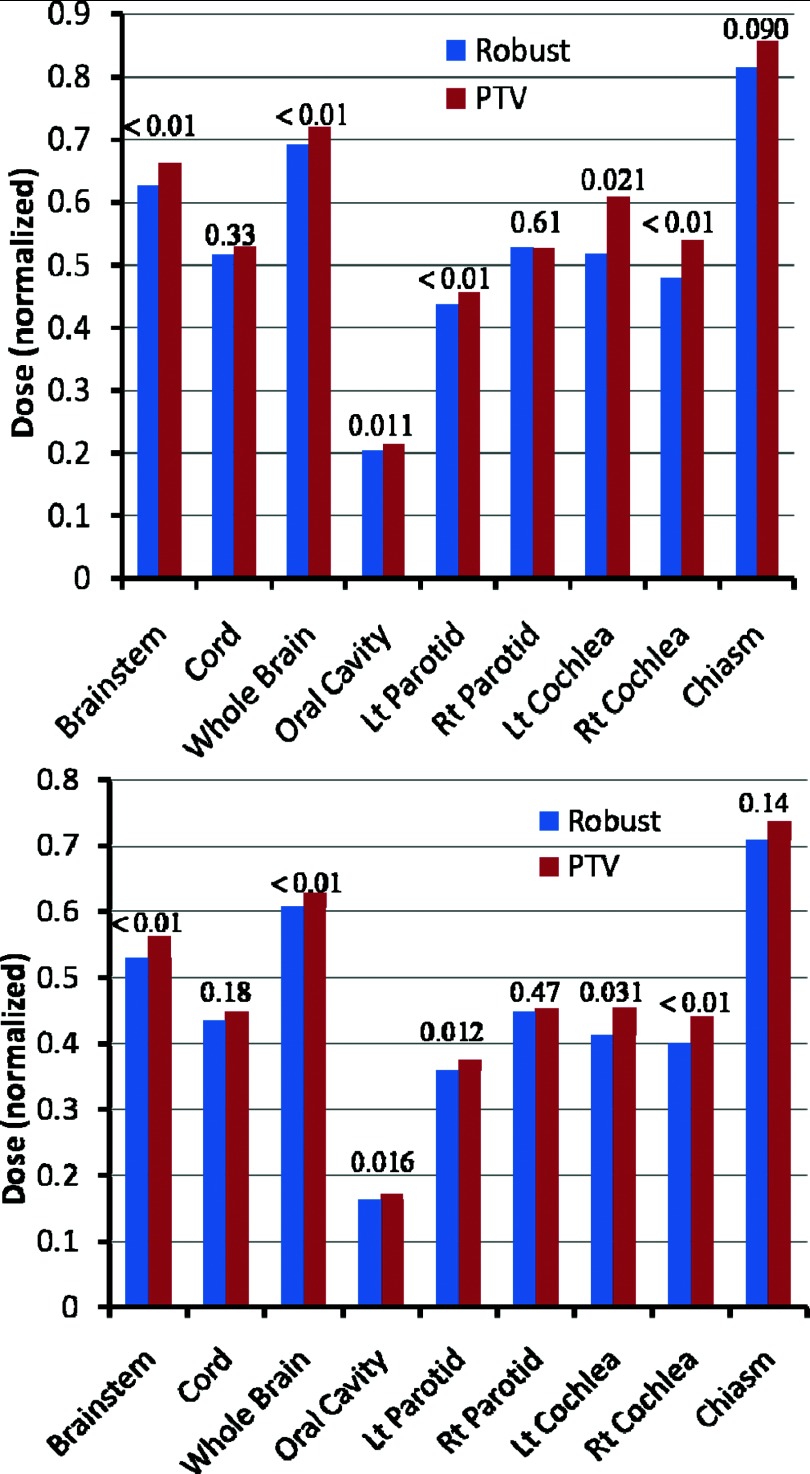
Finally, the robustly optimized plans also reduced the dose to the OARs compared with the PTV-based conventional plans in the worst-case scenario [Fig. 5 (top) and Table IV of the supplementary material²⁷] and in the nominal scenario [Fig. 5 (bottom) and Table V of the supplementary material²⁷], with differences in most endpoints being statistically significant (averaged over the 14 cases).

Figure 5.

Sparing of OARs in the worst-case scenario (top) and in the nominal scenario (bottom) in the robustly optimized plans (left bar for each structure) and the PTV-based plans (right bar for each structure), averaged over 14 H&N cases. Doses shown are D_1cm3 to the spinal cord and brainstem, D_mean to the oral cavity and parotids, and D_1% for other organs. Numbers at the top of the columns are P values. Data indicate improved sparing with robust optimization. The values of each case are normalized to the corresponding prescription doses before averaging [see Table I of the supplementary material (Ref. ²⁷)].

DISCUSSION

Proton therapy in general and IMPT in particular, is highly sensitive to treatment uncertainties. Our results in this paper show that, for the H&N cases studied, robust optimization leads to significantly more robust dose distribution for both targets and OARs than do PTV-based optimization methods while maintaining and possibly even improving the sparing of healthy tissues. Our findings agree with others’ published results.^{14, 15, 19}

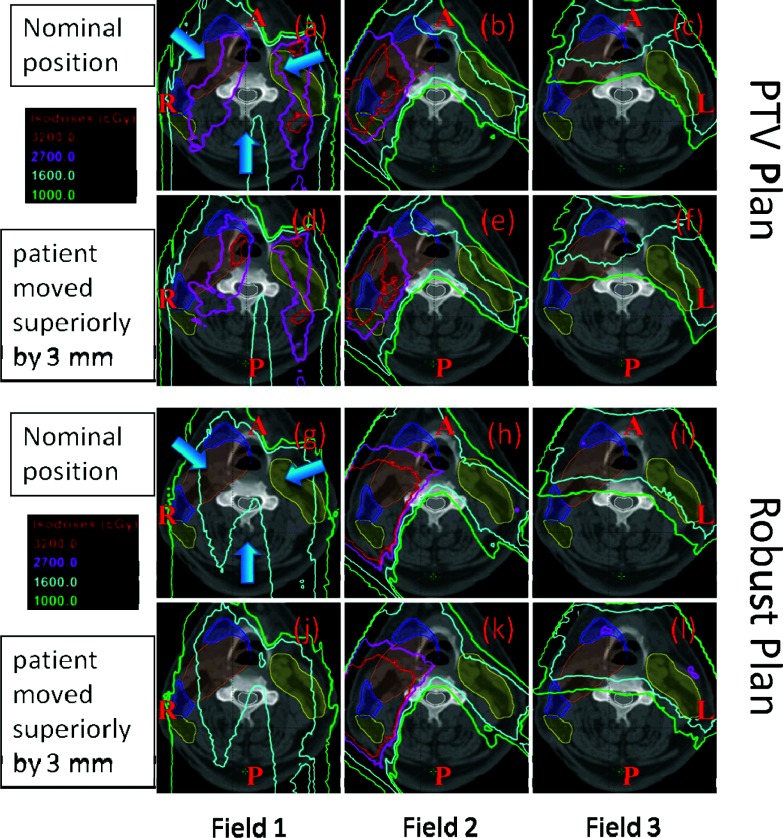
For H&N patients, the proximity of critical normal structures and the high doses necessary to achieve disease control make the safe delivery of radiotherapy challenging. High doses of radiation therapy may injure, sometimes irreversibly, critical normal tissues such as brainstem, spinal cord, oral cavity, optical chiasm, salivary glands, cochleas, etc., within and surrounding the target volume, which may lead to both acute and late side-effects such as loss of auditory, olfactory, gustatory, and visual senses. While IMPT using conventional PTV-based approach may produce dose distributions that may appear to be optimal, what is seen on treatment plans may be quite different from what the patient actually receives. The resulting deviations from expected dose distributions may lead to unexpected local failures and toxicities. Due to intricate heterogeneities involving complex bony structures and air cavities, small displacements in the position may significantly perturb proton dose distributions as illustrated in panels (d)–(f) of Fig. 6. Field 1 appears to be most sensitive to perturbation presumably because it passes through most complex inhomogeneities. Robust optimization automatically reduces the contribution from this field. Furthermore, robust optimization considerably reduces high dose gradients within each of the three fields (see discussion below). We have shown that dose distributions produced by robust optimization represent more closely what is actually delivered in the face of uncertainties as shown in panels (j)–(l) of Fig. 6.

Figure 6.

Dose distributions per field in the transverse plane for a representative patient illustrate the relative insensitivity of the robustly optimized plan (g)–(l) to setup uncertainties compared with the conventional PTV-based optimized plan (a)–(f). Panels (a)–(c) and (g)–(i) show dose distributions in nominal position; whereas the panels (d)–(f) and (j)–(l) show corresponding data with 3 mm superior shift. CTV1: left top big filled area; CTV2: two left small filled area abutting CTV1; CTV3: right filled area disconnected from CTV1. The shift perturbs the dose distribution in the PTV-based plan significantly [e.g., 32 and 27 Gy(RBE) isodose lines]. Field 1 appears to be most sensitive to perturbation presumably because it passes through most complex inhomogeneities. Robust optimization automatically reduces the contribution from this field. Furthermore, robust optimization considerably reduces high dose gradients within each of the three fields.

It is well established that, for protons, assignments of margins for setup uncertainties alone is insufficient because of the additional uncertainty associated with range of protons for each beam and due to the significant perturbation of dose distributions within the structures. In order to fairly evaluate plan qualities of two different plans (e.g., CTV-based robustly optimized IMPT vs PTV-based conventionally optimized IMPT), the effect of uncertainties on dose distributions must be addressed. This point has been articulated for almost three decades;²⁶ but not instituted in routine practice due to high computational costs. For comparing photon plans among themselves, this is not a significant issue, especially if competing plans all have appropriate PTV margins. However, because the concept of conventionally defined PTV is not sufficient for the evaluation of target dose distribution for protons due to beam-specific range uncertainty, a different method of plan evaluation is necessary for comparing one proton plan with another or for comparing a proton plan with a photon plan.

In our previous work, we had used the worst-case dose distributions to compare competing plans. An assertion about that approach one can make is that, since worst-case method is also used for robust optimization, comparing PTV-based plans vs robustly optimized plans using the same underlying methodology would create a bias in favor of the latter. In this paper, we have used this RVH method as an independent way to numerically (via the area under the RVH curves) assess the plan robustness and whether the plan robustness is improved. While the proposed RVH method eliminates bias from the worst-case DVH method and provides a simple metric to cross-compare the robustness of proton plans, it is limited to relative comparison because it does not provide statistically meaningful quantification (e.g., mean or standard deviation). The worst-case based robust optimization method assumes that interfractional variations are of rigid body type; it does not consider deformations and changes in positions of anatomic structures relative to each other. It further assumes that each uncertainty can be considered independently of others. In reality, multiple uncertainties can occur simultaneously but they cannot be negative and positive at the same time as is implicit in the worst-case approach. In theory, one can look at all possible perturbed situations with significant computation time. The current approach is more practical. In our robustness evaluation method, we used 21 dose distributions (seven geometrical positions times three proton ranges), rather than nine to evaluate plan robustness in the face of combined uncertainties.

An important characteristic of robust optimization is that it produces more homogeneous target dose distribution in the worst-case scenarios while showing similar target homogeneity under nominal scenario. The superior homogeneity is highly valuable feature for the treatment of H&N cancers.¹ Improved target dose homogeneity may minimize the toxicity of tissues within the target volume (e.g., base of tongue) which may compromise organ function such as swallowing. Improvement in homogeneity with robust optimization is due to the fact that, if the incorporation of uncertainties reveals hot or cold spots within the target volume, the objective function value (i.e., the plan score) is penalized. Additionally, the improved sparing of the parotid glands, for instance, might avoid severe xerostomia, which could improve patients’ quality of life.¹

In general, the improvement in robustness is thought to be at the expense of normal tissue sparing.^{6, 7, 8, 18} We believe this has been the result of comparing results of CTV-based robust optimization with CTV-based conventional optimization, i.e., without the incorporation of uncertainties in their CTV-based conventional optimization via a PTV margin. Because robustly optimized treatment planning strategy allows us to plan by delivering the prescribed dose directly to CTV rather than PTV, it can potentially reduce doses to normal tissues even under the nominal scenario compared to the PTV-based conventional treatment planning strategy that irradiates the entire PTV. In other words, robust optimization technique is much more efficient in terms of sparing doses to normal tissues while providing better plan robustness than the PTV-based conventional optimization technique.

Two possible mechanisms were reported to improve plan robustness by robust optimization: (1) a localized single-field uniform dose distribution (LSFUD) mechanism,¹⁶ which usually happens within the targets to render per beam dose distribution more homogeneous (Fig. 6); and (2) perturbed dose distribution, which follows the change in anatomical geometry (Fig. 9 of Liu et al.¹⁶). This mechanism usually takes place at the edge of targets and intends to ensure the target coverage despite the presence of the uncertainties. The optimizer can find a desired beamlet weight solution from the degenerate solution space so that the dose distribution follows the changes in anatomical geometry and is minimally perturbed by uncertainties.^{16, 17} Either or both mechanisms are found in the H&N cases studied. Thus, robust optimization resulted in patient-specific, optimizer-determined, and effectively reduced margins compared with a predefined and fixed margin used in the PTV approach based on a patient population model.^{16, 17}

In addition, there are also some advantages of robust optimization in the context of beam delivery over the PTV based optimization. First of all, fewer spots might be needed from robust optimization since either some spots in the PTV margin volume are shut off or their magnitudes are reduced. Additionally, the robust optimization can potentially improve the patient specific quality and assurance (QA) outcome. Currently, in our clinics, both depth dose and 2D planar dose are measured and verified against treatment planning system calculated dose. These measurements are highly sensitive to dose gradient. Because robust optimization tends to penalize highly heterogeneous per field dose delivery, it can increase accuracy of our QA measurement.

CONCLUSIONS

In conclusion, based on the findings of this study, we believe that implementing robust optimization into an IMPT planning for use in clinical practice would significantly improve the quality of IMPT for treating H&N cancers. This effort is currently underway at MD Anderson.

There is still considerable amount of additional work to be done for continued improvement and assessment of robust optimization and robustness evaluation methods. Validity of alternative approaches needs to be evaluated. Nonrigid variations in anatomy and intrafractional motion need to be accounted for. It would also be instructive to use tumor control probability, normal tissue complication probability, and equivalent uniform dose models to evaluate the potential clinical benefits of robust optimization. Recently, we are in the process of implementing robust optimization clinically.