Dosimetric impact of Acuros XB deterministic radiation transport algorithm for heterogeneous dose calculation in lung cancer

Abstract

Purpose: The novel deterministic radiation transport algorithm, Acuros XB (AXB), has shown great potential for accurate heterogeneous dose calculation. However, the clinical impact between AXB and other currently used algorithms still needs to be elucidated for translation between these algorithms. The purpose of this study was to investigate the impact of AXB for heterogeneous dose calculation in lung cancer for intensity-modulated radiation therapy (IMRT) and volumetric-modulated arc therapy (VMAT).

Methods: The thorax phantom from the Radiological Physics Center (RPC) was used for this study. IMRT and VMAT plans were created for the phantom in the Eclipse 11.0 treatment planning system. Each plan was delivered to the phantom three times using a Varian Clinac iX linear accelerator to ensure reproducibility. Thermoluminescent dosimeters (TLDs) and Gafchromic EBT2 film were placed inside the phantom to measure delivered doses. The measurements were compared with dose calculations from AXB 11.0.21 and the anisotropic analytical algorithm (AAA) 11.0.21. Two dose reporting modes of AXB, dose-to-medium in medium (D_m,m) and dose-to-water in medium (D_w,m), were studied. Point doses, dose profiles, and gamma analysis were used to quantify the agreement between measurements and calculations from both AXB and AAA. The computation times for AAA and AXB were also evaluated.

Results: For the RPC lung phantom, AAA and AXB dose predictions were found in good agreement to TLD and film measurements for both IMRT and VMAT plans. TLD dose predictions were within 0.4%–4.4% to AXB doses (both D_m,m and D_w,m); and within 2.5%–6.4% to AAA doses, respectively. For the film comparisons, the gamma indexes (±3%/3 mm criteria) were 94%, 97%, and 98% for AAA, AXB_D_m,m, and AXB_D_w,m, respectively. The differences between AXB and AAA in dose–volume histogram mean doses were within 2% in the planning target volume, lung, heart, and within 5% in the spinal cord. However, differences up to 8% between AXB and AAA were found at lung/soft tissue interface regions for individual IMRT fields. AAA was found to be 5–6 times faster than AXB for IMRT, while AXB was 4–5 times faster than AAA for VMAT plan.

Conclusions: AXB is satisfactorily accurate for the dose calculation in lung cancer for both IMRT and VMAT plans. The differences between AXB and AAA are generally small except in heterogeneous interface regions. AXB D_w,m and D_m,m calculations are similar inside the soft tissue and lung regions. AXB can benefit lung VMAT plans by both improving accuracy and reducing computation time.

INTRODUCTION

Monte Carlo (MC) methods have been widely considered the gold standard for accurate dose calculation in radiation therapy because they stochastically solve the radiation transport problem^{1, 2} instead of correcting for tissue heterogeneities by measurements (correction-based methods) or modeling scatter kernels (convolution methods). However, the developments of intensity-modulated radiation therapy (IMRT), volumetric-modulated arc therapy (VMAT), and stereotactic body radiation therapy (SBRT) have tremendously increased the complexity of modern radiation therapy and made it a challenge for MC to decrease its computation time to the stage that can be routinely used in clinical settings.

A novel deterministic radiation transport algorithm, Acuros XB (AXB), has recently been developed and implemented in the Eclipse treatment planning system (TPS) (Varian Medical Systems, Palo Alto, CA).^{3, 4, 5} Unlike MC algorithms, which simulate individual or small groups of interacting particles within patients, AXB deterministically discretizes the energy, angle, and space variables of the linear Boltzmann transport equation (LBTE) into grids and iteratively solves the LBTE in discrete, multidimensional space. This deterministic algorithm is a version of grid-based Boltzmann solver (GBBS), or discrete ordinates method. Ideally, if a MC algorithm simulates an infinite number of particles and a GBBS discretizes the LBTE variables into infinitely small grids, then the two methods should converge to the real solution; thus they should have the same dose calculation accuracy.⁶ Initially, Gifford et al. investigated a general-purpose GBBS, Attila (Los Alamos National Laboratory, Los Alamos, NM and Transpire Inc., Gig Harbor, WA), for brachytherapy and external photon beam dose calculations.⁷ Since then, we have validated several versions of the GBBS, including AXB,^{8, 9} and it has been well documented that AXB and MC dose calculations are very similar in accuracy.^{9, 10}

Owing to the complex heterogeneities and organ structures in lung cancer, accurate dose calculations are essential for minimizing the toxicity of normal tissue in IMRT and VMAT plans. Currently most clinical TPSs use convolution-based methods, such as anisotropic analytical algorithm (AAA) and the collapsed-cone convolution (CCC), for patient treatment planning. With the AXB algorithm moving forward to clinical implementation and application, this new dose algorithm needs to be compared with current convolution-based algorithms to realize the differences under well-controlled conditions. Based on our previous study in a simple slab phantom, the dose differences between AXB radiation transport algorithm and AAA in the lung region may be as great as 15% in a single open field, which might raise clinical concerns.³ However, according to several other IMRT and VMAT studies, the differences of doses calculated using AXB and AAA were relatively very small [within 3% in lung planning target volumes (PTVs)].¹¹ A fundamental experimental study is necessary to elucidate the dosimetric impact of AXB in lung cancer treatment planning, and thus this study was initiated.

Furthermore, the differences between two dose reporting modes of AXB, dose-to-medium in medium (D_m,m), and dose-to-water in medium (D_w,m), have not been investigated for lung cancer. In a clinical setting, only one report mode is usually reported. The comparison between measurement data to D_m,m and D_w,m in this study can give some useful insight into this issue.

To more closely simulate a real clinical situation using a standardized geometry, we used the thorax phantom from the Radiological Physics Center (RPC) at The University of Texas MD Anderson Cancer Center and followed the RPC irradiation procedure to conduct the experiments.¹² The RPC thorax phantom was designed for credentialing institutions participating in NCI funded lung clinical trials involving IMRT, VMAT, and SBRT and has been used in evaluating the quality of heterogeneity management by various dose algorithms.^{13, 14} An additional benefit of using the RPC phantom for this study is that we were able to test the hypothesis that a better dose algorithm might also improve the credentialing test passing rate by reducing uncertainties in the dose estimates.

MATERIALS AND METHODS

RPC thorax phantom, TLD, and film

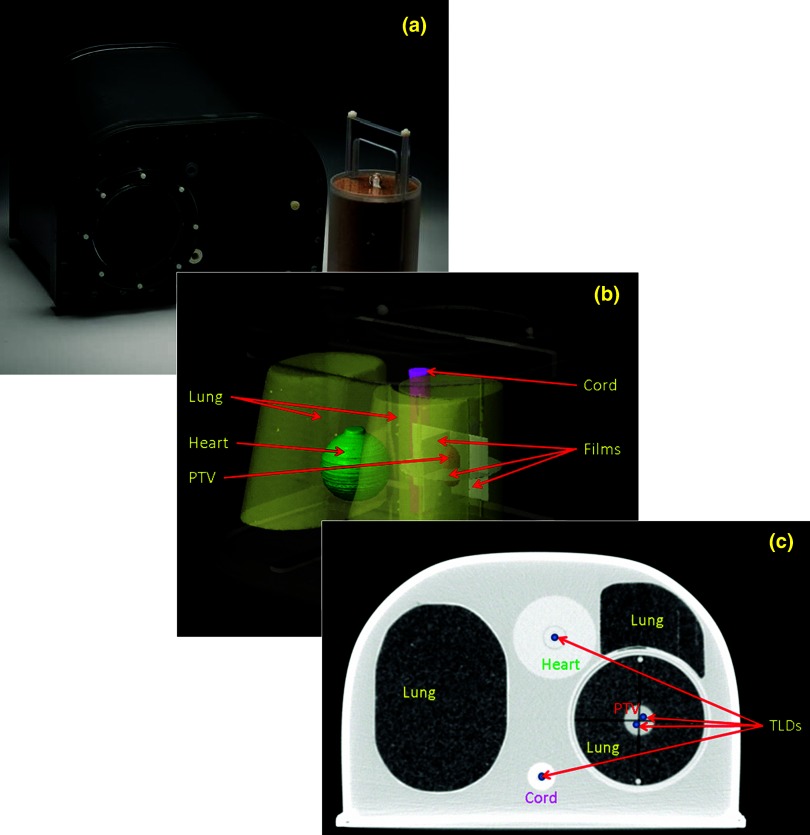
The RPC thorax phantom consists of a chest-shaped outer plastic shell and inserts that simulate lung, heart, and spinal cord tissue, as shown in Fig. 1a. The shell can be filled with water to simulate soft tissue. The lung tissue-equivalent insert can be opened and separated into halves for dosimeter insertion [Fig. 1b]. In our analysis, we included a simulated centrally located NSCL tumor to serve as the PTV in the middle of the dosimeter space/lung insert. In this study, both thermoluminescent dosimeters (TLDs) and film were also incorporated into the lung insert. Four cavities accommodated TLD capsules to measure absolute point doses: two TLDs in the PTV placed inferiorly and superiorly to PTV isocenter and two TLDs in organs at risk, that is, one in the heart and one in the spinal cord [Fig. 1c]. Three slots accommodated radiochromic film (EBT2; Gafchromic, International Specialty Products, Wayne, NJ) to measure the planar dose distributions in the axial, coronal, and sagittal planes. One piece of film was placed at the central axial plane of the lung insert, and two pieces of film were inserted inside the blocks perpendicular to the other film, in the coronal and sagittal planes [Fig. 1b].

Figure 1.

Photograph of the RPC phantom (a), screen capture from the Eclipse TPS depicting the RPC thorax phantom, structure contours (heart, lungs, spinal cord, PTV, and film inserts) (b), and one CT slice depicting the locations of the TLDs (c).

IMRT and VMAT planning

The thorax phantom was simulated with the use of a Brilliance 64-slice computed tomography (CT) scanner (Philips Healthcare, Andover, MA). The slice thickness was set to 1.5 mm to improve TLD visualization. The reconstructed digital imaging and communications in medicine (DICOM) CT data were imported to the Eclipse 11.0 TPS for contouring and both IMRT and VMAT planning. (The Eclipse TPS designates VMAT as “RapidArc,” but we use the more general term VMAT throughout this paper.) The PTV, heart, lungs, spinal cord, and TLDs were manually contoured. All TLD contours were set to high-resolution structures to optimize delineation accuracy.

The prescriptions and optimization objectives used for the IMRT and VMAT treatment plans were based on the RPC phantom irradiation specifications. The planning objectives were that (1) at least 95% of the PTV receive its prescribed dose (D95% ≥ 6.0 Gy), (2) 99% of the PTV receive at least 5.4 Gy (D99% ≥ 5.4 Gy), (3) the OAR receive no more than 4.0 Gy, and (4) hot spots be minimized. The treatment couch, defined using the exact couch with flat-panel structure and the rails in the “out” position as implemented in the Eclipse TPS, was included and set at 0° for treatment planning.

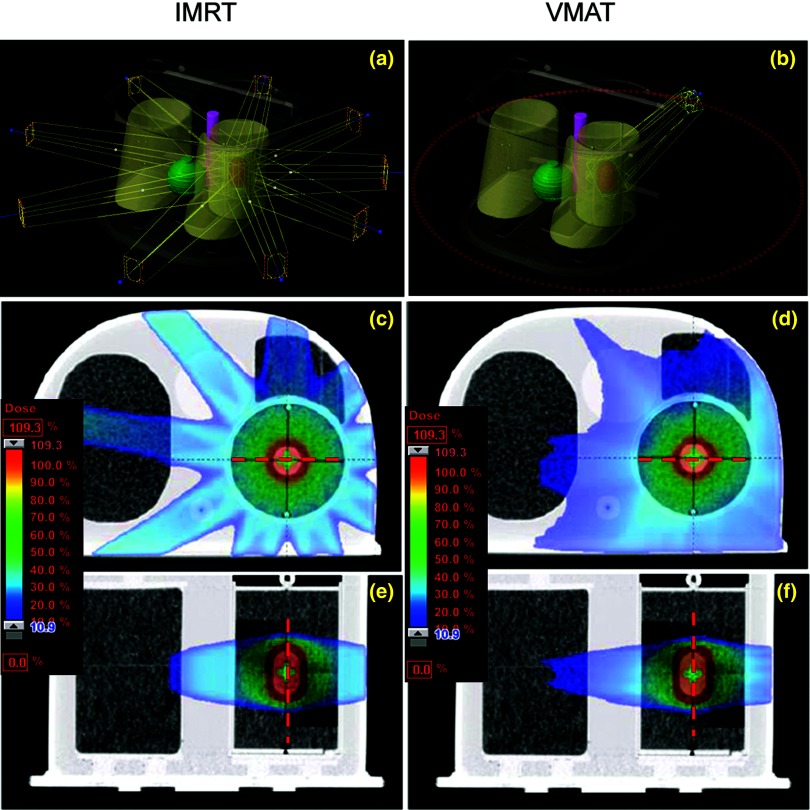
The IMRT plan used nine coplanar, equally spaced 6-MV beams with 0° collimator rotation (beam angles were 200°, 240°, 280°, 320°, 0°, 40°, 80°, 120°, and 160°. The IMRT plan geometry is shown in Fig. 2a. The VMAT plan had two 6-MV arcs and a collimator offset of ±15° (345° and 15°) [Fig. 2d]. Both plans were initially optimized until the planning criteria set by the RPC were met. More optimization attempts were made to improve the homogeneity and conformity of the dose distributions. During the optimization, a fast superposition convolution algorithm (multiresolution dose calculation) was used by the Eclipse TPS to evaluate the volume dose. The final IMRT had 81–95 segments for each field, and the VMAT plans had 178 static control points for each arc. We then calculated the final doses of IMRT and VMAT using the more accurate AAA and AXB algorithms.

Figure 2.

IMRT (left) and VMAT (right) plan geometries (a) and (d) and dose distributions in [the axial (b) and (e) and sagittal (c) and (f)] planes that contain films. The red dashed lines (lateral and inferior–superior) are the position of dose profiles in Fig. 3.

The planned IMRT and VMAT treatments were delivered to the RPC thorax phantom using a Clinac iX linear accelerator (Varian Medical Systems) and the Mosaiq record and verify system (IMPAC Medical Systems, Sunnyvale, CA). Treatment delivery and measurement were repeated three times for both the IMRT and the VMAT plans to ensure reproducibility.

AXB and AAA algorithms

The AXB and AAA dose algorithms (version 11.0.21) were commissioned in Eclipse 11.0 TPS with Varian Golden Beam data and measured data for small fields, for which we have previously validated the fundamental validation in a water phantom.³ The detailed mathematical formulas and implementations, including beam modeling, material assignments, and calculation options, for AXB were described in our previous publications.^{3, 15} Comparing with previous validated version 10.0.24 and 11.0.3, this recent version was built upon new Eclipse 11.0 TPS and has some changes in the material assignments and calculation settings to optimize the accuracy and speed.

Like MC algorithms, which directly solve radiation transport in patients, the default dose reporting mode of AXB is dose-to-medium in medium (D_m,m). AXB also can report dose-to-water in medium (D_w,m) in the Eclipse TPS, since dose-to-water is the traditional measure used in treatment planning. These modes differ only in the postprocessing step, in which the energy-dependent fluence calculated by AXB's transport is multiplied by different flux-to-dose response functions to obtain the local absorbed dose value, similar to the stopping power ratio method used in MC algorithms. For AAA, dose is reported in only one way; although the AAA dose is sometimes referred to as “dose-to-water” since it is based on electron density-scaled water, previous studies have indicated that AAA dose values are closer to D_m,m than D_w,m.^{3, 16} To avoid confusion, we refer to the dose from AAA simply as the AAA dose without classifying it as dose-to-medium or dose-to-water.

Data analysis

TLD

After irradiation, the TLD sample was returned to the RPC for dose read-out and analysis. TLD readout and dose calculations were performed according to the RPC procedure for calculating TLD doses.¹⁷ It should be noted that during each TLD reading session, four control TLDs were included (two controls were read at the beginning and two at the end of the session) in order to minimize random and systematic uncertainties. This assures that each session was consistent from the start to the end and thus can account for any changes in the reader sensitivity during the session. The TLD-measured doses were used to compare with the mean computed dose values inside the TLD contours from the TPS. Kirby et al. has reported on the overall RPC TLD uncertainty indicating 5.8% TLD dose calculation uncertainty at the 95% confidence level.¹⁸

Film

Film irradiation and handling were performed following AAPM TG-55 guidelines and RPC procedure.^{19, 20} The irradiated films were digitized at a 0.4-mm resolution with a CCD100 Microdensitometer (Photoelectron Corporation, North Billerica, MA). Dose–response curves were calibrated following the RPC protocol. For each batch of film, specific dose–response curve were obtained with third order polynomial functions with R² = 0.997.

The film-measured dose was normalized to the corresponding TLD-measured dose in the PTV for absolute dose comparison following the RPC procedure. The films were compared with the treatment plan dose distributions from Eclipse TPS. Considering the uncertainty of the film’ positions for registration relative to their locations on CT images, we visually determined whether a net shift (<1.5 mm) was required. Also, to reduce noise in the film measurements, we smoothed the films’ optical density values using a moving average smoothing function with 9 × 9 data points. The expected overall EBT2 film uncertainty is 4.5% at the 95% confidence level.²¹

Gamma analysis

Gamma analysis was used to quantify the differences between measured and calculated dose distributions²² using criteria of a 3-mm distance-to-agreement (DTA) and a 3% relative dose difference (±3%/3 mm) (Task Group 119 IMRT commissioning standard²³). To study the effects of different criteria on the passing rate, we increased the stringency of the criteria to ±2%/2 mm and ±2%/3 mm and decreased the stringency to ±4%/2 mm, ±4%/3 mm, and ±5%/3 mm. For all the gamma analysis criteria, a passing rate of 90% of the meeting the criteria was defined as acceptable. During the film comparison, we generated a mask to exclude the pixels with large uncertainties, that is, (1) those below a threshold of 20% of the maximum calculated dose because those low dose regions will decrease the total gamma passing rate; or (2) those within 3 mm from the edge of a film because those dose values are less important and might be largely distorted by smooth filter.

Direct comparison between AAA and AXB

To investigate the impact of the dosimetric differences between AAA and AXB, we compared the dose–volume histogram (DVH) plots and parameters for the AAA and AXB plans.

To differentiate the contributions from different fields in the IMRT plan, we also compared the dose profiles of plans for the individual fields in the IMRT plan. The total IMRT dose was assumed to be the sum of the doses from each single field.

Computation time

The computation times for IMRT and VMAT plans using these two algorithms were compared. Both AAA and AXB were calculated in the Eclipse TPS, which was installed on a standard clinical workstation (Dell T5500) with dual 2.27-GHz quad-core Intel processors (E5520), 24-GB RAM, and a 64-bit Windows 7 operating system.

RESULTS

TLDs

Dose estimates for the TLD-measured and the TPS-calculated point doses from AAA and AXB in both dose reporting modes (AXB_D_w,m and AXB_D_m,m) are shown in Table 1. The percent coefficient of variation (%CV) of three repeated irradiations at the eight TLD capsule locations were less than 2% for all locations; with the exception of the TLD in the heart with %CV of 2.6% for the VMAT plan. The calculated dose values within the PTV from AAA and AXB were all within 5% of the measured TLD dose values. The agreements between the measured and calculated doses in the heart and spinal cord were within 6.0%, 4.4%, 4.4%, for AAA, AXB_D_w,m, and AXB_D_m,m, respectively. The differences in the measured and calculated doses did not appreciably differ between the IMRT and VMAT plans. We also found that the differences between the calculated dose values from AXB_D_m,m and AXB_D_w,m were relatively small (within 0.2%) even in the lung region.

Table 1.

Comparison of TLD measurements and the dose calculations from AAA and AXB (D_w,m and D_m,m).

TLD position	Measurement (cGy)	AAA (cGy)	AXB_Dm,m (cGy)	AXB_Dw,m (cGy)	AAA (Δ%)1	AXB_Dm,m (Δ%)1	AXB_Dw,m (Δ%)1
IMRT plan
PTV_inferior	643	669	658	650	−4	−2.4	−1.1
	(1.9)1	(0.2)2	(0.2)2	(0.1)2
PTV_superior	642	669	657	651	−4.2	−2.4	−1.4
	(1.6)1	(0.2)2	(0.3)2	(0.2)2
Heart	175	167	168	168	4.3	4.2	4
	(0.0)1	(3.6)2	(3.9)2	(4.0)2
Spinal cord	136	140	137	137	−2.5	−0.4	−0.4
	(0.2)1	(0.9)2	(0.7)2	(0.9)2
VMAT plan
PTV_inferior	598	622	611	599	−4	−2.2	−0.2
	(1.5)1	(0.9)2	(0.9)2	(0.9)2
PTV_superior	604	619	609	598	−2.5	−0.8	1
	(1.2)1	(1.4)2	(1.2)2	(1.3)2
Heart	88	93	90	88	−5.6	−2.7	−0.8
	(2.6)1	(6.1)2	(6.6)2	(6.7)2
Spinal cord	99	105	103	103	−6.4	−4.4	−4.4
	(1.3)1	(3.0)2	(2.7)2	(2.7)2

Note: Δ% = 100 × (D_TLD − D_XXX)/D_TLD.

¹Percent coefficient of variation (%CV) of measured dose values from repeated measurements (n = 3).

²Percent coefficient of variation (%CV) of calculated dose values inside the TLD contours due to the dose gradient inside each ROI.

Film profiles

The dose profile comparisons between film measurements and calculations are shown for the first delivery of the IMRT [Figs. 3a, 3b] and VMAT [Figs. 3c, 3d] plans; similar results were observed for the second and third irradiations. The DTAs of the measured penumbrae were all within 1.5 mm (passing the RPC criterion of a 4-mm DTA agreeing well with the calculated dose profiles. In general, the profiles calculated using AXB agreed well with those from the films.

Figure 3.

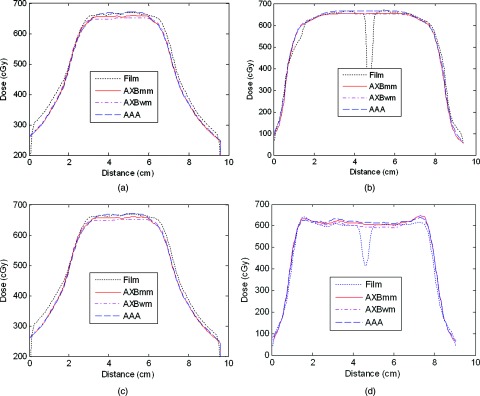
Dose profiles for AAA and AXB calculations and film measurements in the IMRT (a) and (b) and VMAT (c) and (d) plans. The profiles are for the lateral and inferior–superior lines marked in Fig. 2. The dips in the middle of film inferior–superior profiles are because the gaps of sagittal film (see Fig. 4).

Gamma analysis

The distributions of the gamma analyses with ±3%/3 mm criteria for the first delivery of the VMAT and IMRT plans are shown in Figs. 45, respectively; similar results were observed for the second and third irradiations. The differences between film measurements and AAA calculations were slightly larger than the differences between film measurements and AXB calculations. The differences between AXB_D_m,m and AXB_D_w,m were relatively small for both IMRT and VMAT, even in the lung region. The percentages of pixels that passed met the gamma criteria of ±3%/3 mm are provided in Table 2. For the IMRT plan, the AAA and AXB had similar gamma passing rate with ±3%/3 mm criteria (98% for AAA and 99% for AXB both in D_m,m and D_w,m). For VMAT, the AAA had a slightly lower passing rate (90%, 95%, and 97% for AAA, AXB_D_m,m, and AXB_D_w,m, respectively).

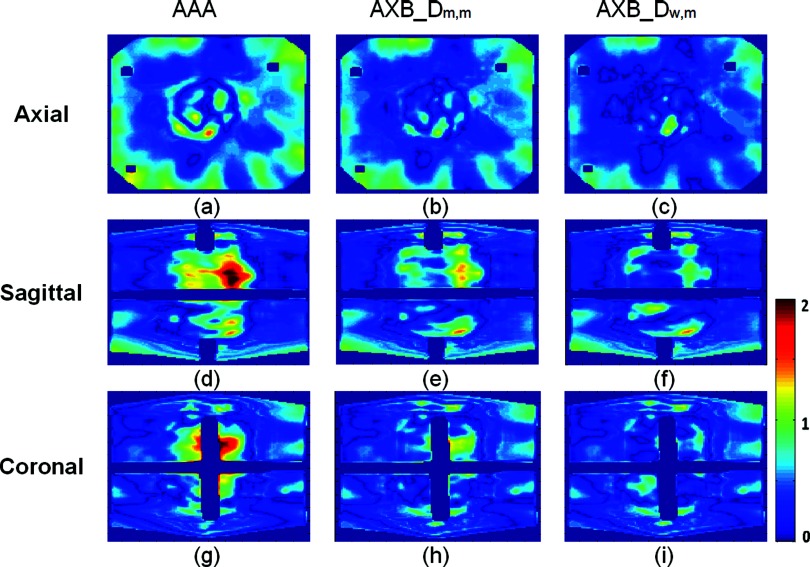
Figure 4.

The distribution of gamma index with ±3%/3 mm criteria for the first IMRT plan delivery (axial on the top, sagittal on the bottom). The results from the dose calculated by (from left to right) AAA, AXB_D_w,m, and AXB_D_m,m. The shadows inside the film region are the gaps of coronal and sagittal films. Bar plot represents gamma-index levels.

Figure 5.

The distribution of gamma index with ±3%/3 mm criteria for the first VAMT plan delivery (axial on the top, sagittal on the bottom). The results from the dose calculated by (from left to right) AAA, AXB_D_w,m, and AXB_D_m,m. The shadows inside the film region are the gaps of coronal and sagittal films. Bar plot represents gamma-index levels.

Table 2.

Percentages of points meeting gamma criteria of ±3%/3 mm criteria.

Film position	AAA	AXB_Dm,m	AXB_Dm,w
IMRT
Axial	97.2	98.2	98.9
	(1.1)1	(0.9)1	(0.8)1
Sagittal	98.3	99.1	99.3
	(0.6)1	(0.5)1	(0.5)1
Coronal	98.6	99.4	99.7
	(0.7)1	(0.4)1	(0.4)1
VMAT
Axial	91.7	96.3	98.5
	(2.0)1	(0.7)1	(0.8)1
Sagittal	89.9	94.1	98
	(0.6)1	(0.4)1	(0.4)1
Coronal	90.2	95.6	98.9
	(0.8)1	(0.5)1	(0.5)1

¹Percent coefficient of variation (%CV) of gamma analysis (±3%/3) from three measurements.

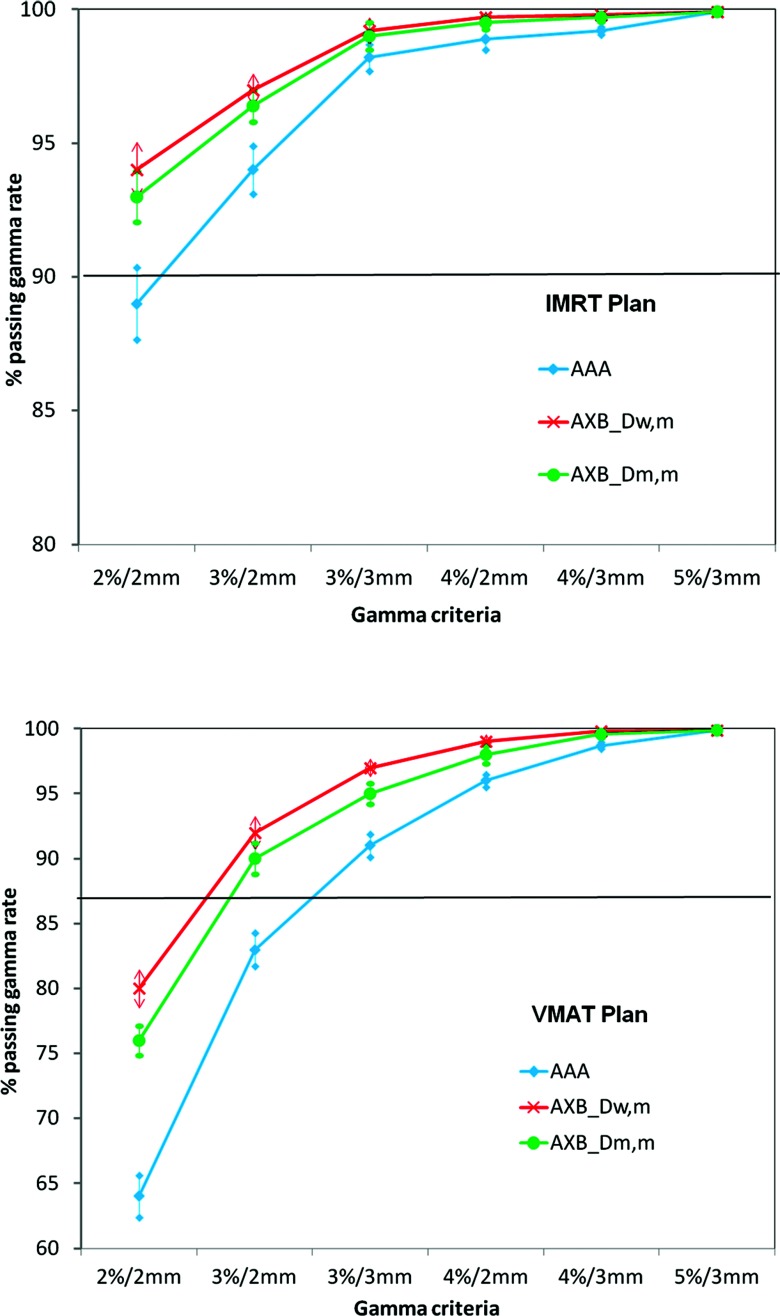
The mean percentages of pixels meeting the criteria for the IMRT and the VMAT plans are plotted for AAA and AXB (D_m,m and D_w,m) as a function of criteria stringency in Fig. 6. As expected, we observed that with less stringent criteria, the passing rate increased for all dose calculation methods. For the criteria less stringent than ±3%/3 mm, AXB (D_m,m and D_w,m) and AAA passing rates did not substantially differ, most of them passed. However, AXB had higher passing rates than AAA for criteria as stringent as ±2%/2 mm for IMRT and ±3%/2 mm for VMAT, indicating that AXB dose calculations were more accurate than AAA calculations in this case.

Figure 6.

Percentage of voxels passing gamma analysis with various criteria.

DVH

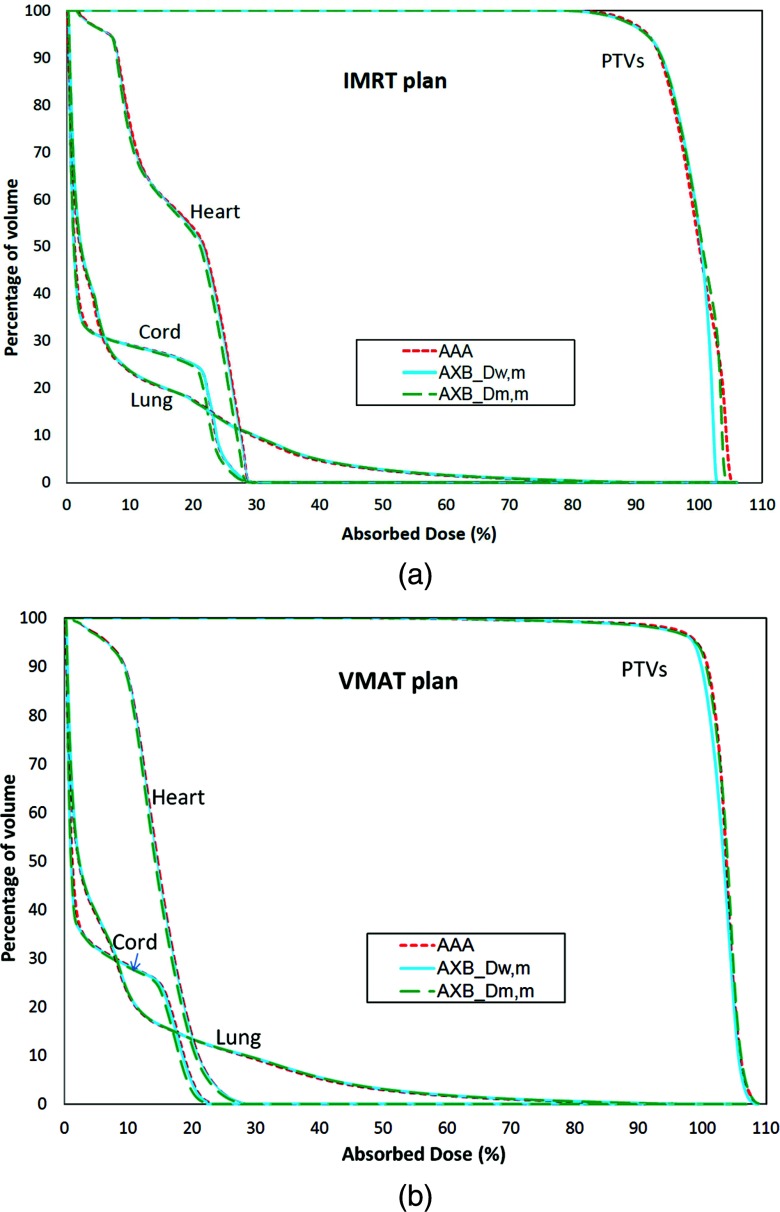
The comparison between DVHs calculated using AAA and AXB for both the IMRT and VMAT plans are shown in Fig. 7. Table 3 shows a detailed quantitative analysis of the DVH comparison: the mean doses (D50) for all structures, the dose to 95% of PTV volume (D95), and maximum dose to 0.1 cubical centimeters of OARs (D_0.1cc) were analyzed. The PTV doses are very similar for all calculation methods (about 1%–2%). For OARs, the differences are larger (within 2%–5%) for both D50 and D_0.1cc. There are notably differences between AAA and AXB_ D_m,m (5% for D50, 3.7% for D_0.1cc) for the spinal cord.

Figure 7.

DVHs calculated by AAA, AXB_D_w,m, and AXB_D_m,m for IMRT (a) and VMAT (b) plans.

Table 3.

DVH comparison between AAA and AXB.

	Mean dose (cGy)			D95 (PTV) or D0.1cc (OARs)
	AAA	AXB_Dm,m	AXB_Dw,m	AAA	AXB_Dm,m	AXB_Dw,m
IMRT plan
PTVs	660	660	657	664	660	649
		(0.1)1	(0.5)1		(0.6)1	(2.3)1
Lung	59	60	60	616	613	614
		(0.8)1	(1.0)1		(0.5)1	(0.4)1
Cord	49	48	49	197	193	197
		(3.3)1	(0.6)1		(1.9)1	(0.2)1
Heart	122	119	121	205	198	202
		(2.9)1	(0.9)1		(3.2)1	(1.6)1
VMAT plan
PTVs	629	630	626	635	640	633
		(0.0)1	(0.5)1		(0.7)1	(0.3)1
Lung	54	54	54	647	625	625
		(0.6)1	(0.7)1		(3.4)1	(3.3)1
Cord	37	35	36	150	144	146
		(4.9)1	(1.9)1		(3.7)1	(2.2)1
Heart	91	88	90	185	180	184
		(3.1)1	(1.0)1		(2.6)1	(0.8)1

¹Δ% to AAA = 100 × abs (D_AXB − D_AAA)/D_AAA.

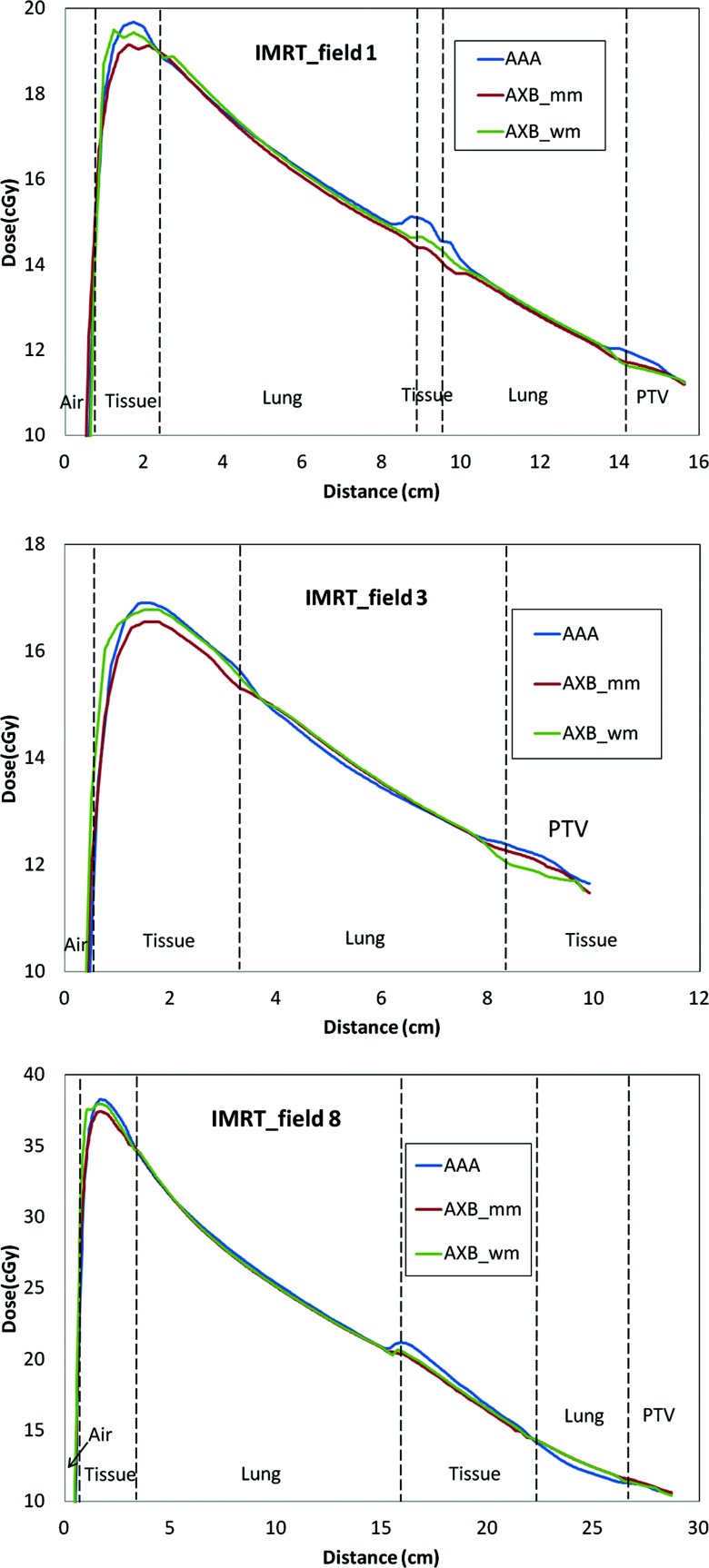
Profiles from single-field plans

Figure 8 shows three examples of central axis profiles for the single-field from IMRT plan (field 1, 3, and 8). It can be noticed that AAA and AXB were very close for most of regions. In some regions, especially the interfaces, the differences can be up to 8% between AAA and AXB_D_w,m and up to 6% between AAA and AXB_D_m,m.

Figure 8.

Central-axis dose profiles for three individual field plans. Each field corresponds to one of the IMRT fields. The total differences in the PTV between AAA and AXB are the summary of all nine fields.

Computation time

The computation times for the IMRT and VMAT plans are listed in Table 4. The AAA computation times were about 5–6 times faster than those of AXB for the IMRT plan, while the AXB computation times were about 4–5 times faster than those of AAA for the VMAT plan.

Table 4.

Computation times (in minutes) of AAA and AXB for IMRT and VMAT plans.

	TAAA	$T_{\mathrm{AXB}\_D\mathrm{m},\mathrm{m}}$	$T_{\mathrm{AXB}\_D\mathrm{w},\mathrm{m}}$
IMRT	0.8	2.5	2.5
VMAT	16	4.2	4.3

DISCUSSION

In this study, we investigated the dosimetric differences between AXB and AAA for IMRT and VMAT plans for lung cancer by comparing AXB and AAA calculations with TLD and film measurements in an anthropomorphic thorax phantom from the RPC. Both AXB and AAA were found to be in good agreement with the TLD measurements and well within the 95% confidence interval of the TLD and film predicated doses. Gamma analysis of the film showed that both AXB and AAA met the ±3%/3 mm criteria (90% passing rate). A comparison of DVHs from AXB and AAA showed that the mean doses in the PTV were similar (about 1%–2%), but larger differences were found between AXB and AAA DVHs for the OARs (2%–4%), mainly because of the lower local dose. Largest difference found in spinal cord is about 5%, indicating that there are still notable differences for AAA and AXB dose calculations.

Controlling the TLD and film measurement uncertainty was important for this study because the differences between AAA and AXB are relatively small. The measurement uncertainty is highly dependent on the handling proficiency. In this study, we followed the standard RPC credentialing procedure to conduct experimental planning and sample irradiation using the thorax phantom. All the TLDs and films were processed in RPC by proficient specialists to reduce the manual uncertainty. The results show that both the TLD (most within 2% except one location in high dose gradient region) and film uncertainty (within 3% for ±3%/3 mm gamma analysis) were well controlled in this study.

Our results are consistent with results from Fogliata et al., which showed that the differences between AAA and AXB in radiation therapy planning for lung cancer were within 3% in PTVs.¹¹ Our comparison of AAA and AXB in individual IMRT fields showed that even though the total dose differences were small, the dose differences for a single beam may be up to 8% in the lung interface regions. When multiple fields irradiate the same location, the total differences were minimized due to compensation of dose prediction errors from other field directions. This result also indicates that the differences between AAA and AXB may also depend on the location of the PTV. If the PTV is very close to the interface region, especially when the bone tissue also involved, the differences between AAA and AXB might be very large. These results are consistent with our findings described previously. Although this potential variation would not impose a significant clinical impact in translating between AAA and AXB, our results show the benefits to be gained by improving the accuracy of dose prediction by using radiation transport methods rather than the water-scaled dose kernel.

Our results showed that both TLD agreement and film gamma passing rate for AXB were slightly better than those of AAA, though it is not statistically significant. This is consistent with our previous study with the RPC head and neck phantom. These results demonstrated the benefits of radiation transport algorithms and indicated that AXB might improve the dose predication. Although such improvements are not profound because convolution-based algorithms have been very effective and accurate in most cases, AXB still has potential advantages in high complexity structures where there are a lot of interfaces between low and high density media. Since the RPC phantom was designed for credentialing institutions to participate in RTOG thorax IMRT and SBRT protocols,^{13, 14} these results also suggest that using AXB instead of AAA may improve the credentialing test passing rate by reducing the uncertainty introduced by the dose algorithm.

We also compared the AXB dose reporting modes D_m,m and D_w,m. Although the D_w,m has historically been considered the appropriate dose reporting mode, it has been recently debated whether the MC dose predictions need to be converted into D_w,m.^{24, 25, 26} Our results showed that there were no clinically significant differences between these two reporting modes in soft-tissue and lung regions. For the cases with bone structure, the differences between D_m,m to D_w,m may become larger, as was observed in our previous studies and other studies.^{3, 26, 27} However, it has been shown that both AAA and the collapsed-cone convolution in the Pinnacle TPS dose predictions are all closer to D_m,m than to D_w,m.^{3, 28, 29} Therefore, we suggest that the D_m,m dose values from AXB or MC algorithms do not need to be converted into D_w,m for dose calculation of clinical lung cases.

It also should be noticed that the material assignment inside the TLD contours may also contribute to the dose differences. If the CT numbers inside the TLD contour are close to water, then we do not need to manually assign the materials to TLDs, otherwise, we must manually define the materials for TLD. In our study, we had placed the TLD tablet inside the phantom during CT simulation and the CT numbers inside the TLD contours are very close to water. Furthermore, the volumes of TLD are very small. Thus, in this study, the dose differences between TLD as water to TLD's CT number are negligible.

We found that the computation speed of AXB was about 4–5 times faster than that of AAA for the VMAT plan, presumably because AXB can calculate scatter components using only one calculation by directly resolving the LBTE that describes the macroscopic scatter distributions from all beams. Thus AXB can markedly reduce the total computation time for VMAT plans which have a large number of orientations. With the increasing interest in VMAT for various clinical applications, AXB might provide both accuracy and fast computation speed for VMAT treatment planning.

CONCLUSIONS

The introduction of the novel deterministic AXB algorithm provides a new option for improving accuracy and efficiency in the clinical practice of radiation therapy, especially for VMAT. Our experimental validation study using the RPC thorax phantom showed that AXB provides dose predictions that are equivalent to or may be slightly better in agreement with TLD and film measurements than AAA. AXB may also improve the RPC credentialing passing rate owing to the reduction of dose calculation uncertainty. AXB can particularly benefit lung VMAT planning by both improving the accuracy of calculations and reducing the computation time. We suggest that D_m,m be the final dose value generated clinically when the MC and AXB algorithms are used.