Limits in decision making arise from limits in memory retrieval

Abstract

Some decisions, such as predicting the winner of a baseball game, are challenging in part because outcomes are probabilistic. When making such decisions, one view is that humans stochastically and selectively retrieve a small set of relevant memories that provides evidence for competing options. We show that optimal performance at test is impossible when retrieving information in this fashion, no matter how extensive training is, because limited retrieval introduces noise into the decision process that cannot be overcome. One implication is that people should be more accurate in predicting future events when trained on idealized rather than on the actual distributions of items. In other words, we predict the best way to convey information to people is to present it in a distorted, idealized form. Idealization of training distributions is predicted to reduce the harmful noise induced by immutable bottlenecks in people’s memory retrieval processes. In contrast, machine learning systems that selectively weight (i.e., retrieve) all training examples at test should not benefit from idealization. These conjectures are strongly supported by several studies and supporting analyses. Unlike machine systems, people’s test performance on a target distribution is higher when they are trained on an idealized version of the distribution rather than on the actual target distribution. Optimal machine classifiers modified to selectively and stochastically sample from memory match the pattern of human performance. These results suggest firm limits on human rationality and have broad implications for how to train humans tasked with important classification decisions, such as radiologists, baggage screeners, intelligence analysts, and gamblers.

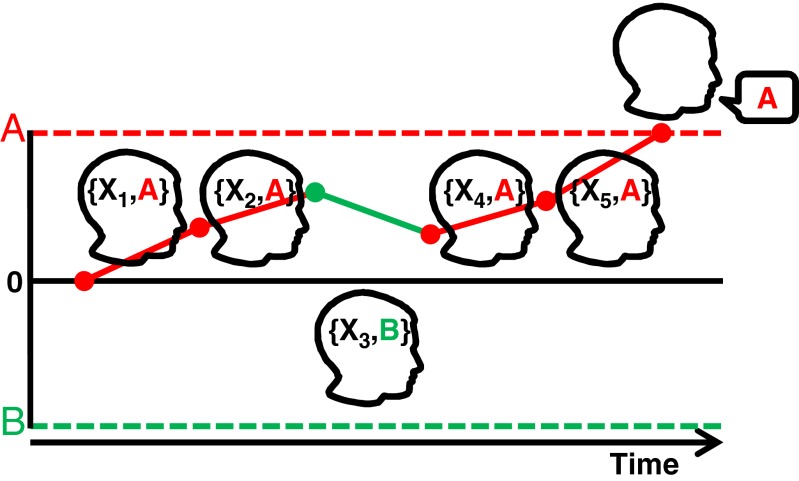
When making decisions, people often retrieve a limited set of items from memory (1–4). These retrieved items provide evidence for competing options. For example, a dark cloud may elicit memories of heavy rains, leading one to pack an umbrella instead of sunglasses. Likewise, when viewing an X-ray, a radiologist may retrieve memories of similar X-rays from other patients. Whether or not these other patients have a tumor may provide evidence for or against the presence of a tumor in the current patient. This process of sequential retrieval from memory, evidence accumulation, and final decision is formalized by diffusion models of choice and response time (Fig. 1). Diffusion models have successfully accounted for human learning and decision performance in a number of domains (1, 5, 6). These models accumulate noisy evidence retrieved from memory until a decision boundary is crossed. Wider boundaries imply higher accuracy and longer response times. For a given boundary, diffusion models optimally integrate evidence.

Fig. 1.

A classification decision modeled as a random-walk diffusion process that stochastically samples from memory. Evidence accumulates through time (from left to right) until the decision boundary for the category A (dotted red line) or B (dotted green line) response is crossed. At the start of trial, the evidence accumulator is set to zero. At each time step, an item from category A or B is retrieved from memory, moving the accumulator (the red/green solid line) toward either decision boundary. The response is determined by which boundary is crossed and the response time is related to the number of steps required to reach a boundary. The drift rate refers to the average rate for this stochastic process to proceed toward the correct boundary.

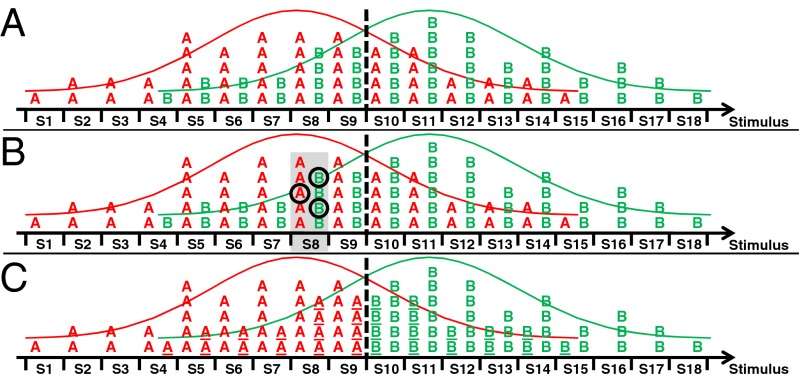
However, according to the diffusion model, it is impossible to make optimal decisions within finite time (i.e., when the boundaries are finite). For probabilistic problems, such as determining whether a tumor is cancerous, whether it will rain, or whether a passenger is a security threat, selectively sampling memory at the time of decision makes it impossible for the learner to overcome uncertainty in the training domain. From a signal-detection perspective, selective sampling from memory results in noisy and inconsistent placement of the criterion across decision trials. Even with a perfect memory for all past experiences, a learner who selectively samples from memory will perform suboptimally on ambiguous category structures (Fig. 2 A and B).

Fig. 2.

(A) Categories A (red curve) and B (green curve) are probabilistic, overlapping distributions. After experiencing many training items (denoted by the red A and green B letters), an optimal classifier places the decision criterion (dotted line) to maximize accuracy, and will classify all new test items to left of the criterion as A and all items to the right of the criterion as B. (B) Thus, the optimal classifier will always judge item S8 to be an A. In contrast, a model that stochastically and nonexhaustively samples similar items from memory may retrieve the three circled items and classify S8 as a B, which is not the most likely category. This sampling model will never achieve optimal performance when trained on ambiguous category structures. (C) Idealizing the category structures during training such that all items to the left of the criterion are labeled as A and to the right as B (underlined items are idealized) leads to optimal performance for both the optimal classifier and the selective sampling model.

In contrast, machine learning models do not stochastically sample from memory in a nonexhaustive fashion. Instead, the complete training set is used and regularization methods (7) adjust model complexity to account for noise in the training data. To achieve optimal performance, a model’s complexity is adjusted to match the dataset, rather than the dataset being altered to match a model’s proclivities.

One implication of the view that people, unlike machine learning models, selectively and stochastically sample from memory when making decisions is that people will be more accurate in predicting future events when trained on idealized distributions of data than when trained on the actual distributions. Although nonsensical from a machine learning perspective, we hypothesize that idealization of training data will boost human performance by reducing the amount of noise introduced by memory retrieval processes (Fig. 2C). Of course, idealization can come with a cost as nuances in the training data are obscured, but these costs are likely eclipsed by gains associated with people better grasping the underlying structure of a domain, thereby boosting test performance.

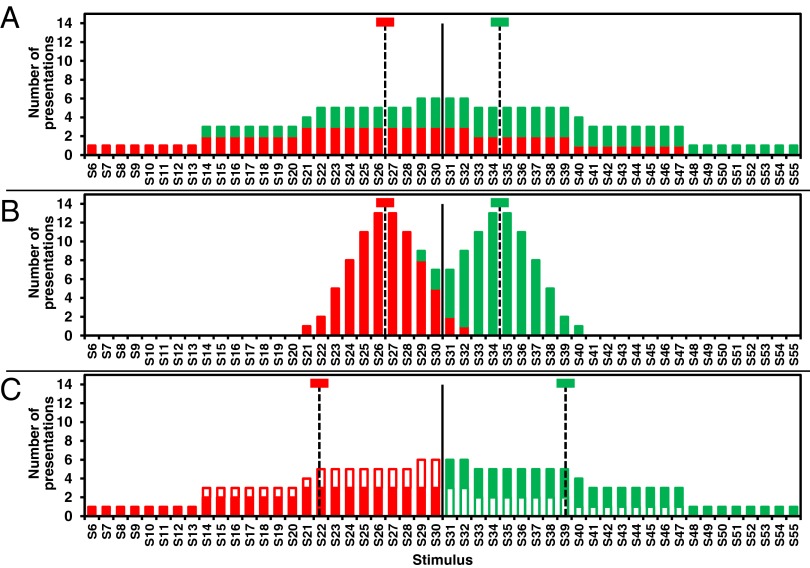
Experiments 1–3 evaluate these hypotheses. In experiments 1 and 2, we trained participants to classify horizontal lines of different lengths. Participants were assigned to either the actual or idealized condition. In the actual condition, participants trained on highly probabilistic category structures (Fig. 3A). In the idealized condition, participants trained on an idealized variant that either reduced category variance (experiment 1, Fig. 3B) or used deterministic feedback (experiment 2, Fig. 3C). Participants were trained over a number of trials using trial-and-error learning (i.e., stimulus → response → feedback). Feedback was omitted on test trials. The test set included training and novel items.

Fig. 3.

Distributions of training items for experiments 1 and 2. Stimulus items varied in length. Each stimulus (S1 to S60) differs from its neighbor by one length unit (1.3 mm). The colored bars indicate the feedback provided during training (red for category A and green for category B). The solid black line is the criterion for the optimal classifier and the dotted lines mark the category means. (A) The highly overlapping distributions from the actual condition in experiments 1 and 2. (B) In experiment 1’s idealized condition, within-category variance is reduced relative to the actual condition. (C) In experiment 2’s idealized condition structure, feedback is a deterministic function of the criterion. Items that have switched categories (compared with the distributions from the actual condition) are shown with a white fill.

Results

Empirical Data.

SI Results gives details of all data analyses and related simulations. Participants in the idealized conditions more closely approximated the optimal classifier at test (Fig. 4). The optimal classifier places the decision criterion (Fig. 1) to maximize performance on the training set. The overall proportion of test responses consistent with the optimal classifier (Fig. 5) was higher in the idealized than in the actual conditions [independent samples two-tailed t tests; experiment 1, t(84) = 2.794, P = 0.006; experiment 2, t(91) = 6.333, P < 0.001]. These results hold at the individual participant level in that response inconsistency (measured by the number of cases in which an individual classifies neighboring stimuli into opposing categories) was also lower in the idealized conditions [independent samples two-tailed t tests; experiment 1, t(84) = 4.433, P < 0.001; experiment 2, t(91) = 6.288, P < 0.001].

Fig. 4.

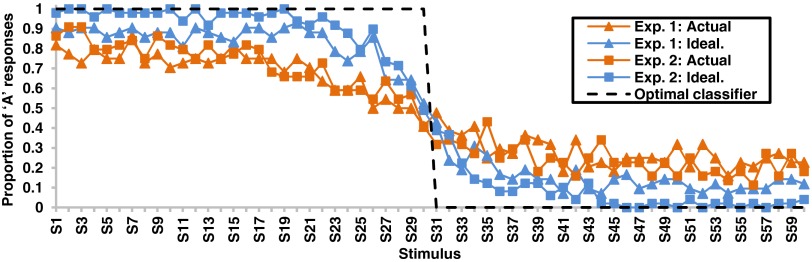
For experiments 1 and 2, the proportion of test items classified as category A members. The black dotted line illustrates the behavior of the optimal classifier, which is better approximated by humans in the idealized than in the actual conditions.

Fig. 5.

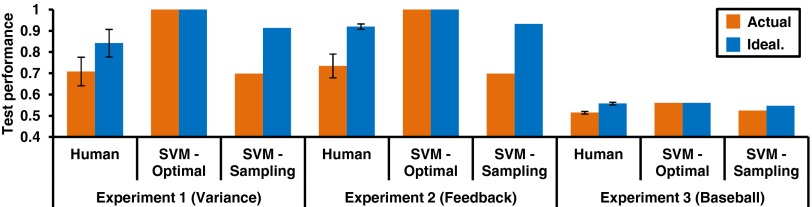
Test performance for human participants and support vector machine (SVM) models. For experiments 1 and 2, test performance is the proportion of trials in accord with the optimal classifier at test, whereas for experiment 3 it is test-phase accuracy. Error bars represent 95% confidence intervals (experiments 1 and 2, between subjects; experiment 3, within subjects).

In experiment 3, we evaluated the benefits of idealization in a complex real-world domain of relevance to professional forecasters, namely, gamblers. Training and test sets were drawn from Major League baseball game outcomes, which constitute a fairly noisy domain (Table S1). The original database can be found at www.retrosheet.org/gamelogs/index.html. Participants were trained using trial-and-error learning on a random subset of games from a season and then were tested on the remaining games from that season. On each trial, two teams were presented and the participant predicted the winner (feedback was omitted on test trials).

In the actual condition, training feedback corresponded to the actual game outcomes. Feedback in the idealized condition was manipulated by the experimenter. From the randomly sampled subset of training games (not the entire season’s games), the teams were ranked according to their total wins, and on every training trial, the higher-ranked team in a head-to-head match was always shown as the game winner. This idealization procedure does not “peek ahead” to the test data and radically alters the actual training distribution. Nevertheless, participants in the idealized condition outperformed those in the actual condition at test [dependent samples two-tailed t test, t(41) = 6.696, P < 0.001], achieving a level of accuracy close to that of an optimally tuned support vector machine (SVM-Optimal) classifier (8, 9) (Fig. 5).

Cognitive Modeling.

We conducted a number of analyses to evaluate whether these striking effects of idealization arise from people’s selectively retrieving examples from memory that are similar to the current item and easily accessible. Items should be available for retrieval to the extent they have been recently presented and are similar to the current stimulus (which acts as a retrieval cue). We evaluated participants’ (actual condition, experiments 1 and 2) propensity to repeat the corrective feedback from the previous trial as a function of similarity (10, 11). Consistent with the sampling account, the average recency score over the studied range was positive [mean = 0.175, SE = 0.02; one-sample t test, t(87) = 10.533, P < 0.001] and waned as the distance (i.e., dissimilarity) between the previous and the current item increased [linear trend analysis, F(1,87) = 97.027, P < 0.001], showing that participants were using feedback from the previous trial to guide their responses (Fig. S1).

As an additional test of whether human performance is shaped by selectively sampling from memory, we fit machine learning models to the data that either retrieved all training examples from memory, or were modified to only retrieve a small set of items similar to the current stimulus, as we hypothesize humans do. As predicted (Fig. 5), the unmodified machine learning models (i.e., SVM-Optimal) did not perform better in the idealized conditions, whereas the sampling variants (i.e., SVM-Sampling) matched the performance profile of human participants. The SVM-Sampling model only differs from the SVM-Optimal model by selectively sampling its memory. The SVM-Sampling model’s predictions converge to those of the SVM-Optimal model as the decision boundaries are moved farther apart, which necessitates retrieving more samples from memory to reach a decision (Fig. 1 gives an overview of this sampling process, and model details are given in Methods). This one change to the SVM-Sampling model was sufficient to capture the basic pattern of human performance, lending credence to our account that people selectively sample from memory.

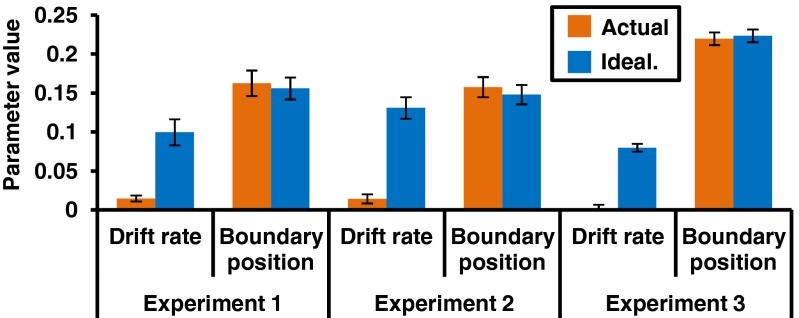
A pillar of our hypothesis is that idealization boosts test accuracy by reducing noise introduced by the retrieval process (i.e., boosting the quality of samples retrieved from memory). According to the diffusion model (Fig. 1), there are two main ways to boost accuracy on a task: raising caution by increasing boundary separation (thus requiring more evidence to be accumulated before reaching a decision) or increasing the drift rate (i.e., boosting the quality of evidence sampled from memory, and therefore the average rate at which the diffusion process moves toward the correct boundary). Idealization is predicted to increase the drift rate (i.e., quality of information sampled from memory) but not boundary separation (i.e., idealization should not make people more cautious).

We fit the EZ-diffusion model (12) to individual participants’ training data to recover parameter estimates for boundary separation and drift rate. As Fig. 6 and Table S2 show, idealization significantly increased drift rate [independent samples two-tailed t tests: experiment 1, t(84) = 9.949, P < 0.001; experiment 2, t(91) = 14.86, P < 0.001; dependent samples two-tailed t test: experiment 3, t(41) = 15.338, P < 0.001], but not boundary separation (all P values are > 0.05). These results support the claim that idealization boosts performance by “cleaning” or “denoising” memory for category information used in the sampling process.

Fig. 6.

Results from diffusion model simulations: mean drift rates and boundary positions for all experiments. Error bars represent 95% confidence intervals (experiments 1 and 2, between subjects; experiment 3: within subjects).

Discussion

In conclusion, we have shown that, contrary to best machine learning practices, it is better to train people on a training distribution that differs from the test distribution. In particular, people perform best at test when trained on an idealized variant of the target-learning problem. The idealization advantage arises because, unlike machine learning systems, people stochastically and selectively retrieve a limited set of memories at the time of decision. This limited retrieval injects noise into the decision process that makes it impossible to achieve an optimal level of performance. Idealization ameliorates many of these negative effects by reducing the noise introduced by limited memory retrieval.

This discovery has implications for learning theories in general. Practically, our results suggest that idealized training regimens should be considered for professionals, such as radiologists. One question is whether the benefits of idealization hold for training situations that extend beyond a single, brief training session, as in experiments 1–3. If, as predicted, the bottleneck for human performance resides at the retrieval stage, then the idealization advantage should persist no matter how extensive the training regimen is (Fig. 1). Preliminary explorations suggest that the benefits of idealization (or more correctly, the limits of training on actual distributions) hold under extended training. As a follow-up to experiment 2, we trained participants for five sessions over 5 d (as opposed to a single session) and found that participants’ test accuracy only slightly improved across sessions and was worse in the fifth session of the actual condition than after the first session in the idealized condition [independent samples two-tailed t tests; t(37) = 3.473, P = 0.001 for accuracy and t(37) = 3.353, P = 0.002 for response inconsistency].

These results suggest that idealization methods are also relevant to tasks involving more extensive training, and that the bottleneck in memory retrieval is not easily overcome by practice alone. More broadly, the observed limits in memory retrieval suggest limits to human rationality because optimal behavior may not be achievable in relatively straightforward decision problems. Although forgetting and other limitations in memory may be adaptive in certain circumstances (13, 14), the present results suggest that limitations in memory retrieval (introduced by stochastic and selective sampling) are not adaptive and simply introduce noise and inconsistency into human judgments. In related tasks, adaptive heuristic approaches often outperform more complex strategies when the decision environment is noisy (15). Our results suggest that when humans implement such strategies, additional noise is introduced by memory retrieval, and this could increase the benefits associated with simpler decision strategies.

One possible concern in adopting idealization methods to influence real-world decision making is that such training could lead to overconfidence (e.g., borderline cases may be treated with an unwarranted degree of certainty because items from the contrasting category are rarely retrieved). Ideally, people would accurately assess the objective uncertainty associated with a stimulus. Unfortunately, our results suggest that people do not have access to this distributional information when making a decision and instead sample from memory. In aggregate, responses may indicate graded confidence reflective of objective uncertainty, but for an individual decision, selective sampling leads to noisy and inconsistent responding. One practical way to optimize real-world decision making, when misses and false alarms are associated with different costs, is to alter feedback for items along the category boundary to shift the decision criterion.

Further work is necessary to determine how to best idealize distributions of various forms to maximize human test performance. What is clear is that, unlike machine learning systems, humans stochastically and selectively retrieve memories when making decisions, and that idealization can significantly boost human performance.

Methods

Participants.

Students from The University of Texas at Austin participated in partial fulfillment of a course requirement or in exchange for a financial compensation. Sample sizes were 86 (experiment 1), 93 (experiment 2), and 84 (experiment 3). All studies were approved by The University of Texas at Austin’s Institutional Review Board. Informed consent was obtained from all participants before they participated in a study.

Experiments 1 and 2.

Material.

We used horizontal lines of various lengths, subtending ∼0.8–13.8° of visual angle at a distance of 45 cm.

Design.

Category structures for experiments 1 and 2 are shown in Fig. 3. Each stimulus (S1 to S60) differs from its neighbor by one length unit (i.e., 1.3 mm on a 1,440- × 900-pixel display). Participants were randomly assigned to one of two conditions, which differed according to the level of variance within both categories (experiment 1) or the type of feedback received after each training trial (experiment 2). Fixed predetermined training samples were used for all participants within each condition (Fig. 3). The ideal between-category decision criterion was always located between stimuli S30 and S31. The test set always included every stimulus from S1 to S60. Condition characteristics are shown in Table 1.

Table 1.

Condition characteristics for experiments 1 and 2

Experiment and condition	n	D	SD
Exp. 1
Actual	44	8	9.9
Idealized	42	8	2.3
Exp. 2
Actual	44	8	9.9
Idealized	49	17.4	9.9

n, number of participants; D, distance between category means (in stimulus units, which are equal to 1.3 mm); SD, within-category SD (in stimulus units).

Procedure.

During the training phase, on every trial, participants were instructed to fixate on a small square appearing in a random position on the screen. After 1 s, a line stimulus replaced the square at the exact same position. Participants were then to press the correct category key as quickly as possible without sacrificing accuracy. If they did not respond within 1.5 s, the stimulus was removed and a message prompting them to respond immediately was shown. Once the participant responded, the stimulus was immediately replaced by the correct category label (shown for 2 s), accompanied by a feedback message (“Correct” or “Wrong”) and an appropriate tone. A blank screen was shown for 0.5 s between trials.

The screen coordinates (horizontal/vertical) defining the stimulus’s (i.e., fixation square and line) position were randomized on each trial to prevent participants from using marks or smudges on the screen as a memory aid. Participants completed 160 training trials. During the test phase, on each trial, a specific line length was sampled without replacement from the test set, until all 60 test line lengths were shown once. Trial procedure differed from that of the training phase in that feedback was not provided, the stimulus remained onscreen until a response was recorded, and participants were not required to respond quickly.

Experiment 3.

Material.

We used stimulus sets composed of Major League baseball (MLB) game outcomes selected from an online database. Each participant was assigned to league outcomes (either MLB’s National or American League) for one season between 1920 and 1960. To prevent use of prior knowledge, actual team names were replaced by fictitious baseball team names (i.e., animal names) and logos were replaced by the associated animal icons. The assignment of animal names to actual baseball teams was random for each participant.

Design.

One separate stimulus set was created for every season and league. For a given season/league combination (e.g., 1934/American League), 5 out of 22 possible games were randomly selected for each pair of teams (8 teams = 28 pairs = 140 games). Teams were then ranked (first to eighth) according to the overall number of wins within that sample. The test set contained every pair of teams from the sample.

A matched-pairs design was used. The same stimulus set and presentation order were used for both participants within a pair. One participant was randomly assigned to the actual condition, for which the feedback for each game was based on the game outcome stemming from the original database. For the other participant (idealized condition), feedback was based on the previously described rankings (i.e., on every trial, the higher-ranked team was shown as the game winner during feedback).

Procedure.

During the training phase, on every trial, a game was randomly selected without replacement from the training set. Logos and team names (in black characters) for this game appeared on each side of the screen. Participants were then asked to pick the winner of the game by clicking on the chosen team’s logo as quickly as possible without sacrificing accuracy. Once the response was recorded, both logos and team names remained onscreen for 2.5 s, and the color of the winning team’s name changed to green, accompanied by a feedback message (Correct or Wrong) and an appropriate tone. Participants completed 140 training trials. During the test phase, on each trial, a pair of teams was randomly selected without replacement from the test set. Once the logos and names appeared (at the start of the trial), participants were asked to click on the logo of the team they believed won more head-to-head games during the remainder of the season. Once the response was recorded, the logos and team names were removed from the screen and the program proceeded to the next trial. The interstimulus interval (during which the screen was blank) lasted 1 s. No feedback was provided. Participants completed 28 test trials; each pair of teams was shown once. For all training and test trials, logo and name positions (left or right) were randomly assigned.

Recency Analyses.

Recency analyses rely on highly probabilistic category structures (11). Thus, these analyses were conducted on the merged training data from the actual conditions in experiments 1 and 2. Only stimuli paired at least once with both category labels (i.e., with probabilistic membership) were entered into the analysis. We divided the stimulus space into eight equally sized regions around the boundary (e.g., region 1: S15–S18; region 8: S43–46), within which items were treated as equivalent. Then, the distance (in terms of number of regions) between the region for the stimulus on the current trial and that for the previous trial was computed. Fig. 7 illustrates the procedure used to compute recency scores, which lie between −1 and 1. At the extremes, a score of 1 indicates that a participant always repeated the feedback from the previous trial, whereas a score of −1 indicates that a participant always chose the opposite of the previous trial’s feedback. Individual recency scores were computed over all trials, as well as for each level of absolute distance (in number of regions) between the stimulus region for the current and the previous trial.

Fig. 7.

(A) Description of trial types used in the recency analysis computations: c1 and c4 represent the number of trials for which the participant’s response matches the feedback from the previous trial, and c2 and c3 represent the number of trials for which the participant’s response does not match the feedback from the previous trial. (B) Equation describing how to calculate a recency score (RS).

SVM Models.

SVMs are machine learning classifiers that attempt to find a plane in multidimensional space that maximally separates the training items from two or more categories, subject to some constraints. To address cases in which a dataset is probabilistic, such that there is no plane that perfectly separates items from the two categories (e.g., Fig. 2), the optimization routines contain a model complexity parameter C that determines how much solutions should be penalized when an item falls on the wrong side of the decision plane. When category structures are nonlinear, a nonlinear kernel is used to project stimuli into a higher dimensional space where there exists a plane that separates the classes.

As noted in ref. 9, this approach renders SVMs remarkably similar to exemplar models from the psychology literature. The weights, α_i, and the intercept term, b, in the SVM are solved (subject to some constraints) using quadratic programming to yield the following classifier:

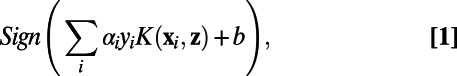where K is the kernel’s function that assesses the similarity between to-be-classified stimulus z and each x_i item stored in memory, and y_i is x_i’s category membership (either +1 or −1). The Sign function indicates deterministic responding, such that the +1 category (e.g., category A) is always chosen when the summation of evidence is positive and the −1 category (e.g., category B) is always chosen when the summation is negative. We refer to such SVMs as SVM-Optimal models.

To reflect the human propensity to selectively sample from memory (2), the SVM-Sampling model feeds evidence for the −1 and +1 categories into a diffusion process (Fig. 1). The SVM-Sampling’s probabilistic decision rule is adapted from that of the exemplar-based random walk (1), with the modification that a decision parameter, γ, is included (16). It has been shown (1) that using this modified decision rule is equivalent, on average, to simulating a diffusion (or sequential sampling) process with γ-wide decision boundary positions. As γ increases, more information is retrieved from memory when making a decision, and predictions from the SVM-Optimal and SVM-Sampling models converge. Building on this demonstration, we used the following formulation of the decision rule to ease analysis:

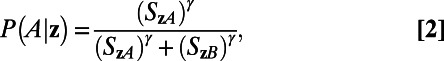where P(A|z) is the probability of choosing category A given new item z, and S_zA and S_zB represent the amount of evidence accumulated for categories A and B respectively. Evidence sums are computed for each category separately. For example, the total evidence for category A, S_zA, is defined by

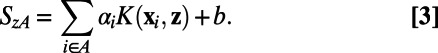For experiments 1 and 2, a Gaussian radial-basis function kernel K was used to train and test all SVM models:

where ε is a parameter that determines the generalization gradient between x_i and z, and ||•|| is the Euclidian norm.

Experiment 3 required a custom kernel to allow for the processing of nominal input data with multivalued outcomes. Each game in the training set was represented as a vector 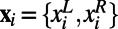, where 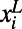and 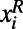are the team names shown on the left and right side of the screen, respectively, for game x_i. Each x_i is associated with a class label, 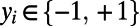, which represents the winning team’s side on the screen (−1 if the left team won the game and +1 if the right team won), thus transforming every trial to a two-category problem (i.e., categories “left” and “right”). For example, if on a specific trial team “Ants” was on the left side of the screen and team “Pigs” on the right side, and team Ants won, the following items were both added to the training set: {Ants, Pigs} with the −1 class label, and {Pigs, Ants} with the +1 class label. This manipulation conveys the exact same information but makes the SVM-Optimal model indifferent to left/right screen positions.

The custom kernel function K, which represents the level of similarity between a game from the training set 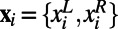and the to-be-classified game z = {z^L, z^R}, was computed as follows:

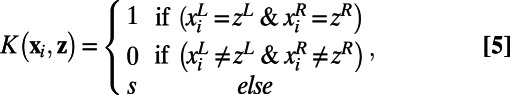where s ε [0, 0.5] determines the similarity between the to-be-classified game and games in memory that match on either the left or right position. With s = 0, no similarity is shared, and the overall decision solely rests on head-to-head outcomes between the two teams forming the stimulus. At the other extreme, with s = 0.5, partial matches are maximal and the classification is driven by whether the left or right team has more total wins. The relative importance of head-to-head wins and total wins smoothly varies for intermediate values of s. The value of s only influences performance in the actual condition.

Diffusion Modeling.

Estimates for the drift rates and boundary positions for individual participants were obtained using the EZ Diffusion model (12), which uses response time means and variances for correct trials, as well as the proportion of correct trials.