Nodal Staging Score: A Tool to Assess Adequate Staging of Node-Negative Colon Cancer

Abstract

Purpose

Adequate nodal staging of colon cancer has been defined as pathologic examination of at least 12 lymph nodes. We sought to refine this definition by quantifying the likelihood that a pathologically node-negative patient has, indeed, no positive nodes.

Patients and Methods

Patients with stage I-III adenocarcinoma of the colon between 1994 and 2005 and had at least one lymph node pathologically examined were identified from the Surveillance, Epidemiology and End Results (SEER) database (n = 131,953). We estimated the sensitivity of the pathologic staging of locoregional spread using a beta-binomial model and developed the nodal staging score (NSS), which is the probability that a patient is correctly staged as node negative. NSS is a function of T stage and the number of examined nodes.

Results

The probability of missing a positive node that is in fact truly present is 29.7% if five nodes are examined, 20.0% if eight are examined, and drops to 13.6% for 12 nodes are examined. An NSS of 90% can be achieved by examining a single node for T1 and four nodes for T2 tumors. To maintain similar levels of NSS for T3, 13 nodes need to be examined and for T4 lesions, 21 nodes need to be examined. Graphical and tabular tools are provided to facilitate calculation of NSS and treatment decision making in practice.

Conclusion

The minimum number of examined nodes for adequate staging depends on the T stage. The score we developed indicates the adequacy of nodal staging for patients with no positive nodes and can assist clinical decision making in the patient without nodal metastasis.

INTRODUCTION

Nodal disease is a critical risk factor for patients who undergo resection for localized colon cancer. Most randomized trials of adjuvant chemotherapy have stratified patients on the basis of the presence of positive lymph nodes and have shown a 30% to 50% improvement in survival for node-positive patients,¹ making adjuvant chemotherapy standard for patients with node-positive colon cancer.¹ Clinical trials have not demonstrated a statistically significant benefit for node-negative patients, so close observation remains the standard of care although some patients and providers opt for adjuvant treatment.^2,3

Since nodal status is the primary determinant of therapeutic course following surgery, adequate nodal retrieval by the surgeon and assessment by the pathologist are considered critical for patient care. Missing nodal disease (false-negative nodal staging) deprives patients of potentially lifesaving adjuvant chemotherapy.¹

In an effort to reduce staging errors, many experts have emphasized a need to evaluate a minimum number of lymph nodes in any colorectal cancer specimen.^4–10 Despite varying recommendations from these studies, National Quality Forum has recommended that at least 12 nodes be examined as a quality indicator.¹¹

When patients have too few lymph nodes examined in their surgical specimen, treating physicians face challenging management decisions. Most will give adjuvant therapy serious consideration to offset the possibility of occult nodal disease. Previous work in this area has focused on correlating the number of examined lymph nodes with progression or survival^4,7,12–22 but does not offer a tool to help patients and physicians judge the adequacy of nodal staging and make an informed treatment decision.

In this article, we present a simple model that calculates the probability of occult nodal disease as a function of the number of examined nodes and the T stage. We use this model to obtain a nodal staging score (NSS), higher values of which reflect a low likelihood of false-negative staging and a greater confidence in the node-negative status of the patient.

PATIENTS AND METHODS

Patients

The Surveillance, Epidemiology, and End Results (SEER) registry, sponsored by the National Cancer Institute, currently collects and publishes cancer incidence and survival data from 14 population-based cancer registries and three supplemental registries covering approximately 26% of the US population. SEER coverage includes 23% of African Americans, 40% of Hispanics, 42% of American Indians and Alaskan natives, 53% of Asians, and 70% of Hawaiian/Pacific Islanders. Using the SEER database, we identified 155,320 cases of stage I-III primary colon cancer diagnosed and resected between 1994 and 2005. Patients for whom the number of examined nodes was zero or unreported were excluded and the final study cohort included 131,953 patients.

The primary limitation of our data is that the data do not include detailed information on all pertinent treatment such as the use of systemic chemotherapy. This limitation, however, is not germane to this analysis. SEER does not record the time of recurrence/progression.

Statistical Analysis

Our analysis is concerned with the probability that node-negative patients are incorrectly staged. Since the true nodal status is unascertainable, we infer the probability of missed nodal disease by examining the number of examined nodes (n) and the number of positive nodes (k) from node-positive patients. A patient is classified as node positive if k is more than 0 and as node negative if k = 0. Consider a patient with large n and small k: if fewer than n nodes had been examined, there would be a chance that this patient would have been incorrectly deemed node negative. Conversely, for a patient with small n and large k, even with fewer examined nodes, it is unlikely that nodal disease would have been missed. Hence the data from node-positive patients are used to interpret the data for node-negative patients.

The probability that a node-negative patient has nodal disease can be computed using the following algorithm:

1. Compute the probability of missing a positive node (one minus sensitivity) as a function of the number of examined nodes. This is inherent to the process of pathologic detection and, as such, depends on the number of examined nodes but not on T stage.

2. Compute the prevalence of nodal disease as a function of T stage, using the probability of missing a positive node. Prevalence is inherent to the disease and independent of the pathologic detection process. Thus, it depends on T stage but not on the number of examined nodes.

3. Compute the NSS. This is the probability that a pathologically node-negative patient has unidentified nodal disease. NSS is calculated from the prevalence and the probability of missing a positive node. Hence, it is a function of both the number of examined nodes and T stage.

Probability of Missing a Positive Node

Probability of missing a positive node can be estimated from the false-negative patients expressed as a proportion of all truly node-positive patients as follows:

1. For a node-positive patient, compute the probability that, had m (m = 1,…,n-1) nodes been examined, all of them would have been negative.

2. Repeat step 1 for all patients.

3. For each m, average the computed probabilities across patients. These are the probabilities of missing nodal disease for each m, that is, each potential value of number of nodes examined.

4. A beta-binomial model that takes into account the potential correlation between the existence of positive nodes for a given patient is used for step 1. For each patient i, represent by x_i the number of positive nodes had m nodes been examined instead of n_i. We keep m less than n_i to avoid extrapolation and seek P(x_i = 0 | m, k_i), which is the probability of missing a positive node. Under the beta-binomial model, this probability is given by

   

   where B(.) represents the beta function and α and β are parameters that characterize the underlying intensity of nodal disease to be estimated from the individual patient data using maximum likelihood.²³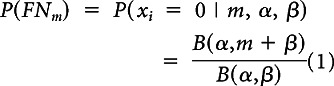

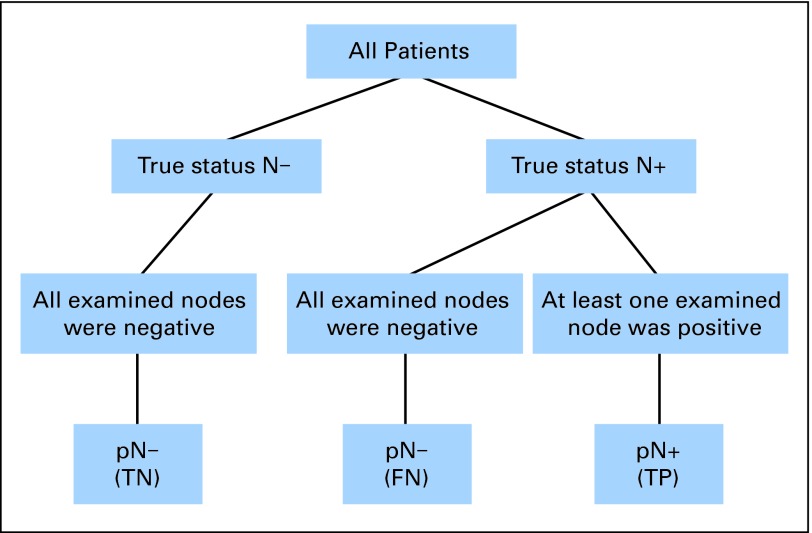
This algorithm relies on three pragmatic assumptions. The first is that there are no false positives (Assumption 1: If an involved node was examined, it would have been identified as such). Figure 1 shows the remaining three possible categories in which a patient can be classified: true positive (TP), true negative (TN), and false negative (FN).

Fig 1.

Description of the three categories in which a patient can be classified (true negative [TN]; false negative [FN]; true positive [TP]). N−, node negative; N+, node positive; p, pathologic.

Assumption 2 is that, for a given patient, all lymph nodes are exchangeable, that is they all have an equal probability of being involved. This enables us to average across patients for each possible number of examined nodes (step 3 of the algorithm). It is a biologically untenable assumption but cannot be relaxed unless examined nodes are individually identified in the data along with their characteristics (size, location, and so on) which is infeasible in all but the smallest studies. For this reason, exchangeability of lymph nodes has been a standard, if unstated, assumption in most previous work. For example, all the studies that analyzed the correlation between survival and number of nodes examined implicitly invoked this assumption.^12–15

Assumption 3 is that the sensitivity is the same for true positives and false negatives. Sensitivity in the above algorithm can be computed only on the pathologically node-positive patients. Making this assumption enables us to generalize the findings to pathologically node-negative patients as well.

Estimation of Prevalence of Nodal Disease

The observed prevalence (called apparent prevalence hereafter) is an underestimate and needs to be adjusted for false negatives. This was done in two steps; the first step invokes Assumption 1 and estimates #FN_k as a function of k:

where #TP_k is the number of true positives for a given k. Since prevalence is not a function of k, the second step obtains the adjusted prevalence by averaging over k:

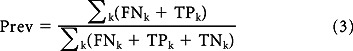Estimation of prevalence is stratified by T stage but is not explicitly noted in the above formula to avoid cumbersome notation.

Nodal Staging Score

Adequate staging was assessed by computing NSS, the probability that a pathologically node-negative patient is indeed free of nodal disease:

CIs

Precision of the reported estimates was assessed by creating 2,000 bootstrap samples from the entire data set and replicating the estimation process. 95% CIs were formed using this bootstrap estimate of the corresponding sampling distributions.

Validation

Since follow-ups for these patients were not used for the estimation of predictive probabilities, they provide a natural way to internally validate our findings. We split the NSS into four quartile groups and constructed survival curves stratified by T stage.

RESULTS

On the basis of a median number of 10 nodes examined, 64.4% of the patients were deemed node negative. Nodal harvest for T3-4N0 patients reaches the levels of that for N1 patients but not for N2 patients (Table 1).

Table 1.

No. of Examined Nodes by T and N Stage

Stage	Patients		Nodes Examined
	No.	%	Mean	SD	Median	IQR
T stage (all patients)
1	16,575	12.6	9.6	8.5	7	4-13
2	20,453	15.5	11.7	8.5	10	6-15
3	78,127	59.2	13.8	9.4	12	7-18
4	16,798	12.7	13.5	9.4	12	7-17
T stage (N0 patients)
1	14,944	17.6	9.5	8.4	7	4-12
2	16,684	19.7	11.6	8.5	10	6-15
3	45,201	53.2	13.4	9.3	11	7-17
4	8,095	9.5	12.8	9.3	11	6-16
N stage
0	84,924	64.4	12.3	9.1	10	6-16
1	31,377	23.8	12.9	9.0	11	7-17
2	15,652	11.9	16.2	9.7	14	10-20

Abbreviations: SD, standard deviation; IQR, interquartile range.

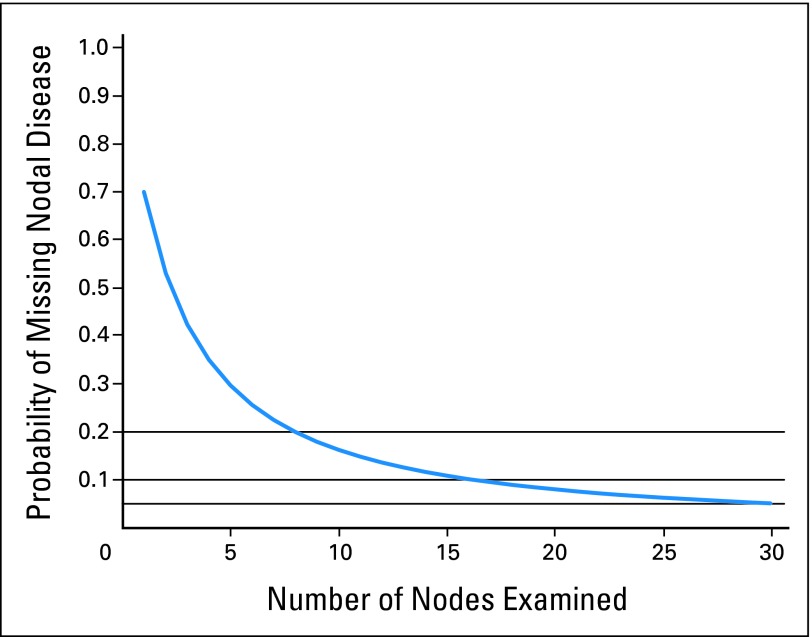
Using our model, the beta-binomial parameters α and β are estimated to be 1.24 (95% CI, 1.22 to 1.26) and 2.89 (95% CI, 2.83 to 2.94). The resulting probability of missing nodal disease (one minus the sensitivity) as a function of nodes examined is plotted in Figure 2. As expected, the probability of missing nodal disease decreases as the number of nodes examined increases (Appendix Table A1, online only): if only a single node was examined on all patients, 70% of all node-positive patients would be misclassified as node negative. Even when 10 nodes are examined (median for our data), 16% would be misclassified. Increasing this to 12 (the current recommendation for adequate staging), the misclassification probabilities remain greater than 13%. Only when the number of nodes examined is 25 does the sensitivity of the method near 95%.

Fig 2.

Sensitivity of the pathologic evaluation of nodal disease. Vertical axis is the probability of missing nodal disease (one minus sensitivity).

The apparent prevalence of nodal disease is 36.6%, but accounting for false negatives, the corrected prevalence is 44.9% (Table 2). Underestimation of prevalence due to false negatives is observed for all T stages, but its extent increases by T stage. As many as 64.9% of T4 colon cancer patients are estimated to have nodal disease, up from an apparent rate of 53.1%.

Table 2.

Apparent and Corrected Prevalence of Nodal Disease

Prevalence (%)	All Patients	T1	T2	T3	T4
Apparent prevalence	36.6	10.0	18.9	43.4	53.1
Corrected prevalence	44.9	13.6	24.1	52.7	64.9

NOTE. Apparent prevalence is based on the final pathologic stage reported to the Surveillance, Epidemiology, and End Results registries, regardless of the number of negative nodes. Corrected prevalence takes into account the probability of false-negative findings based on the number of negative nodes.

Combining Table 2 and Appendix Table A2 (online only), we estimate that approximately 17.6% of all pN0 patients have undetected locoregional spread. The proportion of undetected locoregional spread also increases by T stage: 3.9% for pT1N0, 6.4% for pT2N0, 16.1% for pT3N0, and 24.5% for pT4N0 categories.

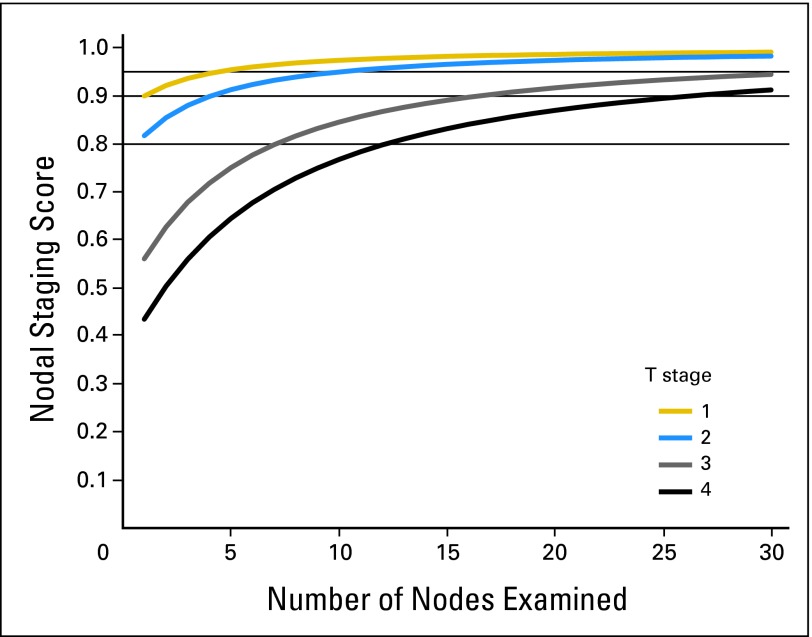
Nodal staging scores are presented in Figure 3 and Appendix Table A2. Patients with T1 and T2 tumors will have more than a 95% chance of a correct pathologic diagnosis of locoregional extent with four and eight examined nodes, respectively. The same levels of accuracy require 25 examined nodes in T3 patients and more than 30 for T4 patients. Bootstrap CIs for all the estimates reported in Table 2 and Appendix Table A2 are all within ± 1% (in absolute terms) of the estimates (data not shown).

Fig 3.

Predictive value a pathologic node–negative (pN–) diagnosis. Vertical axis is the probability of being truly N– for a pN– patient. There is a separate curve for each T stage.

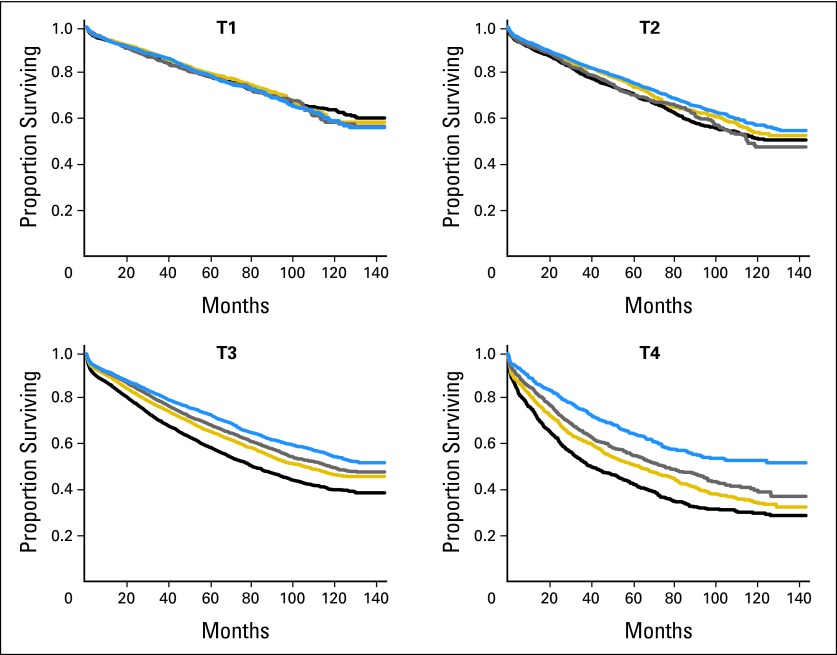
Figure 4 provides survival probability estimates as a function of predictive probabilities grouped on the basis of quartiles stratified by T stage. The four survival curves for T1 coincide (P = .82), but they are significantly separate for T2, T3, and T4 tumors (P < .01 for each of them).

Fig 4.

Survival probabilities as a function of the quartiles of the predictive values, stratified by T stage. The quartiles were 0.956, 0.972, and 0.982 for T1; 0.929, 0.957, and 0.972 for T2; 0.813, 0.874, and 0.913 for T3; and 0.721, 0.805, and 0.862 for T4.

DISCUSSION

Nodal stage is the major determinate of postoperative therapeutic course. If a patient is node negative after only a few nodes have been examined, the likelihood of understaging is nontrivial. Recognizing this, previous work has focused on defining adequate staging as a function of the number of examined nodes. Recommendations range from six to 19 nodes examined, and a minimum of 12 nodes has been embraced as a standard.^13,15

Most proposals regarding the minimum number of lymph nodes that should be examined are based on seeking a threshold for the number of examined nodes that maximizes the prognostic discrimination between the resulting groups. One study used a classification tree¹³ and others used Cox regression with SEER data,¹⁵ institutional data,¹⁴ or data from the National Cancer Data Base (NCDB).²⁵ One study used logistic regression on the number of nodes to predict the likelihood of a false-negative finding.²⁶

Our approach is markedly different from these studies and closer in spirit to the work of Joseph et al.²⁷ We subjected nodal staging to the statistical standards of a diagnostic test by computing the false-negative rate and using the negative predictive value to define a score that captures the adequacy of node-negative classification. These calculations cannot use empirical proportions because a gold standard is not available. Previous work used data from patients with at least 10 nodes examined as the gold standard.²⁷ This is an arbitrary and, in retrospect, an inaccurate choice.

Instead, we relied here on a few key assumptions and used a statistical model to estimate the NSS. One of these assumptions is that there are no false positives: once an involved node is harvested, it will invariably be classified as positive. This is a conservative and reasonable assumption, considering the relatively modest pathologic expertise needed to identify a positive node on the basis of routine histologic criteria. Another modeling assumption was the use of the beta-binomial model, which is considered standard in the analysis of hierarchical binary data. While we did not see lack of model fit, we also considered a hierarchical logistic regression approach which yielded similar results.

The assumption that all nodes within a patient have the same probability of being involved is critical for our work but arguably controversial. This assumption implies that number of examined nodes, and not their location or other specific information, is the only factor that determines whether a truly node-positive patient will be misclassified as node-negative. Strictly speaking, this assumption is unlikely to hold, but it is highly plausible that the number of examined nodes is the strongest factor, in which case the bias resulting from this assumption will be minimal. Further, nodal dissection studies lend support to this argument. For example, a recent study found that in 48% of the patients with a single positive node, the node closest to the primary tumor was negative.²⁸ In a multicenter study of the use of sentinel node in colon cancer, 58% of the sentinel nodes were negative in patients with positive nodes.²⁹ Taken together, these studies suggest a lack of orderly progression in mesenteric lymph node metastases and provide circumstantial support in favor of this assumption.

There are several advantages to our approach. NSS is the probability that a patient who is classified as node-negative is indeed free of nodal disease. It has a direct and familiar interpretation, enabling our results to be easily incorporated into patient counseling and decision making. The effect of T stage on accuracy is naturally incorporated since the prevalence of nodal disease is related to depth of penetration of the primary lesion into the colon wall. It also becomes evident (Figs 2 and 3) that there is no obvious threshold beyond which accuracy improves drastically. Rather, our results indicate a spectrum of small improvements with each additional node examined.

Our method also allows for the estimation of the extent of understaging. After accounting for false negatives, the prevalence of nodal disease in colon cancer is nearly 45%, implying that, of all patients who are diagnosed as pathologic node-negative, approximately 18% are actually node-positive. Presuming that 100,000 patients receive a primary colon cancer diagnosis every year, 65,000 of whom are staged as pN0, this translates to roughly 12,000 patients who are incorrectly staged. Again, by our estimation, approximately 3,000 of these patients (25%) will be misclassified as stage I and the remaining 9,000 (75%) will be misclassified as stage II. Five-year survival rates are approximately 75%, 65%, and 50% for stage I, II, and III patients, respectively, indicating the severity of the consequences of the incorrect prognosis these patients are receiving.

Despite the current joint recommendation from International Union Against Cancer (UICC), American Joint Committee on Cancer (AJCC), and College of American Pathologists to examine at least 12 nodes before nodal status can be established, the compliance with this recommendation is less than 50%.^30,31 This explains our finding that one sixth of all pathologic node-negative and one quarter of all pT4N0 patients have undetected locoregional spread. On the basis of our analysis, the dichotomy of adequate staging based on 12 examined nodes seems to be a misplaced notion for T4 tumors: we estimate that 20% of adequately staged pT4N0 patients have undetected nodal disease. However, insisting on 12 nodes for T1 patients seems equally unjustified: five negative nodes for a T1 patient afford the same level of confidence as 12 negative nodes do for a T2 patient.

It may seem remarkable that examination of even a single node in T1 tumors provides an NSS of 90% or more. The baseline against which all these numbers should be compared is the prevalence of node-negative disease, estimated to be 88% for T1 tumors. In other words, if 88% accuracy was deemed acceptable, there would be no need to examine lymph nodes for T1 tumors. It is unlikely that such a proposal would ever be embraced; it is used here to illustrate that the interpretation of NSS critically depends on prevalence. As a clinical example, consider the decision of adjuvant therapy for a pT4N0 patient with 12 nodes examined. NSS for this patient is 83, indicating a chance of one in six of missed nodal disease (Fig 3 and Appendix Table A2). While this patient would have been considered adequately staged under current guidelines, this number is likely to be deemed unacceptably high by either the treating physician or the patient.

It is important to externally validate the use of the nodal staging score in various clinical settings. Since there is no gold standard (true nodal status), the score needs to be validated against time to recurrence or death to ensure that it can discriminate patients who are at high risk of having missed occult nodal disease.

In brief, we developed a score that is an estimate of the probability that a pN0 patient is indeed free of locoregional spread. The results indicate that NSS exhibits a spectrum with no apparent thresholds. We recommend that thresholds on the required number of nodes be decided on the basis of the desired level of accuracy (NSS) separately for each T stage. Our results may serve as a different, and perhaps more relevant, starting point for the discussion of what constitutes adequate nodal staging. From a clinical standpoint, NSS can effectively be used routinely in clinics as an instrument to decide whether a node-negative colon cancer patient is adequately staged.

Appendix

Table A1.

Probability of Missing Nodal Disease for Selected Values of Examined Nodes

Parameter	No. of Nodes Examined (%)
	1	5	8	10	12	15	18	20	25
Probability of missing nodal disease	70.0	28.8	20.0	16.3	13.6	10.9	9.0	8.0	6.3

NOTE. Probabilities are independent of T stage.

Table A2.

Nodal Staging Score for Selected Values of No. of Nodes Examined

Stage	No. of Nodes Examined (%)
	1	5	8	10	12	15	18	20	25
T1	91.5	96.3	97.5	98.0	98.3	98.7	98.9	99.0	99.2
T2	84.5	92.9	95.2	96.1	96.7	97.4	97.8	98.1	98.5
T3	60.8	78.9	84.9	87.4	89.3	91.3	92.8	93.5	94.9
T4	47.9	68.9	76.9	80.5	83.2	86.2	88.4	89.5	91.7

NOTE. Calculation of the probability of incorrect nodal staging by T stage and number of nodes examined can be used to find the probability of having nodal disease despite a pathological N0 classification. The number corresponding to patient's T stage and the number of examined nodes is the percent probability of the patient not having nodal disease.

AUTHORS' DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

The author(s) indicated no potential conflicts of interest.

AUTHOR CONTRIBUTIONS

Conception and design: Mithat Gönen, Deborah Schrag, Martin R. Weiser

Financial support: Mithat Gönen, Deborah Schrag, Martin R. Weiser

Collection and assembly of data: Mithat Gönen, Deborah Schrag, Martin R. Weiser

Data analysis and interpretation: Mithat Gönen, Deborah Schrag, Martin R. Weiser

Manuscript writing: Mithat Gönen, Deborah Schrag, Martin R. Weiser

Final approval of manuscript: Mithat Gönen, Deborah Schrag, Martin R. Weiser