Finsler Tractography for White Matter Connectivity Analysis of the Cingulum Bundle

Abstract

In this paper, we present a novel approach for the segmentation of white matter tracts based on Finsler active contours. This technique provides an optimal measure of connectivity, explicitly segments the connecting fiber bundle, and is equipped with a metric which is able to utilize the directional information of high angular resolution data. We demonstrate the effectiveness of the algorithm for segmenting the cingulum bundle.

1 Introduction

Since the advent of diffusion weighted magnetic resonance imaging (DW-MRI), a great amount of research has been devoted to finding and characterizing neural connections between brain structures. In this paper, we present a novel approach for the segmentation of white matter tracts based on Finsler active contours [1]. Furthermore, we show results of the algorithm for segmenting the cingulum bundle (CB).

Recently, tractography advances have been made which provide full brain optimal connectivity maps from predefined seed regions. These approaches can be subdivided into stochastic and energy-minimization approaches.

Stochastic approaches produce probability maps of connectivity between a seed region and the rest of the brain. Parker et al. developed PICo, a probabilistic index for standard streamline techniques [2]. Perrin et al. presented probabilistic techniques for untangling fiber crossings using q-ball fields [3]. In other work, Friman et al. proposed a method for probabilistically growing fibers in a large number of random directions and inferring connectivity from the resulting percentages of connections between seed and target regions [4]. While providing a measure of connectivity between brain regions, these stochastic approaches do not provide an explicit segmentation of the fiber bundle itself.

Energy-minimization techniques have also been developed. Parker et al. proposed fast marching tractography which minimizes an energy based on both the position and direction of the normal to a propagating front [5]. O’Donnell et al. cast the tractography problem in a geometric framework finding geodesics on a Riemannian manifold based on diffusion tensors [6]. Similarly, Prados et al. and Lenglet et al. demonstrated a Riemannian based technique, GCM (Geodesic Connectivity Mapping), for computing geodesics using a variant of fast marching methods adapted for directional flows [7,8]. Jackowski et al. also find Riemannian geodesics using Fast Sweeping methods as given by Kao et al. [9,10,11]. In cases of high angular diffusion data, these Riemannian based approaches do not take advantage of the full directional resolution due to the loss of information incurred by the construction of diffusion tensors.

In this paper, we present a technique which provides an optimal measure of connectivity, explicitly segments the connecting fiber bundle, and is based on the richer Finsler metric. Rather than following the traditional approach of finding a large number of fibers (which individually have questionable meaning), clustering them, and then performing statistical analyses on the clusters, we present an alternative approach. We first find the optimal connection, which we term the anchor tract, on the Finsler manifold between the seed and target regions. Then, we initialize an expanding surface level set evolution on the anchor tract which grows until it stops at a local minima on the edge of the fiber bundle. Finally, since the fiber bundle extraction does not rely upon standard statistical measures, such as fractional anisotropy (FA), for the segmentation, we are free to use these measures to statistically compare fiber bundles in clinical studies.

In Section 2, we motivate our interest in segmenting the cingulum bundle. In Section 3, we describe the algorithm for extracting the anchor tracts. Then, in Section 4, we present our surface evolution algorithm for extracting the full cingulum bundle. Finally, in Section 5, we show results for extracting the anchor tracts and the corresponding cingulum bundle.

2 The Cingulum Bundle

The cingulum bundle is a 5–7 mm in diameter fiber bundle that interconnects all parts of the limbic system. It originates within the white matter of the temporal pole, and runs posterior and superior into the parietal lobe, then turns, forming a ”ring-like belt” around the corpus callosum, into the frontal lobe, terminating anterior and inferior to the genu of the corpus callosum in the orbital-frontal cortex [12]. Because of its involvement in executive control and emotional processing, the cingulum bundle has been investigated in several clinical populations, including depression and schizophrenia. Previous studies, using DW-MRI, in schizophrenia, demonstrated decrease of FA in anterior part of the cingulum bundle [13,14], at the same time pointing to the technical limitations restricting these investigations from following the entire fiber tract.

3 Anchor Tracts on a Finsler Manifold

In this section, we present our algorithm for extracting the optimal path, or anchor tract, between two regions in the brain. In this formulation, the optimal path is defined with respect to a Finsler metric. In the case of data acquired with only 6 gradient directions, this reduces to a Riemannian metric because there are 6 independent elements of the diffusion tensor. However, in the case of high angular data, the Finsler metric is more flexible than the Riemannian metric as it is not restricted to an ellipsoidal diffusion profile which results from the Gaussian diffusion assumption.

In order to find the anchor tract, we construct a dynamic programming based approach which uses a Fast Sweeping method, see [15,10,11] for algorithmic details. Also, see the work by Jackowski et al. for a formulation of this algorithm based on the Riemannian metric [9]. For the sake of completeness, we include a brief overview of the algorithm.

For any given starting point p₀, define the value function as the minimum cost for reaching a seed region S ⊂ ℝⁿ from p₀. The resulting Hamilton-Jacobi-Bellman equation is

$$\{\begin{array}{c}0=\underset{\widehat{\mathit{d}}\in S^{n-1}}{\text{inf}}\{\psi (\mathit{p},\widehat{\mathit{d}})+\nabla {ℒ}^{*}(\mathit{p})·\widehat{\mathit{d}}\},\hfill \\ {ℒ}^{*}(\mathit{s})=0\text{for}\mathit{s}\in S,\hfill \end{array}$$ (1)

where ψ is the local cost at each point, p, and for each direction, d̂, and ℒ* is the optimal Finsler length. Numerically, this equation may be solved via Fast Sweeping as shown in Algorithm 1.

Algorithm 1.

Sweeping algorithm for the HJB equation (1)

Require: seed region S, direction-dependent local cost ψ

1: Initialize ℒ* (·) ← +∞, except at starting points s ∈ S where ℒ* (s) ← 0

2: repeat

3:   sweep through all voxels p, in all possible grid directions

4:     d̂′ ← arg mind∈Sn−1 fℒ*,ψ(p,d̂)

5:     if fℒ*,ψ (p,d̂′) < ℒ* (p) then ℒ* (p) ← fℒ*,ψ (p,d̂′) and d̂* (p) ← d̂′ end if

6:   end sweep

7: until convergence of ℒ*

The Fast Sweeping algorithm results in optimal connectivity maps and characteristic vectors at every point in the domain. The anchor tract is then determined by following the characteristic vectors from the target region back to the seed region, not by gradient descent as is standard in direction-independent schemes [16].

There are many numerical schemes which may be used to solve the Hamilton-Jacobi-Bellman equation given above. The number of sweeping iterations required by the Fast Sweeping algorithm depends upon the number of turns in the optimal path. Since neural tracts tend to have few total turns, the Fast Sweeping algorithm is efficient for extracting tracts. We also note that the connections of graph cuts and such directional metrics have been described in [17,18,19]. Of particular note, in [18] the explicit connection between Finsler distances and the flux methods of [20] is considered in some detail.

4 Level Set Fiber Bundle Segmentation

In this section, we discuss the level set surface evolution which we have used to extract the volumetric cingulum bundle. This level set surface is initialized on the anchor tract described in Section 3. By using the calculus of variations, the minimizing flow for a directional cost ψ(p, d̂) is obtained as,

$${\Sigma }_t=-\{{\nabla }_{\mathit{p}}\psi ·N+Tr({\nabla }_{\widehat{\mathit{d}}\widehat{\mathit{d}}}\psi )+(n-1)\psi H\}N,$$ (2)

where Σ is the evolving hypersurface, N is the outward unit normal to the hypersurface, and H denotes the mean curvature. A derivation of this flow can be found in [21]. The expression for the evolution of the level set function ’u’ is obtained as,

$$u_t=\{{\nabla }_{\mathit{p}}\psi ·{\nabla }_u\}+\{Tr({\nabla }_{\widehat{\mathit{d}}\widehat{\mathit{d}}}\psi )+(n-1)\psi H\}\Vert {\nabla }_u\Vert .$$ (3)

We use the sparse field method of Whitaker et al. to efficiently implement this level set surface evolution [22]. We also use the angular interpolation algorithm presented by Tao et al. [23].

In order to find the edge of the cingulum bundle, we construct a cost, ψ, which aligns the tangent plane of the hypersurface with edges in the directions of diffusion of the image volume. To produce a measure of these diffusion edges, we compute the positional gradient of each diffusion direction. We then construct ψ as a function of these positional gradients.

Mathematically the form of the cost function that we desire to extremize can be written as follows.

$$\psi (\mathit{p},\widehat{\mathit{d}})=\psi (\mathit{p},N(\mathit{p}))=f({\nabla }_{\mathit{p}}\varphi (\mathit{p},d_1)·N,{\nabla }_{\mathit{p}}\varphi (\mathit{p},d_2)·N\cdots {\nabla }_{\mathit{p}}\varphi (\mathit{p},{\widehat{\mathit{d}}}_{n_s})·N)$$ (4)

where d₁ through d_ns denote the n_s diffusion directions, ϕ denotes the DWI data, N(p) denotes the normal to the hypersurface at position p, and f is a linear function of the arguments.

There are many possible choices for the function ψ. In this paper, we choose ψ to be the following:

$$\psi =\{\frac{1}{n_s}·\sum _{i=0}^{n_s}\frac{{\nabla }_{\mathit{p}}\varphi (\mathit{p},d_i)·N(\mathit{p})}{\Vert {\nabla }_{\mathit{p}}\varphi (\mathit{p},d_i)\Vert }\}-1.$$ (5)

This cost ranges from [−1,0] and is maximized (at 0) when the normal to the hypersphere is aligned with the mean gradient direction.

5 Experiments and Results

In this section, we present segmentation results for anchor tracts of the right and left cingulum bundles of 12 schizophrenic and 12 normal patients. Further, we present a first implementation of the level set surface flow introduced in Section 4. Scans were acquired on a 3 Tesla GE system (General Electric Medical Systems, Milwaukee, WI). We acquired 51 directions with $b=700\frac{s}{m{m}^2}$, 8 baseline scans with $b=0\frac{s}{m{m}^2}$. The following scan parameters were used: TR 17000 ms, TE 78 ms, FOV 24 cm, 144 × 144 encoding steps, 1.7 mm slice thickness. We acquired 81 axial-oblique slices parallel to the AC-PC line covering the whole brain.

Manually selected endpoints were provided by experts for each case. Masking is necessary to ensure that the tract does not take shortcuts through cerebral spinal fluid (CSF). We used a simple thresholding on the trace of the tensors to mask out CSF regions. Furthermore, we applied a threshold on strong left-right diffusion to mask out the corpus callosum which runs inferior to the cingulum bundle.

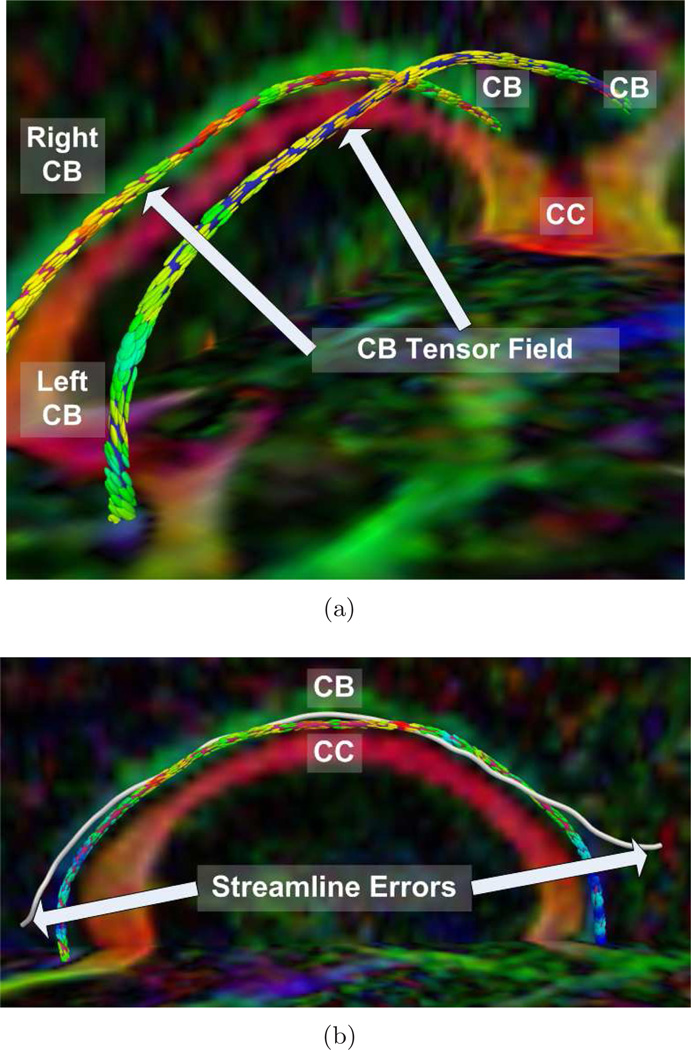
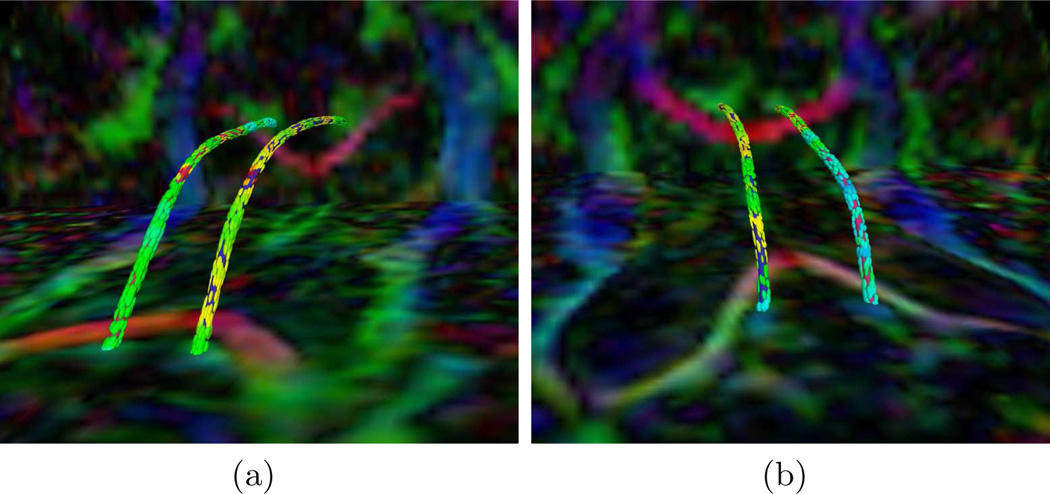
First, we show results of extracting the cingulum bundle anchor tract. In each figure, the tracts are superimposed upon the diffusion data which has been colored by direction (e.g. green signifies high anterior-posterior diffusion). The tensors, shown for convenience, are colored by FA. In Fig. 1, we depict the advantage of this algorithm in segmenting the cingulum bundle. The cingulum bundle curves around the ventricles on both the anterior and posterior ends. In Fig. 1(a), we show how the anchor tracts follow the smoothly varying tensor field around the bend of the ventricles. In Fig. 1(b), we share an example of a streamline based approach (freely available in the 3D Slicer tool) which fails in the same bend around the ventricles. This is the area where large tracts are joining the main bundle from both medial and lateral parts of the parietal lobes. Using the full directional data, our method is able to resolve the cingulum bundle in the presence of the merging fibers. In Fig. 2, we show anterior and posterior zoomed-out views of the anchor tracts.

Fig. 1.

Cingulum Bundle Anchor Tracts from: (a) detailed view of a normal control case, (b) streamline example on a schizophrenic case

Fig. 2.

Cingulum Bundle Anchor Tracts: (a) anterior and (b) posterior views of a normal control case

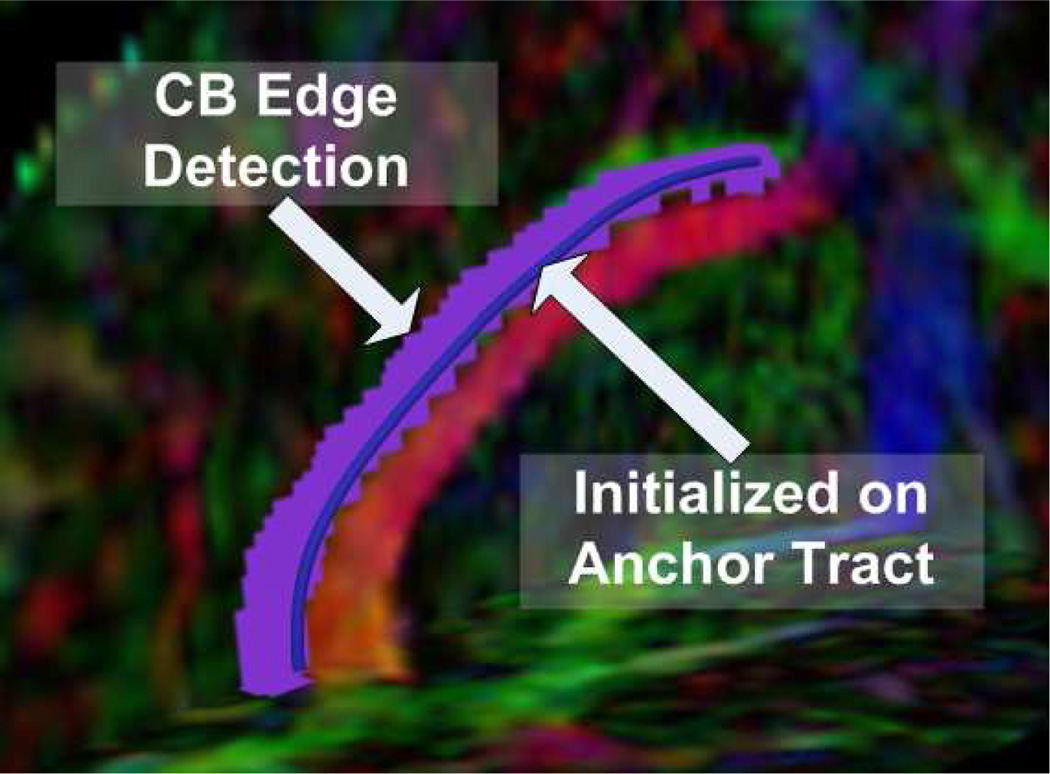
Next, we show the result of an edge-based surface level set evolution on a portion of the cingulum bundle. We present here a proof of concept implementation of the theory from Section 4. In our experiment, the level set flow converged to the edge of the bundle as depicted in the image.

6 Conclusions and Future Work

In this work, we have introduced a novel approach for the segmentation of white matter tracts. We have shown an application of the method for the segmentation of the cingulum bundle. Given manually selected endpoints, the algorithm automatically extracts the cingulum bundle.

We have shown how the method was able to find centerlines, or anchor tracts of the cingulum bundle on 24 cases. We have also shown a first implementation of the edge-based level set surface extraction. In the future, we will run the edge-based level set segmentation on all 24 cases. We will also explore the use of other cost functions, especially region-based costs, for the level set segmentation. Finally, we will be able to compute statistics across the resulting segmented cingulum bundles for the population of schizophrenics and normal controls.

Fig. 3.

Cingulum bundle level set segmentation result on a schizophrenic case