A statistically based flow for image segmentation

Abstract

In this paper we present a new algorithm for 3D medical image segmentation. The algorithm is versatile, fast, relatively simple to implement, and semi-automatic. It is based on minimizing a global energy defined from a learned non-parametric estimation of the statistics of the region to be segmented. Implementation details are discussed and source code is freely available as part of the 3D Slicer project. In addition, a new unified set of validation metrics is proposed. Results on artificial and real MRI images show that the algorithm performs well on large brain structures both in terms of accuracy and robustness to noise.

1. Introduction

The problem of segmentation, that is finding regions in an image that are homogeneous in a certain sense, is central to the field of computer vision. Medical applications, visualization and quantification methods for computer-aided diagnosis or therapy planning from various modalities typically involve the segmentation of anatomical structures as a preliminary step.

We consider the problem of finding the boundaries of only one anatomical region with limited user interaction. Interactivity is desirable since the user is given the opportunity to make use of important implicit external knowledge to guide the algorithm toward a result that makes sense for her task. The segmentation process can be repeated in order to identify as many regions as necessary.

Many different approaches have been proposed to address the segmentation problem which can be dually considered as finding regions or finding boundaries (see (Morel and Solimini, 1994), and references therein). Focusing only on the boundaries is computationally less complex but also less robust since information inside the region is discarded. This is the approach of the snakes and active contours variational methods (Kass et al., 1988; McInerney and Terzopoulos, 1996; Caselles et al., 1995).

While the original region-growing algorithm (Gonzalez and Woods, 2001) formalism is somewhat crude, interesting extensions have been proposed by Adams and Bischof (1994) where some statistical information is derived from the region as it expands. These techniques have been applied to medical image analysis (Justice et al., 1997; Pohle and Toennies, 2001). The relation between region-growing and active contours has been studied by Zhu and Yuille (1996) and more recently active contours have been extended by Chan and Vese (2001) and Paragios and Deriche (2002) to an elegant active regions formalism where regions boundaries are deformed according to an evolution equation derived to minimize an energy based on statistics on the regions.

This paper gives full details of our previously published conference results (Pichon et al., 2003). We briefly present a new variational method for region based segmentation based on non-parametric statistics (Section 2) and discuss how this algorithm has been implemented in the open-source software 3D Slicer (Section 3). We propose a novel validation framework (Section 4) and use it to analyze the performance of the proposed algorithm both on simulated and manually segmented images (Section 5). Appendices A and B give full mathematical details on the fundamental flow and the non-parametric estimation of image statistics.

We believe that the validation metrics outlined here should prove valuable for a number of segmentation problems in medical and other types of imagery.

2. Method

In this section we briefly present a very general flow for image segmentation. This technique is based purely on the statistics of the image. In particular it does not necessitate external information (such as an atlas) nor makes extra anatomy or modality-based assumptions. This method is therefore extremely versatile and we will show in Section 5 that it can compete with more specialized approaches.

Given an image I and a region R, we can write, using Bayes’ rule,

$$P(\mathbf{x}\in R\mid I(\mathbf{x}),||\nabla I(\mathbf{x})||)=P(I(\mathbf{x}),||\nabla I(\mathbf{x})||\mid \mathbf{x}\in R)\times \frac{P(\mathbf{x}\in R)}{P(I(\mathbf{x}),||\nabla I(\mathbf{x})||)}.$$

Assuming uniform priors P(x ∈ R) and P(I(x), ||∇I(x)||) the likelihood P(I(x), ||∇I(x)|||x ∈ R) and the posterior distributions P(x ∈ R|I(x), ||∇I(x)||) are proportional. We use the notation P_R(I(x), ||∇I(x)||) for either the likelihood or the posterior. This can be justified by the facts that:

• we do not know P(x ∈ R).

• using P(I(x), ||∇I(x)||) would introduce undesired global information. The existence in the dataset of another unrelated region with statistics similar to region R should not have any influence.¹

We accordingly define the energy functional

$$E(I,R):={\int }_R{P}_R(I(\mathbf{x}),||\nabla I(\mathbf{x})||)\text{d}\mathbf{x}.$$ (1)

Here, E(I, R) is the volume of the region R where each voxel is weighted by the probability P_R(I(x), ||∇I(x)||) of the intensity and the norm of the gradient of I at this voxel. Likely voxels therefore contribute more to E(I, R) than unlikely voxels and the energy of a region R will be high if and only if its voxels have consistent values in terms of intensity and norm of the gradient.

We can deform an initial region R₀ at t = 0 into a region R(t) to maximize E(I, R). We show in Appendix A that the gradient ascent flow is

$$\frac{\partial S}{\partial t}=P_R(I,||\nabla I||)\mathbf{N},$$ (2)

where S(t) = ∂R(t) the boundary of R at time t and N is the unit outward normal.

As the region is deformed, P_R is estimated in a non-parametric fashion as detailed in Appendix B.

3. Implementation

We implemented our method as a module of the open-source software 3D Slicer. It is freely available at http://www.slicer.org. Thanks to the properties of our flow, we were able to use a very efficient method for evolving the surface. Segmenting a large structure typically² takes less than 1 min.

The flow (2) is unidirectional (the surface can only expand since p_R ≥ 0) any voxel x is eventually reached at a time T (x). Knowing T is equivalent to knowing R or S since by definition

$$\{\begin{array}{l}R(t)=\{\mathbf{x},T(\mathbf{x})\le t\},\hfill \\ S(t)=\partial R(t).\hfill \end{array}$$ (3)

Solving the flow (2) for S(t) is equivalent to solving for T (x) the Eikonal equation

$$\left|\right|\nabla T(\mathbf{x})\left|\right|·p_R(\mathbf{x})=1.$$ (4)

This can be done very efficiently using the Fast Marching method (Tsitsiklis, 1995; Sethian, 1999). Starting from known seed points which define the initial surface, the algorithm marches outward by considering neighboring voxels and iteratively computing arrival times T in increasing order. The seed points are set by the user inside the structure to be segmented. By construction, when computing T (x), the surface contains the voxel x as well as all voxels for which T has already been computed. The algorithm terminates when T is known for all points. Then using (3) we can determine S(t) for any t and let the user determine what time t₀ of the evolution corresponds best to the region she wants.

Note that our method is, in its implementation, reminiscent of region growing. The min-heap data structure which makes Fast Marching efficient is the direct equivalent of the sequentially sorted list in the seeded region growing algorithm (Adams and Bischof, 1994). In fact our algorithm could be made a direct non-parametric extension of seeded region growing simply by artificially forcing arrival times to zero for all points inside the surface S. Relations between region growing and variational schemes have been previously exposed by Zhu and Yuille (1996).

4. Validation framework

Objective and quantitative analysis of performance is absolutely crucial (but often overlooked) when proposing a segmentation algorithm. Since designing a segmentation method is challenging (lack of unifying formalism, high diversity in the applications, subjectivity, implicitness, etc.) it does not come as a surprise that the validation of such an algorithm is also challenging. Different methods have been studied (see (Zhang, 1996), and references therein). We propose a unifying framework for discrepancy measures based on the number and the position of mis-segmented voxels and show how it relates to classical measures. We then apply it to the validation of segmentation of realistic synthetic images (for which the “ground truth”, i.e. perfect segmentation is known) at different levels of noise for accuracy and robustness assessment as well as to manual expert segmentation of real datasets.

4.1. Classical discrepancy measures

Different measures have been proposed to assess the resemblance between a proposed segmentation S and the corresponding ground truth G. The Dice Similarity Coefficient has been widely used and it can be derived as an approximation of the kappa statistic (a chance-corrected measure of agreement, see (Zijdenbos et al., 1994)). It is defined as

$$\text{DSC}(S,G):=\frac{V_{S\cap G}}{\frac{1}{2}(V_S+V_G)},$$

where V_X is the volume (number of voxels) of set X.

One disadvantage of this coefficient is that it only takes into account the number of mis-segmented voxels and disregards their position and therefore the severities of errors. This was corrected in Yasnoff’s discrepancy measure DM (Yasnoff et al., 1977) and the Factor of Merit FOM (Strasters and Gerbrands, 1991):

$$\begin{array}{l}\text{DM}:=\frac{1}{N}\sum _{i=1}^{N}d{(i)}^2,\\ {\text{FOM}}_{\text{e}}:=\frac{1}{N}\sum _{i=1}^N\frac{1}{1+d{(i)}^2},\end{array}$$

where N is the number of mis-segmented voxels and d(i) is the distance from the ith voxel to the ground truth. Another popular measure is the Hausdorff distance

$$H(S,G):=max\{\underset{s\in S}{max}\underset{g\in G}{min}||s-g||,\underset{g\in G}{max}\underset{s\in S}{min}||s-g||\}.$$

H(S,G) is the maximum distance we would have to move the boundaries of one set so that it would encompass completely the other set. As this is extremely sensitive to extreme errors, the partial Hausdorff distance (Huttenlocher et al., 1993) H_f (S,G) can be introduced as the maximum distance we would have to move the boundaries of one set so that it would cover f% of the other set.

4.2. Proposed framework

Consider now the error-distance

$$d(\mathbf{x}):=\{\begin{array}{ll}0,\hfill & \mathbf{x}\in S\cap G,\hfill \\ {min}_{s\in S}\left|\right|\mathbf{x}-s\left|\right|,\hfill & \mathbf{x}\in G\backslash S,\hfill \\ {min}_{g\in G}\left|\right|\mathbf{x}-g\left|\right|,\hfill & \mathbf{x}\in S\backslash G.\hfill \end{array}$$

Assuming that all points x ∈ S ∪ G are equally likely d can be seen as a random variable D which describes completely the discrepancy between the segmentation S and the ground-truth G. Using basic statistical tools we can define the probability of error (PE), mean of errors³ (μ_D>0), standard deviation of errors (σ_D>0) and partial distance-error (D_f) by

$$\begin{array}{l}\text{PE}:=Pr(D>0)\\ {\mu }_{D>0}:=\text{mean}(D\mid D>0),\\ {\sigma }_{D>0}:=\text{stdev}(D\mid D>0),\\ D_f:=f-\text{quantile}(D).\end{array}$$

These measures have a natural intuitive interpretation:

• PE is the probability for a voxel x ∈ S ∪ G to be mis-classified (either over- or under-segmented, i.e. (x ∈ S ∪ G) \ ((S ∩ G))).

• An erroneous voxel is on average μ_D>0 pixels off. This value is very typical if the standard deviation σ_D>0 is small.

• D_1−f is the error distance of the worst f% voxels. For example D_0.5 is the median of errors. Equivalently the maximum distance we would need to move erroneous voxels for the error to be improved to PE = f.

As an example, PE = 10%, μ_D>0 = 3.1, σ_D>0 = 0.3 and D_0.99 = 14 would mean that the overlap between the ground truth and the proposed segmentation is 90%. The 10% remaining pixels are either under-segmented or over-segmented pixels (“false positive” i.e. pixels that are in S and not in G). On average these pixels are 3.1 pixels off. This value is very typical since the standard variation is low (0.3). However there is no reason for the error to be Gaussian and, here, the tail probability is not negligible since the worst 1% pixels are at least 14 pixels off. This could be due to a thin, long finger of mis-segmented pixels.

Fig. 1 illustrates three different cases of mis-segmentation. Figs. 1(a) and (b) have approximately the same probability of error PE (and therefore the same DSC (see Eq. (5)) but Fig. 1(a) has a lower μ_D>0 and partial distance error D_0.95. This is due to the fact that even though Figs. 1(a) and (b) have roughly the same number of mis-segmented pixels, the errors tend to be more severe in Fig. 1(b). Fig. 1(c) illustrates the case of a low probability of error PE and a high μ_D>0. This might seem counter-intuitive. μ_D>0 is the mean of mis-classified points. Here, most points are correctly classified and the few points that are not are rather far off which explains a high μ_D>0. Moreover, the standard deviation of errors σ_D>0 is lower than in Fig. 1(b) since there are less small errors and therefore μ_D>0 is typical. Depending on the end-task Fig. 1(a) might be a better segmentation than Fig. 1(b) or not and any of the above mentioned measures might be the most important metric.

Fig. 1.

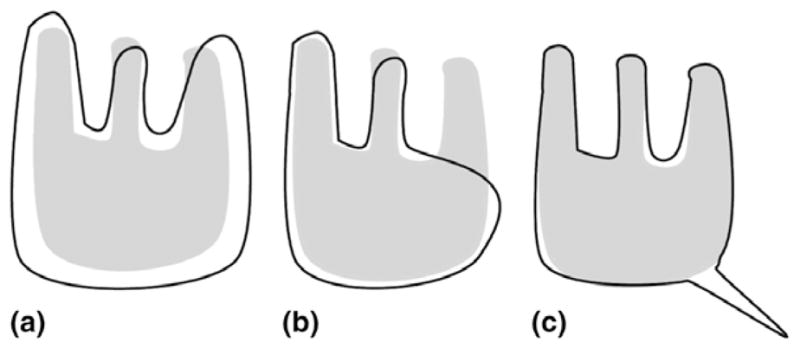
Three synthetic examples of mis-segmentation. The ground truth G is in gray and the segmentation S is in black.

These measures are related to the measures presented in Section 4.1 according to

$$1-\text{DSC}\le \text{PE}=\frac{1-\text{DSC}}{1-\frac{\text{DSC}}{2}},$$ (5)

$$\frac{1}{{\text{FOM}}_{\text{e}}}-1\le {\mu }_{D>0}^2+{\sigma }_{D>0}^2=\text{DM},$$ (6)

$$H_{1-\frac{f}{1-\text{PE}}\le D_{1-f}\le H_{1-\frac{f}{2}}}(\text{in}\text{particular},D_1=H).$$ (7)

Proof

• (5): let a, b, c, d be the true positive, true negative, false negative and false positive probabilities, respectively, then

  $$\begin{array}{l}\text{PE}=(c+d)/(a+c+d),\\ \text{DSC}=2a/[(a+c)+(a+d)].\end{array}$$

  Simple algebra yields the equality. The inequality follows immediately from the fact that 0 < 1 −DSC/2≤1.

• (6): By definition and implying condition D > 0 for all expectancies we have

  $$\begin{array}{l}\text{DM}=E\{D^2\}=E\{{[D-E\{D\}]}^2\}+E{\{D\}}^2\\ ={\sigma }_{D>0}^2+{\mu }_{D>0}^2,\end{array}$$

  which is the equality.

  For the inequality consider Y = D² and f (Y) = 1/(1 + Y). f″ ≥ 0 and therefore f is convex (on ℝ⁺). But FOM is E{f (Y)}. By convexity E{f (Y)}≥ f (E{Y}). Since f⁻¹(x) = 1/x − 1 is decreasing $f^{-1}(\text{FOM})\le E\{Y\}=({\mu }_{D>0}^2+{\sigma }_{D>0}^2)$.

• (7): let D_S = {d(x, G), x ∈ S} and D_G = {d(x, S), x ∈ S} be the distance of all points of one set to the other set. Consider that D_S and D_G are ordered such that value at rank 0 is the minimum. Then the partial Haussdorff distance H_1−f is the max of the values at index (fV_S) and (fV_G) in D_S and D_G. Consider D_S∪G to be the values of D_S and D_G where the points corresponding to S ∩ G (those values are all 0 by construction) are counted only once. We also consider that D_S∪G is sorted. Then the proposed metric D_1−f is the element at index (fV_S∪G). We know that

  $${fV}_{S\cup G}\ge \frac{f}{2}(V_S+V_G).$$
  This means that the value at index (fV_S∪G) of D_S∪G has to be smaller or equal to the largest of the value at index $(\frac{f}{2}{V}_S)$ of D_S and the value at index $(\frac{f}{2}{V}_G)$ of D_G. The equality occurs only when these two values are equal. This proves the right-hand side of (7). For the left side, use

  $${fV}_{S\cup G}=\frac{f}{1-\text{PE}}{V}_{S\cap G}\ge \frac{f}{1-\text{PE}}min\{V_S,V_G\}.$$

5. Validation results

We evaluated the validation algorithm proposed in Section 2 using the validation framework proposed in Section 4 on 2 simulated and 10 real MRI brain datasets. It is fundamental to understand that the proposed algorithm is very general. In particular it is not designed or tuned for any particular structure. Other approaches have been proposed that necessitate (and take advantage of) prior information. For example in (Tsai et al., 2003) a model of brain structures (i.e., an atlas) is deformed to match the dataset; in (McInerney and Terzopoulos, 1996; Zeng et al., 1999), the white and gray matter of the brain are segmented using special geometric constraints based on the neuroanatomical knowledge that the thickness of the cortical mantle is nearly constant; in (Shattuck and Leahy, 2002) the datasets are pre-processed to compensate for bias fields in the MR images and non-brain tissue is removed. Our framework is more general and does not require external information or make extra assumptions on the anatomical region to be segmented or the imaging modality. Because implementations of previously proposed segmentation techniques are typically not publicly available and these algorithms were typically not validated on publicly available datasets it is difficult to quantitatively compare performances. In contrast an implementation of our technique is freely available (as part of the open-source software 3D Slicer). The technique has been validated on publicly available simulated and real datasets.

The work of Shattuck and Leahy (2002) is a notable exception since it has been validated on publicly available images. We will show in Section 5.1 that even though it is very general and assumption free, the performance of the proposed technique is comparable to this more specialized approach.

5.1. Simulated datasets (N=2)

The Brain Web datasets have been generated from a known ground truth using a physical modeling of the MRI process (Kwan et al., 1999). We can assess in a perfectly objective way the performance of our method by comparing the result of our segmentation with the underlying ground truth. Note that even though these datasets are computer-generated they are very realistic (see Fig. 2(b)) Another interesting aspect of this project is that from the same ground truth, datasets with different levels of noise can be simulated which allows us to study the robustness of our method with respect to noise. Using the proposed framework, the authors segmented the lateral ventricle, white matter (WM) and white matter and gray matter (WM+GM) on 2 datasets:

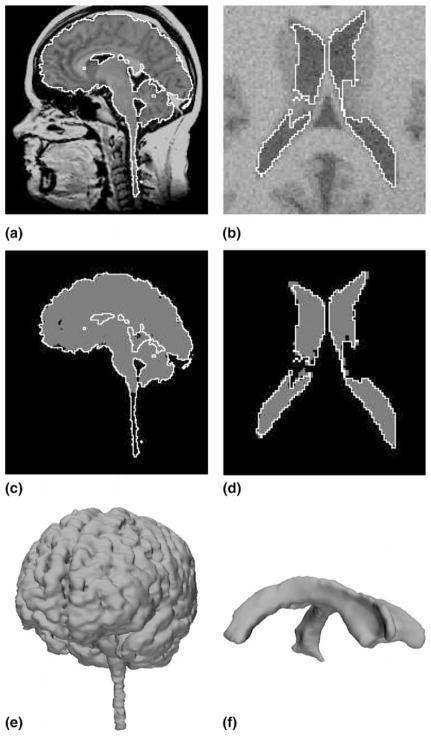
Fig. 2.

Results on real and noisy simulated datasets (left and right respectively): (a) sagittal slice of real dataset and proposed segmentation (WM+GM); (b) axial slice of artificial dataset and proposed segmentation (ventricle); (c) expert segmentation (gray) and proposed segmentation (white); (d) underlying ground truth (gray) and proposed segmentation (white); (e) rendered surface of proposed segmentation (WM+GM); (f) rendered surface of proposed segmentation (ventricle).

• Normal brain, T1, 1 × 1 × 1 mm (181 × 181 × 217 voxels), 3% noise, 20% intensity non-uniformity (“RF”) (standard parameters of the Brain Web model).

• Normal brain, T1, 1 × 1 × 1 mm (181 × 181 × 217 voxels), 9%, 40% (highest levels of noise available).

The results (Table 1) show that the proposed algorithm gives very good results on these structures (according to Zijdenbos et al. (1994), DSC > 0.7 is regarded as good agreement in the literature). The complex structure of the white matter makes its segmentation more challenging and explains the somewhat mediocre performance (in the case of the maximum noise dataset, the cerebellum was not perfectly segmented).

Table 1.

Performance measure on artificial dataset

	DSC (%)	PE (%)	μD>0	σD>0	D0.95	D0.99
Ventricle	92.0 95.1	14.9 9.4	1.07 1.13	0.48 0.61	1.00 1.00	1.00 1.41
WM	91.9 80.3	15.0 32.0	1.59 2.03	1.58 1.94	1.00 2.83	3.61 8.25
WM+GM	96.2 95.2	7.4 9.2	1.42 1.40	1.25 1.15	1.00 1.00	1.41 2.00

Left bold, with standard noise, right, with maximum noise.

In the highest level of noise, connectivity between the lateral and the third ventricles was lost (the intraventricular foramen of Monro disappeared in the noise). This increased the strength of the ventricle edges in the noisy dataset and, paradoxically, simplified the segmentation. Overall the algorithm appears extremely robust to noise.

On the same datasets, Shattuck and Leahy (2002) report⁴ DSC = 93% (standard noise) and DSC = 81% (maximum noise) for the white matter. These scores are slightly better than our own results (DSC = 91.9% and DSC = 80.3%, respectively). However, it is very important to keep in mind that there is a trade-off between performance on a specific problem and versatility. Our technique was not created specifically for white matter extraction and, unlike more specialized techniques, it can be used for a very wide variety of structures and modalities. In summary, the wide applicability of the proposed technique comes at a minor performance cost vis-à-vis the work of Shattuck and Leahy (2002).

5.2. Real datasets (N = 10)

In this section we use, as the ground truth, the expert manual segmentations of 10 full brains and brain tumors from the Brain Tumor Database (Kaus et al., 2001). The semi-automatic segmentation was performed by a student with no special medical training and no inside knowledge of the proposed algorithm.

The 10 patients’ heads were imaged in the sagittal and axial plane with a 1.5 T MRI system⁵ with a postcontrast 3D sagittal spoiled gradient recalled (SPGR) acquisition with contiguous slices. The resolution is 0.975 × 0.975 × 1.5 mm (256 × 256 × 124 voxels). Datasets where manually segmented into three regions:

• tumor

• white and gray matter

• other

Because of inter- and intra-expert variability we should expect these results not to be as good as in the synthetic case. It should also be noted that the arbitrary conventions of the manual segmentations are responsible for a lot of the observed error since for example the ventricle was labeled as gray matter, the medulla oblongata and the spinal cord have been left out etc. (compare Figs. 2(a) and (c)). Overall, nonetheless, results are consistent with the artificial case (Tables 2 and 3).

Table 2.

Performance measure for white and gray matter segmentation on real datasets

	DSC(%)	PE(%)	μD>0	σD>0	D0.95	D0.99
Mean	88.9	19.8	1.79	1.47	2.03	4.91
Std. Dev.	4.0	6.3	0.58	0.79	1.52	2.82
Case 1	89.5	19.0	1.45	0.87	1.41	3.00
Case 2	90.6	17.1	2.29	2.44	2.00	8.25
Case 3	90.9	16.6	1.39	0.80	1.41	2.83
Case 4	84.7	26.5	1.28	0.79	1.41	3.00
Case 5	93.3	12.5	1.58	1.48	1.00	3.00
Case 6	87.0	23.0	1.87	1.66	2.24	5.66
Case 7	86.5	23.8	1.89	1.68	2.24	6.08
Case 8	81.3	31.6	3.15	3.00	6.16	10.67
Case 9	91.4	15.9	1.83	0.48	1.00	1.73
Case 10	93.8	11.8	1.19	0.48	1.00	1.73

Table 3.

Performance measure for tumor segmentation on real datasets

	Tumor Type	DSC (%)	PE(%)	μD>0	σD>0	D0.95	D0.99
Mean	–	83.1	27.6	1.54	0.88	2.35	3.65
Std. Dev.	–	10.9	15.8	0.53	0.72	1.73	2.70
Case 1	meningioma	94.6	10.2	1.07	0.27	1.00	1.41
Case 2	meningioma	87.2	22.8	1.43	0.79	1.73	3.16
Case 3	meningioma	97.5	4.9	1.03	0.15	0.00	1.00
Case 4	low grade glioma	84.0	27.6	1.51	0.90	2.24	2.24
Case 5	astrocytoma	65.7	51.1	1.36	0.56	2.24	3.16
Case 6	low grade glioma	92.1	14.7	1.07	0.24	1.00	1.41
Case 7	astrocytoma	88.9	20.0	1.16	0.35	1.41	2.00
Case 8	astrocytoma	70.6	45.4	2.03	1.49	4.12	6.40
Case 9	astrocytoma	72.7	42.8	2.09	1.80	4.36	7.48
Case 10	low grade glioma	77.7	36.4	2.61	2.20	5.39	8.25

6. Conclusion

We presented a new surface evolution flow based on learned non-parametric statistics of the image. Implementation is straightforward and efficient using the Fast Marching algorithm and is freely available as part of the 3D Slicer project. An extensive validation study as well as a new unified set of validation metrics have also been proposed.

Future work will include a detailed analysis of the variational and statistical aspects of the algorithm. An expansion of the validation framework is also underway.

Appendix A. A fundamental flow

In what follows we only consider the 3D case. The region R is an open connected bounded subset of ℝ³ with smooth boundary S = ∂R and N denotes the corresponding inward unit normal vector to S.

Given an image I, a non-negative weighting function w(·, ·) and a region R we define the energy

$$E(I,w,R):={\int }_{R}w(I(\mathbf{x}),||\nabla I(\mathbf{x})||)\text{d}\mathbf{x}.$$ (A.1)

where E is the weighted volume of the region R. The weight of a voxel x is determined by the function w(·, ·) of the local properties I(x) and ||∇I(x)|| of the image. Ideally, w should reflect the local properties of the region we want to segment. As this is not known a priori we heuristically estimate w as we evolve R to maximize E.

Proposition 1

Notation as above. Then for a given weighting function w, the evolution in which the energy E(I, w, R) is decreasing as fast as possible (using only local information) is $(\frac{\partial S}{\partial t})=w\mathbf{N}$.

Proof

Let ψ^t: R → ℝⁿ be a family of embeddings, such that ψ⁰ is the identity. Let w: ℝⁿ → ℝ be a positive C¹ function. We set R(t):= ψ^t(R) and S(t): = ψ^t(∂R). We consider the family of w-weighted volumes

$$H(t):={\int }_{R}w({\psi }^t(\mathbf{x}))\text{d}{\psi }^t(\mathbf{x})={\int }_{R(t)}w(\mathbf{y})\text{d}\mathbf{y}.$$

Set $X=\frac{\partial {\psi }^t}{\partial t}{\mid }_{t=0}$ then using the area formula (Simon, 1983) and then by the divergence theorem, the first variation is

$$\frac{\text{d}H}{\text{d}t}{\mid }_{t=0}={\int }_R\text{div}(wX)\text{d}\mathbf{x}=-{\int }_{\partial R}(wX)·\mathbf{N}\text{d}\mathbf{y},$$ (A.2)

where N is the inward unit normal to ∂R. Consequently the corresponding w-weighted volume minimizing flow is

$$\frac{\partial S}{\partial t}=w\mathbf{N}.$$

A different derivation of the same result has previously been proposed by Siddiqi et al. (1998).

Since w is a non-negative function, the flow is reversible. In particular, the flow in the reverse direction,

$$\frac{\partial S}{\partial t}=-w\mathbf{N},$$ (A.3)

gives the direction in which the energy is increasing as fast as possible (using local information). In the context of segmentation, one may think of (A.3) as a bubble and of the original flow as a snake.

Given an approximation R₀ of the region to be segmented we can use a maximum likelihood-like approach to determine the weighting function w₀ which would a posteriori justify the segmentation of R₀.

Proposition 2

For a given fixed region R₀, the energy E(I, w, R₀) is maximized by setting w to p_R0 the conditional probability on that region

$$\begin{array}{l}{p}_{R_0}=arg{max}_{w,{\left|\right|w\left|\right|}_1=1}E(I,w,R_0)\\ =P(I(\mathbf{x}),||\nabla I(\mathbf{x})||\mid \mathbf{x}\in R_0).\end{array}$$ (A.4)

Proof

We can rewrite the energy as

$$E(I,w,R_0)={\int }_I{\int }_{\left|\right|\nabla I\left|\right|}{N}_{R_0}(u,v)·w(u,v)\text{d}u\text{d}v,$$

where N_R0 (u, v) is the volume of the set of points x ∈ R₀ such that I(x) = u and ||∇I(x)|| = v. But this is just a constant multiple of p_R0 = P(I(x), ||∇I(x)|||x ∈ R₀) which is therefore by the Schwartz’s inequality is the maximizer of E.

As the region evolves, w is periodically updated according to (A.4). This changes the definition of the energy (A.1) and therefore (A.3) can only be considered a gradient flow for every time interval when w is fixed.

Appendix B. Non-parametric estimation of image statistics

Instead of using the distribution p_R0 = P(I(x), ||∇I(x)|||x ∈ R₀) as described in (A.4) we use p = p_M · p_H, where M and H are the median and inter-quartile range (the difference of between the first and last quartile) operators on a 3 × 3 × 3 neighborhood. M and H convey about the same information as I (gray level) and ||∇I|| (local homogeneity). For example if ||∇I|| is large then values in a 3 × 3 × 3 neighborhood are very dispersed and therefore the interquartile range is large. These measures were chosen primarily because they are robust to noise ⁶ and they respect edges ⁷ of the image better than their linear counterparts.

We use Parzen windows (see for example Duda et al., 2001) to estimate the probability density functions. This is a non-parametric technique and therefore no assumption is required on the shape of the distributions. Given a window function φ and N samples m₁, …, m_N and h₁, …, h_N the densities are estimated by

$$\begin{array}{l}{\widehat{p}}_M(m)=\frac{1}{N}\sum _{i=1}^N\phi (m-m_i),\\ {\widehat{p}}_H(h)=\frac{1}{N}\sum _{i=1}^N\phi (h-h_i).\end{array}$$

This corresponds to convolving the samples histogram with φ. It can be shown that the estimates p̂_M and p̂_H converge toward the true estimates p_M and p_H with n → ∞ and φ → δ. We used φ = g_σ a centered Gaussian kernel of standard deviation σ = σ̂_H/10 to estimate p_H and σ = σ̂_M/10 to estimate p_M.