Abstract
An important element of radiation treatment planning for cancer therapy is the selection of beam angles (out of all possible coplanar and non-coplanar angles in relation to the patient) in order to maximize the delivery of radiation to the tumor site and minimize radiation damage to nearby organs-at-risk. This category of combinatorial optimization problem is particularly difficult because direct evaluation of the quality of treatment corresponding to any proposed selection of beams requires the solution of a large-scale dose optimization problem involving many thousands of variables that represent doses delivered to volume elements (voxels) in the patient. However, if the quality of angle sets can be accurately estimated without expensive computation, a large number of angle sets can be considered, increasing the likelihood of identifying a very high quality set. Using a computationally efficient surrogate beam set evaluation procedure based on single-beam data extracted from plans employing equally-spaced beams (eplans), we have developed a global search metaheuristic process based on the Nested Partitions framework for this combinatorial optimization problem. The surrogate scoring mechanism allows us to assess thousands of beam set samples within a clinically acceptable time frame. Tests on difficult clinical cases demonstrate that the beam sets obtained via our method are superior quality.
1. Introduction
Intensity-modulated radiation therapy (IMRT) treatment plan optimization has been an essential part of the treatment planning environment. In IMRT the radiation beam from each orientation is effectively modulated (that is, radiation is delivered at different levels through different apertures at any given beam angle) in order to deliver a highly conformal dose to the tumor while reducing the dose to surrounding organs at risk (OARs). However, the optimization algorithms implemented in most commercial planning systems require the clinician to enter beam delivery angles as inputs prior to invoking those algorithms. This first planning step in IMRT thus typically requires the selection of 5 to 9 angles (from all possible coplanar and non-coplanar angles in relation to the patient) that distribute radiation among nearby non-cancerous tissues and thereby minimize radiation damage to those tissues. (An alternative treatment modality known as volumetric modulated arc therapy (VMAT) delivers radiation continuously along one or more arcs as the gantry revolves around the patient, hence VMAT does not require or allow the selection of a discrete set of treatment angles. Theoretical comparison of IMRT and VMAT treatment quality is the subject of ongoing research. However, clinical comparison of the two has been shown for a variety of cases, including prostate, cervical, anal canal, lung, brain, breast and head and neck.)
Investigators have demonstrated the added value of carefully selecting beam orientations in IMRT treatment planning with improved dose distributions (Das et al 2003, Liu et al 2006), lowered total body integral dose (Srivastava et al 2011) and reduced number of beams to achieve clinically acceptable plans (Narayanan et al 2012). Considerable research effort has also been devoted to optimizing beam orientations in a treatment plan, including both exact approaches (Bortfeld and Schlegel 1993, Lee et al 2006) and heuristics (Wang et al 2004 and 2005, Pooter et al 2006, Lim et al 2008, Lim and Cao 2012, Bertsimas et al 2012). Most recent work includes utilizing multi-criteria dose optimization to evaluate beam orientations (Breedveld et al 2012), applying adaptive optimization to generate quality angle sets (Jia et al 2011). Fiege et al (2011) and Craft and Donz (2010) incorporated beam orientation parameters directly into Pareto model as criteria during multi-objective optimization. Munawar et al (2010) showed that function imaging, in particular SPECT ventilation images, can be used to select potential beams for IMRT.
IMRT problems are large-scale combinatorial problems and treatment plans must be generated in a reasonable amount of time. In particular, when both dose optimization and beam angle selection are considered at the same time, finding the optimal solution of such a combinatorial problem is an extremely difficult task. Despite overwhelming evidence in the literature that appropriate beam angle choices can lead to improvements in plan quality (Srivastava et al 2011), beam angle selection continues to customarily be performed as a manual process prior to dose optimization. To make the beam angle selection (BAS) methods practical for clinical use, researchers tried to develop fast algorithms by using simple geometric measures of patient anatomy (Potrebko et al 2007), by ranking of the beams (Vaitheeswaran et al 2010), by transforming the problem to a set cover problem (Lee et al 2011) and by using fast heuristic approach (Bangert and Oelfke 2010). Nazareth et al (2009) and Zhang et al (2009) used a distributed computing environment to speed up the computation time.
In this paper, we propose a surrogate-based method in order to enable evaluation of thousands of beam sets quickly. Quick evaluations are embedded within a global search framework, Nested Partitions (NP), coupled with a restricted search heuristic for local improvement. The global viewpoint maintained by NP represents a key difference between this method and other randomized strategies such as simulated annealing and genetic algorithms, which tend to more narrowly focus their search processes. Besides being able to evaluate large number of beam sets efficiently, the scope of this work is to improve the clinical quality of beam angles. Therefore, NP algorithm was benchmarked against clinically-selected beam angle sets, beam angle optimization results from Eclipse™ (Varian Medical Systems, Palo Alto, CA) and conventional NP without restricted search (D’Souza et al 2008). The framework was tested on five challenging clinical head and neck cases. The results given below on these cases via our approach demonstrate clinically significant improvements in treatment plans relative to these other approaches. Our focus in this research has been on head-and-neck cases, since these cases are difficult to treat because of the proximity of several sensitive structures. For less challenging tumors in other sites, there may be less likelihood of significant improvement relative to manually selected beam sets, but the automation of the beam selection process still remains a desirable goal.
2. Methods and Materials
2.1. Clinical Cases and Initial Equi-spaced-beam plans (Eplan) Knowledge Base
We retrospectively selected 5 locally advanced head and neck cancer cases that had undergone radiation therapy in our clinic. The treatment targets involved the primary tumor and the lymph nodes. A simultaneous-integrated boost (SIB) was employed as the mode of delivery, in which the prescribed dose to the primary tumor, high-risk nodes and low-risk nodes was 70 Gy, 59.4 Gy and 54 Gy, respectively in 35 fractions. The OARs included the parotid glands, the oral cavity including the oral mucosa, the brain stem and the spinal cord. We used previously published dose-volume constraints (Lee et al 2007) in the optimization process (see Table 1).
Table 1.
Summary of dose and dose-volume constraints for locally advanced head and neck cases.
| Dose | Volume | Weight |
|---|---|---|
| % volume of left parotid receiving ≥ 26 Gy | 66 | 3 |
| % volume of left parotid receiving ≥ 32 Gy | 33 | 3 |
| % volume of right parotid receiving ≥ 26 Gy | 66 | 3 |
| % volume of right parotid receiving ≥ 32 Gy | 33 | 3 |
| % volume of oral mucosa receiving ≥ 30 Gy | 90 | 8 |
| % volume of oral mucosa receiving ≥ 40 Gy | 30 | 8 |
| Maximum cord dose | 45 Gy | 15 |
| Maximum brain stem dose | 54 Gy | 15 |
| % volume of low-risk PTV receiving ≥ 54 Gy | 95 | 6 |
| % volume of low-risk PTV receiving ≥ 59.4 Gy | 5 | 6 |
| % volume of high-risk PTV receiving ≥ 59.4 Gy | 95 | 6 |
| % volume of high-risk PTV receiving ≥ 70 Gy | 5 | 6 |
| % volume of primary PTV receiving ≥ 70 Gy | 95 | |
| % volume of primary PTV receiving ≥ 77 Gy | 5 |
Equi-spaced-beam plans (eplans) were generated for each of the 5 cases via Pinnacle3 (Philips Healthcare, Fitchburg, WI). Each eplan consists of 7 beams from 5-degree-spaced beams in the range 0-355. A total of eleven 7-beam eplans were generated to contain all 72 beams (5 beams were used twice). These 11 eplans form our initial knowledge base to begin NP.
2.2. Beam Angle Optimization Tool from Eclipse™
Another approach for generating clinical angle set is the Beam Angle Optimization (BAO) tool from Eclipse. BAO generates new angles in accordance with dose optimization, by iteratively optimizing the beam angles to approximately satisfy the set of user defined dose and dose-volume objectives. BAO executes in two steps: global and local optimization. The global optimization creates new coplanar or non-coplanar field geometries. It originates from a set of uniformly distributed beams to eventually reach the number of beams that best fulfills the defined objectives. The number of fields is then decreased by an iterative ranking that excludes the fields of least relative importance. The local optimization commences as the global optimization stops. This optimization only tries combinations of gantry angles and does not change the number of fields. The local optimization can run without first running the global optimization. However, the best results from BAO are achieved by running both the global and the local optimization (please refer to Eclipse user manual for more details). The angle set thus generated by Eclipse was input back to Pinnacle, so that the same dose optimization was used for a fair final comparison.
2.3. The Nested Partitions (NP) Global Optimization Framework
The NP framework is a powerful optimization paradigm that can combine adaptive global sampling with local heuristic search (Shi and Olafsson 2000). It uses a dynamic partitioning method to divide the search space into successive regions that can be analyzed individually via sampling and then coordinates the sampling results to determine how to continue the search, that is, where to concentrate additional computational effort. A brief description of the NP framework is as follows: In each iteration of the algorithm, it determines the current most promising region, i.e., the sub-region that is considered the most likely to contain the global optimum (the best solution with respect to the given objective function over the entire feasible set). This most promising region is then partitioned into a given number of sub-regions; then these sub-regions and the complementary region (the complement of the feasible region with respect to the promising region) are sampled, and the sampling information is used to determine the most promising region in the next iteration. In essence, each iteration of the NP approach consists of 4 processes: (1) partitioning the search space into promising and complementary regions, (2) selecting sample points from the promising and complementary regions, (3) determining the most promising sample, and (4) backtracking out of the current promising region if the best sample resides in the complementary region. We now describe how the NP framework may be applied to the beam angle selection problem. Further details of the NP framework may be found in (Shi and Olafsson 2009).
2.3.1. Partitioning the Beam Angle Space
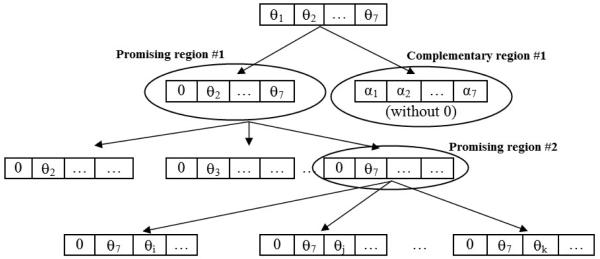
To implement the NP algorithm for beam angle selection, we first need to consider how the solution space may be partitioned into several sub-regions such that they can partitioned further until each sub-region contains only a single solution. This can be conceptually illustrated as shown in figure 1. Consider a treatment plan in which the number of beam angles, N, is 7. The topmost box (at level 0) of figure 1 represents the entire feasible space, which consists of all sets of seven beam angles that meet the spacing and opposition constraints. Suppose that angle “0” is considered to be a good candidate for inclusion in high-quality beam sets and is therefore designated as the “primary” partitioning angle for this iteration and is used to define the initial promising region. The corresponding angle sets that contain angle 0 are indicated schematically in figure 1 in the next level (level 1) by the set beginning with 0, and the initial complementary region thus consists of the angle sets that do not contain angle 0. In order to investigate the desirability of continuing along the path from the promising region and thus retaining angle 0, the promising region is partitioned into 6 left sub-regions (because only one angle out of seven has so far been fixed), in which each sub-region contains angle 0 and at least one of the angles from current best angle set (these angles are considered to be “secondary” partitioning angles in this iteration). We also consider 6 right sub-regions - each contains angle 0 and excludes one of the angles from the current best angle set (for simplicity, these right sub-regions are not shown in figure 1). Sampling is then performed in the entire feasible region by sampling in all left and right sub-regions of the promising region as well as the complementary region. Ideally, the best sample will occur in one of the left sub-regions, and this region would then become the new promising region (in figure 1, the 6th sub-region is new promising region) and the process will continue recursively by inserting additional beams until a “singleton” (region containing a single set of seven angles) is reached. On the other hand, if the best sample is in a right sub-region, that sub-region becomes the next promising region. The case in which the best sample occurs in the complementary region is discussed below.
Figure 1.
Schematic illustrating partitioning in the NP approach to beam angle selection.
2.3.2. Sampling from Each Region
Sampling refers to the generation of the remaining beam angles to complete each of the beam set samples in the promising and complementary region after the angle(s) defining the region have been fixed. Our sampling scheme takes into account the beam angle constraints (minimum spacing between adjacent beams, lack of directly opposed beams). Following the selection of the beam angle for partitioning the solution space, a list of allowable beam angles in each region is defined. Beam angles are chosen sequentially and randomly from the list, such that when an angle is selected, the list of allowable angles is redefined. In this manner, the full beam angle set is defined. Several beam angle sets are defined in similar fashion at each iteration. Using a surrogate-based method (described in section 3.3) enables us to evaluate thousands of beam samples quickly. While a uniform sampling scheme may work well in some cases, incorporation of a simple heuristic into the sampling scheme can drastically improve the sample quality (Shi and Olafsson 2009). For instance, simulated annealing or genetic algorithm can be incorporated to complete the beam set within each region.
2.3.3. Promise Index
To generate the promising region and the complementary region in the NP framework for the next iteration, one has to rank the current regions based on a quality index determined by the sample evaluations. This index is called the promise index. The region with the best promise index determines the next most promising region. Our implementation of beam angle selection in IMRT using the NP framework was based on evaluating treatment plans from which a composite score was calculated for each sample.
In this work, we also embedded Pinnacle3 treatment planning system (Philips Medical Systems, Fitchburg, WI) in the NP framework for partial sample evaluation, i.e., to guide the search of the NP. A few samples are selected based upon composite scores as described below and dose optimization is performed for those samples in the Pinnacle3 planning system. The promise index, for a region, is generated by evaluating the scores for the optimized plans in the region. In this context, scores are weighted deviations from target values, so lower score values correspond to better plans. Specifically, the score is calculated as:
| (1) |
where β is the weight associated with each OAR and target in the score calculation. The last column of Table 1 shows the value of weights used in this work. dOAR and dTAR are specified desired dose or dose volume values for each OAR and target (Table 1), and AOAR and ATAR are the actual dose levels achieve by the treatment plan. In this manner, a beam angle set is penalized for resulting in a plan that violated the constraints.
2.3.4. Backtracking
Backtracking is the ability of the NP algorithm to “jump” out of the promising region if the best sample set is found in the complementary region. We have considered two backtracking rules in our implementation of the beam angle selection problem. In the first rule, in order to backtrack to the super-region of the current most promising region, only those regions that lead from the current most promising region back to the entire feasible region are recorded. In the second backtracking rule it is possible in a single transition to move out of the current promising region to a complementary region that differs in depth from the promising region by more than one angle. The first backtracking rule allows for a slight change in the sample distribution at each iteration while the second rule permits drastic changes.
2.4 Surrogate-Based NP Approach
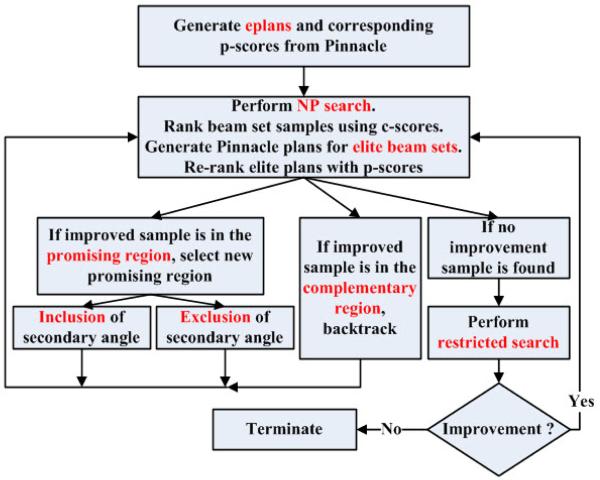
Our surrogate-based NP implementation is illustrated in figure 2. Any BAS algorithm can be incorporated to obtain a warm start in which the initial promising region will contain the initial BAS solution. In this work, we use the best angle set from the 11 eplans as the initial beam set.
Figure 2.
cNP flow chart showing initial warm start (generation of eplans), partitioning into promising region and complementary region, and restricted search.
We considered two NP-based approaches to BAS. In the first method, labeled pNP (to represent Pinnacle-based NP), a treatment quality index referred to as a p-score is computed for each beam-set sample generated by the NP search procedure. A p-score is generated by determining a treatment plan utilizing the beam-set and then computing a quality index for that plan. To assess the quality of a plan, the dose that would be deposited within the tissues of the patient is simulated using Pinnacle and then compared to desired target and OAR doses. Details of this procedure are given below. While the p-score of a beam set represents an accurate estimate of the corresponding treatment quality, a drawback of pNP is the computational expense associated with the generation of a treatment plan. Given that the total computing time generally available for planning for an individual case may only be a few hours at most, this pNP scoring technique allows the consideration of only a small number of samples, which limits the algorithm’s ability to explore the space of feasible beam angle sets.
In order to make better decisions within the NP framework by considering several thousand beam-set samples we developed an approximate scoring mechanism termed a composite score (c-score), which does not require the use of Pinnacle in order to obtain a corresponding treatment plan for a beam set sample. The NP-based framework that involves the computation of c-scores as a surrogate for p-scores is termed cNP.
2.4.1. pNP
In the present work, initialization is based on a collection of equally-spaced seven-beam plans (eplans) generated using the Pinnacle planning system (see section 2.1). This collection of 11 eplans contains all 72 beam angles corresponding to 5 degree spacing.
This dose data was then employed in a search process guided by the random-sample-based NP global framework as described in section 2.3. During the sampling process, the beams to be included in a beam-set sample were selected uniformly. That is, each beam had equal probability to be included in a beam set. A biased-sampling procedure, in which “good” angles (as measured by total monitor units associated with an angle in an eplan, for example) had a higher selection probability, could also be used. A treatment plan corresponding to the sample beam-set was then generated by the Pinnacle planning system and the corresponding doses that would be delivered to patient tissues were analyzed. The dose volume histogram (DVH) is one of the metrics that clinicians are routinely using to evaluate treatment plan quality. For a given organ or structure and a set of dose values for each voxel of that structure, the DVH identifies, for each dose value the fraction of the total volume of the structure that receives at least that much dose. Treatment quality goals are usually set by specifying DVH targets for the PTV and the OARs. For difficult cases it is rarely possible to obtain a treatment that attains all of the specified DVH targets. For a given treatment plan we extracted dose distributions from Pinnacle and used these distributions to obtain the DVH for each target structure and each OAR. (DVHs were normalized so that 95% of the primary PTV received the prescription dose.) The corresponding p-scores of each plan, which reflect the composite violation of DVH constraint settings, were calculated as in (1). In order to achieve quality solutions within a clinically reasonable time, 25 samples (20 from promising region and 5 from complementary region) were evaluated at each NP iteration.. Our empirical testing showed that these sample counts provided good balance between solution quality and computational efficiency. We used the stopping criteria of five iterations, which terminated in two hours on average.
2.4.2. cNP
For a given case, in order to generate data for our alternative approach based on a composite scoring procedure, the equally-spaced seven-beam plans (eplans) generated using the Pinnacle planning system were used to obtain dose matrices for single beams. Single-beam dose distributions were extracted from each eplan. A fast method based on combining these single-beam dose data was used to obtain an approximate quality score (c-score) for each beam set sample generated within the NP search framework. This scoring method starts by adding the dose matrices corresponding to the beams in the sample, scaling the result to obtain an appropriate PTV coverage, and then computes a DVH-based score for this composite plan using the same scoring process as described above. (Note that some beam angles appear in two eplans - when such a repeated angle appears in a sample, both alternatives are considered in evaluating the sample, and the better c-score is used.)
This approach enables us to compute c-scores for 3000 beam set samples in 100 seconds on a 2.8GHz 1GB RAM machine, and, although it does not compute or use optimized dose with respect to the selected beam-sets, our experience has shown that the elite samples with the top 5-10 c-scores generally contain “improved” beam sets and thus are useful in guiding the search process. (Improvement was gauged by generating optimized Pinnacle plans for the best samples, applying the same scoring process described above to these optimized plans, and then comparing these p-scores with the best e-plan p-score.) The justification of the relation between c-scores and p-scores is shown in next section.
Details of this method are as follows: Starting from one angle selected from the best eplan, we try to fix one more angle for the beam angle set at each iteration. For example, suppose the incumbent beam angle set {0, 50, 85, 125, 200, 245, 300} has the best p-score and has angles 0 and 50 fixed. Ideally, we would like to fix one more angle in the set of angles 85, 125, 200, 245 and 300 at the next iteration. There are concerns when we are considering these five candidates: is the best one within 85, 125, 200, 245 and 300? What if none of these angles yield an improved plan? And what if the already fixed angles (0 and 50) are not present in an optimal beam set?
We address the concerns above with three sampling mechanisms. Taking angle 85 as an example, we generate samples with 0, 50 and 85 all fixed and save the best two samples (according to c-scores). We call this process searching the left sub-region. We also collect samples with 0 and 50 fixed and 85 excluded from the samples and save the best two samples according to c-scores. We call this searching the right sub-region. We do this bi-partite search process for each angle in the set {85, 125, 200, 245, 300}. We also collect samples from complementary region with at least one of 0 and 50 excluded and save the best 5 samples. The quality of these samples as measured by p-score will guide our following step. Specifically, if the best sample by p-score is better than previous best p-score and is found in the left region, fix this angle together with 0 and 50 for the next iteration. Thus, the overall process is analogous to strong branching in branch-and-bound. If the best sample is better than the incumbent and found in the right region of an angle, we still fix 0 and 50 but exclude this angle for the sampling in the promising region later on. If the best sample is better than the incumbent and is found in the complementary region, we perform backtracking. In this case we start over with the new best angle set (found in complementary region) to re-define the promising region. This is similar to at the beginning of the method, but instead of using the best eplan, the new best angle set is used. If the best sample is not better than the incumbent, we perform restricted search. During restricted search we fix 6 of the 7 angles of the incumbent and consider all feasible values for the remaining angle. This is analogous to searching an extended neighborhood of the current best angle set for improvement.
Table 2 is an example to illustrate the cNP search process. After comparing the initial 11 eplans, the best eplan has a p-score 166.6, which is chosen as initial warm-start solution for NP search. Using monitor unit data, angle 335, which has the largest MU total, is selected to define the promising region. In iteration 1, the promising region is partitioned into sub-regions based on the other 6 angles, and then 3000 samples are generated as described above. 5 elite samples are collected based on ranking of c-scores and evaluated via p-scores. This NP iteration yields an improved angle set {15, 70, 125, 215, 260, 295, 335} with p-score 132.8. Because this set is from right sub-region of angle 280, that angle will be excluded from the next promising region. Iteration 2 continues NP search with updated promising region and sub-regions (defined by the current best set). Since the best set found in iteration 2 does not provide improvement, restricted search is performed in iteration 3, which identifies an improved set with p-score 128.9. Further improvements are obtained based on the restricted search result in the next two iterations as shown in Table 2.
Table 2.
Illustration of cNP search process.
| Beam angle sets | p-score | Search result | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Best eplan | 5 | 60 | 115 | 170 | 225 | 280 | 335 | 166.6 | Initial solution |
| Iteration 1 | 15 | 70 | 125 | 215 | 260 | 295 | 335 | 132.8 | Improvement |
| Iteration 2 | 15 | 70 | 125 | 165 | 215 | 275 | 335 | 153.2 | No improvement |
| Restricted search | 15 | 70 | 125 | 215 | 260 | 295 | 345 | 128.9 | Improvement |
| Iteration 4 | 15 | 60 | 115 | 160 | 215 | 260 | 295 | 125.8 | Improvement |
| Iteration 5 | 20 | 65 | 120 | 160 | 215 | 260 | 295 | 115.8 | Improvement |
2.4.3 C-score Justification
C-score is considered an alternative for p-score with respect to evaluating beam angle sets. In cNP, c-score is employed to determine a pool of elite samples out of thousands of samples. Therefore, it is critical to justify the utility of c-score to rank the beam sets.
Spearman’s rank correlation coefficient can provide quantified insights on the correlation between the p-score and c-score ranks. It is a number between −1 and 1 which shows the degree of linear dependence of two variables. If the two variables tend to increase or decrease together, the coefficient is positive. If one of the variables tends to increase when the other decreases, the coefficient is negative. A Spearman correlation of zero indicates that there is no tendency for one of the variables to either increase or decrease when the other increases.
For the samples that p-scores were generated after Pinnacle evaluation, we calculated the Spearman’s rank correlation coefficients of the p-score and corresponding c-score for the five cases. Table 3 shows the coefficients and p-values of the one-tailed t-tests on whether the observed coefficients are significantly larger than zero. We can see that all five coefficients were big and it was statistically significant to reject the null hypothesis that the observed coefficients are less than equal to zero. This shows that our c-score surrogate is a useful indicator of actual plan quality.
Table 3.
Spearman’s coefficients and t-test p-values for the five cases
| Case1 | Case2 | Case3 | Case4 | Case5 | |
|---|---|---|---|---|---|
| Spearman’s Coefficient | 0.53 | 0.50 | 0.46 | 0.46 | 0.41 |
| P-value | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
2.5 NP Convergence Analysis
Although c-scores were utilized to define elite samples, the actual quality of these samples was evaluated via p-scores. The convergence property of NP thus holds in this case as shown by Zhang et al (2009). (Note that convergence follows because sample replication is allowed in the initial sampling process, prior to the calculation of p-scores, so that every beam set has a positive probability of being an elite sample and receiving a p-score regardless of c-score.) The sequence of the most promising regions can be seen as a Markov chain. Shi and Olafsson (2000) pointed out that the optimal solutions correspond to the set of absorbing states and the Markov chain will eventually reach one of the absorbing states. Finite time behavior of NP was discussed in Shi and Olafsson (2000) and further analyzed for the beam angle selection problem by Zhang et al (2009). In particular, the expected number E[Y] of iterations until the NP Markov chain gets absorbed is given by,
| (2) |
where P0 is the success probability of NP, which is the probability of the algorithm moving in the correct direction. M is the number of sub-regions in a partition and d* is the maximum depth, which is defined as the maximum number of partition steps needed to reach a singleton region.
It can be seen from (2) that the efficiency of NP is heavily dependent on the success probability P0. Large P0 can significantly reduce the expected number of iterations for NP to reach the optimum. In conventional NP as applied to beam selection, it is not practical to evaluate large numbers of samples for each sub-region, due to the computing expense of Pinnacle. This increases the difficulty of selecting the correct sub-region and achieving high success probability. By introducing the surrogate c-score, however, many more samples can be evaluated, which provides more confidence in the quality assessment of each sub-region .
3. Results
We tested the cNP approach with the five locally advanced head and neck cancer cases (these cases involve complex target geometries and many OARs with competing constraints). The constraint settings used for optimization and evaluation are listed in Table 1. The weights for each OAR and target in the scoring function were selected by clinicians to obtain appropriate clinical plans. To obtain a fair comparison between the clinical plans and our approaches, the same weights were used for all approaches. For our cNP approach, elite samples with the best 25 c-scores were sent to Pinnacle for optimized plan generation and quality evaluation of these plans was done via p-scores. This is the same number of conventional NP samples generated in pNP. We limit our computation time to two hours or five iterations (if reached before two hours). Both NP approaches were compared with angle sets obtained from experienced clinicians (the actual set used in patient’s treatment) and beam sets generated by Eclipse. Before comparing the scores and plan quality, all plans were normalized so that at least 95% of the primary PTV received the prescription dose.
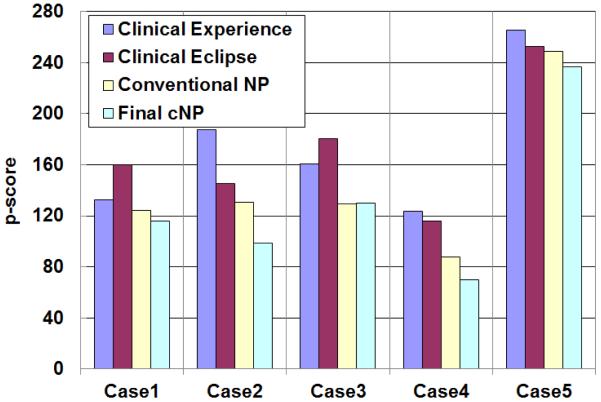
Figure 3 shows the set of p-scores obtained from four different approaches for the five test cases. Current clinical methods performed inconsistently with Eclipse outperforming clinical experience in three out of five cases. Without surrogate c-scores and restricted search, when only Pinnacle was used to guide the search of NP, improvements were obtained relative to both clinical plans. With additional restricted search, more improvement was identified except in case 3. Overall, the cNP approach performed the best. The average improvements in p-scores through the use of cNP were 27%, 27% and 11% comparing to clinical experience, clinical Eclipse and conventional NP, respectively.
Figure 3.
Comparing composite p-scores (weighted violation of dose constraints) for four approaches.
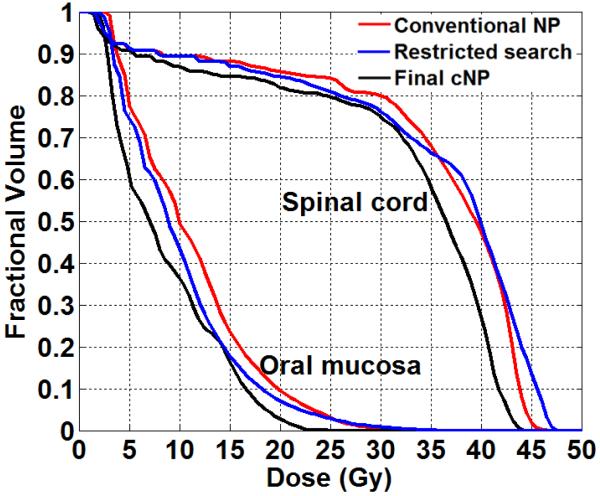
Besides providing improvement in the composite scores, we consider the value of restricted search from a clinical DVH viewpoint. In figure 4 we show the DVHs of spinal cord and oral mucosa from one of the cases to illustrate the value of restricted search. Early conventional NP iterations achieved DVHs were shown in red. From our tests, without restricted search no further improvement could be gained within limited iterations. Restricted search results were shown in blue DVHs. Although the change from restricted search was not significant, that process did identify a new search focus for NP, which led to the final improvement as shown in black. The final improvement was achieved in maximum spinal cord dose and better sparing of oral mucosa.
Figure 4.
Spinal cord and oral mucosa DVHs illustrating the value of restricted search.
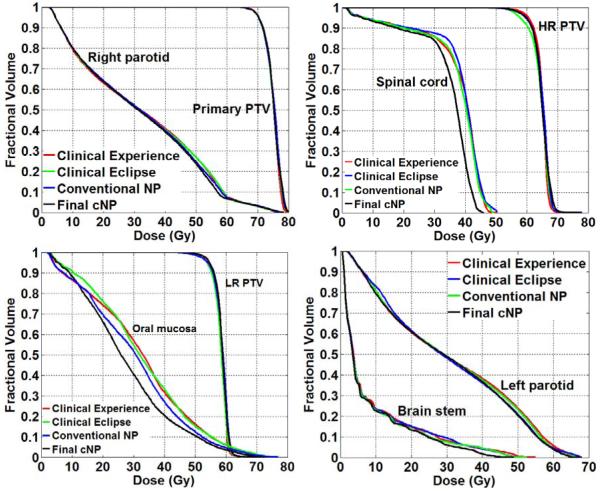
The overall beam angle quality obtained by 4 approaches is shown in figure 5. The average DVHs for the 5 test cases are displayed. For all three PTVs (primary, high risk and low risk), the difference of the 4 approaches was less than 2%. The difference in parotids in high dose region was less than 5%. The bigger differences were achieved for spinal cord, oral mucosa and brain stem. At least 10% improvement was achieved by cNP for sparing of spinal cord comparing to other methods. 12% reduction of the maximum dose delivered to the brain stem was achieved with cNP approach. 15% improvement of oral mucosa sparing was achieved as well. We can see that cNP successfully identified beam angle sets that yielded significantly improved treatment plans relative to clinical plans and conventional NP.
Figure 5.
DVH comparisons of four approaches for beam angle selection (showing the average DVH of the five tested head and neck cases).
4. Discussion
The purpose of this work was to describe a surrogate-based global optimization method for beam angle selection problem that could be implemented with a commercial treatment planning system for clinical practice. Beam angle selection combined with dose optimization, as a single combinatorial optimization problem, is large scale and notoriously difficult to solve to optimality. Consequently, the best that can be expected in most instances is the generation of a high-quality solution within a reasonable time frame, with the indicator of high quality being comparison with previous solutions generated by other approaches (as cited in the introduction section) or comparison with a collection of other feasible solutions generated by clinical judgment, including commercial software, such as Eclipse. We believe knowledge gained from a large number of feasible solutions yields a better chance to identify regions likely to contain high-quality solutions in a global optimization search. NP has the nice property that it uses the feedback information from a large number of feasible solutions spread across the entire solution space to guide the future search effort. The enormous sample-quality information provided by thousands of surrogates allows greater confidence in final solution quality.
One of the reasons that beam angle selection has not been widely adopted in clinical settings is the problem of generating good angle sets in a reasonable amount of time. Recent trends to make the methods practical for clinical use include developing simple/fast methods and harnessing high-throughput computing environment. For fast algorithms, researchers tried simple geometric measures of patient anatomy (Potrebko et al 2007) and ranking of the beams (Vaitheeswaran et al 2010). Nazareth et al (2009) and Zhang et al (2009) used distributed computing environment to speed up the computation time. Our method takes advantage of both aspects. On one hand we could evaluate thousands of sample set within seconds. On the other hand, the structure of the NP algorithm can be easily adapted to parallel computation, in which all samples from different sub-regions could be evaluated by a dose optimization program or clinical planning system simultaneously.
Another reason that beam angle selection continues to be performed as a manual process is a concept of similar plan quality. Some clinicians thought the manually selected angle set would have similar plan quality as those generated by mathematical algorithms. There has been overwhelming evidence in the literature to show that algorithmic beam angle choices can lead to significant improvements in plan quality. Most recently, Srivastava et al (2011) used dosimetric comparisons to conclude that beam angle optimization provides advantage over manual selection for most IMRT cases. The motivation behind improved beam angle selection is the continued need to decrease the dose to critical organs. For locally advanced head and neck cancer cases, the organs-at-risk either sits within the concavity of the targets or is very close to the targets. Mallick and Waldron (2009) has shown that the rate of oral mucositis is very high in patients being treated with fields involving the oral cavity. Because IMRT treatment plans deliver radiation via many beams around the patients, it is difficult to avoid those fields involving the oral cavity. Our results showed that significant preserving of oral cavity can be achieved with better selection of beam angle set.
The final point that we would like to emphasize is the contribution of restricted search in this work. Craft (2007) pointed out that the beam angle selection problem has the structure of many-local-minima. A search strategy of global search followed by local refinement would provide promising beam angle sets. Our results in this work agreed with this conclusion. When sample-based global search could not obtain further solution improvement, a restricted search not only gave us local refinement, but also provided new search direction for even better solutions.
5. Conclusions
Our results show that beam sets superior to those of clinical approaches are produced by a global NP-based search method that utilizes single-beam dose data. Our surrogate-based scoring process enables evaluation of the thousand of samples within seconds, which leads to a “fast” approximate beam-set scoring.
Acknowledgment
This work was supported in part by a grant from the NIH/NCI CA130814.
References
- Bangert M, Oelfke U. Spherical cluster analysis for beam angle optimization in intensity-modulated radiation therapy treatment planning. Phys. Med. Biol. 2010;55:6023–37. doi: 10.1088/0031-9155/55/19/025. [DOI] [PubMed] [Google Scholar]
- Bertsimas D, Cacchiani V, Craft D, Nohadani O. A hybrid approach to beam angle optimization in intensity-modulated radiation therapy. Computers & Operations Research. (In press) [Google Scholar]
- Bortfeld T, Schlegel W. Optimization of beam orientations in radiation therapy: Some theoretical considerations. Phys. Med. Biol. 1993;38:291–304. doi: 10.1088/0031-9155/38/2/006. [DOI] [PubMed] [Google Scholar]
- Breedveld S, Storchi PR, Voet PW, Heijmen BJ. iCycle: Integrated, multicriterial beam angle, and profile optimization for generation of coplanar and noncoplanar IMRT plans. Med. Phys. 2012;39:951–63. doi: 10.1118/1.3676689. [DOI] [PubMed] [Google Scholar]
- Craft D. Local beam angle optimization with linear programming and gradient search. Phys. Med. Biol. 2007;52:N127–35. doi: 10.1088/0031-9155/52/7/N02. [DOI] [PubMed] [Google Scholar]
- Craft D, Monz M. Simultaneous navigation of multiple Pareto surfaces, with an application to multicriteria IMRT planning with multiple beam angle configurations. Med. Phys. 2010;37:736–41. doi: 10.1118/1.3292636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Souza WD, Zhang HH, Nazareth DP, Shi L, Meyer RR. A nested partitions framework for beam angle optimization in intensity-modulated radiation therapy. Phys. Med. Biol. 2008;53:3293–307. doi: 10.1088/0031-9155/53/12/015. [DOI] [PubMed] [Google Scholar]
- Das S, Cullip T, Tracton G, Chang S, Marks L, Anscher M, Rosenman J. Beam orientation selection for intensity-modulated radiation therapy based on target equivalent uniform dose maximization. Int. J. Radiat. Oncol. Biol. Phys. 2003;55:215–24. doi: 10.1016/s0360-3016(02)03817-8. [DOI] [PubMed] [Google Scholar]
- Fiege J, McCurdy B, Potrebko P, Champion H, Cull A. PARETO: A novel evolutionary optimization approach to multiobjective IMRT planning. Med. Phys. 2011;38:5217–29. doi: 10.1118/1.3615622. [DOI] [PubMed] [Google Scholar]
- Jia X, Men C, Lou Y, Jiang SB. Beam orientation optimization for intensity modulated radiation therapy using adaptive l(2,1)-minimization. Phys. Med. Biol. 2011;56:6205–22. doi: 10.1088/0031-9155/56/19/004. [DOI] [PubMed] [Google Scholar]
- Lee CH, Aleman DM, Sharpe MB. A set cover approach to fast beam orientation optimization in intensity modulated radiation therapy for total marrow irradiation. Phys. Med. Biol. 2011;56:5679–95. doi: 10.1088/0031-9155/56/17/014. [DOI] [PubMed] [Google Scholar]
- Lee EK, Fox T, Crocker I. Simultaneous beam geometry and intensity map optimization in intensity-modulated radiation therapy. Int. J. Radiat. Oncol. Biol. Phys. 2006;64:301–20. doi: 10.1016/j.ijrobp.2005.08.023. [DOI] [PubMed] [Google Scholar]
- Lee N, Mechalakos J, Puri DR, Hunt M. Choosing an intensity-modulated radiation therapy technique in the treatment of head-and-neck cancer. Int. J. Radiat. Oncol. Biol. Phys. 2007;68:1299–309. doi: 10.1016/j.ijrobp.2006.11.019. [DOI] [PubMed] [Google Scholar]
- Lim GJ, Cao W. A two-phase method for selecting IMRT treatment beam angles: Branch-and-prune and local neighborhood search. Euro. J. of Operational Research. 2012;217:609–18. [Google Scholar]
- Lim GJ, Choi J, Mohan R. Iterative solution methods for beam angle and fluence map optimization in intensity modulated radiation therapy planning. OR Spectrum. 2008;30:289–309. [Google Scholar]
- Liu HH, Jauregui M, Zhang X, Wang X, Dong L, Mohan R. Beam angle optimization and reduction for intensity-modulated radiation therapy of non-smal-cell lung cancers. Int. J. Radiat. Oncol. Biol. Phys. 2006;65:561–572. doi: 10.1016/j.ijrobp.2006.01.033. [DOI] [PubMed] [Google Scholar]
- Mallick I, Waldron JN. Radiation therapy for head and neck cancers. Semin. Oncol. Nurs. 2009;25:193–202. doi: 10.1016/j.soncn.2009.05.002. [DOI] [PubMed] [Google Scholar]
- Munawar, et al. Intensity modulated radiotherapy of non-small-cell lung cancer incorporating SPECT ventilation imaging. Med. Phys. 2010;37:1863–72. doi: 10.1118/1.3358128. [DOI] [PubMed] [Google Scholar]
- Nazareth DP, Brunner S, Jones MD, Malhotra HK, Bakhtiari M. Optimization of beam angles for intensity modulated radiation therapy treatment planning using genetic algorithm on a distributed computing platform. J. Med. Phys. 2009;34:129–32. doi: 10.4103/0971-6203.54845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan VK, Vaitheeswaran R, Bhangle JR, Basu S, Maiya V, Zade B. An experimental investigation on the effect of beam angle optimization on the reduction of beam numbers in IMRT of head and neck tumors. J. Appl. Clin. Med. Phys. 2012;13:3912. doi: 10.1120/jacmp.v13i4.3912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pooter JA, Romero AM, Jansen WPA, Storchi PRM, Woudstra E, Levendag PC, Heijmen BJM. Computer optimization of noncoplanar beam setups improves stereotactic treatment of liver tumors. Int. J. Radiat. Oncol. Biol. Phys. 2006;66:913–22. doi: 10.1016/j.ijrobp.2006.06.018. [DOI] [PubMed] [Google Scholar]
- Potrebko PS, McCurdy BM, Butler JB, El-Gubtan AS, Nugent Z. A simple geometric algorithm to predict optimal starting gantry angles using equiangular-spaced beams for intensity modulated radiation therapy of prostate cancer. Med. Phys. 2007;34:3951–61. doi: 10.1118/1.2775685. [DOI] [PubMed] [Google Scholar]
- Shi L, Olafsson S. Nested partitions method for global optimization. Operations Research. 2000;48:390–407. [Google Scholar]
- Shi L, Olafsson S. Nested Partitions method, theory and applications. Springer; 2009. [Google Scholar]
- Srivastava SP, Das IJ, Kumar A, Johnstone PA. Dosimetric comparison of manual and beam angle optimization of gantry angles in IMRT. Med. Dosim. 2011;36:313–6. doi: 10.1016/j.meddos.2010.07.001. [DOI] [PubMed] [Google Scholar]
- Vaitheeswaran R, Narayanan VK, Bhangle JR, Nirhali A, Kumar N, Basu S, Maiya V. An algorithm for fast beam angle selection in intensity modulated radiotherapy. Med. Phys. 2010;37:6443–52. doi: 10.1118/1.3517866. [DOI] [PubMed] [Google Scholar]
- Wang X, Zhang X, Dong L, Liu H, Gillin M, Ahmad A, Ang K, Mohan R. Effectiveness of noncoplanar IMRT planning using a parallelized multiresolution beam angle optimization method for paranasal sinus carcinoma. Int. J. Radiat. Oncol. Biol. Phys. 2005;63:594–601. doi: 10.1016/j.ijrobp.2005.06.006. [DOI] [PubMed] [Google Scholar]
- Wang X, Zhang X, Dong L, Liu H, Wu Q, Mohan R. Development of methods for beam angle optimization for IMRT using an accelerated exhaustive search strategy. Int. J. Radiat. Oncol. Biol. Phys. 2004;60:1325–37. doi: 10.1016/j.ijrobp.2004.06.007. [DOI] [PubMed] [Google Scholar]
- Zhang HH, Shi L, Meyer R, Nazareth D, D’Souza W. Solving beam-angle selection and dose optimization simultaneously via high-throughput computing. INFORMS J. on Computing. 2009;21:427–44. [Google Scholar]