Migratory connectivity magnifies the consequences of habitat loss from sea-level rise for shorebird populations

Abstract

Sea-level rise (SLR) will greatly alter littoral ecosystems, causing habitat change and loss for coastal species. Habitat loss is widely used as a measurement of the risk of extinction, but because many coastal species are migratory, the impact of habitat loss will depend not only on its extent, but also on where it occurs. Here, we develop a novel graph-theoretic approach to measure the vulnerability of a migratory network to the impact of habitat loss from SLR based on population flow through the network. We show that reductions in population flow far exceed the proportion of habitat lost for 10 long-distance migrant shorebirds using the East Asian–Australasian Flyway. We estimate that SLR will inundate 23–40% of intertidal habitat area along their migration routes, but cause a reduction in population flow of up to 72 per cent across the taxa. This magnifying effect was particularly strong for taxa whose migration routes contain bottlenecks—sites through which a large fraction of the population travels. We develop the bottleneck index, a new network metric that positively correlates with the predicted impacts of habitat loss on overall population flow. Our results indicate that migratory species are at greater risk than previously realized.

1. Introduction

Anthropogenic habitat loss has precipitated a recent wave of extinctions [1,2]. For non-migratory species, increased extinction risk from habitat loss can be approximated by measuring the area of suitable habitat that has been lost [3]. This method currently underpins assessments of extinction risk [2,4], and global conservation prioritizations [5,6]. However, for migratory species, the impact of habitat loss depends not just on its extent, but also on where it occurs [7–10]. Estimating extinction risk simply from the extent of habitat lost could severely underestimate the vulnerability of migratory species. For example, the Rocky Mountain grasshopper Melanoplus spretus collapsed from some 15 trillion individuals to extinction because habitat loss was concentrated into a small region in which the species contracted during dry years [11].

Millions of shorebirds migrate annually from their Russian and Alaskan Arctic breeding habitats to the coasts of Southeast Asia and Australasia through the East Asian–Australasian Flyway (EAAF) [12,13]. These birds interrupt their journeys to rest and feed in intertidal habitats at staging sites across eastern Asia that can constitute significant bottlenecks for migration [14,15]. For example, over 45 per cent of all red knots Calidris canutus in the flyway use a single site in the Yellow Sea during their migration [15,16]. Habitat loss from sea-level rise (SLR) at such bottleneck sites could disproportionately impact population persistence, but to our knowledge, the magnitude of these effects has not been quantified in this or any other migration system. Here, we estimate the vulnerability of migratory routes for shorebirds to future loss of coastal habitat through SLR across all the EAAF sites used by the birds [17].

To model the impacts of habitat loss on the migratory shorebird populations, we estimate the flow of birds through the network of habitat patches by applying an algorithm widely used to solve the maximum flow problem, developed to calculate the maximum amount of flow running through complex networks (e.g. water in a pipeline system) [18]. There is growing interest in applying graph theory to ecological phenomena, though its application has so far been limited to analyses of network structure such as metapopulations [19,20] and landscape connectivity [21,22]. Using our novel application of graph theory, we estimate the impact of habitat loss on the maximum flow capacity of migratory populations (hereafter referred to as ‘population flow’) of 10 migratory shorebird taxa using the EAAF [12,13]. Migratory pathways are modelled using a graph consisting of nodes connected by edges representing the flow of individuals along the migration route (see figure 1 and electronic supplementary material). We applied an algorithm quantifying the maximum flow that the network could support, given any particular configuration of habitat availability across the nodes.

Figure 1.

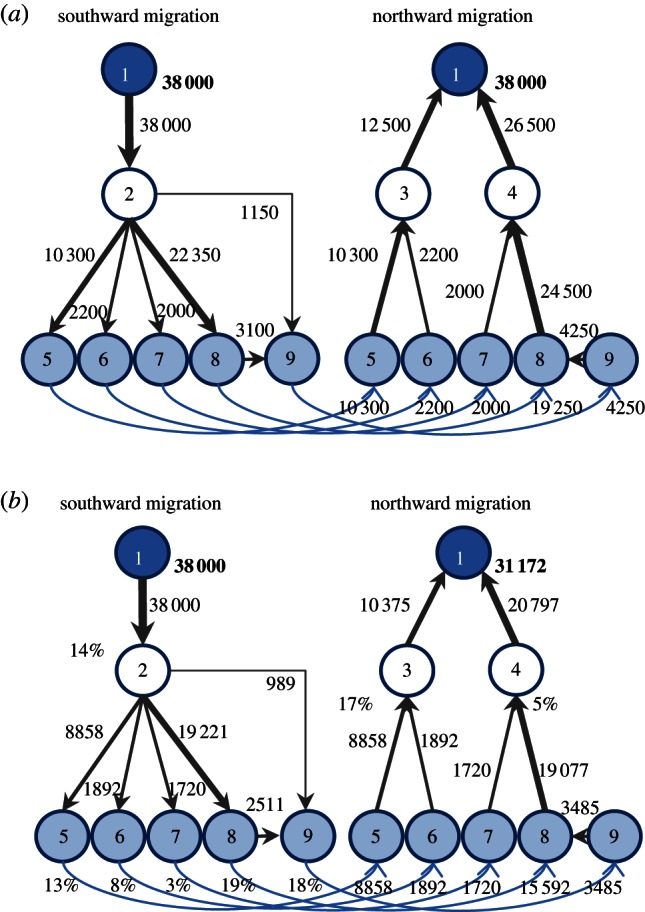
The migratory flyway of the eastern curlew, modelled as a graph consisting of nodes and edges. A node represents a geographical group of internationally important wetland sites that are used as a single unit by the birds. An edge connects two nodes and has direction and weight, representing the flow of birds between nodes. We use linked graphs for southward and northward migration routes, because these often differ. Breeding habitat is shown in dark blue (node 1), connected to non-breeding habitat (pale blue; nodes 5–9) by staging sites (white; nodes 2–4). (a) Current flyway capacity. (b) Predicted future flyway capacity reduced by habitat loss at 50 cm SLR. Percentages indicate habitat loss at each node, which reduces outflow of birds from that node. The total flyway capacity of a network is restricted by the smallest outflows. In this example, the maximum flow of the network is reduced by habitat loss from 38 000 to 31 172 individuals.

2. Material and methods

(a). Network structure

In mathematical graph theory [23], a real-world network is represented as a ‘graph’, a diagram consisting of points called ‘nodes’, joined by lines, called ‘edges’. In ecological applications, nodes typically represent habitats or populations and edges indicate a connection between any two nodes. Edges can have weights and direction to indicate population fluxes, colonization probabilities or internode distances. Here, we represent a flyway as a weighted directional graph, where each node represents a regional group of internationally important shorebird sites. Each node has an attribute indicating habitat loss from SLR and each edge has a weight and direction representing the flux of birds between the two nodes connected by the edge (figure 1). We constructed graphs linking northward and southward migration routes, as these often differ [24,25].

A migratory network structure for each shorebird species was constructed, based on the collective knowledge and experience of a group of experts who have worked in the flyway for several decades ([13,24]; see author list and acknowledgements for a list of workshop members; electronic supplementary material; figure 1). Estimates of network structure were founded on a combination of count data, banding and flagging information, routes of birds fitted with satellite tags and geolocators [12,13,24]. The experts were asked to conceptualize each node as the smallest possible groups of internationally important sites between which there is sufficient information to map the migratory routes of each species in this study (figure 1a). First, sites within a geographical region (e.g. China Seas, northeast Australia) were clustered as groups, then the experts further categorized sites into finer scale groups (e.g. east coast of the Yellow Sea, Gulf of Carpentaria) based on data about migratory patterns for each taxon (see the electronic supplementary material). The weight of each edge, representing a population flow between two nodes, was then defined based on the proportion of the population that moves between the nodes (figure 1a).

(b). Defining migratory networks

We selected 10 shorebird taxa using the EAAF that (i) have declining populations, (ii) depend principally on coastal habitats while on migration, and (iii) have sufficiently comprehensive information available for modelling the spatial structure of their migratory networks. These taxa were bar-tailed godwit (two subspecies treated separately: Limosa lapponica menzbieri and Limosa lapponica baueri), curlew sandpiper (Calidris ferruginea), eastern curlew (Numenius madagascariensis), great knot (Calidris tenuirostris), grey-tailed tattler (Tringa brevipes), lesser sand plover (Charadrius mongolus mongolus and Charadrius mongolus stegmanni combined), red knot (two subspecies treated separately: Calidris canutus rogersi and Calidris canutus piersmai) and terek sandpiper (Xenus cinereus). Bamford et al. [12] catalogued the locations of all sites supporting more than 1 per cent of the flyway population of each taxon. For our study taxa this comprises 163 individual sites, distributed across Alaska, Russia, China, North Korea, South Korea, Japan, Philippines, Vietnam, Thailand, Malaysia, Indonesia, Papua New Guinea, Australia and New Zealand.

Polygon data delineating the extent of each wetland were only available for 76 sites (e.g. Wetland database for Ramsar sites, World Database of Protected Areas, National Wetland Inventory for Australia). Where such data were not available, the extent of each wetland was digitized manually based on satellite images and site descriptions. Wetland boundaries were also compared with mapping from various government and non-government sources, and adjusted where necessary. The accuracy of the digitizing was verified by comparing manually digitized site boundaries with the polygon data when they were available, and agreement between the two was good (average overlap of 78%, n = 31).

To estimate the intertidal area within each wetland site, the area between the low water mark and the high water mark was calculated based on digital elevation maps and tidal range data. The digital elevation model from the Shuttle Radar Topography Mission (SRTM) [26] was combined with digital bathymetry data from SRTM30 Plus (http://topex.ucsd.edu). The SRTM has a spatial grain of 90 m, whereas SRTM30 Plus is provided at 0.5 min resolution. Both have a vertical resolution of 1 m. We resampled the elevation and bathymetry data at 180 m resolution, losing horizontal resolution but gaining vertical resolution to 25 cm. Tidal range at each site was calculated based on the prediction of the high- and low-tide heights at the nearest tidal station using WxTide 32 (copyright Michael Hopper 1999). For sites in the northern hemisphere, tidal ranges at the new moon in August 2010 were used, and for Southern Hemisphere sites, those at the new moon in February 2010 were used, these dates reflecting the periods when the sites are used most intensively by the birds. The highest tidal ranges occur near new moon. During neap tide series, tidal range is smaller, and it is possible that availability of feeding habitat during neap tides limits shorebird numbers at some sites. The estimates of potential habitat loss presented in this paper are, therefore, conservative.

(c). Sea-level rise

SLR predictions vary markedly according to the treatment of Greenland and Arctic ice-sheet melting [27,28], so we estimated habitat loss under six SLR scenarios (50, 100, 150, 200, 250 and 300 cm). The extent of each intertidal area subject to inundation was estimated for each increment of SLR as the total area submerged under water at the low tide of each site. l_i, the loss of intertidal area at site i, was calculated as follows:

where I_ji = 1 if 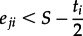, otherwise I_ji = 0, and a_ji is the area of cell j in site i, I_ji indicates whether cell j is inundated or not, which is determined by the elevation of cell j, e_ji, tidal range of site i, t_i, and the degree of SLR S (50, 100, 150, 200, 250 and 300 cm).

(d). Maximum flow problem

We solved the maximum flow problem [18] to estimate change in flyway capacity for each taxon as a result of habitat loss, incorporating both southward and northward migration routes. The loss of population p_k for taxon k is calculated as the reduction in flyway capacity after habitat loss occurs:

where f_k is the function describing the maximum flow between the breeding habitat at the start and at the end of the graph representing the migratory flyway of taxon k (figure 1); 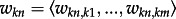is the vector of the capacities of edges connecting node n to other nodes (1, … ,m) of the graph for taxon k; l_kn and a_kn are the loss and the total area of intertidal habitat at node n for taxon k. We also calculated a ‘bottleneck index’ b_k for the migratory route of each taxon, describing the extent of flow concentration based on capacity centrality, the proportion of the flow that passes through each node in comparison with the maximum flow of the network [29] and the magnitude of habitat loss at each node to predict the capacity loss as 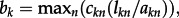where c_kn is the capacity centrality [29] of node n for taxon k.

(e). Sensitivity analysis

We checked the robustness of the results to uncertainty surrounding the connectivity estimates using sensitivity analysis by randomly changing connectivity strengths by ±30%. Other edges from the node subject to the altered connection were also modified such that total connectivity strength remained the same. Monte Carlo simulation was conducted for 1000 iterations per taxon.

(f). Potential expansion of intertidal area

As sea level rises, it is possible that intertidal areas of wetlands could shift inland. We estimated the upper bound of the possible extent of new intertidal areas based on slope, elevation and adjacency to existing intertidal areas for each wetland. In many cases, intertidal areas are bounded by hard infrastructure (e.g. ports and roads) that prevent inland shift, and so we excluded all impermeable surfaces from the analysis using the GlobCover global land cover classification [30]. This is an optimistic scenario, assuming that a wetland can shift freely inland into non-urban landscapes, compensating fully for SLR. We compared the results with a pessimistic scenario assuming there is no inland shift.

3. Results

Our estimates of the total loss of intertidal habitats through SLR varied from 13 to 64 per cent depending on the magnitude of the rise (table 1). Predicted overall habitat loss increased approximately linearly with SLR, though there was marked geographical variation particularly at the medium SLR scenarios. For example, we predicted that a SLR of 100 cm would result in the loss of at least 50 per cent of intertidal habitats in southern Australia and Japan, but only 20 per cent in the Yellow Sea and the East China Sea.

Table 1.

Estimated proportional loss of intertidal habitat through twenty-first century SLR. (Loss of intertidal habitat is shown for the internationally important sites for migratory shorebirds within each region across the flyway, and was calculated by dividing the sum of lost habitat by the total area of present intertidal habitat across the sites within each region.)

	no. sites	50 cm	100 cm	150 cm	200 cm	250 cm	300 cm
Russia	8	0.048	0.101	0.268	0.308	0.361	0.467
Yellow Sea	34	0.133	0.184	0.328	0.401	0.492	0.612
Japan	39	0.225	0.704	0.819	0.851	0.874	0.913
East China Sea (incl. Philippines)	6	0.161	0.280	0.428	0.546	0.744	0.926
Southeast Asia	11	0.387	0.457	0.524	0.619	0.728	0.889
southwest Australia	7	0.261	0.528	0.699	0.867	0.977	0.977
northwest Australia	11	0.071	0.144	0.225	0.322	0.343	0.363
northeast Australia	17	0.062	0.137	0.293	0.567	0.834	0.975
southeast Australia	15	0.222	0.486	0.768	0.921	0.977	0.981
New Zealand	11	0.159	0.329	0.490	0.652	0.811	0.929
Alaska	4	0.399	0.451	0.490	0.523	0.560	0.624
total	163	0.131	0.224	0.350	0.450	0.542	0.639

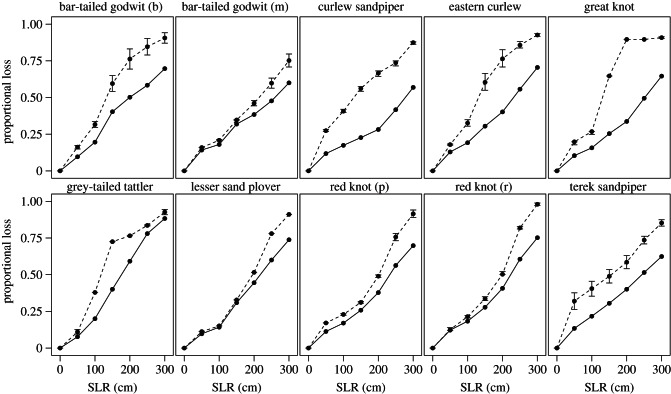
Our analyses indicated that migratory connectivity greatly magnified the impacts of habitat loss upon shorebird populations. Proportional declines in population flow exceeded proportional declines in habitat extent at all SLR scenarios and across all taxa (figure 2; Welch two-sample tests: all p < 0.05). For example, a SLR of 150 cm was predicted to result in the loss of about 35 per cent of intertidal habitat, but decreases in overall population flow of more than 60 per cent for curlew sandpiper, eastern curlew and great knot. The extent to which migratory connectivity magnified the impacts of habitat loss varied markedly among the 10 taxa (figure 2). The patterns can be categorized into those showing a sudden decline in total population flow at a particular sea level (great knot, grey-tailed tattler and eastern curlew), those showing higher capacity loss than that predicted by habitat loss at all SLR scenarios (curlew sandpiper, terek sandpiper and baueri bar-tailed godwit), and those showing declines only slightly exceeding those predicted from habitat loss (lesser sand plover, menzbieri bar-tailed godwit and red knot).

Figure 2.

Proportional losses in habitat extent and population flow in migratory shorebirds. Loss of habitat extent (solid line) and loss of population flow (broken line) both rise with increasing sea level, although the latter always equals or exceeds the former. Taxa vary in the degree to which the impact of habitat loss is magnified by migratory connectivity (the area between the two curves). The sensitivity to uncertainty surrounding the connectivity is estimated by randomly changing the weights of edges by ±30%. Error bars indicate the highest and lowest range of losses in population flow calculated from 1000 iterations. For bar-tailed godwit, (b) indicates subspecies baueri and (m) subspecies menzbieri. For red knot, (p) indicates subspecies piersmai and (r) subspecies rogersi.

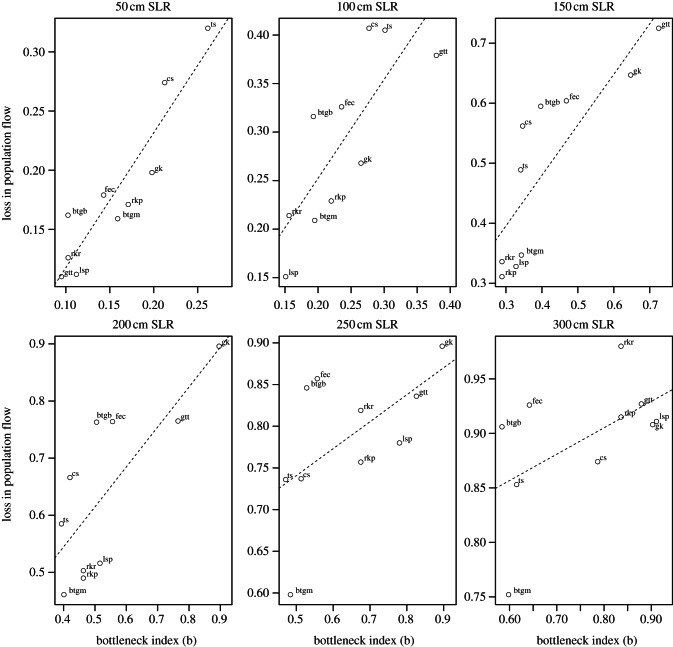
The degree of flow concentration inherent in the migratory network for each taxon predicted the vulnerability of their population to habitat loss. Reductions in population flow were positively related to the bottleneck index in low to medium SLR scenarios, where the heterogeneity of habitat loss was highest (figure 3). The difference between the proportional loss of flyway capacity and loss of habitat extent was much larger at the medium sea-level scenarios (figure 2). At 50 cm SLR, mean loss in population flow across the 10 taxa was only slightly higher than mean habitat loss (mean population flow loss = 0.181, mean habitat loss = 0.113, Welch two-sample tests: p = 0.012), but the difference between these two values is much larger at 150 cm SLR (mean population flow loss = 0.494, mean habitat loss = 0.306, p = 0.004).

Figure 3.

Bottlenecks and loss in population flow. The magnifying effect of migration on the loss of population flow can be predicted with a bottleneck index, a combined metric based on capacity centrality and estimated habitat loss (see the electronic supplementary material for details). The loss in population flow rises with increasing values of the bottleneck index at low to moderate sea-level rise (SLR). Linear regression models are significant from 50 to 200 cm SLR (p < 0.05) and marginally significant at 250 and 300 cm (p = 0.08 and 0.1). Taxa are labelled (bgtb, bar-tailed godwit (baueri); bgtm, bar-tailed godwit (menzbieri); cs, curlew sandpiper; ec, eastern curlew; gk, great knot; gtt, grey-tailed tattler; lsp, lesser sand plover; rkp, red knot (piersmai); rkr, red knot (rogersi); ts, terek sandpiper).

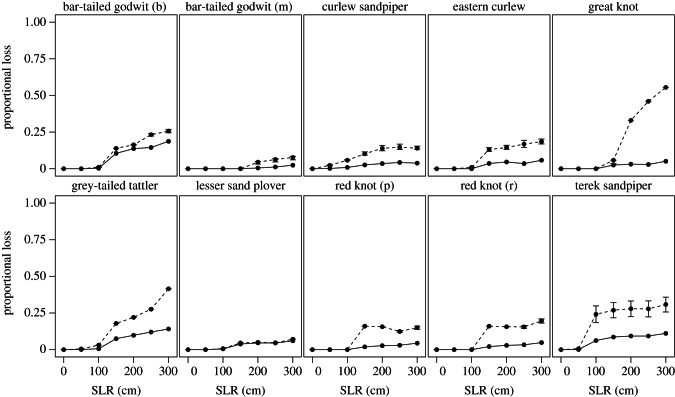
In an optimistic scenario, where an upshore shift of intertidal habitat into all non-urban areas is assumed, the rate of predicted habitat loss unsurprisingly was smaller for all SLR scenarios (figure 4). However, the declines in population flow always remained higher than those predicted by habitat loss alone, and the patterns were generally similar to those when no compensation was assumed (figure 2). For some species such as great knot and terek sandpiper, magnification of the impacts of habitat loss from SLR was as large as in the no compensation scenario, though for others (e.g. lesser sand plover), magnification was much smaller.

Figure 4.

Reductions in habitat extent and maximum population flow for 10 shorebird taxa, assuming upshore shifts of intertidal habitats. The loss of habitat extent (solid line) and loss of population flow (broken line) both rise with increasing sea levels, although the latter always equals or exceeds the former. Species vary in the degree to which the impact of habitat loss is magnified by migratory connectivity (the area between the two curves). Error bars indicate the highest and lowest range of losses in population flow from 1000 iterations.

4. Discussion

Migratory routes often include staging sites where migrants can rest and feed, and the loss of such sites can cause severe ‘bottleneck’ effects on migratory populations [14,31,32]. That is, sudden declines in population flow can be triggered by small amounts of overall habitat loss owing to migratory connectivity [11,14,33]. By developing a method to estimate the amount of population flow travelling through a migratory route subject to habitat loss, we have shown that these effects can be very large across an assemblage of declining long-distance migrants. Importantly from a conservation perspective, the flyway-wide consequences of habitat loss through SLR differ dramatically among the taxa we studied, even though they all use the same geographical region. This is because of variation in the specific patterns of connectivity among sites as well as the absolute extent of habitat loss at the sites used by each taxon. This variation demonstrates that understanding the pattern of migratory connectivity is essential for correctly predicting population declines resulting from habitat loss in migratory species.

SLR threatens to inundate the intertidal habitats upon which migratory shorebirds depend [34,35], but SLR has been relatively understudied in comparison with other drivers of habitat loss such as land conversion and reclamation [33]. This is perhaps because the human consequences are preventable in the short term, and also because the magnitude of SLR was previously underestimated as a result of ice-sheet melting being excluded from SLR models [27,28]. Our results, viewed through the lens of the most recent SLR predictions, suggest that we could witness dramatic collapses of population flow caused by intertidal habitat loss for at least some of the migratory shorebird species in this flyway within a few decades.

By applying the maximum flow algorithm to migratory species, we have built a simple framework in which to estimate the consequences of habitat loss for migratory populations. The newly introduced bottleneck index shows strong correlation with the loss in population flow especially for low to medium SLR scenarios (figure 3). This indicates that habitat loss within a bottleneck node, i.e. a node through which a large proportion of the population passes, can drive large overall declines in population flow, even if only a small fraction of total habitat is lost. Reductions in flyway capacity were strongly positively related to the bottleneck index (figure 3), suggesting that we could begin to estimate the vulnerability of particular migration routes to habitat loss in data-poor situations where a formal connectivity analysis is not possible. Importantly, this index is only based upon information gleaned locally from sites (i.e. how much of the population passes through a site and how much habitat will be lost) and does not require formal models of how individuals traverse an entire network. Our discovery emphasizes the importance of incorporating migratory connectivity into estimates of habitat loss impacts, and also provides an approach to estimate the vulnerability of migratory populations to local habitat loss.

Upshore movement of intertidal habitats in response to SLR would greatly reduce the magnitude of population declines (compare figure 2 with figure 4). Facilitating such movements, therefore, seems a critical conservation tool to protect migratory shorebirds from the impacts of habitat loss through SLR. In reality, the optimistic scenario is less likely to eventuate during the timeframe of the predicted rises in sea level we study here, given that the realization of such new habitat will depend on appropriate sediment patterns and coastal development regimes as well as a concomitant shift in food resources. Furthermore, managed realignment to allow existing intertidal habitat room to move upshore requires careful coastal zone planning and restriction of development footprints [36].

Our analysis does not incorporate the capacity of birds to change their migratory routes in response to environmental change. Such changes certainly do occur in nature [37,38], however, the occurrence of apparently sub-optimal migration routes suggests that flyways are rather constrained [39]. Some long-distance migrants (e.g. bar-tailed godwit) follow extremely tight flight schedules suggesting little room to adapt to major changes in flyway condition [40]. Our new framework for analysing migratory networks could incorporate changes in migratory routes by dynamically modifying the capacity of edges [41], provided the necessary data to parametrize such models were available. In addition to SLR, other aspects of climate change such as changes in temperature and patterns of storm activity could directly impact migratory species. For example, a temporal mismatch between migration times and peak abundance of food resources has been associated with population decline in migratory pied flycatchers Ficedula hypoleuca [42].

We have also assumed that the carrying capacity of each site is presently saturated—further field data would allow for variable carrying capacity to be incorporated into future analyses, perhaps by building spatially explicit population models [43]. Recent developments in remote sensing methodology have made it possible to derive satellite-derived estimates of habitat quality [44], and such data could be useful for estimating carrying capacity of intertidal wetlands across large areas. Varying habitat quality among sites can fundamentally affect how they are used by migratory shorebirds, for example, a site might act only as a minor feeding area prior to a continuing journey to a nearby location, or it might be a major staging area at which significant weight gain occurs and without which the migration would be impossible [32]. Thus, the population impact of losing habitat at a site depends on its quality and ecological context, and while such data are not yet available across the EAAF, it would be fruitful to incorporate habitat quality and context into future analyses.

Compensation of habitat loss by upshore shifts of intertidal areas would greatly reduce the net area of lost habitat, but it has a less predictable impact upon population flows (figure 4). Our results suggest that some species, such as the great knot, will still show large population declines even when full compensation is assumed. This is because many sites along highly developed coastlines, such as large areas of Japan and the Republic of Korea, cannot move upshore at all, thus compensation physically cannot occur. Species relying on sites in such areas for their migration will be those most vulnerable to SLR impacts. Moreover, SLR is not the only driver of intertidal habitat loss in the region, with several large estuaries in East Asia having been reclaimed over the past few decades [16]. This suggests that these species are more likely to experience sudden declines of population flow in future, even though they are currently relatively abundant. As such, careful monitoring of the populations of such species seems appropriate.

Severe declines in migratory shorebirds are becoming apparent around the world, with perhaps the most severe of those in the EAAF [16,45,46]. Intertidal habitats at staging sites in eastern Asia are diminishing rapidly in both area and quality. For example, a single reclamation project in the Yellow Sea recently removed 110 km² of shorebird habitat [16]. Our results (figure 2 and figure 4) indicate that developments around existing habitats severely affect the adaptability of migratory flyways against the threats from SLR. Unless steps are taken to allow the upshore movement of coastal ecosystems, it seems likely that SLR will compound such losses and cause accelerating population declines in migratory shorebirds.