λ-Meta Dynamics Approach To Compute Absolute Solvation Free Energy

Abstract

We present a new approach to combine λ dynamics with meta-dynamics (named λ-meta dynamics) to compute free energy surface with respect to λ. Particularly, the λ-meta dynamics method extends meta-dynamics to a single virtual variable λ, i.e., the coupling parameter between solute and solvent, to compute absolute solvation free energy as an exemplary application. We demonstrate that λ-meta dynamics simulations can recover the accurate potential of mean force surface with respect to λ compared to the benchmark results from traditional λ-dynamics with umbrella sampling. The solvation free energy results for five small organic molecules from λ-meta dynamics simulations using the same filling scheme show that the statistical errors are within ±0.5 kcal/mol. The new λ-meta dynamics method is general and other variables such as order parameters to describe conformational changes can be easily combined with λ-meta dynamics. This should allow for efficient samplings on high-dimension free energy landscapes.

Atomistic simulations to compute free energy difference between two states are pivotal to predict and explain molecular properties. Many simulation techniques have been developed, such as umbrella sampling^1-3, thermodynamics integration⁴, and free energy perturbation⁵. All these methods use a virtual coupling parameter (i.e., λ) to drive the molecular system from one state to another one. To enhance the sampling efficiency on λ, λ dynamics^{6, 7} was developed to treat the coupling parameter as a virtual dynamics variable in conjunction with molecular dynamics of real system. λ dynamics has been applied to study solvation free energy and ligands binding affinity in association with umbrella sampling^{8, 2} and adiabatic molecular dynamics⁹. On the other hand, another efficient sampling method, meta-dynamics, was developed recently to escape the energy minimum¹⁰ and has been further extended to recover the reaction profile^11-14. In meta-dynamics, the free energy surface is obtained efficiently by accumulating and filling history-dependent Gaussian potentials.

In this work, we developed a λ-meta dynamics by combining λ-dynamics with the meta-dynamics method^{12, 15, 16}, to help exploring the potential mean force (PMF) surface with respect to the virtual variable λ. To demonstrate the λ-meta dynamics approach, absolute solvation free energy is taken as one exemplary property. Solvation free energy is an essential property of molecules and is indispensible in drug discovery process¹⁷. Various theoretical approaches have been proposed, ranging from the simple quantitative structure-activity relationship (QSAR) model^18-20 to continuum solvent model^21-27, to molecular mechanics model based on force fields^28-31, and to quantum mechanics/molecular mechanics (QM/MM) model^32-34. We focus on using QM/MM atomistic simulations³⁵ to calculate absolute solvation free energy in aqueous solution. The solute molecule was described with ab initio QM while the solvent with explicit TIP3P water model.

Here, two virtual variables λ_ele and λ_vdw are used to drive the solute from aqueous solution state to vacuum state. λ_ele controls the electrostatic interactions between solute in QM and solution in MM while λ_vdw scales the van der Waals (VDW) between QM and MM. Using the new λ-meta dynamics approach, not only the PMFs were recovered compared to λ dynamics with umbrella sampling, but also absolute solvation free energies for five small organic molecules were computed accurately. A general filling scheme of Gaussian functions required in meta-dynamics was also developed to control the statistical errors in λ-meta dynamics. More importantly, λ-meta dynamics is a general approach for free energy simulations, which can be readily extended to multiple variables and can efficiently explore such high-dimension surfaces.

To elaborate the details of λ-meta dynamics method, we chose absolute free energy computations using the QM/MM Hamiltonian defined by

$$H\left(\lambda \right)=\langle \Phi |H_{QM}+{\lambda }_{\mathit{\text{ele}}}{H}_{\mathit{\text{ESP}}}|\Phi \rangle +H_{QM/MM,\mathit{\text{vdw}}}({\lambda }_{\mathit{\text{vdw}}})+H_{MM}$$ (1)

where H_QM, H_Qm/MM,vdw, and H_MM are the Hamiltonian of QM subsystem, empirical VDW interactions between QM and MM subsystems, and MM internal energy. H_ESP captures the MM point charge electrostatic potential influence on the QM subsystem. The coupling parameters λ_ele and λ_vdw are used to scale the electrostatic and VDW interactions between QM and MM and drive the solute from solution to vacuum environment. To scale the VDW interactions, the soft-core potential is applied to avoid the simulation singularity and instability problems. For λ-dynamics⁶, eq. 1 is extended to the following equation that contains a virtual variable λ,

$$H_{\mathit{\text{extend}}}(\lambda )=H(\lambda )+\frac{1}{2}{m}_{\lambda }{\dot{\lambda }}^2$$ (2)

where λ̇ is velocity of λ and m_λ is the virtual mass of λ. This method has been applied to compute the relative solvation free energies^{6, 37, 9} and binding free energies^{38, 39} between similar molecules.

When meta-dynamics is incorporated into eq. 2, a history-dependent term U^*(λ,t) is added to fill the PMF well. Typically, U^*(λ,t) can be expanded by a set of Gaussian functions as:

$$U^{\ast }(\lambda ,t)=w\sum _{\begin{array}{l}{t}^{\prime }=t_G,2t_G,\dots \\ t^{\prime }<t\end{array}}exp(-\frac{{(\lambda -\lambda (t^{\prime }))}^2}{2\delta s^2})$$ (3)

In this equation, w is the Gaussian height, δs is the Gaussian width, and t_G is the filling frequency. So this external potential U^* (λ, t) depends on the trajectory and filling scheme. When the width of the Gaussians is small and t is sufficiently large, the PMF surface can be recovered by U^*(λ,t), i.e., ΔA(λ) = −U^*(λ). Here, U^* (λ,t) is simplified as U^* (λ) for brevity.

To benchmark our results of λ-meta dynamics simulations, λ-dynamics combined with the classical umbrella sampling was performed. In umbrella sampling, 21 uniformly distributed windows from λ=1 to λ=0 were sampled with 5 ps relaxations and 95 ps MD simulations at T=300 K and 500 kcal/mol force constant on λ for λ_ele and λ_vdw, respectively. (Note that umbrella sampling needs more computational cost to tune up the sampling efficiency such as the number of sampling windows and optimal force constants for each window. In this work, extensive umbrella samplings were applied to obtain the benchmark data.) The Weighted Histogram Analysis (WHAM)^{1, 2} with bin size 0.001 was applied on these trajectories to recover free energy surfaces.

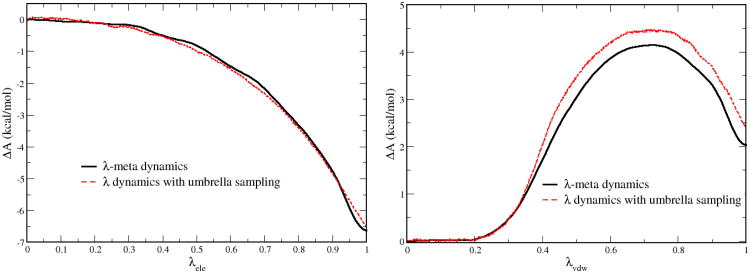
Using methanol as a model system, the PMF surfaces for λ_ele and λ_vdw computed by our λ-meta dynamics approach were plotted in Figure 1 along with the umbrella sampling curves. Both curves of λ_ele and λ_vdw from λ-meta dynamics agree well with umbrella sampling curves. The free energy differences between λ-meta dynamics and umbrella sampling are only 0.3 and 0.5 kcal/mol for ΔA along λ_ele and λ_vdw, respectively. Therefore, the new λ-meta dynamics method can indeed recover the PMF with respect to λ and obtain accurate absolute solvation free energy of methanol compared to umbrella sampling. Note that since the mirror periodic condition was applied for λ-meta dynamics, a cusp appears when λ is close to 1. This is why a relatively small Gaussian width (0.06) should be used in the smoothing period to capture the cusp height. Although the exact cusp shape cannot be reproduced by finite Gaussian functions, these derivations from the cusp on PMF are negligible compared to the umbrella sampling results.

Figure 1.

PMF surfaces computed by λ-meta dynamics (solid black lines) and umbrella sampling (dashed red lines) for methanol in aqueous solution for λ_ele and λ_vdw, respectively.

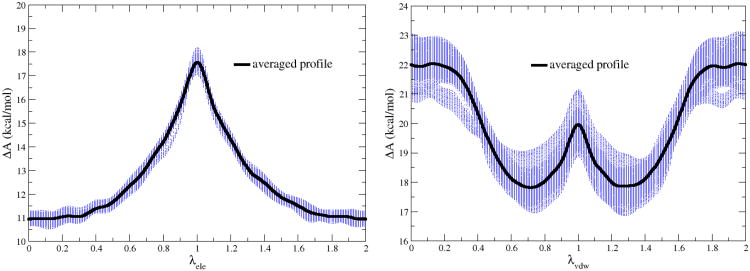
To understand the fluctuations of filling procedure in λ-meta dynamics, Figure 2 shows the PMF profiles (150 curves for λ_ele and 390 curves for λ_vdw in dashed blue lines) from the smoothing period along with their averaged profiles in solid black lines. For λ_ele, the ΔA_ele fluctuations are within 0.5 kcal/mol, while relatively large ΔA_vdw fluctuations of ±1.2 kcal/mol for λ_vdw were observed. Note that these fluctuations during filling procedure are not the statistical errors of λ-meta dynamics. To estimate the statistical errors of λ-meta dynamics, we further carried out eight independent simulations for λ_ele and λ_vdw with different initial velocities in λ-meta dynamics. As list in Table 1, for methanol, the standard deviation for ΔA_ele is 0.17 kcal/mol and is 0.36 kcal/mol for ΔA_vdw Therefore, the absolute solvation free energies can be computed by the new λ-meta dynamics method with small statistical errors (<0.5 kcal/mol for methanol compared to the benchmark result from umbrella sampling). Compared to experimental data in Table 1, theoretical computations (both λ-meta dynamics and umbrella sampling) show the errors around 2 kcal/mol for acetamide and acetic acid. These errors are derived from the interactions between QM and MM subsystems such as vdW, which are beyond the scope of this letter.

Figure 2.

PMF profiles (dotted blue lines) and the averaged PMFs (solid black lines) of λ_ele and λ_vdw for methanol.

Table 1.

The computed solvation free energies from λ-meta dynamics and λ dynamics with umbrella sampling (i.e., λ-US) for five compounds.

Molecule		ΔAele	ΔAvdw	ΔAsolv	ΔAexpa
Methanol	λ-meta	−6.79 ±0.17	1.87 ±0.36	−4.92 ±0.46
	λ-US	−6.50±0.06	2.46±0.10	−4.04±0.08	−5.11
Methane	λ-meta	−0.23 ±0.08	1.77 ±0.30	1.53±0.32
	λ -US	−0.28±0.06	2.21±0.10	1.93±0.06	2.0
Methylamine	λ-meta	−6.58 ±0.22	1.76 ±0.19	−4.82 ±0.28
	λ -US	−6.17±0.10	2.05±0.16	−4.12±0.19	−4.56
Acetamide	λ-meta	−10.14 ±0.30	2.10 ±0.49	−8.04 ±0.70
	λ -US	−9.90±0.05	2.34±0.10	−7.56±0.14	−9.71
Acetic acid	λ-meta	−6.72 ±0.23	2.11 ±0.31	−4.76 ±0.33
	λ -US	−6.46±0.06	2.56±0.17	−3.90±0.14	−6.7

^aExperimental values from Ref. 31

It is worth discussing why ΔA_vdw has the relatively larger error compared to ΔA_ele, which is shown in Figure 1 when comparing Δ-meta dynamics with umbrella sampling and is also observed in Figure 2. Such large errors of ΔA_vdw are caused by the broad VDW force distributions of dH_{QM/MM, vdw}(λ_vdw)/d λ_vdw, especially when the solute VDW sphere is in contact with the solvent molecules for λ_vdw between 0.4 and 1.0. Even though the soft-core potential approach for the VDW part is applied here, as shown in Figure S1 of the supporting information (SI), the inertial movements in VDW make λ dynamics less diffusive for λ_vdw than for λ_ele when the PMF wells are filled. We also plot the curves from eight independent λ-meta dynamics simulations along with the umbrella sampling result in Figure S2. The relatively large derivations (within 1 kcal/mol) between λ-meta dynamics and umbrella sampling appear when λ_vdw is larger than 0.4, and this problem is caused by the empirical VDW energy expression. Nevertheless, the computed solvation free energies still agree well with the umbrella sampling results as shown in Table 1.

The computed solvation free energies for all five small organic molecules are listed in Table 1 with the estimated statistical errors from eight independent simulations for both λ_ele and λ_vdw. For methane, methylamine, acetamide, and acetic acid, the PMF surfaces were plotted in Figures S3-S6 from one of eight independent λ-meta dynamics simulations along with umbrella sampling results. The PMF comparisons between umbrella sampling and λ-meta dynamics demonstrate that λ-meta dynamics with a general filling scheme is robust to obtain the absolute solvation free energies for most five diverse molecules (from large to small solvation free energies) with the errors within 1.0 kcal/mol compared to umbrella sampling results. These deviations of absolute solvation free energies computed by λ-meta dynamics are mainly caused by the cusp when λ=1.

In summary, we developed a new λ-meta dynamics method, which combines λ dynamics with meta-dynamics to enhance the samplings of virtual variables. To our best knowledge, λ-meta dynamics is the first method to demonstrate meta-dynamics can be used to recover PMF surfaces composed of virtual variables. The general filling scheme to accumulate and add Gaussian functions to fill the PMF wells can be used for all five diverse molecules. Our results for solvation free energy calculations show that λ-meta dynamics can reproduce the accurate PMF surface with respect to λ efficiently (120 ps for λ_ele and 240 ps for and λ_vdw). The corresponding solvation free energies are all within 1.0 kcal/mol errors compared to umbrella sampling results. This suggests that the computational cost of solvation free energy calculations can be reduced significantly since one single simulation for λ_ele and λ_vdw is sufficient, respectively. Finally, λ-meta dynamics is a general approach to enhance the samplings on virtual variables, which can be also further applied in other free energy computations such as protein ligand binding free energy. λ-meta dynamics can readily incorporate other order parameters and explore the corresponding high-dimension free energy landscapes efficiently.

Computational Details

The new λ-meta dynamics approach was implemented in our in-house program⁴⁰. In QM/MM simulations, only the solute is included in the QM subsystem at the B3LYP/3-21G level. Since this work focuses on methodology demonstrations, a small Gaussian basis set of QM is applied to save the computational cost in QM/MM simulations. The VDW parameters were chosen for each atom element: C, H, O, and N from CHARMM 22 force field⁴¹ (i.e., atom type C, HA, O, and N). The MD integration step is 1 fs for all forces. The pairlist was updated every 10 fs with electrostatic cutoff as 10 Å. The solute is solvated and centered in a 40×40×40ų water box with more than 2000 TIP3P water molecules depending on the specific solute molecules. NVT ensemble at 300 K was applied in simulations with the Berendsen stat⁴² . For the virtual coordinate, m_λ is chosen as 12 a.m.u., which is same as a carbon atom.

The thermo ensemble on λ is generated using Nose-Hoover Chain technique ⁴³ with 4 chains and the temperature is maintained at 60 K for meta-dynamics.

In λ-meta dynamics, the filling scheme for Gaussian functions in eq. 3 is crucial to reproduce accurate solvation free energy. To accomplish the balance between accuracy and efficiency, a special boundary condition is applied: λ is confined in a [0, 2] region. Particularly, when λ is between 1 and 2, the value of λ is replaced by 2 − λ, which is then used to compute QM/MM energies and the corresponding forces with reverse sign. When λ is larger than 2 or smaller than 0, it is immediately mirrored by λ−2 or λ+2, respectively, to guarantee λ is within [0, 2] region. This mirror periodic condition can help Gaussian functions fill the wells of two end points at 0 and 1, which are essential to compute the accurate solvation free energy.

The entire Gaussian filling procedure is split into two parts: the coarse-filling period and the smoothing period. In the coarse-filling period, Gaussian functions with large Gaussian height from 0.16 to 0.08 in U^*(λ) are applied to construct the rough PMF surface. In the smoothing period, Gaussian functions with height 0.04 are used to refine U^*(λ). All Gaussian functions have the fixed width of 0.06. At every 50 MD steps, a new Gaussian function is added to U^*(λ) and its Gaussian height is gradually changed according to the filling procedure. The detailed scheme to fill the PMF wells and calculate solvation free energies for all five organic molecules is the following:

1. For first 300 Gaussian functions, the Gaussian height is 0.16, then it is decreased to 0.12 for next 300 peaks and to 0.08 for last 300 peaks to accomplish the coarse-filling period with the initial 45 ps MD simulations;

2. The Gaussian height with 0.04 is added to refine U^*(λ) obtained in step a). For λ_ele-meta dynamics, 1,500 Gaussian functions are added in 75 ps simulation. For λ_vdw-meta dynamics, 3,900 functions are added in 195 ps simulations.

In meta dynamics, the free energy profile should be computed by using arithmetic average of profiles after collective variable starts diffusing [Ref 11]. The final solvation free energy surface is constructed by only averaging the curves in the smoothing period after every 10 Gaussian functions are added. Totally, for the λ_ele part, 150 curves, and for λ_vdw 390 curves are generated to reproduce the PMF surface from λ=0 to λ=1. Note that the average value of [0, 1] and [1, 2] regions is also applied here. The solvation free energy (ΔA_solv= ΔA_ele + ΔA_vdw) can be readily computed by two independent terms using the values at λ=0 and λ=1, i.e., ΔA_ele = −U^*(λ_ele=1) +U^*(λ_ele=0) and ΔA_vdw = −U^*(λ_vdw=1) +U^*(λ_vdw=0), respectively.