A 13-bit Noise Shaping SAR-ADC with Dual-Polarity Digital Calibration

Abstract

We present a new noise shaping method and a dual polarity calibration technique suited for successive approximation register type analog to digital converters (SAR-ADC). Noise is pushed to higher frequencies with the noise shaping by adding a switched capacitor. The SAR capacitor array mismatch has been compensated by the dual-polarity digital calibration with minimum circuit overhead. A proof-of-concept prototype SAR-ADC using the proposed techniques has been fabricated in a 0.5-μm standard CMOS technology. It achieves 67.7 dB SNDR at 62.5 kHz sampling frequency, while consuming 38.3μW power with 1.8 V supply.

I. Introduction

Analog-to-digital converters (ADC) using the charge redistribution property of the successive-approximation-register (SAR) show considerable power efficiency, and so they are being widely used in low power and low frequency applications, such as medical devices. As a result of the in-depth research on the SAR architecture and due to prevalence of the CMOS process, the SAR-ADC is aggressively extending into both high frequency domain of several tens of MHz and high resolution in the order of 14-16 bits [1], [1]. However, such performance improvements often come at the cost of increased design complexity or the power/area consumption. Many designers of low power applications, who adopt the SAR-ADC architecture, are still looking for solutions that would increase the ADC resolution without sacrificing its simplicity and the power/area efficiency. In this paper, we present a new noise shaping method, which can be easily added to an existing SAR-ADC structure, along with a dual-polarity digital calibration method, which compensates the capacitor mismatch with minimal circuit burden.

If the error between the analog input and the digitized output can be delivered to the next conversion cycle, the quantization noise is high-pass filtered and pushed into higher frequencies [2]. Researchers have found several ways to incorporate the noise shaping effect in the VCO-based, dual-slope, and flash ADCs. These are either implemented as stand-alone ADCs or used as a single-bit or a multi-bit quantizer for Δ∑ ADCs depending on the application requirements [3]-[7]. The SAR-ADC architecture also has the potential for applying the noise shaping technique considering the fact that the internal charge redistribution digital-to-analog converter (crDAC) capacitors keep a residual charge at the end of the conversion period. If this residual charge can be delivered to the next conversion cycle, the signal-to-noise ratio (SNR) will be increased via noise shaping without significant modifications in the basic SAR architecture [8], [9]. The additional circuit for noise shaping, however, should be carefully designed not to degrade the built-in crDAC performance, which is key in determining the ADC resolution. The proposed noise shaping method delivers the residual charge by adding a single switched capacitor in parallel to the top plate of the crDAC, in a way that it will not degrade the original ADC performance.

For the SAR-ADCs with moderate resolution in the order of 10 effective number of bits (ENOB), resolution is often limited by the capacitor mismatch, as opposed to the small DAC voltage steps, which is the main reason that limits the resolution in high resolution ADCs with low supply voltage [1], [8]. Furthermore, capacitor mismatch is more serious in the low cost processes without high precision multilayer metal-insulator-metal (MIM) capacitors, which should rely on poly-poly capacitors with large bottom plate parasitic capacitance of 10-20% [10]. Therefore, calibration is necessary to minimize capacitor mismatch and the resulting performance degradation.

Calibration can be done either in the analog domain by adding an auxiliary DAC or in the digital domain after the digitized code is generated [11], [12]. Digital calibration has the advantage of low complexity if it is completed in the foreground before the normal ADC operation starts. If the calibration is executed continuously in the background, transparent to the normal ADC operation, it can be more accurate and be responsive to varying environmental conditions, such as temperature. There is, however, a level of circuit overhead in addition to digital code redundancy [1], [12]. We have adopted foreground digital calibration to minimize the burden of calibration circuitry. Moreover, previous calibration methods require a comparator calibration to cut the comparator offset before the capacitor calibration, which is yet another overhead [13], [13]. The proposed dual-polarity digital calibration conducts the comparator calibration along with the capacitor calibration by repeating the calibration of each binary capacitor with two polarities.

II. Noise Shaping

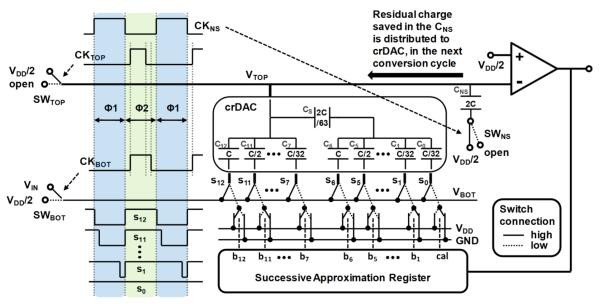
Fig. 1 depicts the overall architecture of the proposed SAR-ADC with the noise shaping. A 12-bit crDAC is implemented as a pair of 6-bit capacitive arrays connected by a splitting capacitor. The split-array topology was adopted to reduce area and dynamic power consumption. A static latched comparator was selected to minimize the kickback noise [14]. By controlling two switches connected each at top and bottom plate of the crDAC (SW_TOP and SW_BOT) with the right sequence described in Fig. 1, the input voltage is sampled at the total capacitance of the crDAC (C_DAC) with the stored charge of,

$$Q_{\mathit{IN}}=C_{\mathit{DAC}}\cdot (V_{\mathit{DD}}∕2-V_{\mathit{IN}}).$$ (1)

Fig. 1.

Overall architecture of the proposed SAR-ADC with timing diagram of its sampling clocks.

Subsequently, a 13-bit serial digital output stream is generated from the comparator output by deciding the status of 12 switches at the bottom plate of each binary scaled capacitor to either supply (V_DD) or ground (GND) from V_DD/2 according to the previous comparator output. At the end of the DAC conversion period, a residual charge will remain and present a residual voltage (ΔV_RES) at the top plate of the crDAC, which is smaller than the minimum DAC output voltage resolution. By adding a capacitor (C_NS) with a switch (SW_NS) for noise shaping, the residual charge can be saved and delivered to the next conversion cycle.

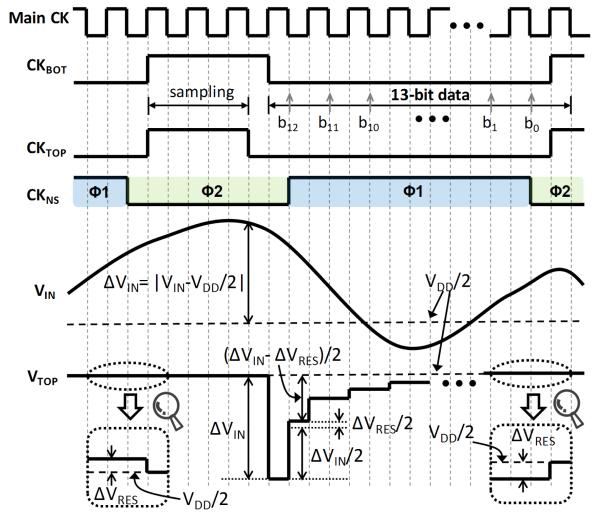
Detailed operating diagram of the noise shaping function is shown in Fig. 2. During the phase Φ₁, the SW_NS is connected to V_DD/2 and the DAC conversion takes place for twelve times till the voltage at the top plate of the crDAC (V_TOP) shows V_DD/2±ΔV_RES. At the end of phase Φ₁, C_NS is charged with a residual charge Q_RES,

$$Q_{\mathit{RES}}=C_{\mathit{NS}}\cdot (V_{\mathit{TOP}}-V_{\mathit{DD}}∕2),$$ (2)

and the SW_NS is opened before the top plate of the crDAC is connected to V_DD/2. Thus, the C_NS maintains its stored charge of Q_RES. During phase Φ₂, the input voltage, V_IN, is sampled while keeping SW_NS open to conserve the Q_RES in C_NS. SW_NS is closed at the beginning of the next Φ₁ phase after both the SW_TOP and the SW_BOT are toggled to low. The residual error charge, Q_RES in C_NS, is then merged with the sampled input charge, Q_IN in C_DAC, as the two capacitors are connected in parallel, and their voltages are averaged (since C_NS = C_DAC) at the onset of Φ₁. As a result, a noise shaping property is achieved.

Fig. 2.

Operating diagram of the SAR-ADC with noise shaping.

The proposed noise shaping method of the SAR-ADC is based on the charge sharing between C_DAC and C_NS. When SW_NS is connected to V_DD/2, the charge captured in C_DAC by the input sampling (Q_IN) is shared with the residual charge in C_NS (Q_RES). Thus, V_TOP is determined according to both the input voltage level and the residual charge from previous conversion cycle. Using the law of conservation of charge, V_TOP at the beginning of the next conversion cycle, V_TOP’, can be calculated from,

$$\begin{array}{cc}\hfill & (C_{\mathit{NS}}+C_{\mathit{DAC}})\times ({V_{\mathit{TOP}}}^{\prime }-V_{\mathit{DD}}∕2)=Q_{\mathit{IN}}+Q_{\mathit{RES}}\hfill \\ \hfill & =C_{\mathit{DAC}}\times (V_{\mathit{DD}}∕2-V_{\mathit{IN}})+C_{\mathit{NS}}\times (V_{TOP}-V_{\mathit{DD}}∕2).\hfill \end{array}$$ (3)

Since C_NS is designed to have the same size as C_DAC, (3) can be simplified to,

$${V_{\mathit{TOP}}}^{\prime }-V_{\mathit{DD}}∕2=(V_{\mathit{DD}}∕2-V_{\mathit{IN}})∕2+(V_{\mathit{TOP}}-V_{\mathit{DD}}∕2)∕2.$$ (4)

Therefore, the sampled input (V_DD/2-V_IN) and the residual error (V_TOP-V_DD/2) are averaged. Accordingly, the relationship between the sampled analog input X[n], the digital output D[n], and the quantization error q_e[n] can be described as,

$$\begin{array}{cc}\hfill & D\left[n\right]=\frac{1}{2}X\left[n\right]+q_e\left[n\right]-\frac{1}{2}{q}_e[n-1]\hfill \\ \hfill & \to D\left(z\right)=\frac{1}{2}X\left(z\right)+q_e\left(z\right)\cdot (1-\frac{1}{2}{z}^{-1}).\hfill \end{array}$$ (5)

The maximum attenuation of the quantization noise that can be achieved is by half, which implies that a maximum improvement of signal to noise ratio (SNR) would be 6 dB from noise shaping. However, the maximum noise attenuation can be increased with the ratio of C_NS to the C_DAC. The ratio between these two capacitors determines the coefficient of the residual error that is delivered to the next conversion cycle. If C_NS = k × C_DAC, then from (3) we can find,

$${V_{\mathit{TOP}}}^{\prime }-V_{\mathit{DD}}∕2=\frac{1}{1+k}\times (V_{\mathit{DD}}∕2-V_{\mathit{IN}})+\frac{k}{1+k}\times (V_{\mathit{TOP}}-V_{\mathit{DD}}∕2)$$ (6)

where k determines the coefficient of the noise shaping component. For example, if k is increased to 3, (5) can be changed to

$$\begin{array}{cc}\hfill & D\left[n\right]=\frac{1}{4}X\left[n\right]+q_e\left[n\right]-\frac{3}{4}{q}_e[n-1]\hfill \\ \hfill & \to D\left(z\right)=\frac{1}{4}X\left(z\right)+q_e\left(z\right)\cdot (1-\frac{3}{4}{z}^{-1}).\hfill \end{array}$$ (7)

and the maximum noise attenuation is ¼ along with maximum SNR improvement of 12 dB.

The size of the C_NS also changes the crDAC step size (ΔV_LSB) based on (6), that is, variations in V_TOP tend to decrease as the weight of noise shaping increases. However, it is not a serious concern in ADCs with moderate resolution considering that the input referred noise of the comparator, V_n-CMP, is much smaller than the minimum voltage resolution of the crDAC, ΔV_LSB. For instance, in the presented 13-bit ADC with k=1, V_n-CMP ≈ 0.1 × ΔV_LSB. Nevertheless, the trade-off between the weight of noise shaping and ΔV_LSB should be considered in the design stage. It should be also noted that C_NS neither needs a high level of accuracy as the crDAC capacitors nor a special care for matching in its layout. This will give designers the flexibility to layout C_NS within the remaining dead space on the chip.

III. Dual-Polarity Digital Calibration

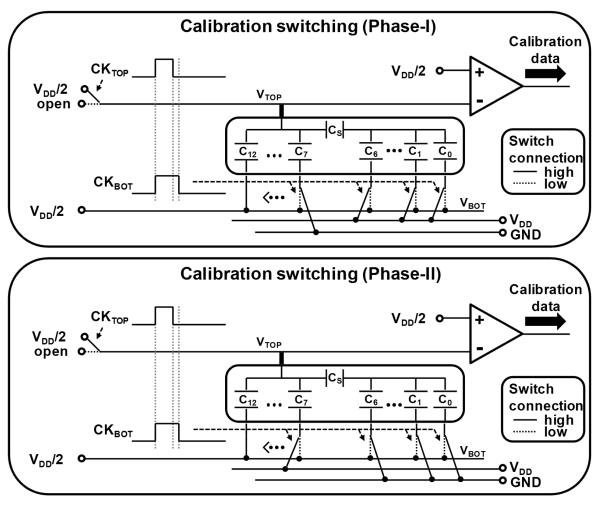
In SAR-ADCs with binary-weighted crDACs, the size of the n^th bit capacitor, C/2^12-n in Fig. 1, is the same as the sum of all smaller capacitors combined. For instance in Fig. 3, C₇ is ideally equal to the series combination of C_S and ∑C_i (i = 0 to 6). Therefore, if we charge C_n up to a certain voltage, e.g. V_DD/2, and also charge the smaller capacitors up to the same voltage but with the opposite polarity, i.e. -V_DD/2, when we connect all of them in parallel, the charges should ideally cancel out and the mismatch voltage should be zero. On the other hand, if there was a mismatch between C₇ and the smaller capacitors, the amount of the mismatch voltage after charge cancellation would be an indicator of the amount of capacitor mismatch, and one can digitize that voltage to calibrate the 7^th bit [11].

Fig. 3.

Switching sequence for the dual-polarity digital calibration.

We applied this calibration method only to the MSB half of the split array (C₇ to C₁₂ in Fig. 3) due to its significance in the SAR-ADC operation, and considered the LSB half to be accurate. The mismatch of the LSB half is negligible because its numerical value (binary weight) is 2⁻⁶ times of its physical size when using the split array architecture. During calibration process, initially all capacitors were discharged by connecting their top and bottom plates to V_DD/2. Then in Phase-I calibration, shown in Fig. 3, the bottom plate of C₇ was connected to GND, charging it to V_DD/2, and the bottom plates of C₀ to C₆ were connected to V_DD, charging the series combination of C_S and C_0:6 to -V_DD/2. At the falling edge of CK_TOP, the top plate detaches from V_DD/2 and at the falling edge of CK_BOT, all bottom plates switch back to V_DD/2, thus connecting all capacitors in parallel. V_TOP at this time represents the mismatch in C₇, and the SAR-ADC digitization function, running only on the LSB half, provides the amount of calibration needed to compensate for this mismatch. The same process is then applied to C₈ to C₁₂. It should be noted that any possible mismatch in the splitting capacitor, C_S, will already be considered after completing the calibration process for each capacitor in the MSB half of the array [13].

Another source of error in the SAR-ADCs is the comparator offset. Because V_TOP after the calibration process is very close to V_DD/2, even a slight offset in the comparator input can affect the calibration results [13]. To address this problem, we have adopted a dual-polarity digital calibration mechanism, which repeats the calibration process that was explained earlier, with two opposite polarities, as shown in Fig. 3. In Phase-I, C_n acquires a positive charge (V_DD/2) and the smaller capacitors acquire a negative charge (−V_DD/2). In Phase-II, however, C_n acquires a negative charge (−V_DD/2) and the smaller capacitors acquire a positive charge (V_DD/2).

Since the comparator offset affects the digitized value of the mismatch voltage by the same amount and in the same direction in each phase, as a common-mode signal, it can be taken care of by subtracting the resulting calibration value in Phase-I from that of Phase-II, and dividing the result by half. The mismatch voltage caused by the capacitor mismatch acquires a different polarity in each calibration phase, like a differential-mode signal, and doubles after subtracting the results. At the end of this dual-polarity calibration process, we will have an averaged calibration value for each MSB capacitor, C₇ to C₁₂.

IV. Measurement Results

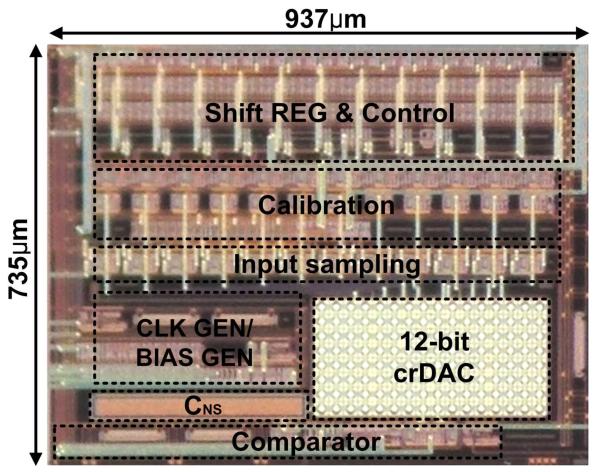
A prototype SAR-ADC was fabricated in the ON-Semi 0.5-μm 3M2P standard CMOS process with poly-insulator-poly (PIP) capacitors. A chip micrograph is shown in Fig. 4 with the active area of 0.689 mm². It can be seen that C_NS, which is added for the noise shaping, occupies a much smaller area compared to the matched crDAC capacitor array, and it has been located within a dead space on the ADC floor plan. The proposed calibration circuitry consumes 13.6% of the entire active area. All measurements were conducted with 1.8V supply and the total SAR-ADC power consumption was 38.3μW at 62.5 kHz sampling rate.

Fig. 4.

Chip micrograph.

Table 1 shows the calibration results of the SAR-ADC, reported in LSB units. Columns two and three show the raw 6-bit digitized outcomes of the mismatch voltage plus comparator offset in Phase-I and Phase-II of the dual-polarity digital calibration process, respectively. In the 4^th column, we have subtract Phase-II from Phase-I and divided it by 2 to cancel out the common-mode comparator offset. However, in order to achieve the net mismatch voltage caused by each capacitor mismatch, which also represents the necessary calibration for each bit in LSB, we should consider the fact that while calibrating C₈ and above, the mismatch of all the lower capacitors will be included in the raw data. Therefore, to find the specific mismatch of each MSB capacitor of the SAR-ADC in column 5, we need to add all the previous values in column 5 to the value in column 4. Finally, the comparator offset can be found by averaging the result of Phase-I and Phase-II, to find the common-mode value, as shown in the 6^th column, with good consistency. These calibration results were delivered to an off-chip microcontroller to compensate the ADC output in the digital domain.

TABLE 1.

SAR-ADC Calibration Results.

Capacitor Under Calibration	Phase-I Cal. Output	Phase-II Cal. Output	(I−II)/2	Capacitor Mismatch	Comp. Offset (I+II)/2
C7	−5	−5	0	0	−5.0
C8	−5	−4	−0.5	−0.5	−4.5
C9	−4	−5	+0.5	0	−4.5
C10	−4	−5	+0.5	0	−4.5
C11	−2	−8	+3.0	+2.5	−5.0
C12	−13	+4	−8.5	−6.5	−4.5

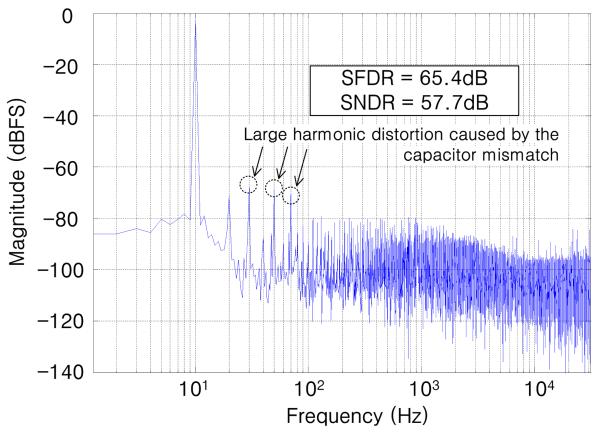
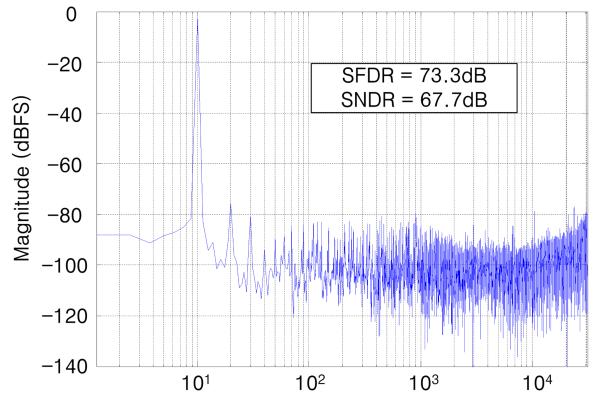
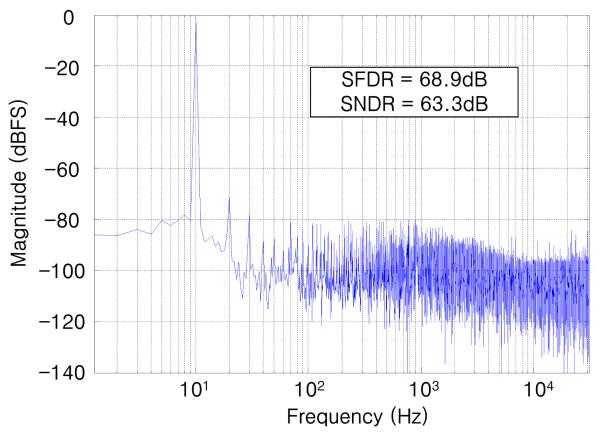
Figs. 5-7 show the spectrum of the SAR-ADC digitized output when a full-scale 1.8 V_p-p sinusoidal input at F_IN = 10 Hz was sampled at F_S = 62.5 kHz, with and without the noise shaping and dual-polarity digital calibration. The 10 Hz input frequency was selected to observe the effects of noise shaping without them being obscured by the harmonic distortion. To calculate the signal-to-noise plus distortion ratio (SNDR), over sampling ratio of 10 was applied to exclude the high frequency noise, resulting in 3.125 kHz signal bandwidth (BW_signal) [7], [8].

Fig. 5.

FFT of a digitized 10 Hz, 1.8 V_p-p sinusoid without noise shaping, before applying the dual-polarity digital calibration.

Fig. 7.

FFT of the same input as in Fig. 5 after applying both noise shaping and dual-polarity digital calibration.

Before calibration and without noise shaping, Fig. 5 shows several large peaks of harmonic distortion, which are caused by capacitive mismatch. The measured spurious free dynamic range (SFDR) and SNDR in this case were 65.4 dB and 57.7 dB, respectively. After compensating for the crDAC capacitor mismatch via calibration, however, the harmonic distortion components were significantly attenuated, as shown in Fig. 6, and consequently the SFDR and SNDR were improved to 68.9 dB and 63.3dB, respectively. Finally, Fig. 7 shows how the noise floor is pushed upward towards the higher frequencies when we activated the noise shaping mechanism in addition to calibration, which in turn decreases the in-band noise and improves the SFDR and SNDR further to 73.3 dB and 67.7 dB, respectively.

Fig. 6.

FFT of the same input as in Fig. 5 after applying dual-polarity digital calibration, but without noise shaping.

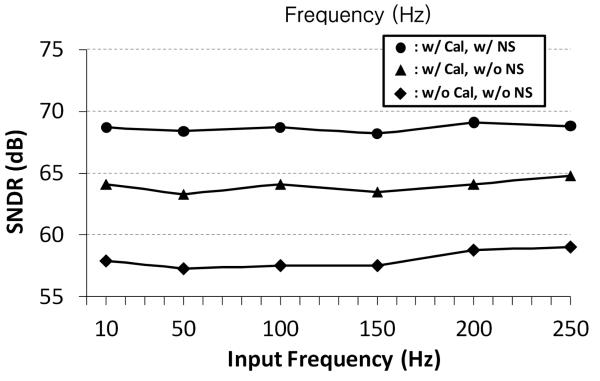
Table 2 summarizes the performance of the SAR-ADC at fixed F_S and F_IN. Total harmonic distortion (THD) was improved by 8.0 dB with calibration, which implies that the distortion caused by the capacitor mismatch was compensated. The SNR was improved by 6.7 dB by activating the proposed noise shaping mechanism. This result means that the noise floor is reduced almost by half and it matches with the theoretical improvement described in section II. The effect of the noise shaping will become even more remarkable when the THD is increased with linearity improvement, considering that the THD is worse than the SNR in the presented ADC. It should be noted that the foreground calibration adopted in this ADC cannot perfectly compensate the capacitance mismatch. It generates some discontinuity, because it has no redundancy in the digital code [1], [12]. The overall improvements in the SAR-ADC performance can be demonstrated by deriving its ENOB from the SNDR, which was improved from 9.3 to 10.2 bits, and eventually to 11.0 bits with calibration and noise shaping, respectively. Fig 8 shows how the measured SNDR of the SAR-ADC varies with the sinusoidal input frequency.

TABLE 2.

SAR-ADC Performance Summary.

Test condition	SFDR (dB)	THD (dB)	SNR (dB)	SNDR (dB)	ENOB (bits)
w/o Cal*, w/o NS**	65.4	60.6	68.6	57.7	9.3
w/ Cal, w/o NS	68.9	68.6	70.1	63.3	10.2
w/ Cal, w/ NS	73.3	71.4	76.8	67.7	11.0

Input signal characteristics: F_S = 62.5 kHz, BW_signal = 3.125 kHz, F_in = 10 Hz

^*Cal: dual-polarity digital calibration,

^**NS: noise shaping

Fig. 8.

SNDR variations vs. sinusoidal input frequency with and without calibration and noise shaping (F_S = 62.5 kHz, BW_signal = 3.125 kHz).

V. Conclusions

A new method for noise shaping has been presented to improve the resolution of the SAR-ADCs with moderate resolution. By simple addition of a switched capacitor to the traditional SAR-ADC architecture, it is possible to deliver the digitization error from one conversion cycle to the next and reduce the in-band noise as a result. We have also demonstrated a dual-polarity digital calibration mechanism to compensate for the capacitor mismatch in the crDAC binary-weighted array with minimum circuit overhead. The presented techniques are easily applicable to a variety of existing SAR-ADCs architectures to improve their performance without adding considerable design burden.

Biography

Hangue Park was born in 1980. He received both B.S. and M.S. degree from Seoul National University, Seoul, Korea, at 2006 and 2008, respectively. From 2001 to 2004, he was with Bluebird-soft, where he designed circuit and system for industrial personal digital assistance (PDA). From 2008 to 2010, he worked for the Samsung-Electronics and designed High-Q RF bandpass filter for SAW-less receiver and PLL for cell-phone applications. He joined GT-Bionics Lab at Georgia Institute of Technology in 2010, where he is currently pursuing his Ph.D. degree. His research interests lies in System and IC design for bio-medical applications, especially in Tongue Drive System.

Maysam Ghovanloo was born in 1973 in Tehran, Iran. He received the B.S. degree in electrical engineering from the University of Tehran, Tehran, Iran, in 1994, the M.S. degree in biomedical engineering from the Amirkabir University of Technology, Tehran, Iran, in 1997, and the M.S. and Ph.D. degrees in electrical engineering from the University of Michigan, Ann Arbor, in 2003 and 2004, respectively.

From 2004 to 2007, he was an Assistant Professor in the Department of Electrical and Computer Engineering, North Carolina (NC) State University, Raleigh. In June 2007, he joined the faculty of Georgia Institute of Technology, Atlanta, where he is currently an Associate Professor and the Founding Director of the GT-Bionics Laboratory in the School of Electrical and Computer Engineering. He has authored or coauthored more than 100 peer-reviewed conference and journal publications.

Dr. Ghovanloo is an Associate Editor of the IEEE TRANSACTIONS ON BIOMEDICAL ENGINEERING, IEEE TRANSACTIONS ON BIOMEDICAL CIRCUITS AND SYSTEMS, and a member of the Imagers, MEMS, Medical, and Displays (IMMD) subcommittee at the International Solid-State Circuits Conference (ISSCC). He is the 2010 recipient of a CAREER award from the National Science Foundation. He has also received awards in the 40th and 41st Design Automation Conference (DAC)/ISSCC Student Design Contest in 2003 and 2004, respectively. He has organized several special sessions and was a member of Technical Review Committees for major conferences in the areas of circuits, systems, sensors, and biomedical engineering. He is a member of the Tau Beta Pi, AAAS, Sigma Xi, and the IEEE Solid-State Circuits Society, IEEE Circuits and Systems Society, and IEEE Engineering in Medicine and Biology Society.