Automatic Segmentation of the Left Atrium from MRI Images using Salient Feature and Contour Evolution

Abstract

We propose an automatic approach for segmenting the left atrium from MRI images. In particular, the thoracic aorta is detected and used as a salient feature to find a seed region that lies inside the left atrium. A hybrid energy that combines robust statistics and localized region intensity information is employed to evolve active contours from the seed region to capture the whole left atrium. The experimental results demonstrate the accuracy and robustness of our approach.

I. Introduction

Automatic segmentation of the left atrium in magnetic resonance imaging (MRI) is a challenge and important task in medical image analysis. For example, it can be used to analyze atrial fibrillation [1]. Challenges arise from the following facts: 1) the size of the left atrium is relatively small as compared to the left ventricle or lungs in cardiac MRI images; 2) boundaries are not clearly defined when the blood pool of the left atrium goes into the pulmonary veins; 3) the shape variability of the left atrium is large between different subjects.

To overcome those difficulties, shape models are widely used in cardiac image segmentation. In general, given a sufficient number of training images, we can either build shape models from source images using machine learning techniques or directly register all of the source images to a target image and then fuse these registration results for one consistent solution which is called multi-atlas based segmentation. One example of the first type is a principal component analysis (PCA) based method [2]. In that work, the shape space of the left atrium is defined as a linear combination of the eigen shapes learned using the PCA technique. Then, segmentation is accomplished via evolving active contours in the shape space. In [3], a probability map is generated by using a majority voting scheme over the pair-wise registration results between all of the atlases and the target image. After that, the map is thresholded to get a binary mask for the left atrium. Finally, the mask is refined using a localized region-based active contour method [4]. Label fusion [5] and whole heart model [6] are also used in the left atrium segmentation.

However, to capture the shape variations of the left atrium, a large number of training data is required for building statistical shape models. In addition, automatic localization of those models is not trivial and much less research has been done on this topic. The purpose of this work was to develop an automatic segmentation technique without using training images or shape models for segmenting the left atrium. To achieve this goal, we define a salient feature that is robust to image variations. Then, we combine the on-line statistics inferred from the salient feature with a localized region-based active contour model to form a hybrid energy functional. Based on this formulation, the left atrium segmentation is solved by using gradient descent flows to drive active contours towards the left atrium. The overall method is fully automatic and easy to implement. Note that the salient feature detection result can be used in other model-based segmentation frameworks for initial localization.

The outline of this paper is as follows. Section 2 starts with the description of the salient feature detection and elaborates on the contour evolution method. Section 3 shows the experimental results with discussions. Finally, Section 4 concludes this paper.

II. Method

One salient feature that can be used to segment the left atrium is the thoracic aorta (TA). It has a circular shape in the axial view that can be detected robustly using the Hough transform technique [7]. Given the location of the TA, we can extract a seed region inside the left atrium using both region and gradient information. After that, an active contour is initialized and driven by robust statistics and a localized region-based force to explore the whole left atrium.

A. Salient Feature Detection

Assume that the left atrium lies close to the center of a cardiac MRI image. We chose the middle slice along the axial direction as the key slice I_key. The Hough transform [7] is performed on I_key to find circles in a predefined region of interest (ROI). It converts the image I_key to a parametric space (a, b, r) and counts the accumulated response of circles, denoted by p(a, b, r), at each (a, b, r). Here (a, b, r) is a circle of radius r centered at (a, b). Finally, it returns a list of circles. A circular response to intensities is assigned to each circle c(a, b, r) as

$$h(a,b,r)=p(a,b,r)(\mu (a,b,r)-\mu (a,b,r,R))/\sigma (a,b,r),$$ (1)

where μ(a, b, r, R) is the mean intensities of a ring centered at (a, b) with radiuses r and R, μ(a, b, r) and σ(a, b, r) are the the mean and standard deviation of the intensities within c(a, b, r), respectively. Here h(a, b, r) favors homogeneous regions with higher intensity values inside c(a, b, r) than c(a, b, r, R). The region with the maximal h(a, b, r) response is chosen as the TA region.

B. Contour Evolution

1) Left Atrium Seed Region Extraction

The seed region inside the left atrium is extracted by first finding the heart region and then searching for seed points that belong to the left atrium.

To segment the heart region, the Otsu’s method [8] is applied to I_key to convert it into a binary image. The largest connected component is chosen as the initial segmentation of the heart. The TA region is excluded from the segmented heart region if they have overlaps. Then, the coarse segmentation is refined using a localized region-based active contour method [4], [9] to minimize an energy functional

$$E_{\text{LG}}(C)=E_{\text{in}}(C)+E_{\text{out}}(C),$$ (2)

where

$$E_{\text{in}}(C(s))={\int }_{C(s)}{\int }_{x\in R}{(I\chi (x,s)-u_l(s))}^2\mathit{dAds}$$ (3)

$$E_{\text{out}}(C(s))={\int }_{C(s)}{\int }_{x\in R^c}{(I\chi (x,s)-v_l(s))}^2\mathit{dAds}$$ (4)

where C(s) denotes a closed curve parameterized by its arclength s, R represents the region inside C(s), R^c is the region outside C(s), and dA is the area element. χ(x, s) is a characteristic function that has value 1 if x is inside a ball B(C(s)) centered at C(s) and 0 otherwise. u_l(s) and v_l(s) are the means of intensities in local neighborhoods around C(s). The area integral defines a Chan-Vese energy [10] that tries to separate the intensity means between the regions divide by C(s) inside B(C(s)). The line integral is the typical geodesic active contour energy [11].

By computing the first variation of E_LG(C) with respect to C(s), we get the gradient descent flow of C(s) [9] as

$$\frac{\partial C(s)}{\partial t}=\left({\int }_R{(I\chi (x,s)-u_l(s))}^{2}dA+{\int }_{R^c}{(I\chi (x,s)-v_l(s))}^{2}dA\right)\kappa N-{\oint }_{C(r)}\left({(I\chi (C(s),r)-u_l(r))}^2+{(I\chi (C(s),r)-v_l(r))}^2\right)dr\mathit{N},$$ (5)

in which N is the inward unit normal vector field on C(s) and κ is the curvature of the contour. This step captures the bright region of the heart which contains the left atrium.

To narrow down the search space, the gradient information of I_key is used to extract the seed region inside the left atrium. To this end, we set the detected heart region as our ROI and compute the magnitude of gradient, I_g, for I_key. Then, I_g is converted into a binary image using a threshold mean(I_g). A distance transform [12] is performed on this binary image. On the distance field image I_dist, we search for a circular region that has the maximal response to the following measurement as the seed region inside the left atrium,

$$S_{\text{LA}}=\frac{\int {\int }_{B(x,r_l)}{I}_{\text{dist}}(x)dA}{\mathit{dist}(x,\text{TA})}$$ (6)

where B(x, r_l) is a ball of radius r_l centered at x and dist(x, TA) is the distance from x to the center of TA.

2) Hybrid Evolution Flow

Note that the energy E_in or E_out is a region-based energy that tends to drive active contours to where regions can be locally divided into two distinct areas. However, the driven force is fairly small if the neighborhood around a contour point is almost homogeneous like near the seed region. To solve this problem, we propose a new energy that adds a region growing term to E_LG. The new functional needs to be minimized is

$$E_H(C)=\alpha (E_{\text{in}}(C)+E_{\text{out}}(C))+\beta E_{\text{RS}}(C)+\gamma {\int }_{C}ds,$$ (7)

where the last term controls the smoothness of C(s), α, β, and γ adjust the contribution of each term. E_RS is a region growing energy [13] that utilizes the robust statistics of the seed region. To compute the robust statistics, a feature vector is defined for each pixel x in an image as

$$\mathit{f}(x)={(\mathit{MED}(x),\mathit{IQR}(x),\mathit{MAD}(x))}^T\in {\mathbb{R}}^3,$$ (8)

where MED(x), IQR(x), and MAD(x) are the intensity median, inter-quartile range, and median absolute deviation around a neighborhood of x, respectively. Then, the seed region is characterized by the probability density function of the feature vectors as

$$p(\mathit{f})=\frac{1}{\mid G\mid }\sum _{x\in G}{K}_{\eta }(\mathit{f}-\mathit{f}(\mathit{x})),$$ (9)

where K is the kernel function. We use Gassian kernel in this work. The robust statistics energy is defined as

$$E_{\text{RS}}(C)=\int {\int }_R-p(\mathit{f}(\mathit{x}))dx,$$ (10)

where R is the region inside contour C. The gradient descent flow of C is

$$\frac{\partial C(s)}{\partial t}=-p(\mathit{f}(C(s))\mathit{N}.$$ (11)

Here N is the inward unit normal vector field on C(s) (see [13] for details).

The gradient descent flow of E_H(C) is just a combination of the flows in equations (5) and (11). Note that we have shown a hybrid evolution flow in 2D. However, the generalization to 3D is straightforward.

III. Experiments and Results

We evaluated the proposed segmentation method using 12 cardiac MRI images that have large variations among the left atrium.

To detect the salient feature, the image I_key was divided into four regions and the bottom right one was chosen as our ROI. The Hough transform only looks for circles with radius 10 < r < 16mm. In all of the test, we set r_l = 0.6r in searching for the seed region. Figure 1 illustrates the process of detecting the seed region. Note that, although boundaries are not clearly defined at where the left atrium connects to other chambers, partial boundaries still exist that separates the left atrium from other heart regions. Specifically, as shown in Figure 1(c), three isolated distance clusters are formed and one of which is contained in the left atrium. Thus, the seed region was successfully identified using the measurement defined in equation 6. Our method was succeeded in detecting seed regions for all of the 12 MRI images. Figure 2 shows four representative detection results where the shapes of the left atrium are significantly different as being viewed from their key slices I_key.

Fig. 1.

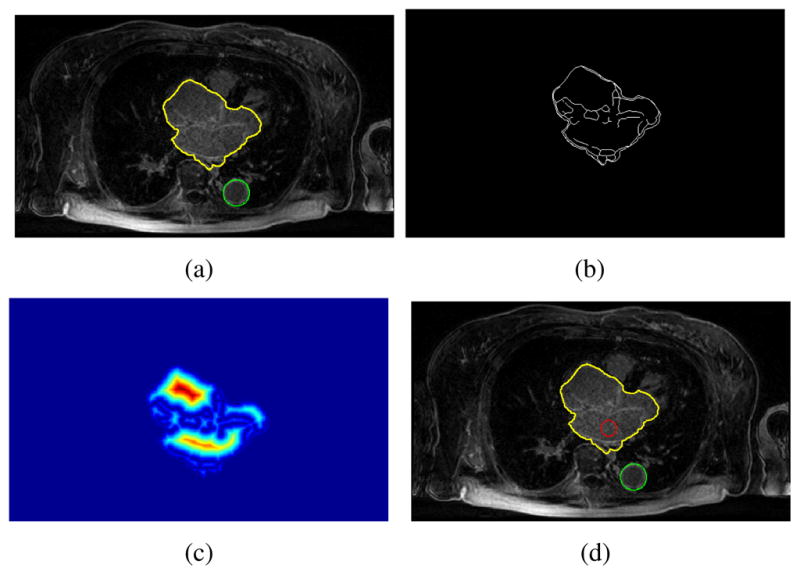
Seed region detection process. (a). TA (green circle) and heart region (yellow contour). (b) Edges within the heart region. (c) Distance field. (d) Seed region (red circle)

Fig. 2.

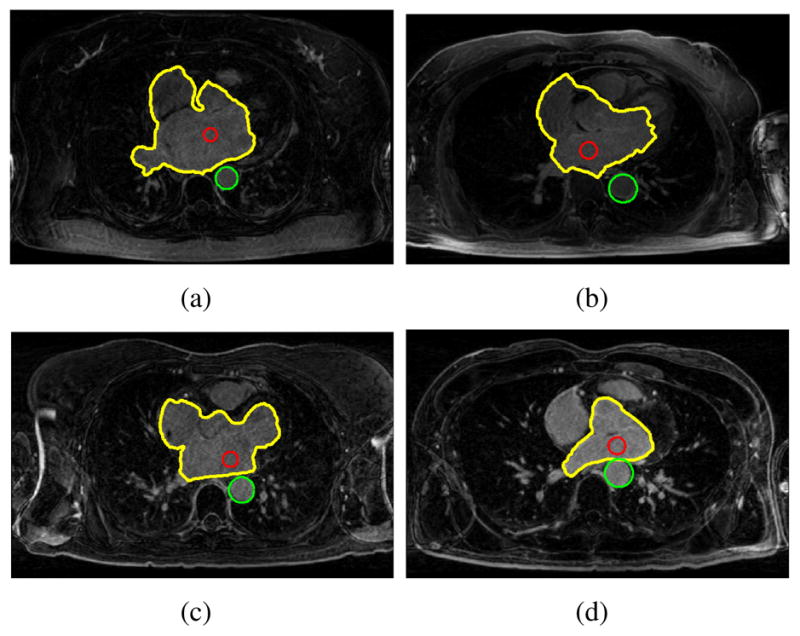
Seed region detection results for different MRI images. The TA is marked with green circle and the seed region with red circle. The yellow contour encloses the heart region.

In the contour evolution stage, the sparse field level set method [14] was used for its efficiency. Also, all of the data were downsampled to 2 × 2 × 2mm³ voxel size before starting active contour evolution. We set α = 0.5, β = 0.5, and γ = 0.3 in all experiments. The contour evolution starts from the seed region and stops when the volume change rate, $\frac{\mid v_i-v_{i-1}\mid }{v_{i-1}}$, between two iterations i − 1 and i is less than a threshold T_v, which is 0.01 in our test. Figure 3 shows an example of the segmentation in the axial view using E_RS only or the hybrid energy E_H. It demonstrates that the robust statistics force pushes the contour from the seed region outwards but provides less stopping force than the hybrid force when the contour is approaching boundaries. Therefore, evolution leakage happens in Figure 3(a). A 3D view of this segmentation result is given in Figure 4.

Fig. 3.

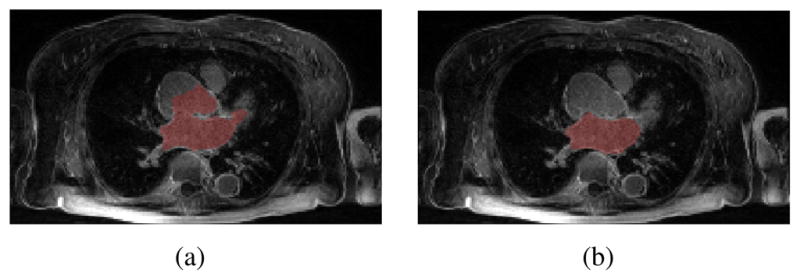
Comparison of segmentation with energy (a) E_RS and (b) E_H.

Fig. 4.

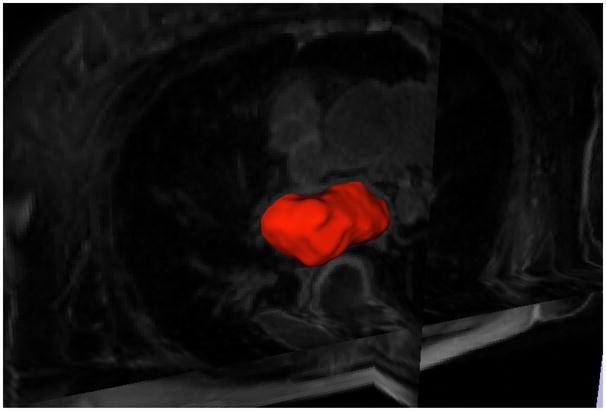
3D view of the segmented left atrium.

To quantify errors, we measure the overlap between automatic segmentations V_a and the ground truth V_m using the standard Dice coefficient [15]

$$D(V_a,V_m)=2\frac{\left|\right|V_a\cap V_m\left|\right|}{\left|\right|V_a\left|\right|+\left|\right|V_m\left|\right|}.$$ (12)

The mean and standard deviation are 0.82 ± 0.06. The most of mismatches are around the pulmonary veins where high-level priors are needed for better segmentations.

IV. Conclusions

We have outlined an automatic segmentation method for extracting the left atrium using salient feature and contour evolution techniques. This method is based on a salient feature for localizing the left atrium. Thus, it is robust to shape variations and image quality. The contour evolution step starts from a seed region inferred via the salient feature and is able to explore the image to find the whole left atrium. The experimental results show the accuracy and robustness of our approach. We will test our algorithm with more MRI images and investigate the application of our approach to the atrial fibrillation analysis in the future.