Hash: a Program to Accurately Predict Protein H^α Shifts from Neighboring Backbone Shifts

Abstract

Chemical shifts provide not only peak identities for analyzing NMR data, but also an important source of conformational information for studying protein structures. Current structural studies requiring H^α chemical shifts suffer from the following limitations. (1) For large proteins, the H^α chemical shifts can be difficult to assign using conventional NMR triple-resonance experiments, mainly due to the fast transverse relaxation rate of C^α that restricts the signal sensitivity. (2) Previous chemical shift prediction approaches either require homologous models with high sequence similarity or rely heavily on accurate backbone and side-chain structural coordinates. When neither sequence homologues nor structural coordinates are available, we must resort to other information to predict H^α chemical shifts. Predicting accurate H^α chemical shifts using other obtainable information, such as the chemical shifts of nearby backbone atoms (i.e., adjacent atoms in the sequence), can remedy the above dilemmas, and hence advance NMR-based structural studies of proteins. By specifically exploiting the dependencies on chemical shifts of nearby backbone atoms, we propose a novel machine learning algorithm, called Hash, to predict H^α chemical shifts. Hash combines a new fragment-based chemical shift search approach with a non-parametric regression model, called the generalized additive model, to effectively solve the prediction problem. We demonstrate that the chemical shifts of nearby backbone atoms provide a reliable source of information for predicting accurate H^α chemical shifts. Our testing results on different possible combinations of input data indicate that Hash has a wide rage of potential NMR applications in structural and biological studies of proteins.

1 Introduction

Chemical shifts play a crucial role in determining protein structures and studying protein dynamics via nuclear magnetic resonance (NMR). They provide peak identities for NMR data analysis (Donald and Martin, 2009; Zeng et al., 2008, 2009, 2011a). In addition, chemical shifts offer an important source of conformational information for studying protein structures (Shen et al., 2008; Wishart et al., 2008; Mulder and Filatov, 2010; Wishart, 2011). In particular, H^α chemical shifts provide important “anchors” for initializing the nuclear Overhauser effect (NOE) assignments, serve as a reliable indicator of secondary structure, and contain rich structural information (e.g., dihedral angles). Despite these important properties of H^α chemical shifts, current studies of protein structures requiring H^α chemical shifts still suffer from the following three problems:

First, the H^α chemical shifts of large proteins can be difficult to assign using conventional NMR triple-resonance experiments on uniformly ¹⁵N- and ¹³C-labelled samples, primarily due to the fast transverse relaxation rate of C^α nuclei in the large systems. Although recent progress (Shen et al., 2008;Wishart et al., 2008; Raman et al., 2010; Rosato et al., 2012; Thompson et al., 2012; Lange et al., 2012) has shown that the atomic or medium resolution structures of some proteins up to 40 kDa can be calculated using molecular modelling and sparse data (e.g., chemical shifts), it is still of interest to assign the dense NOE data that can be collected for large proteins, and use their assignments to calculate high-resolution structure from the data. This is difficult without H^α and side-chain resonance assignments. In (Zeng et al., 2011b), we developed a novel algorithm, called Nasca, to assign both side-chain resonances and NOE distance restraints from NOESY spectra. NASCA takes as input NOESY spectra, backbone chemical shifts, and RDCs, but does not require any TOCSY-type experiments. The current version of NASCA relies on having H^α assignments and geometric data such as NOEs and RDCs that involve H^α nuclei. Therefore it is valuable to develop an algorithm that could predict H^α chemical shifts given neighboring resonances, and backbone structural information determined by RDCs on spatially proximate backbone bond vectors.

For large proteins, two NMR samples are often prepared for determining their solution structures. In the first sample, proteins are deuterated (hence, the NMR signals of H^α are muted) and used in NMR triple-resonance experiments to obtain the resonance assignments of backbone atoms H^N, C^α, C^β and C′ and N. In these experiments, the H^α resonances cannot be assigned. In the second sample, proteins are protonated, and used in NOESY experiments to obtain NOE assignments. Although the NOESY spectra resulting from the second NMR sample contain a substantial number of NOE cross peaks involving H^α that are important for high-quality structure determination, the unassigned H^α resonances make it difficult to assign these H^α-related NOEs. Predicting accurate H^α chemical shifts can alleviate the NOE assignment ambiguity resulting from the corresponding missing resonance assignments, and thus facilitate NOE assignment and enable high-resolution structure determination for large proteins.

Second, most previous chemical shift prediction approaches (Neal et al., 2003; Shen and Bax, 2007; Kohlhoff et al., 2009; Shen and Bax, 2010) require either (a) homologous models with high sequence similarity, or (b) accurate backbone and side-chain structural coordinates. Experimentally, it can be difficult to obtain complete and accurate structural coordinates before assignment, since this requires having an X-ray or NMR structure already. Furthermore, it can be especially difficult to determine the structures of the flexible or disordered loop regions and side-chain conformations at the protein surface. When structural coordinates are absent or of low resolution, we must resort to other information to predict H^α chemical shifts. Resonances of neighboring backbone atoms, including H^N, Cα, Cβ and C′ and N, which can be measured relatively easily from NMR experiments using a deuterated sample, provide an alternative source of information for inferring H^α chemical shifts.

In this paper, we develop a novel machine learning algorithm, called Hash, to predict H^α chemical shifts by specifically exploiting the experimentally-assigned resonances of neighboring backbone atoms (i.e., adjacent backbone atoms in the sequence). Hash applies a combination of a new fragment-based chemical shift search approach and a non-parametric regression model, called the generalized additive model, to effectively solve the chemical shift prediction problem. Using only the assigned resonances of nearby backbone atoms, Hash can still predict accurate H^α chemical shifts for a benchmark set of NMR data extracted from the Biological Magnetic Resonance Bank (BMRB), with RMSD 0.333 ppm and Pearson correlation 0.807. This highly accurate prediction result indicates that the chemical shifts of nearby backbone atoms can provide reliable information for predicting H^α chemical shifts. By combining experimentally-measured chemical shifts of nearby backbone atoms with sequence homology modeling and structural information, Hash achieves excellent prediction accuracy, with RMSD 0.113 ppm and Pearson correlation 0.977. In an application scenario in which only the chemical shifts of nearby backbone atoms plus backbone structural coordinates are available (e.g., when they can be determined from residual dipolar coupling data), Hash outperforms previous structure-based chemical shift prediction approaches and achieves prediction accuracy with RMSD < 0.31 ppm.

The H^α chemical shifts predicted by our approach can be useful for assigning the H^α-related NOEs from NOESY experiments on protonated proteins samples, and thus ensure high-resolution structure determination for large proteins. In summary, the following contributions are made in this paper:

1. The first approach to explicitly use the dependencies between chemical shifts of nearby backbone atoms to predict H^α chemical shifts in NMR structural studies;

2. A novel machine learning algorithm for H^α chemical shift prediction that can use different combinations of obtainable input data, such as primary sequence, backbone structural coordinates determined from residual dipolar couplings (RDCs), and the chemical shifts of nearby backbone atoms;

3. A combination of a new fragment-based search approach and a statistical regression model to effectively solve the chemical shift prediction problem, and a novel application of a non-parametric learning approach (i.e., generalized additive model) into chemical shift prediction and NMR structural biology;

4. Filling the gap in NMR structural studies caused by the missing H^α chemical shifts, which cannot be easily assigned experimentally in large proteins, and the absence of sequence homologues and structural coordinates;

5. Testing and promising results on both a benchmark set of NMR data extracted from the BMRB and a set of NMR data with RDC-defined backbone structures.

1.1 Related Work

Previous chemical shift prediction approaches may be classified into two principal categories: sequence homology search methods (Wishart et al., 1997) and structure-based approaches (Iwadate et al., 1999; Xu and Case, 2001;Moon and Case, 2007; Vila et al., 2009;Meiler, 2003; Neal et al., 2003; Shen and Bax, 2007;Kohlhoff et al., 2009; Shen and Bax, 2010; Han et al., 2011). The sequence homology search methods predict the chemical shifts of the target protein based on sequence homologous models found from the sequence/chemical shift database. These methods require at least 35% sequence identity between the target protein and existing models in the training database (Wishart et al., 1997; Wishart, 2011). On the other hand, two proteins with high sequence identity can still have different global folds, and result in significantly different chemical shifts. For example, although two proteins G_A88 and G_B88 have 88% sequence identity, they have distinct fold topologies and show significantly different chemical shifts (He et al., 2008). Even proteins with almost identical sequences can display different conformations in different states (such as native or denatured states) or different chemical environments (e.g., with different buffer pH) (Morrone et al., 2011). These facts indicate that, in order to robustly predict accurate chemical shifts, other information in addition to protein sequence information must be incorporated.

Most structure-based chemical shift prediction approaches rely heavily on complete and accurate structural coordinates to derive chemical shifts of a protein. Quantum mechanical (QM) methods, one of the early attempts in structure-based chemical shift prediction, calculate nuclear shielding to predict chemical shifts using density functional theory (DFT) (Mulder and Filatov, 2010; Wishart, 2011). Although QM methods can calculate the chemical shifts of nuclei with relatively good accuracy, they are computationally expensive and cannot capture the environmental and dynamic effects (Wishart, 2011). Chemical shifts are related to multiple structure-based factors, such as backbone dihedral angles, hydrogen bonding and ring current (Iwadate et al., 1999; Xu and Case, 2001; Moon and Case, 2007; Vila et al., 2009; Meiler, 2003; Neal et al., 2003; Shen and Bax, 2007; Kohlhoff et al., 2009; Shen and Bax, 2010; Han et al., 2011; Arun and Langmead, 2006; Wishart, 2011). These factors are sometimes called structural factors or structural impact factors on chemical shifts. The large number of high-resolution protein structures in the Protein Data Bank (PDB) and their corresponding assigned resonances deposited in the Biological Magnetic Resonance Bank (BMRB) (Ulrich et al., 2007) have provided rich statistical (i.e., frequency) information for deriving the empirical relationships between various structural factors and chemical shifts. The empirically-derived dependencies between chemical shifts and various structural parameters have been combined with semi-classical methods, which derive simplified or empirical equations from classical physics (Wishart, 2011), to predict chemical shifts from structural coordinates. These approaches, called hybrid approaches, are probably the most popular prediction tools to date, and can efficiently predict chemical shifts to a good accuracy (Xu and Case, 2001; Moon and Case, 2007; Neal et al., 2003; Meiler, 2003; Shen and Bax, 2007; Vila et al., 2009; Kohlhoff et al., 2009; Shen and Bax, 2010; Mulder and Filatov, 2010; Han et al., 2011; Arun and Langmead, 2006; Wishart, 2011). Unfortunately, all these approaches demand accurate and complete (i.e., both backbone and side-chain) structural coordinates. They do not work without prior structural information. In contrast, our approach specifically exploits the chemical shifts of nearby backbone atoms, and can predict accurate H^α chemical shifts in the absence of structural information.

In (Vila et al., 2010), the sequential nearest-neighbor effects on quantum-chemical calculation of ¹³C^α have been investigated. The correlations (i.e., dependencies) between chemical shifts of different backbone atoms have been used in NMR data analysis (Marin et al., 2004; Wang et al., 2005; Wang and Markley, 2009). For example, in (Marin et al., 2004), the patterns of correlations between different backbone atoms have been exploited to predict amino acid types from the NMR-measured chemical shifts. This method has been applied to backbone resonance assignment (Bailey-Kellogg et al., 2000; Langmead and Donald, 2004; Langmead et al., 2004; Xiong et al., 2008; Apaydin et al., 2008, 2010; Jang et al., 2011). In (Wang et al., 2005; Wang and Markley, 2009), a linear analysis of chemical shifts (LACS) has been applied to detect and correct the errors in chemical shift assignments. Despite these applications, to our knowledge, little work has been designed to predict H^α chemical shifts by explicitly using the dependencies between chemical shifts of H^α and nearby backbone atoms.

2 Methods

2.1 Overview

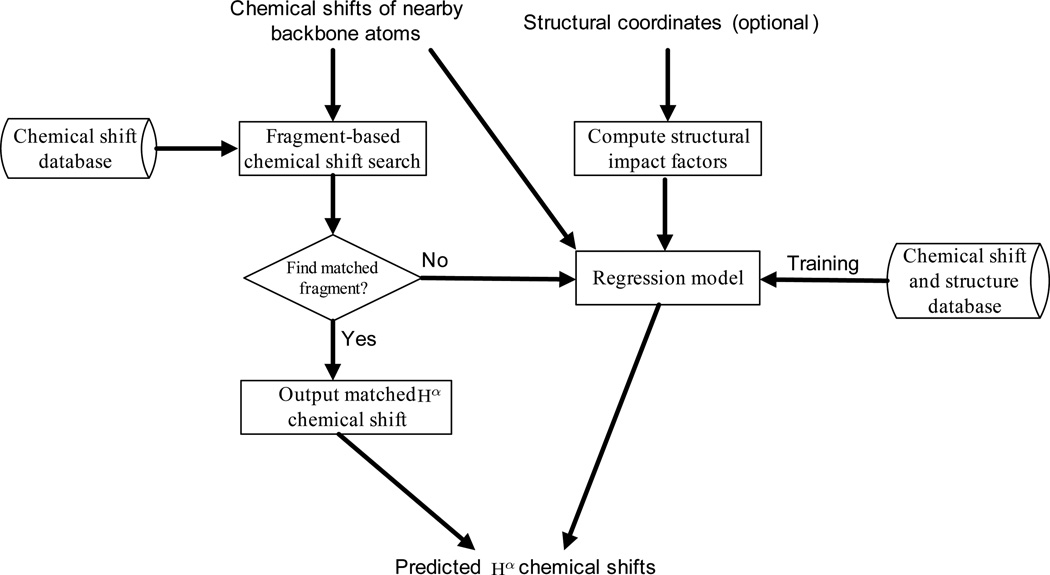
A flow chart of the Hash algorithm is shown in Fig. 1. Hash takes as input the chemical shifts of nearby backbone atoms (i.e., H^N, Cα, Cβ and C′ and N). Protein structural coordinates are optional input data, and can be fed into the program when available. Hash first performs a fragment-based chemical shift search (Section 2.2) over a chemical shift database extracted from the BMRB, and checks whether there exists a chemical shift fragment (i.e., a short sequence segment with known backbone chemical shifts) such that the chemical shifts of nearby backbone atoms in this fragment match those of each fragment in the target protein. If such a matched chemical shift fragment is found, the corresponding H^α chemical shifts are used as the predicted values. Otherwise, the chemical shifts of nearby backbone atoms, together with the obtainable structural impact factors computed from the optional input structural coordinates, are fed into a non-parametric regression model, called the generalized additive model, to predict H^α chemical shifts (Section 2.3).

Figure 1.

A flow chart of the Hash prediction process. Protein structural coordinates are optional input data.

Our algorithm Hash differs from previous chemical shift prediction approaches (Wishart et al., 1997; Iwadate et al., 1999; Xu and Case, 2001; Moon and Case, 2007; Vila et al., 2009; Meiler, 2003; Neal et al., 2003; Shen and Bax, 2007; Kohlhoff et al., 2009; Shen and Bax, 2010; Han et al., 2011) in the following aspects. First, unlike previous chemical shift prediction approaches, which can only use sequence homologues and structural coordinates as input, Hash also exploits the assigned resonances of nearby backbone atoms to predict H^α chemical shifts. In other words, previous approaches heavily depend on sequence homologues or accurate structural coordinates to predict chemical shifts, while in our algorithm, the problem caused by the lack of sequence homologues and accurate structural coordinates can be overcome by introducing the chemical shifts of nearby backbone atoms as effective local chemical environmental indicators to infer accurate H^α chemical shifts. Second, unlike most structure-based chemical shift prediction approaches (Iwadate et al., 1999; Xu and Case, 2001; Moon and Case, 2007; Vila et al., 2009; Meiler, 2003; Neal et al., 2003; Shen and Bax, 2007; Kohlhoff et al., 2009; Shen and Bax, 2010; Han et al., 2011), which mainly rely on specific empirical functions in a parametric fashion to compute the influences on chemical shifts from different structural factors, such as dihedral angles and ring current effect, Hash applies a non-parametric model (see Section 2.3) to calibrate the relationships between different structural factors and chemical shifts. Such a non-parametric approach will allow us to derive a more accurate regression function for H^α chemical shift prediction.

2.2 Fragment-Based Chemical Shift Search

Chemical shift provides a reliable indicator of the local chemical environment for each atom in the protein. Two atoms should have similar chemical shifts if they have similar local chemical environments. Thus, two fragments (i.e., short sequence segments) are likely to share similar H^α chemical shifts if their chemical shifts of nearby atoms are pairwise similar. Based on this observation, we propose a new fragment-based search approach to predict H^α chemical shifts by systematically searching over the available chemical shift database BMRB based on the chemical shifts of nearby backbone atoms.

Our fragment-based chemical shift search approach is described as follows. Let a be the target H^α proton whose chemical shift need to be predicted, w be the length of a chemical shift fragment, and t be the threshold to check whether two chemical shifts are similar. Given a target H^α proton a, we check whether the following criterion is satisfied for each H^α proton b in the chemical shift database: If chemical shifts of all nearby backbone atoms within the residue number window of w/2 from b are within threshold t from those of the corresponding backbone atoms around a, we then output the chemical shift of b as the predicted H^α chemical shift for proton a. We use RefDB (Zhang et al., 2003) as the chemical shift database, which contains the re-referenced chemical shifts of 2372 proteins that were extracted from the BMRB (Ulrich et al., 2007). We choose w = 6 as the length of each chemical shift fragment, and 0.06 ppm for H^N and 0.6 ppm for heavy atoms ¹⁵N and ¹³C as the thresholds to determine whether two chemical shifts are similar to each other during the search.

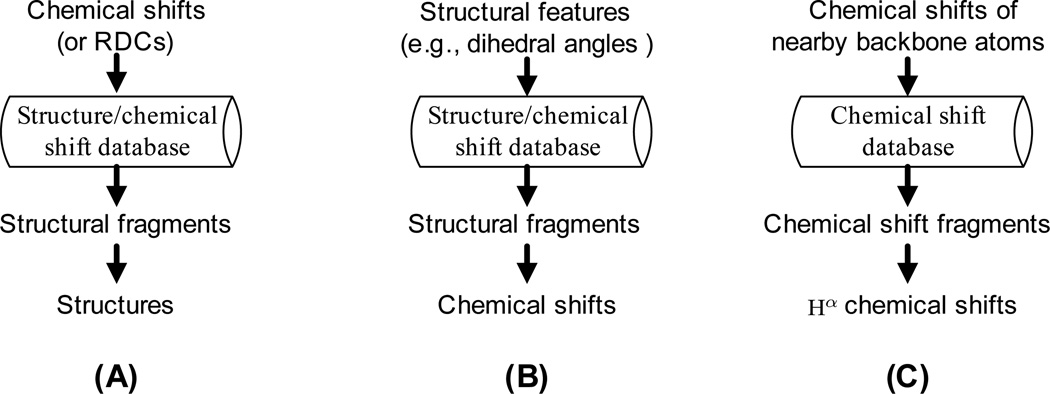
In the NMR structural biology literature, fragment-based search approaches have been widely applied in NMR data analysis and structural studies. Our fragment-based search approach is different from previous fragment-based search methods in that (1) the flow of information is different; (2) our approach searches for chemical shift fragments rather than structural fragments (Fig. 2). Previous fragment-based search approaches can be classified into two categories. The first category is mainly in the application of NMR structure determination, which uses chemical shifts (or RDCs) to search over the structure/chemical shift database and find the structural fragments for structure generation (Delaglio et al., 2000; Shen et al., 2008, 2009). We call these methods chemical shift-to-structure search, in which information flows from chemical shifts to structures (Fig. 2A). The second category is mainly in structure-based chemical shift prediction, which uses structural features (e.g., dihedral angles) to search over the structure/chemical shift database and find the structural fragments to infer the unknown chemical shifts. We call these methods structure-to-chemical shift search, in which information flows from structures to chemical shifts (Fig. 2B). Our fragment-based search is different from all above approaches. As shown in Fig. 2C, our approach uses the chemical shifts of nearby backbone atoms to search over the chemical shift database and find the chemical shift fragments for H^α chemical shift prediction. Our fragment-based search approach can be regarded as chemical shift-to-chemical shift search, in which information flows from the chemical shifts of nearby backbone atoms to H^α chemical shifts.

Figure 2.

Comparison of our approach to other fragment-based search methods. (A) Chemical shift-to-structure search in NMR structure determination (Delaglio et al., 2000; Shen et al., 2008, 2009). (B) Structure-to-chemical shift search in chemical shift prediction (Shen and Bax, 2007). (C) Our chemical shift-to-chemical shift search in chemical shift prediction. In (A) and (B), the structure/chemical shift database contains high-resolution X-ray structural coordinates extracted from the PDB and corresponding chemical shifts extracted from the BMRB. In (C), the chemical shift database contains the chemical shifts extracted from the BMRB. In (A) and (B), structural fragments are short peptide chains with structural coordinates and known backbone chemical shifts. In (C), chemical shift fragments are short sequence segments with known backbone chemical shifts.

2.3 The Regression Model

In most structure-based chemical shift prediction approaches, the predicted chemical shifts are often formulated as an additive model of contributions from different structural factors on chemical shifts, as shown in the following equation:

$${\delta }_p={\delta }_0+{\displaystyle \sum _{i=1}^k{X}_i}$$ (1)

where δ_p represents the predicted chemical shift, δ₀ represents the random coil shift, and X_i represents the contributions on chemical shifts from different structural impact factors, such as hydrogen bonding, ring current effect, and dihedral angles. In the above additive model (Eq. 1), contributions X_i from different structural impact factors are usually calculated using specific empirical functions (i.e., parametric models). In reality, it is difficult to derive a precise empirical function or model to compute contributions X_i on chemical shifts from different structural impact factors. To relieve this problem, we improve the original additive model in Eq. 1 by introducing a non-parametric regression model, called the generalized additive model (GAM) (Hastie and Tibshirani, 1990), into H^α chemical shift prediction. To describe the generalized additive model, we first introduce an additive linear model of the following form:

$$E(Y|X_1,\cdots ,X_k)={\beta }_0+X_1+\cdots +X_k$$ (2)

or

$$E(Y|X_1,\cdots ,X_k)={\beta }_0+{\beta }_1{X}_1+\cdots +{\beta }_k{X}_k$$ (3)

where Y is called the response variable, X_i is called the predictor variable, and β_i is the corresponding coefficient for each predictor variable. The generalized additive model is an extension of the above additive linear model, and has the following form:

$$E(Y|X_1,\cdots ,X_k)={\beta }_0+f_1(X_1)+\cdots +f_1(X_k)$$ (4)

where f_i(X_i) are called the smooth functions, which are non-parametric functions of predictor variables X_i. These non-parametric functions f_i(X_i) can be estimated using current smoothing techniques, such as cubic smoothing spline, LOWESS (locally weighted scatterplot smoothing) (Cleveland and Devlin, 1988), and kernel smoother (Wand and Jones, 1995). In general, a specific distribution, such as Gaussian distribution or Poisson distribution, is used to relate the expected value of the distribution to a set of predictor variables, namely,

$$g(E(Y|X_1,\cdots ,X_k))={\beta }_0+f_1(X_1)+\cdots +f_1(X_k)$$ (5)

where g is also called the link function. The generalized additive model can be solved using the backfitting algorithm (Hastie and Tibshirani, 1990), which is similar to the numerical Gauss-Seidel algorithm for solving a certain linear system of equations.

In the context of H^α chemical shift prediction, the response variable Y is the unknown H^α chemical shift to be predicted, and the predictor variables X_i include the chemical shifts of nearby backbone atoms, and contributions on chemical shifts from different structural impact factors, such as ring current effect and backbone dihedral angles, computed based on input structural coordinates. We apply the cubic smoothing spline method to estimate the non-parametric functions f_i(X_i). We use Gaussian distribution as the link function g in our generalized additive model. This means that our model can compute a probability density distribution by reporting both mean (i.e., expected chemical shift) and standard deviation of a Gaussian distribution for each predicted H^α chemical shift.

To our knowledge, our work is the first application of the generalized additive model in chemical shift prediction and NMR structural biology. Compared to the additive linear model (Eq. 1) used in previous chemical shift prediction approaches, our framework replaces the linear form ${\displaystyle {\sum }_{i=1}^k{X}_i}$ by a sum of smooth functions ${\displaystyle {\sum }_{i=1}^k{f}_i(X_i)}$. Our new statistical model (Eq. 5) is non-parametric and hence less dependent on the assumptions or subjective models employed to describe the influences on chemical shifts from different structural factors. Thus, our algorithm can derive a more accurate regression function from training data to predict H^α chemical shifts.

2.4 Program Description

Hash is implemented in Java and R. Hash calls the library GAM (Hastie, 2011) in the R package to implement the generalized additive model and perform the regression process. Hash runs in a minute for a typical medium-size protein. For example, it takes Hash about 30 seconds to predict H^α chemical shfits for a 197-residue protein on a desktop PC computer with Intel Core 2 Duo processors and 8 GB of physical memory. The source code of Hash can be freely downloaded from our server after publication of this paper, and can be redistributed and modified under the terms of the GNU Lesser General Public License (Gnu, 2002).

3 Results and Discussion

3.1 Training the Regression Model

To evaluate the performance of a chemical shift prediction algorithm, data must be separated into a training data set and a testing data set. Typically, most of the data is used for training the regression model, and a smaller set of the data is used for testing. We used the combination of the talos database (Cornilescu et al., 1999) and the shiftx2 database (Han et al., 2011) to train our generalized additive model (Eq. 5). The talos database contains high-resolution (≤ 2.4 Å) X-ray crystal coordinates and corresponding backbone chemical shifts of 186 proteins, extracted from the PDB and the BMRB, respectively. The shiftx2 database contains high-resolution (≤ 2.1 Å) structural coordinates and corresponding chemical shifts of 174 proteins, most of which are monomeric and free of bound DNA, RNA or other cofactors. For Gly residues, the mean chemical shifts of the two alpha hydrogens were calculated as their H^α chemical shifts. The chemical shifts of the first and last residues in the proteins, and those residues with missing backbone resonance assignments were excluded. In total 12116 residues with available backbone chemical shifts were used as training data. Each residue was considered as a training data point. For all training data points, their secondary chemical shifts were calculated using the reference random coil shift table from (Kohlhoff et al., 2009). The corrections for the effects of different amino acids (Kohlhoff et al., 2009) from the proceeding residues were added to the secondary chemical shifts of nitrogen atoms in the current residues. For each training data point, the influences of hydrogen bonding, ring current and backbone dihedral angles on chemical shifts were computed, using the same methods described in (Pople, 1956; Neal et al., 2003; Kohlhoff et al., 2009). In addition to the backbone dihedral angles of current residue i, we also computed the torsion angles in its neighboring residues, namely residues i − 1 and i + 1. By doing this, we also considered the effects from the nearest neighbors of the current residues.

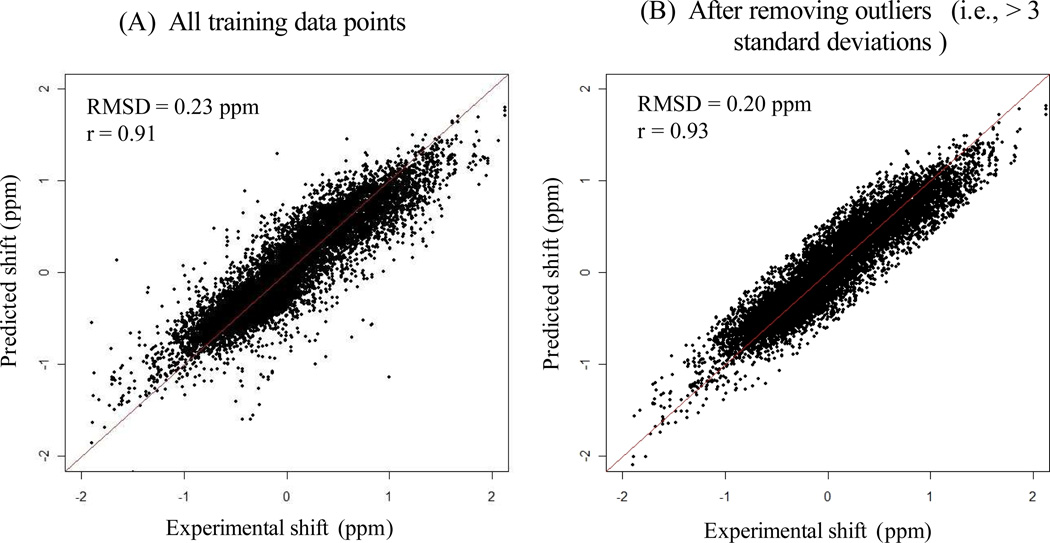
The set of chemical shifts extracted from the talos database and the shiftx2 database, and the computed influences on chemical shifts from different structural factors were then used to train our generalized additive model. The fit between predicted and experimental chemical shifts of H^α on training data is shown in Fig. 3. We measured both RMSD and Pearson correlation between predicted and experimental chemical shifts. The RMSD between predicted and experimental chemical shifts was computed using the equation, $\text{RMSD}=\sqrt{\frac{1}{m}{\displaystyle {\sum }_{i=1}^m{(p_i-e_i)}^2}}$ , where m is the total number of data points, e_i is the experimental chemical shift, and p_i is the corresponding predicted chemical shift. Pearson correlation, denoted by r, measures the strength of linear dependency between two variables. Fig. 3A shows the scatter plot of predicted vs. experimental chemical shifts of H^α for all training data points. The RMSD between predicted and experimental chemical shifts is 0.23 ppm with Pearson correlation r = 0.91. To minimize the impact on parameter estimation from possible chemical shift outliers or mis-assignments in training data, we classified those data points with more than three standard deviations from the predicted values as outliers, and removed them from training data. In total, 226 outliers were removed from the original training data. The scatter plot for the remaining training data points (i.e., after removing outliers) is shown in Fig. 3B. The new RMSD and Pearson correlation between predicted vs. experimental chemical shifts of H^α were improved to 0.20 ppm and r = 0.93, respectively.

Figure 3.

The scatter plots of predicted vs. experimental chemical shifts of H^α on training data. Panel A shows the scatter plot of all training data points. Panel B shows the scatter plot after removing the outliers that deviate more than three standard deviations from the predicted chemical shifts.

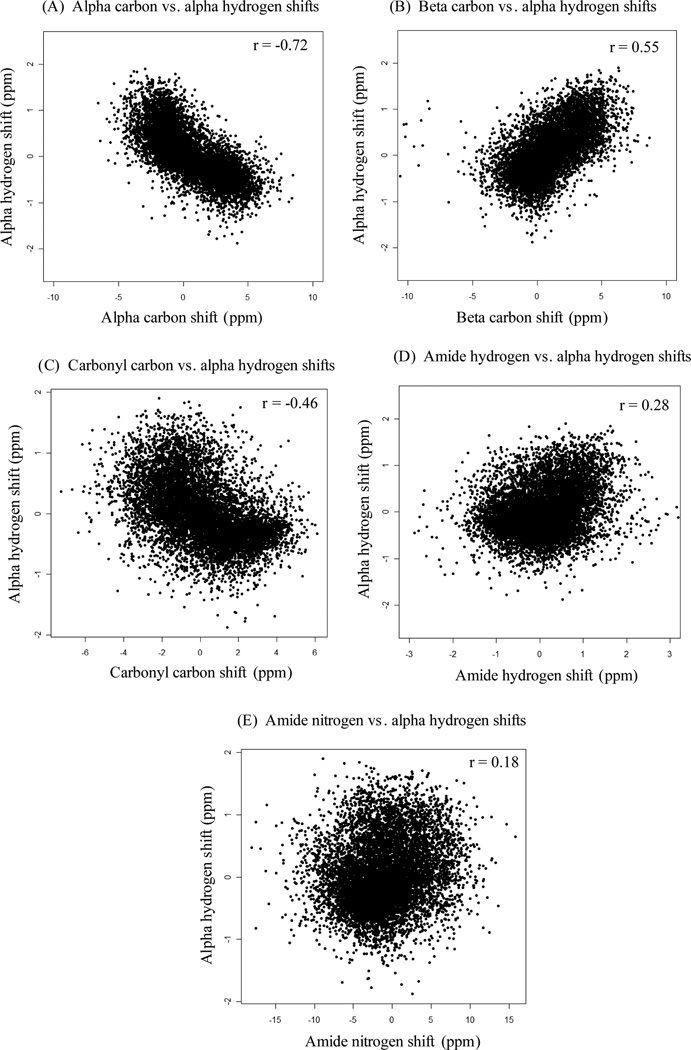
Compared to sparta (Shen and Bax, 2007), which was trained on a similar database and had RMSD 0.27 ppm and Pearson correlation r = 0.85 between predicted and experimental chemical shifts of H^α, our approach achieved better prediction accuracy. Most likely this is because our generalized additive model is less dependent on the assumptions made in the empirical functions to compute the contributions on chemical shifts from different structural impact factors. In addition, our model incorporates the chemical shifts of nearby backbone atoms (e.g., H^N, C^α, C^β, C′ and N). To investigate the relationships between chemical shifts of H^α and nearby backbone atoms, we checked the correlations (i.e., linear dependencies) between them. Fig. 4 shows the scatter plots and Pearson correlations between chemical shifts of H^α and nearby backbone atoms. A certain level of linear dependency has been observed between chemical shifts of H^α vs. Cα, and H^α vs. Cβ (Figs. 4A and 4B). In particular, the Pearson correlation (r = −0.72) between the chemical shifts of H^α and C^α (Fig. 4A) indicates that there exists a strong linear dependency between them. These linear dependencies between chemical shifts of H^α and nearby backbone atoms, which is indicative of local geometry (e.g., secondary structure), can provide a reliable source of information for predicting accurate H^α chemical shifts.

Figure 4.

The scatter plots of chemical shifts of H^α vs. nearby backbone atoms.

3.2 Performance Evaluation

To evaluate the performance of our algorithm, we designed the computational experiments according to different possible combinations of input data (Table 1), which reflect different application scenarios. In all tests, Hash used the chemical shifts of nearby backbone atoms as input. We say that two proteins are sequence homologues if they have > 40 % sequence identity. The same sequence identity cutoff was used in shifty + (Han et al., 2011) to identify the sequence homologues. The first three tests represent the main applications scenarios of Hash, in which only partial or no structural information is available. Two additional tests representing the application scenarios, in which complete structural information is available, are also presented. In Test 1, we assume the existence of sequence homologues but no structural information in chemical shift prediction. Test 2 models the situation in which neither sequence homologues nor structural coordinates are available, but the chemical shifts of nearby backbone atoms can be assigned through conventional NMR triple-resonance experiments. In Test 3, we model the situation in which backbone structural coordinates can be obtained through the RDC-based structure determination approaches (Wang and Donald, 2004;Wang et al., 2006; Zeng et al., 2009; Tripathy et al., 2012; Donald and Martin, 2009) or other methods such as protein threading (Xu et al., 1998), but side-chain conformations are not available.

Table 1.

Design of computational experiments according to different possible combinations of input data. Tests 1–3 represent the application scenarios in which only partial or no structural information is available. Additional Tests 1–2 represent the application scenarios in which complete structural information is available. In Test 2, shiftx, sparta, sparta+, CamShift and shiftx2 cannot run the chemical shift prediction process in the absence of sequence homologue and structural information, while Hash can perform this task.

Test	Sequence homologues	Backbone coordinates	Side-chain coordinates	Chemical shifts of nearby atoms	Programs compared
Test 1	✓			✓	shifty+
Test 2				✓	shiftx, sparta, sparta+, CamShift, Shiftx2
Test 3		✓		✓	shiftx, sparta, sparta+, CamShift, shiftx+
Additional Test 1	✓	✓	✓	✓	shiftx2
Additional Test 2		✓	✓	✓	shiftx, sparta, sparta+, CamShift, Shiftx+

For each test, we compared Hash with other programs in the literature that can take the same input data of sequence and structural information. For example, in Additional Test 1, we compared Hash to the only program in the literature that can take both sequence homologues and structural coordinates as input. In Additional Test 2, we compared our program to several state-of-the-art structure-based chemical shift prediction programs in the literature. In Test 1, we compared our program to the latest version of the only program in the literature that can take only sequence homologues as input.

In Tests 1–2 and Additional Tests 1–2, we used a benchmark data set from (Han et al., 2011) as testing data, which contains structural coordinates and corresponding chemical shifts of 61 proteins extracted from the PDB and the BMRB, respectively. These 61 proteins were not included in training data for fitting the regression model in Section 3.1. Among these 61 proteins in the testing data set, 35 proteins have sequence homologues in the chemical shift database RefDB (Zhang et al., 2003). In Test 3, we tested both the X-ray backbone structures and the NMR-derived backbone structures, which were determined mainly from RDCs using the recently-developed techniques in (Wang and Donald, 2004; Wang et al., 2006; Zeng et al., 2009;Yershova et al., 2011; Tripathy et al., 2012; Donald and Martin, 2009).

3.2.1 Tests with Incomplete or Missing Structural Information

In Test 1, we ran Hash on the primary sequence and the chemical shifts of nearby backbone atoms. Our test showed that Hash performed better than shifty+, which is to our knowledge the latest version of the only program in the literature that takes only sequence homologues as input. In particular, Hash predicts accurate H^α chemical shifts with RMSD 0.012 ppm, which is better than the prediction accuracy of shifty+ (i.e., RMSD 0.085 ppm). Our comparisons indicate that incorporating the obtainable resonances of nearby backbone atoms in addition to sequence homologue information can improve the accuracy of H^α chemical shift prediction. Even a small improvement in chemical shift prediction accuracy is important for NMR structure determination. For example, a 10% improvement in the predicted chemical shifts (a mere 0.02 ppm RMSD) has been shown to narrow the molecular fragment replacement (MFR) search by a factor of 40 (Shen and Bax, 2007). As discussed in the Introduction section, even with high sequence similarity, two proteins can still display different chemical shifts in certain regions (e.g., loop regions in the bound and unbound states). On the other hand, the chemical shifts of nearby backbone atoms can provide accurate local environmental indicators to identify the accurate H^α chemical shifts from the available chemical shift database.

In Test 2, we predicted H^α chemical shifts using only the chemical shifts of nearby backbone atoms. Compared to previous chemical shift prediction programs, including shiftx, sparta, sparta+, CamShift and shiftx2, which cannot run the chemical shift prediction process in the absence of sequence homologue and structural information, Hash can still predict reasonably accurate H^α chemical shifts, with RMSD 0.333 ppm and Pearson correlation 0.807.

In Test 3, we predicted H^α chemical shifts using backbone structural coordinates and the chemical shifts of nearby backbone atoms. To model different application scenarios, we tested both the X-ray backbone structures and the NMR-derived backbone structures. In this test, all the tested proteins were not included in the training data. The X-ray backbone structures were from the same test data as used in (Shen and Bax, 2007), excluding one protein that does not contain H^α chemical shifts. The NMR-derived backbone structures were previously determined from RDCs using the recently-developed techniques (Wang and Donald, 2004; Wang et al., 2006; Zeng et al., 2009; Tripathy et al., 2012; Donald and Martin, 2009). As summarized in Tables 2 and 3, on average Hash outperforms all previous structure-based chemical shift prediction programs, including shiftx, sparta, sparta+, CamShift and shiftx+, when only backbone structural coordinates are available. In our training data (see Section 3.1), most of the high-resolution X-ray structures are monomeric and free of bound DNA, RNA or other cofactors. Here, our test data (Table 3) covers X-ray backbone structures at different resolutions, including those complexes with different ligands, such as RNA or other proteins. As shown in Table 3, even for low resolution X-ray backbone structures, Hash still achieves a decent performance. The bound ligands perturb the local chemical environment, which makes it difficult to predict accurate chemical shifts. In general, chemical shift predictors achieve a below-average performance for these low-resolution structures, when the chemical shifts are perturbed by the bound ligands. On other hand, Hash’s use of neighboring chemical shifts can remedy this situation and improve the chemical shift prediction, since both chemical shifts of H^α and neighboring backbone atoms are correlatively perturbed by the changed local chemical environment caused by the ligand binding.

Table 2.

RMSD results of Test 3, in which the input data includes the RDC-defined backbone structures and the chemical shifts of nearby backbone atoms.

Program	RDC-defined backbone
	GB1	UBQ	hSRI	pol η UBZ	FF2	Average
shiftx	0.495	0.433	0.447	0.382	0.466	0.445
sparta	0.375	0.378	0.300	0.285	0.337	0.335
sparta+	0.445	0.360	0.285	0.321	0.369	0.356
CamShift	0.574	0.492	0.529	0.405	0.455	0.491
shiftx+	0.503	0.388	0.332	0.300	0.413	0.387
Hash	0.341	0.313	0.271	0.333	0.276	0.307

Table 3.

RMSD results of Test 3, in which the input data includes X-ray backbone structures and neighboring chemical shifts of H^α atoms.

Program	X-ray backbone
	3CBS (2.00 Å)a	1KQR (1.40 Å)a	1MMS (2.57 Å)a	2IHB (2.71 Å)a	1KMI (2.90 A)a	1BDO (1.80 Å)a	1IAR (2.30 Å)a	1IGD (1.10 Å)a	Average
shiftx	0.357	0.481	0.377	0.451	0.378	0.275	0.297	0.414	0.379
sparta	0.276	0.412	0.286	0.357	0.272	0.250	0.219	0.386	0.307
sparta+	0.390	0.377	0.287	0.340	0.312	0.318	0.219	0.413	0.332
CamShift	0.330	0.447	0.309	0.358	0.284	0.249	0.376	0.375	0.341
shiftx+	0.406	0.548	0.384	0.416	0.387	0.294	0.228	0.451	0.389
Hash	0.297	0.382	0.271	0.298	0.265	0.270	0.238	0.342	0.295

^aResolution of the X-ray structure.

In summary, for all three main tests, which model different useful application scenarios in NMR structural studies, Hash predicts accurate H^α chemical shifts that agree well with experimental chemical shifts. Previous chemical shift prediction approaches either require sequence homologues or depend heavily on complete and accurate structural coordinates to predict chemical shifts. In practice, it can be challenging to experimentally determine accurate conformations for the flexible or disordered loop regions or surface side-chains. As demonstrated in Tests 1–3, previous approaches cannot run in the absence of sequence homologues and structural coordinates, or perform poorly using only backbone structural coordinates. Previous structure-based prediction programs generally require accurate side-chain structural coordinates to calculate the ring current effect from aromatic side-chain conformations, which plays an important role in chemical shift prediction using structural information alone (Wishart, 2011). As demonstrated in Tables 2 and 3, most structure-based prediction programs performed poorly using only backbone structural coordinates. On the other hand, Hash can remedy this problem by exploiting the chemical shifts of nearby backbone atoms, and still yield decent prediction accuracy even without using side-chain structural information. Therefore, the chemical shifts of nearby backbone atoms (including H^N, C^α, C^β and C′ and N), which can be measured relatively easily from conventional NMR experiments, provide an alternative and reliable source of information for predicting H^α chemical shifts.

3.2.2 Tests with Complete Structural Information

In addition to three main tests (Sec 3.2.1, in which structural information was missing or incomplete), we performed two additional tests in which complete structural information is available. Both additional tests model the potential applications in structure-based NMR assignment (Langmead and Donald, 2004; Lang-mead et al., 2004; Xiong et al., 2008; Apaydin et al., 2008, 2010; Jang et al., 2011), in which known X-ray or NMR structural templates are used to facilitate NMR assignment. In the first additional test, which models the ideal situation with both sequence homologues and structural coordinates available, Hash can predict accurate H^α chemical shifts with RMSD 0.113 ppm, which is slightly better than the prediction result of shiftx2 (RMSD 0.123 ppm, as reported in Table 1 of (Han et al., 2011), which is to our knowledge the only program in the literature that can take both sequence homologues and structural coordinates as input.

Table 4 summarizes the results of the second additional test, and the comparisons to five state-of-the-art structure-based chemical shift prediction approaches, including shiftx (Neal et al., 2003), SPARTA (Shen and Bax, 2007), sparta+ (Shen and Bax, 2010), CamShift (Kohlhoff et al., 2009) and shiftx+ (Han et al., 2011). Using both complete structural coordinates and the chemical shifts of nearby backbone atoms, Hash achieves RMSD 0.213 ppm with Pearson correlation 0.923 for the predicted H^α chemical shifts of 61 proteins in the testing data set. The comparisons show that Hash performs slightly better than shiftx+, and outperforms four other structure-based chemical shift prediction approaches.

Table 4.

Summary of the results of the second additional test, in which the input data includes complete structural coordinates and the chemical shifts of nearby backbone atoms. The test was performed on a benchmark data set of 61 proteins from (Han et al., 2011), whose structural coordinates and chemical shifts were extracted from the PDB and the BMRB, respectively. The prediction results of shiftx, sparta, sparta+, CamShift, and shiftx+ were adapted from Table 1 and Table S9 in (Han et al., 2011).

Program	RMSD (ppm)	Correlation
shiftx	0.253	0.888
sparta	0.334	0.801
sparta+	0.312	0.847
CamShift	0.247	0.893
shiftx+	0.222	0.914
Hash	0.213	0.923

In summary, in both of these additional tests, which probe the suitability of our algorithm for a wide range of applications in structure-based NMR assignment, Hash performs slightly better than the competing programs. These additional test results show that chemical shifts of nearby backbone atoms provide additional information that can be used to enhance the prediction of H^α chemical shifts.

3.3 Application in High-Resolution Structure Determination

To test whether the predicted H^α chemical shifts can contribute to high-resolution protein structure determination, we combined Hash with a high-resolution structure determination protocol previously developed in our lab that does not require TOCSY data. The protocol has been previously described in (Zeng et al., 2011b, 2010; Donald and Martin, 2009; Donald, 2011), which only utilized backbone chemical shift information of H^N, N, C^α, C^β, C′ and H^α. In this study, we took out H^α information and utilized Hash to predict H^α chemical shifts. Then these predicted H^α chemical shifts were used in Nasca (Zeng et al., 2010,2011b) to prune ambiguous resonance assignments which are more than 0.4 ppm away from the predicted values. Next, the remaining possible H^α resonance assignments together with other input data, specifically, the assigned resonances of other backbone atoms, NOE cross peaks and the RDC-defined backbone, were fed into NASCA to perform side-chain resonance and NOE assignments. NASCA does not use any TOCSY data, but assigns side-chain resonances and NOE distance restraints using the NOESY data. After that, the computed NOE assignments were fed into xplor-nih (Schwieters et al., 2003) for structure calculation. We tested this new structure determination protocol on five proteins, including the FF Domain 2 of human transcription elongation factor CA150 (FF2), the B1 domain of Protein G (GB1), human ubiquitin, the ubiquitin-binding zinc finger domain of the human Y-family DNA polymerase Eta (pol η UBZ), and the human Set2-Rpb1 interacting domain (hSRI). The numbers of residues in these proteins are 62, 39, 56, 76 and 112 for FF2, pol η UBZ, GB1, ubiquitin and hSRI, respectively. All NMR data were collected at Duke University, except the RDC data of ubiquitin and GB1 which were downloaded from the Protein Data Bank. The testing results of H^α resonance assignments, side-chain resonance assignments, NOE assignments and final calculated structures are summarized in Table 5. An H^α resonance assignment is said to be correct if it is within the error window (i.e., 0.04 ppm) from the reference shift which was assigned manually. On average, NASCA assigned more than 85% correct H^α chemical shifts using the chemical shifts predicted by Hash (Table 5). Compared to our previous tests in (Zeng et al., 2010, 2011b), in which the manually-assigned H^α chemical shifts were used in the high-resolution structure determination pipeline, the chemical shifts predicted by Hash still led to decent performance on NMR assignment and final structure calculation (Table 5).

Table 5.

Results on NMR assignment and final structure calculation for five proteins, ubiquitin, hSRI, pol η UBZ, GB1 and FF2, using the H^α chemical shifts predicted by Hash. A: Summary of the H^α resonance assignment results computed by Nasca, using the H^α chemical shifts predicted by Hash. B: Summary of side-chain resonance assignment results, computed by Nasca using the H^α chemical shifts predicted by Hash. Nasca (Zeng et al., 2010, 2011b) does not use any TOCSY data, but assigns the side-chain resonances using the NOESY data. C: Summary of NOE assignment results, computed by Nasca using the H^α chemical shifts predicted by Hash. D: Summary of final calculated structures, using the H^α chemical shifts predicted by Hash.

A: Summary of Hα resonance assignments
	ubiquitin	hSRI	pol η UBZ	GB1	FF2
Percentage of correct Hα resonance assignments (%)	90.3	81.8	93.8	77.6	84.5
B: Summary of side-chain resonance assignments
	ubiquitin	hSRI	pol η UBZ	GB1	FF2
Completeness (%)	90.5	88.2	88.1	99.3	92.2
Correctness (%)	80.2	75.8	87.0	78.9	74.1
C: Summary of NOE assignments
	ubiquitin	hSRI	pol η UBZ	GB1	FF2
Total # of assigned NOEs	1588	3367	898	1537	1331
Percentage of correct NOE assignments (%)	80.1	84.6	87.4	86.1	80.8
D: Summary of final calculated structures
	ubiquitin	hSRI	pol η UBZ	GB1	FF2
Average RMSD to mean coordinates SSE region (backbone, heavy) (Å) Ordered region (backbone, heavy) (Å)	0.33, 0.71 0.41, 0.79	0.29, 0.78 0.38, 0.82	0.17, 0.44 0.19, 0.51	0.46, 0.71 0.50, 0.72	0.33, 0.74 0.37, 0.96
RMSD to reference structure SSE region (backbone, heavy) (Å) Ordered region (backbone, heavy) (Å)	0.65, 1.80 1.33, 2.64	1.70, 2.65 1.84, 2.85	0.80, 1.46 1.15, 2.02	1.26, 2.40 1.54, 2.32	0.96, 1.94 1.77, 3.15

The benefit of Hash is best appreciated for a large protein scenario, in which H^α chemical shifts can be difficult to assign, but its NOE cross peaks can be observed in NOESY spectra. We also performed the tests of the large protein scenario for the aforementioned five proteins, in which the H^α chemical shifts were removed from the input data. The results of side-chain resonance assignment, NOE assignment and final structure calculation in these tests are shown in Table 6.

Table 6.

Results on NMR assignment and final structure calculation for five proteins, ubiquitin, hSRI, pol η UBZ, GB1 and FF2, without H^α chemical shifts. Compare to Table 5. A: Summary of side-chain resonance assignment results without H^α chemical shifts. B: Summary of NOE assignment results without H^α chemical shifts. C: Summary of final calculated structures without H^α chemical shifts.

A: Summary of side-chain resonance assignments
	ubiquitin	hSRI	pol η UBZ	GB1	FF2
Completeness (%)	74.1	72.9	78.1	81.0	77.9
Correctness (%)	74.4	67.7	89.6	79.8	73.1
B: Summary of NOE assignments
	ubiquitin	hSRI	pol η UBZ	GB1	FF2
Total # of assigned NOEs	672	2356	571	901	858
Percentage of correct NOE assignments (%)	78.5	79.0	84.6	84.0	77.1
C: Summary of final calculated structures
	ubiquitin	hSRI	pol η UBZ	GB1	FF2
Average RMSD to mean coordinates SSE region (backbone, heavy) (Å) Ordered region (backbone, heavy) (Å)	0.61, 1.15 1.01, 1.62	0.53, 1.09 0.57, 1.09	1.31, 1.60 1.53, 2.06	0.19, 0.48 0.28, 0.57	0.52, 0.92 0.74, 1.43
RMSD to reference structure SSE region (backbone, heavy) (Å) Ordered region (backbone, heavy) (Å)	0.80, 1.56 1.39, 2.12	3.67, 4.36 3.55, 4.34	2.80, 3.34 5.01, 5.94	1.59, 2.52 1.67, 2.38	1.24, 2.30 1.79, 3.08

The benefit of Hash in the large protein scenario is seen by comparing Table 6 to Table 5, in which Hash was employed. As shown in Tables 5 and 6, with the H^α chemical shifts predicted by Hash, the completeness of side-chain resonance assignment computed by NASCA was improved by about 10%. In addition, prediction of the H^α chemical shifts allowed NASCA to assign more NOEs. The presence of a sufficient number of NOE distance restraints can improve the high-resolution structure calculation process. For the structure determination of hSRI using H^α chemical shifts predicted by Hash, the final computed structures deviated from the reference structure by < 1.9 Å backbone RMSD (see Table 5). This is much better than in Table 6, and it shows the value of HASH. These test results indicate that the H^α chemical shifts predicted by Hash play an important role in the downstream side-chain resonance assignment, NOE assignment and structure calculation processes.

4 Conclusions

In this paper, we propose a novel machine learning algorithm for H^α chemical shifts prediction by specifically exploiting the experimentally-assigned resonances of nearby backbone atoms. Our results show that the chemical shifts of nearby backbone atoms can provide a reliable source of information for predicting accurate H^α chemical shifts. In addition, we showed that our chemical shift prediction methodology can contribute to the side-chain and NOE assignment processes using only NOESY data (Zeng et al., 2010). In the future, we will generalize our current approach to predict the chemical shifts of any other backbone atoms that cannot be assigned experimentally from NMR spectra, due to signal loss or peak overlap.