Abstract
Background: The seasonal variation in circulating 25-hydroxyvitamin D [25(OH)D] concentrations is large relative to mean values. Single measurements may misclassify annual exposure, which may lead to bias in research and complicate clinical decision making.
Objective: We aimed to develop and validate a model for adjusting a single measurement of a serum 25(OH)D concentration to the time of year it was measured.
Design: We measured serum 25(OH)D concentrations by using mass spectrometry in 6476 participants from the Multi-Ethnic Study of Atherosclerosis at baseline and again in a subset of 368 participants at a median of 17 mo later. We estimated a cosinor model to describe the seasonal variability in 25(OH)D concentrations and evaluated this model by using follow-up 25(OH)D measurements.
Results: The mean age of subjects was 62.1 y, 61.2% of participants were nonwhite, and 53.3% of participants were women. The cosinor model predicted follow-up 25(OH)D concentrations better than a single measurement [difference in root mean squared error (RMSE): 1.3 ng/mL; P< 0.001]. The cosinor model also better predicted the measured annual mean 25(OH)D concentration (difference in RMSE: 1.0 ng/mL; P< 0.001). Annual mean 25(OH)D concentrations estimated from the cosinor model reclassified 7.1% of participants with regard to 25(OH)D deficiency, which was defined as <20 ng/mL. An estimated annual mean 25(OH)D concentration <20 ng/mL was significantly associated with lower bone mineral density, whereas an untransformed 25(OH)D concentration <20 ng/mL was not.
Conclusions: Cross-sectional data can be used to estimate subject-specific mean annual 25(OH)D concentrations from single values by using a cosinor model. The tool we developed by using this approach may assist research and clinical care of adults in North America by reducing the misclassification of 25(OH)D deficiency.
INTRODUCTION
Vitamin D deficiency is commonly defined by a single measurement of the circulating 25-hydroxyvitamin D [25(OH)D]4 concentration (1). Vitamin D deficiency is a known risk factor for low bone mineral density (BMD) and fracture (2–4). In addition, vitamin D deficiency may promote a number of highly prevalent chronic diseases, including cancer, cardiovascular disease, and diabetes (5, 6). As a result, 25(OH)D concentrations are frequently obtained to guide vitamin D supplementation, which effectively raises 25(OH)D (7).
However, the seasonal variation in circulating 25(OH)D concentrations is large relative to mean values (8–11). As a result, a single 25(OH)D measurement may misclassify year-long 25(OH)D status and potentially lead to bias and imprecision in research studies and inappropriate clinical decisions regarding vitamin D supplementation (11–13). Serum 25(OH)D concentrations generally follow a sinusoidal pattern throughout the calendar year, probably because of the corresponding sinusoidal variation in solar irradiation at most latitudes (8, 9, 11). Other studies have previously shown that a cosinor model approximates seasonal differences in group mean 25(OH)D concentrations (8, 9, 11, 14, 15).
In this study, our goal was to develop and validate a tool to estimate mean annual 25(OH)D concentrations from single measurements in a large, diverse population, building on previous studies that showed the utility of the cosinor model. An accurate estimated mean annual 25(OH)D concentration could facilitate a more accurate classification of vitamin D deficiency for research and clinical care. We use cross-sectional measurements of 25(OH)D from a large, multiethnic cohort to build a cosinor model for seasonal variability in 25(OH)D concentrations and validated this model by using longitudinal 25(OH)D measurements from a subset of participants that were measured a median of 17 mo (range: 16–19 mo) later.
SUBJECTS AND METHODS
Study participants
The Multi-Ethnic Study of Atherosclerosis (MESA), which is a prospective, community-living, cohort study, was designed to examine risk factors for the development and progression of subclinical cardiovascular disease and progression to clinical cardiovascular disease (16). Subjects aged 45–84 y were recruited from the following 6 communities in the United States: Forsyth County, NC; New York, NY; Baltimore, MD; Saint Paul, MN; Chicago, IL; and Los Angeles County, CA. For this study, baseline serum samples drawn in 2000–2002 were available for 6564 of 6814 MESA participants (96%). The 25(OH)D assay failed for 88 participants who did not differ substantially with respect to demographic characteristics. This study included 6476 participants who had successful 25(OH)D measurements. Repeat 25(OH)D measurements at the 2002–2004 study visit were made for a subset of 368 participants who were randomly selected from strata defined by ethnicity and study site. Of the repeat subset, 135 participants had a pair of 25(OH)D measurements that occurred 18 calendar months apart. Because of privacy concerns, the month of the 25(OH)D measurement was the most granular information available about the timing of measurements.
Measurement of 25(OH)D
The serum concentration of total 25(OH)D [sum of 25(OH)D2 and 25(OH)D3] was measured by using high-performance HPLC–tandem mass spectrometry with internal standards at the University of Washington (17–19). The reproducibility over the course of the measurement was ensured by using 2 complementary approaches. First, aliquots of 2 serum samples were run with every plate of MESA samples. Second, a larger panel of aliquots from 20 normal control subjects was run on 9 occasions. Over the course of the measurement, we identified one shift in the 25(OH)D3 concentration. We used quality-control measurements to recalibrate values obtained after the shift to those obtained before the shift. Interassay CVs that were calculated by using 81 repeat measurements of quality-control specimens placed in each plate of MESA samples were 8.5% at 24.8 ng/mL for 25(OH)D3 and 11.8% at 7.0 ng/mL for 25(OH)D2. Calibration was verified by using standard reference material 972 from the National Institute of Standards and Technology (20) with an accuracy of 91–95% for 25(OH)D3 and 100–116% for 25(OH)D2.
Clinical characteristics
Age, sex, and ethnicity were defined by self-report. Medication inventories were completed by MESA staff with the use of medication bottles of participants. Total hours per week of moderate and vigorous physical activity were measured by using a detailed, semiquantitative questionnaire adapted from the Cross-Cultural Activity Participation Study. Total reported hours were categorized into quartiles, and the middle 2 quartiles were combined because of the form of observed associations with 25(OH)D. Diabetes was defined as a fasting serum glucose concentration ≥126 mg/dL or the use of glucose-lowering medications (21). BMI (in kg/m2) was calculated as weight divided by the square of height. The glomerular filtration rate was estimated from serum creatinine and demographics by using the Chronic Kidney Disease Epidemiology Collaboration equation (22). The vertebral BMD at L3 was measured by using computed tomography 1–4 y after the baseline MESA study visit in a subset of 2032 individuals at the second or third MESA examination, ∼18 or 36 mo after the baseline examination and 25(OH)D measurements (23). In participants with baseline 25(OH)D measurements, 1898 of 6476 subjects (29%) had BMD measurements. The serum parathyroid hormone concentration was measured by using the Beckman-Coulter DxI automated immunoassay (Beckman-Coulter) (19).
Statistical methods
On the basis of biological plausibility, published reports that 25(OH)D follows a sinusoidal pattern (8, 9, 11, 14, 15), and observed data, we fit a cosinor model to the cross-sectional measurements made at the baseline MESA study visit. In the cosinor model, 25(OH)D follows a sine wave over time characterized by a phase shift (location of the peak and trough along the time axis), height (vertical shift of the sine wave), and amplitude (maximum variation of the sine wave from its mean height).
In the cosinor model, the time variable t (month) is transformed as
and
which are then fit as predictors of 25(OH)D in a linear model. The coefficients βr and βs of the r and s predictors are transformed to give the amplitude
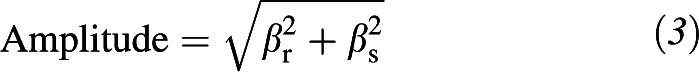 |
and phase shift
of the sine curve. The annual mean is the intercept term of the model.
The addition of main effects of covariates to the model allows the annual mean 25(OH)D concentration to vary on the basis of the covariates, which corresponds to shifting the sine curve up or down. The addition of interaction terms between the covariates and r and s allows the amplitude and shift of the sine curve to differ on the basis of covariate values. In adjusted models, we considered associations with age, sex, study site, ethnicity, BMI, and self-reported hours per week of moderate to vigorous physical activity (in tertiles). SEs of these estimated differences were estimated by using the Δ method (24).
Improvement in the model fit between nested models was assessed by using likelihood ratio tests and adjusted R2 terms. Multivariate Wald tests were used to test the null hypothesis that amplitudes do not differ by the covariate. Model-based SEs for regression variables were used, which assumed that errors were constant as a function of the covariates, independent, and identically distributed. We did not detect any noticeable departures from this assumption.
For a given participant, we predicted their 25(OH)D values at a particular time during the year from the cosinor model. The amplitude and phase shift of a participant-specific sine curve were determined from the fitted sine curve determined by the participant's covariate values. The height of the participant-specific sine curve was determined from the observed value at baseline. This method was equivalent to assuming that an individual's residual departure from the curve estimated by the covariates was constant at both time points. Although the measurements were 16–19 mo apart (median: 17 mo), we did not assume that a person's sine curve would shift up or down over the time between measurements.
To assess the performance of cosinor models, we first compared predicted to measured follow-up 25(OH)D values. For each of the 368 participants whose 25(OH)D was measured at exam 2, we obtained a predicted value from the cosinor model for the month of the exam 2 measurement. In addition, for participants (n = 135) whose pair of 25(OH)D measurements were measured 18 mo apart (ie, participants who had 2 measurements at opposite sides of the sine curve), we estimated their annual mean 25(OH)D exposure by averaging the 2 values. This mean was considered to be the gold-standard estimate of the annual mean exposure that we compared with fitted values (intercepts) from the cosinor model. We compared the cosinor model to carrying forward the measured value, which is the most common method in clinical practice, and to the model with dummy variables for 3 of 4 seasons, which is the most common method in epidemiologic research. Comparisons in prediction performance, as measured by squared error, between models were tested by using the paired t test.
Analyses were done with R version 2.13.1 software (R Foundation for Statistical Computing). No adjustment to CIs or P values was made for multiple comparisons.
RESULTS
Participant characteristics
At baseline, the mean age of participants was 62.1 y (Table 1). Of the 6476 participants included in all analyses, 61.2% of subjects were nonwhite, and 53.3% of subjects were women. Of 368 participants with repeat 25(OH)D measurements at the second MESA study visit, 70.1% of subjects were nonwhite, and 50.2% of subjects were women. Of 135 participants measured at discordant seasons, 72.1% of subjects were nonwhite, and 59.3% of subjects were women.
TABLE 1.
Baseline characteristics of the study population1
| Baseline measurements | All participants (n = 6476) | Participants with follow-up measurements (n = 368) |
| Age (y) | 62.1 ± 10.32 | 62.5 ± 9.2 |
| Age categories [n (%)] | ||
| 45–54 y | 1855 (28.6) | 88 (23.9) |
| 55–64 y | 1779 (27.5) | 107 (29.1) |
| 65–74 y | 1917 (29.6) | 135 (36.7) |
| 75–84 y | 925 (14.3) | 38 (10.3) |
| Ethnicity [n (%)] | ||
| White | 2512 (38.8) | 110 (29.9) |
| Chinese | 787 (12.2) | 74 (20.1) |
| Black | 1763 (27.2) | 107 (29.1) |
| Hispanic | 1414 (21.8) | 77 (20.9) |
| Sex (F) [n (%)] | 3451 (53.3) | 185 (50.2) |
| Sites [n (%)] | ||
| Forsyth County, NC | 1031 (15.9) | 58 (15.8) |
| New York, NY | 1142 (17.6) | 75 (20.4) |
| Baltimore, MD | 1017 (15.7) | 57 (15.5) |
| Saint Paul, MN | 1040 (16.1) | 50 (13.6) |
| Chicago, IL | 971 (15) | 57 (15.5) |
| Los Angeles County, CA | 1275 (19.7) | 71 (19.3) |
| BMI [n (%)] | ||
| <25 kg/m2 | 1867 (28.8) | 110 (29.9) |
| 25 to <30 kg/m2 | 2554 (39.4) | 138 (37.5) |
| 30 to <40 kg/m2 | 1822 (28.1) | 105 (28.5) |
| ≥40 kg/m2 | 233 (3.6) | 15 (4.1) |
| eGFR <60 mL · min−1 · 1.73 m−2 [n (%)] | 606 (9.4) | 39 (10.6) |
| Diabetes [n (%)] | 805 (12.4) | 50 (13.6) |
| Physical activity [n (%)] | ||
| Light | 1615 (24.9) | 95 (25.8) |
| Moderate | 3283 (50.7) | 189 (51.4) |
| High | 1561 (24.1) | 83 (22.6) |
| 25(OH)D (ng/mL) | 25.4 ± 11.5 | 23.5 ± 11 |
| PTH (pg/mL) | 44.8 ± 21.8 | 47.4 ± 28.1 |
eGFR, estimated glomerular filtration rate; PTH, parathyroid hormone; 25(OH)D, 25-hydroxyvitamin D.
Mean ± SD (all such values).
Cross-sectional models
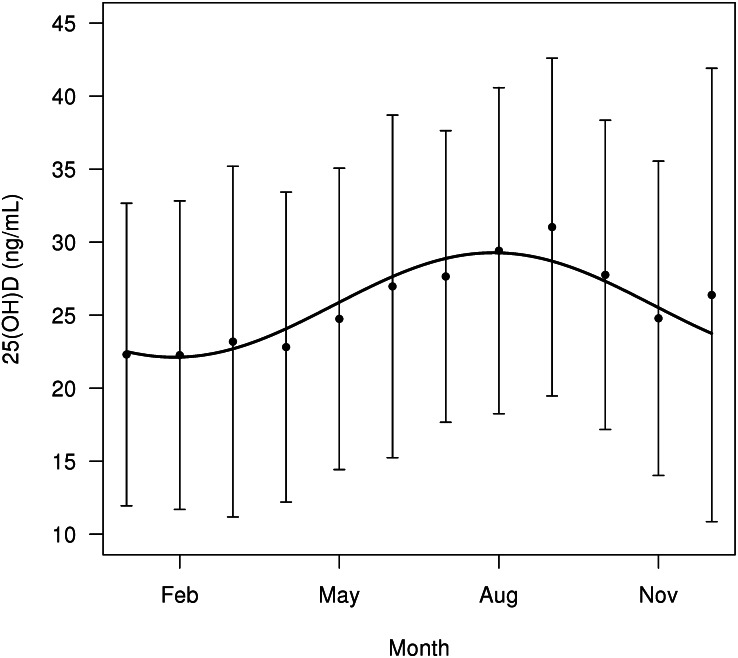
Population mean 25(OH)D concentrations were lowest in January and February and highest in August and September (Figure 1). The cosinor model fit observed baseline data significantly better than did a mean model, which assumed a constant mean 25(OH)D concentration over the course of the year (likelihood ratio test P < 0.0001).
FIGURE 1.
Mean (±SD) seasonal variation in 25(OH)D with the fitted sine curve superimposed. Error bars are ±1 SD. Aug, August; Feb, February; Nov, November; 25(OH)D, 25-hydroxyvitamin D.
In the unadjusted cosinor model, the estimated mean 25(OH)D concentration over the calendar year was 25.7 ng/mL (95% CI: 25.4, 26 ng/mL). The estimated peak-trough difference in the 25(OH)D concentration was 7.2 ng/mL (28% of the mean; 95% CI: 6.4, 7.9 ng/mL), where the estimated peak occurred in August, and the estimated trough occurred in February.
Older age was associated with a higher mean 25(OH)D concentration but smaller amplitude in the seasonal 25(OH)D variation (adjusted P < 0.001) (Table 2). We showed no evidence to suggest that associations with age were nonlinear. Compared with participants of white ethnicity, nonwhite participants had a substantially lower mean 25(OH)D concentration but little or no difference in 25(OH)D amplitude, particularly after adjustment for age, sex, and site (P-heterogeneity in amplitude by ethnicity = 0.07 in the adjusted model). The mean 25(OH)D concentration did not differ by sex, but men tended to have a larger amplitude in both unadjusted and adjusted models. In unadjusted models, the mean 25(OH)D concentration and 25(OH)D amplitude appeared to differ by study site. However, after adjustment for demographics, only the New York study site appeared to have a significantly smaller amplitude (P-heterogeneity in amplitude by study site = 0.18 in the adjusted model). In adjusted models, a higher BMI was associated with a lower mean 25(OH)D concentration but no difference in amplitude. Diabetes was associated with a lower mean 25(OH)D concentration and smaller amplitude. In adjusted models, high physical activity (highest tertile) was associated with a higher mean 25(OH)D concentration and larger amplitude, whereas in unadjusted models, only the amplitude was significantly larger.
TABLE 2.
Differences in the mean and amplitude of 25(OH)D modeled according to the cosinor model1
| Unadjusted |
Adjusted |
|||||
| Clinical characteristic | Difference in mean 25(OH)D | Difference in amplitude | P-difference in amplitude | Difference in mean 25(OH)D | Difference in amplitude | P-difference in amplitude |
| ng/mL | ng/mL | |||||
| Age (/10 y) | 1.1 (0.8, 1.4) | −1.2 (−1.6, −0.8) | <0.001 | 0.9 (0.6, 1.2) | −1.1 (−1.4, −0.7) | <0.001 |
| Age categories | ||||||
| 45–54 y | — | — | — | — | — | — |
| 55–64 y | 0.8 (0, 1.5) | −0.9 (−1.9, 0.2) | 0.094 | — | — | — |
| 65–74 y | 2.4 (1.6, 3.1) | −2.1 (−3.2, −1.1) | <0.001 | — | — | — |
| 75–84 y | 2.6 (1.7, 3.5) | −3 (−4.3, −1.7) | <0.001 | — | — | — |
| Ethnicity | ||||||
| White | — | — | — | — | — | — |
| Chinese | −3.6 (−4.5, −2.7) | −1.3 (−2.6, −0.1) | 0.034 | −5.1 (−6.2, −4.1) | −1 (−2.4, 0.4) | 0.162 |
| Black | −11 (−11.6, −10.4) | −1.3 (−2.3, −0.4) | 0.004 | −11.2 (−11.8, −10.5) | −1 (−2, 0) | 0.042 |
| Hispanic | −5.3 (−6, −4.7) | −0.2 (−1.2, 0.8) | 0.673 | −6.4 (−7.1, −5.6) | 0.1 (−1, 1.2) | 0.868 |
| Sex (M) | 0.1 (−0.5, 0.6) | 1.5 (0.7, 2.2) | <0.001 | −0.2 (−0.7, 0.3) | 1.6 (0.9, 2.4) | <0.001 |
| Study sites | ||||||
| Twin Cities, MN | — | — | — | — | — | — |
| Chicago, IL | −1.3 (−2.3, −0.4) | −0.9 (−2.2, 0.5) | 0.211 | −0.3 (−1.2, 0.7) | −0.4 (−1.8, 0.9) | 0.526 |
| New York, NY | −2.9 (−3.8, −1.9) | −1.4 (−2.8, −0.1) | 0.04 | 0.8 (−0.1, 1.7) | −1.6 (−3, −0.3) | 0.015 |
| Baltimore, MD | −2.6 (−3.6, −1.6) | −0.3 (−1.8, 1.1) | 0.649 | −0.3 (−1.3, 0.7) | 0.1 (−1.4, 1.5) | 0.923 |
| Forsyth County, NC | −1.5 (−2.5, −0.5) | −2.7 (−4.2, −1.3) | <0.001 | 0.7 (−0.2, 1.7) | −1.1 (−2.5, 0.4) | 0.152 |
| Los Angeles, CA | 0.4 (−0.5, 1.3) | −0.9 (−2.2, 0.4) | 0.166 | 3.1 (2.2, 4.1) | −1 (−2.3, 0.4) | 0.154 |
| BMI | ||||||
| <25 kg/m2 | — | — | — | — | — | — |
| 25 to <30 kg/m2 | −2.4 (−3, −1.7) | −1 (−2, −0.1) | 0.032 | −1.7 (−2.3, −1) | −0.8 (−1.7, 0.1) | 0.08 |
| 30 to <40 kg/m2 | −6.1 (−6.8, −5.3) | −0.9 (−1.9, 0.1) | 0.091 | −4.3 (−5, −3.6) | −0.7 (−1.8, 0.3) | 0.155 |
| ≥40 kg/m2 | −9.7 (−11.2, −8.2) | −1 (−3.1, 1.1) | 0.356 | −6.8 (−8.2, −5.3) | −1.2 (−3.2, 0.9) | 0.257 |
| eGFR <60 mL · min−1 · 1.73 m−2 | 4 (3.1, 5) | −0.9 (−2.3, 0.4) | 0.181 | 2 (1.1, 2.9) | 0 (−1.4, 1.3) | 0.942 |
| Diabetes | −3 (−3.8, −2.1) | −2.2 (−3.4, −1) | <0.001 | −1.4 (−2.2, −0.6) | −1.3 (−2.4, −0.2) | 0.019 |
| Physical activity | ||||||
| Light | — | — | — | — | — | — |
| Moderate | 1.8 (1.1, 2.5) | 0.8 (−0.2, 1.7) | 0.107 | 1.7 (1.1, 2.3) | 0.5 (−0.4, 1.4) | 0.311 |
| High | 0.5 (−0.3, 1.3) | 2.3 (1.2, 3.4) | <0.001 | 2 (1.3, 2.8) | 1.5 (0.4, 2.5) | 0.006 |
All values are estimated differences in mean or amplitude (as noted in columns); 95% CIs in parentheses. Adjusted differences were adjusted for age, ethnicity, sex, and study site. P values are from Wald tests of the null hypothesis that differences in amplitude are zero. Multivariate Wald test for ethnicity: P = 0.008 (adjusted), P <0.001 (unadjusted). eGFR, estimated glomerular filtration rate; 25(OH)D, 25-hydroxyvitamin D.
Longitudinal analyses
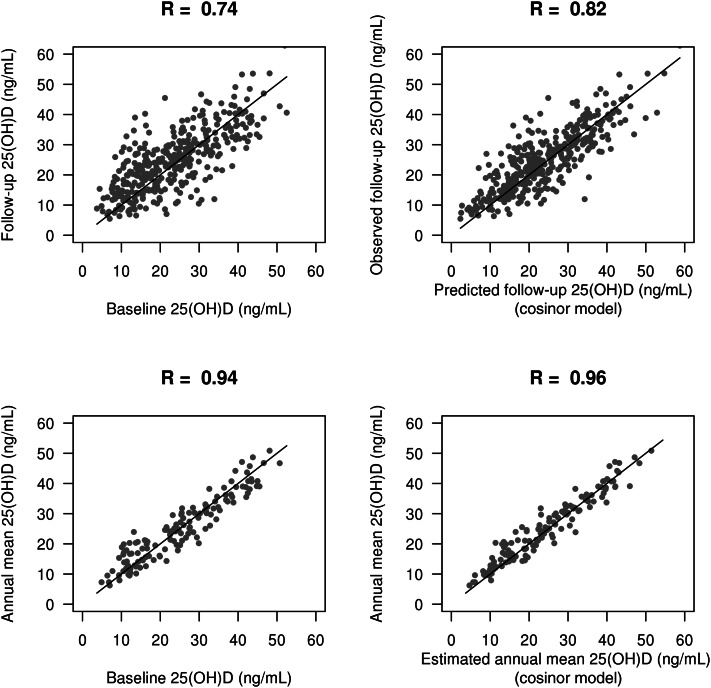
For 368 participants, we repeated serum 25(OH)D measurements a median of 17 mo after the baseline study visit (range: 16–19 mo), which were uniformly distributed over the course of the calendar year. In this subset, the mean 25(OH)D concentration was slightly higher at follow-up than at baseline (25.0 compared with 23.5 ng/mL, respectively). However, the mean 25(OH)D concentration at follow-up was similar to the mean 25(OH)D concentration in the entire cohort (25.0 compared with 25.4 ng/mL, respectively). The correlation between baseline and follow-up 25(OH)D concentrations was 0.74, whereas the correlation between cosinor-predicted follow-up 25(OH)D and measured follow-up 25(OH)D was 0.82 (Figure 2). The empty cosinor model (without covariates) predicted the follow-up 25(OH)D concentration significantly better than simply carrying forward the baseline 25(OH)D concentration (difference in root mean squared error (RMSE): 1.3 ng/mL; P < 0.001; Table 3). For the cosinor model, 57% of predicted values laid within 4 ng/mL of the measured value compared with 43% of predicted values when baseline values were carried forward. The RMSE and bias were similar across categories of relevant demographic and clinical characteristics (see Table 1 under “Supplemental data” in the online issue). The cosinor model had a lower mean squared error than did the model which assumed a different mean 25(OH)D concentration for each of winter (December to February), spring (March to May), summer (June to August), and fall (September to November); however, this difference was not significant (difference in RMSE: 0.3 ng/mL; P = 0.29; Table 3). For the cosinor model without covariates, the estimated intercept for the cosinor curve was 25.7 (95% CI: 25.4, 26), the coefficient for r was −1.9 (95% CI: −2.3, −1.6), and the coefficient for s was −3 (95% CI: −3.4, −2.6). The addition of covariates to the cosinor model did not significantly alter the predictive performance (Table 3).
FIGURE 2.
Scatter plots comparing the predictive performance of baseline 25(OH)D (left) to the null cosinor model (right). The top row shows correlations for predicting the follow-up 25(OH)D value (n = 368), and the bottom row shows correlations for predicting the empirically estimated annual 25(OH)D exposure (n = 135). The cosinor model was unadjusted. Annual mean plots were restricted to participants who were measured 6 mo apart. Solid lines are on the diagonal (y = 1 × x). R, Pearson's correlation coefficient; 25(OH)D, 25-hydroxyvitamin D.
TABLE 3.
Prediction error for follow-up 25(OH)D concentration (top set of rows) and for mean annual 25(OH)D (bottom set of rows)1
| MSE | RMSE | Bias | SD | P compared with baseline model | P compared with cosinor model without covariates | |
| Model for follow-up 25(OH)D (n = 368) | ||||||
| Baseline 25(OH)D carried forward | 58.8 | 7.7 | 1.5 | 7.5 | — | — |
| Dummy variables for season, no covariates | 45.7 | 6.8 | 0.30 | 6.8 | 0.004 | 0.29 |
| Cosinor, no covariates | 39.5 | 6.3 | 0.9 | 6.2 | <0.001 | |
| Cosinor, age, sex | 39.7 | 6.3 | 0.8 | 6.3 | — | 0.987 |
| Cosinor, plus ethnicity | 41.9 | 6.5 | 0.9 | 6.4 | — | 0.782 |
| Cosinor, plus study site | 42.9 | 6.6 | 1.0 | 6.5 | — | 0.572 |
| Cosinor, plus physical activity | 43.2 | 6.6 | 1.0 | 6.5 | — | 0.573 |
| Model for annual mean 25(OH)D (n = 135) | ||||||
| Baseline 25(OH)D carried forward | 15.5 | 3.9 | 0 | 3.9 | — | — |
| Dummy variables for season, no covariates | 13.3 | 3.6 | 0.1 | 3.7 | 0.213 | 0.135 |
| Cosinor, no covariates | 10 | 3.2 | 0.7 | 3.1 | 0.005 | — |
| Cosinor, age, sex | 9.3 | 3 | 0.7 | 3 | — | 0.688 |
| Cosinor, plus ethnicity | 9.8 | 3.1 | 0.7 | 3.1 | — | 0.915 |
| Cosinor, plus study site | 10.1 | 3.2 | 0.6 | 3.1 | — | 0.929 |
| Cosinor, plus physical activity | 10.2 | 3.2 | 0.6 | 3.1 | — | 0.893 |
Bias, average difference between measured and predicted values; MSE, mean squared error (average of squared differences between measured values and predicted values); RMSE, root mean squared error (square root of the mean squared error); SD, SD of predicted values; 25(OH)D, 25-hydroxyvitamin D.
To estimate mean annual 25(OH)D exposure, we investigated the subset of 135 participants with 2 measurements that occurred at opposite sides of the sine curve (ie, 18 mo apart). For those participants, we compared the annual mean 25(OH)D estimated from the cosinor model to the computed mean of observed values, which is considered the gold standard. The cosinor model substantially reduced the bias and variance of the estimated annual mean 25(OH)D exposure compared with simply carrying forward the baseline 25(OH)D concentration (difference in RMSE: 0.8 ng/mL; P = 0.005; Figure 2, Table 3). For the cosinor model, 82% of estimated annual mean values fell within 4 ng/mL of the measured mean compared with 67% when carrying forward baseline values. Again, the addition of covariates to the cosinor model did not significantly improve the predictive performance. An online tool that uses the cosinor model without covariates to calculate the estimated mean annual 25(OH)D concentration and estimated yearly peak and trough 25(OH)D concentrations from a single 25(OH)D measurement and measurement date is available at http://kri.washington.edu/calculator (25).
Classification of vitamin D deficiency
Compared with use of the baseline 25(OH)D concentration alone, the use of the mean annual 25(OH)D concentration estimated from the cosinor model reclassified 7.1% of participants with regard to risk of 25(OH)D deficiency, which was defined as <20 ng/mL as per Institute of Medicine recommendations (Table 4) (1). In the summer, the cosinor model reclassified 11.8% of participants who had a single 25(OH)D concentration ≥20 ng/mL as vitamin D deficient, whereas in the winter, the cosinor model reclassified 19.3% of participants who had a 25(OH)D concentration <20 ng/mL as sufficient.
TABLE 4.
Classification of 25(OH)D concentrations comparing single measured values with estimated annual means1
| Estimated annual mean 25(OH)D |
|||
| Measured baseline 25(OH)D (n = 6476) | ≥20 ng/mL | <20 ng/mL | Percentage reclassified |
| All seasons | |||
| ≥20 ng/mL | 4079 | 179 | 4.2 |
| <20 ng/mL | 279 | 1936 | 12.6 |
| Total | — | — | 7.1 |
| Summer | |||
| ≥20 ng/mL | 889 | 119 | 11.8 |
| <20 ng/mL | 0 | 256 | 0 |
| Total | — | — | 9.4 |
| Winter | |||
| ≥20 ng/mL | 879 | 0 | 0 |
| <20 ng/mL | 124 | 519 | 19.3 |
| Total | — | — | 8.1 |
25(OH)D, 25-hydroxyvitamin D.
Associations with BMD
We examined how the estimation of the annual mean 25(OH)D concentration affected associations of a low 25(OH)D concentration with BMD, which is known to be reduced with vitamin D deficiency (2). Both 25(OH)D and lumbar BMD at L3 were successfully measured in a subset of 1898 MESA participants. After adjustment for age, sex, ethnicity, and BMI, an unadjusted baseline 25(OH)D concentration <20 ng/mL was associated with a 2.5-g/cm3 lower BMD (95% CI: 6.0, −1 g/cm3 lower; P = 0.164). In addition, after adjustment for the season of 25(OH)D measurement as dummy variables, an unadjusted baseline 25(OH)D concentration was <20 ng/mL was associated with a 2.4-g/cm3 lower BMD (95% CI: 6.0, −1.2 g/cm3 lower; P = 0.194). In a parallel adjusted model, an estimated annual mean 25(OH)D concentration <20 ng/mL by using the cosinor model was associated with a 3.9-g/cm3 lower BMD (95% CI: 7.6, 0.2 g/cm3 lower; P = 0.037).
DISCUSSION
In a large, multiethnic, community-based population, the seasonal variation in serum 25(OH)D concentrations was large relative to mean values and was well approximated by a cosinor model. Longitudinal measurements showed that the unadjusted cosinor model improved the prediction of the subsequent 25(OH)D concentration and generated mean annual 25(OH)D concentrations that were highly correlated with observed mean 25(OH)D concentrations. The mean annual 25(OH)D concentration estimated from the cosinor model reclassified 7.1% of participants with regard to 25(OH)D deficiency, which was defined as a concentration <20 ng/mL. The association of a low mean annual 25(OH)D concentration estimated from the cosinor model with BMD was stronger than that of the untransformed low 25(OH)D concentration with BMD, which suggesting that an improved 25(OH)D classification reduced bias. Together, these observations suggested that use of the cosinor model to estimate the mean annual 25(OH)D concentration is a valid approach to improve 25(OH)D classification.
This study built on previous studies that showed a substantial seasonal variation in the 25(OH)D concentration (8, 9, 11, 14, 15) and used cosinor models to describe this variation (8, 9, 11, 15). Like these studies, we began by using cross-sectional data with single measurements per person to evaluate the population mean 25(OH)D concentration. We confirmed that the cosinor model fit the seasonal variation well in a diverse, multi-ethnic population. Notably, the cross-sectional approach assumes that the mean seasonal variation in a population approximates the mean of seasonal variations in its constituents. This assumption may be reasonable in a large population, but cross-sectional studies cannot determine the distribution of within-person seasonal variation or the degree to which modeling fits individual patterns of variation.
Therefore, to our knowledge, the novel component of our study was the use of longitudinal data to validate our approach. Our cosinor model predicted follow-up 25(OH)D concentrations with significantly less bias and more precision than simply carrying forward baseline 25(OH)D values. In addition, the mean annual 25(OH)D concentration estimated from the cosinor model correlated strongly (r = 0.96) with the mean of the 2 measured 25(OH)D concentrations. These observations suggested that the cosinor model is a valid method to estimate 25(OH)D concentration over the year in individuals. Similar results were reported in a longitudinal study from New Zealand (15). Because we studied a diverse North American population, and the prediction with the cosinor model was similar across strata defined by important demographic and clinical characteristics, the tool we developed appears to be broadly applicable to adults in North America.
Compared with a single 25(OH)D measurement, the mean annual 25(OH)D concentration estimated by using the cosinor model reclassified a substantial proportion of participants with regard to risk of 25(OH)D deficiency, defined as <20 ng/mL as recommended by the Institute of Medicine (1). Moreover, the association of estimated mean annual 25(OH)D concentration <20 ng/mL with BMD was stronger than that of a single 25(OH)D measurement with BMD, with both a point estimate further from null and a lower P value. One potential explanation for this observation is that reduced bias in measurement of 25(OH)D facilitates more accurate evaluation of associations with relevant health outcomes.
In cross-sectional analyses, we showed that several clinical characteristics affected the amplitude of seasonal 25(OH)D variation, the overall mean 25(OH)D concentration (height of the sine curve), or both. For example, the amplitude of seasonal variation was greater in younger participants, men, and more physically active participants and varied slightly by study site. Race-ethnicity and BMI were strongly associated with mean 25(OH)D concentration but not amplitude. These findings are consistent with our prior results in the Cardiovascular Health Study (11) and point to age, sex, physical activity and location as potential modifiers of seasonal variation in 25(OH)D. However, in longitudinal analyses, these associations were not sufficiently strong to impact the prediction performance of the cosinor model. Therefore, we believe the simple and conservative approach of applying a cosinor model without covariates is generally most appropriate.
In epidemiologic studies of 25(OH)D, investigators often account for seasonal variation by adjusting for season of 25(OH)D measurement as dummy variables in regression models. We observed that the model for 25(OH)D with dummy variables for season had a smaller bias than that with the cosinor model but a larger variation in predicting follow-up 25(OH)D measurements and the mean annual 25(OH)D. The model with dummy variable was more complex than the cosinor model (estimating 4 compared with 3 variables); therefore, this appears to be an example of the bias-variance tradeoff (26). The concept of the bias-variance tradeoff states that as the complexity of a model increases, a reduction in bias will be observed while observing a corresponding increase in the variance of an out-of-sample prediction. The cosinor model appears to be in the sweet spot where the mean squared error (which includes both bias squared and variance) is minimized. In addition, a recent simulation study suggested that adjustment for seasons as dummy variables in estimating associations with an outcome variable is an ineffective approach to eliminate bias (13).
The use of a cosinor model to estimate the mean annual 25(OH)D concentration or future 25(OH)D concentrations has many potential applications. In clinical care, patients and providers may find estimated mean annual 25(OH)D concentrations or predicted peak and trough concentrations of 25(OH)D over the calendar year to be a useful aid to guide decisions regarding vitamin D supplementation. We have enabled this by installing a free online tool at kri.washington.edu/calculator (25). In research, the use of an estimated mean annual 25(OH)D concentration may reduce bias when testing associations with outcomes that are examined in a cross-section but do not vary by season (as with BMD in this study) and when testing associations with longitudinal outcomes (13). In particular, associations of 25(OH)D with health outcomes have often been described as nonlinear, and the assessment of the mean annual 25(OH)D concentration may help identify appropriate 25(OH)D thresholds (4, 21, 27–31).
Although our study was performed in a diverse, community-based population, it was restricted to communities in North America and, thus, was limited in the range of latitude. Because latitude is the most-important predictor of sunlight intensity, the cosinor model that we have estimated in this study may not be applicable in other populations. In addition, because of limited resources, we had a small sample size of longitudinal measurements. It is possible that we did not detect covariate effects on the accuracy because of a lack of power. However, we have validated the general approach of estimating the cosinor model from cross-sectional data, and we encourage other researchers to consider doing so in other populations around the world.
In conclusion, we developed and validated an approach to estimate the mean annual 25(OH)D concentration from a single 25(OH)D measurement by using a cosinor model. This model represents an acceptably accurate and precise method for classifying vitamin D status and should be considered for use in research and clinical care.
Acknowledgments
We thank the investigators, staff, and participants in the MESA study for their valuable contributions. A full list of participating MESA investigators and institutions can be found at http://www.mesa-nhlbi.org.
The authors’ responsibilities were as follows—MCS: designed the study, analyzed data, wrote the manuscript, and was responsible for the final content of the manuscript; AS: designed the research; GPL and CR-C: designed the research and analyzed data; ANH: conducted the research and provided essential reagents; NS-J and MB: conducted the research; JHI and PLL: wrote the manuscript; DSS: conducted the research and wrote the manuscript; and BK and IHdB: designed the research and wrote the manuscript. None of the authors had a conflict of interest.
Footnotes
Abbreviations used: BMD, bone mineral density; MESA, Multi-Ethnic Study of Atherosclerosis; RMSE, root mean squared error; 25(OH)D, 25-hydroxyvitamin D.
REFERENCES
- 1.IOM (Institute of Medicine) Dietary reference intakes for calcium and vitamin D. Washington, DC: The National Academies Press, 2011 [PubMed] [Google Scholar]
- 2.Dawson-Hughes B, Harris SS, Krall EA, Dallal GE. Effect of calcium and vitamin D supplementation on bone density in men and women 65 years of age or older. N Engl J Med 1997;337:670–6 [DOI] [PubMed] [Google Scholar]
- 3.Cauley JA, Lacroix AZ, Wu L, Horwitz M, Danielson ME, Bauer DC, Lee JS, Jackson RD, Robbins JA, Wu C, et al. Serum 25-hydroxyvitamin D concentrations and risk for hip fractures. Ann Intern Med 2008;149:242–50 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Robinson-Cohen C, Katz R, Hoofnagle AN, Cauley JA, Furberg CD, Robbins JA, Chen Z, Siscovick DS, de Boer IH, Kestenbaum B. Mineral metabolism markers and the long-term risk of hip fracture: the cardiovascular health study. J Clin Endocrinol Metab 2011;96:2186–93 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Holick MF. Vitamin D deficiency. N Engl J Med 2007;357:266–81 [DOI] [PubMed] [Google Scholar]
- 6.Rosen CJ. Clinical practice. vitamin D insufficiency. N Engl J Med 2011;364:248–54 [DOI] [PubMed] [Google Scholar]
- 7.Heaney RP, Davies KM, Chen TC, Holick MF, Barger-Lux MJ. Human serum 25-hydroxycholecalciferol response to extended oral dosing with cholecalciferol. Am J Clin Nutr 2003;77:204–10 [DOI] [PubMed] [Google Scholar]
- 8.Sherman SS, Hollis BW, Tobin JD. Vitamin D status and related parameters in a healthy population: the effects of age, sex, and season. J Clin Endocrinol Metab 1990;71:405–13 [DOI] [PubMed] [Google Scholar]
- 9.Bolland MJ, Grey AB, Ames RW, Mason BH, Horne AM, Gamble GD, Reid IR. The effects of seasonal variation of 25-hydroxyvitamin D and fat mass on a diagnosis of vitamin D sufficiency. Am J Clin Nutr 2007;86:959–64 [DOI] [PubMed] [Google Scholar]
- 10.Jorde R, Sneve M, Hutchinson M, Emaus N, Figenschau Y, Grimnes G. Tracking of serum 25-hydroxyvitamin D levels during 14 years in a population-based study and during 12 months in an intervention study. Am J Epidemiol 2010;171:903–8 [DOI] [PubMed] [Google Scholar]
- 11.Shoben AB, Kestenbaum B, Levin G, Hoofnagle AN, Psaty BM, Siscovick DS, de Boer IH. Seasonal variation in 25-hydroxyvitamin D concentrations in the cardiovascular health study. Am J Epidemiol 2011;174:1363–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Major JM, Graubard BI, Dodd KW, Iwan A, Alexander BH, Linet MS, Freedman DM. Variability and reproducibility of circulating vitamin D in a nationwide U.S. population. J Clin Endocrinol Metab 2013;98:97–104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wang Y, Jacobs EJ, McCullough ML, Rodriguez C, Thun MJ, Calle EE, Flanders WD. Comparing methods for accounting for seasonal variability in a biomarker when only a single sample is available: insights from simulations based on serum 25-hydroxyvitamin D. Am J Epidemiol 2009;170:88–94 [DOI] [PubMed] [Google Scholar]
- 14.Woitge HW, Knothe A, Witte K, Schmidt-Gayk H, Ziegler R, Lemmer B, Seibel MJ. Circaannual rhythms and interactions of vitamin D metabolites, parathyroid hormone, and biochemical markers of skeletal homeostasis: a prospective study. J Bone Miner Res 2000;15:2443–50 [DOI] [PubMed] [Google Scholar]
- 15.Bolland MJ, Chiu WW, Davidson JS, Grey A, Bacon C, Gamble GD, Reid IR. The effects of seasonal variation of 25-hydroxyvitamin D on diagnosis of vitamin D insufficiency. N Z Med J 2008;121:63–74 [PubMed] [Google Scholar]
- 16.Bild DE, Bluemke DA, Burke GL, Detrano R, Roux AVD, Folsom AR, Greenland P, Jacob DR, Kronmal R, Liu K, et al. Multi-ethnic study of atherosclerosis: objectives and design. Am J Epidemiol 2002;156:871–81 [DOI] [PubMed] [Google Scholar]
- 17.Hoofnagle AN, Laha TJ, Donaldson TF. A rubber transfer gasket to improve the throughput of liquid-liquid extraction in 96-well plates: application to vitamin D testing. J Chromatogr B Analyt Technol Biomed Life Sci 2010;878:1639–42 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Strathmann FG, Laha TJ, Hoofnagle AN. Quantification of 1α,25-dihydroxy vitamin D by immunoextraction and liquid chromatography-tandem mass spectrometry. Clin Chem 2011;57:1279–85 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bosworth CR, Levin G, Robinson-Cohen C, Hoofnagle AN, Ruzinski J, Young B, Schwartz SM, Himmelfarb J, Kestenbaum B, de Boer IH. The serum 24,25-dihydroxyvitamin D concentration, a marker of vitamin D catabolism, is reduced in chronic kidney disease. Kidney Int 2012;82:693–700 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Phinney KW. Development of a standard reference material for vitamin D in serum. Am J Clin Nutr 2008;88:511S–2S [DOI] [PubMed] [Google Scholar]
- 21.American Diabetes Association. Standards of medical care for patients with diabetes mellitus. Diabetes Care 2003;26(suppl 1):S33–50 [DOI] [PubMed] [Google Scholar]
- 22.Levey AS, Stevens LA, Schmid CH, Zhang YL, Castro AF, Feldman HI, Kusek JW, Eggers P, Lente FV, Greene T, et al. A new equation to estimate glomerular filtration rate. Ann Intern Med 2009;150:604–12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hyder JA, Allison MA, Wong N, Papa A, Lang TF, Sirlin C, Gapstur SM, Ouyang P, Carr JJ, Criqui MH. Association of coronary artery and aortic calcium with lumbar bone density: the MESA Abdominal Aortic Calcium Study. Am J Epidemiol 2009;169:186–94 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cramér H. Princeton, NJ: Princeton University Press, 1946 [Google Scholar]
- 25.Sachs MC. Hydroxyvitamin D calculator for seasonal adjustment. November 2012. Available from: http://kri.washington.edu/calculator (cited March 2013). [Google Scholar]
- 26.Hastie T, Tibshirani R, Friedman JH. The elements of statistical learning. New York, NY: Springer, 2009 [Google Scholar]
- 27.Wang TJ, Pencina MJ, Booth SL, Jacques PF, Ingelsson E, Lanier K, Benjamin EJ, D'Agostino RB, Wolf M, Vasan RS. Vitamin D deficiency and risk of cardiovascular disease. Circulation 2008;117:503–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Giovannucci E, Liu Y, Hollis BW, Rimm EB. 25-hydroxyVitamin D and risk of myocardial infarction in men: a prospective study. Arch Intern Med 2008;168:1174–80 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Melamed ML, Michos ED, Post W, Astor B. 25-hydroxyVitamin D levels and the risk of mortality in the general population. Arch Intern Med 2008;168:1629–37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.de Boer IH, Kestenbaum B, Shoben AB, Michos ED, Sarnak MJ, Siscovick DS. 25-hydroxyVitamin D levels inversely associate with risk for developing coronary artery calcification. J Am Soc Nephrol 2009;20:1805–12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.de Boer IH, Levin G, Robinson-Cohen C, Biggs ML, Hoofnagle AN, Siscovick DS, Kestenbaum B. Serum 25-hydroxyVitamin D concentration and risk for major clinical disease events in a community-based population of older adults: a cohort study. Ann Intern Med 2012;156:627–34 [DOI] [PMC free article] [PubMed] [Google Scholar]