Abstract
The cardiac ganglion (CG) of Homarus americanus is a central pattern generator that consists of two oscillatory groups of neurons: “small cells” (SCs) and “large cells” (LCs). We have shown that SCs and LCs begin their bursts nearly simultaneously but end their bursts at variable phases. This variability contrasts with many other central pattern generator systems in which phase is well maintained. To determine both the consequences of this variability and how CG phasing is controlled, we modeled the CG as a pair of Morris-Lecar oscillators coupled by electrical and excitatory synapses and constructed a database of 15,000 simulated networks using random parameter sets. These simulations, like our experimental results, displayed variable phase relationships, with the bursts beginning together but ending at variable phases. The model suggests that the variable phasing of the pattern has important implications for the functional role of the excitatory synapses. In networks in which the two oscillators had similar duty cycles, the excitatory coupling functioned to increase cycle frequency. In networks with disparate duty cycles, it functioned to decrease network frequency. Overall, we suggest that the phasing of the CG may vary without compromising appropriate motor output and that this variability may critically determine how the network behaves in response to manipulations.
Keywords: neuronal oscillators, central pattern generator, morris-lecar model, phase relationships
the timing of neuron firing in central pattern generators (CPGs) is often described in terms of phase, the latency from the start of a periodic cycle normalized to cycle period. For example, the pyloric CPG of the stomatogastric ganglion (STG) produces a stereotyped triphasic motor pattern, in which the phase relationships are highly conserved between individuals despite significant variability in the cycle frequency of the motor pattern, as well as in the maximal conductances of intrinsic currents (Hooper 1997a, 1997b; Bucher et al. 2005; Schulz et al. 2006, 2007; Goaillard et al. 2009; Tang et al. 2010). Other systems exhibiting phase constancy include undulatory locomotive circuits within lampreys and other aquatic animals (Grillner 1974; Cohen et al. 1992), swimmeret beating in crayfish (Skinner and Mulloney 1998; Mulloney and Smarandache-Wellmann 2012), the leech heart system (Wenning et al. 2004; Calabrese et al. 2011), and the motor pattern controlling gill ventilation in shore crabs (Dicaprio et al. 1997). The phase relationships of these motor patterns are actively maintained throughout the animal's life, presumably through homeostatic mechanisms that tune network components to produce appropriately timed network activity (Bucher et al. 2005; Davis 2006; Marder and Goaillard 2006).
For each of these systems, phase maintenance among motor neurons is necessary to produce an adaptive behavioral output. However, it is unclear whether the relative phasing of motor neuron and interneuron firing is always maintained. In the cardiac system of decapod crustaceans, the motor behavior is a single-phase contraction of the heart, but the cardiac CPG contains two oscillatory groups of neurons: motor neurons [“large cells” (LCs)] and premotor neurons [“small cells” (SCs)]. The strength and timing of heart contractions are exclusively controlled by the motor neurons, and thus the phase relationships between the motor and premotor neurons can vary without affecting motor output. In this report, we show that certain phase relationships of the CG motor pattern vary substantially across experimental preparations in the lobster, Homarus americanus. While previous studies have considered how CPG networks may be built to produce stereotypical activity patterns (e.g., Prinz et al. 2004), our results suggest that networks can be more flexibly tuned to produce appropriate behavioral output in certain biological systems.
We reproduced the variability in the CG motor pattern by constructing a two-cell model of the CG using Morris-Lecar (1981) oscillators and catalogued the behavior of 15,000 simulations in which the maximal conductance parameters of the model were randomized. The database approach allowed us to examine networks in which the cell parameters and chemical synaptic strengths were strongly heterogeneous. Our results show that heterogeneity has important consequences for network activity and is indeed necessary to reproduce the variability of the biological system. Thus, our modeling results provide insights into the dynamics of coupled heterogeneous oscillators that may be generalized to other neuronal circuits.
METHODS
Experimental methods.
The CG consists of nine neurons: five motor neurons (LCs) and four premotor neurons/interneurons (SCs). Both classes of cells fire during the same phase of muscle contraction, but the SC burst tends to outlast the LC burst. These two classes of cells are connected by electrical and excitatory chemical synapses (Fig. 1A). We performed extracellular in vitro recordings of the CG motor pattern using stainless steel pin electrodes that were isolated from the bath with a petroleum jelly well, as previously described by Stevens et al. (2009). Our primary recordings were taken from the anterior trunk of the CG (Fig. 1B). These recordings contained both SC and LC spikes, which were distinguishable by their amplitude, with LC spikes having the larger amplitude. To ensure that we correctly disambiguated the spike train recorded from the anterior trunk, we performed an additional extracellular recording from the motor nerve at a position anterior to cell 1 or cell 2, in which only LC spikes were present (Fig. 1B). Neuronal activity was recorded for ∼2–4 min, resulting in ∼100–250 cycles/experiment.
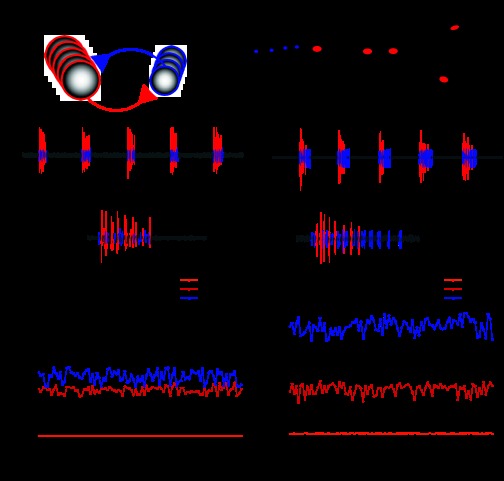
Fig. 1.
Extracellular recordings of the cardiac ganglion (CG) showing variable phase relationships. A: schematic network diagram of the CG. The network consists of nine neurons: five motor neurons [“large cells” (LCs)] and four interneurons [“small cells” (SCs)]. B: anatomic schematic diagram of the CG showing extracellular recording sites. Blue circles represent SC soma; red circles represent LC soma. Dotted circles represent extracellular recording wells. Our primary recordings were from the site in the middle of the ganglion, the anterior trunk. The additional recording site on the motor nerve was used to ensure that spikes recorded from the anterior trunk were correctly identified. C and D: extracellular recordings from the anterior trunk in two experimental preparations of the CG. SC and LC spikes are colored as blue and red, respectively. Note that LC activity was similar in terms of frequency and burst duration, meaning that cardiac output was likely to be similar in both preparations. In C, LCs and SCs initiate and terminate their bursts nearly simultaneously. In D, LCs and SCs initiate their bursts together but terminate their bursts at different time points. E and F: cycle-to-cycle calculation of phase for 100 cycles of the recordings shown in C and D. Note that the phases of SC and LC burst offset were substantially different between the two preparations as well as more variable over the course of the experiment on a cycle-to-cycle basis. E: cycle-to-cycle calculation of phase for the preparation shown in C. F: cycle-to-cycle calculation of phase for the preparation shown in D.
Extracellular recordings were amplified using a model 1700 A-M Systems differential alternating current amplifier (A-M Systems, Sequim, WA) and a model 440 Brownlee Precision Instrumentation amplifier (Brownlee Precision, San Jose, CA). This signal was digitized through a Micro 1401 digitizer (CED, Cambridge, UK) and recorded using the Spike2 software package (version 7, CED). All dissections and experiments were carried out in chilled (8–12°C) physiological saline solution [containing (in mM) 479.12 NaCl, 12.74 KCl, 13.67 CaCl2, 20.00 MgSO4, 3.91 Na2SO4, 11.45 Trizma base, and 4.82 maleic acid; pH 7.45]. The chemicals used to make the saline solution were obtained from Sigma-Aldrich (St. Louis, MO). Over the course of each recording, the temperature was maintained by an in-line Peltier temperature regulator (CL-100 bipolar temperature controller and SC-20 solution heater/cooler, Warner Instrument, Hamden, CT). Saline was superfused over the preparation at a flow rate of 5 ml/min.
Data analysis.
The phase relationships of SC and LC activity were calculated using programs written in the Spike2 script language (D. Bucher, University of Florida). The reference point for all phase measurements was chosen to be the start of the SC burst (phase = 0). The phase of all other events was calculated by the following equation: phase = lev/P, where lev is the latency of the event from the start of the SC burst and P is the cycle period (calculated as the time between the start of consecutive SC bursts). Phase was also calculated in this fashion for the model networks.
Because the phase resets every cycle, we considered phase to be a circular variable in all statistical analysis (see Zar 2010). Statistical tests and bootstrap confidence intervals were performed using the statistics toolbox in the MATLAB computing environment (The MathWorks, Natick, MA) in conjunction with a freely available circular statistics MATLAB toolbox (Berens 2009). Bootstrap confidence intervals were computed with 10,000 bootstrap samples. Values are given as means ± SD or circular means ± angular deviation for circular data unless otherwise noted. Angular deviation is analogous to SD but for a circular variable. Each data point was represented as a vector of unit length with the direction signifying the phase of oscillation. Angular deviation was calculated as follows:
| (1) |
where s is angular deviation and r is the length of the mean vector (Berens, 2009).
Model description.
The CG was modeled as a pair of Morris-Lecar oscillators connected by electrical and excitatory chemical coupling to reflect the basic connectivity of the biological network (see Fig. 1A). Each Morris-Lecar neuron includes a fast noninactivating Ca2+ current, a slow noninactivating K+ current, and a leak current (Morris and Lecar 1981). Together, these currents produce slow oscillations in membrane potential in the model neuron. The model therefore captures the slow dynamics of bursting biological neurons while ignoring the fast dynamics associated with action potentials. An isolated Morris-Lecar oscillator can be simulated by numerically integrating the following equations:
| (2) |
| (3) |
where C is the total capacitance of the neuron; V is the membrane potential of the model neuron; t is time; gL, gCa, and gK are the maximal conductances for leak, Ca2+, and K+ currents, respectively; VL, VCa, and VK are the reversal potentials for leak, Ca2+, and K+ currents, respectively; and M∞ and W∞ are sigmoidal functions that describe the steady-state activation curves for Ca2+ and K+ currents, respectively. Note that the activation of the Ca2+ current instantaneously follows its activation curve, whereas the activation of the K+ current (given by the state variable W) evolves according to the time constant of K+ channel opening (τW).
The sigmoidal activation curves were determined as follows:
| (4) |
| (5) |
where V1 and V3 are the parameters that set the half-activation for Ca2+ and K+ currents, respectively, and V2 and V4 are the parameters that control the steepness of the activation curves. τW was determined as follows:
| (6) |
where λW is a parameter that defines the rate constant of K+ channel opening and ϕW is the minimum value of λW for all values of V.
We added excitatory chemical coupling as well as electrical coupling between a pair of neurons, each modeled by Eqs. 1 and 2. The entire network was governed by the following equations:
| (7) |
| (8) |
| (9) |
| (10) |
where the superscripts “A” and “B” mark parameters and variables that take on different values for the two model oscillators within the network. For example, VA is the membrane potential of the first cell and VB is the membrane potential of the other oscillator within the network. gsynA and gsynB are the parameters that set the maximal conductances for the excitatory chemical synapses, and ggap is a parameter that sets the strength of the direct electrical coupling. With the exception of ggap, all maximal conductance parameters are heterogeneous, whereas the reversal potential parameters are homogeneous between the two oscillators. S∞ is a sigmoidal function that describes the steady-state activation curve of the chemical synapses based on presynaptic membrane potential. The functions M∞, W∞, S∞, and τW are identical in the two oscillators, with S∞ using the same formalism as the other steady-state activation curves, as follows:
| (11) |
where V5 is a parameter that reflects synaptic half-activation and V6 is a parameter that reflects the synaptic activation slope. We simulated a population of randomly configured model networks as specified by the above equations. To create this population, we randomly selected values for the nine maximal conductance parameters (gLA, gLA, gCaA, gCaA, gKA, gKA, gsynA, gsynA, and ggap) from uniform random distributions, as shown in Table 1. The remaining parameters were set to fixed values, as shown in Table 1, and were based on the simulations done by Skinner et al. (1993). In a subset of simulations, we further manipulated the parameter values of gsyn and Vsyn as described in the results.
Table 1.
Parameter values used for the simulated model networks
| Parameter | Variable | Value Used |
|---|---|---|
| Cell surface area, cm2 | 0.001 | |
| Total cell capacitance, nF | C | 10 |
| Ca2+ reversal potential, mV | VCa | 100 |
| K+ reversal potential, mV | VK | −80 |
| Leak reversal potential, mV | VL | −10 |
| Synaptic reversal potential, mV | Vsyn* | −15 |
| Ca2+ current half-activation, mV | V1 | 0 |
| Ca2+ current activation slope, mV | V2 | 15 |
| K+ current half-activation, mV | V3 | 0 |
| K+ current activation slope, mV | V4 | 15 |
| Synaptic half-activation, mV | V5 | 0 |
| Synaptic activation slope, mV | V6 | 5 |
| K+ current minimum rate constant, ms | ϕW | 0.002 |
| Parameter | Variable | Minimum Value Used | Maximum Value Used |
|---|---|---|---|
| Ca2+ current maximal conductance, μS/cm2 | gCa | 0 | 100 |
| K+ current maximal conductance, μS/cm2 | gK | 0 | 100 |
| Leak current maximal conductance, μS/cm2 | gL | 1 | 10 |
| Chemical synaptic strength, μS/cm2 | gsyn* | 0 | 50 |
| Electrical coupling strength, μS/cm2 | ggap | 5 | 40 |
In portions of the simulations, the parameter values for the synaptic reversal potential and chemical synaptic strengths were manipulated as described in the results.
To match what is known about the biological system, we instituted a number of constraints on our simulations. First, because both the SCs and LCs have been shown to be endogenous bursters (Tazaki and Cooke 1983; García-Crescioni and Miller 2011), we ensured that each Morris-Lecar neuron produced spontaneous oscillations in isolation before we included them in a network. Once two endogenously bursting oscillators were found, we coupled them into a network and simulated the system until it reached a steady-state pattern of activity (as done by Prinz et al. 2003a). Networks were excluded from our analysis if either neuron did not produce bursts in the integrated network, if the two neurons burst at different rates (most often in a 2:1 ratio), or if the phase of burst overlap was <0.01. For this last criterion, we calculated the phase of burst overlap as follows: lov/P, where lov is the length of time over which both oscillators were simultaneously bursting in a single cycle and P is the cycle period of the rhythm.
All simulations were integrated with an exponential Euler method (Dayan and Abbott 2001) using a custom written C++ code. Network frequency, phase relationships, and other measures of network activity were calculated in MATLAB.
RESULTS
Phase relationships of the biological motor pattern.
We recorded the extracellular bursting activity of 38 isolated CGs to characterize the phase relationships between the SCs and LCs. In some preparations (e.g., Fig. 1C), LCs and SCs produced bursts in unison, with approximately equal durations. In other cases (e.g., Fig. 1D), the SC burst was noticeably longer than the LC burst. Across preparations with different relative burst durations, the frequency and burst duration of motor neuron activity could be approximately identical (compare Fig. 1, C with D). In such cases, the frequency and amplitude of heart contractions are likely to be similar, even though the phasing of SC and LC activity is strikingly different.
To quantify the phase relationships of the two neuronal types in the CG, four events were examined for each cycle of the CG motor pattern: the first SC spike (SC start phase), the last SC spike (SC end phase), the first LC spike (LC start phase), and the last LC spike (LC end phase). The SC start phase was considered to be the start of each cycle (phase = 0). The phases of the remaining three events were calculated as the latency from the first SC spike normalized to the cycle period (see methods).
Figure 1, E and F, shows the results of the phase analysis for 100 cycles of the 2 experiments shown in Fig. 1, C and D, respectively. Although phase relationships were variable on a cycle-to-cycle basis, they were stable over the course of the experiment. Strikingly, the LC start phase showed less cycle-to-cycle variability than the LC and SC end phases. We analyzed this variability in terms of angular deviation, a standard measurement of dispersion for a circular variable (Zar 2010). Within preparations, the angular deviation for the LC start phase was several orders of magnitude lower than the deviations of the LC end phase and the SC end phase (median deviations in cycles: LC start, 4.03 × 10−4; LC end, 1.45 × 10−2; and SC end, 1.46 × 10−2). The within-preparation variance of the LC start phase was significantly lower than the variances of the LC end and SC end phases (Mann-Whitney test, P < 0.001, Bonferroni correction for multiple comparisons). The within-preparation variance was not significantly different for the LC and SC end phases (Mann-Whitney test, P = 0.75). The cycle period of the rhythm did not significantly correlate with the degree of cycle-to-cycle variability in network phasing (data not shown).
In addition to being more variable over the course of individual preparations, LC and SC end phases displayed greater variability across preparations (Fig. 2, A and B). Average LC start phases ranged from −0.031 to 0.019 (mean: 0.005 ± 0.010). LC and SC end phases were more variable, ranging from 0.039 to 0.356 (mean: 0.169 ± 0.080) and from 0.068 to 0.413 (mean: 0.248 ± 0.090), respectively. The variances of the end phases were significantly greater than the variance of the LC start phase [Mann-Whitney test on the angular distances (Fig. 2B), Bonferroni-corrected P < 0.001 (see Zar 2010)]. To determine whether this variability was greater than that often observed in CPGs known to maintain phase, we compared these results with previously published data taken from the pyloric rhythm in Cancer borealis (Goaillard et al. 2009). LC and SC end phases were two to four times more variable than all five phases of the pyloric rhythm; all of these differences were significant (data not shown; Mann-Whitney test on the angular distances, P < 0.05). Interestingly, the LC start phase was significantly less variable than all the phases of the STG rhythm (P < 0.01).
Fig. 2.

Pooled analysis of variability in the phase relationships of the CG motor pattern. A: dot and box plots showing the distribution of the LC start, LC end, and SC end phases in n = 38 preparations. The lines within the box plot denote the median, upper, and lower quartiles, with the whiskers denoting the most extreme data within 1.5 times the interquartile range from the nearest quartile. Outliers beyond these extremes are denoted by the “+” symbol. B: angular deviation for each phase of the CG rhythm. Error bars denote SEs, as estimated by bootstrapping with 10,000 bootstrap samples. LC end and SC end phases were significantly more variable than the LC start phase (P < 0.001, Bonferonni correction for multiple comparisons). C: dot and box plots showing the distribution of LC and SC duty cycles and the duty cycle difference (SC − LC). D: pairwise regressions between SC (gray) and LC (black) burst durations and the cycle period. For each regression, the coefficient of determination and 95% confidence interval for the y-intercept are shonw. Note that neither regression line passed through the origin (y-intercepts were both negative), indicating that burst duration does not proportionally scale with cycle period.
In all preparations, LC and SC bursts began nearly simultaneously on each cycle. Because the LC start phase was approximately zero, LC and SC end phases were nearly equal to the LC and SC duty cycles (compare Fig. 2, A with C). Thus, the phasing of the CG motor pattern can be conveniently captured by just two variables (the SC and LC duty cycles) rather than three (the LC start phase, LC end phase, and SC end phase). The SC duty cycle is equal to the SC end phase, by definition, and the LC duty cycle is nearly identical to the LC end phase (compare Fig. 2, C with A).
LC and SC duty cycles were very similar in some preparations, whereas they were distinct in others (Fig. 1, C and D). We quantified this by calculating the difference between the duty cycles (SC duty cycle − LC duty cycle) in each preparation. The duty cycle difference varied from −0.016 to 0.197 (mean: 0.083 ± 0.047), indicating that the relative phasing of the LC and SC burst ends, like the duty cycle of each individual neuronal type, was variable (Fig. 2C).
The duty cycles of the LCs and SCs are determined by their burst durations and the cycle period of the rhythm, both of which are individually important indicators of network activity. We plotted LC and SC burst durations as a function of cycle period to examine the variability in these two additional measures of network activity (Fig. 2D). We observed significant positive correlations between the burst durations and cycle period (linear regression; slopes significantly greater than zero, P < 0.001, with SC: R2 = 0.756 and LC: R2 = 0.707). However, neither regression line passed through the origin (P < 0.05), indicating that burst duration does not scale proportionately with cycle period.
The cycle period of the CG rhythm was also variable, ranging from 1.10 to 5.85 s (mean: 2.60 ± 1.22, coefficient of variation = 0.47). This is more extreme than the variability observed for the cycle period of the pyloric rhythm in the STG in the same species and at comparable temperatures [mean: 1.52 ± 0.27 s, coefficient of variation = 0.18 (Bucher et al. 2005)]. The variability in LC and SC burst durations were comparable with each other, with LC durations ranging from 0.059 to 1.446 s (mean: 0.479 ± 0.403) and SC durations ranging from 0.147 to 1.949 s (mean: 0.636 ± 0.433). The variances of LC and SC burst durations were not significantly different (F-test, P = 0.26; Fligner-Killeen test, P = 0.23).
Phase analysis of a population of computational models.
We developed a simple two-cell computational model to address three questions raised by these experimental data. First, do the synchronization patterns of the CG follow directly from network architecture or is it necessary to tune network parameters to replicate the phase relationships of the biological system? Second, which network parameters control the phase relationships of the biological rhythm? Specifically, because the SC and LC duty cycles captured the most salient features of CG phasing, we examined the parameters that determined the duty cycles of the two oscillators within the model networks. Third, do the phase relationships of the CG affect the response of the network to perturbation? In particular, we examined the effect of perturbing the strength of synaptic coupling.
The model consisted of two Morris-Lecar oscillators coupled by an electrical synapse and by reciprocal excitatory chemical synapses. Although the CG consists of nine neurons in H. americanus, a two-cell model is sufficient to capture basic network dynamics, because 1) the electrical properties of each individual LC and SC are similar to those of other members of its respective group (but see Berlind 1993) and 2) the bursting activity of each group of neurons (LC and SC) is synchronized by strong electrical coupling among those neurons (Cooke 2002). Thus, the basic dynamics of the CG arise from the interactions of two oscillators, one representing the population of SCs and the other representing the population of LCs (Ball et al. 2010).
Each model neuron has three currents: a fast noninactivating Ca2+ current, a slow noninactivating K+ current, and a leak current. In the biological network, slow-wave oscillations are driven by an interplay between inward Ca2+ currents and outward voltage- and Ca2+-dependent K+ currents (Tazaki and Cooke 1979a, 1990). We also included a depolarizing leak current because it has been hypothesized that a depolarizing pacemaker potential may work as an initial stimulus to trigger the Ca2+-dependent currents that produce the burst (Cooke 2002).
Fast oscillations that resemble action potentials were not produced in this simple model. Thus, we considered an oscillator to be “bursting” whenever its membrane potential was depolarized above 0 mV. Because synaptic release is triggered by bursting in the biological network, we set V5 to 0 mV in all simulations.
Previous studies have suggested that the chemical synapses in the CG are excitatory (Tazaki and Cooke 1979b; Morganelli and Sherman 1987), but we are unaware of any measurement of the reversal potential of these excitatory synapses. We first set the synaptic reversal potential to −15 mV, which is comparable with the reversal potentials of excitatory synapses in many vertebrate and invertebrate systems. This reversal potential was between the voltage maxima and minima of a typical Morris-Lecar oscillator within our parameter ranges.
We simulated 15,000 randomly configured two-cell model networks. From this simulation pool, 13,141 networks produced in-phase synchronous oscillations (those in which bursts significantly overlapped and occurred in a 1:1 ratio) and were further analyzed. This population of 13,141 networks displayed substantially variable oscillation patterns in terms of cycle frequency and phasing (Fig. 3). For example, Fig. 3, A and B, shows two networks that have different cycle frequencies but display similar phase relationships: the bursts begin and terminate at nearly identical phases in each network (similar to the experimental data shown in Fig. 1C). In contrast, the networks shown in Fig. 3, C and D, display a different phasing pattern: the bursts begin at nearly identical phases but end at distinct phases (similar to Fig. 1D).
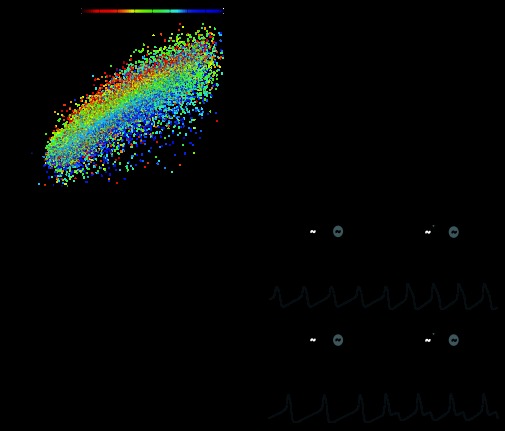
Fig. 3.
Example model network voltage traces with accompanying bar plots showing parameter values. The dashed line marks the burst threshold (0 mV) in A–D. All parameters were plotted in units of μS/cm2 to the right of each voltage trace. Scale bars = 30 mV and 500 ms. A and B: two different model networks in which the two cells exhibited nearly identical oscillation patterns, with bursts beginning and ending concurrently. While having similar phasing, these two networks displayed drastically different cycle frequencies. C and D: two model networks in which the two cells initiated their bursts at nearly identical phases but terminated their bursts at different phases. Again, note the large difference in cycle frequency between these two examples, despite having similar phase relationships.
As in our experimental results, we measured the phase of all the burst onsets and offsets in each network. We used the burst onset of the oscillator with the larger duty cycle as the arbitrary reference point (phase = 0). This is analogous to using the SC burst onset as the reference point in the biological network, because SCs have the larger duty cycle in experimental preparations. Remarkably, with minimal parameter tuning, the entire population of model networks exhibited a pattern of phase relationships that closely resembled the biological networks (Fig. 4; compare with Fig. 2, A and C). Specifically, the burst onsets of the two model cells occurred nearly simultaneously in all networks, whereas the duty cycles and duty cycle differences were highly variable from network to network. Taken together, these data indicate that the two model cells usually begin their bursts together and terminate their bursts either together or apart, depending on the network. These trends are apparent in the example voltage traces shown in Fig. 3.
Fig. 4.
Pooled phase analysis of the simulated population of model networks (n = 13,141). The burst onset of the oscillator with the larger duty cycle was taken as the starting reference point for phase analysis (analogous to the SC burst start in the biological system). Dot plots and box plots show the distribution of start and end phases for the small duty cycle oscillator (analogous to LCs), the end phase of the large duty cycle oscillator (analogous to the SC end phase), and the phase delay between end phases. The pattern of variability observed within these model networks resembled the experimental data shown in Fig. 2, A and C. The lines within the box plot denote the median, upper, and lower quartiles, with the whiskers denoting the most extreme data within 1.5 times the interquartile range from the nearest quartile. Due to the large number of points, outliers beyond these extremes were not marked.
The intrinsic duty cycle of the oscillators strongly influences network phasing.
As in the experimental data, the duty cycles of the model cells captured the basic phasing of network output, because the bursts began nearly simultaneously for each cycle. To understand how network parameters determine the phase relationships of the model networks, we investigated the relationship between four measures: 1) “intrinsic duty cycle” (the duty cycle of each oscillator when simulated in isolation), 2) “network duty cycle” (the duty cycle of each oscillator when coupled to its partner), 3) “intrinsic duty cycle difference” (the difference between the intrinsic duty cycles of the oscillators), and 4) “network duty cycle difference” (the difference between the duty cycles of the oscillators within the coupled network). The duty cycle difference was always calculated by subtracting the duty cycle of oscillator A from oscillator B (see Eqs. 6–9 in methods). Because of the symmetry of the network, it would have been equally valid to subtract the duty cycle of oscillator B from oscillator A.
The duty cycle of each oscillator within the coupled network was very similar to its intrinsic duty cycle (linear regression, R2 = 0.78, P < 0.001; Fig. 5A). Secondary effects were exerted by the intrinsic duty cycle of the other oscillator in the network (Fig. 5A; see color scheme). As an extension of this finding, the duty cycle difference between two coupled oscillators was largely determined by the difference in the intrinsic duty cycles of the two oscillators that comprised that network (linear regression, R2 = 0.68, P < 0.001; Fig. 5B). In contrast, the intrinsic frequency of the two oscillators hardly influenced the phasing of network activity (linear regression, R2 = 0.08, P < 0.001; Fig. 5C). We did not observe a significant interaction between the intrinsic frequency and intrinsic duty cycle (data not shown).
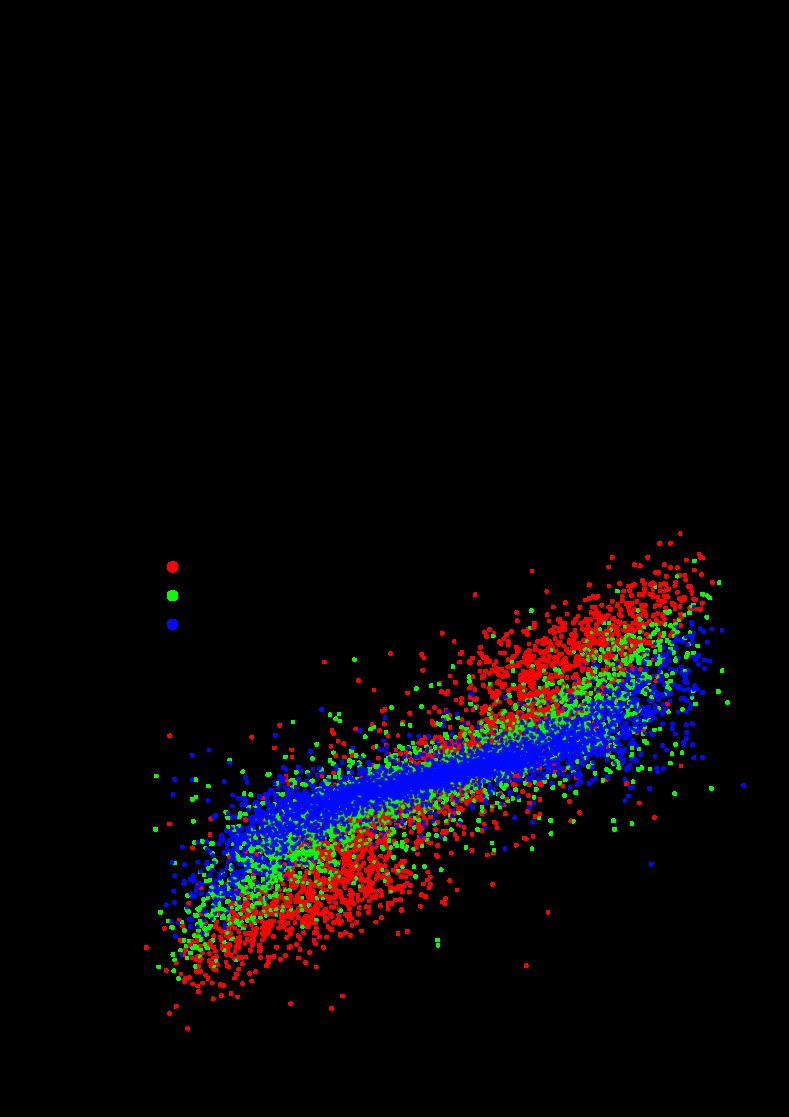
Fig. 5.
The phasing of the model networks is strongly determined by the intrinsic duty cycles of the two oscillators. A: scatterplot of the intrinsic duty cycle versus the network duty cycle for all model oscillators (n = 26,282), showing a strong positive correlation (pairwise linear regression, R2 = 0.78). The color of each point represents the intrinsic duty cycle of the other oscillator within the network (see color bar). B: the difference in intrinsic duty cycle displayed a strong positive correlation with the network duty cycle difference (R2 = 0.68). C: the difference between the intrinsic frequencies had only marginal effects on network phasing in the models (R2 = 0.08). D: voltage traces showing intrinsic oscillator activity and network activity. Chemical and electrical coupling were absent at the beginning of each trace (see schematics above traces) and were inserted into the model at the time points marked by the arrows. Scale bars = 30 mV and 500 ms. The left trace shows oscillators with similar intrinsic duty cycles but different intrinsic frequencies. When coupled, the oscillators continued to display similar duty cycles. Model parameters were as follows: top oscillator [maximal conductance for Ca2+ current (gCa), 65.5; maximal conductance for K+ current (gK), 80.5; maximal conductance for leak current (gL), 2.41; and maximal conductance for excitatory chemical synapses (gsyn), 22.3], bottom oscillator (gCa, 19.6; gK, 58.1; gL, 9.15; and gsyn, 0.785), and electrical coupling [strength of electrical coupling (ggap), 36.3]. The right trace shows oscillators with similar intrinsic frequencies but different intrinsic duty cycles. Once coupled, the oscillators displayed disparate duty cycles. Model parameters were as follows: top oscillator (gCa, 24.8; gK, 93.6; gL, 1.87; and gsyn, 5.25), bottom oscillator (gCa, 63.5; gK, 62.6; gL, 7.62; and gsyn, 2.67), and electrical coupling (ggap, 11.9).
Thus, in this population of models, the phase relationships of a network were largely determined by the intrinsic duty cycles of its component oscillators. Networks composed of oscillators with similar intrinsic duty cycles produced in-phase bursting patterns, even when their intrinsic frequencies were dissimilar (Fig. 5D, top). Networks composed of oscillators with dissimilar intrinsic duty cycles produced in-phase burst onsets and out-of-phase burst offsets, even when their intrinsic frequencies were similar (Fig. 5D, bottom).
If intrinsic duty cycle is the principal determinant of the phasing of network activity, which parameters predict the intrinsic duty cycle of a model neuron? We observed a strong, positive relationship between the ratio of gCa/gK and the intrinsic duty cycle of a model neuron (cubic regression: R2 = 0.72, P < 0.001; Fig. 6A). In essence, this fit shows that when the inward current was strong relative to the outward current, the cell remained active for a larger proportion of each periodic cycle.
Fig. 6.
The proportion gCa/gK and the electrical coupling influence the phasing of network activity. A: gCa/gK displayed a strong nonlinear relationship with the intrinsic duty cycle (cubic regression, R2 = 0.72, n = 26,282). B: the difference between gCa/gK in two oscillators predicts the duty cycle difference for those oscillators when they are coupled (R2 = 0.71, n = 13,141). The color scheme shows that increasing the electrical coupling (ggap) decreased the slope of the relationship between gCa/gK and duty cycle difference.
Due to the correlation between gCa/gK and the intrinsic duty cycle of a model cell, the difference in gCa/gK between the two model cells was positively correlated with the difference in network duty cycle (linear regression, R2 = 0.71, P < 0.001; Fig. 6B). This result was consistent with the example traces shown in Fig. 3 if one examines the parameter values for each trace. In networks in which the two model cells have similar duty cycles, the proportion of gCa to gK is similar in each model cell (Fig. 3, A and B). In contrast, in networks where the two model cells have disparate duty cycles, this proportion is dissimilar between the two cells (Fig. 3, C and D).
The strength of electrical coupling (ggap) also influenced the phase relationships in the model networks. The value of ggap influenced the strength of the relationship between the difference in gCa/gK and the duty cycle difference. For small values of ggap, the slope of this relationship was large, meaning that the difference in duty cycle was sensitive to the difference in gCa/gK (Fig. 6B, red circles). For larger values of ggap, this relationship was weaker, indicating that the difference in duty cycle was less sensitive to the difference in gCa/gK (Fig. 6B, blue circles). The duty cycle difference was also influenced by the strength of the excitatory chemical synapses (see below).
Excitatory chemical synapses function to increase or decrease cycle frequency depending on the phase relationships of the network.
To investigate the role of the chemical synapses within the model networks, we characterized the effect of changing the synaptic strengths in each network. Networks were simulated with the synaptic strengths doubled from their initial values (each gsyn multiplied by 2 from the initial parameters) and with both of the chemical synapses silenced (each gsyn set to zero).
The effects of scaling the strengths of the chemical synapses were dependent on the phasing of the network at baseline (i.e., before the perturbation). In networks with similar duty cycles, increasing gsyn tended to increase cycle frequency, whereas decreasing gsyn decreased frequency. In these networks, the duty cycle difference was not often affected by scaling the chemical synapses (Fig. 7A). In contrast, in networks with disparate duty cycles, increasing gsyn tended to decrease cycle frequency, whereas decreasing gsyn increased frequency. In these networks, increasing gsyn tended to increase the duty cycle difference, whereas decreasing gsyn tended to make the duty cycles more similar (Fig. 7B).
Fig. 7.
Chemical synapses function to increase cycle frequency in networks with similar duty cycles but decrease cycle frequency in networks with disparate duty cycles. A and B: voltage traces of network activity with baseline parameters (middle), chemical synaptic strengths doubled (top), and chemical synapses silenced (bottom). Scale bars = 500 ms and 50 mV. A: network with similar duty cycles in the baseline simulation. Increasing the synaptic strength increased cycle frequency. Baseline model parameters were as follows: top oscillator (gCa, 57.7; gK, 64.5; gL, 3.81; and gsyn, 24.5), bottom oscillator (gCa, 12.4; gK, 12.3; gL, 7.98; and gsyn, 16.1), and electrical coupling (ggap, 27.9). B: network with disparate duty cycles in the baseline simulation. Increasing synaptic strength decreased cycle frequency. Baseline model parameters were as follows: top oscillator (gCa, 73.0; gK, 96.6; gL, 1.63; and gsyn, 2.99), bottom oscillator (gCa, 73.4; gK, 79.1; gL, 6.39; and gsyn, 17.0), and electrical coupling (ggap, 6.1). C: the initial duty cycle difference predicted whether cycle frequency increases or decreases in response to silencing the chemical synapses (n = 12,946). As the absolute value of duty cycle difference increased, the change in cycle frequency changed from negative to positive. D: the initial duty cycle difference predicted how the duty cycle changes in response to silencing the chemical synapses (n = 12,946). Silencing the chemical synapses tended to make the duty cycles more similar. If the duty cycle difference was initially positive, then silencing the synapses tended to produce a negative change, and vice versa. The color scheme in C and D shows the mean strength of the two chemical synapses. The magnitude of the effect of silencing the synapses was positively related to the initial synaptic strengths (larger changes in frequency and duty cycle for stronger initial synapses). The n values here were less than the original simulation set because we excluded networks that failed to meet our criteria with the synapses turned off.
The results shown in Fig. 7, C and D, in which the changes in network activity elicited by silencing the chemical synapses are plotted as a function of the duty cycle difference, demonstrates that these trends hold for the population of analyzed networks. The change in frequency followed a U-shaped pattern, increasing from negative to positive as the absolute value of the duty cycle difference increased (Fig. 7C), that is, cycle frequency tended to decrease in networks with initially similar duty cycles but increase in networks with disparate duty cycle difference. The change in duty cycle difference elicited by silencing the chemical synapses displayed a negative, roughly linear, relationship with the initial duty cycle difference (Fig. 7D). When the initial duty cycle difference was negative, silencing the chemical synapses produced a positive change, making the duty cycles more similar in the final state. When the initial duty cycle difference was positive, a negative change was produced, again making the duty cycles more similar in the final state. When the initial duty cycles were similar (near zero), silencing the chemical synapses did not significantly change the duty cycle difference.
The mean synaptic strength within the baseline model influenced the magnitude of the changes in frequency and phase (see color scheme in Fig. 7, C and D). Unsurprisingly, networks with weaker synapses produced smaller changes in frequency and duty cycle, whereas networks with stronger synapses produced larger changes. For changes in frequency, this trend was particularly apparent in networks with similar duty cycles (Fig. 7C, center of the x-axis). Taken together, the initial phasing of the network and average chemical synaptic strength strongly predict how the network responds to the removal of chemical synapses.
Changing the synaptic reversal potential alters how network phasing interacts with the chemical synapses to influence cycle frequency.
The function of the chemical synapses in the model depends on the synaptic reversal potential. In the baseline models, Vsyn is equal to −15 mV, which sits at the base of the synaptic activation curve (Fig. 8A) and between the voltage minima and maxima of a typical cell within the model networks (Fig. 8B). With these parameters, the onset of the chemical synaptic current to a cell at resting membrane potential (V = −60 mV) elicits a depolarization. However, these excitatory synapses produce hyperpolarizations when applied during the bursting phase of an oscillation. Thus, the synaptic current hyperpolarizes the oscillator in its active state and depolarizes the oscillator in its resting state. In contrast, if the synaptic reversal potential were higher, the chemical synapses would elicit depolarizations even when the oscillator was bursting (e.g., if Vsyn were equal to +45 mV, then depolarizations during bursting would be elicited whenever 0 mV < V < +45 mV).
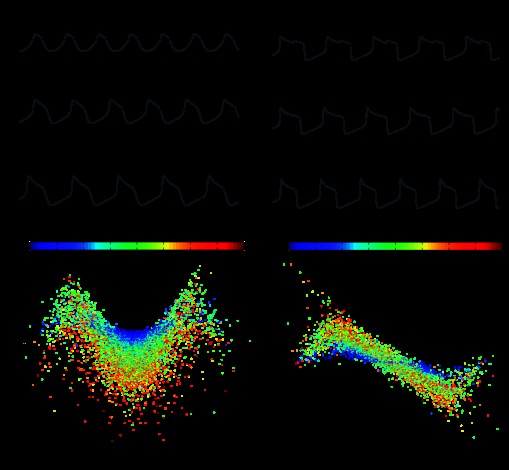
Fig. 8.
Modifying the reversal potential of the chemical synapses substantially affects how the chemical synapses control network frequency. A: locations of the four reversal potentials tested (−15, 0, 15, and 45 mV) on the activation curve of the chemical synaptic current. Letters correspond to the panels of the corresponding reversal potential. B: locations of the six reversal potentials tested on a histogram showing the voltage minima and maxima of all oscillators within the model networks. Chemical synapses were turned off in the simulations used to gather these data. Letters indicate the panels corresponding to each reversal potential. C–F: relationships between the differences in duty cycle and changes in cycle frequency in response to silencing the chemical synapses for each reversal potential. For consistency, all plots contained exactly 10,000 points, which were randomly chosen from simulations in each condition. C: gsyn = −15 mV (same as baseline parameters). D: gsyn = 0 mV. E: gsyn = 15 mV. F: gsyn = 45 mV.
Therefore, we simulated and characterized network activity at three additional synaptic reversal potentials (0, +15, and +45 mV). Figure 8A shows the location of all four reversal potentials in relation to the synaptic activation curve. Figure 8B shows their location with respect to the minima and maxima of the oscillators in electrically coupled networks. Figure 8, C–F, shows the relationship between the difference in duty cycle and change in frequency elicited by silencing the chemical synapses for each level of synaptic reversal potential. As in Fig. 7, C and D, these plots show the effect of silencing the chemical synapses on cycle frequency as a function of the initial difference in the duty cycles of the oscillators. As before, when Vsyn = −15 mV, frequency decreased in response to this perturbation in networks with similar duty cycles but increased in networks with disparate duty cycles (Fig. 8C). This trend was maintained as Vsyn increased to 0 mV (Fig. 8D) but changed when Vsyn increased further. When Vsyn = +15 mV, networks with similar duty cycles tended to speed up, whereas networks with different duty cycles tended to slow down (Fig. 8E). Additionally, on average, the differences between oscillator duty cycle appeared less variable for more depolarized values of Vsyn, i.e., the range of data points along the x-axis was smaller (Fig. 8, E and F). Thus, the function of the chemical synapses within the model networks appears to be highly sensitive to changes in the reversal potential of chemical synapses.
How phasing effects the response of the networks to perturbations.
To understand why variability in CG phasing may influence the dynamics of the excitatory chemical synapses within the circuit, consider the two model networks shown in Fig. 9. The first network is a representative case in which the duty cycles are very similar, and silencing the chemical synapses caused a decrease in cycle frequency (Fig. 9A). The second network is a representative case in which the duty cycles are dissimilar, and silencing the chemical synapses caused an increase in cycle frequency (Fig. 9B). These traces can be loosely thought of as representing the CG, with the top traces showing SC activity and the bottom traces showing LC activity.
Fig. 9.
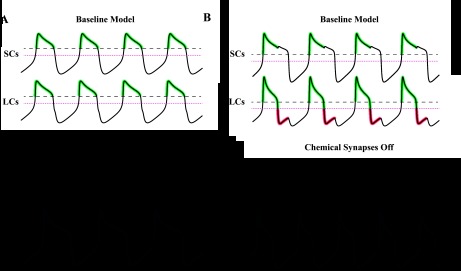
Qualitative explanation of how chemical synapses can differentially influence cycle frequency based on network phasing. Green portions of the traces mark periods where the postsynaptic current is active and acting to hyperpolarize membrane potential. Red portions of the traces mark periods where the postsynaptic current is active and acting to depolarize membrane potential. Black dotted lines mark burst threshold (0 mV). Magenta dotted lines mark the synaptic reversal potential (−15 mV). Scale bars = 500 ms and 30 mV. A: network with similar duty cycles, in which cycle frequency decreased after chemical synapses were removed. Model parameters were as follows: top oscillator (gCa, 46.8; gK, 48.4; gL, 3.07; and gsyn, 37.28), bottom oscillator (gCa, 27.7; gK, 30.6; gL, 6.72; and gsyn, 14.7), and electrical coupling (ggap, 35.2). B: network with disparate duty cycles, in which cycle frequency increased after chemical synapses were removed. Model parameters were as follows: top oscillator (gCa, 77.6; gK, 73.9; gL, 8.74; and gsyn, 25.9), bottom oscillator (gCa, 69.6; gK, 91.5; gL, 9.68; and gsyn, 1.94), and electrical coupling (ggap, 35.2).
In the first network, the burst onsets and offsets were temporally aligned (Fig. 9A). The two chemical synapses were activated over the interval where both oscillators were bursting and were otherwise inactive. During the interval where the synapses were active (green portion of traces), both oscillators were more depolarized than the reversal potential of the synapses (−15 mV). As a result, the effect of the synapses was primarily a hyperpolarization of the oscillators. This terminated the SC and LC bursts early, which increased network frequency. When the synapses were silenced, the oscillators exhibited prolonged bursts and therefore a lower frequency.
In the second network, the burst onsets were aligned, but the offsets occurred out of phase (Fig. 9B). Each periodic burst can be divided into two segments: the first, in which both oscillators are depolarized, and the second, during which one oscillator remains depolarized and the other is hyperpolarized. During the first segment, the chemical synapses function to hyperpolarize both oscillators and increase network frequency (similar to the effect shown in Fig. 9A). In the second segment, one oscillator remains depolarized while the other repolarizes, causing its synapse to fall silent. During this period, only the oscillator with the short duty cycle receives input from the chemical synapses. This input induces a depolarization (red portion of traces) because the short duty cycle oscillator has a membrane potential below −15 mV. This premature depolarization decreases cycle frequency by prolonging the burst of the long duty cycle oscillator. Without this depolarization (with the chemical synapses turned off), the small duty cycle oscillator hyperpolarizes the large duty cycle oscillator more effectively during this period, via the electrical synapse (Fig. 9B, bottom).
DISCUSSION
It is now well established that the cellular and molecular components of neuronal networks are highly variable across preparations. This result was first demonstrated within the STG, in which ion channel mRNA expression varies two- to sixfold across preparations in neurons of the same cell type, as do measurements of maximal conductance in voltage-clamp (Golowasch et al. 1999; Goldman et al. 2001; Schulz et al. 2006, 2007; Goaillard et al. 2009). More recent studies have replicated this result in other neuronal systems (Swensen and Bean 2005; Amendola et al. 2012; Roffman et al. 2012), including the CG (Tobin et al. 2009). Although it is often discounted as experimental noise, variability is an intrinsic and important feature of neuronal systems, which arises from the stochastic nature of biochemical processes (Marder 2011; Marder and Taylor 2011).
A fundamental question facing neuroscientists today is how certain features of neuronal activity are constant across preparations, even though the underlying network components are variable. One widely conserved feature of many CPG networks is their ability to maintain phase, meaning that the latencies between neuron bursts scale proportionally with the cycle period of the rhythm. Phase constancy has been extensively investigated in the pyloric motor pattern of the STG (Hooper 1997a, 1997b; Bucher et al. 2005; Goaillard et al. 2009; Tang et al. 2010) and in the undulatory swimming motor pattern in lampreys and similar aquatic species (Grillner 1974; Cohen et al. 1992; Williams 1992). Phase maintenance has also been examined within the crayfish swimmeret system (Skinner and Mulloney 1998; Jones et al. 2003; Mulloney and Smarandache-Wellmann 2012), the leech heart system (Wenning et al. 2004), and the motor pattern controlling gill ventilation in shore crabs (Dicaprio et al. 1997).
In this report, we document a case in which the phasing of a CPG rhythm is significantly variable. By itself, this result challenges our conventional understanding that CPG systems produce stable and precise oscillation patterns. In addition, we present modeling results that suggest that this variability in phasing can considerably influence network behavior. We therefore propose that the oscillation pattern produced by a neuronal network can vary substantially in certain systems and that this variation may cause networks to respond to perturbations differentially.
Comparison of the CG with other CPGs.
In many CPGs, each phase of the motor rhythm induces a phase of muscle contraction. Additionally, the phasing of muscle contractions must be strictly preserved in many of these systems to produce effective behaviors (e.g., Grillner 1974). The cardiac CPG is fundamentally different from these networks because the rhythm contains two classes of bursting neurons, only one of which induces a phase of muscle contraction. As a result, the relative phasing of the two neuron types can vary while motor neuron activity remains constant (see Fig. 1, C and D, or the model networks in Fig. 9). Thus, there may be no evolutionary advantage to maintaining the phasing of the CG through homeostatic mechanisms, as has been hypothesized for other CPG networks (Bucher et al. 2005). Previously published results have suggested that CPGs systems involved in stick insect locomotion (Fischer et al. 2001) and Aplysia feeding (Horn et al. 2004) may also exhibit variable phasing within and across preparations.
The CG model and its limitations.
We used well-studied Morris-Lecar equations to explore the dynamics of two heterogeneous oscillators coupled by excitatory and electrical coupling. The purpose of the model was to highlight the consequences of having variable phase relationships in a rhythmic network as well as to provide basic insights into how network phasing is determined in a network that resembles the CG. However, due to its simplicity and a lack of experimental data, the model was limited in making detailed predictions about the biological system.
Model networks were highly sensitive to the synaptic reversal potential (see Fig. 8), which has not been experimentally determined to our knowledge. It is possible that a more depolarized synaptic reversal potential is more relevant to the biological system, because the slow-wave oscillations appeared to peak around −30 mV (Tazaki and Cooke 1979c). The sensitivity of the model to the synaptic reversal potential does not, however, alter any of our major conclusions. As shown in Fig. 9, for instance, networks still responded differentially to silencing the chemical synapses, depending on their baseline phasing. Network phasing was also qualitatively similar when the synaptic reversal potential was altered or the chemical synapses were removed entirely (data not shown).
In most of the model networks, the intrinsic duty cycles of the oscillators were similar to their duty cycles within the coupled network. However, when LCs and SCs are synaptically isolated in the biological system, their duty cycles can change significantly; on average, the SC duty cycle increases, whereas the LC duty cycle decreases (Tazaki and Cooke 1983; García-Crescioni and Miller 2011). While the models do not always reproduce this behavior over the random parameter ranges we searched, our results provide insights into these experimental observations. Oscillators with disparate intrinsic duty cycles are drawn toward a compromise value through synaptic coupling (see Fig. 5A), especially with high levels of electrical coupling (see Fig. 6B). The model therefore predicts that the biological network requires strong electrical coupling to synchronize two oscillators with disparate intrinsic duty cycles. The observed experimental variability in network phasing likely results from either variability in the strength of electrical coupling between LCs and SCs or variability in the intrinsic duty cycles of LCs and SCs.
Ca2+ and K+ currents can be coregulated to preserve oscillator duty cycle and network phasing.
An important insight from the coupled oscillator model was that network phasing was strongly influenced by gCa/gK in the two oscillators (see Fig. 6B). Similarly, within an individual Morris-Lecar oscillator, gCa/gK strongly determined the intrinsic duty cycle (see Fig. 6A) and therefore strongly influenced the duty cycle of that oscillator within the coupled network (see Fig. 5A). Thus, the duty cycle of a Morris-Lecar oscillator can be largely preserved if gCa and gK are coregulated such that their ratio is maintained. Furthermore, network phasing can be specified by a set of correlations within the larger conductance space of the network model.
These results speak to the hypothesis that neurons coregulate the expression levels of different ion channels to define and maintain their electrophysiological phenotype (Marder and Goaillard 2006). Previous modeling studies have observed that covarying ionic maximal conductances in high-dimensional, conductance-based models can preserve certain characteristics of neural activity (Taylor et al. 2009; Ball et al. 2010; Franklin et al. 2010; Hudson and Prinz 2010). However, because it is difficult to gain intuition from these high-dimensional models, it useful to develop insights by coregulating conductances in low-dimensional models (Olypher and Prinz 2010). For example, the positive relationship between gCa/gK and the duty cycle of an isolated Morris-Lecar oscillator has a simple and intuitive explanation that may generalize to more complicated models and biological neurons: the greater the balance of inward to outward currents, the larger the duty cycle. In conjunction with this theoretical work, recent experiments have observed linear correlations in ion channel mRNA levels within the STG (Schulz et al. 2006, 2007; Goaillard et al. 2009) and the CG (Tobin et al. 2009). However, these experimentally observed correlations do not match the correlations produced by modeling studies (Taylor et al. 2009), suggesting that a deeper understanding of ion channel regulation is necessary to understand how correlations between ionic currents arise in biological systems.
Electrically coupled Morris-Lecar oscillators generically synchronize at burst onset.
A striking feature of our experimental data is that the LC and SC burst onsets are nearly simultaneous both within and across preparations (see Figs. 1, E and F, and 2, A and B). The LC start phase of the lobster CG rhythm is, on average, less variable than all phases of the pyloric rhythm of the crab (data not shown and Goaillard et al. 2009). One could interpret this result as suggesting that the synchronous onset of SCs and LCs is functionally important to the system and that the network is tightly tuned to maintain this behavior.
However, when we randomly varied the parameters of the model networks, the burst onsets almost always occurred in rapid succession, whereas the phasing of the burst offsets was more variable. This suggests an alternative explanation: intrinsic neuronal properties may predispose SC and LC bursts to align at their onsets but permit them to have variable burst offset phases. This implies that the Morris-Lecar oscillators, in the moments before burst onset, are hovering very close to threshold. When one oscillator activates, it immediately pushes the other oscillator above threshold. Conversely, the oscillators are less sensitive to synaptic input immediately before the burst offset. This intuition is consistent with a more rigorous mathematical analysis, which shows that a Morris-Lecar oscillator with “type I” membrane excitability is least sensitive to synaptic input near its peak voltage value and most sensitive towards its minimum voltage (Ermentrout 1996).
Variability in the phasing of the CG rhythm may account for variability in how the system responds to neuromodulators.
Electrophysiological studies of CPG behavior often characterize the changes in CPG output that result from experimental perturbations, such as the application of neuromodulator or the introduction of a neurotoxin. These perturbations usually produce similar effects in most preparations (Grashow et al. 2009). However, in other cases, the same experimental perturbation produces qualitatively different effects in different preparations. For example, the perfusion of the neuropeptide C-type allatostatin through the lobster heart increases the strength of heart contractions in some preparations but decreases contraction force in other preparations (Wiwatpanit et al. 2012). Additionally, in spiny lobsters, bath application of serotonin to the STG can cause either an increase or decrease in cycle frequency, depending on the balance of serotonin receptors that are expressed in the preparation (Spitzer et al. 2008).These observations can be difficult to understand, especially in cases where the majority of preparations respond in a particular way and only a small subset of preparations are anomalous (Grashow et al. 2009). As a result, variability in the responses of CPGs to neuromodulatory input is still poorly understood.
In the population of CG models, we observed variable responses to the perturbation of scaling the strengths of the excitatory chemical synapses. Silencing the chemical synapses decreased cycle frequency in networks composed of oscillators with similar duty cycles but increased cycle frequency in networks composed of oscillators with disparate duty cycles. In addition, silencing the chemical synapses decreased the duty cycle difference in networks with initially disparate duty cycles but did not significantly affect the phasing of networks with initially similar duty cycles. Thus, the variability in the baseline phasing of the networks strongly influenced how the networks responded to these perturbations.
These results are reminiscent of previous experimental studies that demonstrated that the baseline frequency of a rhythmic motor pattern may affect how the pattern responds to perturbation. For example, in the stomatogastric nervous system of spiny lobsters, the anterior pyloric modulator neuron increases the cycle frequency of the pyloric rhythm in networks that cycle slowly but does not significantly affect cycle frequency in networks with a faster baseline rhythm (Nagy and Dickinson 1983). Other studies of the STG have reported similar findings for different neuromodulators (Nusbaum and Marder 1989; Skiebe and Schneider 1994; Fu et al. 2007; Ma et al. 2009). Our results predict that network phasing may also influence how CPGs respond to modulatory input or to other experimental perturbations. More generally, our analysis illustrates how relatively subtle deviations in network activity across preparations can have important experimental consequences and how these consequences might be accounted for by simple and easily understandable models of neuronal oscillators.
GRANTS
This work was supported by a grant from the Arnold and Mabel Beckman Foundation, National Science Foundation Awards 1121973 and 0832788, and National Institutes of Health Grants 5-P20-RR-016463-12, 8-P20-GM-103423-12, and R01-MH-46742-22.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
Author contributions: A.H.W., E.M., and P.S.D. conception and design of research; A.H.W., M.A.K., and A.L.M. performed experiments; A.H.W., M.A.K., and A.L.M. analyzed data; A.H.W., E.M., M.L.Z., and P.S.D. interpreted results of experiments; A.H.W. prepared figures; A.H.W. and P.S.D. drafted manuscript; A.H.W., E.M., M.L.Z., and P.S.D. edited and revised manuscript; A.H.W., M.A.K., A.L.M., E.M., M.L.Z., and P.S.D. approved final version of manuscript.
ACKNOWLEDGMENTS
The authors thank Olaf Ellers, Tim O'Leary, and Jon Caplan for comments on the manuscript.
Present address of M. A. Kwiatkowski: Center for Women's Mental Health, Massachusetts General Hospital, Simches Research Bldg., 185 Cambridge St., Suite 2200, Boston, MA 02114.
REFERENCES
- Amendola J, Woodhouse A, Martin-Eauclaire MF, Goaillard JM. Ca2+/cAMP-sensitive covariation of IA and IH voltage dependences tunes rebound firing in dopaminergic neurons. J Neurosci 32: 2166–2181, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ball JM, Franklin CC, Tobin AE, Schulz DJ, Nair SS. Coregulation of ion channel conductances preserves output in a computational model of a crustacean cardiac motor neuron. J Neurosci 30: 8637–8649, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P. Journal of Statistical Software. CircStat: a Matlab Toolbox for Circular Statistics (online). http://www.jstatsoft.org/v31/i10 [7 March 2013].
- Berlind A. Heterogeneity of motorneuron driver potential properties along the anterior-posterior axis of the lobster cardiac ganglion. Brain Res 609: 51–58, 1993 [DOI] [PubMed] [Google Scholar]
- Bucher D, Prinz AA, Marder E. Animal-to-animal variability in motor pattern production in adults and during growth. J Neurosci 25: 1611–1619, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calabrese RL, Norris BJ, Wenning A, Wright TM. Coping with variability in small neuronal networks. Integr Comp Biol 51: 845–855, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen AH, Ermentrout GB, Kiemel T, Kopell N, Sigvardt KA, Williams TL. Modelling of intersegmental coordination in the lamprey central pattern generator for locomotion. Trends Neurosci 15: 434–438, 1992 [DOI] [PubMed] [Google Scholar]
- Cooke IM. Reliable, responsive pacemaking and pattern generation with minimal cell numbers: the crustacean cardiac ganglion. Biol Bull 202: 108–136, 2002 [DOI] [PubMed] [Google Scholar]
- Davis GW. Homeostatic control of neural activity: from phenomenology to molecular design. Annu Rev Neurosci 29: 307–323, 2006 [DOI] [PubMed] [Google Scholar]
- Dayan P, Abbott LF. Theoretical Neuroscience. Cambridge, MA: Massachusetts Institute of Technology Press, 2001 [Google Scholar]
- Dicaprio R, Jordan G, Hampton T. Maintenance of motor pattern phase relationships in the ventilatory system of the crab. J Exp Biol 200: 963–974, 1997 [DOI] [PubMed] [Google Scholar]
- Ermentrout B. Type I membranes, phase resetting curves, and synchrony. Neural Comput 8: 979–1001, 1996 [DOI] [PubMed] [Google Scholar]
- Fischer H, Schmidt J, Haas R, Büschges A. Pattern generation for walking and searching movements of a stick insect leg. I. Coordination of motor activity. J Neurophysiol 85: 341–353, 2001 [DOI] [PubMed] [Google Scholar]
- Franklin CC, Ball JM, Schulz DJ, Nair SS. Generation and preservation of the slow underlying membrane potential oscillation in model bursting neurons. J Neurophysiol 104: 1589–1602, 2010 [DOI] [PubMed] [Google Scholar]
- Fu Q, Tang LS, Marder E, Li L. Mass spectrometric characterization and physiological actions of VPNDWAHFRGSWamide, a novel B type allatostatin in the crab, Cancer borealis. J Neurochem 101: 1099–1107, 2007 [DOI] [PubMed] [Google Scholar]
- García-Crescioni K, Miller MW. Revisiting the reticulum: feedforward and feedback contributions to motor program parameters in the crab cardiac ganglion microcircuit. J Neurophysiol 106: 2065–2077, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goaillard JM, Taylor AL, Schulz DJ, Marder E. Functional consequences of animal-to-animal variation in circuit parameters. Nat Neurosci 12: 1424–1430, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman M, Golowasch J, Marder E, Abbott L. Global structure, robustness, and modulation of neuronal models. J Neurosci 21: 5229–5238, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Abbott LF, Marder E. Activity-dependent regulation of potassium currents in an identified neuron of the stomatogastric ganglion of the crab Cancer borealis. J Neurosci 19: RC33, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grashow R, Brookings T, Marder E. Reliable neuromodulation from circuits with variable underlying structure. Proc Natl Acad Sci USA 106: 11742–11746, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grillner S. On the generation of locomotion in the spinal dogfish. Exp Brain Res 20: 459–470, 1974 [DOI] [PubMed] [Google Scholar]
- Hooper SL. Phase maintenance in the pyloric pattern of the lobster (Panulirus interruptus) stomatogastric ganglion. J Comput Neurosci 4: 191–205, 1997a [DOI] [PubMed] [Google Scholar]
- Hooper SL. The pyloric pattern of the lobster (Panulirus interruptus) stomatogastric ganglion comprises two phase-maintaining subsets. J Comput Neurosci 4: 207–219, 1997b [DOI] [PubMed] [Google Scholar]
- Horn CC, Zhurov Y, Orekhova IV, Proekt A, Kupfermann I, Weiss KR, Brezina V. Cycle-to-cycle variability of neuromuscular activity in Aplysia feeding behavior. J Neurophysiol 92: 157–180, 2004 [DOI] [PubMed] [Google Scholar]
- Hudson AE, Prinz AA. Conductance ratios and cellular identity. PLoS Comput Biol 6: e1000838, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones SR, Mulloney B, Kaper TJ, Kopell N. Coordination of cellular pattern-generating circuits that control limb movements: the sources of stable differences in intersegmental phases. J Neurosci 23: 3457–3468, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma M, Szabo T, Jia C, Marder E, Li L. Mass spectrometric characterization and physiological actions of novel crustacean C-type allatostatins. Peptides 30: 1660–1668, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, Goaillard JM. Variability, compensation and homeostasis in neuron and network function. Nat Rev Neurosci 7: 563–574, 2006 [DOI] [PubMed] [Google Scholar]
- Marder E, Taylor AL. Multiple models to capture the variability in biological neurons and networks. Nat Neurosci 14: 133–138, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E. Variability, compensation, and modulation in neurons and circuits. Proc Natl Acad Sci USA Suppl 108: 15542–15548, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morganelli PM, Sherman RG. Nerve terminals and synapses in the cardiac ganglion of the adult lobster Homarus americanus. J Morphol 191: 177–191, 1987 [DOI] [PubMed] [Google Scholar]
- Morris C, Lecar H. Voltage oscillations in the barnacle giant muscle fiber. Biophys J 35: 193–213, 1981 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulloney B, Smarandache-Wellmann C. Neurobiology of the crustacean swimmeret system. Prog Neurobiol 96: 242–267, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagy F, Dickinson PS. Control of a central pattern generator by an identified modulatory interneurone in crustacea. I. Modulation of the pyloric motor output. J Exp Biol 105: 33–58, 1983 [DOI] [PubMed] [Google Scholar]
- Nusbaum M, Marder E. A modulatory proctolin-containing neuron (MPN). II. State-dependent modulation of rhythmic motor activity. J Neurosci 9: 1600–1607, 1989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olypher AV, Prinz A. Geometry and dynamics of activity-dependent homeostatic regulation in neurons. J Comput Neurosci 28: 361–374, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz AA, Billimoria CP, Marder E. Alternative to hand-tuning conductance-based models: construction and analysis of databases of model neurons. J Neurophysiol 90: 3998–4015, 2003 [DOI] [PubMed] [Google Scholar]
- Prinz AA, Bucher D, Marder E. Similar network activity from disparate circuit parameters. Nat Neurosci 7: 1345–1352, 2004 [DOI] [PubMed] [Google Scholar]
- Roffman RC, Norris BJ, Calabrese RL. Animal-to-animal variability of connection strength in the leech heartbeat central pattern generator. J Neurophysiol 107: 1681–1693, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schulz DJ, Goaillard JM, Marder E. Variable channel expression in identified single and electrically coupled neurons in different animals. Nat Neurosci 9: 356–362, 2006 [DOI] [PubMed] [Google Scholar]
- Schulz DJ, Goaillard JM, Marder EE. Quantitative expression profiling of identified neurons reveals cell-specific constraints on highly variable levels of gene expression. Proc Natl Acad Sci USA 104: 13187–13191, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skiebe P, Schneider H. Allatostatin peptides in the crab stomatogastric nervous system: inhibition of the pyloric motor pattern and distribution of allatostatin-like immunoreactivity. J Exp Biol 194: 195–208, 1994 [DOI] [PubMed] [Google Scholar]
- Skinner FK, Mulloney B. Intersegmental coordination of limb movements during locomotion: mathematical models predict circuits that drive swimmeret beating. J Neurosci 18: 3831–3842, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skinner FK, Turrigiano GG, Marder E. Frequency and burst duration in oscillating neurons and two-cell networks. Biol Cybern 69: 375–383, 1993 [PubMed] [Google Scholar]
- Spitzer N, Cymbalyuk G, Zhang H, Edwards DH, Baro DJ. Serotonin transduction cascades mediate variable changes in pyloric network cycle frequency in response to the same modulatory challenge. J Neurophysiol 99: 2844–2863, 2008 [DOI] [PubMed] [Google Scholar]
- Stevens JS, Cashman CR, Smith CM, Beale KM, Towle DW, Christie AE, Dickinson PS. The peptide hormone pQDLDHVFLRFamide (crustacean myosuppressin) modulates the Homarus americanus cardiac neuromuscular system at multiple sites. J Exp Biol 212: 3961–3976, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swensen AM, Bean BP. Robustness of burst firing in dissociated Purkinje neurons with acute or long-term reductions in sodium conductance. J Neurosci 25: 3509–3520, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang LS, Goeritz ML, Caplan JS, Taylor AL, Fisek M, Marder E. Precise temperature compensation of phase in a rhythmic motor pattern. PLoS Biol 8: e1000469, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor AL, Goaillard JM, Marder E. How multiple conductances determine electrophysiological properties in a multicompartment model. J Neurosci 29: 5573–5586, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tazaki K, Cooke IM. Ionic bases of slow, depolarizing responses of cardiac ganglion neurons in the crab, Portunus sanguinolentus. J Neurophysiol 42: 1022–1047, 1979a [DOI] [PubMed] [Google Scholar]
- Tazaki K, Cooke IM. Spontaneous electrical activity and interaction of large and small cells in cardiac ganglion of the crab, Portunus sanguinolentus. J Neurophysiol 42: 975–999, 1979b [DOI] [PubMed] [Google Scholar]
- Tazaki K, Cooke IM. Isolation and characterization of slow, depolarizing responses of cardiac ganglion neurons in the crab, Portunus sanguinolentus. J Neurophysiol 42: 1000–1021, 1979c [DOI] [PubMed] [Google Scholar]
- Tazaki K, Cooke IM. Separation of neuronal sites of driver potential and impulse generation by ligaturing in the cardiac ganglion of the lobster, Homarus americanus. J Comp Physiol A 151: 329–346, 1983 [Google Scholar]
- Tazaki K, Cooke IM. Characterization of Ca current underlying burst formation in lobster cardiac ganglion motorneurons. J Neurophysiol 63: 370–384, 1990 [DOI] [PubMed] [Google Scholar]
- Tobin AE, Cruz-Bermúdez ND, Marder E, Schulz DJ. Correlations in ion channel mRNA in rhythmically active neurons. PloS One 4: e6742, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wenning A, Hill AA, Calabrese RL. Heartbeat control in leeches. II. Fictive motor pattern. J Neurophysiol 91: 397–409, 2004 [DOI] [PubMed] [Google Scholar]
- Williams TL. Phase coupling by synaptic spread in chains of coupled neuronal oscillators. Science 258: 662–665, 1992 [DOI] [PubMed] [Google Scholar]
- Wiwatpanit T, Powers B, Dickinson PS. Inter-animal variability in the effects of C-type allatostatin on the cardiac neuromuscular system in the lobster Homarus americanus. J Exp Biol 215: 2308–2318, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zar J. Biostatistical Analysis( 5th ed.). Upper Saddle River, NJ: Pearson Education, 2010 [Google Scholar]