Facet-Dependent Catalytic Activity of Platinum Nanocrystals for Triiodide Reduction in Dye-Sensitized Solar Cells

Abstract

Platinum (Pt) nanocrystals have demonstrated to be an effective catalyst in many heterogeneous catalytic processes. However, pioneer facets with highest activity have been reported differently for various reaction systems. Although Pt has been the most important counter electrode material for dye-sensitized solar cells (DSCs), suitable atomic arrangement on the exposed crystal facet of Pt for triiodide reduction is still inexplicable. Using density functional theory, we have investigated the catalytic reaction processes of triiodide reduction over {100}, {111} and {411} facets, indicating that the activity follows the order of Pt(111) > Pt(411) > Pt(100). Further, Pt nanocrystals mainly bounded by {100}, {111} and {411} facets were synthesized and used as counter electrode materials for DSCs. The highest photovoltaic conversion efficiency of Pt(111) in DSCs confirms the predictions of the theoretical study. These findings have deepened the understanding of the mechanism of triiodide reduction at Pt surfaces and further screened the best facet for DSCs successfully.

Dye-sensitized solar cells (DSCs)¹,²,³,⁴,⁵,⁶, based on sensitizer dye adsorbed nanocrystalline TiO₂ anode, an electrolyte solution containing a redox couple (I₃⁻/I⁻) and platinum (Pt) coated counter electrode (CE) show great promise as an alternative to conventional p-n junction solar cells because of their superior light harvesting efficiency, low cost and ease of fabrication. As an important component in DSCs, the CE usually utilizes a fluorine-doped tin oxide (FTO) glass coated with a thin layer of Pt⁷,⁸,⁹,¹⁰ to catalyze the triiodide (I₃⁻) reduction at the counter electrode/electrolyte interface. Although a number of other materials such as carbon¹¹,¹²,¹³,¹⁴, conductive polymer¹⁵,¹⁶,¹⁷, and some inorganic compounds¹⁸,¹⁹,²⁰,²¹,²² have been investigated as inexpensive alternatives, Pt is still the primary material because of its superior chemical and electrochemical stabilities and extremely high catalytic activity for I₃⁻ reduction.

The performance of Pt nanoparticles in various heterogeneous catalytic processes have been found to be highly dependent on the exposed facets²³, which determines the surface atomic arrangement and coordination. For instance, {111} faceted Pt nanotetrahedrons have been shown to exhibit higher catalytic activity compared to spherical particles²⁴, and typically the catalytic activity can be enhanced with high-index facets that are rich in stepped and dangling atoms²⁵,²⁶,²⁷,²⁸. Pt nanocrystals with various facets have shown diverse pioneer catalytic activities in different reaction processes. For example, El-Sayed and coworker observed that in the case of the electron transfer reaction between [Fe(CN)₆]³⁻ and S₂O₃²⁻, Pt nanocubes bounded only by {100} facets exhibit higher catalytic activity than Pt tetrahedrons enclosed by {111} facets²⁴,²⁹,³⁰, and while the star-like nanocrystals contained high-index facets such as {311} could reduce the activation energy of the reaction by 1.6 times compared to the tetrahedral nanocrystals³¹. Otherwise, little difference in the catalytic activity was found for the Suzuki coupling reaction regarding different shapes Pt nanocrystals³². For methanol electro-oxidation, the {100}-facet-enclosed Pt-Pd nanocubes demonstrate a higher activity when compares to {111}-facet-enclosed Pt-Pd nanotetrahedrons. However, to the best of our knowledge, the suitable facet of Pt nanocrystals with highest catalytic activity for I₃⁻ reduction in DSCs has not been reported in the literature, although there are some reports on the relationship between nano Pt crystallinity and the catalytic activity in DSCs³³. Commonly, Pt nanoparticles coated on FTO as CEs in DSCs via thermal decomposition, electrodeposition or sputtering are ill-defined mixtures of surface species, which also hamper the understanding of the catalytic phenomena and the catalytic mechanism of I₃⁻ reduction at Pt electrode³⁴,³⁵,³⁶. Hence, in order to enhance catalytic performance while minimizing the use of precious metal Pt, it is worthwhile to find the best suitable facet. Herein, we show that quantum chemical calculations combined with the synthesis of Pt nanocrystals with various well-defined crystal shapes can be used to study the catalytic mechanism of I₃⁻ reduction at Pt electrode and screen the best facet with higher catalytic activity for I₃⁻ reduction.

Results

Theoretical calculation

As the first step, the catalytic activity of I₃⁻ reduction over three common characteristic surface structures of Pt nanoparticles, containing the most stable close-packed {111}, open-packed {100} facets and a typical high-index facet, the stepped {411} facet, was investigated by means of density functional theory (DFT) calculations. The overall I₃⁻ reduction reaction on the CE can be written as: I₃⁻(sol) +2e⁻ → 3I⁻(sol). The general consensus of the I₃⁻ reduction mechanism can be described as:

where * represents the free site on the electrode surface and sol indicates the acetonitrile solution phase. The solution phase reaction step (1) has been verified to be usually fast and considered to be in equilibrium³⁷. Accordingly, one can see that the overall catalytic activity would be determined by the molecular iodine reduction reaction (IRR: I₂(sol) +2e⁻ → 2I⁻(sol)) occurring at the liquid-solid interface, i.e. steps (2) and (3). Hence we focused our studies on these two elementary reaction steps at the liquid-solid interface to explore the facet-dependent activity trend for different surfaces of Pt.

We firstly apply the previously verified thermodynamics model³⁸,³⁹ to estimate the catalytic activity, demanding that the Gibbs free energy of a multistep reaction system should decrease step by step. Regarding IRR, the total Gibbs free energy change (ΔG₀ = 2μ_Ι⁻_(sol) − μ_I2(sol) − 2μ_e) provides the thermodynamic driving force, and would achieve maximum energy as the electrode voltage U determining the electronic chemical potential μ_e (μ_e = eU) is the most negative (U = U_VBM^TiO2 − U_SHE, ~ −0.06 V vs SHE, see SI for details). We have demonstrated in our previous work that under this condition, the adsorption energy of I atom (E_ad^I) at the CH₃CN/electrode interface, serving as a good descriptor for the iodine reduction activity, should usually range from around 0.33 to 1.20 eV for good catalysts³⁹. When E_ad^I is large, the overall activity is limited by I removal to form I⁻(sol); while E_ad^I is small, I₂ molecular dissociation is hindered. Based on the DFT calculation, Pt(111) possesses a E_ad^I of 0.52 eV at the CH₃CN/Pt(111) interface, being within this range and thus accounting for the high catalytic activity of Pt catalyst. However, on Pt(411) and Pt(100) with a low-coordinate surface atom exposed, the adsorption energies of I atom at the corresponding interface are largely enhanced, being 1.38 eV and 1.56 eV, respectively. These two E_ad^I on Pt(411) and Pt(100) are beyond the suitable range and their catalytic activities may therefore be speculated to be less active.

To further demonstrate the activity trend of different Pt surfaces and establish the structure-activity relationship, a full reaction energetic involving thermodynamics and kinetic are considered in the DFT framework. Herein, three large surfaces (p(4×4) Pt(111), p(4×4) Pt(100) and p(1×4) Pt(411)) with several CH₃CN molecule layers introduced above them at a desity of 0.79 g/cm³ were constructed to simulate the interface, respectively. All the spin-polarized density functional theory (DFT) calculations were performed with Perdew-Burke-Ernzerhof (PBE) functional within the generalized gradient approximation (see details in SI).

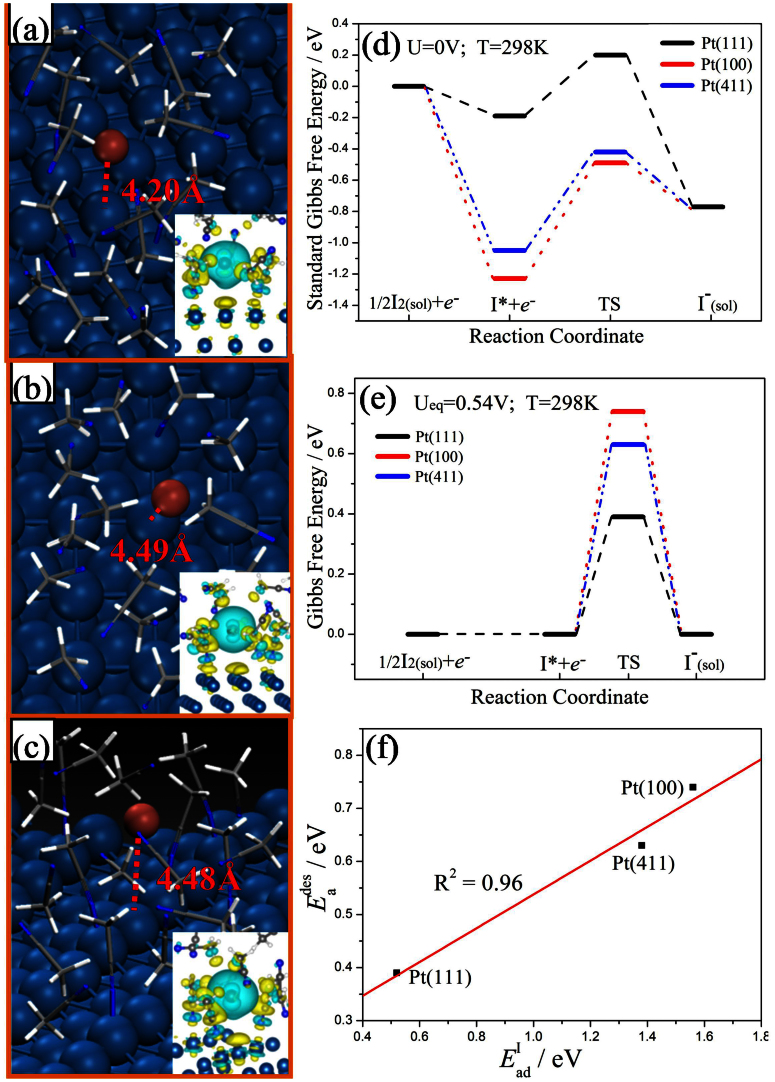
Upon adsorption at these three CH₃CN/electrode interfaces, it is found that the iodine molecule can readily dissociate into two I* atoms without an obvious dissociation barrier (E_a^dis), resulting in I* sitting preferably on the top of Pt atom at a distance (d_(Pt-I)) of ~2.6 Å (see Figure S1). The adsorption energies of I atom were calculated to be 0.52, 1.38 and 1.56 eV at the interfaces of CH₃CN/Pt(111), CH₃CN/Pt(411) and CH₃CN/Pt(100), respectively, as reported above. The adsorbed iodine atom (I*) can receive one electron and then desorb into solution in the form of I⁻. The structures of transition states (TSs) with a much elongated d_(Pt-I) are showed in Figure 1a–c, from which we can see that d_(Pt-I) are 4.20 Å, 4.48 Å, 4.49 Å for Pt (111), (411) and (100) surface respectively, and I* is surrounded by CH₃CN molecules with H atoms in methyl pointing to I*. The corresponding I* desorption barrier (E_a^des) were calculated to be 0.39, 0.63 and 0.74 eV, respectively. The charge density differences are illustrated to show the bond properties between I and the surface Pt atom in forming TS, as inserted in Figure 1a–c. On these investigated surfaces, it is found that the electrons accumulate at I atom resulting from the electron depletion at the surface Pt atom and the surface adsorbed CH₃CN molecules. Interestingly, there is no orbital overlap between the p-orbital of ion-like I and d-orbital of surface Pt atom, indicating a typical ionic bond of Pt-I. Bader charge analyses show that I* at TS is charged with 0.55, 0.64 and 0.63 e at CH₃CN/Pt(111), Pt(100) and Pt(411) interfaces, respectively.

Figure 1. Transition state structures at CH₃CN/Pt(111), CH₃CN/Pt (100), and CH₃CN/Pt(411) interfaces, respectively, as well as Energy profiles of the whole counter electrode reaction.

(a), transition state structure on Pt(111) surface in the presence of CH₃CN solvent. Inserts: charge density difference map of TS, and light-blue color represents for electron accumulation while yellow for electron depletion. (b–c) are for the Pt(100) and Pt(411) surface, similar with (a). (d), Standard Gibbs free energy profiles of IRR on Pt(111), Pt(100), Pt(411), respectively. (e), Gibbs free energy profiles of IRR on Pt(111), Pt(100), Pt(411), respectively, under the I₃⁻/I⁻ equilibrium voltage of 0.54 V. (f), the linear relationship between I* desorption barrier (E_a^des) and adsorption energy (E_ad^I).

Figure 1d and Figure 1e show the reaction energy profile of IRR on the three surfaces. For the Standard Gibbs free energy profiles in Figure 1d, we set U = 0 V vs SHE to remove the effect of electrode voltage on electron potential, providing almost the largest thermodynamic driving force. From these profiles, one can see that the iodine atom adsorbs on Pt(100) and Pt(411) so strongly that it is difficult to desorb (the barriers as high as 0.74 and 0.63 eV, respectively). By comparison, the adsorption energy of iodine atom on Pt(111) is relative low, being 0.52 eV, and the corresponding desorption barrier is as low as 0.39 eV. A more straightforward approach is to compare free energy profile under the equilibrium voltage condition, as shown in Figure 1e. Under the equilibrium voltage (0.54 V) of I₃⁻/I⁻ redox couple, the free energy change of IRR reaches zero. Then, considering that iodine molecule can readily dissociate on all three surfaces, it is reasonable to suggest that the dissociation of I₂ molecule is very fast and could be approximately considered in equilibrium. Therefore, the overall activity is determined by the desorption barrier of I atom. From Figure 1e, we can predict that the effective barrier of IRR for the three surface follows in the order of Pt(111) < Pt(411) < Pt(100), meaning that the I₃⁻ reduction activity follows the same order as Pt(111) > Pt(411) > Pt(100).

It is worth to further elucidate the desorption barrier of I atom. The results demonstrated that there is a linear relationship between E_a^des and E_ad^I, as shown in Figure 1f; the bigger E_ad^I is, the higher E_a^des would be. In addition, the effect of electrode voltage on desorption barrier was considered approximately, which shows that as the electrode voltage is increased, E_a^des increases slightly on all three models investigated, corresponding to small transfer coefficients (see Figure S3 and details in SI).

Experimental validation

On the basis of the theoretical studies, a Pt catalyst for CE in DSCs should preferentially possess the exposed {111} facets and avoid {100} facets or {411} facets. Three well-defined Pt nanocrystals, Pt truncated nanooctahedrons, Pt nanocubes, and Pt nanooctapods were therefore fabricated with preferentially exposed {111}, {100} and {411} facets. The detailed synthesis of different faceted Pt nanocrytals²⁸,⁴⁰,⁴¹,⁴² is described in the Supporting Information. The morphology and crystallinity of the as-prepared Pt nanocrystals were analyzed using transmission electron microscopy (TEM), high-resolution TEM (HRTEM) and X-ray diffraction (XRD) (SI, Figure S5). A TEM image for Pt truncated nanooctahedrons is shown in Figure 2a and Figure 2d. From Figure 2d, it can be seen that the truncated nanooctahedron is mainly bounded by {111} facets. The average edge lengths were about 7 nm for these truncated octahedral nanocrystals. The corresponding d-spacings for the (111) facets were found to be 0.224 nm (Figure 2d), which was consistent with the XRD result (SI, Figure S5). Figure 2b illustrates a TEM image of Pt nanocubes monolayer assembly. The average side length of these selected nanocubes was measured as about 10 nm. An HRTEM images of a selected Pt nanocube (Figure 2e) reveals a highly crystalline cube with clearly resolved lattice fringes having a {200}-d-spacing of about 0.19 nm (SI, Figure S5). These two nanocrystals prepared via the same method were measured in details in the literature⁴². A TEM image of the third Pt nanocrystal with high-index facets is shown in Figure 2c. According to the Zheng's model²⁸, the Pt octapod nanocrystal has eight trigonal-pyramidal arms and 24 identical kite-shaped {411} facets. The as-prepared Pt nanocrystals have an average apex-to-apex diameter of about 70 nm, and every arm has a length of about 20 nm. When octapod crystals were oriented along the [110] zone axis, the (411) facets were driven parallel to the TEM beam, allowing the direct observation of the atomic arrangement by HRTEM. As illustrated in Figure 2f, the ([2n − 1], 1, 1) steps made of subfacets of (111) and (100) planes can be observed in the (411) facet oriented in the [110] direction, matching the Zheng's model. Based on the above analysis, Pt truncated nanooctahedrons, Pt nanocubes, and Pt nanooctapods offer crystallographically and obvious distinct facets. The performances of the three facets bounded nanocrystals on I₃⁻ reduction and resultant photovoltaic conversion efficiency of DSCs were characterized in the following parts.

Figure 2. Representative morphologies and structures of three types Pt nanocrystals.

Respectively with single kind of facets in TEM (a–c) and HRTEM (d–f) images: (a,d) Pt(111), (b,e) Pt(100), (c,f) Pt(411).

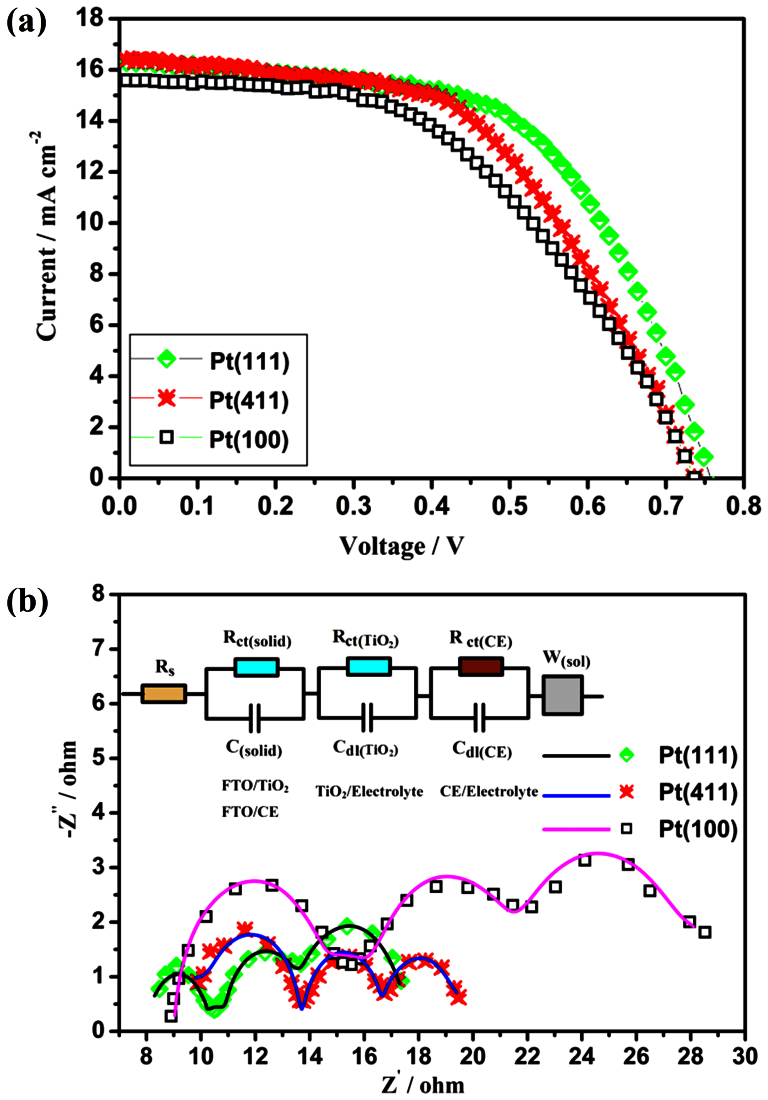
Figure 3 shows the photocurrent-voltage (J–V) curves and Nyquist plots of electrochemical impedance spectra (EIS) of three DSCs fabricated with Pt(111), Pt(100), and Pt(411) CEs. The detailed photovoltaic parameters from the J–V curves are summarized in Table 1. It was found that DSC equipped with Pt(111) yields energy conversion efficiency (η) of 6.91%, which is superior to that of the DSCs with a Pt(411) CE (6.46%), and Pt(100) CE (5.66%). These interesting results demonstrate that the {111} facets surely possess an excellent catalytic activity toward I₃⁻ reduction, in well agreement with the DFT predictions. To reveal the electrochemical characteristics of the Pt(111), Pt(100) and Pt(411) electrodes, EIS experiments of the DSCs with the three types Pt CEs were carried out at 20°C, and the results are shown in Figure 3b. The semicircle in the high frequency region (the left one) arises from the parallel connection of coupling between the Helmholtz capacity and the charge-transfer resistance of Pt electrode (the width of the first arc in Figure 3b), while the response in the intermediate-frequency region is associated with the TiO₂ film (the anode)⁴³,⁴⁴,⁴⁵. The low-frequency region reflects the diffusion in the electrolyte, which is well described by a Nernst diffusion impedance Z_N³⁷,⁴³,⁴⁴,⁴⁵,⁴⁶. Using Fick's law and appropriate boundary conditions Z_N becomes

where ω is the angular frequency and α equals to 0.5 for a finite length Warburg impedance (FLW). W and τ_d are respectively the Warburg parameter and characteristic diffusion time constant, which can be expressed by

where R is the molar gas constant, T the absolute temperature, c₀ the bulk concentration of I₃⁻, A the electrode surface area, F the Faraday constant, n the number of electrons involved in the electrochemical reaction, D the diffusion coefficient of I₃⁻ species and d the diffusion length, which is taken as half of the distance between the electrodes (l).³⁷,⁴³,⁴⁵,⁴⁶. Fitting Z_N, the diffusion coefficient D can be determined from the value of W, which has been given in Table S2. The EIS parameters were determined by fitting the impedance spectra using the ZSimpWin software via the circuit model inserted in Figure 3b⁴⁴, and a good agreement between the measured and the fitted data was achieved for all cases.

Figure 3. Photocurrent-voltage (I–V) curves (a) and electrochemical impedance spectra (b) of DSCs fabricated with the three types Pt nanocrystals as counter electrodes, where the lines express fit results for corresponding EIS data, and the insert gives the equivalent circuit.

R_s: series resistance; R_ct(solid): charge-transfer resistance of TiO₂-FTO or Pt-FTO interface; C_(solid): capacitance of TiO₂-FTO or Pt-FTO interface; R_ct(TiO2): charge-transfer resistance of dye-sensitized TiO₂ layer; C_dl(TiO2): double layer capacitance of dye-sensitized TiO₂/electrolyte interface; R_ct(Pt): charge-transfer resistance at the CE/electrolyte interface; C_dl(Pt): double layer capacitance of CEs; W_(sol): Warburg parameter describing the diffusion of I₃⁻ in the electrolyte.

Table 1. Photovoltaic performance of the DSCs with different Pt facets CEs[a] and EIS parameters of the same DSCs[b].

Samples	Jsc/mA cm−2	Voc/mV	FF	η/%	Rs/Ω	W(sol)/Ω	Cdl(Pt)/μF	Rct(Pt)/Ω	Rsct(Pt)/Ω cm2
Pt (111)	16.29	757	0.58	6.91	8.21	2.99	2.03	2.32	1.31
Pt (411)	16.41	737	0.53	6.46	9.84	3.83	2.72	3.01	2.42
Pt (100)	15.59	736	0.49	5.66	9.13	6.86	3.21	6.24	8.74

[a] J_sc: short-circuit current density; V_oc: open-circuit voltage; FF: fill factor; η: energy conversion efficiency.

[b] For spectra, see Figure 3(b). R_s: series resistance; R_ct(Pt): charge-transfer resistance at the CE/electrolyte interface; C_dl(Pt): double layer capacitance of CEs; W_(sol): Warburg parameter; R^s_ct(Pt): R_ct(Pt) normalized by the active surface area of the three Pt counter electrodes.

Since the prime concern of this study is to compare the catalytic activity of the CEs, we have avoided the anode. The high-frequency intercept on the real axis represents the series resistance (R_s), which is mainly composed of the bulk resistance of CEs materials, resistance of FTO glass substrate, contact resistance, etc, and hence the low value of R_s is beneficial to the performance of DSCs. Charge transfer resistance (R_ct(Pt)) is a measure of the ease of electron exchange between the Pt electrode and the redox species in the electrolyte and thus varies inversely with the I₃⁻ reduction activity of the CEs²¹,⁴⁷. It is directly proportional to the diameter of the left semicircle that appears in Nyquist plots. C_dl(pt) stands for double layer capacitance which develops at the Pt electrode/electrolyte interface due to the accumulation of ions at the electrode surface and could qualitatively represent real surface areas of the electrodes. Warburg parameter (W_(sol)) shows the Nernst diffusion of I₃⁻ in electrolyte, which is proportional to the width of the third arc in Figure 3b⁴⁵. In Table 1, the R_ct(Pt) of Pt(111) is 2.32 Ω, significantly smaller than that of Pt(411) (3.01 Ω) and Pt(100) (6.24 Ω), which means that the {111} facets of Pt have a higher catalytic activity toward I₃⁻ reduction than that of the high-index {411} facets, while the {100} facets are less effective in catalyzing the I₃⁻ reduction. In order to eliminate the influence of active surface area on electrocatalytic activity of the samples, the active surface areas were determined from the hydrogen adsorption-desorption charges⁴⁸,⁴⁹,⁵⁰. The Pt(111), Pt(411) and Pt(100) electrodes (0.36 cm²) respectively own the real total surface area of about 0.565, 0.804, and 1.401 cm² (Table S3 in SI). R_ct(Pt) was normalized by the active surface area, as R^s_ct(Pt) which reflects the material's intrinsic catalytic performance. From the results in Table 1, variation trend of R^s_ct(Pt) is in accordance with that of R_ct(Pt), which ensures that the variation in electrocatalytic activity of the samples is related with the change in crystal facet of Pt. In order to eliminate the influence of Pt loading amount on the electrocatalytic activity of the three sample, the charge-transfer resistance at the CE/electrolyte interface R_ct(Pt) was also normalized by the actual masses used in Pt CEs, as R^m_ct(Pt) which reflects the mass activity of the catalyst. The values of R^m_ct(Pt) are listed in Table S3 in SI. The order of mass activity becomes apparent, with Pt(100) being the least active, followed by Pt(411) and Pt(111), which is in line with the device's performance and DFT results. From Table 1, the C_dl(pt) decreases in the order of Pt(111) < Pt(411) < Pt(100), which is consistent with the results of measurements of active surface area, since the C_dl(Pt) is proportional to the active surface area of Pt electrode. Pt nanooctahedron owns the lowest C_dl(pt), which may be attributed to its higher degree of aggregation (also shown in Figure 2a). On the other hand, particle aggregation benefits the electric conductivity of material, so Pt nanooctahedron owning the lowest R_s is reasonable. Meanwhile, the C_dl(pt) value of Pt nanooctapods is a bit larger than that of nanooctahedrons, which means that although the particle size of Pt nanooctapods is larger than that of nanooctahedrons and nanocubes, the surface areas of the formed CEs have little difference, which may be owing to the multi-pods for preventing the aggregation of Pt nanooctapods. In diffusion zone, W_(sol) increases in the order of Pt(111) (2.99 Ω) < Pt(411) (3.83 Ω) < Pt(100) (6.86 Ω). Judged from equation (5), the diffusion coefficients (D) of I₃⁻ species vary in the inverse order (see Table S2), which indicates that the diffusion velocity of redox couple near the interface of Pt(111) electrode and electrolyte is higher, benefiting the reduction of I₃⁻ to I⁻. Above all, the low R_ct(Pt), low R_s and low W_(sol) of Pt(111) increase fill factor(0.58), resulting in the high conversion efficiency. Comparing the EIS parameters and conversion efficiencies of Pt(100) and Pt(411), it can be obtained that although Pt(100) owns the lower R_s and higher C_dl(pt) than that of Pt(411), the highest R_ct(Pt) leads to its poorer performance, which means that R_ct(Pt) corresponding to catalytic activity plays a extremely important role on DSCs performance.

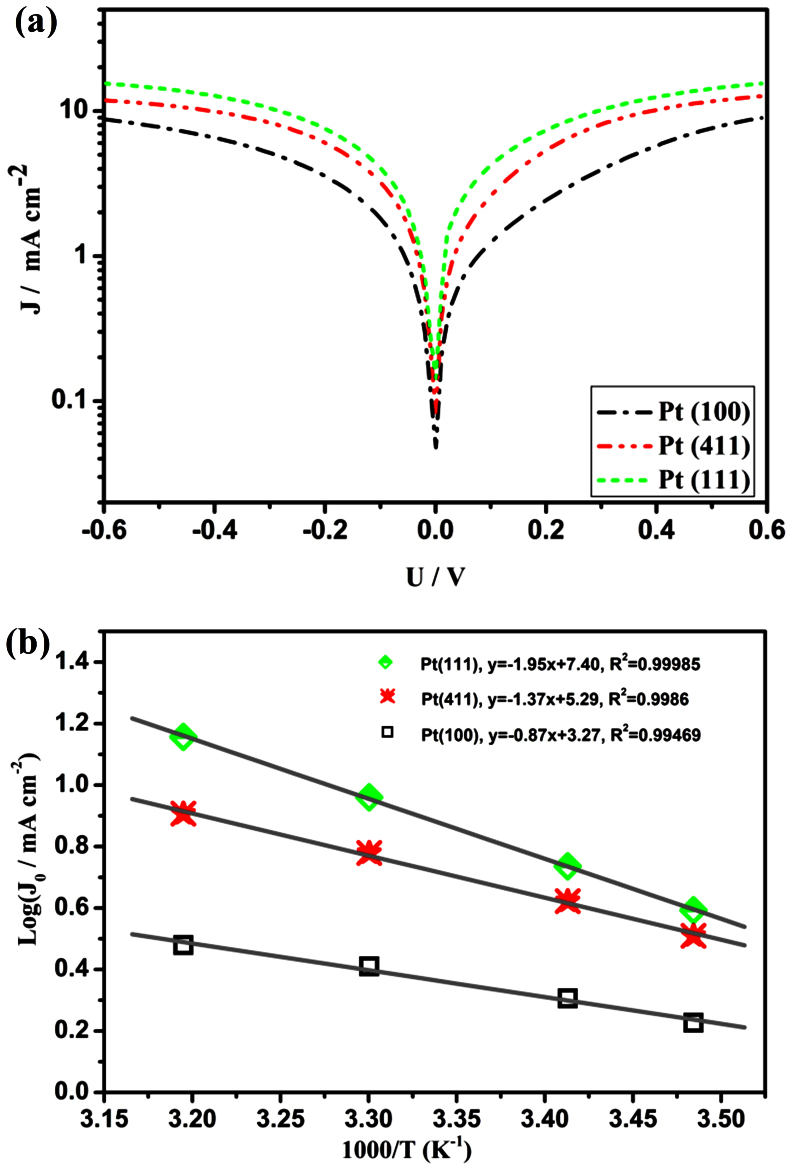
To further examine the interfacial charge-transfer properties of the I₃⁻/I⁻ couple on the electrode surface, Tafel polarization measurements were carried out with dummy cells fabricated with two identical electrodes (CE//IL//CE). Figure 4a shows the current density (J) as a function of voltage (U) at room temperature for the redox reactions of I₃⁻ to I⁻. Theoretically, the Tafel curve can be divided into three zones via the value of overpotential, which are the polarization zone at low overpotential (|U| < 120 mV), Tafel zone at middle overpotential (with a sharp slope), diffusion zone at high overpotential. From the Tafel zone and diffusion zone, we can obtain the exchange current density (J₀) and the limiting diffusion current density (J_lim) which are closely related to the catalytic activity of the catalysts. In Tafel zone, the anodic and cathodic branches of the J–U plot (Figure 4a in logarithm scale) show the largest slope for the Pt(111), indicating the highest Tafel exchange current density (J₀) on this electrode in terms⁵¹,⁵², suggesting that Pt(111) has the higher catalytic activity. While, the Pt(411)'s slope gets moderate level, and the Pt(100)'s is the least, suggesting relatively lower catalytic activities. In order to further characterize the catalytic activity, EIS experiments were carried out at different temperature. And the exchange current density (J₀) was further calculated from R_ct (using equation (7)).

where R_ct is the kinetic component of the resistance determined by EIS data, and R, T, n and F have their usual significance. It is obtained that the J₀ shows temperature dependence (Figure 4b), following the Arrhenius equation:

where I₀ is the exchange current density at T = infinite and E_a is the activation energy. From Figure 4b, Pt(111) has the highest catalytic activity, and Pt(100) shows the lowest. In diffusion zone, Pt(111) exhibits a highest J_lim, whereas Pt(100) owns the lowest. Based on equation (9), the diffusion coefficient (D) value of the I₃⁻ species can also be obtained.

where D is the diffusion coefficient of the I₃⁻, l is the distance between the electrodes, C is the I₃⁻ concentration and the rest retain their usual significance. The diffusion coefficients obtained in this way were compared with the data obtained above from transient-state state measurements (see Table S2). It can be seen that the orders of diffusion coefficients of the three Pt electrodes in the two measurements are consistent: Pt(111) > Pt(411) > Pt(100). From the results of the EIS and Tafel-polarization measurements, it can be concluded that the catalytic activity of Pt(111) exceeds that of Pt(411) and Pt(100), which is in a good accordance with results of the DFT predictions.

Figure 4. Electrochemical investigations of the Pt electrodes prepared with three different nanocrystals.

(a) Tafel curves of the symmetrical cells fabricated with two identical Pt electrodes; (b) exchange current density-temperature data in the Arrhenius coordinates.

Discussion

In summary, first-principles calculations show that the Pt catalysts for I₃⁻ reduction can be optimized by changing the crystal shape, and the reduction activity should follow in the order: Pt(111) > Pt(411) > Pt(100) owing to the increasing I* desorption barriers. The performance of the three synthesized structure-directed Pt nanocrystals mainly exposing {111}, {411} and {100} facets, respectively, confirms the predictions of the theoretical study. An optimum catalyst consisting of Pt nanooctahedron enclosed by {111} facets has been developed and shown to be highly active for I₃⁻ reduction and high photovoltaic conversion efficiency (6.91%) in DSCs.

Methods

Materials

All chemicals (ACS grade) were purchased from Sigma-Aldrich and used without further purification. Synthesis of Pt nanooctapods (Pt(411))²⁸, Pt nanocubes (Pt(100))⁴⁰,⁴¹,⁴², and Pt truncated nanooctahedrons (Pt(111))⁴² were prepared according to the literature and described in the Supporting Information (SI). The fabrication of DSCs is also listed in the Supporting Information.

Materials characterizations

The morphology and structure of the samples were characterized by high-resolution transmission electron microscopy (HRTEM, JEOL 2100, operating at 200 kV). The photocurrent–voltage performance of the DSCs was measured with a Keithley digital source meter (Keithley 2601, USA) and simulated under AM 1.5 illumination. The power of the simulated light was calibrated to 100 mW·cm⁻² using a Newport Oriel PV reference cell system (model 91150 V). All the electrochemical experiments were conducted by using a computer-controlled electrochemical workstation (Parstat 2273, Princeton) in the dark. The measured frequency of electrochemical impedance spectra (EIS) experiments ranged from 100 mHz to 1 MHz with an AC modulation signal of 10 mV and bias DC voltage of 0.60 V. The spectra were fitted by the ZSimpWin software. Tafel polarization measurements were carried out in a dummy cell with a scanning rate at 50 mV s⁻¹. CV experiments for electrochemically active Pt surface area (ECASA, refer to Table S3 in SI) were conducted in a three-electrode system in 0.5 M H₂SO₄ with a scanning rate of 50 mV s⁻¹ and with a Hg/HgSO₄/K₂SO₄(sat) reference electrode (MSE). The working electrodes were Pt nanocrystals loaded FTO, exposing an area of about 0.36 cm².

Theoretical calculation

All the spin-polarized density functional theory (DFT) calculations were performed with Perdew-Burke-Ernzerhof (PBE) functional within the generalized gradient approximation using the VASP code⁵³. The project-augmented wave (PAW) method was used to represent the core-valence electron interaction. For total energy calculations, the valence electronic states were expanded in plane wave basis sets with a cutoff energy of 450 eV. Atomic positions were relaxed until the sum of the absolute forces was less than 0.05 eV/Å. The adsorption energy of I (E_ad^I) is defined as: E_ad^I = E(interface) + 1/2E(I₂) − E(I/interface), where E(interface), E(I₂) and E(I/interface) are the energies of the liquid/electrode interface, I₂ in the gas phase and I adsorbed on the liquid/electrode interface, respectively, and each of them can be achieved from DFT calculation. To model the interface environment, several acetonitrile layers were explicitly introduced and fully optimized in the surface slab with a density of 0.79 g/cm³, in which the coverage effect of adsorbed solvent molecule at the interface on E_ad^I have been discussed (see calculation details in SI).

Author Contributions

B. Zhang, H.G. Yang and D. Wang, H.F. Wang wrote the main manuscript. D. Wang, H.F. Wang prepared Figure 1, and B. Zhang prepared other Figures and Table 1. J. Liu helped to prepare Figure 2. Y. Hou, S. Yang, X.H. Yang, J.H. Zhong and H.J. Zhao discussed the electrochemical section, and P. Hu provided several advices for theoretical calculation. All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Revised supporting information