Iterative Image Reconstruction for PROPELLER-MRI using the NonUniform Fast Fourier Transform

Abstract

Purpose

To investigate an iterative image reconstruction algorithm using the non-uniform fast Fourier transform (NUFFT) for PROPELLER (Periodically Rotated Overlapping parallEL Lines with Enhanced Reconstruction) MRI.

Materials and Methods

Numerical simulations, as well as experiments on a phantom and a healthy human subject were used to evaluate the performance of the iterative image reconstruction algorithm for PROPELLER, and compare it to that of conventional gridding. The trade-off between spatial resolution, signal to noise ratio, and image artifacts, was investigated for different values of the regularization parameter. The performance of the iterative image reconstruction algorithm in the presence of motion was also evaluated.

Results

It was demonstrated that, for a certain range of values of the regularization parameter, iterative reconstruction produced images with significantly increased SNR, reduced artifacts, for similar spatial resolution, compared to gridding. Furthermore, the ability to reduce the effects of motion in PROPELLER-MRI was maintained when using the iterative reconstruction approach.

Conclusion

An iterative image reconstruction technique based on the NUFFT was investigated for PROPELLER MRI. For a certain range of values of the regularization parameter the new reconstruction technique may provide PROPELLER images with improved image quality compared to conventional gridding.

Introduction

PROPELLER-MRI (1,2) (Periodically Rotated Overlapping parallEL Lines with Enhanced Reconstruction) has attracted the attention of the MR community due to its significantly reduced sensitivity to bulk motion compared to conventional multiple-shot fast spin echo (FSE), and its ability to reduce the contribution of corrupted data in the image formation process. Both advantages originate from the unique k-space sampling strategy used in PROPELLER-MRI, according to which, several k-space lines are acquired in each TR, forming a blade that is then rotated around its center, and acquisition is repeated to cover the desired region of k-space. Consequently, a central disk of k-space is acquired in each blade that can be used as a two-dimensional (2D) navigator to correct motion between blades, as well as to identify blades with corrupted data. Since the k-space samples in PROPELLER and its variants (Turboprop (3), PROPELLER-EPI (4)) are not located on a Cartesian grid, images are typically reconstructed using gridding (5,6). However, when applied to noise contaminated data, gridding methods can produce images with suboptimal statistical properties. In contrast, iterative image reconstruction methods have been applied in various medical imaging modalities, and are known to mitigate artifacts that arise from data inconsistencies, as well as to minimize image noise by use of regularization strategies (7). In iterative reconstruction, by manipulating the value of the regularization parameter, one can explore the trade-off between image properties such as the signal to noise ratio (SNR), spatial resolution, amount of artifacts, and select the operating point depending on the requirements of the imaging application.

For iterative image reconstruction with non-Cartesian k-space samples, Fessler et al. demonstrated that the transformation between image-space and k-space in each iteration of the algorithm can be accomplished rapidly and accurately by means of the Non Uniform Fast Fourier Transform (8) (NUFFT). This method has been successfully applied in different imaging modalities, such as computed tomography (CT) (9), diffraction ultra-sound tomography (10) and spiral MRI with sensitivity encoding (11) (SENSE), with significant improvement in image quality. In this work, an iterative image reconstruction algorithm using NUFFT was investigated for PROPELLER-MRI. Correlation weighting (1,2) was also incorporated to compensate for through-plane motion. The tradeoff between spatial resolution, SNR and image artifacts was investigated for different values of the regularization parameter, and the results were compared to those produced with gridding using an apodization filter with different widths. It was demonstrated that, for a certain range of values of the regularization parameter, iterative image reconstruction for PROPELLER produces a more desirable trade-off between SNR, spatial resolution and bias than gridding.

Theory

Conventional PROPELLER Image Reconstruction

In conventional PROPELLER image reconstruction, phase correction is performed first, followed by in-plane motion correction between blades (2). The non-uniform k-space samples are then gridded onto a Cartesian grid, and a 2D inverse fast Fourier transform (FFT) is applied on the Cartesian k-space data. Gridding is completed using:

$$M_c=\{[(M_p•W)\otimes C]•\mathit{III}\}{\otimes }^{-1}C$$ [1]

where M_C is the k-space data in a Cartesian grid, M_P is the data in the PROPELLER grid, W is the weighting function that compensates for the non-uniform sampling density, C is the convolution function, III is the Cartesian grid, ⊗ and ⊗⁻¹ represent the convolution and deconvolution operations, respectively. The weighting function, W, is non-zero only at the sampling locations of the PROPELLER grid, and is estimated iteratively (5,12). The convolution function, C, is also estimated iteratively. Comparison of the central disc of k-space of each blade with the mean central disc of k-space provides the blade that best represents the mean of all blades, therefore named the “reference” blade. Comparison of the central disc of k-space between each blade and the reference blade provides an estimate of the quality of the data in the blade, and is incorporated as an additional weight (2) (correlation weight) during estimation of W.

Iterative Image Reconstruction for PROPELLER MRI using NUFFT

The goal in PROPELLER image reconstruction is to produce an image residing on a Cartesian grid from non-uniformly spaced, noisy k-space samples. If f(r) is the true object and ϕ is the Fourier transform of f,

$$\varphi (k)=\int f(r)e^{-i2\pi kr}dr,$$ [2]

where r denotes location in image space and k location in k-space, then,

$$M_p=\varphi +\eta ,$$ [3]

where η is the noise in k-space. Therefore, the goal in PROPELLER image reconstruction is to reconstruct f from the noisy k-space samples M_p. However, this is a continuous-to-discrete mapping, and the inverse problem is ill-posed problem since there are infinite solutions f that exactly match the samples M_p (13). One approach to address this issue is by means of the pseudo-inverse of this continuous-to-discrete mapping (14). However, this is a computationally intensive procedure. In this work, the image to be reconstructed is first discretized using rectangular basis functions as follows (13):

$$f(r)=\sum _{i=1}^N{x}_{i}b(r-r_i),$$ [4]

where x_i is the value of f at location r_i, b is a rectangular basis function centered at r_i, and N is the total number of samples in image space. Thus, the image reconstruction problem is converted into determining the unknown coefficients x_i from measured data M_p using:

$$M_p=Ax+\eta ,$$ [5]

where x is a vector containing the coefficients x_i, and A is a matrix the elements of which are the Fourier coefficients multiplied by the 2D FFT of the rectangular basis function b. The operator A maps the discrete representation of the object residing on a Cartesian grid to k-space samples on the PROPELLER grid. In this discrete-to-discrete formulation of the image reconstruction problem, the estimate of the object on a Cartesian grid can be obtained by weighted least squares (WLS) minimization:

$$\widehat{x}=\underset{x}{\text{arg}\text{min}}{\Vert M_p-Ax\Vert }_w^2,$$ [6]

which corresponds to a solution of:

$$A^{\ast }\mathit{WAx}=A^{\ast }{WM}_p,$$ [7]

where A^* is the adjoint of A, and W is the weighting function that compensates for the non-uniform sampling density and incorporates correlation weighting (2) (similar to conventional PROPELLER image reconstruction). Correlation weighting mitigates through-plane motion artifacts by reducing the contribution of data from blades affected by through-plane motion. In this work, the estimate of the object on a Cartesian grid was obtained by minimizing a penalized weighted least squares cost function:

$$\psi (x)=1/2{\Vert M_p-Ax\Vert }_w^2+\beta R(x),$$ [8]

where R(x) is a quadratic regularization function that penalizes the roughness of the estimated image, and β is a penalty parameter that controls the influence of R(x) on the cost function. R(x) is given by the summation over all voxels in the image, of the sum of squared intensity differences between a voxel and its 8 neighboring voxels. The cost function in Equation 8 was minimized using the conjugate gradient (CG) method with the Fletcher-Reeves update formula. The key step in this procedure was to compute the gradient of the cost function:

$$\nabla \psi (x)=-A^{\ast }W(M_p-Ax)+\beta \nabla R(x)$$ [9]

The operations Ax and A^* were performed using NUFFT (8). In the rest of this work, this iterative reconstruction method is referred to as quadratic penalized weighted least squares (QPWLS) image reconstruction approach. The phase correction (1–3) and in-plane motion correction (1,15) of conventional PROPELLER image reconstruction were incorporated at the beginning of the QPWLS iterative reconstruction.

Methods

Numerical simulations, as well as experiments on a phantom and a healthy human subject were used to evaluate the performance of QPWLS for PROPELLER, and compare it to that of conventional gridding. Three sampling patterns with 16, 24 and 32 blades were used in this investigation. All sampling patterns contained 20 k-space lines per blade and 128 k-space samples per line. In all cases, images were reconstructed using both, conventional gridding and QPWLS. All images were reconstructed into 256×256 matrices. For the purposes of gridding, a pre-sampled Kaiser-Bessel function with 300 samples within a width=[5/(field of view)] was used as the convolution kernel. Linear interpolation was used to estimate values of the Kaiser-Bessel function corresponding to different distances between k-space samples in the PROPELLER and Cartesian grids. Deconvolution was performed in image space by dividing the reconstructed image by the inverse Fourier transform of the convolution kernel. For the purposes of iterative reconstruction, a k-space Cartesian grid over-sampled by a factor of 2 was used for NUFFT, and the k-space value in each location of the non-uniform grid was estimated by interpolation from the eight nearest neighbors of the over-sampled grid.

Numerical Simulations

PROPELLER k-space data were simulated using the Shepp-Logan phantom (16). The k-space representation of the Shepp-Logan phantom is known analytically. Therefore, it was possible to accurately simulate sampling with any pattern.

In order to assess the convergence rate of the QPWLS algorithm, images of the Shepp-Logan phantom were reconstructed from noise-free k-space data, and at each iteration of the CG algorithm the root mean square (RMS) error of the reconstructed image was calculated. The RMS error was defined as:

$$\text{RMS}=\sqrt{\frac{{\displaystyle \sum _{i=1}^{\text{N}}}{(f_i-f_{ni})}^2}{\text{N}}},$$ [10]

where f_n is the image produced in the n^th iteration, f is the true object, i is the index number of a voxel, and N is the number of voxels in each image. A plot of RMS error versus the number of iterations was generated, and the number of iterations for which the algorithm appeared to converge was determined. The same procedure was repeated for several penalty values β = {0.01, 0.03, 0.05, 0.07, 0.1, 0.2, 0.3, 0.5, 0.7, 0.9, 1}.

Numerical Monte-Carlo simulations were conducted to assess the performance of QPWLS image reconstruction, and compare it to that of conventional gridding. For that purpose, zero-mean Gaussian noise was added to k-space samples of the Shepp-Logan phantom, and an ensemble of 1000 noisy images were reconstructed using conventional gridding with apodization filters with width of {54.7%, 62.5%, 70.3%, 78.1%, 85.9%, 93.7%, 100%} of 2*K_max, where K_max is the maximum sampled k-space frequency, as well as QPWLS with each of the penalty values shown above. The mean and standard deviation of the signal in each voxel were empirically estimated from the 1000 noisy images. The ratio of the empirically estimated mean and standard deviation of the signal in each voxel provided empirical estimates of SNR for each voxel. The average of the empirical estimates of SNR in a uniform region inside the high intensity ellipse near the bottom of the Shepp-Logan phantom was then measured. The variance of the added Gaussian noise was such that the average SNR in the selected region was approximately 20 when reconstructing from the 32-blades pattern using gridding without apodization (i.e. the width of the apodization filter was 100% of 2* K_max). Spatial resolution was assessed, for both gridding and iterative reconstruction by means of the full width at half maximum (FWHM) of the point spread function (17) (PSF). Finally, for each reconstruction approach, the 1000 noisy images were averaged, and the absolute bias of the average image, f_av, defined as ||f − f_av||, was estimated. The simulations were repeated for all sampling patterns, as well as for k-space noise with a variance equal to half of that used above.

The performance of QPWLS reconstruction in the presence of bulk, in-plane motion, was evaluated, before and after motion correction. Noisy k-space samples of the Shepp-Logan phantom were produced for the sampling pattern with 32 blades as described above, and image-space rotations and translations were simulated by rotating and adding phase to each PROPELLER k-space blade, respectively (15). The amount of rotation and translation was determined by randomly sampling from gaussian distributions with a mean of 0 and standard deviation of 5° and 5 pixels, respectively. Images were reconstructed from the motion-affected blades with conventional gridding and iterative reconstruction, before and after motion correction.

Finally, the performance of the iterative image reconstruction algorithm in the presence of through-plane motion was evaluated. Noisy k-space samples of the Shepp-Logan phantom were produced for the sampling pattern with 32 blades as described above. Through-plane motion was simulated by shifting three of the ellipses contained in the Shepp-Logan phantom for 10 of the blades. Images were reconstructed with and without correlation weighting using conventional gridding and QPWLS.

Experiments on Phantoms and Humans

Scans were performed on an actual phantom and the brain of a healthy human subject using a 3T GE MRI scanner (General Electric, Waukesha, WI) and the standard GE head coil. Informed consent was obtained from the human volunteer. Data were acquired with a Turboprop-MRI sequence and the following imaging parameters: TR=5000 ms, echo train length (ETL) = 8, turbo-factor = 5, field of view of 24 cm × 24 cm, slice thickness of 3 mm, and the sampling patterns mentioned above. SNR measurements in the images of the actual phantom and human brain were obtained using measurements of noise as described in references (18,19). Regions of interest (ROIs) were selected in areas of the phantom and the brain with relatively uniform signal intensity, and the average SNR over each ROI was estimated.

Results

Numerical Simulations

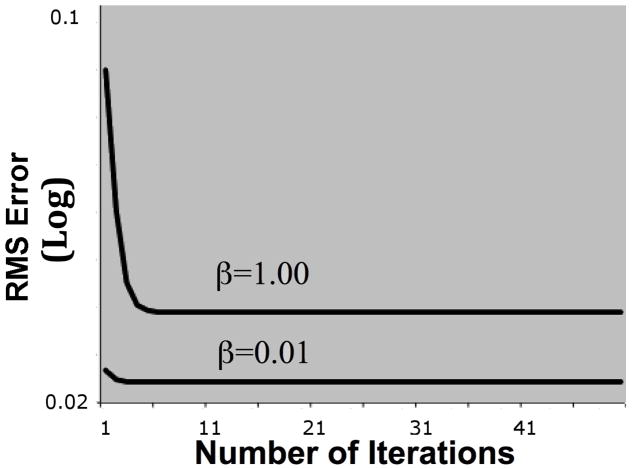
When no noise was added in k-space, and the Shepp-Logan phantom was reconstructed iteratively, the RMS error remained almost constant after 5–10 iterations, for all penalty values (Fig. 1). In this study, iterative reconstruction was terminated after 20 iterations (a conservative termination criterion was used, since reconstruction speed was not considered in this study). In addition, the FWHM of the PSF was approximately constant for various image-space locations. Therefore, in the discussion that follows, only the FWHM of the PSF in the center of the field of view in image space is used. For β≤0.03, the SNR was lower and the bias was higher in images obtained with iterative reconstruction compared to gridding without apodization (filter width = 100% of 2*K_max) (Fig. 2). For iterative reconstruction with β>0.03, as well as for gridding with an apodization filter of width less than 100% of 2*K_max, SNR was increased at the cost of spatial smoothing (Fig. 2). For β>0.03 and β<0.35 approximately, the SNR was higher and the bias was lower in images obtained with iterative reconstruction compared to gridding with apodization (Fig. 2). For iterative reconstruction, the bias was lowest at β=0.2 (among all penalty values considered) with an FWHM of the PSF equal to 2.7 mm (Fig. 2). At this spatial resolution, the SNR for QPWLS was approximately 16% higher, and the bias 4.8% lower than gridding. Similar SNR to that of QPWLS with β=0.2 can be achieved with gridding using an apodization filter of width equal to 78.1% of 2*K_max, at the cost of lower spatial resolution (8.51% increase in the FWHM of the PSF), and 3.5% higher bias (Figs. 2, 3a1, 3a2). When compared to gridding with no apodization, QPWLS with β=0.2 resulted in 33.8% higher SNR, 6.4% lower bias, for a 3.4% increase in the FWHM of the PSF (Fig. 2). The lowest bias for gridding was obtained by using an apodization filter of width equal to 70.3% of 2*K_max (among the different apodization filters considered) (Fig. 2). At this point, the FWHM of the PSF for gridding was 12.6% higher, and the SNR was at least 50% lower, than QPWLS with β=0.2.

Figure 1.

Plot of the RMS error in iterative reconstruction (in logarithmic scale) as a function of the number of iterations, for penalty values of 0.01 and 1.

Figure 2.

Plot of the SNR (black curves) and bias (grey curves) for images of the Shepp-Logan phantom reconstructed with QPWLS (triangles) and gridding (squares). The penalty values used in QPWLS, and the width of the apodization filter used for gridding, are placed on the bottom horizontal axis at corresponding values of the FWHM of the PSF (top horizontal axis) and not in any specific scale.

Figure 3.

Images of the Shepp-Logan phantom (a1, a2), an actual phantom (b1, b2), and a healthy human brain (c1, c2), reconstructed with conventional gridding with an apodization filter of width 70.3% of 2*K_max (top row), as well as with QPWLS and β = 0.2 (bottom row). In the simulations, that apodization filter and penalty value resulted in the lowest bias for gridding and iterative reconstruction, respectively. The SNR measured in a region of uniform signal is shown below each image.

When bulk, in-plane motion was simulated and not corrected, images of the Shepp-Logan phantom reconstructed with conventional gridding or the iterative technique contained significant artifacts (Fig. 4A, 4C, respectively). In contrast, after compensation for motion, both gridding and QPWLS produced high-quality estimates of the true object (Fig. 4B, 4D, respectively). Similar findings were obtained for through-plane motion and reconstruction with and without correlation weighting (Fig. 5).

Figure 4.

Images of the Shepp-Logan phantom for acquisitions with simulated in-plane motion and reconstruction using conventional gridding, without (A) and with (B) motion correction. Images C and D were produced using iterative reconstruction without and with compensation for in-plane motion, respectively.

Figure 5.

Images A and B represent the difference between the true Shepp-Logan phantom and the average image reconstructed with gridding in the presence of simulated through-plane motion, without and with correlation weighting, respectively. Similarly, images C and D are the difference maps for reconstruction with QPWLS without and with correlation weighting, respectively.

Experiments on Phantoms and Humans

Similar results were obtained for the scans on the phantom and human volunteer. Figure 3 shows T₂-weighted images of the phantom (Fig. 3b1, 3b2) and human brain (Fig. 3c1, 3c2) reconstructed with gridding using an apodization filter of width equal to 78.1% of 2*K_max, as well as QPWLS with a penalty value of 0.2. Images obtained with gridding showed similar SNR but reduced spatial resolution, which is in agreement with the simulation results (Figs. 2, 3a1, 3a2).

Discussion

PROPELLER-MRI is characterized by significantly lower sensitivity to various sources of image artifacts compared to conventional FSE, primarily due to its unique k-space sampling pattern that permits reduction of data inconsistencies during image reconstruction. Currently, reconstruction from k-space samples residing on the non-Cartesian grid used in the PROPELLER family of sequences is conducted with gridding. In this study, an iterative PROPELLER image reconstruction approach using NUFFT was investigated, and the performance of the new technique was compared to that of conventional gridding.

By selecting different penalty values β, the iterative image reconstruction method allows manipulation of the tradeoff between SNR, spatial resolution, amount of artifacts and bias, according to the requirements of the particular imaging task. In order to be able to evaluate the results of iterative image reconstruction, an apodization filter was used with gridding, and the width of the filter was varied to be able to compare the characteristics of images reconstructed with the two techniques for the same SNR or spatial resolution. In this study, it was demonstrated that for β≤0.03, iterative reconstruction provided PROPELLER images of the Shepp-Logan phantom with lower SNR, and higher bias than gridding (Fig. 2). Therefore, for β≤0.03, conventional gridding without apodization provided generally higher quality images than iterative reconstruction. For β>0.03 and β<0.35 approximately, the SNR was higher and the bias was lower in images obtained with iterative reconstruction compared to gridding with apodization (Fig. 2). Therefore, for β>0.03 and β<0.35 approximately, iterative reconstruction provided generally higher quality images than gridding. The lowest bias was achieved for iterative reconstruction with β=0.2 (among all penalty values considered) (Fig. 2). When compared to gridding with apodization, iterative PROPELLER image reconstruction using NUFFT and β=0.2 provided lower bias and higher SNR. When compared to gridding without apodization, iterative PROPELLER image reconstruction using NUFFT and β=0.2 provided lower bias, higher SNR, for only a small increase in FWHM of the PSF.

In this work, the bias was used as a global measure of errors included in the reconstructed images compared to the true object. However, the bias depends on the object being imaged. For iterative reconstruction of the Shepp-Logan phantom and β>0.4, most of the increase in the bias originated from smoothing the sharp outside edges of that phantom. When the bias was not calculated considering all voxels, but instead only voxels inside a uniform region of the Shepp-Logan phantom, the bias remained lower than that produced with gridding for almost the whole range of β values investigated, and decreased for increasing penalty values. Therefore, the bias depends on the imaged object. The β value for which the bias of the Shepp-Logan phantom was minimized is not necessarily the optimal operating point for PROPELLER imaging on any object. However, for PROPELLER-MRI on human tissue, there exists a range of β values for which iterative reconstruction may improve the image characteristics compared to conventional gridding.

It is well known in the medical imaging research community that iterative image reconstruction can be particularly advantageous in cases of insufficient sampling, where conventional gridding techniques lead to artifacts due to Nyquist holes (20). It is anticipated that, in under-sampled PROPELLER-MRI, the iterative reconstruction algorithm that was investigated in this study may provide images with fewer image artifacts than gridding (21). However, motion correction in PROPELLER is performed prior to gridding or iterative reconstruction, and certain levels of under-sampling may introduce errors that reduce the accuracy of motion compensation. Therefore, further research is necessary in order to evaluate the application of iterative reconstruction using NUFFT in under-sampled PROPELLER-MRI data.

The experiments on the phantom and human subject were performed using the Turboprop sequence. The same reconstruction algorithm can be applied in other sequences from the PROPELLER family, such as Turboprop and PROPELLER-EPI. The fact that T₂ and T₂* decays were not included in the simulations with the Shepp-Logan phantom may be related to the different SNR increases for increasing β values in the simulations and actual experiments. Also, a quadratic regularization function was used in this study. Incorporating a non-quadratic penalty needs further investigation for different applications of PROPELLER imaging. Additionally, other iterative and non-iterative reconstruction approaches have been developed for non-Cartesian trajectories (22–24), and further investigation on the performance of such methods in PROPELLER imaging is necessary. Finally, although the reconstruction speed for gridding and iterative reconstruction with NUFFT was not optimized in this research, the latter is certainly slower than the former. A detailed analysis of the number of operations needed for the two reconstruction methods can be found elsewhere (10).

In conclusion, an iterative image reconstruction technique based on the NUFFT was investigated for PROPELLER MRI. It was shown that, for a certain range of β values the new reconstruction technique may provide PROPELLER images with improved image quality compared to gridding. The motion correction and correlation weighting procedures were also incorporated in the iterative image reconstruction algorithm, thereby maintaining the main advantages of PROPELLER MRI over conventional multishot FSE.