Adjusting for High-dimensional Covariates in Sparse Precision Matrix Estimation by ℓ₁-Penalization

Abstract

Motivated by the analysis of genetical genomic data, we consider the problem of estimating high-dimensional sparse precision matrix adjusting for possibly a large number of covariates, where the covariates can affect the mean value of the random vector. We develop a two-stage estimation procedure to first identify the relevant covariates that affect the means by a joint ℓ₁ penalization. The estimated regression coefficients are then used to estimate the mean values in a multivariate sub-Gaussian model in order to estimate the sparse precision matrix through a ℓ₁-penalized log-determinant Bregman divergence. Under the multivariate normal assumption, the precision matrix has the interpretation of a conditional Gaussian graphical model. We show that under some regularity conditions, the estimates of the regression coefficients are consistent in element-wise ℓ_∞ norm, Frobenius norm and also spectral norm even when p ≫ n and q ≫ n. We also show that with probability converging to one, the estimate of the precision matrix correctly specifies the zero pattern of the true precision matrix. We illustrate our theoretical results via simulations and demonstrate that the method can lead to improved estimate of the precision matrix. We apply the method to an analysis of a yeast genetical genomic data.

1. Introduction

Estimation of high-dimensional covariance/precision matrix has attracted a great deal of interest in recent years [1, 2, 3, 4, 5, 6]. The problem is related to sparse Gaussian graphical modeling where the precision matrix provides information on the conditional independency among a large set of variables. Application of estimating the precision matrix includes analysis of gene expression data, spectroscopic imaging, FMRI data, numerical weather forecasting. Under the assumption of sparsity and some regularity conditions on the underlying precision matrix, regularization methods have been proposed to estimate such precision matrices. Some explicit rates of convergence of the resulting estimates have been obtained [1, 2, 7, 6]. Furthermore, [4] and [3] have studied the optimal convergence rate of the estimates in Frobenius and operator norms, as well as the matrix ℓ₁ norm.

Almost all current methods for precision matrix estimation or Gaussian graphical model estimation assume that the random vector has zero or constant mean. However, in many real applications, it is often important to adjust for the covariate effects on the mean of the random vector in order to obtain more precise and interpretable estimate of the precision matrix. One such example is related to analysis of genetical genomic data, where we have both high dimensional genetic marker data and high dimensional gene expression data measured on the same set of samples in a segregation population. One important goal is to study the conditional independency structure among a set of genes at the expression level. This is related to estimating the precision matrix when the data are assumed to be normally distributed. However, it is now known that genetic marker data can affect the mean gene expression levels for many genes [8]. It is therefore important to adjust for the marker effects on gene expression when the conditional independency structure is studied.

In this paper, we consider the problem of adjusting for high-dimensional covariates in precision matrix estimation by ℓ₁-penalization. It can be formulated as the sparse multivariate regression with correlated errors. The model has both high dimensional regression coefficient matrix and high dimensional covariance matrix. Estimation of such multivariate regressions with correlated errors have been studied in literature. [9] focused on estimating the regression coefficient matrix and presented several algorithms based on ℓ₁ penalization. However, no theoretical results were provided. [10] developed an estimation procedure that iteratively estimates the regression coefficients and the precision matrix based on ℓ₁-penalization. They provided asymptotic results on estimation bounds and consistency. However, the computation is quite intensive.

We propose a two-stage ℓ₁ penalization procedure that first jointly estimates the multiple regression coefficients to obtain a sparse estimation of the regression coefficient matrix. We extend the results of [11] on sharp recovery and convergence rate for sparsity in single regression to multiple regression setting. The estimates of the regression coefficients are then used to adjust for the means in estimating the precision matrix. Under the assumption of a matrix version of the irrepresentable condition [12, 11] on the covariate matrix as well as a matrix version of the irrepresentable condition on the precision matrix, we obtain the consistency results. We additionally obtain the explicit convergence rates for both the estimates of the regression coefficient matrix and estimates of precision matrix in element-wise ℓ_∞ norm, hence also in spectral and Frobenius norms. The theoretical property of our estimates depends on the method of primal dual witness construction [11, 5]. If the primal-dual witness construction succeeds, it acts as a witness to the fact that the solution to the restricted problem is equivalent to the solution to the original problem. When further conditions on the minimum values of the true coefficient matrix and the precision matrix are assumed, we also establish the sign consistency results for the estimates.

2. Model and notation

Consider a random vector Y ∈ ℝ^p and a deterministic covariate vector X ∈ ℝ^q, we assume that

$$Y=\mathrm{\Gamma }X+\epsilon ,$$ (1)

where Γ is the p × q regression coefficient matrix, ε is a mean-zero error vector and is assumed to distribute as a sub-Gaussian vector with covariance matrix Σ = Θ⁻¹ and precision matrix Θ. Specifically, we assume that for each ε^j in ε = (ε¹, …, ε^p), ${\epsilon }^j/\sqrt{{\mathrm{\Sigma }}_{jj}}$ is sub-Gaussian with parameter σ. A zero-mean random variable Z is sub-Gaussian if there exists a constant σ ∈ (0, ∞) such that E[exp(tZ)] ≤ exp(σ²t²/2), for all t ∈ ℝ. By Chernoff bound, this upper bound on the moment generating function implies a two-sided tail bound of the form pr(|Z| > z) ≤ 2 exp(−z²/(2σ²)). If every element in the vector ε is sub-Gaussian, we call the vector ε sub-Gaussian.

Given n independent and identically distributed observations of a random vector (Y |X), we propose to estimate the regression coefficient matrix Γ and precision matrix Θ in model (1) in a two-step ℓ₁ penalization procedure. To simplify the problem, we assume the X_i are fixed observations for i = 1, ⋯, n. Denote X = (X₁, ⋯, X_n)^⊤ = (X⁽¹⁾, ⋯, X^(q)) as the design matrix. Denote $W={({\epsilon }_1^{\top },\cdots ,{\epsilon }_n^{\top })}^{\top }$ as the realized noise matrix and Y = (Y₁, ⋯, Y_n)^⊤. We further denote $C_X=X^{\top }X/n={\sum }_{i=1}^n{X}_i{X}_i^{\top }/n,C_{YX}=Y^{\top }X/n={\sum }_{i=1}^n{Y}_i{X}_i^{\top }/n$ and $C_Y=Y^{\top }Y/n={\sum }_{i=1}^n{Y}_i{Y}_i^{\top }/n$.

We first introduce notation related to vector and matrix norms. We use the notation A ≻ 0 for the positive definiteness of matrix A. We denote A̅ = vec(A) as the vectorization of an arbitrary matrix A. Define ‖A‖₁ = ∑_i,j |A_ij | as the element-wise ℓ₁ norm for a matrix A and ‖A‖_1,off = ∑_i≠j |A_ij| as the off-diagonal ℓ₁ norm of matrix A. We denote ‖A‖_∞ = max_i,j |A_ij| and ${\Vert |A|\Vert }_{\infty }={\text{max}}_{i=1,\cdots ,p}{\sum }_{j=1}^p|A_{ij}|$ as the element-wise ℓ_∞ norm and the matrix ℓ_∞ norm of a matrix A, respectively. Furthermore, we use ‖A‖_F as the Frobenius norm, which is the square-root of the sum of the squares of the entries of A, and ‖A‖₂ as the spectral norm, which is the largest singular value of A. Finally, we use Γ*, Σ* and Θ* to denote the true matrix parameters in model (1), while Γ̂, Σ̂ and Θ̂ as their estimates.

As commonly used in Gaussian graphical model, we similarly relate the nonzero elements of the precision matrix Σ* to the edges between two variables, and define the support of the precision matrix as

$$E({\mathrm{\Theta }}^{*})≔\{i,j\in (1,\cdots ,p)|i\ne j,{\mathrm{\Theta }}_{ij}^{*}\ne 0\},$$

and the maximum degree or row cardinality of Θ* as

$$d_1≔\underset{i=1,\cdots ,p}{\text{max}}|\{j\in (1,\cdots ,p)|{\mathrm{\Theta }}_{ij}^{*}\ne 0\}|.$$

Similarly, for the regression coefficient matrix, let T(Γ*) be the support of a matrix Γ*, defined as

$$T({\mathrm{\Gamma }}^{*})≔\{(i,j):{\mathrm{\Gamma }}_{i,j}^{*}\ne 0,\text{where}i\in (1,\cdots ,p),j\in (1,\cdots ,q)\}.$$

Also define $T(i)≔\{j:{\mathrm{\Gamma }}_{i,j}^{*}\ne 0,j=(1,\cdots ,q)\}$, which is the support of the regression coefficients for the ith variable. We define the maximum degree or row cardinality of Γ* as

$$d_2≔\underset{i=1,\cdots ,p}{\text{max}}\left|\right\{j\in \{1,\cdots ,q\}|{\mathrm{\Gamma }}_{ij}^{*}\ne 0\}|,$$

which corresponds to the maximum number of non-zeros in any row of Γ*. Denote the cardinality of T(Γ*) as k_n = |T(Γ*)|. Finally, we define the extended sign matrix of Γ* as

$$S_{\pm }({\mathrm{\Gamma }}_{ij}^{*})≔\{\begin{array}{ccc}+1,\hfill & \hfill \text{if}\hfill & \hfill {\mathrm{\Gamma }}_{ij}^{*}>0\hfill \\ -1,\hfill & \hfill \text{if}\hfill & \hfill {\mathrm{\Gamma }}_{ij}^{*}<0\hfill \\ 0,\hfill & \hfill \text{if}\hfill & \hfill {\mathrm{\Gamma }}_{ij}^{*}=0.\hfill \end{array}$$

3. Two-stage Penalized log-Determinant Bregman Divergence Estimation

We propose to develop a two-stage penalized estimation procedure for estimating the regression coefficient matrix Γ and the precision matrix Θ, where in the first stage, we estimate Γ through a penalized joint least square estimation and in the second stage, we estimate Θ by minimizing a penalized log-determinant Bregman divergence after plugging in the regression coefficient estimates. This algorithm can be summarized as the following:

• Step 1. Estimate Γ by minimizing a joint penalized residual sum of squares,

  $$\mathrm{\Gamma ̂}=\text{arg min}[\frac{1}{2n}\sum _{i=1}^{n}tr\{(Y_i-\mathrm{\Gamma }{X}_i){(Y_i-\mathrm{\Gamma }{X}_i)}^{\top }\}+{\rho }_n{\Vert \mathrm{\Gamma }\Vert }_1],$$ (2)

  where ρ_n is a tuning parameter.
• Step 2. Compute

  $${\mathrm{\Sigma ̂}}_{\mathrm{\Gamma ̂}}=\frac{1}{n}\sum _{i=1}^n(Y_i-\mathrm{\Gamma ̂}{X}_i){(Y_i-\mathrm{\Gamma ̂}{X}_i)}^{\top }.$$ (3)
• Step 3. Solve the optimization problem,

  $${\mathrm{\Theta ̂}}_{\mathrm{\Gamma ̂}}=\text{arg}\underset{\mathrm{\Theta }\succ 0}{\text{min}}\{\mathrm{t}\mathrm{r}({\mathrm{\Sigma ̂}}_{\mathrm{\Gamma ̂}}\mathrm{\Theta })-\text{log det}\mathrm{\Theta }+{\lambda }_n{\Vert \mathrm{\Theta }\Vert }_{1,\text{off}}\},$$ (4)

  where λ_n is a tuning parameter.

• Step 4. Output the solution (Γ̂, Θ̂_Γ̂).

Note that in Step 1, we ignore the correlation among the Y variables when estimating the multiple regression coefficients. [9] showed that only when the correlation of the errors is high, incorporation of of such an dependency can lead to increased efficiency in estimating Γ. Theorem 1 in the next section shows that the maximum estimation error is controlled in a certain rate. The estimate Σ̂_Γ̂ in Step 2 is a plug-in estimate based on the estimated residuals. This leads to our two-stage estimate of the precision matrix Θ̂_Γ̂ in Step 3, formulated as the ℓ₁-penalized log-determinant divergence problem [5]. Efficient coordinate descent algorithm can be applied to implement the optimization problems in Step 1 and Step 3 [13]. The tuning parameters can be chosen based on the BIC. The convergent rate in element-wise ℓ_∞ norm of this estimate is established in Theorem 2, followed by rates in other norms.

4. Theoretical properties

4.1. Estimation bound and sign consistency of Γ̂

Let T ≡ T(Γ*), T(i) and C_X be defined as above and denote I_p as the identity matrix of dimension p. In addition, for any matrix A, let A_S,T be the submatrix with the row indices given in set S and column indices given in set T. We first make several assumptions on the covariate matrix X.

Assumption 1. There exists a γ ∈ (0, 1], such that

$${\Vert |{(C_X\otimes I_P)}_{T^c,T}{[{(C_X\otimes I_P)}_{T,T}]}^{-1}|\Vert }_{\infty }\le 1-\gamma .$$ (5)

This is the matrix extension of the irrepresentable condition used in ℓ₁ penalized regression setting [12]. This assumption is equivalent to the irrepresentable assumption for Lasso for each of the p components of the response, i.e., ‖|(C_X)_T(i)^c,T(i)[(C_X)_T(i),T(i)]⁻¹|‖_∞ ≤ 1 − γ, for i = 1 ⋯, p. This can be further written as

$${\text{sup}}_i{\Vert |{(C_X)}_{T{(i)}^c,T(i)}{[{(C_X)}_{T(i),T(i)}]}^{-1}|\Vert }_{\infty }\le 1-\gamma .$$

The assumption implies that the number of non-zero elements in each row of Γ should be less than n.

Assumption 2. There exists a constant C_max, such that the largest eigenvalue

$${\lambda }_{\mathit{\text{max}}}\left({[{(C_X\otimes I_P)}_{T,T}]}^{-1}{(C_X\otimes \mathrm{\Sigma })}_{T,T}{[{(C_X\otimes I_P)}_{T,T}]}^{-1}\right)\le C_{\mathit{\text{max}}}.$$ (6)

This condition assumes an upper bound on the operator norm of the matrix [(C_X ⊗ I_p)_T,T]⁻¹(C_X ⊗ Σ)_T,T[(C_X ⊗ I_p)_T,T]⁻¹, which is a combination of the assumptions (26b) and (26c) in [11]. It is easy to check that this assumption holds if

$$\frac{{\lambda }_{\text{max}}\left({(C_X\otimes \mathrm{\Sigma })}_{T,T}\right)}{{\lambda }_{\text{min}}^2\left({(C_X\otimes I_p)}_{T,T}\right)}\le C_{\text{max}}.$$

Since C_X ⊗ Σ is no longer a block diagonal matrix, we cannot obtain an equivalent assumption for each of the p components of the response and then take the supreme over all p components.

Assumption 3. For all n > 0, the largest eigenvalue of C_X has a common upper bound Λ_max, that is

$${\lambda }_{\text{max}}(C_X)\le {\mathrm{\Lambda }}_{\text{max}}.$$

This is also commonly used assumption in sparse high dimensional regression analysis ([12] and [11]).

Theorem 1. Suppose that the design matrix X satisfies the Assumptions (1) and (2) and X is column-standardized such that

$$n^{-1/2}\underset{i\in \{1,\cdots ,p\}}{\text{max}}\underset{j\in {\{T(i)\}}^c}{\text{max}}{\Vert X^{(j)}\Vert }_2\le 1.$$ (7)

If the sequence of regularization parameters {ρ_n} satisfies

$${\rho }_n>\frac{2}{\gamma }\sqrt{\frac{2{\text{max}}_i{\mathrm{\Sigma }}_{ii}^{*}\{\text{log}(p_n)+\text{log}(q_n)\}}{n}},$$ (8)

then for some constant C₁ > 0, the following properties hold with probability greater than $1-4\text{exp}(-C_{1}n{\rho }_n^2)\to 1$,

1. The minimization of Step 1 of the algorithm has a unique solution Γ̂ ∈ ℝ^p×q with its support contained within the true support, i.e. T(Γ̂) ⊆ T(Γ*). In addition, the element-wise ℓ_∞ norm and the Frobenius norm have the following bounds

   $${\Vert {\mathrm{\Gamma ̂}}_T-{\mathrm{\Gamma }}_T^{*}\Vert }_{\infty }\le {\rho }_n\{{\Vert |{\{{(C_X\otimes I_p)}_{T,T}\}}^{-1}|\Vert }_{\infty }+\frac{\gamma }{2}\sqrt{\frac{C_{\mathit{\text{max}}}}{{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}}}\}≔{\rho }_n{M}_n(X,T,{\mathrm{\Sigma }}^{*}),{\Vert \mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*}\Vert }_F\le \sqrt{k_n}{\rho }_n{M}_n(X,T,{\mathrm{\Sigma }}^{*}).$$

2. If the minimum absolute value of the regression coefficient matrix Γ* on its support is bounded below as |Γ*|_min > ρ_nM_n(X, T, Σ*), then Γ̂ has the correct signed support, i.e. S_±(Γ̂) = S_±(Γ̂*).

Theorem 1 is an extension of the results for single regression of [11] to multiple regressions when we simultaneously estimate the regression coefficients of multiple regressions. A lower bound on the minimum absolute value of elements of Γ* is required for sign consistency. Such an estimation bound on the regression coefficient matrix is required to establish the theoretical property of Θ̂_Γ̂

4.2. Estimation bound and sign consistency of Θ̂

We next present results on the estimate of the precision matrix Θ̂ = Θ̂_Γ̂. Define Ω* = Θ*⁻¹ ⊗ Θ*⁻¹, which is the Hessian of the log-determinant objective function respect to Θ* [5]. Since ${\mathrm{\Omega }}_{(j,k),(l,m)}^{*}=\text{cov}\{{\epsilon }_j{\epsilon }_k,{\epsilon }_l{\epsilon }_m\}$, it can be viewed as an edge-based counterpart to the usual covariance matrix Σ* [5]. Let S(Θ*) = {E(Θ*) ∪ {(1, 1), ⋯, (p, p)} } be the augmented set including the diagonals. With slight abuse of notation, we also use S and S^c to denote S(Θ*) and its complement. We further define

$$K_{{\mathrm{\Sigma }}^{*}}≔{\Vert |{\mathrm{\Sigma }}^{*}|\Vert }_{\infty }=(\underset{i}{\text{max}}\sum _{j=1}^p|{\mathrm{\Sigma }}_{ij}^{*}|),$$

as the matrix ℓ_∞ norm of the true covariance matrix Σ*, and

$$K_{{\mathrm{\Omega }}^{*}}≔{\Vert |{({\mathrm{\Omega }}_{SS}^{*})}^{-1}\Vert |}_{\infty }={|\Vert {({[{\mathrm{\Theta }}^{*-1}\otimes {\mathrm{\Theta }}^{*-1}]}_{SS})}^{-1}|\Vert }_{\infty }.$$

Before we present the theorem on Θ̂_Γ̂, we need one assumption on the Heissian matrix Ω*,

Assumption 4. There exists an α ∈ (0, 1], such that

$${\Vert |{\mathrm{\Omega }}_{S^{c}S}^{*}{({\mathrm{\Omega }}_{SS}^{*})}^{-1}|\Vert }_{\infty }\le 1-\alpha .$$

This assumption is the mutual incoherence or irrepresentable condition introduced in [5], which controls the influence of the non-edge terms on the edge-based terms.

Define ${\mathrm{\delta ̄}}_f(n,p_n^{\tau })≔\sqrt{(\text{log}4+\tau \text{log}{p}_n)/(C_{*}n)}$ for some τ > 2, where $C_{*}={[128{(1+4{\sigma }^2)}^2{\text{max}}_i{\{{\mathrm{\Sigma }}_{ii}^{*}\}}^2]}^{-1}$. We then have the following main theorem on the estimation error bound and edge selection.

Theorem 2. Under the model of Theorem 1 and additional Assumptions (3) and (4), assume that ε is a sub-Gaussian random vector with parameter σ². Let Γ̂ be the estimate of Γ from Step 1 of two-stage procedure and Θ̂_Γ̂ be the unique solution in Step 3 of the procedure, that is

$${\mathrm{\Theta ̂}}_{\mathrm{\Gamma ̂}}≔\text{arg}\underset{\mathrm{\Theta }\succ 0}{\text{min}}\{\mathrm{t}\mathrm{r}(\mathrm{\Theta }{\mathrm{\Sigma ̂}}_{\mathrm{\Gamma ̂}})-\text{log det}\mathrm{\Theta }+{\lambda }_n{\Vert \mathrm{\Theta }\Vert }_{1,\text{off}}\},$$

where Σ̂_Γ̂ is defined in (3). Suppose that d₂ in Γ* satisfies the following upper bound

$$d_2<\frac{\gamma }{2M_n(X,T,{\mathrm{\Sigma }}^{*})\sqrt{{\mathrm{\Lambda }}_{\text{max}}}}\sqrt{\frac{\text{log}{q}_n}{\text{log}{p}_n+\text{log}{q}_n}}\times \left[\sqrt{\{\frac{C^{*}}{\text{log}{q}_n}\sqrt{2n(\text{log}4+\tau \text{log}{p}_n)}+1\}-1}\right],$$

where $C^{*}=4(1+4{\sigma }^2)(1-\sqrt{2/\tau })$, and tuning parameter ρ_n satisfies

$$\frac{2}{\gamma }\sqrt{\frac{2{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}\text{log}(p_n{q}_n)}{n}}<{\rho }_n^2<\frac{1-\sqrt{2/\tau }}{C_2{M}_2{(X,T,{\mathrm{\Sigma }}^{*})}^2{\mathrm{\Lambda }}_{\text{max}}{d}_2^2}\sqrt{\frac{\text{log}4+\tau \text{log}{p}_n}{C_{*}n},}$$

where C² is some constant. Choosing the regularization parameter

$${\lambda }_n=(8/\alpha ){\mathrm{\delta ̄}}_f(n,p_n^{\tau }).$$

If the sample size exceeds the lower bound

$$n>2(\text{log}4+\tau \text{log}{p}_n)\text{max}\{C_{*}^{*2}{d}_1^2{(1+\frac{8}{\alpha })}^2,1\},$$ (9)

where $C_{*}^{*}=48(1+4{\sigma }^2){\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}\text{max}\{K_{{\mathrm{\Sigma }}^{*}}{K}_{{\mathrm{\Omega }}^{*}},K_{{\mathrm{\Sigma }}^{*}}^3{K}_{{\mathrm{\Omega }}^{*}}^2\}$, then with probability greater than

$$1-\frac{4}{p_n^{{\tau }^{*}-2}}-8\text{exp}(-C_{1}n{\rho }_n^2)-2\text{exp}(-C_{2}n{\rho }_n^2)\to 1,$$

where

$${\tau }^{*}=\tau {(1-\frac{C_2{M}_n{(X,T,{\mathrm{\Sigma }}^{*})}^2{\mathrm{\Lambda }}_{\text{max}}{\rho }_n^2{d}_2^2\sqrt{C_{*}n}}{\sqrt{\text{log}4+\tau \text{log}{p}_n}})}^2>2,$$

we have:

1. The estimate Θ̂_Γ̂ satisfies the element-wise ℓ_∞-bound:

   $${\Vert {\mathrm{\Theta ̂}}_{\mathrm{\Gamma ̂}}-{\mathrm{\Theta }}^{*}\Vert }_{\infty }\le \{16\sqrt{2}(1+4{\sigma }^2)(1+8{\alpha }^{-1})\underset{i}{\text{max}}\{{\mathrm{\Sigma }}_{ii}^{*}\}{K}_{{\mathrm{\Omega }}^{*}}\}\sqrt{\frac{\text{log}4+\tau \text{log}{p}_n}{n}.}$$
2. The edge set E(Θ̂) is a subset of the true edge set E(Θ*) and includes all edges (i, j) with

   $$|{\mathrm{\Theta }}_{ij}^{*}|>\{16\sqrt{2}(1+4{\sigma }^2)(1+8{\alpha }^{-1})\underset{i}{\text{max}}\{{\mathrm{\Sigma }}_{ii}^{*}\}{K}_{{\mathrm{\Omega }}^{*}}\}\sqrt{(\text{log}4+\tau \text{log}{p}_n)/n}.$$

The proof of this theorem is based on the primal-dual witness method used in [5]. The key difference between our approach and that of [5] is the result on controlling the sampling noise. Define U ≔ Σ̂_Γ̂ − Σ*, where ${\mathrm{\Sigma ̂}}_{\mathrm{\Gamma ̂}}={\sum }_{i=1}^n(Y_i-\mathrm{\Gamma ̂}{X}_i){(Y_i-\mathrm{\Gamma ̂}{X}_i)}^{\top }/n$. Our proof is mainly on the control of ‖U‖_∞. As part of the proof of this theorem, a new result on controlling the sampling noise in our setting is given as Lemma 2 in the Appendix, taking into account that Γ has to be estimated. [5] on the other hand considered the model with zero mean and only has to consider the noise control for ${\sum }_{i=1}^n{Y}_i{Y}_i^{\top }/n-{\mathrm{\Sigma }}^{*}$. Theorem 2 indicates that we have the same bound on the element-wise ℓ_∞ norm of the discrepancy between the estimate and the truth as that in [5], but with a slower convergence probability, which is the price we pay for estimating Γ.

Based on the result on of the element-wise ℓ_∞ norm bound, we can get the results on Frobenius and spectral norm bounds. Denote s_n = |E(Θ*)| as the total number of off-diagonal non-zeros in Θ*. We have following corollary:

Corollary 1 (Rates in Frobenius and spectral norm). Under the same assumptions as Theorem 2, with probability at least $1-4/p_n^{{\tau }^{*}-2}-8\text{exp}(-C_{1}n{\rho }_n^2)-2\text{exp}(-C_{2}n{\rho }_n^2)$, the estimator Θ̂_Γ̂ satisfies

$${\Vert {\mathrm{\Theta ̂}}_{\mathrm{\Gamma ̂}}-{\mathrm{\Theta }}^{*}\Vert }_F\le \{2K_{{\mathrm{\Omega }}^{*}}(1+\frac{8}{\alpha })\}\sqrt{\frac{(s_n+p_n)(\text{log}4+\tau \text{log}{p}_n)}{C_{*}n},}{\Vert {\mathrm{\Theta ̂}}_{\mathrm{\Gamma ̂}}-{\mathrm{\Theta }}^{*}\Vert }_2\le \{2K_{{\mathrm{\Omega }}^{*}}(1+\frac{8}{\alpha })\}\text{min}(\sqrt{s_n+p_n,}{d}_1)\sqrt{\frac{\text{log}4+\tau \text{log}{p}_n}{C_{*}n},}$$

where $C_{*}={[128{(1+4{\sigma }^2)}^2{\text{max}}_i{\{{\mathrm{\Sigma }}_{ii}^{*}\}}^2]}^{-1}$.

Our final theoretical result is on sign consistency, which requires a lower bound on the minimum value of Θ*. Define ${\theta }_{\text{min}}≔{\text{min}}_{(i,j)\in E({\mathrm{\Theta }}^{*})}|{\mathrm{\Theta }}_{ij}^{*}|$ and the sign recovery event $ℳ(\mathrm{\Theta ̂},{\mathrm{\Theta }}^{*})≔\{\text{sign}({\mathrm{\Theta ̂}}_{ij})=\text{sign}({\mathrm{\Theta }}_{ij}^{*}),\forall (i,j)\in E({\mathrm{\Theta }}^{*})\}$. We have the following theorem on sign consistency:

Theorem 3. Under the same conditions as in Theorem 2, suppose that the sample size satisfies the lower bound

$$n>2(\text{log}4+\tau \text{log}{p}_n)\text{max}\{2K_{{\mathrm{\Omega }}^{*}}^2{(1+\frac{8}{\alpha })}^2{\theta }_{\text{min}}^{-2},{C_{*}}^2{d}_1^2{(1+\frac{8}{\alpha })}^2,1\},$$

then the estimator is model selection sign consistent with high probability,

$$pr(ℳ({\mathrm{\Theta ̂}}_{\mathrm{\Gamma ̂}},{\mathrm{\Theta }}^{*}))\ge 1-4/p_n^{{\tau }^{*}-2}-8\text{exp}(-C_{1}n{\rho }_n^2)-2\text{exp}(-C_{2}n{\rho }_n^2)\to 1.$$

5. Monte Carlo simulations

5.1. Models for comparisons and generation of data

We present results from Monte Carlo simulations to examine the performance of the proposed two-stage estimates. We simulated data to mimic genetical genomic data, where both binary genetic marker data and continuous gene expression data are simulated. We compare our estimate with several other procedures in terms of estimating the precision matrix and neighborhood selection, including the standard Gaussian graphical model implemented as GLASSO [13] using only the gene expression data, a procedure that iteratively updates the regression coefficient matrix and the precision matrix [9, 10] and a neighbor-based graphical model selection procedure of [14], where each gene is regressed on other genes and also the genetic markers using the ℓ₁ regularized regression, and a link is defined between gene i and j if gene i is selected for gene j and gene j is also selected by gene i. Note that in our setting, the neighbor-based procedure does not provide an estimate of the precision matrix. For each simulated data set, we chose the tuning parameters ρ and λ based on the BIC.

To compare the performance of different estimators for the precision matrix, we use the quadratic loss function LOSS(Θ, Θ̂) = tr(Θ⁻¹Θ̂ − I)², where Θ̂ is an estimate of the true precision matrix Θ. We also compare ‖Δ‖_∞, ‖|Δ|‖_∞, ‖Δ‖₂ and ‖Δ‖_F, where Δ = Θ − Θ̂ is the difference between the true precision matrix and its estimate. In order to compare how different methods recover the true graphical structures, we consider the specificity (SPE), sensitivity (SEN) and Matthews correlation coefficient (MCC) scores, which are defined as

$$\mathrm{S}\mathrm{P}\mathrm{E}=\mathrm{T}\mathrm{N}/(\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}),\mathrm{S}\mathrm{E}\mathrm{N}=\mathrm{T}\mathrm{P}/(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}),$$

and

$$\mathrm{M}\mathrm{C}\mathrm{C}=(\mathrm{T}\mathrm{P}\times \mathrm{T}\mathrm{N}-\mathrm{F}\mathrm{P}\times \mathrm{F}\mathrm{N})/\{(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P})(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N})(\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P})(\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{N})\},$$

where TP, TN, FP and FN are the numbers of true positives, true negatives, false positives and false negatives in identifying the non-zero elements in the precision matrix. Here we consider the non-zero entry in a sparse precision matrix as “positive.”

In the following simulations, we consider a general sparse precision matrix, where we randomly generate a link (i.e., non-zero elements in the precision matrix, indicated by δ_ij) between variables i and j with a success probability proportional to 1/p. Similar to the simulation setup of Li and Gui [15], Fan et al. [16] and Peng et al. [17], for each link, the corresponding entry in the precision matrix is generated uniformly over [−1, −0.5]∪[0.5, 1]. Then for each row, every entry except the diagonal one is divided by the sum of the absolute value of the off-diagonal entries multiplied by 1.5. Finally the matrix is symmetrized and the diagonal entries are fixed at 1. To generate the p × q coefficient matrix Γ = (γ_ij), we first generated a p × q sparse indicator matrix (δ_ij), where δ_ij = 1 with a probability proportional to 1/q. If δ_ij = 1, we generated γ_ij from Unif ([υ_m, 1] ∪ [−1, −υ_m]), where υ_m is the minimum absolute non-zero value of Θ generated.

After Γ and Θ were generated, we generated the marker genotypes X = (X₁, ⋯, X_q) by assuming X_i ~ Bernoulli(1, 1/2), for i = 1, ⋯, q. Finally, given X, we generated Y the multivariate normal distribution Y |X ~ 𝒩(ΓX, Σ). For a given model and a given simulation, we generated a data set of n independent and identically distributed random vectors (X, Y). The simulations were repeated 50 times.

5.2. Simulation results

We first consider the setting when the sample size n is larger than the number of genes p and the number of genetic markers q. We simulated data from three models with different values of p, q (See Table 1 Model 1 – Model 3) and present the simulation results in Table 2. We observe that the two-stage procedure performs very similarly to the iterative procedure. Clearly, the two-stage procedure and the iterative procedure provide much improved estimates of the precision matrix over the Gaussian graphical model for all three models considered in all measurements. This is expected since the Gaussian graphical model assumes a constant mean of the multivariate vector, which is a misspecified model. In addition, the two-stage procedure resulted in higher sensitivities, specificities and MCC than the Gaussian graphical model and the neighbor-based method. We observed that the Gaussian graphical model often resulted in much denser graphs than the real graphs. This is partially due to the fact that some of the links identified by Gaussian graphical model can be explained by shared common genetic variants. By assuming constant means, in order to compensate for the model misspecification, the Gaussian graphical tends to identify many non-zero elements in the precision matrix. The results indicate that by adjusting the effects of the covariates on the means, we can reduce both false positives and false negatives in identifying the non-zero elements of the precision matrix. The neighbor-based selection procedure using multiple LASSO accounts for the genetic effects in modeling the relationship among the genes. It performed better than the Gaussian graphical in graph structure selection, but worse than the two-stage procedure. This procedure, however, did not provide an estimate of the precision matrix.

Table 1.

Six models considered in simulations, where p is the number of the variables, q is the number of covariates and n is the sample size. pr(Θ_ij ≠ 0) and pr(Γ_ij ≠ 0) specify the sparsity of the model.

Model	(p, q, n)	pr(Θij ≠ 0)	pr(Γij ≠ 0)
1	(100, 100, 250)	2/p	3/q
2	(50, 50, 250)	2/p	4/q
3	(25, 10, 250)	2/p	3.5/q
4	(1000, 200, 250)	1.5/p	20/q
5	(800, 200, 250)	1.5/p	25/q
6	(400, 200, 250)	2.5/p	20/q

Table 2.

Comparison of the performances on estimating the precision matrix Θ by the two-stage procedure, the iterative selection procedure of [10], a neighbor-based selection procedure [14] and the Gaussian graphical model using glasso [13], where Δ = Θ − Θ̂.

Method	AUC	SPE	SEN	MCC	‖Δ‖∞	‖|Δ|‖∞	‖Δ‖2	‖Δ‖F
Model 1: (p, q, n)=(100, 100, 250)
Two-stage	0.91	0.99	0.49	0.56	0.32	1.18	0.68	3.24
Iterative	0.91	0.99	0.48	0.56	0.33	1.17	0.67	3.18
glasso	0.81	0.97	0.24	0.21	0.69	1.89	1.12	5.19
Neighbor	0.86	0.99	0.38	0.48
Model 2: (p, q, n)=(50, 50, 250)
Two-stage	0.91	0.97	0.69	0.65	0.35	1.31	0.73	2.43
Iterative	0.92	0.98	0.69	0.66	0.37	1.30	0.72	2.36
glasso	0.74	0.87	0.37	0.18	0.75	2.12	1.20	4.57
Neighbor	0.88	0.95	0.60	0.48
Model 3: (p, q, n)= (25, 10, 250)
Two-stage	0.89	0.91	0.76	0.62	0.23	0.90	0.51	1.20
Iterative	0.89	0.91	0.76	0.62	0.24	0.90	0.52	1.21
glasso	0.57	0.43	0.73	0.12	0.65	1.99	1.12	2.77
Neighbor	0.85	0.84	0.68	0.44
Model 4: (p, q, n)=(1000, 200, 250)
Two-stage	0.93	1	0.32	0.51	0.46	1.77	0.91	13.42
Iterative	0.90	1	0.31	0.47	0.59	1.81	0.97	13.48
glasso	0.88	0.98	0.08	0.02	0.71	2.86	1.31	19.82
Neighbor	0.87	1	0.12	0.16
Model 5: (p, q, n)=(800, 200, 250)
Two-stage	0.93	1	0.21	0.45	0.48	1.80	0.97	12.58
Iterative	0.89	1	0.21	0.34	0.75	2.30	1.20	12.82
glasso	0.87	0.97	0.07	0.02	0.76	2.97	1.40	18.39
Neighbor	0.87	0.96	0.61	0.19
Model 6: (p, q, n)=(400, 200, 250)
Two-stage	0.79	1	0.05	0.20	0.39	1.56	0.79	7.13
Iterative	0.75	1	0.05	0.21	0.44	1.55	0.77	6.86
glasso	0.71	0.95	0.03	−0.01	0.69	2.72	1.22	11.01
Neighbor	0.73	0.99	0.08	0.10

We next consider the setting when p > n and simulated data from three models with different values of n, p and q (see Table 1 Model 4 – Model 6). Note that for all three models, the graph structure is very sparse due to the large number of genes considered. The performances over 50 replications are reported in Table 2 for the optimal tuning parameters chosen by the BIC. For all three models, we observed much improved estimates of the precision matrix from the proposed two-stage procedure as reflected by smaller norms of the difference between the true and estimated precision matrices. In terms of graph structure selection, in general, we observe that when p is larger than the sample size, the sensitivities from all four procedures are much lower than the settings when the sample size is larger. This indicates that recovering the graph structure in a high-dimensional setting is statistically difficult. However, the specificities are in general very high, agreeing with our theoretical result of the estimates.

Finally, Table 3 presents the comparison of the estimates of Γ of three different procedures. Overall, we observe no differences in estimates of Γ from the two-stage and the iterative procedures, both perform better than the neighbor-based procedure.

Table 3.

Comparison of the performances on estimating the regression coefficient matrix Γ from the two-stage procedure, an iterative selection procedure of [10] and a neighbor-based procedure [14], where Δ = Γ − Γ̂.

Algorithm	AUC	SPE	SEN	MCC	‖Δ‖∞	‖|Δ|‖∞	‖Δ‖F
Model 1: (p, q, n)=(100,100,250)
Two-stage	0.98	0.99	0.87	0.77	0.38	1.03	2.39
Iterative	0.98	0.98	0.90	0.64	0.36	1.01	2.16
Neighbor	0.97	0.99	0.87	0.78	0.38	1.06	2.39
Model 2: (p, q, n)=(50,50,250)
Two-stage	0.98	0.99	0.89	0.84	0.37	1.65	2.48
Iterative	0.98	0.98	0.90	0.81	0.36	1.70	2.32
Neighbor	0.97	0.96	0.91	0.75	0.35	1.48	2.21
Model 3: (p, q, n)=(25,10,250)
Two-stage	0.98	0.75	0.98	0.68	0.24	0.74	0.97
Iterative	0.97	0.81	0.98	0.74	0.25	0.75	1
Neighbor	0.98	0.90	0.95	0.81	0.31	1.02	1.30
Model 4: (p, q, n)=(1000,200,250)
Two-stage	0.96	1	0.82	0.82	0.48	1.90	11.86
Iterative	0.96	1	0.83	0.79	0.62	2.98	11.98
Neighbor	0.83	1	0.65	0.80	0.81	3.51	18.75
Model 5: (p, q, n)=(800,200,250)
Two-stage	0.97	1	0.83	0.82	0.48	2.49	11.69
Iterative	0.96	1	0.81	0.79	0.89	6.52	12.75
Neighbor	0.79	0.97	0.77	0.46	0.76	4.21	14.48
Model 6: (p, q, n)=(400,200,250)
Two-stage	0.96	1	0.82	0.82	0.45	2.03	7.29
Iterative	0.96	0.99	0.86	0.65	0.44	2.27	6.40
Neighbor	0.86	1	0.78	0.83	0.56	2.64	8.35

6. Real data analysis

To demonstrate the proposed method, we present results from the analysis of a data set generated by [18], where 112 yeast segregants, one from each tetrad, were grown from a cross involving parental strains BY4716 and wild isolate RM11-1A and gene expression levels of 6,216 genes were measured. These 112 segregants were individually genotyped at 2,956 marker positions throughout the genome. Since many of these markers are in high linkage disequilibrium, we combined the markers into 585 blocks where the markers within a block differed by at most one sample. For each block, we chose the marker that had the least number of missing values as the representative marker.

To demonstrate our methods, we focused our analysis on a set of genes of the protein-protein interaction (PPI) network obtained from a previously compiled set by [19] combined with protein physical interactions deposited in Munich information center for protein sequences. We further selected 1,207 genes with variance greater than 0.05. Based on the most recent yeast protein-protein interaction database BioGRID [20], there are a total of 7,619 links among these 1,207 genes. Our goal is to construct a conditional independent network among these genes based on the sparse Gaussian graphical model adjusting for possible genetic effects on gene expression levels.

Results from several different procedures are summarized in Table 4. We observe that the neighbor-based method resulted in sparsest graph and the standard Gaussian graphical model without adjusting for the effects of genetic markers resulted in the densest graph, and the two-stage procedure was in between. A summary of the degrees of the graphs estimated by these three procedures is given in Table 4. We observe that the standard Gaussian graphical model gave a much denser graph than the other two procedures, agreeing with what we observed in simulation studies. The Gaussian graphical selected a lot more links than the other two methods, among the links that were identified by the Gaussian graphical model only, 476 pairs are associated with at least one common genetic marker based on the two-stage procedure, further explaining that some of the links identified by gene expression data alone can be due to shared comment genetic variants. The neighbor-based selection procedure identified only 1,917 edges, out of which 1880 were identified by the two-stage procedure and 1,916 were identified by the graphical model. There was a common set of 1749 links that were identified by all three procedures.

Table 4.

Comparison of the results of the two-stage procedure, the neighbor-based procedure [14] and the Gaussian graphical model using glasso [13] for the yeast protein-protein interaction data where n = 112, p = 1207, q = 578.

	Two-stage	Neighbor	Gaussian graph
No. of edges in Θ̂	13522	7518	18987
No. of links in Γ̂	1030	330	NA
Tuning parameter	(0.326, 0.362)	0.324	0.224
Mean degree	27.16	3.18	31.5
Max degree	53	12	60

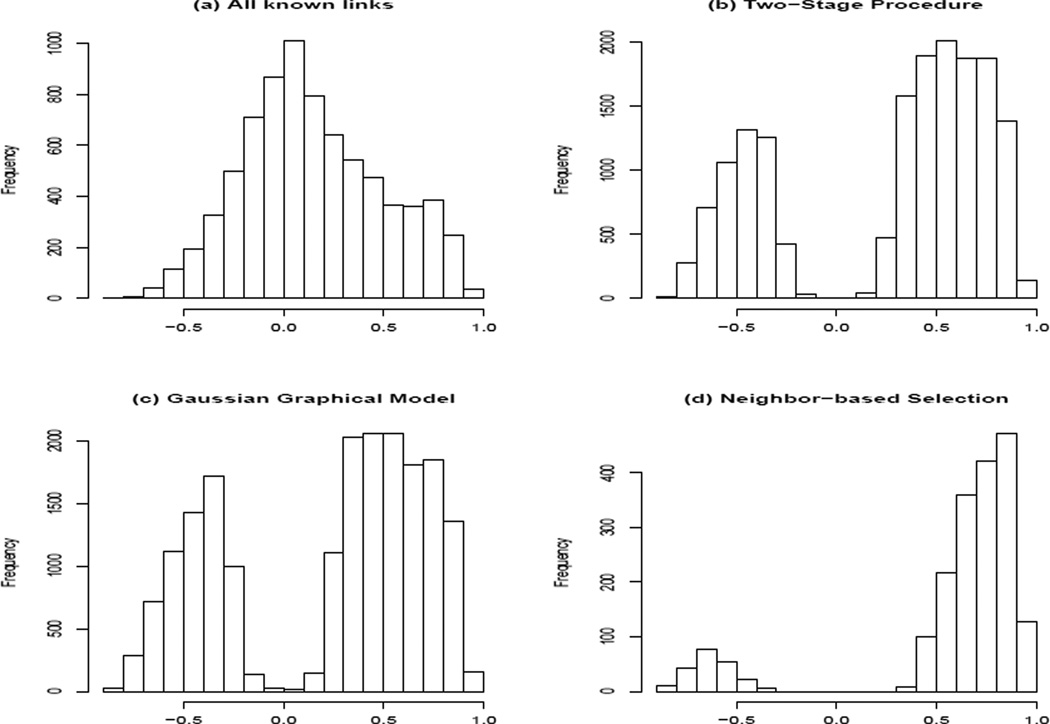
If we treat the PPI of the BioGRID database as the true network among these genes, the true positive rate from the two-stage procedure, the Gaussian graphical model and the neighbor-based selection procedure was 0.068, 0.071 and 0.019, respectively, and the false positive rate was 0.018, 0.026 and 0.0025, respectively. The reason for having low true positive rates is that many of the protein-protein interactions cannot be reflected at the gene expression level. Figure 1 (a) shows the histogram of the correlations of genes that are linked on the BioGRID PPI network, indicating that many linked gene pairs have very small marginal correlations. The Gaussian graphical models are not able to recover these links. Figure 1 plots (b) – (d) show the marginal correlations of the gene pairs that were identified by the two-stage procedure, the Gaussian graphical model and the neighbor-based procedure, clearly indicating that the linked genes identified by the two-stage procedure have higher marginal correlations. In contrast, some linked genes identified by the Gaussian graphical model have quite small marginal correlations.

Figure 1.

Histograms of marginal correlations for pairs of linked genes based on BioGRID (a) and linked genes identified by the two-stage procedure (b), the Gaussian graphical model (c) and a neighbor-based selection procedure (d).

7. Discussion

The proposed two-stage procedure is computationally efficient through coordinate descent algorithm and can be applied to high dimensional settings. Our simulation results show that this two-stage procedure performs very similarly to the iterative procedure of [9, 10]. To ensure model selection consistency and to derive the estimation bounds, our main theoretical assumption is an irrepresentable or mutual incoherence condition on both the covariates matrix and the true precision matrix. These conditions are similar to those required for model selection consistency of the LASSO or precision matrix estimation. Compared to the asymptotic results in [10], the results in this paper provide more explicit bounds in different matrix norms and present conditions for correct sign support. Our theoretical results on the estimate of the precision matrix parallel to those in [5]. However, the proofs are more difficult since the estimation biases of the regression coefficients have to be accounted for when studying the properties of the estimate of the precision matrix. This is achieved by proving an important lemma on control of sampling noise.

Partially due to computational consideration, we used the ℓ₁-penalization to obtain sparse results for both regression coefficient matrix and the precision matrix. However, other non-convex penalty functions can be applied in our two-stage algorithm, although computationally the optimizations are more challenging. Alternatively, one can extend the Dantzig selector [21] to estimate the regression coefficient matrix and the constrained ℓ₁ minimization [22] to estimate the precision matrix. It would be interesting to compare the performances of these different approaches. Finally, we can also consider to impose low-rank sparsity in stage 1 of the estimation using a penalty proportional to the rank of Γ [23]. This approach yields a closed form solution and different rates of convergence. It is interesting to compare these alternatives with the proposed approach in this paper.

Appendix

We present the proofs of the theorems in this Appendix. Proof of Theorem 1 extends that of [11] to multiple regressions and coefficient matrix settings. The key of the proof of Theorem 2 is a lemma on control of sampling noise, which we present detailed proof. Using this lemma, the proof of Theorem 2 is mainly based on the technique of primal-dual witness method [5].

Proof of Theorem 1.

From equation (2) and the model Y_i = Γ*X_i+ε_i, the estimation equation becomes

$$(\mathrm{\Gamma }-{\mathrm{\Gamma }}^{*})C_X-\frac{1}{n}{W}^{\top }X+{\rho }_{n}B=0,$$

where B is the sub-differential of ‖Γ‖₁, defined as B_ij = sign(Γ_ij) if Γ_ij ≠ 0 and ∈ [−1, 1], if Γ_ij = 0. With these definitions, we have the following lemma

Lemma 1. (a) A matrix Γ̂ ∈ ℝ^p×q is optimal to the ℓ₁ penalization problem (2) if and only if there exists an element B̂ of the sub-differential ∂‖Γ̂‖₁ such that

$$(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})C_X-\frac{1}{n}{W}^{\top }X+{\rho }_n\mathrm{B̂}=0.$$

(b) Suppose that the sub-different matrix satisfies the strict dual feasibility condition |B̂_ij| < 1 for all (i, j) ∉ T(Γ̂). Then any optimal solutione Γ̃ to the ℓ₁ penalization problem (2) satisfiese Γ_ij = 0 for all (i, j) ∉ T(Γ̂).

(c) Under the condition of part (b), if the |T(Γ̂)|×|T(Γ̂)| matrix (C_X⊗I_p)_{T(Γ̂),T(Γ̂)} is invertible, then Γ̂ is the unique optimal solution of the ℓ₁ penalization problem (2).

Similar technique as in [11] can be used to prove this Lemma. From Lemma 1, we know that strict dual feasibility conditions are sufficient to ensure the uniqueness of Γ̂. We construct the primal-dual witness solution (Γ̃, B̃) as follows:

1. First, we determine the matrix Γ̃ by solving the restricted LASSO problem

   $$\mathrm{\Gamma ̃}=\text{arg}\underset{{\mathrm{\Gamma }}_{T^c}=0}{\text{min}}\{\frac{1}{2n}\sum _{i=1}^n\mathrm{t}\mathrm{r}\{(Y_i-\mathrm{\Gamma }{X}_i){(Y_i-\mathrm{\Gamma }{X}_i)}^{\top }\}+{\rho }_n{\Vert \mathrm{\Gamma }\Vert }_1\}.$$ (.1)

2. Second, we choose B̃_T as an element of the sub-differential of the regularizer ‖ · ‖₁, evaluated at Γ̃.

3. Third, we set e B̃_T^c to satisfy the zero sub-differential condition (.1), and check whether or not the dual feasibility condition B̃_ij ≤ 1 for all (i, j) ∈ T^c is satisfied. To ensure the uniqueness, we check for strict dual feasibility B̃_ij < 1 for all (i, j) ∈ T^c.

4. Fourth, we check whether the sign consistency condition ${\mathrm{B̃}}_T=\text{sign}({\mathrm{\Gamma }}_T^{*})$ is satisfied.

PROOF OF THEOREM 1. From the primal-dual witness construction, denote Λ = Γ̃ − Γ*, where Γ̃ is the solution to (.1) and Γ* is the true parameter. The equation (.1) can be rewritten as:

$${(C_X\otimes I_p)}_{T,T}{\mathrm{\Lambda ̅}}_T-\frac{1}{n}{(X^{\top }\otimes I_p)}_{T,·}\overline{W^{\top }}+{\rho }_n{\overline{\tilde{B}}}_T=0,$$ (.2)

$${(C_X\otimes I_p)}_{T^c,T}{\mathrm{\Lambda ̅}}_T-\frac{1}{n}{(X^{\top }\otimes I_p)}_{T^c,·}\overline{W^{\top }}+{\rho }_n{\overline{\tilde{B}}}_{T^c}=0.$$ (.3)

Since Λ̅_T^c = 0, in order to establish strict dual feasibility, we need to check whether ${\Vert {\overline{\tilde{B}}}_{T^c}\Vert }_{\infty }<1$. From (.2), we have

$${\mathrm{\Lambda ̅}}_T={[{(C_X\otimes I_p)}_{T,T}]}^{-1}[\frac{1}{n}{(X^{\top }\otimes I_p)}_{T,·}\overline{W^{\top }}-{\rho }_n{\overline{\tilde{B}}}_T],$$

substituting this into (.3) leads to

$${\overline{\tilde{B}}}_{T^c}=-\frac{1}{{\rho }_n}{(C_X\otimes I_p)}_{T^c,T}{[{(C_X\otimes I_p)}_{T,T}]}^{-1}[\frac{1}{n}{(X^{\top }\times I_p)}_{T,·}\overline{W^{\top }}-{\rho }_n{\overline{\tilde{B}}}_T]+{(C_X\otimes I_p)}_{T^c,T}{[{(C_X\otimes I_p)}_{T,T}]}^{-1}{\overline{\tilde{B}}}_T·=\frac{1}{n{\rho }_n}{(X^{\top }\otimes I_p)}_{T^c,·}\{I_{np}-{(\frac{1}{n}X\otimes I_p)}_{·,T}{[{(C_X\otimes I_p)}_{T,T}]}^{-1}{(X^{\top }\otimes I_p)}_{T,·}\}\times \overline{W^{\top }}+{(C_X\otimes I_p)}_{T^c,T}{[{(C_X\otimes I_p)}_{T,T}]}^{-1}{\overline{\tilde{B}}}_T=(\mathrm{I})+(\mathrm{I}\mathrm{I}).$$ (.4)

For the second term (II) of (.4), from the Assumption (1) and ${\Vert {\overline{\tilde{B}}}_{T^c}\Vert }_{\infty }\le 1$, we have

$${\Vert {(C_X\otimes I_p)}_{T^c,T}{[{(C_X\otimes I_p)}_{T,T}]}^{-1}{\overline{\tilde{B}}}_T\Vert }_{\infty }<1-\gamma .$$

From the sub-Gaussian (sG for short) distribution assumption on ε, $\overline{W^{\top }}~sG(0,I_n\otimes {\mathrm{\Sigma }}^{*})$. Denote the projection matrix as

$${\Pi }_{{(C_X\otimes I_p)}_{T,T}}≔I_{np}-{(\frac{1}{n}X\otimes I_p)}_{·,T}{[{(C_X\otimes I_p)}_{T,T}]}^{-1}{(X^{\top }\otimes I_p)}_{T,·}≔I_{np}-A.$$

Choosing a particular element (j, i) in the first term (I) of (.4),

$$\frac{1}{n{\rho }_n}(X^{(j)T}\otimes {\mathbf{e}}_i^{\top })(I_{np}-A)\overline{W^{\top }}$$

with $\overline{W^{\top }}~sG(0,I_n\otimes {\mathrm{\Sigma }}^{*})$ and e_i is ith row of identity matrix I_p, then

$$\frac{1}{n{\rho }_n}(X^{(j)T}\otimes {\mathbf{e}}_i^{\top })(I_{np}-A)\overline{W^{\top }}~sG(0,{\sigma }_{(j,i)}^2),$$

where using the fact that I_np − A is a projection matrix and the condition (7) in the theorem, we have

$${\sigma }_{(j,i)}^2=\frac{1}{n^2{\rho }_n^2}(X^{(j)T}\otimes {\mathbf{e}}_i^{\top })(I_{np}-A)(I_n\otimes {\mathrm{\Sigma }}^{*})(I_{np}-A)(X^{(j)}\otimes {\mathbf{e}}_i)\le \frac{1}{n^2{\rho }_n^2}(X^{(j)T}{X}^{(j)})\otimes ({\mathbf{e}}_i^{\top }{\mathrm{\Sigma }}^{*}{\mathbf{e}}_i)\le \frac{1}{n{\rho }_n^2}{\mathrm{\Sigma }}_{ii}^{*}\le \frac{1}{n{\rho }_n^2}\underset{i}{\text{max}}({\mathrm{\Sigma }}_{ii}^{*}).$$

By applying the Chernoff bound, we have,

$$\mathrm{p}\mathrm{r}(\underset{i}{\text{max}}\underset{j\in {(T(i))}^c}{\text{max}}|{(\mathrm{I})}_{(j,i)}|\ge t)\le 2(p_n{q}_n-k_n)\text{exp}\{-\frac{n{\rho }_n^2{t}^2}{2{\text{max}}_i({\mathrm{\Sigma }}_{ii}^{*})}\},$$

where (I)(_j,i) is the (j, i)th element in the first term (I) in (.4) and k_n is the number of nonzero elements in the true parameter Γ*. Setting t = γ/2 yields

$$\mathrm{p}\mathrm{r}(\underset{i}{\text{max}}\underset{j\in {(T(i))}^c}{\text{max}}|{(\mathrm{I})}_{(j,i)}|\ge \frac{\gamma }{2})\le 2\text{exp}\{\frac{n{\rho }_n^2{\gamma }^2}{8{\text{max}}_i({\mathrm{\Sigma }}_{ii}^{*})}+\text{log}(p_n{q}_n-k_n)\}.$$

Putting together the pieces and using our choice (8) of ρ_n, we have

$$\mathrm{p}\mathrm{r}({\Vert {\overline{\tilde{B}}}_{T^c}\Vert }_{\infty }>1-\frac{\gamma }{2})\le 2\text{exp}(-c_{1}n{\rho }_n^2)\to 0,$$

for some constant c₁. So from Lemma 1, the estimated support T̂(Γ̂) is contained in the support T̃ hence in the true support T*(Γ*) with probability at least $1-2\text{exp}(-c_{1}n{\rho }_n^2)$.

Next we establish the ℓ_∞ bounds, from (.4) we know

$${\overline{{\mathrm{\Lambda }}^{*}}}_T≔{(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})}_T={[{(C_X\otimes I_p)}_{T,T}]}^{-1}[\frac{1}{n}{(X^{\top }\otimes I_p)}_{T,·}\overline{W^{\top }}-{\rho }_n{\overline{\widehat{B}}}_T],$$

where B̂_T is in the sub-differential of ‖Γ̂‖₁. So

$${\Vert {\overline{{\mathrm{\Lambda }}^{*}}}_T\Vert }_{\infty }\le {\Vert {[{(C_X\otimes I_p)}_{T,T}]}^{-1}{(X^{\top }\otimes I_p)}_{T,·}\frac{1}{n}\overline{W^{\top }}\Vert }_{\infty }+{\rho }_n{\Vert |{[{(C_X\otimes I_p)}_{T,T}]}^{-1}|\Vert }_{\infty }$$

Note that the second term in (.4) is a fixed term. Since $\overline{W^{\top }}~sG(0,I_n\otimes {\mathrm{\Sigma }}^{*})$, then

$${[{(C_X\otimes I_p)}_{T,T}]}^{-1}{(X^{\top }\otimes I_p)}_{T,·}\frac{1}{n}\overline{W^{\top }}~sG(0,\mathrm{\Omega }),$$

where

$$\mathrm{\Omega }=\frac{1}{n^2}{[{(C_X\otimes I_p)}_{T,T}]}^{-1}{(X^{\top }\otimes I_p)}_{T,·}(I_n\otimes {\mathrm{\Sigma }}^{*}){(X\otimes I_p)}_{·,T}{[{(C_X\otimes I_p)}_{T,T}]}^{-1}=\frac{1}{n}{[{(C_X\otimes I_p)}_{T,T}]}^{-1}{(C_X\otimes {\mathrm{\Sigma }}^{*})}_{T,T}{[{(C_X\otimes I_p)}_{T,T}]}^{-1}.$$

Define the first term in (.4) as ξ, then the (j, i)-th element of ξ where j ∈ T(i) is distributed as sub-Gaussian with parameter σ², that is ξ_(j,i) ~ sG(0, σ²), with σ² ≤ 1/nC_max, where C_max is defined in the Assumption 2. Again from Chernoff bound,

$$\mathrm{p}\mathrm{r}(\underset{i}{\text{max}}\underset{j\in T(i)}{\text{max}}|{\xi }_{(j,i)}|>t)\le 2\text{exp}(-\frac{n{t}^2}{2C_{\text{max}}}+\text{log}{k}_n).$$

Setting $t={\rho }_n\gamma /2\sqrt{C_{\text{max}}/{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}}$, then $n{t}^2/2C_{\text{max}})=n{\rho }_n^2{\gamma }^2/(8{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\})$. Since ρ_n satisfies (8), $n{\rho }_n^2{\gamma }^2/(8{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\})>\text{log}(p_n{q}_n)>\text{log}(k_n)$. So $\mathrm{p}\mathrm{r}({\text{max}}_i{\text{max}}_{j\in T(i)}|{\xi }_{(j,i)}|>{\rho }_n\gamma /2\sqrt{C_{\text{max}}/{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}})$ vanishes at the rate at least $2\text{exp}(-c_{2}n{\rho }_n^2)$, where c₂ is a constant. Overall, we conclude that

$${\Vert \mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*}\Vert }_{\infty }\le {\rho }_n\{\frac{\gamma }{2}\sqrt{\frac{C_{\text{max}}}{{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}}}+{\Vert |{[{(C_X\otimes I_p)}_{T,T}]}^{-1}|\Vert }_{\infty }\}$$

with probability greater than $1-4\text{exp}(-C_{1}n{\rho }_n^2)$ where C₁ is a constant (for example C₁ can be chosen as min{c₁, c₂}). Thus assertion (1) in Theorem 1 is proved and the (2) directly follows when (1) is proved. Thus complete the proof of Theorem 1.

Proof of Theorem 2:

We define

$$M_n(X,T,{\mathrm{\Sigma }}^{*})={\Vert |{[{(C_X\otimes I_p)}_{T,T}]}^{-1}|\Vert }_{\infty }+\frac{\gamma }{2}\sqrt{\frac{C_{\text{max}}}{{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}}},$$

and C_max is the constant in Assumption 2. Define U ≔ Σ̂_Γ̂ − Σ*, where ${\mathrm{\Sigma ̂}}_{\mathrm{\Gamma ̂}}={\sum }_{i=1}^n(Y_i-\mathrm{\Gamma ̂}{X}_i){(Y_i-\mathrm{\Gamma ̂}{X}_i)}^{\top }/n$. Our proof is mainly on the control of ‖U‖_∞, which is the major difference between our Theorem 2 and Theorem 1 in [5]. We state this noise control result in the following lemma:

Lemma 2 (Control of Sampling Noise). Under the assumptions that log p_n = o(n), $\text{log}{q}_n=o(\sqrt{n})$, d₂ = o(q_n) and furthermore, for some real number τ > 2,

$$d_2<\frac{\gamma }{2M_n(X,T,{\mathrm{\Sigma }}^{*})\sqrt{{\mathrm{\Lambda }}_{\text{max}}}}\sqrt{\frac{\text{log}{q}_n}{\text{log}{p}_n+\text{log}{q}_n}}\times \{\sqrt{[\frac{C^{*}}{\text{log}{q}_n}\sqrt{2n(\text{log}4+\tau \text{log}{p}_n)}+1]}-1\},$$

where $C^{*}=4(1+4{\sigma }^2)(1-\sqrt{2/\tau })$ and Λ_max is the constant in Assumption 3 and σ is the parameter in the tail condition on ε_i. Choose a constant C₂ > 1, such that

$$C_2>1+\frac{\gamma }{M_n(X,T,{\mathrm{\Sigma }}^{*})\sqrt{{\mathrm{\Lambda }}_{\text{max}}}{d}_2}\sqrt{\frac{\text{log}{q}_n}{\text{log}{p}_n+\text{log}{q}_n}}.$$ (.5)

Assume the conditions in Theorem 1 are satisfied and in addition to the tuning parameter ρ_n satisfying condition (8), ρ_n also satisfies

$${\rho }_n^2<\frac{1-\sqrt{2/\tau }}{C_2{M}_n{(X,T,{\mathrm{\Sigma }}^{*})}^2{\mathrm{\Lambda }}_{\text{max}}{d}_2^2}\sqrt{\frac{\text{log}4+\tau \text{log}{p}_n}{C_{*}n}},$$

where $C_{*}={[128{(1+4{\sigma }^2)}^2{\text{max}}_i{\{{\mathrm{\Sigma }}_{ii}^{*}\}}^2]}^{-1}$. Under this condition, denote

$${\tau }^{*}=\tau {[1-\frac{C_2{M}_n{(X,T,{\mathrm{\Sigma }}^{*})}^2{\mathrm{\Lambda }}_{\text{max}}{\rho }_n^2{d}_2^2\sqrt{C_{*}n}}{\sqrt{\text{log}4+\tau \text{log}{p}_n}}]}^2>2,$$ (.6)

then

$$pr({\Vert U\Vert }_{\infty }\ge \sqrt{\frac{\text{log}4+\tau \text{log}{p}_n}{C_{*}n}})\le \frac{4}{p_n^{{\tau }^{*}-2}}+8\text{exp}\{-C_{1}n{\rho }_n^2\}+2\text{exp}\{-C_{2}n{\rho }_n^2\},$$

where C₁ and C₂ are constants.

PROOF OF LEMMA 2. From the definition of U, we have

$$U=\frac{1}{n}{W}^{\top }W-{({\mathrm{\Theta }}^{*})}^{-1}+(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})C_X{(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})}^{\top }-(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})(\frac{1}{n}{X}^{\top }W)-(\frac{1}{n}{W}^{\top }X){(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})}^{\top }.$$

We want to bound the element-wise ℓ_∞ norm ‖U‖_∞,

$${\Vert U\Vert }_{\infty }\le {\Vert \frac{1}{n}{W}^{\top }W-{({\mathrm{\Theta }}^{*})}^{-1}\Vert }_{\infty }+{\Vert (\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})C_X{(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})}^{\top }\Vert }_{\infty }+{\Vert (\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})(\frac{1}{n}{X}^{\top }W)\Vert }_{\infty }+{\Vert (\frac{1}{n}{W}^{\top }X){(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})}^{\top }\Vert }_{\infty }․\le {\Vert \frac{1}{n}{W}^{\top }W-{({\mathrm{\Theta }}^{*})}^{-1}\Vert }_{\infty }+{\Vert |(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})\otimes (\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})|\Vert }_{\infty }{\Vert C_X\Vert }_{\infty }+2{\Vert (\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})(\frac{1}{n}{X}^{\top }W)\Vert }_{\infty }.$$

Let 𝒜 be the event that T̂(Γ̂) ⊆ T(Γ*) and ${\Vert ({\mathrm{\Gamma ̂}}_T-{\mathrm{\Gamma }}_T^{*})\Vert }_{\infty }\le {\rho }_n{M}_n(X,T,{\mathrm{\Sigma }}^{*})$. Then $\mathrm{p}\mathrm{r}(𝒜)\ge 1-4\text{exp}(-C_{1}n{\rho }_n^2)$. Under event $𝒜,\overline{(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})(X^{\top }W/n)}={\{(W^{\top }X/n)\otimes I_p\}}_{·,T}\overline{{(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})}_T}$. So

$${\Vert (\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})(\frac{1}{n}{X}^{\top }W)\Vert }_{\infty }={\Vert {[(\frac{1}{n}{W}^{\top }X)\otimes I_p]}_{·,T}\overline{{(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})}_T}\Vert }_{\infty }\le {\Vert |{[(\frac{1}{n}{W}^{\top }X)\otimes I_p]}_{·,T}|\Vert }_{\infty }{\Vert {(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})}_T\Vert }_{\infty }.$$

So under event 𝒜,

$${\Vert U\Vert }_{\infty }\le \mathrm{I}+\mathrm{I}\mathrm{I}+\mathrm{I}\mathrm{I}\mathrm{I},$$

where

$$\mathrm{I}=\Vert \frac{1}{n}{W}^{\top }W-{({\mathrm{\Theta }}^{*})}^{-1}\Vert ,\mathrm{I}\mathrm{I}={\Vert |(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})\otimes (\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})|\Vert }_{\infty }{\Vert C_X\Vert }_{\infty },\mathrm{I}\mathrm{I}\mathrm{I}=2{\Vert |{[(\frac{1}{n}{W}^{\top }X)\otimes I_p]}_{·,T}|\Vert }_{\infty }{\Vert {(\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*})}_T\Vert }_{\infty }.$$

From Lemma 1 of [5] on sub-Gaussian tail condition, we have

$$\mathrm{p}\mathrm{r}(\mathrm{I}>\delta )\le 4p^2\text{exp}\{-\frac{n{\delta }^2}{128{(1+4{\sigma }^2)}^2{\text{max}}_i{\{{\mathrm{\Sigma }}_{ii}^{*}\}}^2}\}.$$ (.7)

Since λ_max(C_X) ≤ Λ_max, then ${\Vert C_X\Vert }_{\infty }\le {\mathrm{\Lambda }}_{\text{max}}{\Vert |\mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*}|\Vert }_{\infty }^2$ because of ‖| A ⊗ B |‖_∞ ≤ ‖|A|‖_∞ ‖|B|‖_∞. Then II ≤ Λ_max(d₂‖Γ̂ −Γ*‖_∞)². Under event 𝒜, T̂(Γ̂ ⊆ T(Γ*)) and ${\Vert \mathrm{\Gamma ̂}-{\mathrm{\Gamma }}^{*}\Vert }_{\infty }={\Vert {\mathrm{\Gamma ̂}}_T-{\mathrm{\Gamma }}_T^{*}\Vert }_{\infty }\le M_n(X,T,{\mathrm{\Sigma }}^{*}){\rho }_n$. So

$$\mathrm{p}\mathrm{r}(\mathrm{I}\mathrm{I}>{\mathrm{\Lambda }}_{\text{max}}{d}_2^2{g}^2({\rho }_n))\le 1-\mathrm{p}\mathrm{r}(𝒜)\le 4\text{exp}\{-C_{1}n{\rho }_n^2\}.$$

Next we bound (III).We know under event 𝒜, ‖(Γ̂−Γ*)^T‖_∞ ≤ ρ_nM_n(X, T,Σ*). We need further bound each row’s ℓ₁ norm in [(W^⊤X/n)⊗I_p]_·,T. Since $\overline{W^{\top }X/n}$ is a p_nq_n × 1 random vector with mean zero and covariance matrix C_X ⊗ Σ*/n, for certain index (i, j), the (i, j)-th row in [(W^⊤X/n) ⊗ I_p]_·,T is $[e_i^{\top }(W^{\top }X/n)]\otimes e_j^{\top }$, and e_i, e_j ∈ ℝ^p are the simple base functions for i, j = 1, ⋯, p. Since $\overline{e_i^{\top }(W^{\top }X/n)}=(I_q\otimes e_i^{\top })\overline{(W^{\top }X/n)},\overline{e_i^{\top }(W^{\top }X/n)}$ is with mean zero and covariance matrix

$$(I_q\otimes e_i^{\top })(\frac{1}{n}{C}_X\otimes {\mathrm{\Sigma }}^{*})(I_q\otimes e_i)=\frac{1}{n}{C}_X\otimes {\mathrm{\Sigma }}_{ii}^{*}=\frac{1}{n}{\mathrm{\Sigma }}_{ii}^{*}{C}_X.$$

The non-zero elements in $[e_i^{\top }(W^{\top }X/n)]\otimes e_j^{\top }$ is ${[e_i^{\top }(W^{\top }X/n)]}_{T(j)}\otimes 1$, so $\overline{{[e_i^{\top }(W^{\top }X/n)]}_{T(j)}}$ is mean zero with covariance matrix $\frac{1}{n}{\mathrm{\Sigma }}_{ii}^{*}{(C_X)}_{T(j),T(j)}$, and ‖|[(W^⊤X/n) ⊗ I_p]_·,T|‖_∞ equals the maximum value for all (i, j) pair, the ℓ₁ norm of $\overline{{[e_i^{\top }(W^{\top }X/n)]}_{T(j)}}$. Obviously variables in vector $\overline{{[e_i^{\top }(W^{\top }X/n)]}_{T(j)}}$ are sub-Gaussian. In next lemma, we bound the ℓ₁ norm of such type of sub-Gaussian vectors.

Lemma 3. For any j ∈ {1, ⋯, p}, let T(j) be defined as before. Suppose that |T(j)| ≥ 1. If y ∈ ℝ^|T(j)| is a random vector with mean zero and covariance matrix ${\mathrm{\Sigma }}_{ii}^{*}{(C_X)}_{T(j),T(j)}/n$, and every variable in y is sub-Gaussian. Then

$$pr({\Vert y\Vert }_1>t)\le 2|T(j)|\text{exp}\{-\frac{n{t}^2}{2|T(j){|}^2{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}{\mathrm{\Lambda }}_{\text{max}}}\}.$$

PROOF OF LEMMA 3: First we have:

$$\mathrm{p}\mathrm{r}({\Vert y\Vert }_1>t)=\mathrm{p}\mathrm{r}(|y_1|+\cdots +|y_{|T(j)|}|>t)\le \mathrm{p}\mathrm{r}(|y_1|>\frac{t}{|T(j)|})+\cdots +\mathrm{p}\mathrm{r}(|y_{|T(j)|}|>\frac{t}{|T(j)|}).$$

Note that y_k is sub-Gaussian with parameter ${\mathrm{\Sigma }}_{ii}^{*}{(C_X)}_{kk}/n\le {\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}{\mathrm{\Lambda }}_{\text{max}}/n\forall k\in \{1,\cdots ,|T(j)|\}$ and i ∈ {1, ⋯, |T(j)|}. From Chernoff bound,

$$\mathrm{p}\mathrm{r}({\Vert y\Vert }_1>t)\le 2|T(j)|\text{exp}\{-\frac{n{t}^2}{2|T(j){|}^2{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}{\mathrm{\Lambda }}_{\text{max}}}\},$$

which completes the proof.

Since f(x) = x exp{−a/x²} for some a > 0 is an increasing function of x and ∀_j ∈ {1, ⋯, p}, |T(j)| ≤ d₂, we have

$$\mathrm{p}\mathrm{r}({\Vert |{[(\frac{1}{n}{W}^{\top }X)\otimes I_p]}_{·,T}|\Vert }_{\infty }>t)\le 2d_2\text{exp}\{-\frac{n{t}^2}{2d_2^2{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}{\mathrm{\Lambda }}_{\text{max}}}\}.$$ (.8)

If we choose $t^2=\frac{1}{4}{\mathrm{\Lambda }}_{\text{max}}{d}_2^2{\rho }_n^2{\gamma }^2\text{log}{q}_n/(\text{log}{p}_n+\text{log}{q}_n)$, we have

$$\frac{n{t}^2}{2d_2^2{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}{\mathrm{\Lambda }}_{\text{max}}}=\frac{n{\rho }_n^2{\gamma }^2}{8{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}}\frac{\text{log}{q}_n}{\text{log}{p}_n+\text{log}{q}_n}.$$

From the choice of ρ_n in (8), we can see

$$n{\rho }_n^2{\gamma }^2/[8\underset{i}{\text{max}}\{{\mathrm{\Sigma }}_{ii}^{*}\}(\text{log}{p}_n+\text{log}{q}_n)]>1,$$

so

$$\frac{n{t}^2}{2d_2^2{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}{\mathrm{\Lambda }}_{\text{max}}}>\text{log}{q}_n$$

and from the condition d₂ = o(q_n), we know in (.8), the exponential part dominates and converges to zero at some exponential rate. On the other hand the term on the exponential shoulder is bounded by $n{\rho }_n^2{\gamma }^2/[8{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}]=C_{2}n{\rho }_n^2$ for some constant $C_2>0(C_2={\gamma }^2/[8{\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}])$. Denote for any event B, $\mathrm{p}{\mathrm{r}}_{𝒜}^{*}(B)=\mathrm{p}\mathrm{r}(B\cap 𝒜)$, then

$$\mathrm{p}{\mathrm{r}}_{𝒜}({\Vert |{[(\frac{1}{n}{W}^{\top }X)\otimes I_p]}_{·,T}|\Vert }_{\infty }>\frac{1}{2}\sqrt{\frac{{\mathrm{\Lambda }}_{\text{max}}\text{log}{q}_n}{\text{log}{p}_n+\text{log}{q}_n}}\gamma d_2{\rho }_n)\le 2\text{exp}\{-C_{2}n{\rho }_n^2\}.$$

So

$$\mathrm{p}\mathrm{r}(\mathrm{I}\mathrm{I}\mathrm{I}>\sqrt{\frac{{\mathrm{\Lambda }}_{\text{max}}\text{log}{q}_n}{\text{log}{p}_n+\text{log}{q}_n}}\gamma d_2{\rho }_n^2{M}_n(X,T,{\mathrm{\Sigma }}^{*}))\le \mathrm{p}{\mathrm{r}}_{𝒜}(\mathrm{I}\mathrm{I}\mathrm{I}>\sqrt{\frac{{\mathrm{\Lambda }}_{\text{max}}\text{log}{q}_n}{\text{log}{p}_n+\text{log}{q}_n}}\gamma d_2{\rho }_n^2{M}_n(X,T,{\mathrm{\Sigma }}^{*}))+\mathrm{p}\mathrm{r}({𝒜}^c)\le \mathrm{p}{\mathrm{r}}_{𝒜}({\Vert |{[(\frac{1}{n}{W}^{\top }X)\otimes I_p]}_{·,T}|\Vert }_{\infty }>\frac{1}{2}\sqrt{\frac{{\mathrm{\Lambda }}_{\text{max}}\text{log}{q}_n}{\text{log}{p}_n+\text{log}{q}_n}}\gamma d_2{\rho }_n)+\mathrm{p}\mathrm{r}({𝒜}^c)$$

That is

$$\mathrm{p}\mathrm{r}(\mathrm{I}\mathrm{I}\mathrm{I}>\sqrt{\frac{{\mathrm{\Lambda }}_{\text{max}}\text{log}{q}_n}{\text{log}{p}_n+\text{log}{q}_n}}\gamma d_2{\rho }_n^2{M}_n(X,T,{\mathrm{\Sigma }}^{*}))\le 2\text{exp}\{-C_{2}n{\rho }_n^2\}+4\text{exp}\{-C_{1}n{\rho }_n^2\},$$ (.9)

where C₂ is defined above and C₁ is defined in Theorem 1.

Denote

$${\mathrm{\delta ̄}}_f(n,p_n^{\tau })=\sqrt{(\text{log}4+\tau \text{log}{p}_n)/(C_{*}n)},$$

where $C_{*}={[128{(1+4{\sigma }^2)}^2{\text{max}}_i{\{{\mathrm{\Sigma }}_{ii}^{*}\}}^2]}^{-1}$. Define

$$\alpha =\sqrt{\frac{{\mathrm{\Lambda }}_{\text{max}}\text{log}{q}_n}{\text{log}{p}_n+\text{log}{q}_n}}\frac{\gamma d_2{\rho }_n^2{M}_n(X,T,{\mathrm{\Sigma }}^{*})}{{\mathrm{\delta ̄}}_f(n,p_n^{\tau })}$$

and

$$\beta =\frac{{\mathrm{\Lambda }}_{\text{max}}{d}_2^2{M}_n{(X,T,{\mathrm{\Sigma }}^{*})}^2{\rho }_n^2}{{\mathrm{\delta ̄}}_f(n,p_n^{\tau })}.$$

So

$$\alpha +\beta =\frac{M_n{(X,T,{\mathrm{\Sigma }}^{*})}^2{\mathrm{\Lambda }}_{\text{max}}{\rho }_n^2{d}_2^2}{{\mathrm{\delta ̄}}_f(n,p_n^{\tau })}\times \left(1+\frac{\gamma }{M_n(X,T,{\mathrm{\Sigma }}^{*})\sqrt{{\mathrm{\Lambda }}_{\text{max}}{d}_2}}\sqrt{\frac{\text{log}{q}_n}{\text{log}{p}_n+\text{log}{q}_n}}\right)<\frac{C_2{M}_n{(X,T,{\mathrm{\Sigma }}^{*})}^2{\mathrm{\Lambda }}_{\text{max}}{\rho }_n^2{d}_2^2}{{\mathrm{\delta ̄}}_f(n,p_n^{\tau })}<1-\sqrt{\frac{2}{\tau }},$$

from the choice of C₂ in (.5) and inequality (.6). We have

$$\mathrm{p}\mathrm{r}({\Vert U\Vert }_{\infty }\ge {\mathrm{\delta ̄}}_f(n,p_n^{\tau }))\le \mathrm{p}\mathrm{r}(\mathrm{I}+\mathrm{I}\mathrm{I}+\mathrm{I}\mathrm{I}\mathrm{I}\ge {\mathrm{\delta ̄}}_f(n,p_n^{\tau }))\le \mathrm{p}\mathrm{r}(\mathrm{I}\ge (1-\alpha -\beta ){\mathrm{\delta ̄}}_f(n,p_n^{\tau }))+\mathrm{p}\mathrm{r}(\mathrm{I}\mathrm{I}\ge \beta {\mathrm{\delta ̄}}_f(n,p_n^{\tau }))+\mathrm{p}\mathrm{r}(\mathrm{I}\mathrm{I}\mathrm{I}\ge \alpha {\mathrm{\delta ̄}}_f(n,p_n^{\tau })).$$

Choosing the parameter $\delta =(1-\alpha -\beta ){\mathrm{\delta ̄}}_f(n,p_n^{\tau })$ in (.7), so from (.7),

$$\mathrm{p}\mathrm{r}(\mathrm{I}\ge (1-\alpha -\beta ){\mathrm{\delta ̄}}_f(n,p_n^{\tau }))\le 4p_n^2\text{exp}\left\{-{(1-\alpha -\beta )}^2[\text{log}4+\tau \text{log}{p}_n]\right\}=\frac{4^{1-{(1-\alpha -\beta )}^2}}{p_n^{\tau {(1-\alpha -\beta )}^2-2}}.$$

So

$$\mathrm{p}\mathrm{r}(\mathrm{I}\ge (1-\alpha -\beta ){\mathrm{\delta ̄}}_f(n,p_n^{\tau }))\le \frac{4}{p_n^{{\tau }^{*}-2}}$$

Note that

$$\beta {\mathrm{\delta ̄}}_f(n,p_n^{\tau })={\mathrm{\Lambda }}_{\text{max}}{d}_2^2{({\rho }_n{M}_n(X,T,{\mathrm{\Sigma }}^{*}))}^2$$

and

$$\alpha {\mathrm{\delta ̄}}_f(n,p_n^{\tau })=\gamma d_2{\rho }_n^2{M}_n(X,T,{\mathrm{\Sigma }}^{*})\sqrt{{\mathrm{\Lambda }}_{\text{max}}\text{log}{q}_n/[\text{log}{p}_n+\text{log}{q}_n]},$$

further with (.8) and (.9),

$$\mathrm{p}\mathrm{r}({\Vert U\Vert }_{\infty }\ge {\mathrm{\delta ̄}}_f(n,p_n^{\tau }))\le \frac{4}{p_n^{{\tau }^{*}-2}}+8\text{exp}\{-C_{1}n{p}_n^2\}+2\text{exp}\{-C_{2}n{\rho }_n^2\}.$$

Thus we proved Lemma 2.

Based on Lemma 2, the rest of the proof follows closely to the proof to Theorem 1 in [5]. We only outline the proof here.

Lemma 4. For any λ_n > 0 and sample covariance of ε_i based on the estimate Γ̂, Σ̂_Γ̂ with strictly positive diagonal, the ℓ₁-penalized log-determinant problem (4) has a unique solution Θ̂_Γ̂ ≻ 0 characterized by

$${\mathrm{\Sigma ̂}}_{\mathrm{\Gamma ̂}}-{\mathrm{\Theta ̂}}_{\mathrm{\Gamma ̂}}^{-1}+{\lambda }_nẐ=0,$$ (.10)

where Ẑ is an element of the sub-differential ∂‖Θ̂_Γ̂‖_1,off.

This lemma is a slightly revised version of Lemma 3 in [5] and hence we omit the proof here. Based on this lemma, we construct the primal-dual witness solution (Θ̃, Z̃) as follows:

1. Determine the matrix Θ̃ by solving the restricted log-determinant problem

   $$\mathrm{\Theta ̃}≔{\text{arg}}_{\mathrm{\Theta }\succ 0,}\underset{{\mathrm{\Theta }}_{S^c}=0}{\text{min}}\{\mathrm{t}\mathrm{r}({\mathrm{\Sigma ̂}}_{\mathrm{\Gamma ̂}}\mathrm{\Theta })-\text{log det}\mathrm{\Theta }+{\lambda }_n{\Vert \mathrm{\Theta }\Vert }_{1,\text{off}}\}.$$ (.11)

   Note that by construction, we have Θ̃ ≻ 0 and Θ̃_S^c = 0.

2. We choose Z̃_S as a member of the sub-differential of the regularizer ‖·‖_1,off, evaluated at Θ̃.

3. Set Z̃_S^c as

   $${\mathrm{Z̃}}_{S^c}=\frac{1}{{\lambda }_n}\{-{\mathrm{\Sigma ̂}}_{S^c}+{[{\mathrm{\Theta ̃}}^{-1}]}_{S^c}\},$$

   where Σ̂ is short for Σ̂_Γ̂ and the constructed (Θ̃, Z̃) satisfy the optimality condition (.10).
4. We verify the strict dual feasibility condition

   $$|{\mathrm{Z̃}}_{ij}|<1\text{for all}(i,j)\in S^c.$$

If the primal-dual witness construction succeeds, then it acts as a witness to the fact that the solution Θ̃ to the restricted problem (.11) is equivalent to the solution Θ̂ to the original unrestricted problem (4) [5]. The proof proceeds as this: we first show that the primal-dual witness technique succeeds with high probability, hence the support of the optimal solution Θ̂ is contained within the support of the true Θ*. In addition, the characterization of Θ̂ provided by the primal-dual witness construction can establish the element-wise ℓ_∞ bounds claimed in Theorem 2. Note we define the ”effective noise” in the sample covariance matrix Σ̂_Γ̂ in the appendix as U ≔ Σ̂_Γ̂ − (Θ*)⁻¹ and we use Δ ≔ Θ̃ − Θ* to measure the discrepancy between the restricted estimate Θ̃ in (.11) and the truth Θ*. We define R(Δ) ≔ Θ̃⁻¹ − Θ*⁻¹ + Θ*⁻¹ΔΘ*⁻¹.

PROOF OF THEOREM 2. We first show that with high probability the witness matrix Θ̃ is equal to the solution Θ̂ to the original log-determinant problem (4), by showing that the primal-dual witness construction succeeds with high probability. Let ℬ denote the event that ${\Vert U\Vert }_{\infty }\le {\mathrm{\delta ̄}}_f(n,p_n^{\tau })=\sqrt{(\text{log}4+\tau \text{log}{p}_n)/(C_{*}n)}$ where $C_{*}={[128{(1+4{\sigma }^2)}^2{\text{max}}_i{\{{\mathrm{\Sigma }}_{ii}^{*}\}}^2]}^{-1}$. Condition (9) on sample size n implies ${\mathrm{\delta ̄}}_f(n,p_n^{\tau })\le 8(1+4{\sigma }^2){\text{max}}_i\{{\mathrm{\Sigma }}_{ii}^{*}\}$, which indicates that sub-Gaussian tail condition can be used in our control of sampling noise. Lemma 2 can guarantee $\mathrm{p}\mathrm{r}(ℬ)\ge 1-4/p_n^{{\tau }^{*}-2}-8\text{exp}(-C_{1}n{\rho }_n^2)-2\text{exp}(-C_{2}n{\rho }_n^2)$.

Conditioning on event ℬ, the following analysis follows as that of [5]. The choice of regularization penalty ${\lambda }_n=(8/\alpha ){\mathrm{\delta ̄}}_f(n,p_n^{\tau })$ implies ‖U‖_∞ ≤ (α/8)λ_n. Following the same steps as [5], we can show that ‖R(Δ)‖_∞ ≤ αλ_n/8. We can then show that the matrix Z̃_S^c constructed in step (c) satisfies ‖Z̃_S^c‖_∞ < 1 and therefore Θ̃ = Θ̂. The estimator Θ̂ then satisfies the ℓ_∞ bound as claimed in Theorem 2 (1), and moreover, Θ̂_S^c = Θ̃_S^c = 0, as claimed in the first part Theorem 2 (2). Second part of Theorem 2 (2) follows directly after (1). Since the above is conditioned on the event ℬ, these statements hold with probability

$$\mathrm{p}\mathrm{r}(ℬ)\ge 1-4/p_n^{{\tau }^{*}-2}-8\text{exp}(-C_{1}n{\rho }_n^2)-2\text{exp}(-C_{2}n{\rho }_n^2).$$

Hence we proved Theorem 2.

Proof of Theorem 3:

The proof of Theorem 3 depends on the following lemma.

Lemma 5 (Sign Consistency). Suppose the minimum absolute value θ_min of nonzero entries in the true precision matrix Θ* is bounded from below by

$${\theta }_{\text{min}}\ge 2{\Vert \mathrm{\Theta ̃}-{\mathrm{\Theta }}^{*}\Vert }_{\infty },$$ (.12)

then $\text{sign}({\mathrm{\Theta ̃}}_S)=\text{sign}({\mathrm{\Theta }}_S^{*})$ holds.

Proof of Lemma 5. This claim follows from the bound (.12), which guarantees for all (i, j) ∈ S, the estimate Θ̃_ij cannot differ enough from ${\mathrm{\Theta }}_{ij}^{*}$ to change sign.

Proof of Theorem 3. Using the notation ${\mathrm{\delta ̄}}_f(n,p_n^{\tau })=\sqrt{(\text{log}4+\tau \text{log}{p}_n)/(C_{*}n)}$, where $C_{*}={[128{(1+4{\sigma }^2)}^2{\text{max}}_i{\{{\mathrm{\Sigma }}_{ii}^{*}\}}^2]}^{-1}$, the lower bound on n implies

$${\theta }_{\text{min}}>4K_{{\mathrm{\Omega }}^{*}}(1+\frac{8}{\alpha }){\mathrm{\delta ̄}}_f(n,p_n^{\tau }).$$

As in the proof of Theorem 2, with probability greater than

$$1-4/p_n^{{\tau }^{*}-2}-8\text{exp}(-C_{1}n{\rho }_n^2)-2\text{exp}(-C_{2}n{\rho }_n^2),$$

we have Θ̃_Γ̂ = Θ̂_Γ̂ and ‖Θ̃_Γ̂ − Θ*‖_∞ ≤ θ_min/2. Consequently, Lemma 5 implies that $\text{sign}({\mathrm{\Theta ̃}}_{ij})=\text{sign}({\mathrm{\Theta }}_{ij}^{*})$ for all (i, j) ∈ E(Θ*). Overall, we can conclude that with probability greater than

$$1-4/p_n^{{\tau }^{*}-2}-8\text{exp}(-C_{1}n{\rho }_n^2)-2\text{exp}(-C_{2}n{\rho }_n^2),$$

the sign consistency condition $\text{sign}({\mathrm{\Theta ̂}}_{ij})=\text{sign}({\mathrm{\Theta }}_{ij}^{*})$ holds for all (i, j) ∈ E(Θ*). This proves the theorem.