Arousal state feedback as a potential physiological generator of the ultradian REM/NREM sleep cycle

Abstract

Human sleep episodes are characterized by an approximately 90-minute ultradian oscillation between rapid eye movement (REM) and non-REM (NREM) sleep stages. The source of this oscillation is not known. Pacemaker mechanisms for this rhythm have been proposed, such as a reciprocal interaction network, but these fail to account for documented homeostatic regulation of both sleep stages. Here, two candidate mechanisms are investigated using a simple model that has stable states corresponding to Wake, REM sleep, and NREM sleep. Unlike other models of the ultradian rhythm, this model of sleep dynamics does not include an ultradian pacemaker, nor does it invoke a hypothetical homeostatic process that exists purely to drive ultradian rhythms. Instead, only two inputs are included: the homeostatic drive for Sleep and the circadian drive for Wake. These two inputs have been the basis for the most influential Sleep/Wake models, but have not previously been identified as possible ultradian rhythm generators. Using the model, realistic ultradian rhythms are generated by arousal state feedback to either the homeostatic or circadian drive. For the proposed ‘homeostatic mechanism’, homeostatic pressure increases in Wake and REM sleep, and decreases in NREM sleep. For the proposed ‘circadian mechanism’, the circadian drive is up-regulated in Wake and REM sleep, and is down-regulated in NREM sleep. The two mechanisms are complementary in the features they capture. The homeostatic mechanism reproduces experimentally observed rebounds in NREM sleep duration and intensity following total sleep deprivation, and rebounds in both NREM sleep intensity and REM sleep duration following selective REM sleep deprivation. The circadian mechanism does not reproduce sleep state rebounds, but more accurately reproduces the temporal patterns observed in a normal night of sleep. These findings have important implications in terms of sleep physiology and they provide a parsimonious explanation for the observed ultradian rhythm of REM/NREM sleep.

1. Introduction

Human sleep is composed of both rapid eye movement (REM) and non-REM (NREM) sleep states. These states are defined by physiological and behavioral features: REM sleep is characterized by a low-amplitude high-frequency EEG signals similar to Wake, rapid eye movements, and muscle atonia, whereas NREM sleep is characterized by high-amplitude low-frequency EEG signals and little to no eye movements (Iber et al., 2007). One of the most distinctive features of sleep in healthy adults is the approximately 90-minute ultradian oscillation between REM and NREM sleep states (Kleitman, 1963). However, the physiological mechanism that generates this ultradian oscillation is currently unknown.

Neurophysiological studies have identified numerous brain regions that regulate Sleep and Wake states (Jouvet, 1967; Pace-Schott and Hobson, 2002). These include monoaminergic and cholinergic nuclei in the hypothalamus and brainstem that have ascending diffuse projections to the cerebrum. Monoaminergic nuclei are generally silent during REM sleep, slightly active during NREM sleep, and most active during Wake, while cholinergic nuclei are generally active during REM sleep and Wake, and silent during NREM sleep (Hobson et al., 1975; Saper et al., 2010). Mutual inhibition between the wake-active monoaminergic nuclei and the sleep-active ventrolateral preoptic region of the hypothalamus (VLPO) results in a switch-like mechanism, such that only the wake-active or sleep-active region is able to be activated at a given time. This switch is believed to be responsible for the discrete separation of Sleep and Wake states (Saper et al., 2001).

The circuitry involved in the generation and expression of REM and NREM sleep states is less well understood. One approach to understanding how ultradian rhythms are generated has been to develop mathematical models that include key neuronal populations. In 1975, McCarley and Hobson proposed a reciprocal interaction model, in which the REM-active cholinergic nuclei are self-excitatory and excite the NREM-active monoaminergic nuclei, while the monoaminergic nuclei are self-inhibitory and inhibit the cholinergic nuclei (McCarley and Hobson, 1975). Using a simple first order model of population interactions, they showed that with appropriate parameter values, the network could act as a pacemaker (i.e., a clock that spontaneously generates rhythms with a fixed period). Later experimental work showed that the locus for the cholinergic nuclei was different from that proposed in the original model (Armstrong et al., 1983), and the model was accordingly revised (McCarley and Massaquoi, 1986). Subsequently, more detailed models of neuronal dynamics in a reciprocal interaction network have been used to generate ultradian rhythms (Diniz Behn et al., 2007; Diniz Behn and Booth, 2012; Diniz Behn and Booth, 2010). A limitation of these models, however, is that they rely on fitting the values of numerous unconstrained parameters to achieve oscillatory behavior with the desired ultradian period. They therefore fall short of identifying what precise aspect of the underlying physiology generates the oscillation and its period. Furthermore, a recent study proposed that REM/NREM sleep regulation involves a switch-like (mutually inhibitory) network, rather than a reciprocal interaction (excitatory/inhibitory) network (Lu et al., 2006), although it is unclear what would drive this switch between REM and NREM sleep states. Rempe et al. (2010) used a switch-like network to simulate sleep, generating REM/NREM cycles by using intrinsically oscillatory neurons in each population. Given the lack of consensus on this topic (Datta and Maclean, 2007), it seems likely that the relevant neurobiology has yet to be fully described. Such uncertainty over the underlying physiology does not preclude neuronal modeling from having a useful purpose in this domain – and perhaps even predicting the correct network structure – but it means the theoretical results should be interpreted with caution.

Human and animal experiments have revealed various properties of the ultradian rhythm that can be used to identify candidate mechanisms. As Hartmann (1966) first recognized, the ultradian rhythm could potentially be generated by either an autonomous pacemaker with an intrinsic period close to 90 minutes (analogous to the circadian pacemaker), or by a homeostatic process (i.e., an hourglass mechanism) in which REM sleep propensity increases during time spent in Wake or NREM sleep, and is dissipated by time spent in REM sleep. The latter mechanism would presumably involve the accumulation and clearance of some currently unidentified biochemical substance or network property (Feinberg, 1974; Feinberg and Evarts, 1969), similar to the sleep homeostatic mechanism, for which nitric oxide and adenosine have been identified as possible constituents (Kalinchuk et al., 2011).

Several lines of evidence point away from the ultradian rhythm being generated solely by a pacemaker and indicate the need for some type of homeostatic process. First, the period of the ultradian rhythm is imprecise (unlike circadian rhythms); the coefficient of variation is about 20% in adults (Feinberg and Floyd, 1979). Second, there is evidence to suggest that REM sleep homeostatically rebounds following selective REM deprivation (Brunner et al., 1990; Dement et al., 1966; Endo et al., 1998; Morden et al., 1967). Third, the length of a REM sleep bout (i.e., a continuous block of REM sleep epochs) is positively correlated with the length of the preceding NREM sleep bout. If a pacemaker generated the rhythm, one would expect a negative correlation, so as to maintain a constant period length (Hartmann, 1966). Interestingly, REM sleep propensity (i.e., the likelihood of entering and maintaining REM sleep) appears to be increased by periods of NREM sleep (Benington and Heller, 1994b), suggesting a homeostatic balance between REM and NREM sleep (Benington and Heller, 1994a). To account for these findings, some models have included a hypothetical homeostatic process which builds during REM sleep and is dissipated during NREM sleep, in addition to the better studied sleep homeostatic process that increases during Wake and decreases during Sleep (Tamakawa et al., 2006). However, no corresponding biological factor has yet been identified for the hypothetical homeostatic process.

The two classic processes involved in sleep regulation – sleep homeostasis and endogenous circadian rhythms, which together comprise the Two-Process model (Daan et al., 1984) – also interact with the ultradian rhythm. In a typical night, about 20% of Sleep is spent in REM sleep, but REM sleep is not uniformly distributed across the night (Hirshkowitz, 2004). For an individual sleeping at a normal circadian phase, REM sleep bouts tend to be longer in the second half of the night. One reason for this is that the circadian pacemaker promotes REM sleep near the time of the circadian core body temperature minimum that occurs near the end of the night in people sleeping at their habitual times (Dijk and Czeisler, 1995). On the other hand, NREM sleep is promoted by sleep homeostatic pressure: NREM sleep duration and intensity are increased after extended periods of Wake, and EEG delta power, a validated marker of sleep homeostasis, decreases approximately exponentially across a night of sleep (Borbély et al., 1981; Daan et al., 1984). The sleep homeostatic process may therefore act both to promote Sleep over Wake and to promote NREM sleep over REM sleep (an idea that we test explicitly using our model). The decrease in sleep homeostatic pressure across the night may thus be another reason for the lengthening of REM sleep bouts in the second half of the night (Khalsa et al., 2002). These modulatory effects of the sleep homeostatic and circadian processes on the stages of Sleep have been well studied. To date, however, these two processes have not been directly considered as possible generators of ultradian rhythmicity.

Here, we test the hypothesis that interactions between arousal state (i.e., the state of Wake, REM sleep or NREM sleep) and the classic circadian and sleep homeostatic processes are sufficient to generate the ultradian rhythm of REM and NREM sleep. To achieve this, we use a simple mathematical model that has three stable states, corresponding to Wake, REM sleep, and NREM sleep. This model includes no ultradian pacemaker mechanism, nor any hypothetical REM/NREM sleep homeostat. The only drives to the system are the circadian and sleep homeostatic processes, as have been used widely in models of Sleep and Wake (Daan et al., 1984; Mallis et al., 2004). For this model, we adopt established terminology for the “sleep homeostat” and the “circadian drive for wakefulness”. However, our implementation does not restrict these drives to only promote Wake over Sleep or vice versa. As described in Section 2, they can also differentially promote REM sleep over NREM sleep or vice versa. Within this framework, we test two specific mechanisms for generating ultradian rhythms.

1. The homeostatic mechanism

The original Two-Process model of sleep assumes that sleep homeostatic pressure builds during Wake and is dissipated during NREM sleep (Daan et al., 1984). However, it does not provide a clear role for REM sleep. If sleep homeostasis reflects cerebral metabolism (Kalinchuk et al., 2011) or changes in synaptic density (Massimini et al., 2009), it seems reasonable to assume that both Wake and REM sleep should have similar effects on sleep homeostasis, given their similar EEG and metabolic characteristics (Maquet and Phillips, 1998). We therefore test the effects of homeostatic pressure increasing during Wake and REM sleep, and decreasing during NREM sleep. This mechanism is expected to cause ultradian rhythmicity due to the opposing effects of REM and NREM sleep on the homeostatic drive, and the fact that higher homeostatic pressure is associated with a greater tendency to enter NREM sleep.

2. The circadian mechanism

Circadian rhythms originate in the mammalian master clock, the suprachiasmatic nucleus (SCN) of the hypothalamus and are expressed by SCN neurons, which typically fire at their highest rates during the biological day (Ibuka and Kawamura, 1975; Inouye and Kawamura, 1982). Outputs from the SCN are relayed to both VLPO and monoaminergic nuclei (Saper et al., 2005). There are also projections back to the SCN from monoaminergic (Legoratti-Sánchez et al., 1989; Moore et al., 1978) and cholinergic (Bina et al., 1993) nuclei, meaning SCN firing patterns are affected by arousal state. At a given circadian phase, SCN neurons fire at similar rates during Wake and REM sleep, but at a significantly lower rate during NREM sleep (Deboer et al., 2003). In humans, the circadian drive for wakefulness is highest during the mid-late biological day, corresponding to the time when SCN neurons are most active (Dijk and Czeisler, 1994). We therefore test the effects of the circadian drive for wakefulness decreasing during NREM sleep and increasing during Wake and REM sleep, via an hourglass mechanism; this is a modulation of the endogenous circadian drive. This mechanism is expected to cause ultradian rhythmicity due to the opposing effects of REM and NREM sleep on the circadian drive, and the fact that times of low circadian drive for wakefulness (e.g., near the time of the core body temperature minimum in humans) are also associated with higher REM sleep propensity.

These two mechanisms rely, respectively, on the two underlying assumptions that increasing homeostatic pressure promotes NREM sleep and that decreasing circadian drive promotes REM sleep. As detailed above, there is considerable experimental support for these two assumptions. However, the two proposed mechanisms for REM/NREM sleep cycling are described and theoretically tested here for the first time.

2. Theory

We previously developed a simple physiologically-based model of the Sleep/Wake switch (Phillips and Robinson, 2007). This model included the VLPO and monoaminergic nuclei, and produced stable Wake and Sleep states, but did not differentiate between REM and NREM sleep. We then showed that the dynamics of this model are mathematically equivalent to the motion of a particle along one dimension in a two-well potential (Phillips and Robinson, 2009). In this model, one well represented Wake, and the other represented Sleep. Frictional terms caused the particle to settle in one well or the other, while circadian and homeostatic drives pushed the particle between wells. Here, we extend that model to a three-well potential, with the three wells representing Wake, REM sleep, and NREM sleep. The particle now moves in two dimensions, with position along the x -axis representing Wake/Sleep state, and position along the y -axis representing REM/NREM sleep state.

We use this three-well potential model as a test-bed for our proposed mechanisms for three reasons. First, it has fewer parameters than a physiological model would. Second, it allows us to test our proposed mechanisms without making restrictive assumptions about the underlying physiology. This is particularly important given the existing uncertainties that were presented in Section 1. Third, this model has greater transparency than a neuronal model would. Because the model is relatively simple, we can easily understand the basis for its dynamics. This would not necessarily be true of a more physiological model, where the dynamics could depend in a non-obvious way on the particular choice of neuronal model used.

Ultimately, this approach may also allow us to relate dynamics to physiology, as we did previously with the one-dimensional model (Phillips and Robinson, 2009). There, we were able to derive analytic expressions relating the parameters of the potential model to the parameters of the physiological model. Under appropriate assumptions, we may therefore be able to work back from the three-well potential formulation to a physiological model by inferring the neuronal equations that correspond to the potential surface and forces. This approach could also yield estimates on some physiological parameter values.

2.1 Two dimensional potential

Our previous one-dimensional potential model used a quartic function to create two wells. The basic mathematical form of this model was

$$\lambda F(x,\stackrel{.}{x})=x^2{(x-1)}^2+hx\stackrel{.}{x}+Dx,$$ (1)

where F(x, ẋ) is the non-conservative potential along which the particle moves, and x and ẋ represent the position and velocity of the particle, respectively. The hxẋ term is a frictional term (h > 0) included so that the particle settles within a well, rather than continuing to oscillate following state transitions. Circadian and homeostatic drives to the system are represented by the variable D. The Dx term generates a force on the particle in either the positive or negative x -direction, depending on the sign of D. The parameter λ is a constant that determines the rate at which the model moves when transitioning between wells. For D = 0, the model has stable states at x = 0 and x = 1, which we label as Sleep and Wake, respectively.

The equation of motion for the particle is defined by the partial derivative of F with respect to position, x, with λ playing the effective role of mass, but with different units:

$$\lambda \frac{d^{2}x}{{dt}^2}=-\lambda \frac{\partial F}{\partial x}=-4x^3+6x^2-2x-h\stackrel{.}{x}-D.$$ (2)

Here, we extend the model to a two-dimensional potential, F, that is quartic in both x and y,

$$\lambda F(x,y,\stackrel{.}{x},\stackrel{.}{y})=x^2{(x-1)}^2+y^2{(y-1)}^2+{kx}^2{y}^2+h(x\stackrel{.}{x}+y\stackrel{.}{y})+D_{x}x+D_{y}y.$$ (3)

We choose λ = 0.2 min² to generate realistic transitions (on the timescale of minutes) and use h = 10 min to achieve overdamping. This is done to avoid excessive oscillations (ringing) of the particle within a well following any state transition.

For k = D_x = D_y = 0, the potential has four stable states: {(0,0),(0,1),(1,0),(1,1)}. Since we are interested in studying a three state system (Wake, REM sleep, and NREM sleep), without loss of generality we eliminate the stable state at (1,1) by including the kx²y² term in Eq. (3). This addition does not change the positions of the other stable states and it maintains positive curvature as x and y go to ±∞, ensuring all solutions converge. The fourth well is eliminated for k > 1/4, so we choose k = 0.3. We label the three remaining states as follows: (0,0) is NREM sleep, (0,1) is REM sleep, and (1,0) is Wake.

More generally, we divide the phase space as follows:

1. If x ≥ 1/2, the state is defined as Wake;

2. If x < 1/2, the state is defined as Sleep. For y ≥ 1/2, the state is defined as REM sleep, and for y < 1/2, the state is defined as NREM sleep.

Thus, the x -axis represents Wake/Sleep state and the y -axis represents REM/NREM sleep state, as shown in Figure 1. While standardized sleep scoring has defined sub-states (e.g., stages N1–N3 of NREM sleep, or phasic vs. tonic REM sleep), this discrete partitioning of states is justified by experimental data showing that the states of Wake, NREM sleep, and REM sleep are each distinctly separated by EEG characteristics (Diniz Behn et al., 2010). We assume symmetry in the shape of the potential in x and y. In future, we could consider asymmetries or the inclusion of other cross-terms (e.g., xy², x² y, etc.), but here we keep the model as simple as possible.

Figure 1.

Map of the three-well potential surface, U = x² (x − 1)² + y² (y − 1)² + xD for different values of D: (A) D = 0.2, (B) D = 0, (C) D = −0.2. This surface is the conservative part of the potential given in Eq. (3) (i.e., omitting frictional terms), with only a horizontal force, −D, acting. Shading shows the value of U, with darker shading corresponding to lower values. Lines in (B) indicate how the space is zoned into REM sleep, NREM sleep, and Wake. The xD term provides a horizontal force (arrows), pushing the particle towards Sleep (REM sleep or NREM sleep) in (A) and Wake in (C). For D = 0, all three potential wells are equally stable.

We note that the thresholds x = 1/2 and y = 1/2 are chosen without loss of generality. For a different arbitrary choice of thresholds, the other model parameters could be rescaled to achieve identical dynamics. Furthermore, because our model rapidly transitions across these thresholds, the results are not particularly sensitive to the threshold value, producing similar results with 50% changes in threshold values.

Figure 1 shows the effect of a horizontal force, D, on the shape of the conservative potential for −0.2 ≤ D ≤ 0.2. Negative values of D induce a force to the right (towards Wake), while positive values of D induce a force to the left (towards Sleep). Note that vertical forces have an exactly equivalent effect on the shape of the potential, forcing the particle either up or down; therefore, they are not shown here. For comparison, the model presented below generates forces of −0.9 ≤ D_x ≤ 0.0 and −0.3 ≤ D_y ≤ 10.9 for the homeostatic mechanism, and −0.5 ≤ D_x ≤ 0.5 and −0.2 ≤ D_y ≤ 2.3 for the circadian mechanism.

From the potential, F, the equations of motion for the particle are defined by partial derivatives (assuming the particle has an effective mass of λ):

$$\lambda \frac{d^{2}x}{{dt}^2}=-\lambda \frac{\partial F}{\partial x}=-4x^3+6x^2-2x-2{\mathit{kxy}}^2-h\stackrel{.}{x},$$ (4)

$$\lambda \frac{d^{2}y}{{dt}^2}=-\lambda \frac{\partial F}{\partial y}=-4y^3+6y^2-2y-2{kx}^{2}y-h\stackrel{.}{y}.$$ (5)

2.2 Circadian and homeostatic drives

To model the circadian drive, C, we assume entrainment to a 24-h day and use a sinusoidal form,

$$C(t)=\frac{1}{2}\left[1+cos\left(\omega t\right)\right],$$ (6)

where ω = 2π/(24 h). The circadian drive is considered here to represent the wake-promoting signal from the SCN, which has its maximum near the time of the endogenous core body temperature maximum and its minimum near the time of the endogenous core body temperature minimum (Dijk and Czeisler, 1994). We refer to C = 1 as the circadian maximum (strongest drive to Wake) and C = 0 (weakest drive to Wake) as the circadian minimum. Note that this can equivalently be thought of as a circadian drive to Sleep, with the strongest drive to Sleep at C = 0 and the weakest drive to Sleep at C = 1.

To model the homeostatic drive, H, we use a linear differential equation that depends on arousal state,

$$\chi \frac{dH}{dt}=-H\left(1+N{e}^{-\beta y}\right)+{\mu }_{W}W+{\mu }_{R}R.$$ (7)

In this equation, N = 1 in NREM sleep and 0 otherwise, W = 1 in Wake and 0 otherwise, and R = 1 in REM sleep and 0 otherwise. These step functions are necessary to generate approximately exponential saturation and decay in the dynamics of H. Using linear terms instead (e.g., x in place of W) instead results in smooth oscillations. The dissipation term, −H (1+Ne^−βy) includes an exponential function because homeostatic dissipation is more rapid in deeper NREM sleep (i.e., more negative y) (Achermann and Borbély, 1990); this particular functional form is found to yield realistic dynamics for β = 2 and the effects of changing β are shown in Section 3.1. The parameter χ = 18 h is a time constant that determines the characteristic timescale of exponential saturation in Wake, the value of which we take from the Two-Process model (Daan et al., 1984). The parameters μ_W and μ_R determine the rates of homeostatic increase in Wake and REM sleep, respectively. We use μ_W = 1 so that H ranges from 0 to 1. With this value, dH/dt > 0 in Wake, and dH/dt < 0 in NREM sleep. The value of μ_R and the sign of dH/dt in REM sleep depend on the ultradian mechanism modeled, which is discussed in the next Section.

The effects of the circadian and homeostatic drives are modeled as horizontal or vertical forces on the particle. These forces are produced by the linear terms D_x x and D_y y in Eq. (3), respectively, using

$$D_x={\nu }_{xc}C+{\nu }_{xh}H+M_x,$$ (8)

$$D_y={\nu }_{yc}C+{\nu }_{yh}H+M_y.$$ (9)

The ν_ij parameters represent the strength of circadian (c) and homeostatic (h) forces in the x and y directions, while the M_x and M_y parameters are constant offsets. The signs of the ν_ij parameters can be determined based on experimental evidence. The circadian drive promotes Wake near its maximum, so C should exert a force in the positive x direction. Therefore ν_xc < 0, because the force is opposite in sign from the partial derivative of the potential, as per Eqs. (4) and (5). The circadian drive also promotes REM sleep near its minimum, so C should exert a force in the negative y direction, i.e., ν_yc > 0. The homeostatic drive promotes Sleep, so H should exert a force in the negative x direction, i.e., ν_xh > 0. The homeostatic drive also promotes NREM sleep, as higher homeostatic pressure results in greater NREM intensity. Therefore, H should exert a force in the negative y direction, i.e., ν_yh > 0.

The values of the ν_xc and ν_xh parameters can be estimated based on the size of a perturbation needed to induce a state transition. Considering the simple case of Sleep/Wake transitions (y = 0), the conservative potential reduces to

$$\lambda U(x,y)=x^2{(x-1)}^2+Dx,$$ (10)

where D is the total drive to the system in the horizontal direction. For D = 0, the system has both stable Wake (x = 1) and Sleep (x = 0) states. For a sufficiently large positive or negative drive, D, the Wake or Sleep state loses stability, respectively. The limits can be determined by calculating the partial derivative,

$$\lambda \frac{\partial U}{\partial x}=4x^3-6x^2+2x+D.$$ (11)

Equilibriums correspond to zeroes of this equation, which has three real solutions (i.e., two stable states) for $-1/\sqrt{27}<D<1/\sqrt{27}$, and only one real solution (i.e., one stable state) outside of this range. The length of this interval is $2/\sqrt{27}\approx 0.38$. The circadian and homeostatic drives must therefore induce perturbations at least this large to cause state switching, and the same analysis holds for perturbations in the y -direction, by symmetry. Here, we choose ν_xc = −1.0 to achieve sufficiently large circadian perturbations. We then choose ν_xh = 0.6 to give a similar ratio of circadian to homeostatic contributions as in our previous physiological model (Phillips and Robinson, 2008).

2.3 Mechanisms for ultradian rhythmicity

To model ultradian oscillations, we consider two possible mechanisms. First, the homeostatic mechanism, in which arousal state feedback to the homeostatic drive generates oscillations. Second, the circadian mechanism, in which arousal state feedback to the circadian drive generates oscillations. Experimental support for each mechanism is considered in detail in Section 4. In fitting the parameters of the model for each mechanism, we use a combination of fitting methods. Some parameters in the model can be easily estimated due to the fact that they dictate a particular feature of the model’s dynamics. Others must be fit in combination with other parameters and in these cases we use a fixed grid search of the parameter space to estimate parameter values. Final model parameters for each mechanism are given in Tables 1 and 2.

Table 1.

Model parameter values that are the same for both the homeostatic and circadian mechanisms. Methods used to determine parameter values are discussed in the text.

Parameter	Value
λ	0.2 min2
k	0.3
h	10 min
ω	2π/(24 h)
χ	18 h
β	2
μW	1

Table 2.

Model parameter values that differ between the homeostatic and circadian mechanisms. Methods used to determine parameter values are discussed in the text.

Parameter	Homeostatic mechanism value	Circadian mechanism value
νxc	−1.0	−0.5
νxh	0.6	2.0
νyc	3.0	1.3
νyh	25.0	1.0
μR	1	0
Mx	−0.2	−0.63
My	−7.5	−1.07
η	-	1.0 h
γ	-	1.5

2.3.1 The homeostatic mechanism

REM sleep propensity has been found to increase during NREM sleep (Benington and Heller, 1994a). One possible mechanism to explain this finding is an increase in homeostatic pressure in Wake and REM sleep, and a dissipation of homeostatic pressure in NREM sleep. To model this, we assume the same rate of homeostatic increase in REM sleep as in Wake, i.e., μ_R = μ_W = 1. This generates oscillations between REM and NREM sleep, because increasing H forces the particle towards NREM sleep and away from REM sleep. To achieve an appropriate rate of REM/NREM sleep cycling, the system must be more sensitive to perturbations in H in the y -direction than in the x -direction. We therefore require that ν_yh ≫ ν_xh. A value of ν_yh = 25 is found to generate an oscillation with a period close to the experimentally observed ~90 minutes. We then choose M_x = −0.2 and M_y = −6.0 to achieve approximately 8 hours of sleep, with approximately 20% of sleep spent in REM sleep.

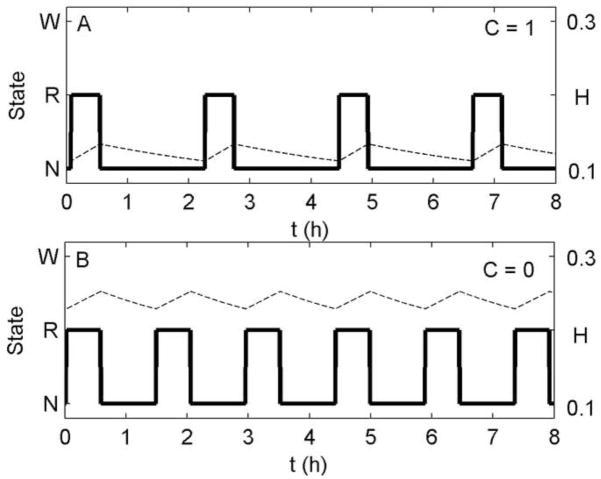
To estimate the strength of circadian control of REM sleep, which is determined by ν_yc, we refer to forced desynchrony data from protocols in which participants live on non-24-h “days” to “force” desynchrony of sleep/wake schedules from endogenous circadian rhythms. In participants living on a 28-h day, the percentage of total sleep time spent in REM sleep varied from 17% at circadian phases near the time of the core body temperature maximum to 33% at circadian phases near the time of the core body temperature minimum (Dijk and Czeisler, 1995). We simulate these conditions by holding the system in Sleep at a fixed circadian phase. This is achieved by setting x = 0 and then setting C to a constant value between 0 (circadian minimum) and 1 (circadian maximum). Note that for later results, this condition is not imposed. Under this condition, the model oscillates between REM (y = 1) and NREM sleep (y = 0), as shown in Figure 2. We find that a value of ν_yc = 3 results in a change in percentage REM sleep similar to that observed in the data, ranging from 21% of total sleep time for C = 1 to 38% of total sleep time for C = 0.

Figure 2.

Ultradian oscillations of NREM sleep and REM sleep at a fixed circadian phase during 8 h of enforced Sleep (x = 0) using the homeostatic mechanism. The y-axis shows arousal state, W = Wake, R = REM sleep, N = NREM sleep. Simulations are at (A) the circadian wakefulness maximum, C = 1, and (B) the circadian wakefulness minimum, C = 0. Plotted are arousal state (thick solid line) and homeostatic drive (dashed line).

The percentages from the above simulation are slightly higher than those in the data, because our simulation is of the stable limit cycle achieved once the homeostatic drive has stabilized, thereby excluding the longer NREM sleep episodes observed at the beginning of sleep when the homeostatic drive is transiently higher. This is consistent with the experimental observation that REM sleep increases from 17% of total sleep time in the first 2 h of sleep to 26% of total sleep time in the last 2 h when averaged across all circadian phases (Dijk and Czeisler, 1995). In our model, the increase in REM sleep percentage with circadian phase is also associated with a lengthening of REM sleep bouts from 28 min to 33 min, but a shortening of the ultradian period from 131 min to 88 min. These changes are both qualitatively consistent with data (Czeisler et al., 1980b). Finally, because the ν_ycC term introduces a force in the positive y direction, we decrease M_y to −7.5 to maintain approximately 20% of time in REM sleep during a normal ~8-h night.

2.3.2 The circadian mechanism

Recordings from SCN neurons in rats reveal lower firing rates in NREM sleep than in Wake and REM sleep, even at the same circadian phase (Deboer et al., 2003). Furthermore, the absolute differences in firing rates between NREM sleep and Wake/REM sleep at a given circadian phase are slightly larger than the differences in firing rates between the circadian maximum and minimum within each state. Whether these changes play any causal role in generating state switching is unclear from existing data. Here, we propose that they do play a causal role. Specifically, we propose that decreased SCN firing rates promote REM sleep. Therefore, a decrease in SCN firing rate during NREM sleep could result in a transition to REM sleep, while an increase in SCN firing rate during REM sleep could result in a transition to NREM sleep.

To test this mechanism without interference from the sleep homeostat, we remove the assumption that REM sleep results in an increase in homeostatic pressure by setting μ_R = 0 in Eq. (7). This change means that the homeostatic drive decreases in both REM and NREM sleep, with faster dissipation in NREM sleep.

To model changes in SCN firing rate with arousal state, we amend Eq. (6) to

$$C(t)=\frac{1}{2}\left[1+cos\left(\omega t\right)\right]+Z,$$ (12)

where Z varies with arousal state, increasing in Wake and REM sleep, and decreasing in NREM sleep. Since C − Z varies between 0 and 1, and the variations in SCN firing rate with arousal state are slightly larger in magnitude than those between circadian maximum and minimum, we allow Z to vary between 0 and 1.5. We model these variations using the differential equation

$$\eta \frac{dZ}{dt}=\gamma \left(W+R\right)-Z,$$ (13)

where γ = 1.5 and η is a time constant that determines the rate at which Z changes at state transitions. We use η = 1.0 h to achieve an ultradian rhythm with a period close to 90 minutes. Since the addition of Z in Eq. (12) approximately doubles the range of C compared to Eq. (6), we halve ν_xc to a value of −0.5.

For the circadian mechanism, REM/NREM sleep transitions are driven by changes in the circadian rather than the homeostatic drive. Therefore, the parameter ν_yh is necessarily much smaller for the circadian mechanism than for the homeostatic mechanism. We find that ν_yh = 1.0 generates a reasonable variation in REM sleep propensity across a night of sleep. Decreasing ν_yh or ν_xh results in sleep occurring at an earlier circadian phase. We find that we must therefore increase ν_xh to 2.0 to achieve an appropriate circadian phase for the timing of sleep.

To fit the remaining parameters, ν_yc, M_x, and M _y, we use a fixed grid exploration of the three dimensional parameter space spanned by the three parameters. At each point in space, we generate a model time series and score it based on how many of the following 6 criteria are satisfied:

1. Nightly sleep duration is between 7 and 8 h.

2. 20–25% of total sleep time is REM sleep.

3. The ultradian rhythm has an average period between 1.5 and 2.0 h.

4. The last bout of sleep before awakening (either NREM or REM sleep) is less than 1.5 h in duration.

5. The midpoint of sleep occurs 2.5 to 4.0 h before the minimum of C − Z.

6. The first bout of NREM sleep is less than 1.5 h in duration.

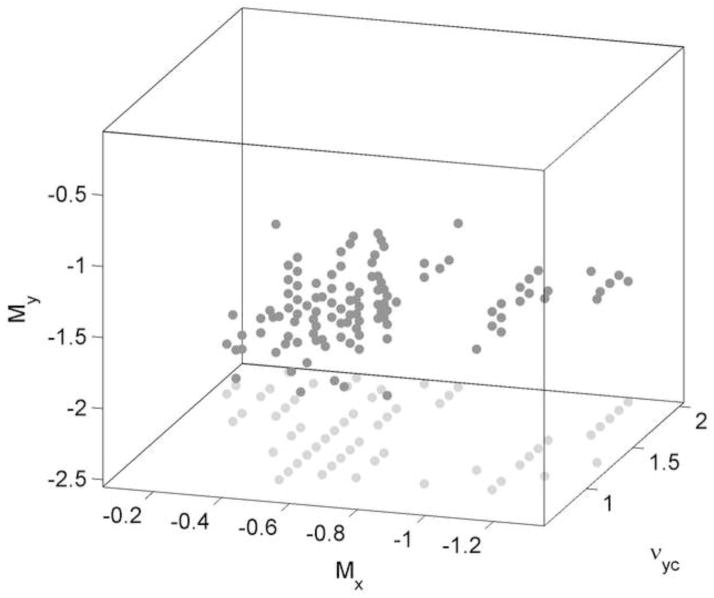
Figure 3 shows points in the space that satisfy at least 4 criteria; no points satisfy more than 5 criteria. We select the following parameter values from near the middle of the cloud of points: ν_yc = 1.3, M_x = −0.63, and M_y = −1.07. These values satisfy all but criterion 6; in Section 4 we consider why the model fails to satisfy all criteria and suggest how it might be improved in the future. Final model parameters are given in Tables 1 and 2.

Figure 3.

Points in the parameter space spanned by ν_yc, M_x, and M_y that satisfy at least 4 of the 6 criteria listed in Section 2.3.2 are shown as dark gray dots. Projections of these points onto the M_x − ν_yc plane are shown as light gray dots. A fixed step size of 0.1 was used for all 3 dimensions in exploring the space.

3. Results

We first show the generation of ultradian rhythms by each of the proposed mechanisms in Section 3.1. We then examine the effects of total sleep deprivation and selective REM sleep deprivation on the architecture (i.e., structure and pattern of the different sleep stages) of recovery sleep in Section 3.2.

3.1 Normal sleep

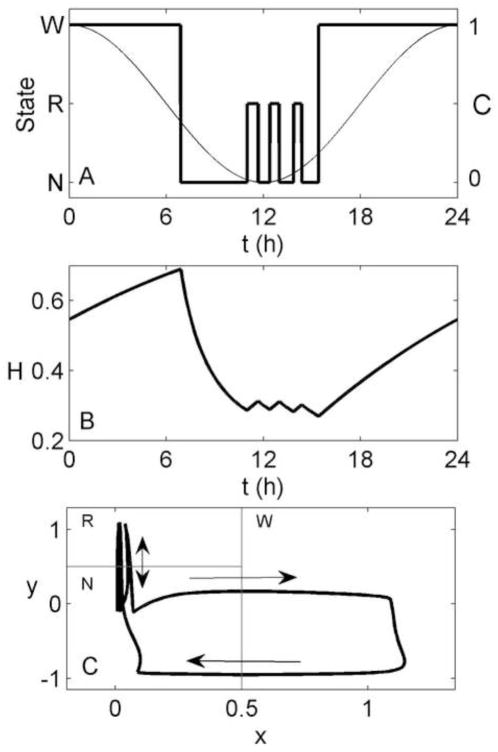
Both of our proposed mechanisms successfully generate ultradian rhythms during a spontaneous (i.e., non-scheduled) night of sleep, with REM sleep bouts longest near the circadian minimum. Figure 4 shows a night of sleep generated using the homeostatic mechanism. After transitioning to Sleep, there is a long NREM sleep bout due to high homeostatic pressure. Once the homeostatic drive has dissipated below a critical level, a transition to REM sleep occurs. This begins an oscillation between REM and NREM sleep states with a period close to 90 minutes. REM sleep bouts range in duration from 30 to 40 minutes and make up 20% of total sleep time.

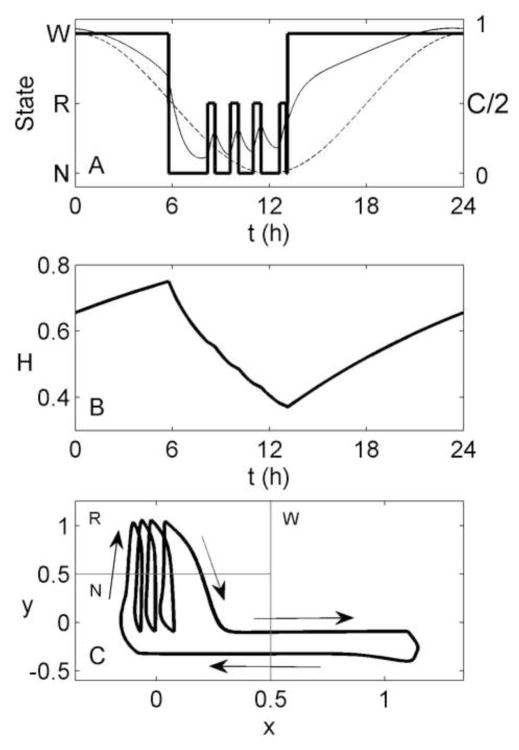
Figure 4.

Simulation of 24 h of spontaneous sleep/wake, generated using the homeostatic mechanism. (A) Arousal state (thick line), and the circadian drive (thin line) as functions of time. (B) Homeostatic drive (H) as a function of time. (C) Path of the system in phase space (thick line), with arrows indicating the direction of motion. Thin gray lines indicate the demarcations between arousal states, as per Figure 1.

Using the homeostatic mechanism, sleep onset occurs about 5 h before the circadian minimum, rather than the 6–7 h seen in experiments in normally entrained individuals. As a result, the first REM sleep bout is the longest, since it occurs near the circadian minimum. This is consistent with experiments in which spontaneous sleep duration is very long or initiated near the circadian minimum (Czeisler et al., 1980a), as NREM sleep propensity may increase again late in sleep due to the rising circadian drive. For normally entrained individuals, however, the last REM sleep bout (now occurring at the time of the circadian minimum) is the longest. Another slight discrepancy between model and data is the excessive length of the first NREM sleep bout of ~4 h, compared to observed first NREM sleep bouts of ~70 min (Czeisler et al., 1980a). This is due to the time taken to dissipate the high homeostatic pressure at the beginning of the night. This cannot be simply addressed by increasing β in Equation (7). As shown in Figure 5A, if we set β = 4 and use M_x = −0.1 to maintain the same total sleep duration, the very rapid dissipation of H at the beginning of the night causes a brief return to Wake, producing a biphasic sleep pattern. Alternative ways of addressing this issue are considered in Section 4. In Figure 5B, we show the effects of setting β = 0, and using M_y = −10 to maintain the same REM sleep duration. The model still produces an ultradian rhythm, demonstrating that the rhythm is not reliant on the exponential term in Eq. (7). However, the first NREM sleep bout is lengthened due to the slower rate of homeostatic dissipation.

Figure 5.

Simulation of 24 h of spontaneous sleep/wake, generated using the homeostatic mechanism, with (A) β = 4 and M_x = −0.1, and (B) β = 0 and M_y = −10. All other parameter values are as in Tables 1 and 2. Arousal state (thick line), circadian drive (thin line) and homeostatic drive (dashed line) are plotted as functions of time.

Figure 6 shows a night of spontaneous sleep generated using the circadian mechanism. This mechanism is able to realistically capture most aspects of a normal night of sleep, including a long first NREM sleep bout and an approximately 90 minute ultradian rhythm. REM sleep bouts increase in duration across the night, from 26 to 29 minutes, and are longest near the circadian minimum, which occurs approximately 6.5 h after sleep onset. The most notable discrepancy between model and data is that the first NREM sleep bout is slightly too long at ~2 h. This aside, the model provides a good reproduction of experimental data, including timing of sleep relative to the minimum of C − Z (the non-evoked sinusoidal component of C).

Figure 6.

Simulation of 24 h of spontaneous sleep/wake, generated using the circadian mechanism. (A) Arousal state (thick line) as a function of time, shown with the circadian drive, C/2 (thin solid line), which varies with arousal state, and the sinusoidal component, C − Z (thin dashed line). The latter is not divided by 2 so that they can be seen on the same axes. (B) Homeostatic drive as a function of time. (C) Path of the system in phase space (thick line), with arrows indicating the direction of motion. Thin gray lines indicate the demarcations between arousal states, as per Figure 1.

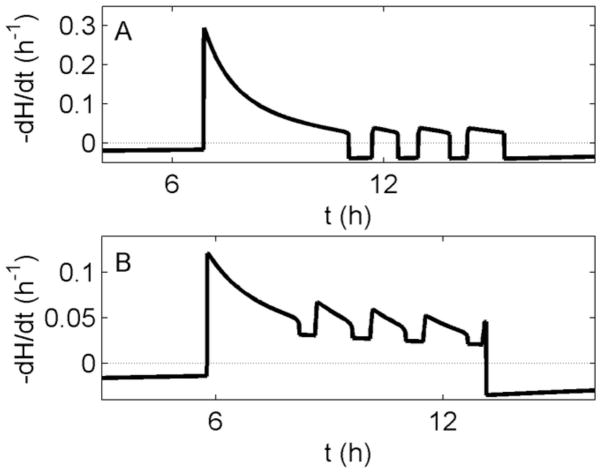
Previous models of the homeostatic process have assumed that slow wave activity (SWA) in the EEG, defined by power in the 0.75–4.5 Hz range, is related to the rate of dissipation of the homeostatic process (Achermann et al., 1993). In Figure 7, we plot the rate of dissipation of H for our model during a night of sleep, using either the homeostatic or circadian mechanism. The graphs show a similar profile to SWA, generally decreasing across the night and being higher in NREM sleep than in REM sleep (Achermann and Borbély, 1990). The dissipation rate of H will therefore be used as a proxy for NREM sleep intensity in our model. The circadian and homeostatic mechanisms generate similar dissipation profiles, the key difference being that the homeostatic mechanism has negative dissipation in REM sleep, due to the inherent assumption of homeostatic increase in that state.

Figure 7.

Dissipation rate of H (solid lines) during a single night of sleep for (A) the homeostatic mechanism and (B) the circadian mechanism. Dashed horizontal lines indicate zero. Note the time axes are shifted between panels due to slightly different timing of sleep for each mechanism.

3.2 Sleep deprivation

A model of the ultradian rhythm should be tested for its ability to reproduce rebounds of REM and NREM sleep following selective REM sleep deprivation or total sleep deprivation. To date, however, ultradian models have been almost entirely unsuccessful in this respect. The only notable exception is the model of Franken (2002) that we consider in Section 4. Of the mechanisms proposed here, only the homeostatic mechanism has the potential to reproduce appropriate sleep state rebounds. This is because the circadian mechanism requires an acute change in SCN firing rate following a state transition. This change occurs on a timescale of η = 1 h, meaning the mechanism is unable to track sleep history on timescales much longer than this. By contrast, the homeostatic mechanism operates on a considerably longer timescale, defined by χ = 18 h.

Using the homeostatic mechanism, we simulate both a 3-day total sleep deprivation and a 3-day selective REM sleep deprivation. Selective NREM sleep deprivation would be essentially equivalent to total sleep deprivation, as disruption of NREM sleep also prevents REM sleep from occurring; therefore, we do not simulate selective NREM sleep deprivation. In both total and selective REM sleep deprivation cases, simulations begin at t = 0, corresponding to C = 1. We simulate a 3-day pre-deprivation baseline and a 3-day post-deprivation recovery during which sleep is unrestricted. Total deprivation is simulated by checking the arousal state every 30 seconds. If the model is found to be in Sleep (x < 1/2), it is instantaneously moved into the Wake state (x = 1, y = 0). This method is used to mimic experimental deprivation techniques. Similarly, selective REM sleep deprivation is simulated by checking arousal state every 30 seconds. If the model is found to be in REM sleep (x < 1/2, y ≥ 1/2), it is instantaneously moved into the Wake state (x = 1, y = 0).

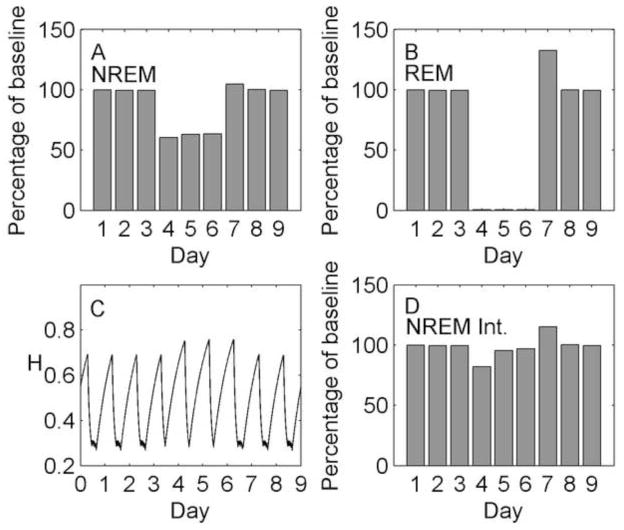
The results of the simulated total sleep deprivation are shown in Figure 8. The deprivation method (days 4–6) causes a total loss of REM sleep and an approximately 90% reduction in NREM sleep duration relative to baseline. This sleep deprivation results in increased homeostatic pressure, which causes an increase in NREM sleep duration on days 5 and 6 relative to day 4, from 8% to 12% of baseline. During recovery (days 7–9), NREM sleep duration is slightly increased relative to baseline (+4% on day 7), and REM sleep duration is slightly decreased as it is displaced by NREM sleep (−3% on day 7). While the changes in time spent in each state are relatively small, we observe a large rebound in NREM sleep intensity (+30% on day 7), represented by the rate of homeostatic dissipation. This finding is consistent with experimental results from a 40.5 h total sleep deprivation (Borbély et al., 1981); during the first night of recovery sleep, NREM sleep duration was slightly increased relative to baseline (+4%) and NREM sleep intensity in the delta band was significantly increased (approx. +20%).

Figure 8.

Simulation of total sleep deprivation and recovery using the homeostatic mechanism. Days 1–3 are baseline, days 4–6 are total sleep deprivation, and days 7–9 are recovery. (A) Total NREM sleep duration per day as a percentage of baseline. (B) Total REM sleep duration per day as a percentage of baseline. (C) Homeostatic drive H as a continuous function of time. (D) Total homeostatic dissipation per day (integrated with respect to time) as a percentage of baseline, used as a marker of NREM sleep intensity.

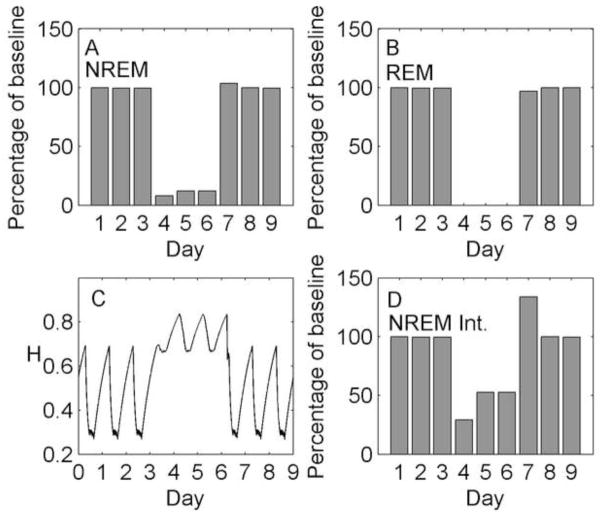
The results of the simulated REM sleep deprivation are shown in Figure 9. This deprivation method (days 4–6) causes a greater than 99% loss of REM sleep and also decreases NREM sleep duration by approximately 40% due to the frequent awakenings. The net effect is a slight increase in homeostatic sleep pressure. This causes an increase in NREM sleep duration across the deprivation, from 60% of baseline on day 4 to 63% of baseline on day 6. Similarly, there is an increase in NREM sleep intensity across the deprivation, from 82% of baseline on day 4 to 97% of baseline on day 6. During recovery, there are rebounds in NREM sleep duration (+5% on day 7) and intensity (+15% on day 7). Interestingly, we also observe a large rebound in REM sleep duration during the recovery phase (+33% on day 7). The size of this rebound is consistent with Endo et al., (1998), who reported a large rebound in REM sleep duration relative to baseline (+40%) following three consecutive days of selective REM sleep deprivation. However, the rebound is unexpected given the mechanism we are using. The increase in H is expected to bias the model towards NREM sleep, yet we see rebounds in both REM and NREM sleep. To understand this result, it is necessary to look at more than just percentage time spent in each state; we must also examine the patterns of transitions among REM sleep, NREM sleep and Wake within a sleep episode.

Figure 9.

Simulation of selective REM sleep deprivation and recovery using the homeostatic mechanism. Days 1–3 are baseline, days 4–6 are selective REM sleep deprivation, and days 7–9 are recovery. (A) Total NREM sleep duration per day as a percentage of baseline. (B) Total REM sleep duration per day as a percentage of baseline. (C) Homeostatic drive H as a continuous function of time. (D) Total homeostatic dissipation per day (integrated with respect to time) as a percentage of baseline, used as a marker of NREM sleep intensity.

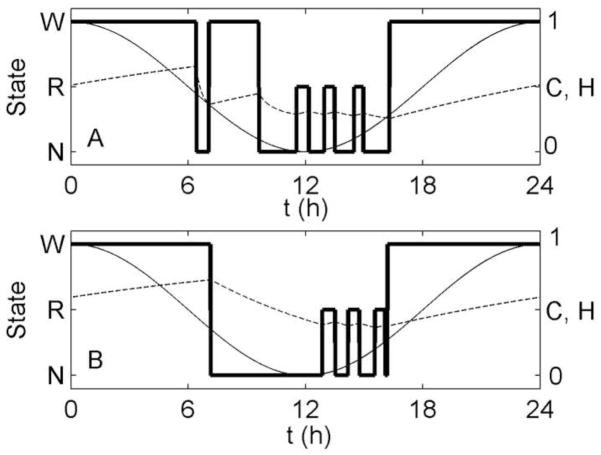
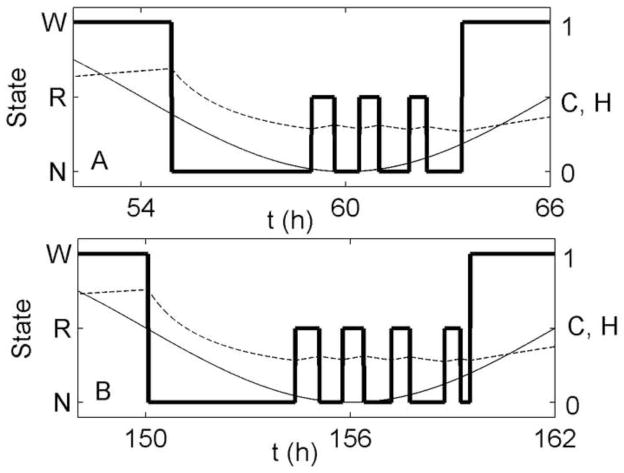
Figure 10 shows the sleep architecture for baseline (day 3) and for recovery (day 7). During recovery, sleep is not only longer by 1 h, due to the effects of homeostatic pressure in the x -direction, but also initiated 1 h earlier. As a result, once the homeostatic pressure is reduced by the first NREM sleep bout, more time is spent cycling between REM and NREM sleep near the circadian minimum (C = 0), resulting in an additional REM sleep cycle and increased total REM sleep duration. These findings emphasize the importance of considering sleep transitions and timing when interpreting experimental results.

Figure 10.

Two nights of sleep taken from the selective REM sleep deprivation simulation, using the homeostatic mechanism: (A) The third night of baseline, and (B) The first night of recovery from 3 days of selective REM deprivation. Arousal state (thick line), circadian drive (thin line), and homeostatic drive (dashed line) are shown in each case.

4. Discussion

Identifying the physiological mechanisms that generate and regulate the ultradian REM/NREM sleep rhythm is a significant unsolved problem in the field of sleep research. In this paper, we used a Two-Process model of sleep to test the plausibility of two novel mechanisms, both of which involve arousal state feedback to the circadian and homeostatic drives to the system. Traditionally, the Two-Process model has included a single arousal state feedback mechanism: the dissipation of homeostatic pressure by SWA, which is highest in NREM sleep. Generation of ultradian rhythms has previously only been achieved by invoking additional processes, such as a reciprocal interaction oscillator (Achermann and Borbély, 1992; Massaquoi and McCarley, 1992). Here, we showed that ultradian rhythms can be generated by the addition of arousal state feedback, through either a homeostatic or a circadian mechanism. These mechanisms have the advantage of parsimony, as they use the well-established circadian and homeostatic processes.

Given the similarity between Wake and REM sleep in terms of EEG waveforms and complex mentations, it is appealing to treat them as parallel states that differ in circadian phase. This sentiment was previously expressed by Wurts and Edgar (2000) when they wrote that “the SCN may actively promote cortical EEG arousal that manifests as wakefulness or REM sleep depending on the time of day”. In our model, the circadian and homeostatic mechanisms treat Wake and REM sleep identically in terms of their feedback effects. If these mechanisms are involved in the generation of ultradian rhythms, they may have important implications for how the ultradian rhythm evolved.

The states of REM and NREM sleep have been ascribed various complementary functions, mostly involving maintenance of different aspects of brain function. These have included consolidation of different types of memories (Stickgold and Walker, 2007), synaptic pruning (Massimini et al., 2009), and energy balance or thermoregulation of the central nervous system (Benington and Heller, 1995; Wehr, 1992). However, the functional significance of the nightly REM/NREM sleep cycle remains unknown. Determining the mechanisms that generate and regulate the ultradian rhythm could therefore advance our understanding of the function of sleep. Specifically, if Wake and REM sleep are demonstrated to have similar effects on the sleep homeostat, it would suggest similar functional roles for these two states (possibly explaining how unihemispheric sleepers are apparently able to function without REM sleep (Siegel, 2005), by substituting Wake in its place). It is interesting to note that previous use of the Two-Process model to simulate REM/NREM sleep cycles assumed that Process S increases in Wake and REM sleep, and decreases in NREM sleep (Achermann et al., 1993). In that case, the assumption was made not to generate REM/NREM sleep cycles – which were externally imposed – but rather to provide the closest fit to SWA. Future studies could investigate the effects of different arousal states on adenosine accumulation and clearance in greater detail. We hypothesize that adenosine

While our focus here was on reproducing the ultradian rhythms of healthy human adults, our approach could potentially also yield insights into the mechanisms that underlie the effects of sleep pathologies and drugs on the ultradian rhythm. Experimental data suggest that narcolepsy causes a reduction in the height of the boundaries between the potential wells (Diniz Behn et al., 2010). In addition, our model could be applied to understanding developmental changes in ultradian period, REM/NREM sleep balance, and the ability to directly enter REM sleep from Wake. In infants, the ultradian period is approximately half as long as in adults (Stern et al., 1969). Using our model, there are three possible explanations for this finding: (i) The mechanisms that generate ultradian rhythms could function identically, but the boundaries between the potential wells could be lower, allowing more rapid state transitions; (ii) In the circadian mechanism, the SCN neurons could respond more rapidly to a change in state (i.e., a smaller value of η); (iii) In the homeostatic mechanism, the rates of homeostatic increase and dissipation could be more rapid (i.e., a smaller value of χ). Future work should explore each of these possibilities.

Our goal in this paper was to demonstrate the plausibility of the two proposed mechanisms for reproducing features of the ultradian rhythm. We achieved this using a relatively simple model with minimal degrees of freedom, rather than beginning with a more complex model that could potentially achieve a closer fit to experimental data. For the homeostatic mechanism, the circadian minimum occurred slightly too early relative to sleep, and for both mechanisms, the first NREM sleep bout tended to be slightly too long. These issues could be addressed by using more complex functions for the circadian waveform and for homeostatic increase and dissipation, e.g., separate time constants. We also do not rule out the possibility of achieving a slightly better fit to data with different parameter fitting methods using the existing model.

For the homeostatic mechanism, we assumed that homeostatic pressure is increased by Wake and REM sleep, and decreased by NREM sleep. We also assumed that decreasing homeostatic pressure forces the particle in the positive y -direction, thereby promoting REM sleep. Consequently, one might expect REM sleep propensity to be increased by periods of NREM sleep, but not by equivalent periods of Wake. Below, however, we show that this reasoning is flawed, as it neglects the effects of homeostatic pressure on the particle in the x -direction. Experimental data support the idea that REM sleep propensity is increased by NREM sleep, consistent with some form of homeostatic balance between REM and NREM sleep (Feinberg, 1974). Debate continues regarding the effects of Wake on REM sleep propensity (Benington and Heller, 1994a; Endo et al., 1997; Ocampo-Garces et al., 2000; Whitehead et al., 1969).

Benington and Heller (1994a) argued that REM sleep propensity is increased only by NREM sleep and not by Wake. This hypothesis was subsequently challenged by experiments that found equivalent REM sleep rebounds following sleep deprivation protocols that variably decreased NREM sleep duration (Endo et al., 1997; Ocampo-Garces et al., 2000). The authors of those experiments concluded that NREM sleep could not be the only state in which REM sleep propensity increases, and that Wake must also increase REM sleep propensity. However, our results from simulating selective REM sleep deprivation reveal an alternative possibility. Despite homeostatic pressure increasing due to a decrease in NREM sleep duration, our REM sleep deprivation simulation produced a REM sleep rebound. Moreover, the size of this rebound (~130% of baseline REM sleep duration) was very similar to that found in human experiments (Endo et al., 1998). Superficially, this result seems at odds with the homeostatic mechanism, as an increase in homeostatic pressure is expected to translate into reduced REM sleep propensity, and therefore reduced REM sleep duration. But this simple interpretation fails to account for two important factors.

First, our model makes explicit the idea that the same homeostatic process could have multiple effects; although increased homeostatic pressure drives the model away from REM sleep in the y -direction, it also drives the model towards Sleep in the x -direction. REM sleep is therefore increased due to increased time in Sleep and more REM/NREM sleep cycles. Physiologically, this dual action of the sleep homeostat could represent the action of adenosine on two or more neuronal populations or circuits. As we have shown here, the additional degree of freedom afforded by having the same homeostatic process act on the system in two different ways can supplant the need for a second hypothetical homeostatic process.

Second, rebounds in REM and NREM sleep may be affected by the timing of recovery sleep relative to circadian phase. In Figure 10, we showed that a REM sleep rebound can occur due to sleep being centered closer to the circadian minimum. This underlines the importance of considering sleep structure and timing in addition to raw stage percentages. Unfortunately, neither of the cited experiments measured or adequately controlled for circadian phase (Endo et al., 1997; Ocampo-Garces et al., 2000). In addition, sleep deprivations were conducted with lights on, meaning different experimental groups would have received different retinal light exposures due to having different Wake durations. Since ocular light exposure is the most potent stimulus for shifting circadian phase in mammals (Rusak, 1979), the different experimental groups may have had recovery sleep at different circadian phases. It is thus unclear whether these experiments constitute sufficient basis to reject Benington and Heller’s hypothesis. Nonetheless, we cannot exclude the possibility of REM sleep propensity increasing in Wake, nor can we exclude the possibility of homeostatic processes secondary to those explored in this paper. In future, we could consider including a dynamic circadian model to simulate the effects of light exposure patterns on subsequent sleep, as we have done with the physiological Sleep/Wake model (Phillips et al., 2011).

An issue that we have not directly considered in this paper is that of delayed rebounds in REM or NREM sleep following deprivation. Some studies have found that total sleep deprivation is followed by a NREM sleep rebound on the first night of recovery, and then a REM sleep rebound on the second night of recovery (Berger and Oswald, 1962). This may be interpreted as the regulation of sleep by two separate homeostats – a dominant NREM homeostat and a subordinate REM homeostat – or it could be due to an overshoot in the initial NREM sleep rebound resulting in REM sleep ‘debt’. Alternatively, the delayed REM sleep rebound may simply be the result of differences in circadian phase between the nights of recovery, due to differences in daily light exposure or sleep timing during the protocol. For example, an earlier bedtime on the first night of recovery could result in an effective phase advance due to absence of phase-delaying light exposure at night. Circadian phase has seldom been tightly controlled for in such experiments, and therefore clouds interpretation of the data. In addition, there is the possibility of sleep components entering Wake (Leemburg et al., 2010), and even the occurrence of local sleep, at high homeostatic pressures (Vyazovskiy et al., 2011). Both of these possibilities could alter the observed rebound and should be considered in future work with the model.

It is worth noting some important similarities and differences between the homeostatic mechanism we propose here and the reciprocal interaction model (McCarley and Massaquoi, 1986). In the homeostatic mechanism model, REM sleep is associated with increasing homeostatic pressure; in the reciprocal interaction model, the occurrence of REM sleep induces partial activation of wake-promoting populations that could potentially also result in increases in sleep homeostatic pressure. The key difference is that REM sleep is terminated by increased homeostatic pressure in the homeostatic mechanism model, whereas it is terminated by inhibition of REM-active nuclei in the reciprocal interaction model. In addition, the reciprocal interaction model does not account for NREM and REM sleep rebounds following sleep deprivation without the addition of new processes, whereas the homeostatic mechanism was shown to reproduce both types of sleep rebound.

As an alternative to the homeostatic mechanism, we showed that the circadian mechanism can also generate ultradian rhythms. Both of the proposed circadian and homeostatic mechanisms involve hourglass (relaxation oscillator) mechanisms, and both are motivated by experimental findings. An important distinction between the homeostatic and circadian mechanisms is the inability of the latter to reproduce REM sleep rebounds following selective REM sleep deprivation. This is because the circadian mechanism has a much shorter timescale than the homeostatic mechanism. As we have modeled them here, the two mechanisms are independent. However, we do not rule out the possibility of an interaction. For example, the homeostatic drive could have a direct effect on the SCN and its response to arousal state. Indeed, experimental evidence suggests that circadian clock genes may be directly involved in sleep homeostasis (Dijk and Archer, 2010; Franken and Dijk, 2009). Currently, however, it is difficult to obtain direct measures of SCN activity in humans, and therefore difficult to directly assess how the human SCN responds to arousal state. One possible avenue for measuring SCN activity in vivo may be the development of advanced imaging technologies (Vimal et al., 2009).

State-dependent changes in SCN firing rates were originally observed in rats (Deboer et al., 2003). By basing our circadian mechanism on these experimental observations, we were able to generate human ultradian rhythms. However, it is not so clear how these state-dependent changes may function in rats. Because rats are nocturnal, REM sleep propensity is greatest when SCN firing rates are high. A decrease in SCN firing rate during NREM sleep would therefore be expected to reinforce NREM sleep, not promote a transition to REM sleep. In fact, this conjectured reinforcement of NREM sleep was confirmed by Fleshner et al. (2011), who modeled arousal state feedback onto the SCN in rats. In their model, arousal state feedback was used for fine-tuning sleep/wake patterns, not for generating ultradian rhythms. This is not to say that arousal state feedback to the SCN is not involved in state switching at all, but it suggests the need for another mechanism – possibly the homeostatic mechanism – to generate REM/NREM sleep cycling in rats. This view is bolstered by the fact that ultradian rhythms and REM sleep rebounds appear to persist in animals with SCN lesions (Edgar et al., 1993; Mistlberger et al., 1983; Wurts and Edgar, 2000), in which any circadian mechanism presumably no longer functions.

Interestingly, the two mechanisms we propose here are each able to capture different aspects of REM/NREM sleep regulation. In fact, it is plausible that both mechanisms occur physiologically. Previously, it has been proposed that regulation of REM and NREM sleep can be best understood in terms of two separate regulatory processes: (i) a long-term process that homeostatically regulates REM sleep propensity, and (ii) a short-term process that generates the REM/NREM sleep cycle (Franken, 2002). These two hypothetical processes bear some resemblance to the two mechanisms we propose here; the homeostatic mechanism is a long-term process and the circadian mechanism is a short-term process. The details are not identical: for example, Franken assumes the long-term process only increases during REM sleep, whereas our homeostatic mechanism assumes the homeostatic drive increases during both Wake and REM sleep. Nonetheless, the structure of the model is conceptually similar; the key difference is that we identify our mechanisms as being directly related to the homeostatic and circadian drives. In future we could develop a combined model that includes both the circadian and homeostatic mechanisms. Since the two mechanisms would interact with each other, it would be necessary to re-estimate the values of all 9 parameters in Table 2, which is an additional research project not pursued here. Nevertheless, given that each mechanism alone is able to reproduce different and complementary features of REM/NREM sleep regulation, the development of a combined model appears to be a promising direction for future development of the model and possibly a unified understanding of the REM/NREM sleep cycle.

As another future direction, we could test the effects of stochastic inputs to the model, since the deterministic model used here does not produce any nighttime arousals, which are normal even in healthy individuals. It would be interesting to consider the effects of such arousals on subsequent sleep architecture, including the likelihood of transitions between each of the model’s arousal states: Wake, REM sleep, and NREM sleep. It may also be fruitful to consider the roles of different SCN sub-regions in mediating the effects of arousal state feedback. Here, we modeled the SCN as a single oscillator, but experimental data indicate that SCN sub-regions independently promote different sleep stages (Lee et al., 2009).

In summary, using a simplified model of sleep dynamics, we were able to demonstrate the plausibility of two novel mechanisms for generating ultradian rhythms. Together, these mechanisms were able to explain both normal sleep architecture, and state-specific rebounds following total sleep deprivation and selective REM sleep deprivation. Each mechanism alone captured some but not all features of REM/NREM sleep regulation and the features captured by each mechanism were complementary. Collectively, these findings point towards a possible synthesis of both arousal state feedback mechanisms in physiology. The next stage of our research will involve developing a combined model and seeking direct experimental tests of our two proposed mechanisms. This work may therefore focus greater attention on the role of bidirectional interactions between arousal state and the two fundamental processes of sleep.